Abstract
This paper presents a comparative analysis of machine learning-based methods for predicting shaft power in ships, a key factor in optimizing ship performance. Accurate shaft power prediction facilitates efficient operations, reducing fuel consumption, emissions, and maintenance costs, aligning with environmental regulations and promoting sustainable maritime practices. The proposed approach evaluates three machine learning methods, analyzing 431 models to determine the most accurate and reliable option for VLCC tankers. XGBoost emerged as the top-performing model, delivering a 13% improvement in accuracy over traditional methods. Using the SHAP framework, key factors influencing shaft power predictions—such as GPS speed, draft, days from dry dock, and wave height—were identified, enhancing model transparency and decision-making clarity. This explainability fosters trust in the use of AI within marine engineering. The results demonstrate that machine learning can optimize maintenance scheduling by reducing unnecessary cleaning procedures, mitigating propulsion system wear, and improving reliability. By using predictive insights, ship operators can achieve better fuel efficiency, lower emissions, and cost savings. The study underscores the potential of explainable machine learning models as transformative tools for ship performance monitoring, supporting greener and more efficient maritime operations.
1. Introduction
In 2018, global shipping was responsible for approximately 1.076 million tonnes of CO2, accounting for 2.9% of total anthropogenic emissions. At the EU level, maritime transport contributed around 3–4% of total CO2 emissions—over 124 million tonnes in 2021. In response, regulatory frameworks have expanded: as of January 2024, the European Union Emissions Trading System (EU ETS) includes CO2 emissions from all large ships calling at EU ports, regardless of flag [1]. This initiative complements the IMO’s 2023 GHG Strategy [2], both aiming to reduce carbon intensity in international shipping. Among the strategies endorsed by the IMO is Shaft Power Limitation (ShaPoLi) as a method for curbing emissions [3]. These regulatory developments have intensified the need for accurate, data-driven tools to support energy efficiency in shipping, including predictive models for routing, fuel management, and emissions mitigation [4,5,6,7]. Traditional shaft power prediction methods rely on simplified assumptions and often fall short in complex maritime conditions. Machine learning offers a more accurate and adaptable alternative, aiding emission reduction efforts.
In 2018, emissions from global shipping accounted for 1.076 million tonnes of CO2, contributing approximately 2.9% to total global emissions resulting from human activities. At the EU level, maritime transport accounts for approximately 3 to 4% of the total CO2 emissions of the EU, equivalent to over 124 million tonnes of CO2 in 2021. In January 2024, the European Union’s Emissions Trading System (EU ETS) expanded its coverage to include carbon dioxide (CO2) emissions from all large ships, regardless of their flag, when entering EU ports [1]. The EU ETS, coupled with the IMO 2023 GHG Strategy [2] aimed at reducing the intensity of carbon in international shipping, represent two significant pillars in reducing emissions within the shipping industry. According to IMO regulations [3], Shaft Power Limitation is among the proposed methods for reducing CO2 emissions. Therefore, it is evident that there is a significant push within the scientific community toward researching, developing, and applying predictive models related to ship efficiency issues, such as optimizing routes, managing fuel consumption, and mitigating gas emissions [4,5,6,7].
However, conventional methods for predicting shaft power typically rely on empirical models built on simplified assumptions, which may constrain their accuracy and relevance in dynamic and complex maritime settings. The rise of machine learning (ML) techniques presents a promising avenue to enhance predictive capabilities across various sectors, including maritime operations, thus aiding in the reduction of emissions within the shipping industry.
An accurate prediction allows for better optimization of vessel performance [8]. When knowing the expected power requirements under different operating conditions, ship operators can adjust speed, route, and other parameters to achieve the desired balance between efficiency, speed, and fuel consumption [9]. Anticipating shaft power requirements can help in proactive maintenance planning. The monitoring of power output trends over time helps operators to detect deviations from expected values, which may indicate underlying mechanical issues or degradation. Early detection allows for timely maintenance interventions, minimizing downtime and preventing costly breakdowns [10]. Efficient use of shaft power results in reduced greenhouse gas emissions and environmental impact [11]. Efficient prediction of shaft power can lead to substantial cost savings for shipowners and operators. By optimizing fuel consumption [12], reducing maintenance costs through proactive planning, and improving overall operational efficiency, companies can achieve significant financial benefits and improve their competitive position in the maritime industry [13]. Additionally, the minimization of fuel consumption and the optimization of engine performance allows vessels to operate more sustainably, contributing to efforts aimed at reducing the carbon footprint of maritime transportation [14]. Through rigorous experimentation and analysis, we seek to emphasize the strengths and limitations of different ML techniques, thereby contributing to the advancement of predictive modeling in maritime operations. This paper’s contribution can be summed up as follows:
- Pioneering the application of explainable machine learning algorithms for shaft power prediction, shedding light on the decision-making process and enhancing transparency in model outputs.
- Applying explainable AI methods to offer a deeper understanding of how shaft power predictions affect fuel usage and emissions. This contributes to more transparent and actionable insights for monitoring and controlling emissions, thereby improving environmental compliance and performance tracking.
- Pioneering the use of machine learning algorithms to predict shaft power and optimize operational parameters, which helps in reducing fouling rates by maintaining consistent and efficient engine performance. This approach aids in minimizing the frequency and impact of fouling-related maintenance, thereby enhancing vessel efficiency.
- Conducting a comprehensive comparative analysis between machine learning methods and current industry practices for shaft power prediction, offering insights into the potential improvements and advancements achievable through novel approaches.
- The recommended method can be embedded in a system that enables real-time monitoring of shaft power and performance parameters. Additionally, the system can promptly alert operators to anomalies or deviations from expected performance, allowing for quick intervention and correction.
2. Related Work
The maritime sector is actively pursuing sustainable shipping objectives, in order to strike a balance between economic viability and environmental concerns. Previous studies have investigated a multitude of methodologies and approaches to tackle this challenge; an overview of them is shown in Table 1. In [15] artificial neural networks were used to estimate the shaft power of a microhydroelectric plant. In the context of shipping, ref. [16] investigated machine learning models to predict the power of the hull to optimize the voyages and reduce carbon emissions. Other studies have focused on predicting the performance of the hull form [17] and comparing different machine learning algorithms for modeling the speed and power of the ship [18]. In addition, a comprehensive review of biofouling and its impact on vessel performance has been conducted, exploring various monitoring and evaluation techniques [19]. In the study by [20], the researchers utilized a linear regression approach driven by data to estimate shaft power, fuel consumption, and vessel speed. This process involved extensive data preprocessing and feature engineering to improve model accuracy. The modeling began with the development of the shaft power prediction, which was then used as a key input for building the subsequent models that predict fuel consumption and vessel speed.
The authors of [21] explored the application of neural networks for predicting towboat shaft power. In [22] the authors propose a data-driven approach to develop a predictive model for fuel consumption using a multiple linear regression model that considers propeller rotational speed, with a particular focus on weather factors such as wind, waves, and currents. In a separate study [23], the authors employed two machine learning techniques—Huber regression and Light Gradient Boosting Machines (LGBMs)—to estimate ship fuel consumption. Their findings emphasize the effectiveness of machine learning in achieving accurate predictions, offering significant potential for optimizing fuel efficiency and lowering greenhouse gas emissions. In [24], the authors present an approach that uses data collection from similar ships over time to train neural networks to forecast power use, considering variables such as weather conditions. Support vector machines (SVMs) were employed in [25] for classification with the aim of detecting shaft misalignment. In [26], the authors examined five models for shaft power prediction and underscored the significance of preprocessing steps. The inclusion of environmental variables, such as wave statistics, enhanced the models’ predictive performance, with the Random Forest (RF) algorithm outperforming the others. Several deep learning models have been investigated in [27] with Recurrent Neural Network (RNN) identified as the most effective in balancing accuracy and efficiency for power prediction. The energy efficiency of a general cargo ship was researched by analyzing its shaft power utilization over a 16-month voyage [28]. A shaft power prediction model was developed using the Random Forest Regressor, incorporating oceanographic conditions and maneuvering parameters. To enhance model interpretability, the SHapley Additive exPlanations (SHAP) technique was applied, offering valuable insights into the model’s decision-making process and the contribution of each input feature.
Various studies have explored the prediction of fuel consumption in container ships. The authors in [29] constructed prediction models such as Multiple Linear Regression (MLR), Ridge Regression (RR), LASSO Regression, and Support Vector Regression (SVR) to broaden the application of machine learning algorithms in prediction tasks, comparing their accuracy using error metrics. In another study [30], the artificial neural network (ANN) and Gaussian Process Regression (GPR) were applied to forecast fuel consumption. In a more recent approach [31], the researchers found that artificial neural networks (ANNs) outperformed multiple linear regression (MLR) to predict container ship behavior. ANNs were also used in [32] to predict the fuel consumption and speed of container ships. Multiple regression algorithms such as support vector machines (SVMs), random forest regressions (RFRs), extra tree regressions (ETRs), and artificial neural networks (ANNs) were utilized in [33] to predict the fuel oil consumption of the main engine of the ship (FOC).

Table 1.
An overview of related work: the problem they focused on and the machine learning method used to solve it.
Table 1.
An overview of related work: the problem they focused on and the machine learning method used to solve it.
| Literature | Methods | Prediction |
|---|---|---|
| [20] | LR | Shaft Power |
| [18] | XGBoost | Ship Propulsion Power |
| [15] | ANN | Shaft Power |
| [16] | ANN | Shaft Power |
| [22] | MLR | Fuel Consumption |
| [23] | LGBM | Fuel Consumption |
| [21] | Ensemble NN, ANN | Shaft Power |
| [24] | ANN | Shaft Power |
| [25] | SVM | Misalignment defects detection |
| [26] | MLR, DT, K-NN ANN, RF | Shaft Power |
| [27] | RNN, CNN | Power Output of Turbines |
| [28] | RF | Shaft Power |
| [29] | MLR, Ridge, LASSO SVR, Tree-Based Algorithms. | Fuel Consumption |
| [30] | ANN, GPR | Fuel Consumption |
| [31] | ANN, MLR | Fuel Consumption |
| [17] | CNN | Hull Form Performance |
| [32] | ANN | Ship Speed Fuel Consumption |
| [33] | SVM, RFR, ETR, ANN | Fuel Consumption |
3. Tools and Methods
3.1. Dataset
This research uses a dataset collected using the Internet of Vessels platform [10,34] that gathers data from numerous sensors on the vessel, along with weather conditions from external APIs. Our dataset consists of 19,234 entries from a 36-month period (March 2020 until March 2023, reported hourly) of a single tanker VLCCs and contains various parameters such as time, location, speed, power, environmental conditions, and vessel characteristics. Together, these variables offer a comprehensive understanding of the factors influencing ship performance and navigation, allowing a thorough analysis of maritime operations, efficiency, and safety. The first step was to refine the dataset by excluding entries where the GPS speed was below 5 units. After applying the filtering criterion to exclude entries with GPS speed below 5 knots, the final dataset consists of 17,523 records. This filtering step was essential to ensure that the data used for model training and evaluation reflects realistic operational conditions, as very low speeds typically correspond to port operations, anchoring, or maneuvering—scenarios that are not relevant to shaft power prediction during a normal voyage. Including such entries would introduce noise and reduce the model’s ability to generalize to actual propulsion conditions, where shaft power prediction is operationally meaningful.
The dataset comprises the following 10 variables: (1) GPS Speed, (2) Draft, (3) Days from Dry Dock, (4) Days from Delivery, (5) Wave height, (6) Wave Relative Direction, (7) Wind Speed, (8) Wind Relative Direction, (9) Current Velocity, and (10) Current Relative Direction. These variables collectively capture key operational and environmental factors that influence the ship’s performance. Days from Dry Dock and Days from Delivery represent the time elapsed since the ship’s last dry docking and initial delivery, respectively, offering insight into its maintenance status and age. GPS Speed measures the vessel’s velocity as determined by GPS, serving as a primary metric of its motion. Draft indicates the vertical distance between the waterline and the bottom of the hull, critical for evaluating the ship’s buoyancy and stability. Wave height quantifies the vertical size of waves encountered, reflecting prevailing sea conditions. Wave Relative Direction specifies the angle at which waves approach the ship, shedding light on their interaction with vessel motion. Wind Speed measures the intensity of wind impacting the ship, which can affect propulsion efficiency and handling. Wind Relative Direction refers to the wind’s orientation relative to the ship’s heading, important for assessing aerodynamic forces and navigational control. Current Velocity captures the speed of surrounding ocean currents, influencing travel speed and fuel consumption. Lastly, Current Relative Direction denotes the direction of these currents relative to the ship’s course, affecting its drift and required navigational adjustments. This dataset contains the same features as those used in the study presented in [35].
Finally, for all those entries, we also calculate the shaft power as predicted by Kreitner’s method [36], which is the method currently being used in the Angelicoussis shipping group and will serve as the baseline during the evaluation. A widely used and industry-standard approach for ship performance modeling combines sea trial curves with theoretical correction methods, such as Kreitner’s method [36] or ISO 15016 [37]. These methods adjust for environmental factors like wind, waves, and currents, offering improved accuracy over raw sea trial data. Their simplicity and low computational demand make them suitable for onboard use. At the Angelicoussis Group, a refined version of this method, developed internally by the Energy Efficiency Department, is employed to estimate shaft power under ideal conditions (e.g., clean hull, calm seas), as shown in Figure 1.

Figure 1.
Power model for the group of sister vessels examined in this paper. On the x-axis is the vessel speed in knots, on the y-axis is shaft power in kilo-watt and the legend is the draft in meters.
3.2. Methodology
At first, we shuffle the initial dataset to avoid clustering of features and have a representative representation of all possible conditions. Then we divide the dataset into two portions: the model selection dataset comprising the first 80% of the data, and the model assessment dataset containing the remaining 20%. For the model selection process, we combine two methodologies for evaluating our machine learning algorithms: the shuffling method and 5-fold cross-value. We first randomized the order of entries within the model selection dataset, and then split our data into training and validation data pairs using a split ratio of 80–20%. Then, we further divided the trained dataset into five subsets, utilizing the 5-fold cross-validation method, and performed the standardization, described in Section 3.3, for each split for the 5-cross-validation split. This process was repeated 10 times overall. By combining these two methodologies, we created 50 pairs of training and validation sets, allowing a robust evaluation of various interpolation methods. Although the shuffling method introduces variability randomness into the selection process, k-fold cross-validation ensures systematic coverage of the dataset in a systematic manner. Finally, to assess the performance of our selected model, we used the remaining 20% of the initial dataset, referred to as the model assessment dataset. The entire process is visually represented in Figure 2.
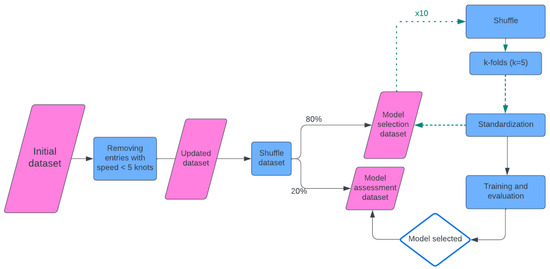
Figure 2.
Methodology flowchart.
3.3. Standardization
We standardized the data using the z-score method, which involves subtracting the mean and dividing by the standard deviation for each value of each feature. This process ensures that after standardization, all features have a mean of zero and a standard deviation of one, thereby placing them on the same scale. We applied the z-score method with information extracted by each respective training dataset, and standardized the data before training and assessed the models, respectively.
3.4. Machine Learning Algorithms
Supervised learning can be utilized with datasets containing known information, which, after a ‘training’ process, can be used to make predictions on new unseen data. The goal in such cases is to train a model to recognize patterns within the initial dataset (referred to as the ‘training dataset’) and use these patterns to predict the missing or desired information. Supervised learning is generally divided into two main categories: classification and regression. In classification, the objective is to predict the category or group to which the missing information belongs, while in regression, the goal is to predict numerical values. In this study, the first step involved determining the appropriate type of supervised learning to apply. Regression learning was chosen to be used to predict shaft power.
3.4.1. k-Nearest Neighbors
The k-nearest neighbors (k-NN) algorithm is one of the oldest, simplest, and most efficient machine learning algorithms [38]. For classification problems, it assigns the majority class among the k-nearest neighbors, while for regression, it estimates the target using a weighted average:
with extensions such as inverse distance weighting:
It is worth mentioning that in k-NN, the selection of the distance metric also plays a crucial role. Typically, researchers choose natural numbers for p in the formula Specifically, the choice of distance metric in k-NN significantly influences performance, as it determines how similarity between data points is calculated. For example, the Manhattan distance (p = 1) is often more effective in cases with varied feature scales or sparse data, while the Euclidean distance (p = 2) assumes more uniform, continuous relationships across features.
3.4.2. Decision Trees
Decision trees are versatile, nonparametric models widely used for both classification and regression tasks. These models aim to predict the value of a target variable by learning a series of hierarchical decision rules derived from the input data features [39]. At each node of the tree, a decision is made based on a specific feature, splitting the data into subsets that are progressively more homogeneous with respect to the target variable. For regression tasks, decision trees predict continuous values by partitioning the data space into regions and assigning a predicted value, typically the mean of the target variable within each region. Moreover, for regression, tree depth controls model complexity, balancing performance, and overfitting.
3.4.3. XGBoost
XGBoost is a tree boosting algorithm known for its high performance and efficiency in machine learning tasks. It offers a scalable, end-to-end solution and has gained widespread recognition for delivering top-tier results across a variety of predictive modeling challenges [40].
3.5. SHapley Additive exPlanations (SHAP)
SHAP (SHapley Additive exPlanations) [41] is a state-of-the-art explainability method that quantifies the importance of features in a model’s decisions. It is based on the principles of local accuracy, missingness, and consistency, providing reliable and interpretable explanations across a wide range of models. SHAP can explain linear regression models, generalized additive regression models, non-additive boosted tree models, linear logistic regression models, non-additive boosted tree logistic regression models, and even transformer-based NLP models. In addition, it effectively handles correlated input features, making it a versatile and powerful tool for understanding both simple and complex machine learning models.
3.6. Emissions Estimation Methodology
To evaluate the environmental impact of vessel operations, we apply the bottom-up emissions estimation method as outlined in the [42]. This approach calculates pollutant emissions based on operational power output and fuel-specific emission factors.
The total emission output of a given pollutant is computed using the following equation:
where:
- is the estimated emission output (e.g., CO2, NOx),
- is the emission factor specific to the pollutant and fuel type (e.g., gCO2/kWh),
- is the total power output of the main engine during the operation period (in kWh).
The main engine power output is further defined as:
where:
- shaftpower is the average shaft power delivered by the engine during the voyage (in kW),
- workingtime is the total engine operating time over the analyzed period (in hours).
By integrating the predicted shaft power from our machine learning models with operational time data, this method enables estimation of emissions under various voyage and environmental conditions. This facilitates the use of data-driven performance monitoring for compliance evaluation and emissions reduction strategies.
4. Results
4.1. Model Selection
As was mentioned earlier in Section 3, each method has a number of hyper-parameters that need to be fine-tuned in order to find the best-performing model. In order to evaluate their performance, we utilized two key metrics: R-Squared () and the Root Mean Square Error (RMSE). The R-Squared metric, often referred to as the coefficient of determination, measures the proportion of the variance in the dependent variable that is predictable from the independent variables, providing insight into the goodness of fit of the model. A higher R-Squared value indicates a model that can better explain the variability of the output with respect to the input variables. On the other hand, the RMSE is a standard way to measure the error of a model in predicting quantitative data. It quantifies the square root of the average squared differences between the predicted and actual values, offering a clear gauge of the prediction accuracy. Lower RMSE values signify a model with higher precision [43,44].
Starting with Decision Tree regressor, we examined the model for different depth values and their performance in terms of R-Squared and RMSE are shown in Figure 3, respectively. We found that a model with a depth of 10 performed best based on both scores. Increasing the complexity (depth) beyond 10 did not provide any significant improvement, as both the R-Squared value and the RMSE level off. Thus, to save on computational resources, we chose the model with depth equal to 10.
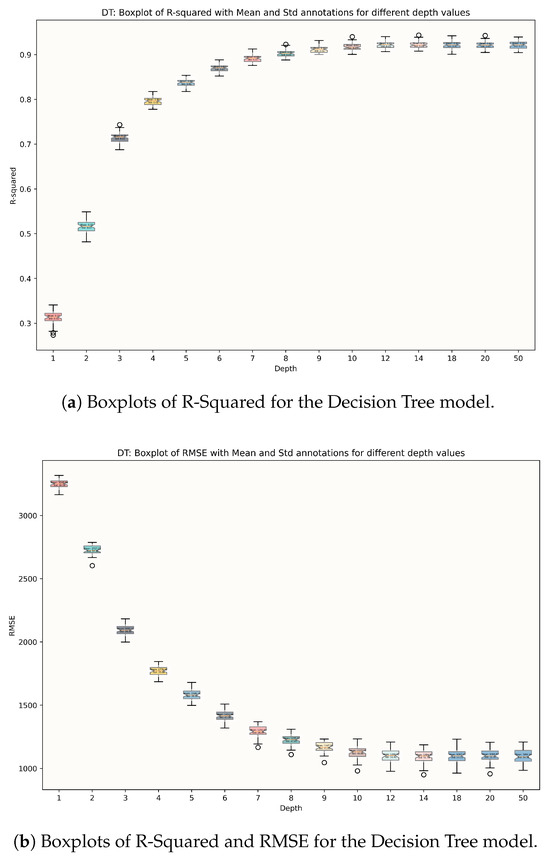
Figure 3.
DecisionTree models: Boxplots of R-Squared and RMSE for different depth values.
In the model selection process for the k-NN method, we examined the model by varying the number of neighbors, different Minkowski distances, and weighted functions. Regarding the number of neighbors, we tested for to adjust the granularity of the local decision boundary. For the Minkowski distance, we tested for catering to different geometric considerations in feature space. Finally, for the weight functions, we tested with both ‘uniform’- and ‘distance’-based weight functions, where the latter assigns importance to neighbors based on their proximity, potentially enhancing prediction accuracy in more irregular data distributions. As observed in Figure 4, the number of nearest neighbors is the hyper-parameter that most significantly affects the model’s performance. With three neighbors, the k-NN method exhibits the best values for both R-Squared and RMSE, indicating that, in comparison, the rest of the hyper-parameters have a minimal impact on performance. The optimal model identified utilized 3 nearest neighbors and employed the Minkowski distance metric with a p-value of 1 (Manhattan Distance) and the ‘distance’ weight function.
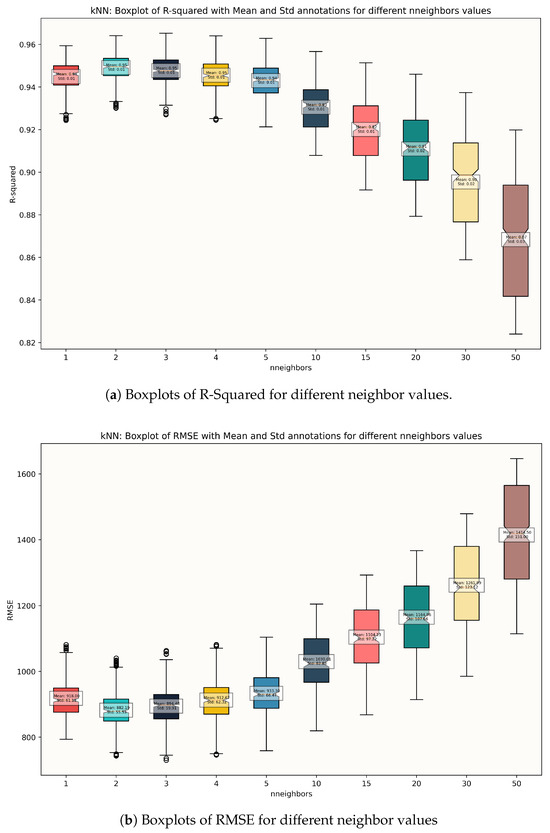
Figure 4.
K-NN models: Boxplots of R-Squared and RMSE for different neighbor values. (a) Boxplots of R-Squared for different neighbor values. (b) Boxplots of RMSE for different neighbor values.
The XGBoost method was evaluated based on three hyper-parameters. More specifically, we explore a wide range of estimators from 5 to 200, which allows for extensive examination of the trade-off between model complexity and overfitting. Different learning rates (0.001, 0.01, 0.1, 1) are set to control the speed and refinement with which the model learns, aiming to find a balance that avoids both underfitting and rapid overfitting. Additionally, various tree depths (3, 4, 5, 7, 9, 15, 20) were tested to assess how well deeper or shallower trees capture the data’s underlying patterns. As illustrated in Figure 5 and Figure 6, the model configured with 100 and 200 estimators achieved the highest R-Squared and the lowest RMSE, respectively. Additionally, the depth parameter did not show any significant impact on the model after a depth of 7; therefore, we decided to select the model with depth 7 for computational reasons, as shown in Figure 6. The learning rate appeared to have a significant influence on performance at levels of 0.1 and 1 as is presented in Figure 6. Consequently, we selected two models with 100 and 200 estimators, a depth of 7, and a learning rate of 0.1.

Figure 5.
XGBoost models: Boxplots of R-Squared and RMSE for different estimator values.
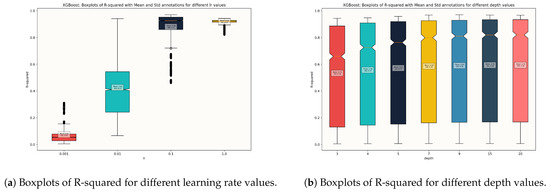
Figure 6.
XGBoost Models: Boxplots of R-Squared and RMSE for different learning rate and depth values.
Regarding the Decision Tree model, we observed that although outperforming the baseline model, as illustrated in Figure 7, it also shows statistically significant differences () in performance metrics when compared to the k-NN and XGBoost models. Specifically, both the mean R-squared and RMSE for the Decision Tree models were not on par with those obtained from the k-NN and XGBoost configurations. Given this disparity, we decided against further detailed evaluations of the Decision Tree models for this particular study. Nonetheless, it is worth noting that the Decision Tree models did demonstrate substantial improvement over the baseline, indicating that they could still be considered viable options in contexts where simpler or less computationally intensive models are required.
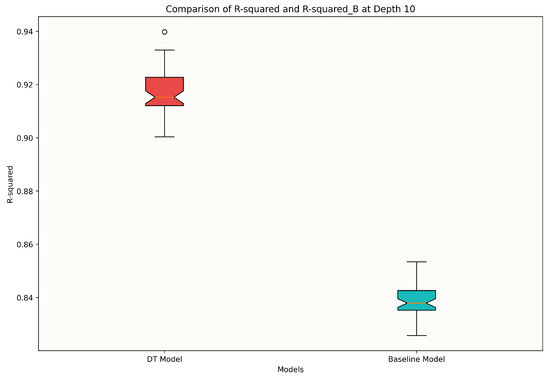
Figure 7.
DT models: Boxplots of R-squared for DT and baseline models.
As shown in Figure 8, we chose 12 k-NN models for their excellent performance, each outperforming the baseline model. The selection criteria for these models in the assessment phase were based purely on computational efficiency. We chose a model configured with two neighbors using the Manhattan distance ( in Minkowski terms) and a distance-weighted function. This model demonstrated a robust performance, achieving an R-Squared value of 0.854 on the assessment dataset, indicating strong predictive accuracy.

Figure 8.
k-NN models: Boxplots of R-squared for k-NN and baseline models.
Regarding the XGBoost models, it is clear from Figure 9 that all four selected models performed significantly better than the baseline model. It is evident that the models of learning rate 0.1 had better scores; thus, we selected two configurations with the same learning rate but different numbers of estimators. The first model, configured with 100 estimators, a learning rate of 0.1, and a depth of 7, reached an R-squared of 0.93. Building on this setup, the second model increased the number of estimators to 200 while maintaining the same learning rate and depth. This adjustment further enhanced the model’s accuracy, bringing the R-squared to 0.94. These results underscore the effectiveness of the XGBoost models in handling complex predictive tasks and their capacity for incremental improvement with increased estimators.
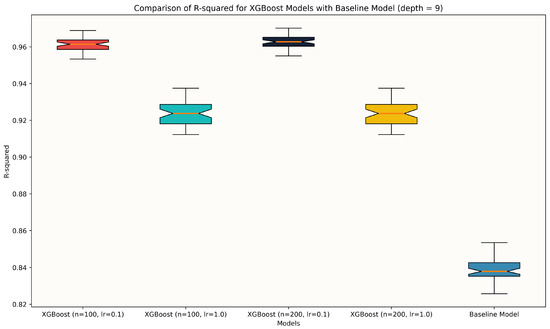
Figure 9.
XGBoost models: Boxplots of R-squared for XGBoost and baseline models.
4.2. Model Assessment
During the model assessment process, we trained the selected models on 80% of our shuffled initial dataset. The models were trained and then tested on the model assessment dataset, i.e., the shuffled 20% of the initial dataset, a part of the dataset that has not been involved in the model selection process. As we can observe in Figure 10, the two XGBoost models exhibit optimal behavior according to the assessment dataset, achieving 13% higher accuracy (R squared) compared to the baseline model. In the case of k-NN, although it exhibits better performance than the baseline model, this improvement is not statistically significant.
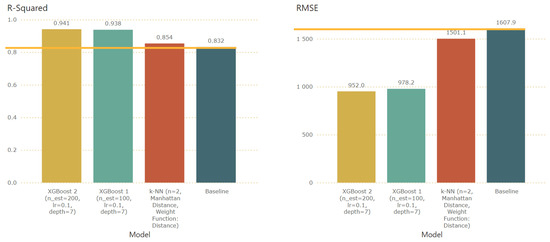
Figure 10.
Model assessment: results of the three evaluated models.
4.3. Explainable Machine Learning with SHAP Framework
The beeswarm plot aims to present a concise overview of how the most influential features in a dataset affect the model’s output. Each instance of the explanation is depicted by a single dot on each feature row. The horizontal position of the dot is determined by the SHAP value. Additionally, the features are arranged based on their impact on prediction. This order allows us to visualize how the values of a feature influence the prediction outcome. Each dot on the plot corresponds to a single observation. The horizontal axis indicates the SHAP value, and the color of the dot indicates whether the observation has a higher or lower value compared to others.
For our optimal model (XGBoost with 200 estimators, learning rate 0.1, and depth 7), in Figure 11, a higher GPS speed, draft, days from dry doc, and wave height positively affect the prediction, whereas lower values have a negative impact. On the other hand, lower days from delivery have positively affected the prediction, whereas higher values have a negative impact.
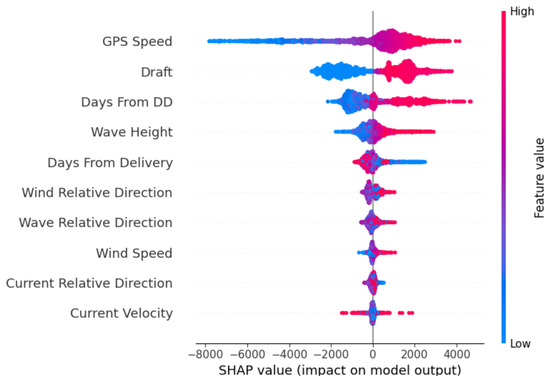
Figure 11.
The beeswarm plot.
5. Discussion
This research proposes a novel method for applying machine learning to predict shaft power in ships. Precise shaft power prediction enables more efficient operation, directly translating to reduced fuel consumption and lower emissions. These efficiency gains not only benefit operational costs but also significantly shrink the environmental footprint of maritime transportation.
Furthermore, an accurate shaft power prediction model can serve as a foundation for future research on pathfinding optimization and could also replace the Kreitner method currently utilized in this area. Beyond fuel savings, the model facilitates optimal maintenance scheduling based on predicted power requirements. This minimizes unnecessary dry-docking and cleaning procedures, leading to significant cost savings and a further reduction in emissions associated with maintenance activities. Additionally, timely maintenance interventions prevent excessive wear and tear on the propulsion system, extending its lifespan and further reducing overall maintenance needs. The combined impact of these factors translates to a trifecta of benefits: enhanced operational reliability, improved overall vessel performance, and a substantial reduction in transportation emissions. This shift toward sustainable practices fosters a greener future for maritime operations.
Our study employs three different machine learning methods—k-NN, Decision Trees, and XGBoost—to predict the shaft power of VLCC tankers, utilizing input data gathered from numerous sensors on the vessel and weather conditions from external APIs. Although some of the input variables are gathered from sensors on the vessel and such sensors may not be available to all vessels, to ensure the model’s adaptability to a wide range of vessels, we utilize input parameters that are universally measured during a voyage. Furthermore, for future work, we plan to explore alternative methods to estimate or replace such parameters with more widely available data or multiple sources of information making the model more practical and applicable to diverse ships.
We focus on accurate shaft power prediction as it is essential for optimizing tanker performance and ensuring operational efficiency. Our research highlights the importance of maintaining a representative relationship between the input variables while striving for the highest prediction accuracy. Historically, many machine learning applications in this domain have overlooked the critical task of understanding how these variables interact. Therefore, our study integrates explanatory artificial intelligence (AI) methods to offer a deeper understanding of the features influencing prediction accuracy. By utilizing explainable AI techniques, specifically the SHAP framework, this research provides valuable insights into the decision-making processes of machine learning models. This transparency helps identify which features—such as GPS speed, draft, days from dry dock, and wave height—are most influential in predicting shaft power. Understanding these relationships not only enhances the accuracy and reliability of predictions but also contributes to more informed decision making in real-world maritime operations.
Our findings reveal that the XGBoost method significantly outperforms other approaches, achieving 13% greater accuracy than traditional prediction methods. This improvement is crucial for enhancing the operational efficiency of tankers. More accurate predictions lead to better management of fuel consumption, which directly reduces fuel emissions and minimizes the environmental impact of maritime transportation. Moreover, accurate shaft power predictions play a pivotal role in addressing fouling issues. By optimizing operational efficiency and maintenance schedules, we can reduce the frequency of fouling-related problems, leading to fewer cleaning procedures and decreased fuel consumption. This reduction in fouling not only prolongs the lifespan of propulsion systems but also contributes to lower emissions by ensuring that vessels operate at peak efficiency.
While k-NN demonstrated improved performance over the baseline model during validation, its results on unseen data were not statistically significant. This is likely due to k-NN’s sensitivity to novel input configurations, making it less stable in generalization compared to tree-based methods like XGBoost. This reinforces the suitability of XGBoost for real-world deployment, given its superior robustness and predictive consistency across varying operational conditions.
The application of explainable AI models (XAI models) in performance monitoring is equally transformative. The recommended method can be embedded in a system that enables real-time monitoring of shaft power and performance parameters. Additionally, the system can promptly alert operators to anomalies or deviations from expected performance, allowing for quick intervention and correction. This real-time capability enhances the proactive management of ship performance, ensuring that issues are addressed before they escalate into significant problems. By providing clear explanations of the predictions and highlighting the key factors driving these predictions, operators gain a deeper understanding of the underlying causes of performance deviations, leading to more effective troubleshooting and maintenance strategies.
In addition to enhancing shaft power prediction, the proposed framework can be extended to emissions estimation by leveraging the relationship between engine power output and fuel-based emission factors, as defined in the 4th IMO GHG Study (Section 3.6). By accurately predicting shaft power and combining it with operational time, the model can indirectly estimate total emissions using a bottom-up approach. This capability enables not only real-time performance tracking but also emissions forecasting under varying voyage conditions. Furthermore, the integration of explainable AI (XAI) methods, such as SHAP, provides transparency into how environmental and operational variables influence both power output and derived emissions. This interpretability supports regulatory compliance, improves trust in data-driven systems, and aids operators in making informed decisions to reduce fuel consumption and environmental impact.
Although the dataset used in this study originates from a single VLCC tanker, it spans a duration of 36 months, capturing a wide range of operational, environmental, and maintenance conditions. This long-term data collection provides high variability and richness, enabling the development of robust models that reflect real-world ship behavior under diverse scenarios. However, we acknowledge that using data from a single vessel introduces certain limitations. Specifically, the model may capture vessel-specific patterns that limit generalizability to other ships. Additionally, the absence of data from multiple vessel types means the current model cannot yet account for structural and operational differences across ship classes. These limitations are noted for future work, where we aim to extend the dataset to include multiple vessels to enhance model generalization and applicability across the broader maritime fleet.
The shaft power is used because it more accurately reflects the energy transmitted by the engines compared to the indicated horsepower, which measures the power generated internally within the engine. Overall, the introduction of explainable AI models, such as those based on the SHAP framework, represents a significant advancement in the field of explainable AI. These models bridge the gap between complex machine learning algorithms and human understanding, enhancing the transparency, trustworthiness, and fairness of predictive systems. By improving the accuracy of shaft power predictions and addressing fouling and emissions, this research supports more sustainable and efficient maritime operations, ultimately contributing to a greener and more environmentally responsible shipping industry.
6. Conclusions
This study demonstrates the effectiveness of machine learning models for accurately predicting shaft power in VLCC tankers. Through a comprehensive comparative analysis involving k-NN, Decision Trees, and XGBoost, the latter showed a 13% improvement over traditional baseline methods. The integration of SHAP explainability enhances model transparency by identifying critical predictors such as GPS speed, draft, days from dry dock, and wave height. These insights enable not only improved operational efficiency and fuel economy but also more effective maintenance planning and emissions monitoring. Although data was sourced from a single vessel, the results underline the potential of scalable, explainable AI systems for real-time performance monitoring and emissions forecasting, supporting more sustainable maritime operations. Future work will aim to generalize the model across diverse vessel types using broader datasets.
Author Contributions
Conceptualization, S.Z., Y.K., T.P., and I.F.; methodology, S.Z., K.G., D.K., and Y.K.; software, S.Z., K.G., and D.K.; validation, S.Z., K.G., Z.L., D.P., I.F., and Y.K.; formal analysis, Y.K.; investigation, Z.L., D.P., I.F., and Y.K.; resources, Z.L., D.P., and I.F.; data curation, S.Z., K.G., Z.L., D.P., I.F., and Y.K.; writing—original draft preparation, S.Z. and K.G.; writing—review and editing, S.Z., K.G., I.F., and Y.K.; visualization, S.Z.; supervision, T.P., I.F., and Y.K.; project administration, Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Zoran Lajic and Dimitris Papathanasiou was employed by the company Angelicoussis Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| API | Application Programming Interface |
| DT | Decision Tree |
| EU | European Union |
| EU ETS | European Union Emissions Trading System |
| IMO | International Maritime Organization |
| IoT | Internet of Things |
| k-NN | k-Nearest Neighbors |
| ML | Machine Learning |
| NN | Neural Network |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| SHAP | SHapley Additive exPlanations |
| SVM | Support Vector Machine |
| VLCC | Very Large Crude Carrier |
| XAI | Explainable Artificial Intelligence |
| XGBoost | eXtreme Gradient Boosting |
References
- European Commision. Reducing Emissions from the Shipping Sector; European Commision: Brussels, Belgium, 2023. [Google Scholar]
- International Maritime Organization (IMO). 2023 IMO Strategy on Reduction of GHG Emissions from Ships; International Maritime Organization (IMO): London, UK, 2023. [Google Scholar]
- International Maritime Organization (IMO). 2021 Guidelines on the Shaft/Engine Power Limitation System to Comply with the EEXI Requirements and Use of a Power Reserve; International Maritime Organization (IMO): London, UK, 2021. [Google Scholar]
- Gupta, P.; Rasheed, A.; Steen, S. Ship performance monitoring using machine-learning. Ocean Eng. 2022, 254, 111094. [Google Scholar] [CrossRef]
- Fahrnholz, S.F.; Caprace, J.D. A machine learning approach to improve sailboat resistance prediction. Ocean Eng. 2022, 257, 111642. [Google Scholar] [CrossRef]
- Aizpurua, J.I.; Knutsen, K.E.; Heimdal, M.; Vanem, E. Integrated machine learning and probabilistic degradation approach for vessel electric motor prognostics. Ocean Eng. 2023, 275, 114153. [Google Scholar] [CrossRef]
- Panagiotakopoulos, T.; Filippopoulos, I.; Filippopoulos, C.; Filippopoulos, E.; Lajic, Z.; Violaris, A.; Chytas, S.P.; Kiouvrekis, Y. Vessel’s trim optimization using IoT data and machine learning models. In Proceedings of the 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA), Corfu, Greece, 18–20 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Guo, B.; Gupta, P.; Steen, S.; Tvete, H.A. Evaluating vessel technical performance index using physics-based and data-driven approach. Ocean Eng. 2023, 286, 115402. [Google Scholar] [CrossRef]
- Graf von Westarp, A. A new model for the calculation of the bunker fuel speed–consumption relation. Ocean Eng. 2020, 204, 107262. [Google Scholar] [CrossRef]
- Filippopoulos, I.; Panagiotakopoulos, T.; Skiadas, C.; Triantafyllou, S.M.; Violaris, A.; Kiouvrekis, Y. Live Vessels’ Monitoring using Geographic Information and Internet of Things. In Proceedings of the 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA), Corfu, Greece, 18–20 July 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, S.; Papanikolaou, A.; Shang, B. Regulating the safe navigation of energy-efficient ships: A critical review of the finalized IMO guidelines for assessing the minimum propulsion power of ships in adverse conditions. Ocean Eng. 2022, 249, 111011. [Google Scholar] [CrossRef]
- Li, X.; Sun, B.; Jin, J.; Ding, J. Ship speed optimization method combining Fisher optimal segmentation principle. Appl. Ocean Res. 2023, 140, 103743. [Google Scholar] [CrossRef]
- Hua, R.; Yin, J.; Wang, S.; Han, Y.; Wang, X. Speed optimization for maximizing the ship’s economic benefits considering the Carbon Intensity Indicator (CII). Ocean Eng. 2024, 293, 116712. [Google Scholar] [CrossRef]
- Issa, M.; Ilinca, A.; Martini, F. Ship Energy Efficiency and Maritime Sector Initiatives to Reduce Carbon Emissions. Energies 2022, 15, 7910. [Google Scholar] [CrossRef]
- Delgado-Currín, R.; Calderon-Munoz, W.R.; Elicer-Cortos, J.C. Artificial Neural Network Model for Estimating the Pelton Turbine Shaft Power of a Micro-Hydropower Plant under Different Operating Conditions. Energies 2024, 17, 3597. [Google Scholar] [CrossRef]
- Kriezis, A.C.; Sapsis, T.; Chryssostomidis, C. Predicting Ship Power Using Machine Learning Methods. In Proceedings of the SNAME Maritime Convention, Houston, TX, USA, 27–29 September 2022. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kim, K.S.; Yeon, S.; Lee, Y.Y.; Kim, G.D.; Kim, M. Power Prediction Method for Ships Using Data Regression Models. J. Mar. Sci. Eng. 2023, 11, 1961. [Google Scholar] [CrossRef]
- Lang, X.; Wu, D.; Mao, W. Comparison of supervised machine learning methods to predict ship propulsion power at sea. Ocean Eng. 2022, 245, 110387. [Google Scholar] [CrossRef]
- Valchev, I.; Coraddu, A.; Kalikatzarakis, M.; Geertsma, R.; Oneto, L. Numerical methods for monitoring and evaluating the biofouling state and effects on vessels hull and propeller performance: A review. Ocean Eng. 2022, 251, 110883. [Google Scholar] [CrossRef]
- Kim, H.S.; Roh, M.I. Interpretable, data-driven models for predicting shaft power, fuel consumption, and speed considering the effects of hull fouling and weather conditions. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100592. [Google Scholar] [CrossRef]
- Radonjic, A.; Vukadinovic, K. Application of ensemble neural networks to prediction of towboat shaft power. J. Mar. Sci. Technol. 2015, 20, 64–80. [Google Scholar] [CrossRef]
- Hajli, K.; Rönnqvist, M.; Dadouchi, C.; Audy, J.F.; Cordeau, J.F.; Warya, G.; Ngo, T. A fuel consumption prediction model for ships based on historical voyages and meteorological data. J. Mar. Eng. Technol. 2024, 23, 439–450. [Google Scholar] [CrossRef]
- Le, T.T.; Sharma, P.; Pham, N.D.K.; Le, D.T.N.; Van Vang Le, S.M.O.; Rowinski, L.; Tran, V.D. Development of comprehensive models for precise prognostics of ship fuel consumption. J. Mar. Eng. Technol. 2024, 23, 451–465. [Google Scholar] [CrossRef]
- Parkes, A.; Sobey, A.; Hudson, D. Physics-based shaft power prediction for large merchant ships using neural networks. Ocean Eng. 2018, 166, 92–104. [Google Scholar] [CrossRef]
- Lee, Y.E.; Kim, B.K.; Bae, J.H.; Kim, K.C. Misalignment detection of a rotating machine shaft using a support vector machine learning algorithm. Int. J. Precis. Eng. Manuf. 2021, 22, 409–416. [Google Scholar] [CrossRef]
- Laurie, A.; Anderlini, E.; Dietz, J.; Thomas, G. Machine learning for shaft power prediction and analysis of fouling related performance deterioration. Ocean Eng. 2021, 234, 108886. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Kim, D.; Handayani, M.P.; Lee, S.; Lee, J. Feature Attribution Analysis to Quantify the Impact of Oceanographic and Maneuverability Factors on Vessel Shaft Power Using Explainable Tree-Based Model. Sensors 2023, 23, 1072. [Google Scholar] [CrossRef] [PubMed]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Transp. Res. Part D Transp. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Hu, Z.; Jin, Y.; Hu, Q.; Sen, S.; Zhou, T.; Osman, M.T. Prediction of fuel consumption for enroute ship based on machine learning. IEEE Access 2019, 7, 119497–119505. [Google Scholar] [CrossRef]
- Kim, Y.R.; Jung, M.; Park, J.B. Development of a fuel consumption prediction model based on machine learning using ship in-service data. J. Mar. Sci. Eng. 2021, 9, 137. [Google Scholar] [CrossRef]
- Moreira, L.; Vettor, R.; Guedes Soares, C. Neural network approach for predicting ship speed and fuel consumption. J. Mar. Sci. Eng. 2021, 9, 119. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Filippopoulos, I.; Stamoulis, G. Collecting and using vessel’s live data from on board equipment using “Internet of Vessels (IoV) platform” (May 2017). In Proceedings of the 2017 South Eastern European Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Kastoria, Greece, 23–25 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Kiouvrekis, Y.; Gkirtzou, K.; Zikas, S.; Kalatzis, D.; Panagiotakopoulos, T.; Lajic, Z.; Papathanasiou, D.; Filippopoulos, I. An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels. Future Internet 2025, 17, 264. [Google Scholar] [CrossRef]
- Kreitner, J. Heave, pitch, and resistance of ships in a seaway. Trans. R. Inst. Nav. Archit. 1939, 87. [Google Scholar]
- ISO 15016:2015; Ships and Marine Technology—Guidelines for the Assessment of Speed and Power Performance by Analysis of Speed Trial Data. The International Organization for Standardization: Geneva, Switzerland, 2015.
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When Is “Nearest Neighbor” Meaningful? In Database Theory—ICDT’99, Proceedings of the 7th International Conference, Jerusalem, Israel, 10–12 January 1999; Beeri, C., Buneman, P., Eds.; Springer: Berlin/Heidelberg, 1999; pp. 217–235. [Google Scholar]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- International Maritime Organization (IMO). Fourth IMO GHG Study 2020—Full Report and Annexes; International Maritime Organization (IMO): London, UK, 2020; Available online: https://wwwcdn.imo.org/localresources/en/OurWork/Environment/Documents/Fourth%20IMO%20GHG%20Study%202020%20-%20Full%20report%20and%20annexes.pdf (accessed on 10 May 2025).
- Colin Cameron, A.; Windmeijer, F.A. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).