Abstract
Computing-in-memory (CIM) with emerging non-volatile resistive memory devices has demonstrated remarkable performance in data-intensive applications, such as neural networks and machine learning. A crosspoint memory array enables naturally parallel computation of matrix–vector multiplication (MVM) in the analog domain, offering significant advantages in terms of speed, energy efficiency, and computational density. However, the intrinsic device non-ideality residing in analog conductance state distorts the MVM precision and limits the application to high-precision scenarios, e.g., scientific computing. Yet, a theoretical framework for guiding reliable computing-in-memory designs has been lacking. In this work, we develop an analytical model describing the constraints on bit precision and row parallelism for reliable MVM operations. By leveraging the concept of capacity from information theory, the impact of non-ideality on computational precision is quantitively analyzed. This work offers a theoretical guidance for optimizing the quantized margins, providing valuable insights for future research and practical implementation of reliable CIM.
1. Introduction
Over the past decade, extensive research has focused on emerging memory technologies [1,2,3], such as resistive random-access memory (RRAM) devices, which offer significant advantages in high area efficiency, fast switching speed, and low power consumption compared to conventional CMOS-based memories, etc. [4]. Notably, they are non-volatile (a feature rare in traditional memories) and allowed to be programmed in an analog manner, through continuous modulation of their internal state variables [5]. These capabilities are critical for emerging computing paradigms [6,7,8], as substantial research has demonstrated their significant advantages in accelerating matrix–vector multiplication (MVM) operations. This acceleration, in turn, enables faster processing of numerous data-intensive tasks, including neural network inference and training, as well as recommendation systems [9,10,11,12], and shows promise for extension to dynamic collaborative adversarial domain adaptation network, residual frequency attention regularized network, and other deep learning-based methods [13,14,15]. It has also contributed to high-precision scenarios, such as scientific computing (Figure 1a) [16,17] and signal processing [18,19].
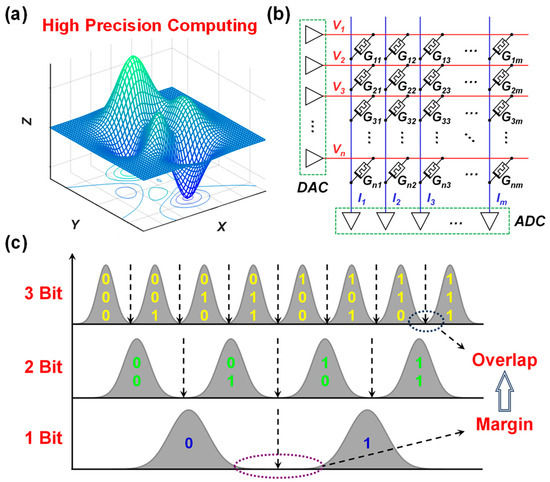
Figure 1.
Applications, principles, and challenges of high-precision MVM computation. (a) Example of high-precision computing. (b) Schematic diagram of the principle to perform in situ MVM computation in one-step based on a crosspoint RRAM array. (c) The problem and challenge of precision loss caused by non-ideality input distribution in analog MVM operation.
A crosspoint RRAM array is illustrated in Figure 1b. By leveraging Ohm’s and Kirchhoff’s laws for multiplication and addition, respectively, it performs in situ MVM computations in the analog domain. Thus, it not only solves the problem of significant overhead for data movement in traditional digital approaches [20] but also reduces the computational complexity from O(N2) to O(1) [21]. In the MVM circuit, digital-to-analog converters (DACs) are used to provide input voltages (vector V) to the word lines of the RRAM array, the matrix G is encoded as the conductance values of the device cells, then the currents on the bit lines (vector I) represent the MVM product result in real time. To read out the MVM result, the currents are usually converted by transimpedance amplifiers (TIAs) and subsequently quantized by analog-to-digital converters (ADCs).
Despite the notable advantages in terms of computational parallelism, integration density, and low latency, the analog MVM operation is fundamentally more susceptible to non-ideality than digital counterparts [22,23]. In particular, the multi-level conductance programming capability is limited by the reduced readout margin due to inherent device variations and fluctuations, as illustrated in Figure 1c. The device non-ideality is reasonably abstracted as a normal distribution of conductance [24,25,26]. As a result, when participated in the analog MVM operation, the non-idealities would be accumulated and eventually limit the computing precision, otherwise lead to quantization errors during output digitization. While such errors may be tolerated in neural networks due to the robustness provided by nonlinear activation functions, their presence becomes problematic in high-precision tasks such as scientific computing and signal processing, posing a significant challenge for high-precision analog computing systems. Therefore, performing rigorous precision analysis of analog MVM is crucially important.
According to the basic statistical principles, the output current distribution should scale with (where NRow is the number of cells involved in MVM computation) [27], but the precise quantitative relationship remains unexplored. A recent study examined the deviation in output current caused by the device’s low-conductance state (which is not strictly zero), ultimately affecting computational accuracy [28]. However, this work primarily focused on 1-bit precision inputs and lacked a comprehensive analysis of multi-bit inputs, limiting its applicability and generalizability. Here, we develop an analytical model describing the input-output precision relationship of the analog MVM circuit. It captures the inherent limitations imposed by hardware constraints and non-ideality characteristics, shedding light on the fundamental trade-off between bit precision and row parallelism. The capacity concept in information theory is utilized as a quantitative tool to evaluate the impact of non-ideality distribution on output precision, and thus measuring the degradation behavior of analog MVM precision.
2. MVM Product Result Precision Model
2.1. Definition of Physical Quantities
To study the precision of the analog MVM result in Figure 1b, we define that precision of the input voltage V is CV bits (with NV levels), and precision of the device conductance matrix G is CG bits (with NG levels). COUT represents the precision of the MVM result per operation cycle, corresponding to the number of current states that needs to be quantized by the ADC. It is worth noting that, although the conductance range varies significantly across various RRAM devices (or broadly other nonvolatile resistive memory devices, e.g., phase change memory), the absolute value of these physical quantities should not affect the modeling result. It is well known that, in the ideal case, when NROW rows in the array are simultaneously turned on, the nominal output precision of MVM is
COUT = CV + CG + log2NROW
Equation (1) has been frequently used to guide the selection of ADCs and the determination of quantization interval in existing studies [29,30,31], especially on the field of microarchitecture design, which is understandable, as objects at architecture level are abstracted. However, in practical, the individual discrete conductance levels are never ideal, rather they follow specific distributions, as illustrated in Figure 1c, which, in turn, should change the effectiveness of Equation (1).
2.2. MVM Output Precision Model
To perform MVM output precision analysis, we assume that all voltage and conductance levels are distributed uniformly in their ranges, respectively, and that all levels of each variable follow a normal distribution with the same standard deviations (σV and σG) [32]. The levels are normalized with respect to the lowest level, namely the means of all levels (μV and μG) are positive integers within the ranges 1 to NV and 1 to NG, respectively. As DAC is a much more mature technology, the voltage input V it provides is relatively stable with a small non-ideality distribution. For simplicity, we first assume the ideal voltage input (σV = 0) and analyze only the impact of non-ideal conductance levels on MVM precision. Figure 2a illustrates such a consideration for two specific cases, in each of which the non-ideal conductance vector G = [N(μG1, σG12), N(μG2, σG22), …, N(μGN, σGN2)], where N(μ, σ2) represents the normal distribution, is multiplied by an ideal voltage vector V = [μV1, μV2, …, μVN]. According to basic statistical principle, the resulting MVM product currents should also normal distribution, with each element dictated by
where Σ represents the summation of currents through all RRAM devices, and the subscript i = 1, 2, …, N represents the index of the RRAM device through which the current is accumulated. When the non-ideal input voltage is taken into account, the product of these two distributions results in a more complex distribution for the current output. However, the maximum distribution still occurs only when all elements of the voltage and conductance vectors reach their respective maximum values. Specifically, this is represented as σI2 = NROW(σV2σG2 + NV2σG2 + NG2σV2). Notably, when σV = 0, the analysis corresponds to the ideal voltage input case shown in Figure 2a.
I = Σi N(μViμGi, μVi2σGi2),
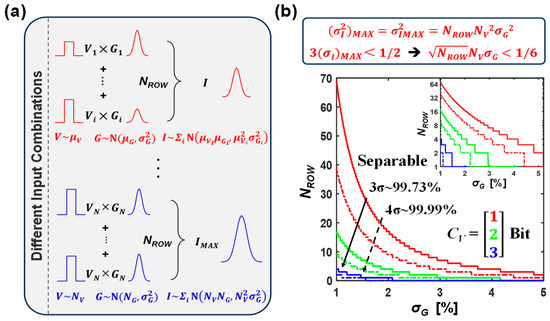
Figure 2.
Analysis of the MVM precision when the voltage input is ideal. (a) Decomposition diagram of the MVM process. (b) The limiting relationship between bit precision and row parallelism, along with the results based on 3σ and 4σ as the criteria, respectively. The inset displays the corresponding results in a semi-logarithmic coordinate system.
It is revealed that the standard deviation of the MVM product current is controlled by the input voltages, in addition to the device conductance variation σG. In the worst-case scenario, all voltage inputs μV are assumed with the maximum value NV, and the resulting current vector is I = Σi N(NVμGi, NV2σG2), the standard deviation of MVM current is σI = NVσG. To accurately quantize two adjacent current levels with ADC, there should be no overlap between the two distributions. Under the 3σ (4σ) criteria with 99.73% (99.99%) probability, the following inequality should be satisfied:
where k is 3 or 4. Equation (3) reflects the constraint on bit precision σG and row parallelism NROW. The results for 99.73% (corresponding to using 3σ as the criterion) and 99.99% quantized accuracy (4σ criterion) are calculated, respectively.
Figure 2b illustrates these constraints according to Equation (3). The maximum number of row parallelism NROW is greatly restricted by the voltage input precision NV and the non-ideality characteristics σG of the device. When the input voltage is limited to the simplest 1-bit case and the conductance distribution is confined to 1% (percent of the device’s maximum conductance), NROW can reach 64. However, as the conductance distribution deteriorates, for example, under parameter conditions where σG = 3~5%, which is a common range of metal-oxide RRAM devices [33,34], NROW will quickly drop below 10. For example, when the input voltage is 1-bit and σG = 4%, the maximum allowable row parallelism is merely 4. When the input voltage is 3 bits, multi-row MVM computations with NROW less than 4 achieve at least 3σ accuracy, only if the condition of σG = 1% is met. This result underscores again the importance of accounting for non-ideal factors when implementing high-precision MVM computations on current RRAM devices.
In addition to RRAM, a variety of emerging non-volatile memory (NVM) technologies—such as magnetoresistive random-access memory (MRAM), phase-change memory (PCM), and ferroelectric field-effect transistors (FeFETs)—have also been explored for MVM applications. MRAM offers exceptional endurance (up to 1015 cycles), but its narrow resistance window limits its suitability for multi-bit storage and analog computing [35]. PCM is among the most mature NVM technologies at advanced fabrication nodes, yet it suffers from relatively high read/write currents and power consumption [36,37]. FeFETs, in contrast, feature lower write currents and reduced power consumption, which significantly enhance energy efficiency in programming computational units [38,39]. However, like RRAM, FeFETs also face challenges in endurance, particularly in scenarios requiring frequent weight updates.
Our proposed model serves as a mathematical abstraction of the MVM process. Crucially, the output precision depends solely on the statistical characteristics of input noise and device variability, rather than on any specific memory type. As such, the model applies broadly to MVM implementations that rely on analog programming and operate under fundamental circuit laws—such as Ohm’s and Kirchhoff’s laws. It can be directly applied to resistive memory devices like PCM and MRAM, which follow similar analog computing paradigms. For non-resistive devices such as FeFETs, although the underlying switching mechanism is based on threshold voltage modulation, the core assumptions of the model remain valid. These devices can be treated as special cases—such as binary-state (1-bit) systems—within the same analytical framework. Therefore, our method retains its applicability and provides meaningful insights into precision degradation and design constraints across a wide range of NVM-based MVM architectures.
3. Information Loss in Non-Ideal MVM
Equation (3) discloses the constraints for producing distinguishable MVM output levels. The increase in memory precision and row parallelism would eventually cause overlaps between neighboring MVM result levels, for which the use of ADC according to Equation (1) becomes invalid. To obtain reliable, error-free ADC outputs, the bit precision of the ADC can be reduced to increase the margin between neighboring levels [40]. However, this approach is mostly empirical and lacks theoretical investigation. To measure the precision loss in non-ideal MVM caused by nonideality distribution, we adopt information capacity to quantify the degradation in computational precision by utilizing the concept of information entropy (a measure of the uncertainty or randomness in the information theory). It should also help gain a deeper understanding of how non-ideality and computational errors impact the overall performance of the system. Previous works [41] have modeled the storage problem in memory devices as a communication problem, in which storage capacity is represented by information capacity. Similarly, the MVM process can also be interpreted within the framework of information theory, where the precision of computation and the system’s ability to handle and transmit information are closely related to information capacity.
We performed a series of numerical simulations to comprehensively evaluate the effects of the input bits, bit precision and row parallelism under practical conditions. The parameters are presented in Table 1. The input voltage V and conductance G were all set to [1, 2, 3] bits, with their respective non-ideality distributions ranging from [0.1, 0.3, 0.5]% and [3, 5, 10]% based on data disclosed in the literature [32,42]. In addition, the number of rows (NROW) considered across the range [4, 8, 16, 32, 64]. The information capacity is defined as
where P(i) represents the probability of each possible level. Considering that ADCs design typically assumes a uniform quantization of the analog MVM results over the full dynamic range, we described the MVM result levels as being uniformly distributed (namely P(i) = 1/NVNGNROW). There is COUT = −ΣP(i)log2P(i) = log2NVNGNROW = CV + CG + log2NROW, that is, Equation (4) is reduced to Equation (1). In the non-ideal case, the probability P(i) associated with different current levels will be different. Additionally, each current level transitions from a discrete level to a continuous distribution (corresponding to i changing from a positive integer to a continuous variable).
COUT = −ΣP(i)log2P(i),

Table 1.
Model parameters, including input bits, bit precision, and row parallelism.
Figure 3a illustrates the case of CV = CG = 2 Bits, with its parameters specified in the graph. Specifically, by running 106 times simulations, we obtained the occurrence probability of each individual level, corresponding to the ideal output case. Based on these ideal individual levels, non-idealities were introduced to each input to generate the normal distribution for each level. It is evident that the distribution of each state inevitably has some overlap. Moreover, since the occurrence of the minimum or maximum levels is relatively infrequent, the overall output distribution closely approximates a normal distribution. There are some works [31,40] that use lower-precision ADCs and discard quantization for these extreme cases, with results showing that the overall output is only minorly affected. However, for reliable high-precision MVM computation, all output levels should be covered in the consideration. Therefore, each level is normalized so that the area under each curve is the same (Figure 3b). Because the distribution is wider when the current output is larger, the corresponding peak value is lower.
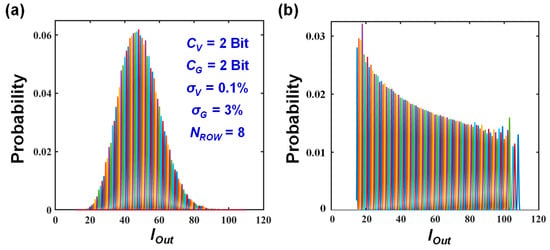
Figure 3.
Output distribution obtained from repeated MVM operations, with the corresponding parameter settings indicated in the graph. (a) Unnormalized and (b) normalized.
Subsequently, the output capacity COUT is computed using Equation (4) to quantitatively assess the output precision loss. As shown in Figure 4a, the yellow plane represents the ideal precision, CIDEAL, under ideal conditions as calculated by Equation (1), while the red polyline connects the actual capacity values obtained under various parameter settings, illustrating how precision changes as those parameters vary. It can be seen that as σG increases, COUT decreases rapidly. Although raising NROW can boost COUT, it eventually saturates and diverges from CIDEAL. We also examined the impact of σV on output precision and found that, within a hypothetical range, it has a virtually negligible effect on COUT. Figure 4b shows the precision loss resulting from increased σG and NROW, which clearly demonstrates the limits on bit precision and row parallelism required to prevent precision degradation.
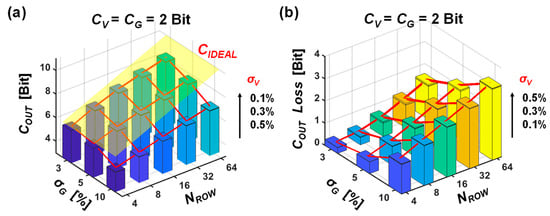
Figure 4.
Numerical simulation of MVM output precision using information theory capacity. (a) Example of CV = CG = 2 Bits, where COUT represents the normalized information capacity, depicted by the red line, and CIDEAL denotes the theoretical accuracy, represented by the yellow plane. (b) Illustrative example of precision loss caused by row parallelism and conductance distribution.
4. Discussion
We have systematically investigated output precision under different row parallelism settings and non-ideal input distributions (both voltage and conductance). As shown in Figure 5, when non-ideal factors are small, increasing input precision and row parallelism improves output precision almost described by Equation (1). However, as the variances of the voltage and conductance distributions increase, the output precision measured via information theory capacity rapidly decreases and eventually saturates, highlighting inherent constraints on bit precision and row parallelism for any input combination.
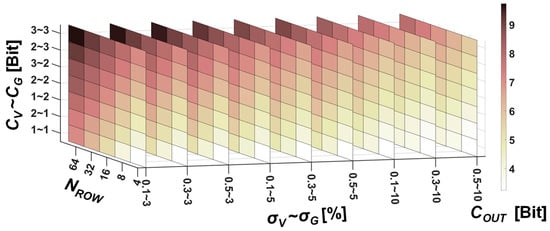
Figure 5.
Illustration of the combined effect of bit numbers, bit precision, and row parallelism on output precision for normalized inputs.
While the above results are obtained with the consideration of normalizing output levels, we have also considered the scenario with unnormalized levels (Figure 6), which show that the overall capacity is significantly reduced, mainly due to potential inconsistencies between states. In other words, the probability of an extreme value (either large or small) appearing in the output state is extremely low, leading to a reduction in information content and a corresponding decrease in capacity contribution. In addition, the overall normal distribution will also mask the capacity loss caused by other factors, making the impact of the bit numbers or fluctuations in conductance and voltage distribution less apparent.
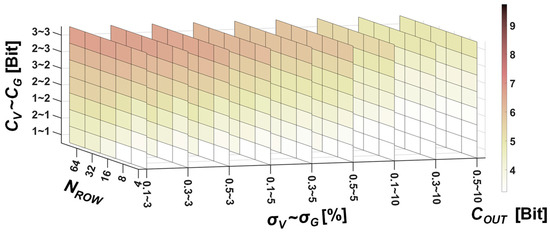
Figure 6.
Illustration of the combined effect of bit numbers, bit precision, and row parallelism on output precision for unnormalized inputs.
Finally, considering that the assumption of normal distribution may not hold under closed-loop write–verify methods, where the resulting conductance distributions tend to deviate from normality, we have extended our analysis by introducing two additional models: (1) a simple uniform distribution model and (2) a mixed distribution model that combines a weighted superposition of uniform and normal distributions. Since repeated multiplication and addition operations on uniform distributions also broaden their effective width, the maximum output level remains a valid representation of the worst-case scenario. As a result, the analytical and simulation methodologies presented previously are still applicable. We performed numerical simulations to evaluate whether all output states could be reliably distinguished. The results are shown in Figure 7, formatted consistently with Figure 2b. Specifically, Figure 7a presents the uniform distribution case G~U(μG − σG, μG + σG), while Figure 7b shows a representative case of the mixed model (G~αU(μG − σG, μG + σG) + βN(μG, σG2), with α = 2β = 2/3). Compared with the baseline results under the normal distribution in Figure 2b, the impact of σG is more moderate in the uniform and mixed distribution models. These findings indicate that using a write–verify programming scheme can substantially enhance row parallelism and increase the bit precision achievable per RRAM cell.
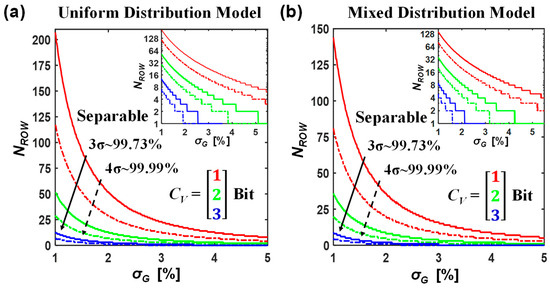
Figure 7.
The limiting relationship between bit precision and row parallelism based on (a) a uniform distribution model and (b) a mixed distribution model.
5. Conclusions
In this work, we have investigated the sensitivity of analog-domain MVM computation to input voltage bit precision, device conductance precision, and row parallelism—all of which contribute to output precision loss. Building on this, we conducted a comprehensive analysis to examine how bit precision and row parallelism influence computational accuracy. Furthermore, we expanded the scope of our model by discussing its applicability to both resistive (e.g., PCM, MRAM) and non-resistive (e.g., FeFET) memory technologies. By introducing a mixed uniform–normal distribution model under write–verify programming conditions, we significantly enhanced the generalizability and robustness of our framework for diverse application scenarios. We also applied information-theoretic concepts to quantitatively evaluate output precision degradation. The results of our analysis establish rigorous fabrication requirements and highlight the need for high-precision write–verify schemes across various emerging memory technologies. Additionally, our findings emphasize the importance of high-resolution ADC design in analog computing systems and provide theoretical guidance for determining ADC quantization margins—ultimately contributing to the design and optimization of precise, efficient, and practically viable MVM systems.
Author Contributions
Conceptualization, Y.L. and Z.S.; methodology, Y.L.; software, Y.L. and S.W.; validation, Y.L., S.W. and Z.S.; formal analysis, Y.L.; investigation, Y.L.; resources, Y.L. and Z.S.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Z.S.; visualization, Y.L. and S.W.; supervision, Z.S.; project administration, Z.S.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Beijing Natural Science Foundation (4252016), National Key R&D Program of China (2020YFB2206001), and the 111 Project (B18001).
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ielmini, D.; Wong, H.-S.P. In-Memory Computing with Resistive Switching Devices. Nat. Electron. 2018, 1, 333–343. [Google Scholar] [CrossRef]
- Rao, M.; Tang, H.; Wu, J.; Song, W.; Zhang, M.; Yin, W.; Zhuo, Y.; Kiani, F.; Chen, B.; Jiang, X.; et al. Thousands of Conductance Levels in Memristors Integrated on CMOS. Nature 2023, 615, 823–829. [Google Scholar] [CrossRef]
- Borghetti, J.; Snider, G.S.; Kuekes, P.J.; Yang, J.J.; Stewart, D.R.; Williams, R.S. “Memristive” Switches Enable “Stateful” Logic Operations via Material Implication. Nature 2010, 464, 873–876. [Google Scholar] [CrossRef] [PubMed]
- Ielmini, D. Resistive Switching Memories Based on Metal Oxides: Mechanisms, Reliability and Scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Pan, F.; Gao, S.; Chen, C.; Song, C.; Zeng, F. Recent Progress in Resistive Random Access Memories: Materials, Switching Mechanisms, and Performance. Mater. Sci. Eng. R Rep. 2014, 83, 1–59. [Google Scholar] [CrossRef]
- Sun, Z.; Kvatinsky, S.; Si, X.; Mehonic, A.; Cai, Y.; Huang, R. A Full Spectrum of Computing-in-Memory Technologies. Nat. Electron. 2023, 6, 823–835. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Ambrosi, E.; Bricalli, A.; Wang, W.; Ielmini, D. Solving Matrix Equations in One Step with Cross-Point Resistive Arrays. Proc. Natl. Acad. Sci. USA 2019, 116, 4123–4128. [Google Scholar] [CrossRef]
- Wang, S.; Luo, Y.; Zuo, P.; Pan, L.; Li, Y.; Sun, Z. In-Memory Analog Solution of Compressed Sensing Recovery in One Step. Sci. Adv. 2023, 9, eadj2908. [Google Scholar] [CrossRef]
- Mannocci, P.; Farronato, M.; Lepri, N.; Cattaneo, L.; Glukhov, A.; Sun, Z.; Ielmini, D. In-Memory Computing with Emerging Memory Devices: Status and Outlook. APL Mach. Learn. 2023, 1, 010902. [Google Scholar] [CrossRef]
- Yu, S.; Shim, W.; Peng, X.; Luo, Y. RRAM for Compute-in-Memory: From Inference to Training. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2753–2765. [Google Scholar] [CrossRef]
- Moon, K.; Lim, S.; Park, J.; Sung, C.; Oh, S.; Woo, J.; Lee, J.; Hwang, H. RRAM-Based Synapse Devices for Neuromorphic Systems. Faraday Discuss. 2019, 213, 421–451. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.; Spetalnick, S.D.; Crafton, B.; Khwa, W.-S.; Chih, Y.-D.; Chang, M.-F.; Raychowdhury, A. A 40nm 60.64TOPS/W ECC-Capable Compute-in-Memory/Digital 2.25MB/768KB RRAM/SRAM System with Embedded Cortex M3 Microprocessor for Edge Recommendation Systems. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 1–3. [Google Scholar]
- Zhang, Y.; Huang, P.; Gao, B.; Kang, J.; Wu, H. Oxide-Based Filamentary RRAM for Deep Learning. J. Phys. D Appl. Phys. 2021, 54, 083002. [Google Scholar] [CrossRef]
- Yin, S.; Kim, Y.; Han, X.; Barnaby, H.; Yu, S.; Luo, Y.; He, W.; Sun, X.; Kim, J.-J.; Seo, J.-S. Monolithically Integrated RRAM- and CMOS-Based in-Memory Computing Optimizations for Efficient Deep Learning. IEEE Micro 2019, 39, 54–63. [Google Scholar] [CrossRef]
- Hsieh, E.R.; Zheng, X.; Nelson, M.; Le, B.Q.; Wong, H.-S.P.; Mitra, S.; Wong, S.; Giordano, M.; Hodson, B.; Levy, A.; et al. High-Density Multiple Bits-per-Cell 1T4R RRAM Array with Gradual SET/RESET and Its Effectiveness for Deep Learning. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 35.6.1–35.6.4. [Google Scholar]
- Zidan, M.A.; Jeong, Y.; Lee, J.; Chen, B.; Huang, S.; Kushner, M.J.; Lu, W.D. A General Memristor-Based Partial Differential Equation Solver. Nat. Electron. 2018, 1, 411–420. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, B.; Liu, J.; Sun, Z.; Hu, H.; Zhang, J.; Zhan, X.; Chen, J. Design-Technology Co-Optimizations (DTCO) for General-Purpose Computing in-Memory Based on 55nm NOR Flash Technology. In Proceedings of the 2021 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–16 December 2021; pp. 12.1.1–12.1.4. [Google Scholar]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An Overview of Massive MIMO: Benefits and Challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Song, W.; Rao, M.; Li, Y.; Li, C.; Zhuo, Y.; Cai, F.; Wu, M.; Yin, W.; Li, Z.; Wei, Q.; et al. Programming Memristor Arrays with Arbitrarily High Precision for Analog Computing. Science 2024, 383, 903–910. [Google Scholar] [CrossRef]
- Xiao, T.P.; Feinberg, B.; Bennett, C.H.; Prabhakar, V.; Saxena, P.; Agrawal, V.; Agarwal, S.; Marinella, M.J. On the Accuracy of Analog Neural Network Inference Accelerators. IEEE Circuits Syst. Mag. 2023, 22, 26–48. [Google Scholar] [CrossRef]
- Zuo, P.; Sun, Z.; Huang, R. Extremely-Fast, Energy-Efficient Massive MIMO Precoding with Analog RRAM Matrix Computing. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2335–2339. [Google Scholar] [CrossRef]
- Lepri, N.; Glukhov, A.; Ielmini, D. Mitigating Read-Program Variation and IR Drop by Circuit Architecture in RRAM-Based Neural Network Accelerators. In Proceedings of the 2022 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 27–31 March 2022; pp. 3C.2-1–3C.2-6. [Google Scholar]
- Lee, S.; Jung, G.; Fouda, M.E.; Lee, J.; Eltawil, A.; Kurdahi, F. Learning to Predict IR Drop with Effective Training for ReRAM-Based Neural Network Hardware. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Zanotti, T.; Zambelli, C.; Puglisi, F.M.; Milo, V.; Perez, E.; Mahadevaiah, M.K.; Ossorio, O.G.; Wenger, C.; Pavan, P.; Olivo, P.; et al. Reliability of Logic-in-Memory Circuits in Resistive Memory Arrays. IEEE Trans. Electron Devices 2020, 67, 4611–4615. [Google Scholar] [CrossRef]
- Perez, E.; Maldonado, D.; Perez-Bosch Quesada, E.; Mahadevaiah, M.K.; Jimenez-Molinos, F.; Wenger, C.; Roldan, J.B. Parameter Extraction Methods for Assessing Device-to-Device and Cycle-to-Cycle Variability of Memristive Devices at Wafer Scale. IEEE Trans. Electron Devices 2023, 70, 360–365. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Wang, Z.-Q.; Sills, S.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Understanding Pulsed-Cycling Variability and Endurance in HfOx RRAM. In Proceedings of the 2015 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015; pp. 5B.3.1–5B.3.6. [Google Scholar]
- Luo, Y.; Han, X.; Ye, Z.; Barnaby, H.; Seo, J.-S.; Yu, S. Array-Level Programming of 3-Bit per Cell Resistive Memory and Its Application for Deep Neural Network Inference. IEEE Trans. Electron Devices 2020, 67, 4621–4625. [Google Scholar] [CrossRef]
- Lele, A.S.; Zhang, B.; Khwa, W.-S.; Chang, M.-F. Assessing Design Space for the Device-Circuit Codesign of Nonvolatile Memory-Based Compute-in-Memory Accelerators. Nano Lett. 2025, 25, 1243–1249. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, B.; Wang, S.; Ipek, E. Making Memristive Neural Network Accelerators Reliable. In Proceedings of the 2018 IEEE International Symposium on High Performance Computer Architecture (HPCA), Vienna, Austria, 24–28 February 2018; pp. 52–65. [Google Scholar]
- Feinberg, B.; Vengalam, U.K.R.; Whitehair, N.; Wang, S.; Ipek, E. Enabling Scientific Computing on Memristive Accelerators. In Proceedings of the 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 1–6 June 2018; pp. 367–382. [Google Scholar]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A Convolutional Neural Network Accelerator with in-Situ Analog Arithmetic in Crossbars. Comput. Archit. News 2016, 44, 14–26. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Sun, Z. The Maximum Storage Capacity of Open-Loop Written RRAM Is around 4 Bits. In Proceedings of the 2024 IEEE 17th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Zhuhai, China, 22–25 October 2024; pp. 1–3. [Google Scholar]
- Li, X.; Gao, B.; Qin, Q.; Yao, P.; Li, J.; Zhao, H.; Liu, C.; Zhang, Q.; Hao, Z.; Li, Y.; et al. Federated Learning Using a Memristor Compute-in-Memory Chip with in Situ Physical Unclonable Function and True Random Number Generator. Nat. Electron. 2025, 1–11. [Google Scholar] [CrossRef]
- Zanotti, T.; Puglisi, F.M.; Pavan, P. Low-Bit Precision Neural Network Architecture with High Immunity to Variability and Random Telegraph Noise Based on Resistive Memories. In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 21–25 March 2021; pp. 1–6. [Google Scholar]
- Deaville, P.; Zhang, B.; Verma, N. A 22nm 128-Kb MRAM Row/Column-Parallel in-Memory Computing Macro with Memory-Resistance Boosting and Multi-Column ADC Readout. In Proceedings of the 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 12–17 June 2022; pp. 268–269. [Google Scholar]
- Khaddam-Aljameh, R.; Stanisavljevic, M.; Fornt Mas, J.; Karunaratne, G.; Braendli, M.; Liu, F.; Singh, A.; Muller, S.M.; Egger, U.; Petropoulos, A.; et al. HERMES Core—A 14nm CMOS and PCM-Based In-Memory Compute Core Using an Array of 300ps/LSB Linearized CCO-Based ADCs and Local Digital Processing. In Proceedings of the 2021 Symposium on VLSI Circuits, Kyoto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar]
- Lu, Y.; Li, X.; Yan, B.; Yan, L.; Zhang, T.; Song, Z.; Huang, R.; Yang, Y. In-Memory Realization of Eligibility Traces Based on Conductance Drift of Phase Change Memory for Energy-Efficient Reinforcement Learning. Adv. Mater. 2022, 34, e2107811. [Google Scholar] [CrossRef]
- Jooq, M.K.Q.; Moaiyeri, M.H.; Tamersit, K. A New Design Paradigm for Auto-Nonvolatile Ternary SRAMs Using Ferroelectric CNTFETs: From Device to Array Architecture. IEEE Trans. Electron Devices 2022, 69, 6113–6120. [Google Scholar] [CrossRef]
- Saito, D.; Kobayashi, T.; Koga, H.; Ronchi, N.; Banerjee, K.; Shuto, Y.; Okuno, J.; Konishi, K.; Di Piazza, L.; Mallik, A.; et al. Analog In-Memory Computing in FeFET-Based 1T1R Array for Edge AI Applications. In Proceedings of the 2021 Symposium on VLSI Technology, Kyoto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar]
- Wen, T.-H.; Hung, J.-M.; Huang, W.-H.; Jhang, C.-J.; Lo, Y.-C.; Hsu, H.-H.; Ke, Z.-E.; Chen, Y.-C.; Chin, Y.-H.; Su, C.-I.; et al. Fusion of Memristor and Digital Compute-in-Memory Processing for Energy-Efficient Edge Computing. Science 2024, 384, 325–332. [Google Scholar] [CrossRef]
- Zarcone, R.V.; Engel, J.H.; Burc Eryilmaz, S.; Wan, W.; Kim, S.; BrightSky, M.; Lam, C.; Lung, H.-L.; Olshausen, B.A.; Philip Wong, H.-S. Analog Coding in Emerging Memory Systems. Sci. Rep. 2020, 10, 6831. [Google Scholar] [CrossRef]
- Verreault, A.; Cicek, P.-V.; Robichaud, A. Oversampling ADC: A Review of Recent Design Trends. IEEE Access 2024, 12, 121753–121779. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).