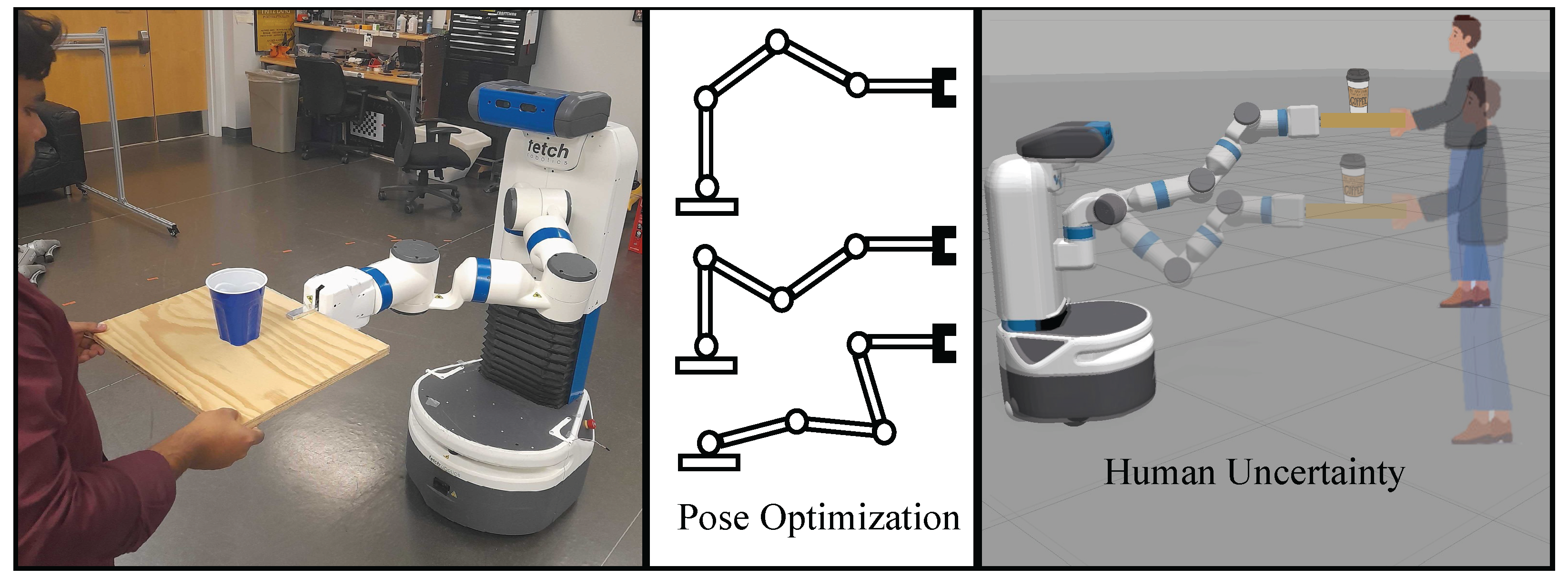
DARC: Disturbance-Aware Redundant Control for Human–Robot Co-Transportation
Abstract
1. Introduction
- We formulate a high-level Model Predictive Control (MPC) planner problem that incorporates disturbances along with a low-level pose optimization mechanism and the robot’s whole-body kinematics. We propose a two-step iterative optimization approach to holistically solve the high-level and low-level problems.
- For the high-level MPC problem, we estimate control costs under disturbances and generate optimal control inputs. The initial state of the MPC controller depends on the low-level pose optimization.
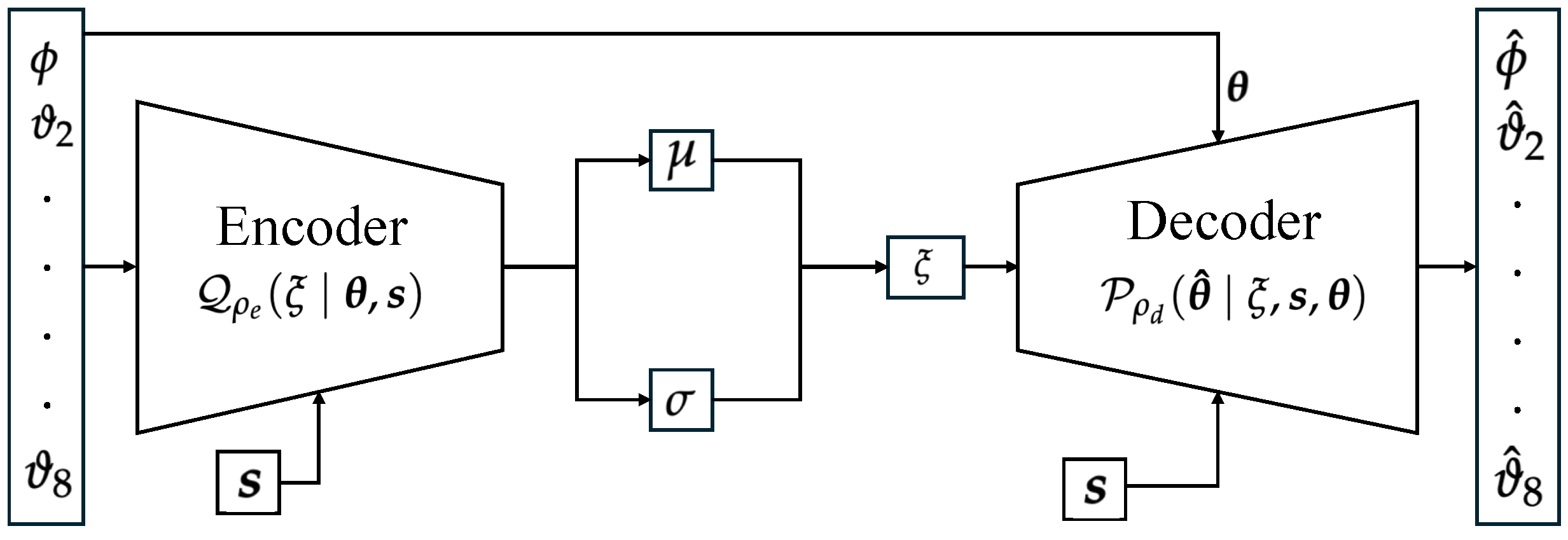
- For the low-level pose optimization, we optimize the robot’s pose selected from a joint configuration set generated using Conditional Variational Autoencoder (CVAE). The selection criteria are informed by the expected cost of the high-level MPC.
- We provide theoretical derivations and simulated experiments with a Fetch mobile manipulator to validate the DARC framework. Quantitative comparisons highlight the advantages of our method over different baselines.
2. Literature Review
3. Preliminaries and Problem Formulation
3.1. Trajectory with External Human Disturbances
3.2. End-Effector Kinematics
3.3. MPC-Based Tracking with Pose Optimization
4. Main Result
4.1. Optimal Control Law:
- We first generate a set of candidate joint angle configurations around . Then, for each candidate pose in this set, we compute the sequence of optimal control inputs and associated cost-to-go.
- We compare the estimated cost-to-go for each configuration in the candidate set and choose the one that yields the minimum cost-to-go.
| Algorithm 1 Disturbance-Aware MPC Tracking with Pose Optimization |
| Require: Reference trajectory , disturbance parameters , initial pose Ensure: Sequence of optimal inputs and optimized pose control
|
4.2. Generation of Candidate Set with Conditional Variational Autoencoder (CVAE):
| Algorithm 2 Training Algorithm for Conditional Variational Autoencoder (CVAE) |
| Require: Joint angle data , end-effector pose data , initial configurations , learning rate , weight coefficients , , number of epochs E, and batch size . Ensure: Trained CVAE model parameters.
|
5. Experiments
5.1. Evaluation of CVAE Method
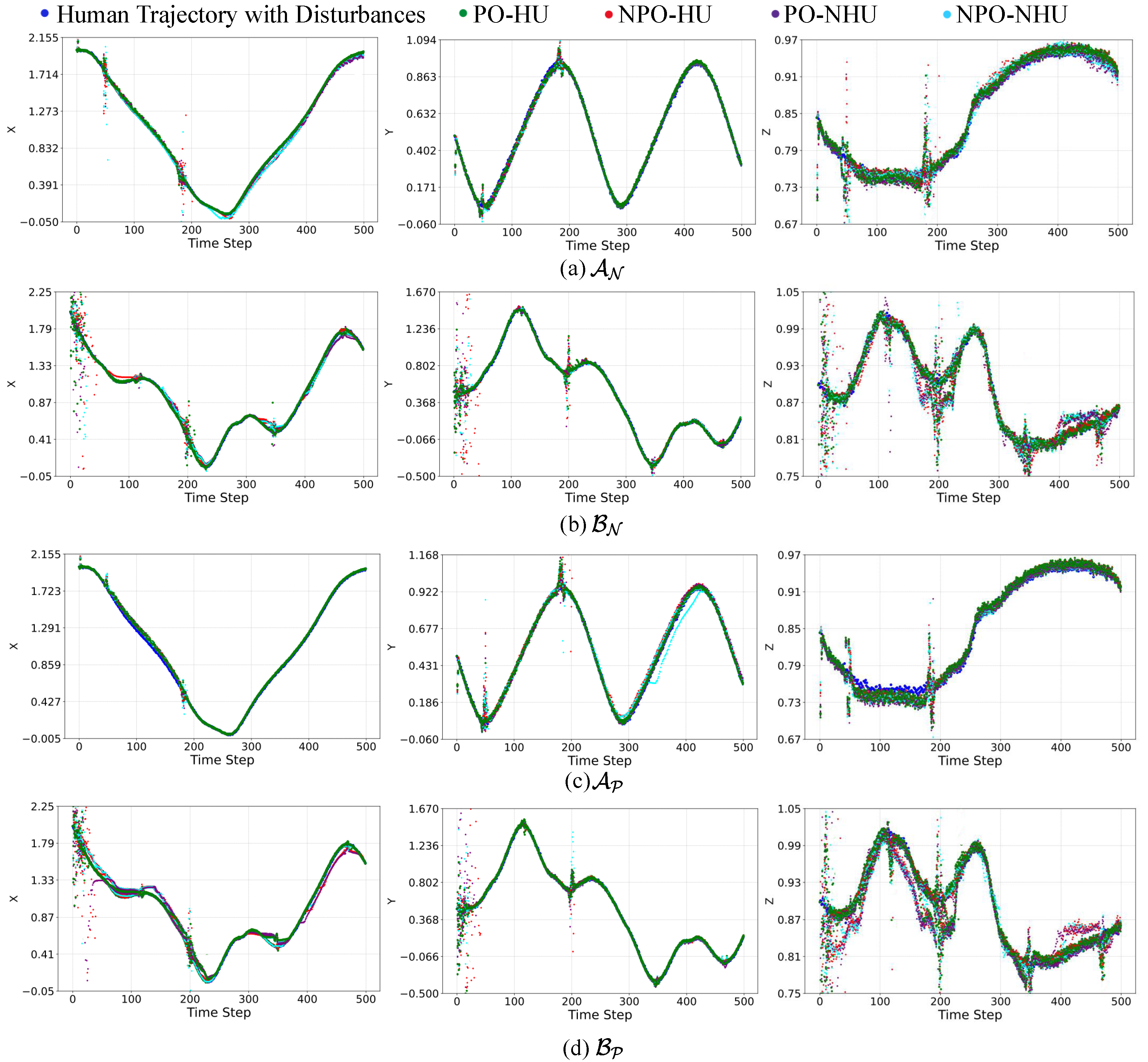
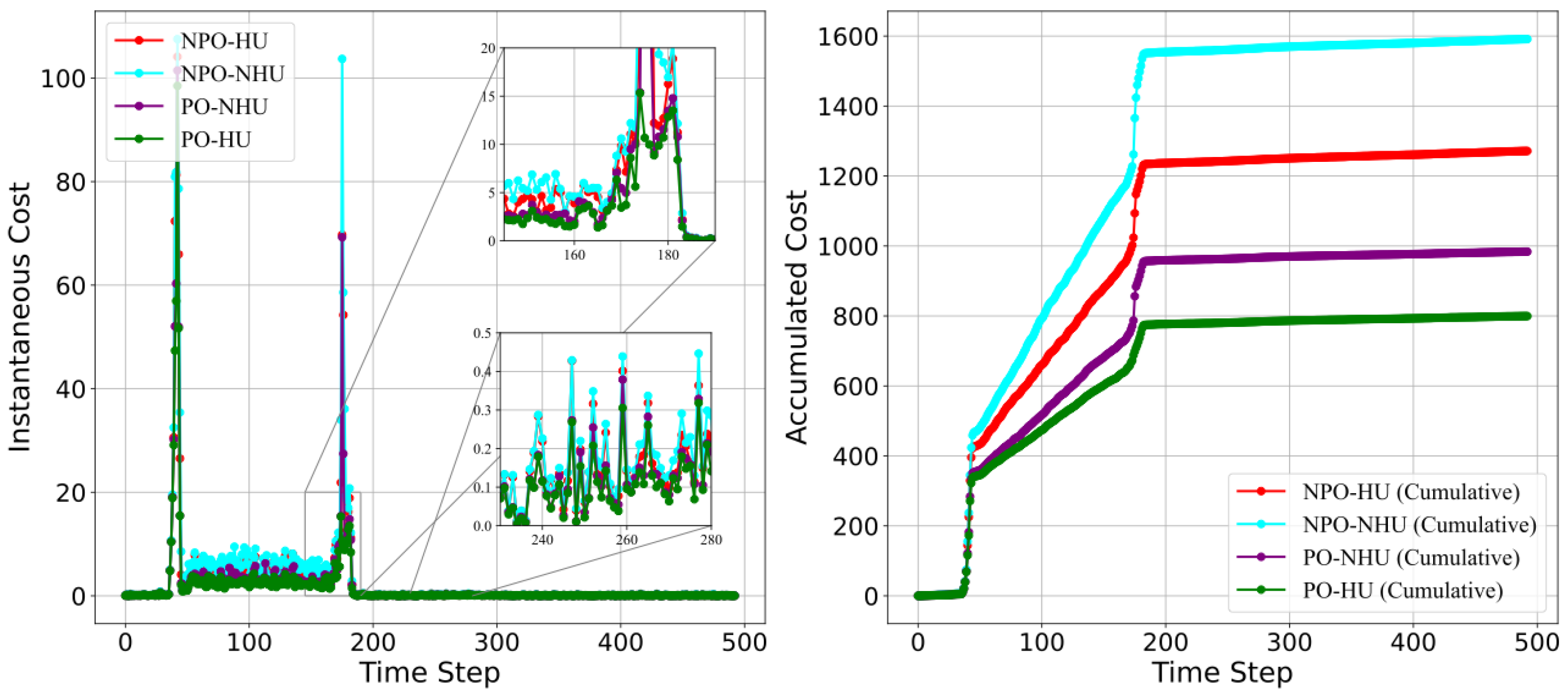
5.2. Evaluation of DARC Framework
5.3. Hardware Demonstration
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Prewett, M.S.; Johnson, R.C.; Saboe, K.N.; Elliott, L.R.; Coovert, M.D. Managing workload in human–robot interaction: A review of empirical studies. Comput. Hum. Behav. 2010, 26, 840–856. [Google Scholar] [CrossRef]
- Liu, L.; Schoen, A.J.; Henrichs, C.; Li, J.; Mutlu, B.; Zhang, Y.; Radwin, R.G. Human robot collaboration for enhancing work activities. Hum. Factors 2024, 66, 158–179. [Google Scholar] [CrossRef] [PubMed]
- Bischoff, R.; Kurth, J.; Schreiber, G.; Koeppe, R.; Albu-Schäffer, A.; Beyer, A.; Eiberger, O.; Haddadin, S.; Stemmer, A.; Grunwald, G.; et al. The KUKA-DLR Lightweight Robot arm—A new reference platform for robotics research and manufacturing. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; VDE: Berlin, Germany; pp. 1–8. [Google Scholar]
- Pedrocchi, N.; Vicentini, F.; Matteo, M.; Tosatti, L.M. Safe human-robot cooperation in an industrial environment. Int. J. Adv. Robot. Syst. 2013, 10, 27. [Google Scholar] [CrossRef]
- Broekens, J.; Heerink, M.; Rosendal, H. Assistive social robots in elderly care: A review. Gerontechnology 2009, 8, 94–103. [Google Scholar] [CrossRef]
- Cai, S.; Ram, A.; Gou, Z.; Shaikh, M.A.W.; Chen, Y.A.; Wan, Y.; Hara, K.; Zhao, S.; Hsu, D. Navigating real-world challenges: A quadruped robot guiding system for visually impaired people in diverse environments. In Proceedings of the 2024 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 11–16 May 2024; pp. 1–18. [Google Scholar]
- Ajoudani, A.; Zanchettin, A.M.; Ivaldi, S.; Albu-Schäffer, A.; Kosuge, K.; Khatib, O. Progress and prospects of the human–robot collaboration. Auton. Robot. 2018, 42, 957–975. [Google Scholar] [CrossRef]
- Sharkawy, A.N.; Koustoumpardis, P.N. Human–robot interaction: A review and analysis on variable admittance control, safety, and perspectives. Machines 2022, 10, 591. [Google Scholar] [CrossRef]
- Hayes, B.; Scassellati, B. Challenges in shared-environment human-robot collaboration. Learning 2013, 8. [Google Scholar]
- Brosque, C.; Galbally, E.; Khatib, O.; Fischer, M. Human-robot collaboration in construction: Opportunities and challenges. In Proceedings of the 2020 IEEE International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26–28 June 2020; pp. 1–8. [Google Scholar]
- Cursi, F.; Modugno, V.; Lanari, L.; Oriolo, G.; Kormushev, P. Bayesian neural network modeling and hierarchical MPC for a tendon-driven surgical robot with uncertainty minimization. IEEE Robot. Autom. Lett. 2021, 6, 2642–2649. [Google Scholar] [CrossRef]
- Mahmud, A.J.; Li, W.; Wang, X. Mutual Adaptation in Human-Robot Co-Transportation with Human Preference Uncertainty. arXiv 2025, arXiv:2503.08895. [Google Scholar]
- Haninger, K.; Hegeler, C.; Peternel, L. Model predictive control with gaussian processes for flexible multi-modal physical human robot interaction. In Proceedings of the 2022 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 6948–6955. [Google Scholar]
- Donelan, P. Singularities of robot manipulators. In Singularity Theory: Dedicated to Jean-Paul Brasselet on His 60th Birthday; World Scientific: Singapore, 2007; pp. 189–217. [Google Scholar]
- Chiaverini, S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators. IEEE Trans. Robot. Autom. 1997, 13, 398–410. [Google Scholar] [CrossRef]
- Chiacchio, P.; Chiaverini, S.; Sciavicco, L.; Siciliano, B. Closed-loop inverse kinematics schemes for constrained redundant manipulators with task space augmentation and task priority strategy. Int. J. Robot. Res. 1991, 10, 410–425. [Google Scholar] [CrossRef]
- Wittmann, J.; Kist, A.; Rixen, D.J. Real-Time Predictive Kinematics Control of Redundancy: A Benchmark of Optimal Control Approaches. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 11759–11766. [Google Scholar]
- Faroni, M.; Beschi, M.; Tosatti, L.M.; Visioli, A. A predictive approach to redundancy resolution for robot manipulators. IFAC-Pap. Online 2017, 50, 8975–8980. [Google Scholar] [CrossRef]
- Erhart, S.; Sieber, D.; Hirche, S. An impedance-based control architecture for multi-robot cooperative dual-arm mobile manipulation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 315–322. [Google Scholar]
- Mahmud, A.J.; Raj, A.H.; Nguyen, D.M.; Xiao, X.; Wang, X. Human-Robot Co-Transportation with Human Uncertainty-Aware MPC and Pose Optimization. arXiv 2024, arXiv:2404.00514. [Google Scholar]
- Aaltonen, I.; Salmi, T.; Marstio, I. Refining levels of collaboration to support the design and evaluation of human-robot interaction in the manufacturing industry. Procedia CIRP 2018, 72, 93–98. [Google Scholar] [CrossRef]
- Magrini, E.; Ferraguti, F.; Ronga, A.J.; Pini, F.; De Luca, A.; Leali, F. Human-robot coexistence and interaction in open industrial cells. Robot. Comput.-Integr. Manuf. 2020, 61, 101846. [Google Scholar] [CrossRef]
- Roveda, L.; Maskani, J.; Franceschi, P.; Abdi, A.; Braghin, F.; Molinari Tosatti, L.; Pedrocchi, N. Model-based reinforcement learning variable impedance control for human-robot collaboration. J. Intell. Robot. Syst. 2020, 100, 417–433. [Google Scholar] [CrossRef]
- Peternel, L.; Tsagarakis, N.; Caldwell, D.; Ajoudani, A. Robot adaptation to human physical fatigue in human–robot co-manipulation. Auton. Robot. 2018, 42, 1011–1021. [Google Scholar] [CrossRef]
- Mujica, M.; Crespo, M.; Benoussaad, M.; Junco, S.; Fourquet, J.Y. Robust variable admittance control for human–robot co-manipulation of objects with unknown load. Robot. Comput.-Integr. Manuf. 2023, 79, 102408. [Google Scholar] [CrossRef]
- Zhang, Y.; Pezzato, C.; Trevisan, E.; Salmi, C.; Corbato, C.H.; Alonso-Mora, J. Multi-Modal MPPI and Active Inference for Reactive Task and Motion Planning. IEEE Robot. Autom. Lett. 2024, 9, 7461–7468. [Google Scholar] [CrossRef]
- Bhardwaj, M.; Sundaralingam, B.; Mousavian, A.; Ratliff, N.D.; Fox, D.; Ramos, F.; Boots, B. Storm: An integrated framework for fast joint-space model-predictive control for reactive manipulation. In Proceedings of the Conference on Robot Learning, Auckland, New Zealand, 14–18 December 2022; pp. 750–759. [Google Scholar]
- De Schepper, D.; Schouterden, G.; Kellens, K.; Demeester, E. Human-robot mobile co-manipulation of flexible objects by fusing wrench and skeleton tracking data. Int. J. Comput. Integr. Manuf. 2023, 36, 30–50. [Google Scholar] [CrossRef]
- Sirintuna, D.; Giammarino, A.; Ajoudani, A. An Object Deformation-Agnostic Framework for Human–Robot Collaborative Transportation. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1986–1999. [Google Scholar] [CrossRef]
- Sirintuna, D.; Ozdamar, I.; Gandarias, J.M.; Ajoudani, A. Enhancing Human-Robot Collaboration Transportation through Obstacle-Aware Vibrotactile Feedback. arXiv 2023, arXiv:2302.02881. [Google Scholar]
- Bussy, A.; Gergondet, P.; Kheddar, A.; Keith, F.; Crosnier, A. Proactive behavior of a humanoid robot in a haptic transportation task with a human partner. In Proceedings of the 2012 IEEE RO-MAN: The 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 962–967. [Google Scholar]
- Agravante, D.J.; Cherubini, A.; Sherikov, A.; Wieber, P.B.; Kheddar, A. Human-humanoid collaborative carrying. IEEE Trans. Robot. 2019, 35, 833–846. [Google Scholar] [CrossRef]
- Berger, E.; Vogt, D.; Haji-Ghassemi, N.; Jung, B.; Amor, H.B. Inferring guidance information in cooperative human-robot tasks. In Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, GA, USA, 15–17 October 2013; pp. 124–129. [Google Scholar]
- Zanon, M.; Gros, S. Safe reinforcement learning using robust MPC. IEEE Trans. Autom. Control 2020, 66, 3638–3652. [Google Scholar] [CrossRef]
- Saltık, M.B.; Özkan, L.; Ludlage, J.H.; Weiland, S.; Van den Hof, P.M. An outlook on robust model predictive control algorithms: Reflections on performance and computational aspects. J. Process Control 2018, 61, 77–102. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Scherer, C.W. Control of Linear Parameter Varying Systems with Applications; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Patel, S.; Sobh, T. Manipulator performance measures-a comprehensive literature survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of robotic mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Cheong, H.; Ebrahimi, M.; Duggan, T. Optimal design of continuum robots with reachability constraints. IEEE Robot. Autom. Lett. 2021, 6, 3902–3909. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L.; Gao, L. Minimizing energy consumption for robot arm movement. Procedia Cirp 2014, 25, 400–405. [Google Scholar] [CrossRef]
- Zhang, M.M.; Atanasov, N.; Daniilidis, K. Active end-effector pose selection for tactile object recognition through monte carlo tree search. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3258–3265. [Google Scholar]
- Wang, J.; Zhang, T.; Wang, Y.; Luo, D. Optimizing Robot Arm Reaching Ability with Different Joints Functionality. In Proceedings of the 2023 32nd IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), Busan, Republic of Korea, 28–31 August 2023; pp. 1778–1785. [Google Scholar]
- Schneider, U.; Posada, J.R.D.; Verl, A. Automatic pose optimization for robotic processes. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2054–2059. [Google Scholar]
- George Thuruthel, T.; Ansari, Y.; Falotico, E.; Laschi, C. Control strategies for soft robotic manipulators: A survey. Soft Robot. 2018, 5, 149–163. [Google Scholar] [CrossRef]
- Kumar, V.; Hoeller, D.; Sundaralingam, B.; Tremblay, J.; Birchfield, S. Joint space control via deep reinforcement learning. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3619–3626. [Google Scholar]
- Hua, X.; Wang, G.; Xu, J.; Chen, K. Reinforcement learning-based collision-free path planner for redundant robot in narrow duct. J. Intell. Manuf. 2021, 32, 471–482. [Google Scholar] [CrossRef]
- Shen, Y.; Jia, Q.; Huang, Z.; Wang, R.; Fei, J.; Chen, G. Reinforcement learning-based reactive obstacle avoidance method for redundant manipulators. Entropy 2022, 24, 279. [Google Scholar] [CrossRef] [PubMed]
- Soleimani Amiri, M.; Ramli, R. Intelligent trajectory tracking behavior of a multi-joint robotic arm via genetic–swarm optimization for the inverse kinematic solution. Sensors 2021, 21, 3171. [Google Scholar] [CrossRef] [PubMed]
- Parque, V.; Miyashita, T. Smooth curve fitting of mobile robot trajectories using differential evolution. IEEE Access 2020, 8, 82855–82866. [Google Scholar] [CrossRef]
- Sun, L.; Zhan, W.; Hu, Y.; Tomizuka, M. Interpretable modelling of driving behaviors in interactive driving scenarios based on cumulative prospect theory. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 4329–4335. [Google Scholar]
- Zhang, J.; Liu, H.; Chang, Q.; Wang, L.; Gao, R.X. Recurrent neural network for motion trajectory prediction in human-robot collaborative assembly. CIRP Ann. 2020, 69, 9–12. [Google Scholar] [CrossRef]
- Kratzer, P.; Toussaint, M.; Mainprice, J. Prediction of human full-body movements with motion optimization and recurrent neural networks. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1792–1798. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Manh, H.; Alaghband, G. Scene-lstm: A model for human trajectory prediction. arXiv 2018, arXiv:1808.04018. [Google Scholar]
- Rossi, L.; Paolanti, M.; Pierdicca, R.; Frontoni, E. Human trajectory prediction and generation using LSTM models and GANs. Pattern Recognit. 2021, 120, 108136. [Google Scholar] [CrossRef]
- Fetch Robotics. Fetch & Freight Research Edition Documentation. Available online: https://github.com/fetchrobotics/docs (accessed on 16 June 2025).
- Campa, R.; De La Torre, H. Pose control of robot manipulators using different orientation representations: A comparative review. In Proceedings of the 2009 IEEE American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2855–2860. [Google Scholar]
- Zheng, H.; Negenborn, R.R.; Lodewijks, G. Trajectory tracking of autonomous vessels using model predictive control. IFAC Proc. Vol. 2014, 47, 8812–8818. [Google Scholar] [CrossRef]
- Shi, Q.; Zhao, J.; El Kamel, A.; Lopez-Juarez, I. MPC based vehicular trajectory planning in structured environment. IEEE Access 2021, 9, 21998–22013. [Google Scholar] [CrossRef]
- Ho, C.K.; Chan, L.W.; King, C.T.; Yen, T.Y. A deep learning approach to navigating the joint solution space of redundant inverse kinematics and its applications to numerical IK computations. IEEE Access 2023, 11, 2274–2290. [Google Scholar] [CrossRef]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016; pp. 1–4. [Google Scholar]


| Sample | Joint Angles (rad) | Position (m) | Orientation (rad) | MSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Given | 0.0 | 0.2 | −0.18 | −0.5 | −0.68 | −0.24 | 0.95 | 2.1 | 0.987 | 0.201 | 1.105 | 1.266 | −0.046 | −0.093 | - |
| 1 | 0.017 | 0.177 | −0.301 | −0.528 | −0.454 | −0.129 | 0.814 | 1.788 | 1.003 | 0.185 | 1.103 | 1.198 | −0.036 | −0.064 | 0.00101 |
| 2 | 0.023 | 0.174 | −0.199 | −0.575 | −0.497 | −0.071 | 0.844 | 1.868 | 1.020 | 0.213 | 1.018 | 1.253 | 0.064 | −0.033 | 0.00411 |
| 3 | 0.005 | 0.251 | −0.275 | −0.444 | −0.428 | −0.311 | 0.711 | 1.860 | 1.002 | 0.222 | 1.114 | 1.210 | −0.122 | −0.039 | 0.00586 |
| 4 | −0.005 | 0.217 | −0.197 | −0.381 | −0.379 | −0.236 | 0.761 | 1.791 | 1.044 | 0.174 | 0.996 | 1.224 | 0.084 | −0.075 | 0.00581 |
| 5 | 0.037 | 0.250 | −0.155 | −0.548 | −0.579 | −0.265 | 0.818 | 1.905 | 0.990 | 0.291 | 1.050 | 1.183 | −0.065 | 0.006 | 0.00492 |
| 6 | 0.033 | 0.158 | −0.251 | −0.464 | −0.456 | −0.140 | 0.810 | 1.709 | 1.018 | 0.181 | 1.062 | 1.159 | 0.019 | −0.054 | 0.00340 |
| 7 | 0.017 | 0.195 | −0.110 | −0.355 | −0.444 | −0.246 | 0.805 | 1.830 | 1.048 | 0.181 | 0.940 | 1.267 | 0.149 | −0.075 | 0.01162 |
| 8 | 0.004 | 0.153 | −0.169 | −0.410 | −0.405 | −0.193 | 0.708 | 1.730 | 1.055 | 0.143 | 0.994 | 1.167 | 0.050 | −0.074 | 0.00661 |
| 9 | 0.014 | 0.137 | −0.181 | −0.431 | −0.451 | −0.114 | 0.865 | 1.814 | 1.040 | 0.137 | 0.979 | 1.294 | 0.157 | −0.100 | 0.01077 |
| 10 | −0.005 | 0.145 | −0.133 | −0.379 | −0.452 | −0.136 | 0.829 | 1.748 | 1.053 | 0.127 | 0.947 | 1.252 | 0.175 | −0.092 | 0.01397 |
| 11 | 0.011 | 0.199 | −0.256 | −0.352 | −0.430 | −0.098 | 0.818 | 1.691 | 1.020 | 0.196 | 1.046 | 1.275 | 0.082 | 0.011 | 0.00531 |
| 12 | 0.005 | 0.151 | −0.175 | −0.410 | −0.383 | −0.092 | 0.781 | 1.762 | 1.055 | 0.144 | 0.958 | 1.274 | 0.163 | −0.061 | 0.01237 |
| 13 | 0.035 | 0.174 | −0.279 | −0.572 | −0.463 | −0.152 | 0.817 | 1.696 | 1.004 | 0.201 | 1.090 | 1.045 | −0.040 | −0.071 | 0.00831 |
| 14 | −0.003 | 0.245 | −0.184 | −0.489 | −0.475 | −0.098 | 0.778 | 1.845 | 1.020 | 0.252 | 1.015 | 1.289 | 0.051 | 0.041 | 0.00661 |
| 15 | 0.022 | 0.273 | −0.186 | −0.548 | −0.523 | −0.174 | 0.807 | 1.832 | 0.993 | 0.301 | 1.041 | 1.171 | −0.013 | 0.045 | 0.00721 |
| 16 | 0.003 | 0.112 | −0.178 | −0.636 | −0.455 | −0.126 | 0.757 | 1.812 | 1.048 | 0.127 | 1.007 | 1.092 | 0.013 | −0.131 | 0.00900 |
| 17 | 0.032 | 0.238 | −0.276 | −0.448 | −0.512 | −0.050 | 0.863 | 1.701 | 0.980 | 0.276 | 1.087 | 1.237 | 0.026 | 0.086 | 0.00734 |
| 18 | 0.031 | 0.166 | −0.142 | −0.458 | −0.479 | −0.270 | 0.784 | 1.727 | 1.038 | 0.178 | 0.999 | 1.065 | 0.030 | −0.099 | 0.01009 |
| 19 | 0.022 | 0.180 | −0.232 | −0.454 | −0.477 | −0.045 | 0.827 | 1.798 | 1.017 | 0.212 | 1.040 | 1.322 | 0.070 | 0.020 | 0.00576 |
| 20 | 0.015 | 0.182 | −0.126 | −0.376 | −0.479 | −0.114 | 0.747 | 1.762 | 1.043 | 0.206 | 0.975 | 1.294 | 0.092 | 0.028 | 0.00908 |
| No. of Samples | Computation Time (s) | MSE |
|---|---|---|
| 10 | 0.0011 ± 0.0001 | 0.0215 ± 0.0057 |
| 30 | 0.0027 ± 0.0004 | 0.0177 ± 0.0049 |
| 60 | 0.0047 ± 0.0011 | 0.0125 ± 0.0032 |
| 100 | 0.0061 ± 0.0019 | 0.0103 ± 0.0015 |
| 200 | 0.0112 ± 0.0031 | 0.0099 ± 0.0010 |
| Traj | Q | PO-HU () | PO-HU () | pPO-HU () | NPO-HU | PO-NHU | NPO-NHU | |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 879.02 ± 32.1 | 1012.59 ± 43.2 | 993.12 ± 38.7 | 2467.55 ± 158.4 | 1289.69 ± 52.1 | 8421.79 ± 402.1 § | ||
| 0.6 | 1008.45 ± 42.5 | 1289.51 ± 60.1 | 1217.44 ± 54.8 | 4664.03 ± 279.3 † | 1855.11 ± 83.7 ‡ | 9107.12 ± 445.6 § | ||
| 0.3 | 911.56 ± 29.8 | 986.14 ± 38.5 | 957.71 ± 35.2 | 2395.09 ± 142.1 | 1051.24 ± 63.2 | 7916.18 ± 365.9 § | ||
| 0.6 | 994.99 ± 38.11 | 1079.52 ± 51.4 | 1042.36 ± 46.3 | 3674.88 ± 201.1 † | 1102.45 ± 58.4 | 9363.44 ± 481.2 § | ||
| 0.3 | 799.66 ± 26.4 | 891.38 ± 36.5 | 851.45 ± 31.8 | 1271.54 ± 81.2 | 983.87 ± 56.2 | 1591.42 ± 102.4 | ||
| 0.6 | 871.97 ± 36.1 | 968.91 ± 46.3 | 924.18 ± 42.6 | 1564.94 ± 104.8 | 1092.47 ± 64.9 | 3206.33 ± 189.7 | ||
| 0.3 | 735.71 ± 30.1 | 809.48 ± 39.1 | 786.72 ± 35.6 | 1165.65 ± 75.4 | 869.09 ± 50.8 | 1778.19 ± 107.8 | ||
| 0.6 | 861.07 ± 36.2 | 953.16 ± 45.8 | 902.42 ± 42.9 | 1334.66 ± 88.2 | 1013.35 ± 59.4 | 1819.98 ± 119.2 | ||
| 0.3 | 852.84 ± 33.6 | 1091.48 ± 57.1 | 983.47 ± 43.4 | 1891.23 ± 127.4 | 1431.73 ± 71.3 | 5721.94 ± 314.5 § | ||
| 0.6 | 976.77 ± 43.1 | 1186.40 ± 61.7 | 1098.75 ± 54.3 | 2880.69 ± 162.2 † | 1569.67 ± 77.8 ‡ | 6452.61 ± 338.4 § | ||
| 0.3 | 861.766 ± 30.2 | 1019.72 ± 49.1 | 971.33 ± 44.5 | 6407.73 ± 285.1 † | 1260.28 ± 61.8 | 10531.81 ± 490.9 § | ||
| 0.6 | 1001.92 ± 43.4 | 1218.77 ± 59.1 | 1179.25 ± 53.7 | 7243.09 ± 327.8 † | 1461.87 ± 70.5 | 11355.08 ± 517.6 § | ||
| 0.3 | 615.81 ± 26.1 | 701.63 ± 36.3 | 679.55 ± 33.7 | 1259.24 ± 92.1 | 764.59 ± 49.2 | 2558.78 ± 175.5 | ||
| 0.6 | 828.87 ± 38.3 | 897.28 ± 52.6 | 866.41 ± 48.1 | 2483.88 ± 150.7 | 927.36 ± 62.1 | 3495.15 ± 198.8 | ||
| 0.3 | 651.76 ± 32.1 | 762.99 ± 48.2 | 711.81 ± 39.5 | 2214.90 ± 12.3 | 969.85 ± 59.4 | 5278.04 ± 261.9 § | ||
| 0.6 | 778.93 ± 40.2 | 937.81 ± 59.4 | 894.11 ± 48.9 | 2758.48 ± 142.6 † | 1172.75 ± 60.7 | 5661.65 ± 297.6 § |
| Trajectory | H = 1 | H = 4 | H = 6 | H = 8 |
|---|---|---|---|---|
| 0.049 ± 0.027 | 0.072 ± 0.027 | 0.091 ± 0.031 | 0.104 ± 0.039 | |
| 0.034 ± 0.019 | 0.056 ± 0.034 | 0.072 ± 0.038 | 0.082 ± 0.043 | |
| 0.041 ± 0.024 | 0.062 ± 0.039 | 0.077 ± 0.045 | 0.085 ± 0.049 | |
| 0.031 ± 0.017 | 0.057 ± 0.031 | 0.065 ± 0.035 | 0.075 ± 0.038 |
| Planning Horizon | PO-HU | NPO-HU | PO-NHU |
|---|---|---|---|
| 4 | 0.013286 ± 0.00116 | 0.010474 ± 0.00094 | 0.013164 ± 0.00102 |
| 8 | 0.013633 ± 0.00121 | 0.011300 ± 0.00109 | 0.013295 ± 0.00107 |
| 12 | 0.013866 ± 0.00119 | 0.012736 ± 0.00113 | 0.013668 ± 0.00115 |
| 16 | 0.014126 ± 0.00124 | 0.012807 ± 0.00119 | 0.014003 ± 0.00119 |
| 20 | 0.014951 ± 0.00128 | 0.013287 ± 0.00116 | 0.014205 ± 0.00124 |
| 24 | 0.015287 ± 0.00131 | 0.013888 ± 0.00125 | 0.014257 ± 0.00129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmud, A.J.; Raj, A.H.; Nguyen, D.M.; Xiao, X.; Wang, X. DARC: Disturbance-Aware Redundant Control for Human–Robot Co-Transportation. Electronics 2025, 14, 2480. https://doi.org/10.3390/electronics14122480
Mahmud AJ, Raj AH, Nguyen DM, Xiao X, Wang X. DARC: Disturbance-Aware Redundant Control for Human–Robot Co-Transportation. Electronics. 2025; 14(12):2480. https://doi.org/10.3390/electronics14122480
Chicago/Turabian StyleMahmud, Al Jaber, Amir Hossain Raj, Duc M. Nguyen, Xuesu Xiao, and Xuan Wang. 2025. "DARC: Disturbance-Aware Redundant Control for Human–Robot Co-Transportation" Electronics 14, no. 12: 2480. https://doi.org/10.3390/electronics14122480
APA StyleMahmud, A. J., Raj, A. H., Nguyen, D. M., Xiao, X., & Wang, X. (2025). DARC: Disturbance-Aware Redundant Control for Human–Robot Co-Transportation. Electronics, 14(12), 2480. https://doi.org/10.3390/electronics14122480






