BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD
Abstract
1. Introduction
- Medical data of CKD and RA patients were extracted from the MIMIC database and preprocessed. To ensure analytical reliability, we implemented three distinct feature selection methods and addressed dataset imbalance through targeted techniques.
- We designed a model that tuned the hyperparameters of FT-Transformer using the Bayesian optimization algorithm. By continuously optimizing the parameters and improving the classifier’s performance, we successfully achieved accurate predictions about the likelihood of CKD patients developing RA.
- A comprehensive evaluation and interpretability analysis were conducted on the trained model, through which key risk factors predictive of clinical outcomes were identified. By integrating these findings with the existing medical literature, we further validated the identified risk factors, strengthening their clinical relevance and implications.
2. Related Work
3. Materials and Methods
3.1. Datasets
- RA patients were defined as ICU patients with clinically diagnosed CKD and hemoglobin (Hb) levels ≤ 110 g/L.
- For patients with multiple ICU admissions, only data from their first hospitalization were included.
- Patients under 18 years of age were excluded.
- Patients with excessive missing data were excluded.
3.2. Data Preprocessing
3.3. Feature Selection
3.4. Deep Learning Model Based on Bayesian Optimization
3.4.1. Bayesian Optimization Algorithm
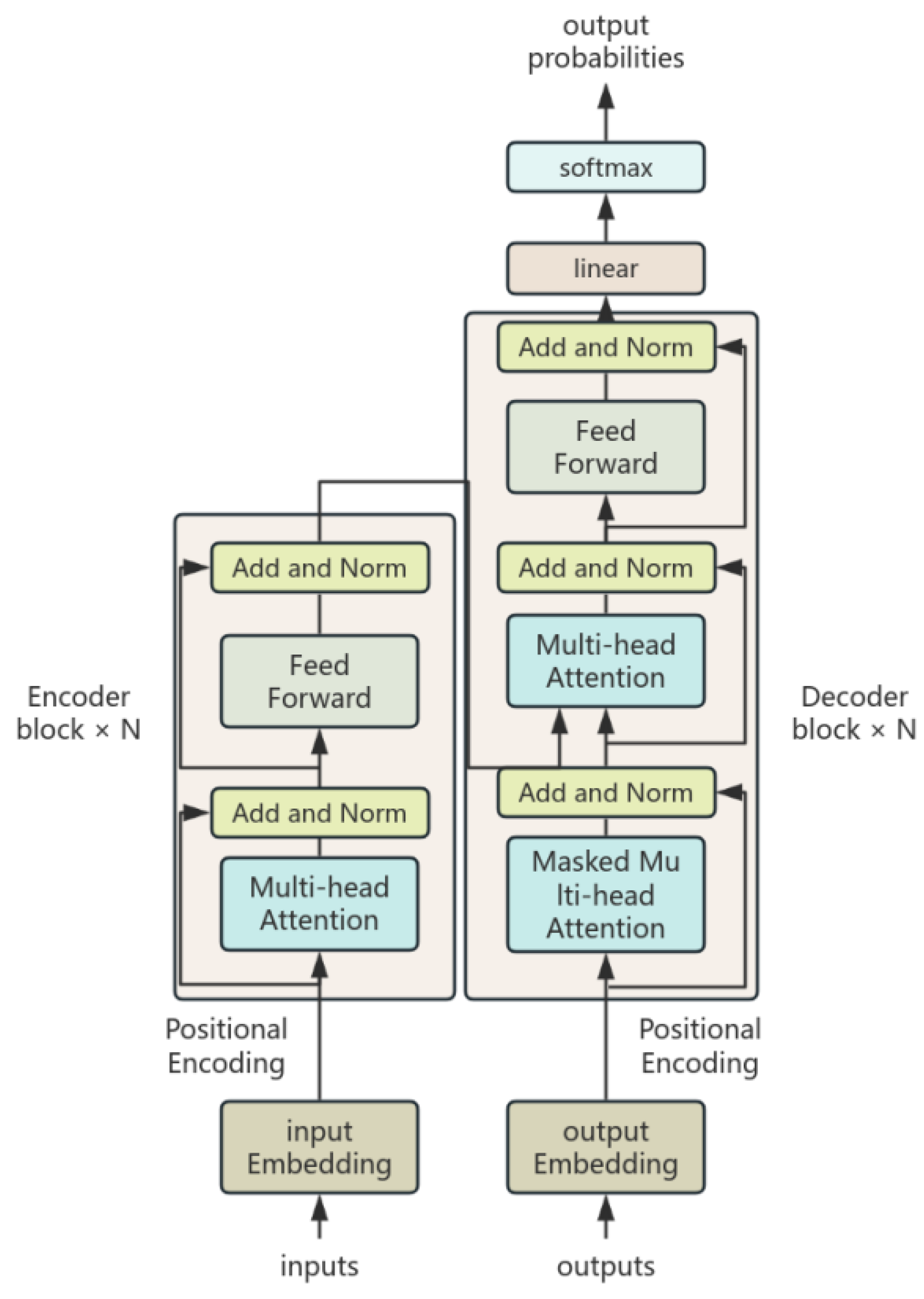
3.4.2. FT-Transformer
3.4.3. BO–FTT
- The objective function was configured as accuracy with init_points = 12, n_iter = 15, and a random seed of 1234. In addition, the five key parameters selected in this paper include core structural parameters, input_embed_dim, num_attn_blocks, and num_heads, and regularization parameters, attn_dropout and ff_dropout. Among them, num_heads determines the diversity of the multi-attention mechanism; input_embed_dim determines the vector representation capability of categorical features, which directly affects the model’s ability to capture feature differences; num_attn_blocks controls the model depth, where increased layers enhance feature interactions but heighten overfitting risks; attn_dropout can control the sparsity of the attention matrix through randomly masking some attention connections to prevent overfitting; ff_dropout is mainly used to regulate the overfitting risk of the feedforward network. The parameters and their value ranges are shown in Table 1.
- 2.
- Randomly select a set of parameters as initial evaluation points and compute the objective function values
- 3.
- Use the current surrogate model and acquisition function to choose the next most promising site for sampling and assessing accuracy. Add the new observation point to the training data, and then update the surrogate model.
- 4.
- Repeat the sampling, evaluation, updating, and checking process from Step 3 until either the maximum number of iterations of 100 times is reached or there is no improvement in the model’s accuracy within 20 iterations. At the end of each loop, output the parameters that maximize the accuracy of FTT.
4. Results
- Accuracy
- 2.
- Recall
- 3.
- Precision
- 4.
- F1 score
- 5.
- AUC-ROC curve
4.1. Performance Evaluation of BO–FTT
4.2. Comparative Experiments
4.3. Interpretability of BO–FTT
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Selected Features | |
|---|---|
| Correlation Analysis | gender, age, rbc, wbc, hematocrit, platelet, neutrophils_abs, creatinine, calcium, severe_liver_disease, chronic_pulmonary_disease, mild_liver_disease, diabetes_with_cc, diabetes_without_cc, peripheral_vascular_disease, charlson_comorbidity_index, metastatic_solid_tumor, malignant_cancer, paraplegia, bilirubin_total |
| Recursive Feature Elimination | gender, rbc, wbc, hemoglobin, platelet, creatinine, hematocrit, neutrophils_abs, severe_liver_disease, chronic_pulmonary_disease, mild_liver_disease, diabetes_with_cc, diabetes_without_cc, metastatic_solid_tumor, malignant_cancer, paraplegia, alp |
| ElasticNet | gender, age, wbc, hematocrit, neutrophils_abs, lymphocytes_abs, calcium, chronic_pulmonary_disease, mild_liver_disease, diabetes_with_cc, diabetes_without_cc, peripheral_vascular_disease, charlson_comorbidity_index, malignant_cancer, bilirubin_total |
| Final Feature Set | gender, age, rbc, wbc, hematocrit, platelet, neutrophils_abs, creatinine, calcium, severe_liver_disease, chronic_pulmonary_disease, mild_liver_disease, diabetes_with_cc, diabetes_without_cc, peripheral_vascular_disease, charlson_comorbidity_index, metastatic_solid_tumor, malignant_cancer, paraplegia, bilirubin_total |
References
- Pramod, S.; Goldfarb, D.S. Challenging patient phenotypes in the management of anemia of chronic kidney disease. Int. J. Clin. Pract. 2021, 75, e14681. [Google Scholar] [CrossRef] [PubMed]
- Comini, L.D.O.; de Oliveira, L.C.; Borges, L.D.; Dias, H.H.; Batistelli, C.R.S.; Ferreira, E.D.S.; da Silva, L.S.; Moreira, T.R.; da Costa, G.D.; da Silva, R.G.; et al. Prevalence of chronic kidney disease in Brazilians with arterial hypertension and/or diabetes mellitus. J. Clin. Hypertens. 2020, 22, 1666–1673. [Google Scholar] [CrossRef] [PubMed]
- Gansevoort, R.T. Too much nephrology? The CKD epidemic is real and concerning. A PRO view. Nephrol. Dial. Transplant. 2019, 34, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Smemr, A.; Hallmark, B.F. Complications of Kidney Disease. Nurs. Clin. N. Am. 2018, 53, 579–588. [Google Scholar]
- Pazianas, M.; Miller, P.D. Osteoporosis and chronic kidney disease–mineral and bone disorder (CKD-MBD): Back to basics. Am. J. Kidney Dis. 2021, 78, 582–589. [Google Scholar] [CrossRef]
- Farinha, A.; Mairos, J.; Fonseca, C. Anemia in Chronic Kidney Disease: The State of the Art. Acta Medica Port. 2022, 35, 758–764. [Google Scholar] [CrossRef]
- Odawara, M.; Nishi, H.; Nangaku, M. A spotlight on using HIF-PH inhibitors in renal anemia. Expert Opin. Pharmacother. 2024, 25, 1291–1299. [Google Scholar] [CrossRef]
- Figurek, A.; Rroji, M.; Spasovski, G. FGF23 in chronic kidney disease: Bridging the heart and anemia. Cells 2023, 12, 609. [Google Scholar] [CrossRef]
- Fishbane, S.; Pollock, C.A.; El-Shahawy, M.; Escudero, E.T.; Rastogi, A.; Van, B.P.; Frison, L.; Houser, M.; Pola, M.; Little, D.J.; et al. Roxadustat versus epoetin alfa for treating anemia in patients with chronic kidney disease on dialysis: Results from the randomized phase 3 ROCKIES study. J. Am. Soc. Nephrol. 2022, 33, 850–866. [Google Scholar] [CrossRef]
- Guzzo, I.; Atkinson, M.A. Anemia after kidney transplantation. Pediatr. Nephrol. 2023, 38, 3265–3273. [Google Scholar] [CrossRef]
- Cui, J.; Yang, J.; Zhang, K.; Xu, G.; Zhao, R.; Li, X.; Liu, L.; Zhu, Y.; Zhou, L.; Yu, P.; et al. Machine learning-based model for predicting incidence and severity of acute ischemic stroke in anterior circulation large vessel occlusion. Front. Neurol. 2021, 12, 749599. [Google Scholar] [CrossRef] [PubMed]
- Bahrainwala, J.; Berns, J.S. Diagnosis of iron-deficiency anemia in chronic kidney disease. Semin. Nephrol. 2016, 36, 94–98. [Google Scholar] [CrossRef] [PubMed]
- Agoro, R.; Montagna, A.; Goetz, R.; Aligbe, O.; Singh, G.; Coe, L.M.; Mohammadi, M.; Rivella, S.; Sitara, D. Inhibition of fibroblast growth factor 23 (FGF23) signaling rescues renal anemia. FASEB J. 2018, 32, 3752. [Google Scholar] [CrossRef] [PubMed]
- Tirmenstajn-Jankovic, B.; Dimkovic, N.; Perunicic-Pekovic, G.; Radojicic, Z.; Bastac, D.; Zikic, S.; Zivanovic, M. Anemia is independently associated with NT-proBNP levels in asymptomatic predialysis patients with chronic kidney disease. Hippokratia 2013, 17, 307. [Google Scholar]
- el Din Afifi, E.N.; Tawfik, A.M.; Abdulkhalek, E.E.R.S.; Khedr, L.E. The relation between vitamin D status and anemia in patients with end stage renal disease on regular hemodialysis. J. Ren. Endocrinol. 2021, 7, e15. [Google Scholar] [CrossRef]
- Kamei, D.; Nagano, M.; Takagaki, T.; Tomotaka, S.; Ken, T. Comparison between liquid chromatography/tandem mass spectroscopy and a novel latex agglutination method for measurement of hepcidin-25 concentrations in dialysis patients with renal anemia: A multicenter study. Heliyon 2023, 9, e13896. [Google Scholar] [CrossRef]
- Akchurin, O.; Patino, E.; Dalal, V. Interleukin-6 contributes to the development of anemia in juvenile CKD. Kidney Int. Rep. 2019, 4, 470–483. [Google Scholar] [CrossRef]
- Verma, A.; Jain, M. Predicting the Risk of Diabetes and Heart Disease with Machine Learning Classifiers: The Mediation Analysis. Meas. Interdiscip. Res. Perspect. 2024, 42, 1–18. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Tomašev, N.; Glorot, X.; Rae, J.W. A clinically applicable approach to continuous prediction of future acute kidney injury. Nature 2019, 572, 116–119. [Google Scholar] [CrossRef]
- Yue, S.; Li, S.; Huang, X. Machine learning for the prediction of acute kidney injury in patients with sepsis. J. Transl. Med. 2022, 20, 215. [Google Scholar] [CrossRef]
- She, S.; Shen, Y.; Luo, K.; Zhang, X.; Luo, C. Prediction of Acute Kidney Injury in Intracerebral Hemorrhage Patients Using Machine Learning. Neuropsychiatr. Dis. Treat. 2023, 19, 2765–2773. [Google Scholar] [CrossRef] [PubMed]
- Qu, C.; Gao, L.; Yu, X.; Wei, M.; Fang, G.Q.; He, J.; Li, W.Q. Machine learning models of acute kidney injury prediction in acute pancreatitis patients. Gastroenterol. Res. Pract. 2020, 2020, 3431290. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Yin, M.; Jiang, A.; Zhang, S.; Xu, X.; Liu, L. Automated machine learning for early prediction of acute kidney injury in acute pancreatitis. BMC Med. Inform. Decis. Mak. 2024, 24, 16. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.L.; Wu, C.C.; Lee, S.P.; Chen, Y.K.; Su, W.; Su, S.L. A predictive model for progression of CKD. Medicine 2019, 98, e16186. [Google Scholar] [CrossRef]
- Galloway, C.D.; Valys, A.V.; Shreibati, J.B.; Treiman, D.L.; Petterson, F.L.; Gundotra, V.P.; Friedman, P.A. Development and validation of a deep-learning model to screen for hyperkalemia from the electrocardiogram. JAMA Cardiol. 2019, 4, 428–436. [Google Scholar] [CrossRef]
- Chittora, P.; Chaurasia, S.; Chakrabarti, P.; Kumawat, G.; Chakrabarti, T.; Leonowicz, Z.; Bolshev, V. Prediction of chronic kidney disease—A machine learning perspective. IEEE Access 2021, 9, 17312–17334. [Google Scholar] [CrossRef]
- Song, W.; Zhou, X.; Duan, Q.; Wang, Q.; Li, Y.; Li, A.; Zhou, W.; Sun, L.; Qiu, L.; Li, R.; et al. Using random forest algorithm for glomerular and tubular injury diagnosis. Front. Med. 2022, 9, 911737. [Google Scholar] [CrossRef]
- Swain, D.; Mehta, U.; Bhatt, A.; Patel, H.; Patel, K.; Mehta, D.; Acharya, B.; Gerogiannis, V.C.; Kanavos, A.; Manika, S. A robust chronic kidney disease classifier using machine learning. Electronics 2023, 12, 212. [Google Scholar] [CrossRef]
- Zheng, J.X.; Li, X.; Zhu, J.; Guan, S.Y.; Zhang, S.X.; Wang, W.M. Interpretable machine learning for predicting chronic kidney disease progression risk. Digit. Health 2024, 10, 20552076231224225. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Dong, Z.; Wang, Q.; Pei, Z.; Chen, Y.; Zheng, Y.; Wang, Y.; Chen, P.; Feng, Z.; et al. New diagnostic model for the differentiation of diabetic nephropathy from non-diabetic nephropathy in Chinese patients. Front. Endocrinol. 2022, 13, 913021. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Fang, J.; Yu, T.; Liu, L.; Zou, G.; Gao, H.; Zhuo, L.; Li, W. Novel model predicts diabetic nephropathy in type 2 diabetes. Am. J. Nephrol. 2020, 51, 130–138. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.; Bulgarelli, L.; Pollard, T.; Horng, S.; Celi, L.A.; Mark, R. MIMIC-IV (version 2.0). PhysioNet 2022, 24, 49–55. [Google Scholar]
- Aljrees, T. Improving prediction of cervical cancer using KNN imputer and multi-model ensemble learning. PLoS ONE 2024, 19, e0295632. [Google Scholar] [CrossRef]
- Balaram, A.; Vasundra, S. Prediction of software fault-prone classes using ensemble random forest with adaptive synthetic sampling algorithm. Autom. Softw. Eng. 2022, 29, 6. [Google Scholar] [CrossRef]
- Marcos-Zambrano, L.J.; Karaduzovic-Hadziabdic, K.; Loncar Turukalo, T.; Przymus, P.; Trajkovik, V.; Aasmets, O.; Berland, M.; Gruca, A.; Hasic, J.; Hron, K. Applications of machine learning in human microbiome studies: A review on feature selection, biomarker identification, disease prediction and treatment. Front. Microbiol. 2021, 12, 634511. [Google Scholar] [CrossRef]
- Pudjihartono, N.; Fadason, T.; Kempa-Liehr, A.W.; O′Sullivan, J.M. A review of feature selection methods for machine learning-based disease risk prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar] [CrossRef]
- Domingo, D.; Kareem, A.B.; Okwuosa, C.N.; Custodio, P.M.; Hur, J.W. Transformer Core Fault Diagnosis via Current Signal Analysis with Pearson Correlation Feature Selection. Electronics 2024, 13, 926. [Google Scholar] [CrossRef]
- Zhou, S.; Li, T.; Li, Y. Recursive feature elimination based feature selection in modulation classification for MIMO systems. Chin. J. Electron. 2023, 32, 785–792. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, W.; Sheng, Y. Variable selection for uncertain regression models based on elastic net method. Commun. Stat.-Simul. Comput. 2024, 49, 1–22. [Google Scholar] [CrossRef]
- Cao, Y.; Li, B.; Xiang, Q.; Zhang, Y. Experimental Analysis and Machine Learning of Ground Vibrations Caused by an Elevated High-Speed Railway Based on Random Forest and Bayesian Optimization. Sustainability 2023, 15, 12772. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting deep learning models for tabular data. Adv. Neural Inf. Process. Syst. 2021, 34, 18932–18943. [Google Scholar]
- Kumar, P.; Nair, G.G. An efficient classification framework for breast cancer using hyper parameter tuned Random Decision Forest Classifier and Bayesian Optimization. Biomed. Signal Process. Control 2021, 68, 102682. [Google Scholar]
- Özkale, M.R.; Abbasi, A. Iterative restricted OK estimator in generalized linear models and the selection of tuning parameters via MSE and genetic algorithm. Stat. Pap. 2022, 63, 1979–2040. [Google Scholar] [CrossRef]
- Liwei, T.; Li, F.; Yu, S.; Yuankai, G. Forecast of lstm-xgboost in stock price based on bayesian optimization. Intell. Autom. Soft Comput. 2021, 29, 855–868. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Rossi, A.; Lancellotti, S.; Romaniello, F. Parameter tuning in the radial kernel-based partition of unity method by Bayesian optimization. J. Comput. Appl. Math. 2024, 451, 116108. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2960–2968. [Google Scholar]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Jaffari, Z.H.; Abbas, A.; Kim, C.M.; Shin, J.; Kwak, J.; Son, C.; Lee, Y.-G.; Kim, S.; Chon, K.; Cho, K.H. Transformer-based deep learning models for adsorption capacity prediction of heavy metal ions toward biochar-based adsorbents. J. Hazard. Mater. 2024, 462, 132773. [Google Scholar] [CrossRef]
- Isomura, T.; Shimizu, R.; Goto, M. Optimizing FT-Transformer: Sparse Attention for Improved Performance and Interpretability. Ind. Eng. Manag. Syst. 2024, 23, 253–266. [Google Scholar]
- Yu, Z.; Li, X.; Sun, L. A transformer cascaded model for defect detection of sewer pipes based on confusion matrix. Meas. Sci. Technol. 2024, 35, 115410. [Google Scholar] [CrossRef]
- Joo, Y.; Namgung, E.; Jeong, H.; Kang, I.; Kim, J.; Oh, S.; Lyoo, I.K.; Yoon, S.; Hwang, J. Brain age prediction using combined deep convolutional neural network and multi-layer perceptron algorithms. Sci. Rep. 2023, 13, 22388. [Google Scholar] [CrossRef] [PubMed]
- Joseph, L.P.; Joseph, E.A.; Prasad, R. Explainable diabetes classification using hybrid Bayesian-optimized TabNet architecture. Comput. Biol. Med. 2022, 151, 106178. [Google Scholar] [CrossRef] [PubMed]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, A.I.; Samsudin, A.S.; Rashid, M.I.M. Battery state of charge estimation for electric vehicle using Kolmogorov-Arnold networks. Energy 2024, 311, 133417. [Google Scholar] [CrossRef]
- Street, W.N.; Wolberg, W.H.; Mangasarian, O.L. Nuclear feature extraction for breast tumor diagnosis. In Proceedings of the Biomedical Image Processing and Biomedical Visualization, San Jose, CA, USA, 29 July 1993; SPIE: Bellingham, WA, USA, 1993; Volume 1905, pp. 861–870. [Google Scholar]
- Islam, M.M.F.; Ferdousi, R.; Rahman, S.; Bushra, H. Likelihood prediction of diabetes at early stage using data mining techniques. Adv. Intell. Syst. Comput. 2020, 992, 113–125. [Google Scholar]
- Sterratt, D.C. On the importance of countergradients for the development of retinotopy: Insights from a generalised Gierer model. PLoS ONE 2013, 8, e67096. [Google Scholar] [CrossRef]
- Frisbie, J.H. Anemia and hypoalbuminemia of chronic spinal cord injury: Prevalence and prognostic significance. Spinal Cord 2010, 48, 566–569. [Google Scholar] [CrossRef]
- Bozzini, C.; Busti, F.; Marchi, G.; Vianello, A.; Cerchione, C.; Martinelli, G.; Girelli, D. Anemia in patients receiving anticancer treatments: Focus on novel therapeutic approaches. Front. Oncol. 2024, 14, 1380358. [Google Scholar] [CrossRef]
- Mehdi, U.; Toto, R.D. Anemia, diabetes, and chronic kidney disease. Diabetes Care 2009, 32, 1320–1326. [Google Scholar] [CrossRef]
- Singh, S.; Manrai, M.; Kumar, D.; Srivastava, S.; Pathak, B. Association of liver cirrhosis severity with anemia: Does it matter? Ann. Gastroenterol. 2020, 33, 272. [Google Scholar] [CrossRef]
- Santos, S.; Lousa, I.; Carvalho, M.; Sameiro-Faria, M.; Santos-Silva, A.; Belo, L. Anemia in Elderly Patients: Contribution of Renal Aging and Chronic Kidney Disease. Geriatrics 2025, 10, 43. [Google Scholar] [CrossRef]
- Tefferi, A.; Hanson, C.A.; Inwards, D.J. How to interpret and pursue an abnormal complete blood cell count in adults. In Mayo Clinic Proceedings; Elsevier: Amsterdam, The Netherlands, 2005; Volume 80, pp. 923–936. [Google Scholar]








| Parameter | Value Range |
|---|---|
| num_heads (int) | (0, 10) |
| num_attn_blocks (int) | (0, 10) |
| input embed dim (int) | (0, 100) |
| attn_dropout (float) | (0.1, 0.5) |
| ff_dropout (float) | (0.1, 0.5) |
| Parameter | Value |
|---|---|
| num_heads (int) | 7 |
| num_attn_blocks (int) | 8 |
| input embed dim (int) | 77 |
| attn_dropout (float) | 0.21 |
| ff_dropout (float) | 0.20 |
| Evaluation Metrics | Value |
|---|---|
| Accuracy | 91.81% |
| Precision | 87.71% |
| Recall | 89.10% |
| F1-score | 88.37% |
| Model | Value |
|---|---|
| BO–FTT | ‘input_embed_dim’: 77; ‘attn_dropout’: 0.21; ‘num_heads’: 7; ‘ff_dropout’: 0.20; ‘num_attn_blocks’: 8 |
| BO–tabnet | ‘cat_emb_dim_label’: 9; ‘mask_type_label’: softmax; ‘optimizer_params’: 0.03; |
| BO–MLP | ‘alpha’: 0.02; ‘hidden_layer_sizes’: 402; |
| BO–KAN | ‘grid_eps’: 0.03; ‘grid_range_max’: 6; ‘grid_range_min’: −6; ‘grid_size’: 8; ‘scale_base’: 0.23; ‘scale_noise’: 0.27; ‘scale_spline’: 2.11; ‘spline_order’: 8 |
| Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| BO–FTT | 91.81% | 87.71% | 89.10% | 88.37% |
| BO–tabnet | 79.16% | 77.31% | 78.79% | 78.04% |
| BO–MLP | 86.40% | 85.84% | 86.40% | 85.99% |
| BO–KAN | 83.90% | 81.05% | 73.90% | 71.88% |
| Evaluation Metrics | Value |
|---|---|
| accuracy | 88.01% |
| precision | 82.35% |
| recall | 83.83% |
| f1-score | 83.05% |
| Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| BO–FTT | 96.49% | 96.37% | 96.01% | 96.37% |
| BO–tabnet | 94.74% | 94.70% | 94.70% | 94.70% |
| BO–MLP | 95.32% | 95.37% | 94.94% | 95.14% |
| BO–KAN | 92.41% | 92.42% | 91.00% | 91.63% |
| Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| BO–FTT | 97.12% | 97.19% | 96.81% | 96.99% |
| BO–tabnet | 87.65% | 82.34% | 83.11% | 87.62% |
| BO–MLP | 94.87% | 94.84% | 94.22% | 94.51% |
| BO–KAN | 87.50% | 85.76% | 85.17% | 85.45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, J.; Wang, M. BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD. Electronics 2025, 14, 2471. https://doi.org/10.3390/electronics14122471
Liu Y, Chen J, Wang M. BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD. Electronics. 2025; 14(12):2471. https://doi.org/10.3390/electronics14122471
Chicago/Turabian StyleLiu, Yuqi, Jiaqing Chen, and Molan Wang. 2025. "BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD" Electronics 14, no. 12: 2471. https://doi.org/10.3390/electronics14122471
APA StyleLiu, Y., Chen, J., & Wang, M. (2025). BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD. Electronics, 14(12), 2471. https://doi.org/10.3390/electronics14122471




