Abstract
In a biological nervous system, neurons are connected to each other via synapses to transmit information. Synaptic crosstalk is the phenomenon of mutual interference or interaction of neighboring synapses between neurons. This phenomenon is prevalent in biological neural networks and has an important impact on the function and information processing of the neural system. In order to simulate and study this phenomenon, this paper proposes a memristor model based on hyperbolic tangent function for simulating the activation function of neurons, and constructs a three-neuron HNN model by coupling two memristors, which brings it close to the real behavior of biological neural networks, and provides a new tool for studying complex neural dynamics. The intricate nonlinear dynamics of the MHNN are examined using techniques like Lyapunov exponent analysis and bifurcation diagrams. The viability of the MHNN is confirmed through both analog circuit simulation and FPGA implementation. Moreover, an image encryption approach based on the chaotic system and a dynamic key generation mechanism are presented, highlighting the potential of the MHNN for real-world applications. The histogram shows that the encryption algorithm is effective in destroying the features of the original image. According to the sensitivity analysis, the bit change rate of the key is close to 50% when small perturbations are applied to each of the three parameters of the system, indicating that the system is highly resistant to differential attacks. The findings indicate that the MHNN displays a wide range of dynamical behaviors and high sensitivity to initial conditions, making it well-suited for applications in neuromorphic computing and information security.
1. Introduction
Synaptic connections are vital for transmitting information between neurons. Prior research has confirmed the existence of synaptic crosstalk in biological synapses [1], which significantly impacts brain activity and function. However, this phenomenon is rarely taken into account in neural network studies. The interactions between neurotransmitters at synaptic sites are crucial for maintaining normal brain function, especially in terms of behavioral cognition and synaptic plasticity [2]. By emulating the interactions between neurons and synapses observed in the brain [3], researchers can obtain a more profound understanding of brain mechanisms and apply these insights to the development of advanced neural network models.
The memristor is a nonlinear circuit element whose resistance can vary in response to changes in current and voltage, which possesses a memory property, and is considered the fourth fundamental circuit component, in addition to resistance, capacitance, and inductance [4]. By regulating the voltage applied across the memristor, its resistance can be adjusted in a nonlinear and continuous manner. This resistance change is retained even after power is removed, corresponding, respectively, to the plasticity [5] and memorability [6] of synaptic weights, respectively [7]. In recent years, memristive neural networks have gained increasing prevalence [8,9,10,11]. Among them, the Hopfield neural network (HNN) [12] has emerged as a prominent artificial neural network, attracting substantial interest from scholars [13,14]. The ability of the HNN to stimulate complex dynamical behaviors observed in the brain, particularly chaotic phenomena, is largely due to its strong nonlinearity and flexible algebraic formulations. Leveraging the distinct advantages of memristors, researchers have developed memristive Hopfield neural networks (MHNNs) [13,14,15,16,17], which have been widely applied in diverse research areas such as associative memory, image processing, and combinatorial optimization [16,17,18,19,20].
Conducting circuit experiments is a common approach for analyzing and verifying dynamic behaviors of neurons and neural networks. However, due to the impact of fabrication processes and environmental variations, transistor mismatch in practical circuits remains difficult to eliminate. Field Programmable Gate Arrays (FPGAs) are primarily based on digital logic design, and digital circuits require less stringent signal accuracy than analog circuits. Signals in digital circuits usually have a large noise tolerance, so some small parameter deviations are unlikely to cause significant changes in dynamics. In addition, compared to traditional analog circuits, FPGAs are usually manufactured using advanced manufacturing processes which have stricter control of component parameters during the manufacturing process, thus reducing the possibility of mismatches. To further uncover the mechanisms underlying complex phenomena in neural network computation and to replicate the dynamic behavior of neuronal models, the development of efficient brain-inspired computing hardware is essential [21]. Among various digital design platforms, FPGA is distinguished by its high flexibility, real-time performance, and portability, making it well suited to the diverse requirements of memristive neural network systems. H. Lin et al. verified the physical realizability of memristive neural networks and demonstrated a medical image encryption design using FPGA [22]. HNN is also widely used in industrial applications [21,22,23,24]. Q. Lai et al. incorporated the amnesia model into HNN, modeled the synaptic components with memristive properties, proposed a novel high-dimensional HNN structure with multiple double-scroll chaotic attractors, and applied it to a 3D image encryption scheme [25].
Existing studies on the chaotic dynamics of memristive neurons and neural networks explore a variety of models such as memristive self-synaptic neurons and synaptic coupled networks, and present rich nonlinear phenomena such as multistability and extreme multistability and their applications in areas such as secure communications. In this paper, a MHNN with synaptic crosstalk is proposed, and the physical feasibility of the model is verified by FPGA implementation and simulation circuits, and finally, a dynamic key image encryption scheme based on chaotic sequences is developed.
Based on the above-mentioned research, this study aims to make following contributions, which are shown in Figure 1:
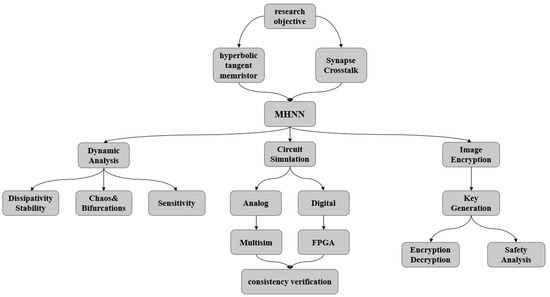
Figure 1.
Structure of the study.
(1) A memristor model based on the hyperbolic tangent function is proposed to simulate the activation function of neurons. Utilizing this memristor model, a three-neuron HNN incorporating synaptic crosstalk is constructed by coupling two memristors.
(2) The complex nonlinear dynamical behavior of the memristor-based HNN is analyzed using multiple methods. The results reveal that, as system parameters vary, the network displays a wide range of dynamic behaviors, such as period-doubling bifurcations, chaotic states, and periodic oscillations.
(3) The physical realizability of the MHNN is validated through both circuit simulation and FPGA implementation. First, a circuit module capable of realizing the MHNN is designed, and its output is verified against the theoretical model using Multisim simulation, ensuring the reproducibility of the system’s dynamical behavior. Subsequently, the FPGA implementation of the MHNN further demonstrates its potential for simulating complex dynamical behaviors and for real-world applications.
(4) A novel image encryption approach utilizing a five-dimensional chaotic system and a dynamic key generation mechanism is presented. The chaotic system is iterated via the Runge–Kutta-4th (RK4) method to generate a key matrix that is highly correlated with the pixel positions of the original image. Additionally, image encryption and decryption are accomplished through exclusive OR (XOR) operations. Experimental findings demonstrate that this method effectively disrupts the statistical properties of the original image, and the histogram of the encrypted image displays a uniform distribution.
In conclusion, dynamical analysis establishes the MHNN’s nonlinear behaviors as a theoretical foundation while circuit simulation and image encryption test these behaviors in a real-world task requiring both chaos and hardware efficiency.
2. HNN Based on Hyperbolic Tangent Memristor
2.1. Hyperbolic Tangent Memristive Model
In biological theory, the activation function is used to represent the potential firing rate of a neuron and is often mathematically approximated by a hyperbolic function. Designing a mathematical model, along with a corresponding equivalent circuit model that closely reflects the characteristics of neuronal activation functions, holds significant research value. Such models contribute to the mathematical and structural development of memristive neural networks.
In neural network studies, activation functions are typically defined as monotonic functions bounded by upper and lower limits, with the hyperbolic tangent function being a commonly selected choice. Building on traditional memristor models, a memristor employing the hyperbolic tangent function has been proposed [16], and it can be expressed as
where is the input voltage, is the output current, is the state variable of the memristor, is the conductance of memristor and a, b are internal parameters of the memristor, which are positive real numbers.
In order to prove the characteristics of memristors, the parameters are set as , . When the excitation signal is , the hysteresis loop of a memristor is simulated, where and represent the amplitude and frequency of the cosinoidal voltage input. Let and , the relationship between and is a hysteresis loop, and the variation in memristive conductance with are presented in Figure 2, which prove the basic memristive characteristics.
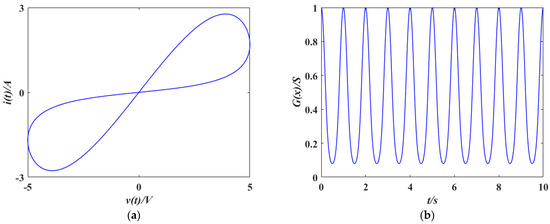
Figure 2.
Simulation results of hyperbolic tangent memristors: (a) Hysteresis loop of the memristor; (b) time-domain waveform of memristive conductance.
Considering the effects of amplitude and frequency of input cosinoidal voltage on the operating characteristics of the memristor, the two parameters are modified separately. First, with , and fixed, the amplitude is set to 1 V, 3 V, and 5 V, respectively. As shown in Figure 3a, the area enclosed by the hysteresis loop rises with the amplitude of the input signal. Then, with , is set to 1 Hz, 3 Hz, and 5 Hz, respectively. As the frequency increases, the area of the hysteresis loop diminishes and ultimately converges to a linear function, as depicted in Figure 3b. The simulation results presented in Figure 3 demonstrate that the hyperbolic tangent memristor exhibits the essential features of conventional memristor models.
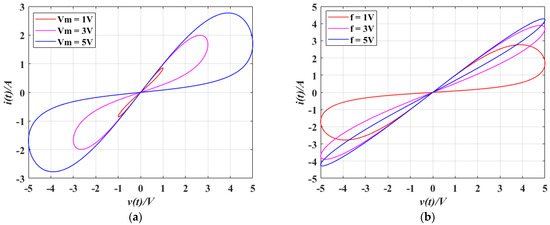
Figure 3.
Hysteresis loops of the memristor under different parameters: (a) ; (b) .
2.2. Construction of the Three-Neuron Memristive Hopfield Neural Network
The Hopfield neural network is the neural network with complete interconnections commonly employed to simulate dynamic behaviors of the human brain [12]. The circuit state equations can be expressed as
where , , and are the capacitance, resistance, and voltage of the memristor, is the activation function of neuron , is the synaptic weight between neurons and , and is the biasing current of neuron .
To simulate the crosstalk behaviors between neuronal synapses, the two memristors are coupled, which can be expressed as
where and are the internal state variables of the memristors separately, and are internal parameters of the memristor, and is the crosstalk strength between two memristors.
Based on the conventional Hopfield neural network containing three neurons, a MHNN coupling two memristors with synaptic crosstalk is constructed by expressing the connection weights between the second and third neurons with hyperbolic tangent memristors and setting the deviation of the model as zero. The newly built MHNN system is shown in Figure 4.
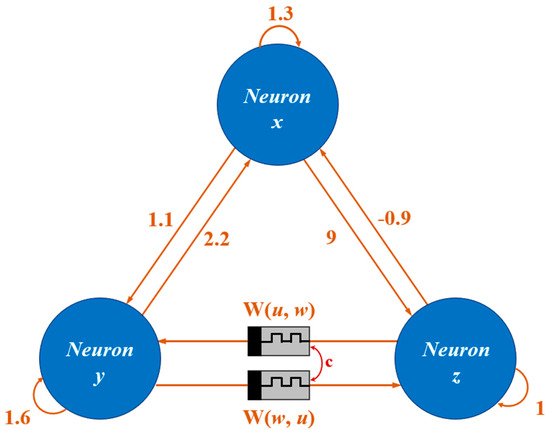
Figure 4.
Model of MHNN with synaptic crosstalk.
After extensive experiments, the synaptic weight matrix is chosen as
According to the parameters given in Equation (4), the model can be expressed as the following set of nondimensionalized autonomous ordinary differential equations:
where , , are the membrane voltage of three neurons, , are the internal state variables of two memristors, is the memristive synapse of neuron to , and is the memristive synapse of neuron to .
3. Dynamic Analysis of MHNN
This section focuses exclusively on characterizing crosstalk-driven dynamics. In this part, a range of fundamental dynamic analysis techniques are applied to investigate the complex nonlinear chaotic behavior of the MHNN in this study. These methods include dissipativity evaluation, equilibrium point assessment, phase space visualization, bifurcation analysis, Lyapunov exponent computation, and time series inspection.
3.1. Dissipativity Analysis
Based on the Lyapunov stability criterion [26], a five-variable Lyapunov function can be constructed as follows:
The partial derivative of time for Equation (6) is
where
For all , there is , so it can be obtained that
Let . According to Equation (9), Equation (8) satisfies
Let us suppose that all the state variables satisfy . A sufficiently large domain is selected, and in a limited domain, it is always true that . It is required that
where is a positive constant.
Since , it is obvious that
Based on Equation (12), it can be concluded that the confined domain of the solutions in Equation (5) can be given as
From the analysis above, the system is bounded and has the possibility to generate chaotic behaviors.
3.2. Equilibria Analysis
Setting the left-hand side of Equation (5) to zero yields the following result:
Hence, the equilibrium point of Equation (5) corresponds to the solution of Equation (14), which can be reformulated as
where the equilibria of HNN are the intersections of surfaces of , , and .
Let , , and be equal to zero, and setting , and , the three surfaces are shown in Figure 5. As can be visualized from the figure, there are two intersections in total, which are equilibriums of the system within the given parameters.
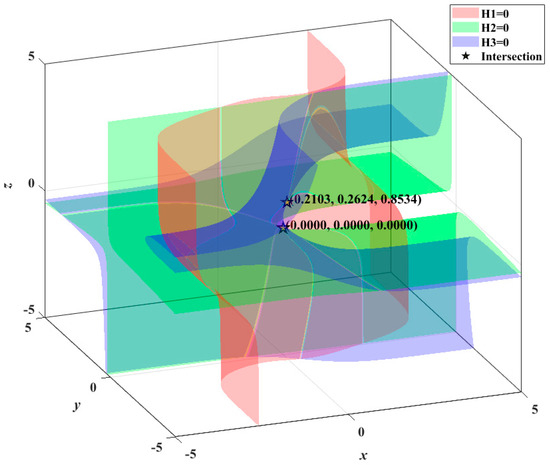
Figure 5.
Equilibria of the MHNN.
By linearizing Equation (5) at the equilibrium point, the Jacobian matrix can be expressed as
where .
The characteristic equation at can be formulated as
Obviously,
where
Based on the partitioned matrix determinant equations, Equation (17) can be calculated as
where
Therefore, the coefficients in Equation (17) are
According to the Routh–Hurwitz stability criterion, the Routh Array can be given as [25]
When , , so the system is unstable in the given condition and it can produce chaotic or hyperchaotic phenomena.
Based on the analysis above, the eigenvalues and stabilities of other equilibrium points within different synaptic crosstalk strengths are shown in Table 1, which demonstrate no significant effect on the stability of the system within a certain range.

Table 1.
Equilibrium points, eigenvalues, and stabilities related to synaptic crosstalk strength.
3.3. Dynamic Behaviors
When , the representative Lyapunov exponents are
Since the maximum Lyapunov exponent , the system can produce chaos.
By numerically simulating the time evolution of the system, the trajectories of the state variables can be plotted and the system’s dynamic behaviors can be examined. For Equations (3) and (5), the parameters are set as , and with the initial conditions defined as . The chaotic behaviors of the system under the given conditions are, respectively, illustrated in the subplots of Figure 6.
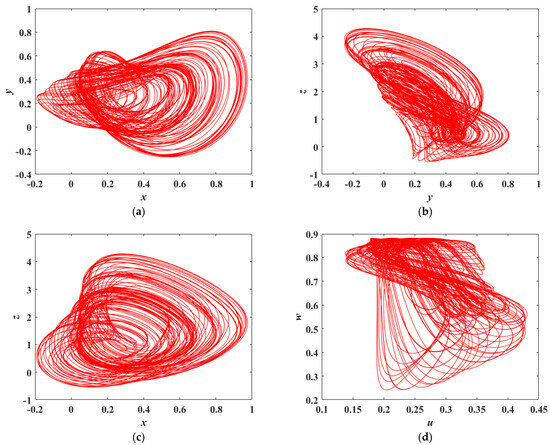
Figure 6.
Phase portraits of MHNN: (a) x-y phase; (b) y-z phase; (c) x-z phase; (d) u-w phase.
The Poincaré map is a method commonly used to verify the presence of chaotic phenomena. It reveals the dynamic characteristics of a system by selecting a specific hyperplane in the phase space and recording the state values each time the system trajectory intersects this hyperplane.
Figure 7 presents the Poincaré map in the x-y-z space with cross-sections defined by and , in which it can be seen that the points on the cross-section form a piece of discrete two-dimensional shapes, which indicates the existence of chaotic attractors.
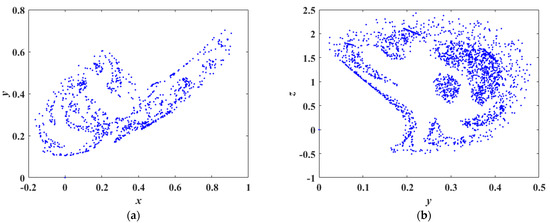
Figure 7.
Poincaré map in x-y and y-z phase: (a) ; (b) .
3.4. Memristive Parameter b-Associated Dynamics
The internal memristive parameter is selected as the bifurcation parameter of the system, and numerical simulations are performed in MATLAB 2023b using the RK4 method with a step size . When is selected as the sole bifurcation parameter, with and held constant, the corresponding single-parameter bifurcation diagram of the state variable and the associated Lyapunov exponents can be generated to characterize the system’s dynamic behavior. The initial state is set as . To accurately track the system’s evolution over time, suitable simulation configurations are employed. For the bifurcation diagram, the start time, time step size, and end time are configured to 500 s, 0.01 s, and 2500 s, respectively. For the computation of the finite-time Lyapunov exponents, the time step and end time are set to 0.01 s and 10,000 s, respectively. The system’s dynamic behaviors as the parameter increases from 14 to 18 are depicted in Figure 8.
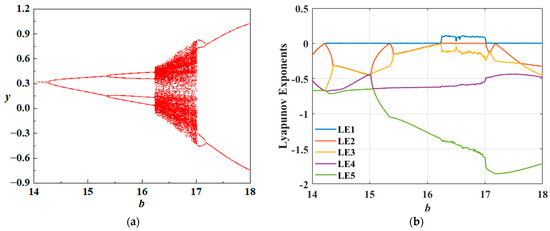
Figure 8.
The b-dependent dynamics: (a) bifurcation diagram of the variable y; (b) finite-time Lyapunov exponent spectra.
Figure 8 presents the bifurcation diagram in the y phase along with the corresponding Lyapunov exponent spectrum of the system. It can be observed that the dynamic behaviors revealed by both methods exhibit consistent trends. Specifically, as the parameter increases within the interval , the system maintains a stable fixed point. When reaches 14.26, the first periodic bifurcation occurs, during which the system undergoes a supercritical Andronov–Hopf bifurcation and transitions into a period-1 oscillatory state. As b continues to increase, the system experiences a second bifurcation at , entering a period-2 oscillatory state. Subsequently, within the interval , the number of branches in the bifurcation diagram increases significantly and becomes densely distributed, indicating that the system gradually transitions from a quasi-periodic state to a chaotic state. Finally, at , the system undergoes a sudden transition from chaos back to a periodic oscillatory state.
To more effectively reveal the coexisting symmetric behaviors, the phase portraits of the HNN under parameter b and the time-domain waveforms are drawn in x-y phase, as illustrated in Figure 9.
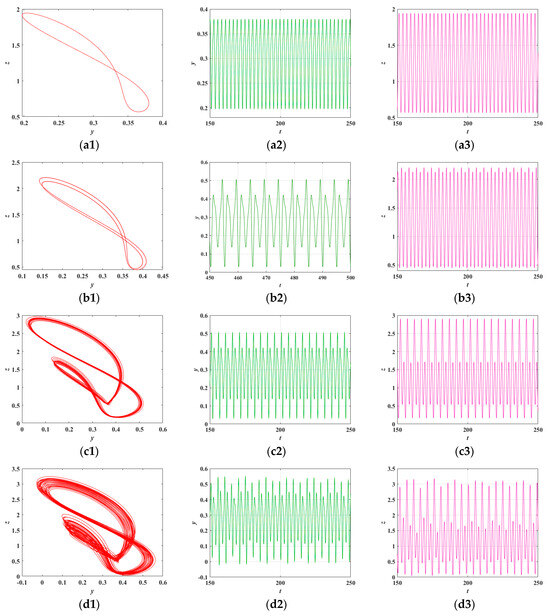
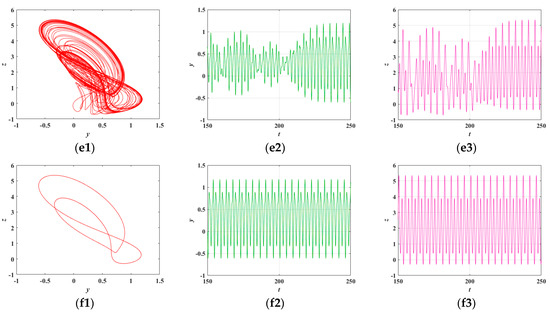
Figure 9.
b-dependent phase portraits and time-domain waveforms: (a1) ; (a2) ; (a3) ; (b1) ; (b2) ; (b3) ; (c1) ; (c2) ; (c3) ; (d1) ; (d2) ; (d3) ; (e1) ; (e2) ; (e3) ; (f1) ; (f2) ; (f3) .
The results illustrate the nonlinear dynamical evolution of the system as the parameter increases. Initially, at , the system exhibits periodic oscillations, suggesting that the magnetic field has minimal influence on the neurons and that the system maintains the intrinsic periodic spiking behavior of neuronal activity. As increases to 16, the system undergoes a period-2 bifurcation. The previously stable limit cycle splits into two distinct cycles, resulting in alternating behavior between two closed loops in the phase portrait. In this state, the neurons display period-2 bursting oscillations. With a further increase in to 16.2, the system undergoes additional bifurcations and transitions into a quasi-periodic state. The corresponding phase portrait reveals densely packed oscillatory patterns, indicating that the system is no longer constrained to a simple limit cycle but instead exhibits more intricate and irregular dynamics. This evolution also implies a growing degree of coupling between the magnetic field and the neural system. As continues to increase, the system reaches a chaotic regime at , characterized by hyperchaotic bursting behavior in the neurons. Remarkably, a slight increase to results in a rapid transition back to a period-2 oscillatory state, further highlighting the system’s sensitivity to parameter changes and the richness of its nonlinear dynamical responses.
Based on the combined analysis of the bifurcation diagram, phase portraits, and waveform evolution, it can be concluded that the system is capable of generating both periodic and chaotic behaviors. This confirms that the system exhibits rich and complex dynamical characteristics.
3.5. Memristive Crosstalk Strength c-Associated Dynamics
Here, with parameters set as and , the bifurcation behavior of the HNN within the interval is illustrated in Figure 10.
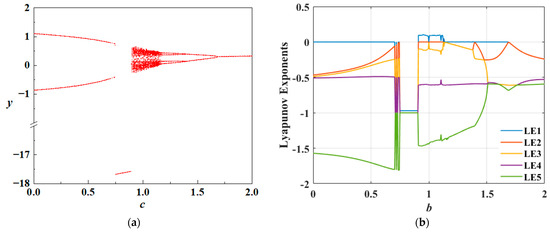
Figure 10.
The c-dependent dynamics: (a) bifurcation diagram of the variable y; (b) finite-time Lyapunov exponent spectra.
When the crosstalk intensity is low, the highest Lyapunov exponent is negative, and the system exhibits periodic oscillations. As increases within the interval , the Lyapunov exponents undergo a sudden change, and the maximum value remains below zero, indicating that the system enters a stable fixed-point state. When , the maximum Lyapunov exponent and the system begins to generate sustained periodic oscillations. As further increases to 1.17, the system undergoes a subcritical Hopf bifurcation, transitioning into a period-2 bursting oscillatory state. In the interval , the system exhibits periodic oscillations once again, and when , the system stabilizes.
By setting and , the HNN exhibits different attractors depending on the value of the crosstalk parameter , as illustrated in Figure 11. When the crosstalk strength is low, neurons display periodic spike firing, suggesting that external stimuli have limited influence on neuronal dynamics. As the crosstalk intensity increases, the firing pattern changes, giving rise to chaotic spike firing or cluster firing behaviors. When the crosstalk intensity reaches a high level, the firing activity of the neurons stabilizes and the overall system becomes dynamically stable.
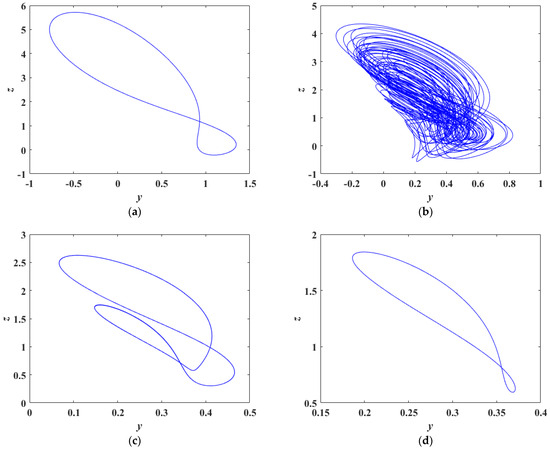
Figure 11.
The c-dependent dynamics: (a) ; (b) ; (c) ; (d) .
To examine the signal spectrum under various crosstalk strengths, the Fast Fourier Transform (FFT) algorithm is employed. The frequency-domain signal characteristics of the system for different values of the parameter , corresponding to , , and , are presented in Figure 12. Each subfigure contains the amplitude response curves of the y phase and z phase. The analysis results show that for all values of the parameter , the amplitude responses of both y phase and z phase show significant peaks in the mid-frequency band (about 49.6 Hz), indicating that the system has a strong response at this frequency. However, with the increase in parameter , the amplitude response of y phase and z phase decreased. This indicates that the parameter has a significant effect on the frequency response characteristics of the system, especially on the response strength in the middle frequency band.
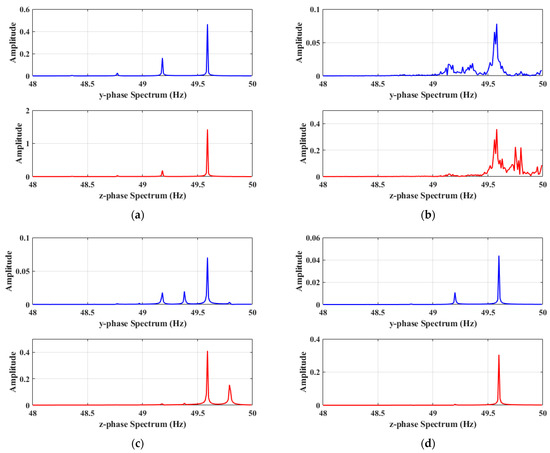
Figure 12.
The c-dependent frequency-domain signal: (a) ; (b) ; (c) ; (d) .
4. Hardware Implementation of MHNN
4.1. Analog Circuit Simulation
In order to verify the dynamics of the system, it is first necessary to build an analog circuit capable of realizing the ‘−tanh(.)’ hyperbolic tangent function [27]. The circuit module consists of eight resistors, two operational amplifiers, two transistors, and a DC source. The circuit schematic is shown in Figure 13.
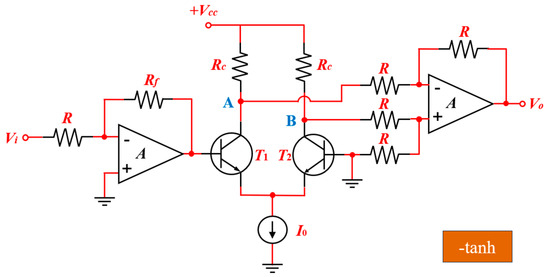
Figure 13.
Circuit schematics of ‘−tanh(.)’.
In the circuit diagram, let and represent the input and output voltages of the hyperbolic tangent module, respectively. The relationship between the input and output voltages can be characterized as
where refers to the thermal voltage of the transistor, typically a value of 26 mV at room temperature. The corresponding parameters are configured as , , , and . Notice that the circuit realizes the ‘tanh(.)’ hyperbolic tangent function when nodes A and B are interchanged.
Referring to [28,29], the analog circuit used to realize the MHNN model in Equation (5) is constructed and implemented.
where
and are the voltages across capacitors, respectively.
To facilitate the design of the analog circuit, the detailed simulation circuits of the system are designed and synthesized [30,31] based on Equations (26) and (27). In this design, the reverse hyperbolic tangent function ‘−tanh(.)’ is realized using independent functional modules. The primary circuit is composed of four operational amplifiers, four modules of the ‘−tanh(.)’ function, and a number of resistors and capacitors. Additionally, the memristive synapses between neurons y and z incorporate four multipliers along with multiple resistors, as illustrated in Figure 14 and Figure 15.
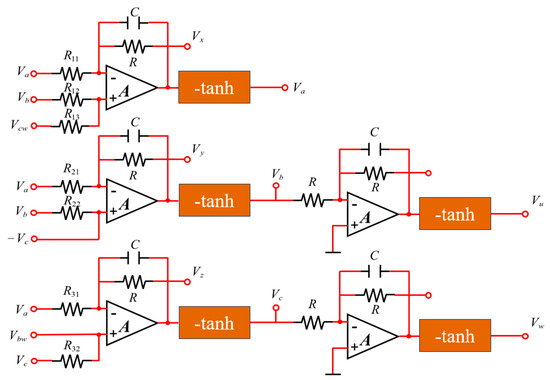
Figure 14.
Primary circuit of MHNN.
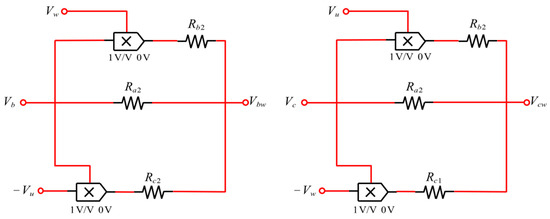
Figure 15.
Circuit schematics of memristive synapse crosstalk.
The time constant is set as , where and . The parameters of other resistors in the circuit are shown in Table 2.

Table 2.
Value of resistors in the MHNN simulation circuit.
Multisim is an EDA platform based on interactive simulation technology, and its outstanding advantages are reflected in the deep integration of virtual instruments and real-time debugging capabilities. After several repetitive experiments, the simulation results show good repeatability and are in perfect agreement with the numerical calculations, as illustrated in Figure 16.
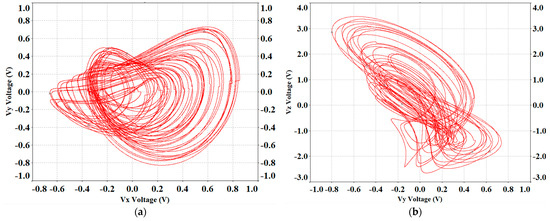
Figure 16.
Phase portraits of Multisim simulation: (a) x-y phase; (b) y-z phase.
The simulation results of the analog circuits show chaotic states that are in general agreement with those presented by the numerical results shown in Figure 6. However, due to the differences between the values of the discrete components and the system parameters, and the influence of the initial values, the final simulated waveforms deviate a little from the numerical results. In summary, the simulation results validate the feasibility of the HNN circuit, supporting its potential for physical implementation and offering a basis for investigating synaptic crosstalk in neural systems.
4.2. FPGA Implementation
FPGA is a type of silicon chip that can be reprogrammed, offering the benefits of high integration, abundant on-chip resources, and theoretically unlimited programming cycles. The initial conditions and component parameters of the system can be set using hardware programming languages to achieve precise control. This allows for accurate verification of the system’s dynamic behavior and is highly suitable for implementing nonlinear oscillators that are extremely sensitive to changes in parameters and initial values.
To solve the problem of the difficulty of accurately matching the actual parameters of the system with the mismatch of components by taking the values of discrete components in analog circuits, we further used FPGAs to compute and verify the dynamical behavior of the system.
In this study, a digital circuit was designed on Xilinx Spartan-7 series FPGA based on Vivado 2023.2 platform to discretize the chaotic system using the RK4 method. By controlling the algorithmic flow through the state machine, and using 5 adders, 5 multipliers and ROM ip-core, the mathematical operations were realized. The code was compiled into a binary bitstream file and input into the board for simulation experiments, which successfully generated the chaotic signal. The implementation flow is given below in Figure 17.
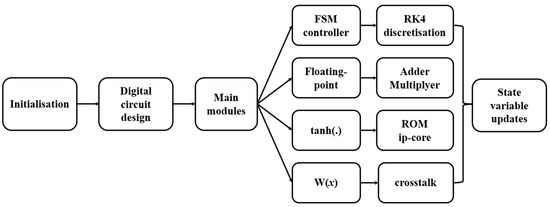
Figure 17.
Implementation flow of MHNN.
First, Equation (5) is discretized using the RK4 method:
The core computation process is divided into four phases to compute respectively, and each phase computes the derivatives of the state variables by invoking the floating-point ip-core and accumulates the intermediate results, and ultimately, the state variables are updated by weighted fusion of the derivative results of the four phases.
The output waveforms of the FPGA are shown in Figure 18a,b. Considering the output limitations of the module as well as the ease of observation, the waveform values of the FPGA are finally scaled by a factor of 2.5, and the results match the numerical simulation results presented in Figure 6 and Figure 16.
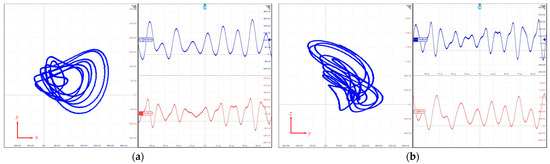
Figure 18.
FPGA phase portraits and time-domain waveforms: (a) x-y phase; (b) y-z phase.
To evaluate the implementation’s efficiency, resource usage of the FPGA is given below in Table 3. The results show that the resource occupancy of each part of the FPGA remains at a relatively low level while achieving a high level of accuracy, proving the superiority of using FPGA for the analysis of system dynamics.

Table 3.
Resource usage of the FPGA.
Through FPGA implementation, the feasibility of the proposed scheme is verified and the experimental results are consistent with the simulation analysis, which effectively proves the correctness of the system.
5. Image Encryption Application
Image encryption plays a vital role in the realm of information security. Traditional methods, such as the Arnold transform and Logistic mapping, often suffer from limitations including a small key space and the tendency to preserve statistical features of the original image. In contrast, chaotic systems exhibit extreme sensitivity to initial conditions, where even slight changes can lead to entirely different key matrices. Moreover, the ergodicity of chaotic systems ensures a random distribution of key matrix elements. Additionally, since the elements of the key matrix are strongly correlated with pixel positions, the unpredictability and security of the encryption process are significantly enhanced.
Here, we utilize the MHNN’s chaos verified in Section 3 and Section 4, where encryption performance is assessed via sensitivity of the key. In this study, a grayscale image is used as the encryption target, and the MHNN serves as the underlying chaotic model. The initial conditions are set to (0.01, 0.01, 0.01, 0, 0), with internal memristor parameters configured as and synaptic crosstalk . Under these conditions, chaotic sequences are generated and subsequently processed with the original image to produce the encrypted image.
The key generation algorithm is based on the dynamics of high-dimensional chaotic systems. By numerically solving the chaotic equations, a key matrix that is strongly correlated with the pixel positions of the image is generated, as illustrated in Figure 19.
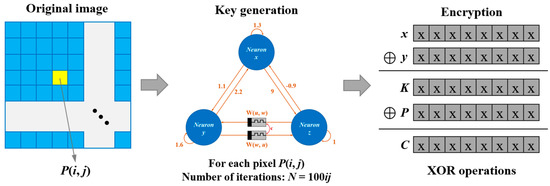
Figure 19.
Image encryption process.
The specific steps of the algorithm are as follows:
(1) Define the dynamical equations of the five-dimensional chaotic system as given in Equation (5), and numerically solve them using the RK4 method with a step size of .
(2) Initialize the variables as (0.01, 0.01, 0.01, 0, 0). For each pixel in the image, iterate the chaotic system times to obtain the chaotic variables x and y. These variables are then mapped to the integer range [0, 255] and used to compute the key matrix K, which can be expressed as
The encryption process is implemented based on the key matrix generated in Equation (26). When encrypting, each pixel of the plaintext is subjected to a pixel-wise XOR operation with the corresponding element of the key matrix , which can be expressed as
where C is the ciphertext image. The pixel values of the ciphertext image C are uniformly distributed shown in Figure 20, effectively concealing the information of the original image.
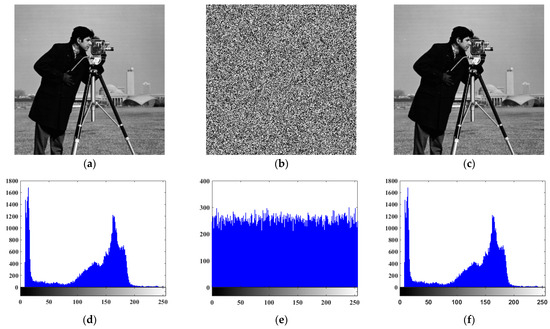
Figure 20.
Image encryption and histogram analysis: (a) Original image; (b) encrypted image; (c) decrypted image; (d) histogram of the original image; (e) histogram of the encrypted image; (f) histogram of the decrypted image.
When it comes to the decryption process, the same key matrix K is used to perform pixel-wise XOR operations on the ciphertext image C, recovering the original image by
where P’ is the decrypted image. Due to the reversibility of the XOR operation, the decrypted image P’ is identical to the original image P, ensuring lossless recovery of the information.
The histogram of the original image shows a highly uneven distribution, featuring distinct variations in sparsity and density, a broad dynamic range, and sharp peaks. In contrast, the histogram of the encrypted image exhibits a uniform distribution, with no significant spikes and a much narrower variation range, indicating that the encryption algorithm effectively disrupts the statistical features of the original image.
Key sensitivity is a vital metric for assessing the security performance of an encryption system. It is widely acknowledged that key sensitivity that satisfies the avalanche principle meets standard security requirements. Bit change rate refers to the ratio of the number of bits of the encrypted image’s octet binary value per pixel that change to the total number of bits when a small perturbation is applied to the system parameters. The avalanche principle states that an extremely small change in the key should result in a random alteration of each bit in the ciphertext sequence, with the bit change rate approaching 50%. In this study, slight perturbations were introduced to the parameters of the memristive neural network, and the corresponding changes in the encrypted ciphertext were observed. Specifically, the parameters , , and were individually varied by 10−8. The results presented in Table 4 clearly exhibit the avalanche effect, demonstrating strong key sensitivity and dependence. These findings further confirm the inherent sensitivity of chaotic systems to initial conditions.

Table 4.
Sensitivity analysis of the MHNN encryption algorithm.
The experimental results demonstrate that the proposed algorithm effectively disrupts the statistical features of the original image. In addition, the histogram of the ciphertext image exhibits a uniform distribution, and the decrypted image is completely identical to the original image.
6. Conclusions
This research proposes a novel MHNN that incorporates synaptic crosstalk, utilizing hyperbolic tangent memristors to simulate complex neuronal dynamics. The constructed three-neuron MHNN displays a wide range of nonlinear behaviors, including chaotic states, periodic oscillations, and bifurcations, as uncovered through comprehensive dynamical analyses. Methods such as Lyapunov exponent analysis, bifurcation diagrams, and phase portraits illustrate the system’s sensitivity to internal parameters, particularly the memristive parameter b and the crosstalk strength c. The observed transitions between stable and chaotic regimes underscore the model’s potential for applications that demand adaptability and dynamic response.
The feasibility of the proposed MHNN is further validated through hardware implementation. Circuit simulations in Multisim and FPGA-based realizations confirm the reproducibility of the theoretical dynamics. The integration of hyperbolic tangent memristors into the neural network enhances biological plausibility while bridging the gap to artificial models, thereby demonstrating the practical potential of memristive systems in neuromorphic computing. Moreover, the application of the MHNN to image encryption proves effective in generating position-dependent key matrices with uniform pixel distribution, offering strong resistance to statistical attacks. The high sensitivity of the encryption scheme to initial conditions and parameter variations further underscores its robustness for real-world security applications.
Overall, this work advances the understanding of memristive neural networks by integrating synaptic crosstalk and providing a comprehensive framework for their modeling, analysis, and implementation. Nevertheless, there remains ample room for algorithmic refinement. In future research, the exploration of memristive synapses in chaotic HNN is expected to extend to areas such as intelligent control, artificial intelligence, and the Internet of Things, potentially establishing memristive computing as a core technology in next-generation intelligent systems.
Author Contributions
Conceptualization, M.S. and F.M.; methodology, M.S.; software, M.S.; validation, Y.Y.; formal analysis, Y.Y.; investigation, X.H.; resources, M.S.; data curation, M.S.; writing—original draft preparation, M.S.; writing—review and editing, Q.T.; visualization, M.S.; supervision, F.M.; project administration, M.S.; funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Natural Science Foundation of China] grant number [62471237]. The APC was funded by Fuhong Min.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kawahara, M.; Kato-Negishi, M.; Tanaka, K. Cross talk between neurometals and amyloidogenic proteins at the synapse and the pathogenesis of neurodegenerative diseases. Metallomics 2017, 9, 619–633. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, G.W. Grounding neuroscience in behavioral changes using artificial neural networks. Curr. Opin. Neurobiol. 2024, 84, 102816. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Biophysical neurons, energy, and synapse controllability: A review. J. Zhejiang Univ.-Sci. A 2023, 24, 109–129. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Sun, J.; Kang, K.; Sun, Y.; Hong, Q.; Wang, C. A multivalue 3d crossbar array nonvolatile memory based on pure memristors. Eur. Phys. J. Spec. Top. 2022, 231, 3119–3130. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Liu, R.; Zhao, K.; Dou, G. An associative memory circuit based on physical memristors. Neurocomputing 2022, 472, 12–23. [Google Scholar] [CrossRef]
- Qiu, R.; Dong, Y.; Jiang, X.; Wang, G. Two-Neuron Based Memristive Hopfield Neural Network with Synaptic Cross-talk. Electronics 2022, 11, 3034. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Xu, Q.; Ding, X.; Chen, B.; Parastesh, F.; Iu, H.H.C.; Wang, N. A universal configuration framework for mem-element-emulator-based bionic firing circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4120–4130. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Iu, H.H.C.; Wang, N.; Bao, H. Locally active memristor based neuromorphic circuit: Firing pattern and hardware experiment. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3130–3141. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, X.; Wu, H.; Iu, H.H.C.; Parastesh, F.; Wang, N. ReLU function-based locally active memristor and its application in generating spiking behaviors. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4551–4555. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of 2-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Min, F.; Cai, J.; Bao, H. Memristor Synapse-Driven Simplified Hopfield Neural Network: Hidden Dynamics, Attractor Control, and Circuit Implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 2308–2319. [Google Scholar] [CrossRef]
- Chen, C.; Min, F.; Zhang, Y.; Bao, B. Memristive electromagnetic induction effects on Hopfield neural network. Nonlinear Dyn. 2021, 106, 2559–2576. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, X.; Yang, Q.; Liu, P.; Wang, Y. Memristor-based Hopfield Network Circuit for Recognition and Sequencing Application. AEU-Int. J. Electron. Commun. 2021, 134, 1536984. [Google Scholar] [CrossRef]
- Bao, B.; Qian, H.; Xu, Q.; Chen, M.; Wang, J.; Yu, Y. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based Hopfield neural network. Front. Comput. Neurosci. 2017, 11, 81. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J.; Bao, H.; Chen, M.; Bao, B. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn. 2019, 95, 3385–3399. [Google Scholar] [CrossRef]
- Citko, W.; Sienko, W. Inpainted image reconstruction using an extended Hopfield neural network based machine learning system. Sensors 2022, 22, 813. [Google Scholar] [CrossRef]
- Rubio-Manzano, C.; Segura-Navarrete, A.; Martinez-Araneda, C.; Vidal-Castro, C. Explainable Hopfield neural networks using an automatic video-generation system. Appl. Sci. 2021, 11, 5771. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P. Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors 2021, 21, 4567. [Google Scholar] [CrossRef]
- Yang, C.; Hu, Q.; Yu, Y.; Zhang, R.; Yao, Y.; Cai, J. Memristor-Based Chaotic Circuit for Text/Image Encryption and Decryption. In Proceedings of the 2015 8th International Symposium on Computational Intelligence and Design, Hangzhou, China, 12–13 December 2015; Volume 1, pp. 447–450. [Google Scholar]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-Like Initial-Boosted Hyperchaos and Application in Biomedical Image Encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Gonzalez, J.A.G.; de Magdaleno, J.J.R.; Pacheco, J.M.M. FPGA Implementation of a Multi-PRNG Based on a Multiscroll Chaotic Hopfield Neural Network. IEEE Trans. Ind. Inform. 2025, 21, 3097–3106. [Google Scholar] [CrossRef]
- Chen, C.; Bao, H.; Zhang, Y.; Yu, Y.; Zhao, S.; Yang, Y.; Chen, L. Synchronization and Coupling Dynamics in Memristive Homogeneous and Heterogeneous Hopfield Neural Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 71, 1–14. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Zhang, H.; Chen, G. Design and Analysis of Multiscroll Memristive Hopfield Neural Network With Adjustable Memductance and Application to Image Encryption. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7824–7837. [Google Scholar] [CrossRef]
- Parks, P.C. A new proof of the Routh-Hurwitz stability criterion using the second method of Lyapunov. Math. Proc. Camb. Philos. Soc. 1962, 58, 694–702. [Google Scholar] [CrossRef]
- Chen, C.; Min, F. Memristive bi-neuron Hopfield neural network with coexisting symmetric behaviors. Eur. Phys. J. Plus 2022, 137, 841. [Google Scholar] [CrossRef]
- Bao, B.C.; Qian, H.; Wang, J.; Xu, Q.; Chen, M.; Wu, H.; Yu, Y.J. Numerical analyses and experimental validations of coexisting multiple attractors in Hopfield neural network. Nonlinear Dyn. 2017, 90, 2359–2369. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.; Wang, X. Dynamical characteristics of an HP memristor based on an equivalent circuit model in a chaotic oscillator. Chin. Phys. B 2015, 24, 207–215. [Google Scholar] [CrossRef]
- Bao, B.C.; Chen, C.J.; Bao, H.; Zhang, X.; Xu, Q.; Chen, M. Dynamical Effects of Neuron Activation Gradient on Hopfield Neural Network: Numerical Analyses and Hardware Experiments. Int. J. Bifurc. Chaos 2019, 29, 1930010. [Google Scholar] [CrossRef]
- Huang, L.L.; Wang, Y.L.; Jiang, Y.C.; Lei, T.F. A Novel Memristor Chaotic System with a Hidden Attractor and Multistability and Its Implementation in a Circuit. Math. Probl. Eng. 2021, 2021, 7457220. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).