MSGformer: A Hybrid Multi-Scale Graph–Transformer Architecture for Unified Short- and Long-Term Financial Time Series Forecasting
Abstract
1. Introduction
- We developed MSGformer to forecast financial time series, effectively capturing short-term volatility and long-term dependencies in market data;
- To address the challenges of capturing local short-term dependencies in high-dimensional financial data, we incorporated a multi-scale graph neural network (MSGnet) to model complex market dynamics at multiple scales, improving the model’s ability to handle varied time resolutions;
- By combining MSGnet’s ability to handle multi-dimensional data and Transformer’s attention mechanism, the proposed model overcomes the limitations of single-model approaches, achieving improved prediction accuracy across different financial forecasting tasks.
2. Related Work
2.1. Traditional Methods
2.2. Deep Learning Approaches
2.3. Transformer Methods
3. Methodology
3.1. MSGNet
- Identify the scale of the input time series;
- Use adaptive graph convolution blocks to reveal the inter-sequence correlation of scale links;
- Capture intra-sequence correlation through multi-head attention;
- Use the SoftMax function to adaptively aggregate representations from different scales.
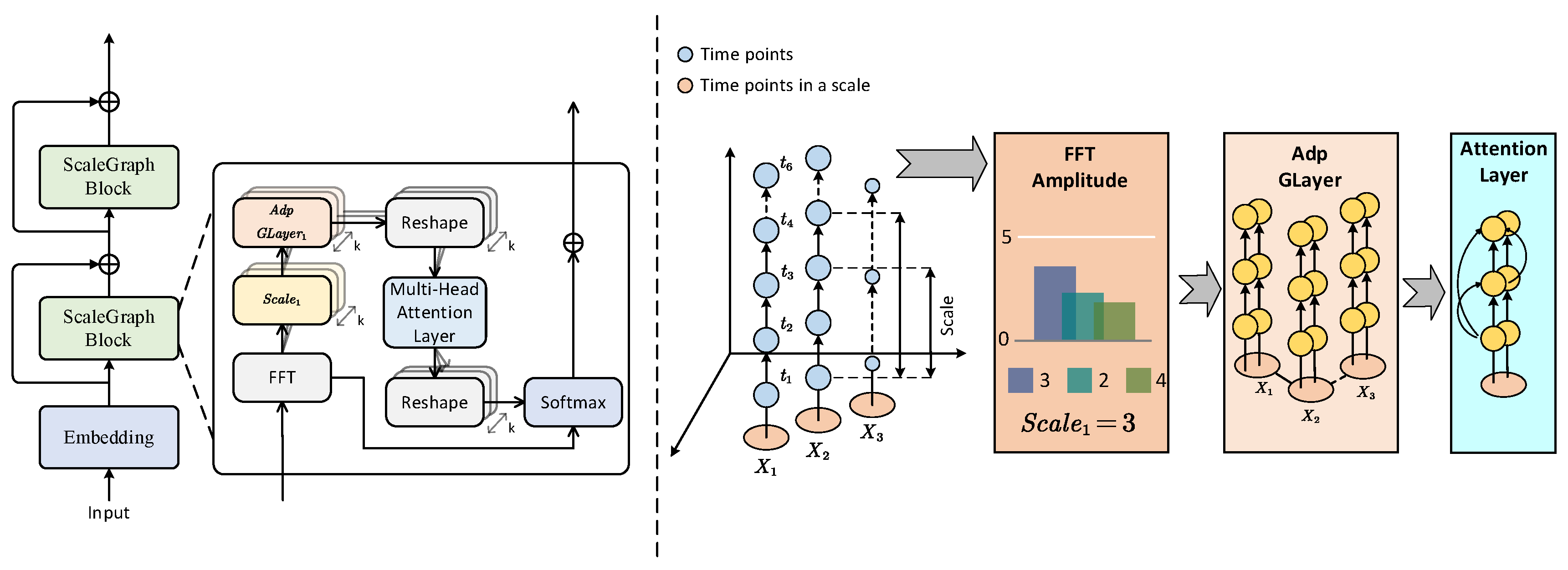
3.1.1. Scale Identification
3.1.2. Adaptive Graph Convolution
3.1.3. Multi-Head Attention and Scale Aggregation
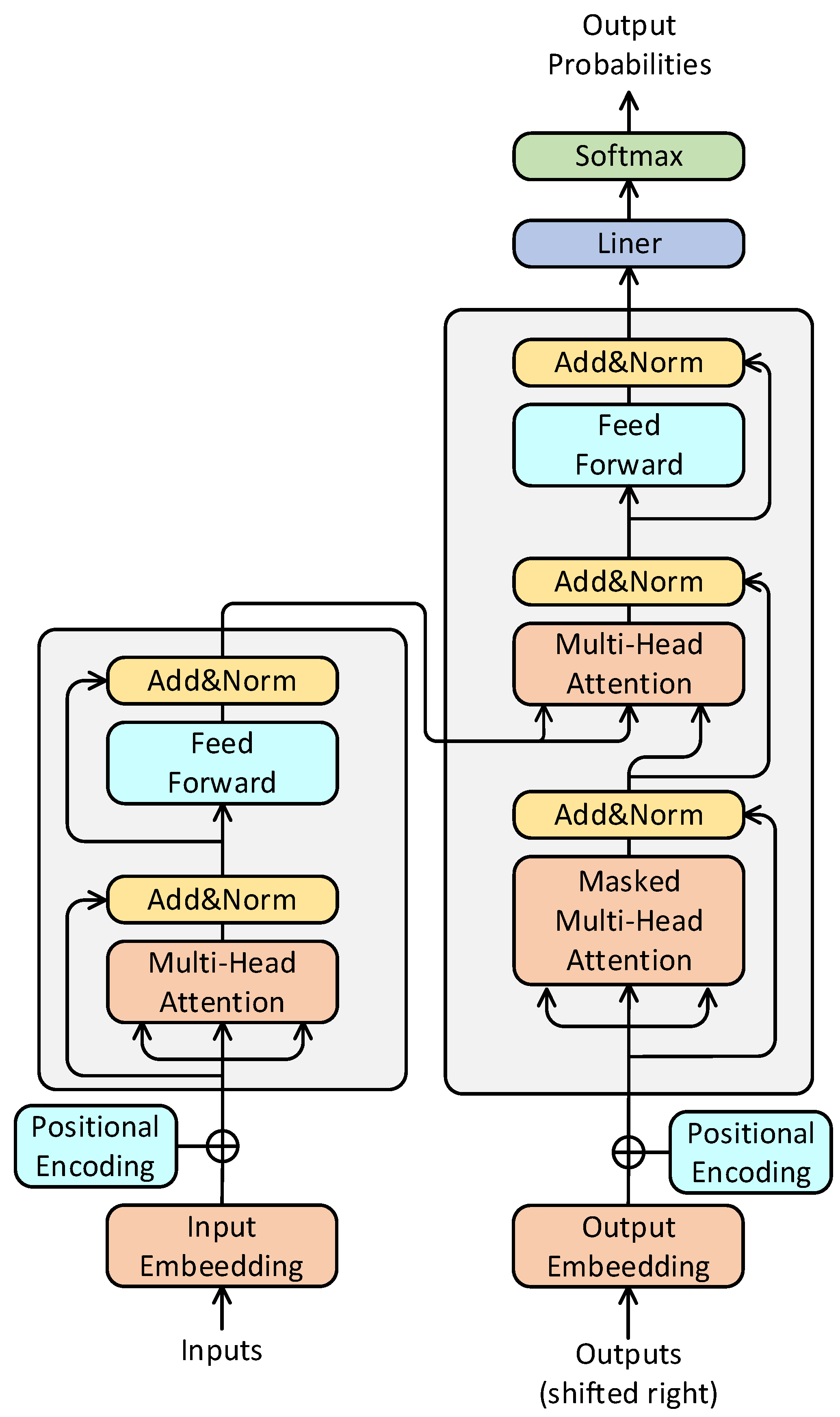
3.2. Transformer
3.2.1. Self-Attention
- Query: Each input element is mapped into a query vector (Q);
- Key: Each input element is also mapped to a bond vector (K);
- Value: Each input element is mapped to a value vector (V).
3.2.2. Multi-Head Attention
3.2.3. Positional Encoding
3.2.4. Encoder and Decoder Structures
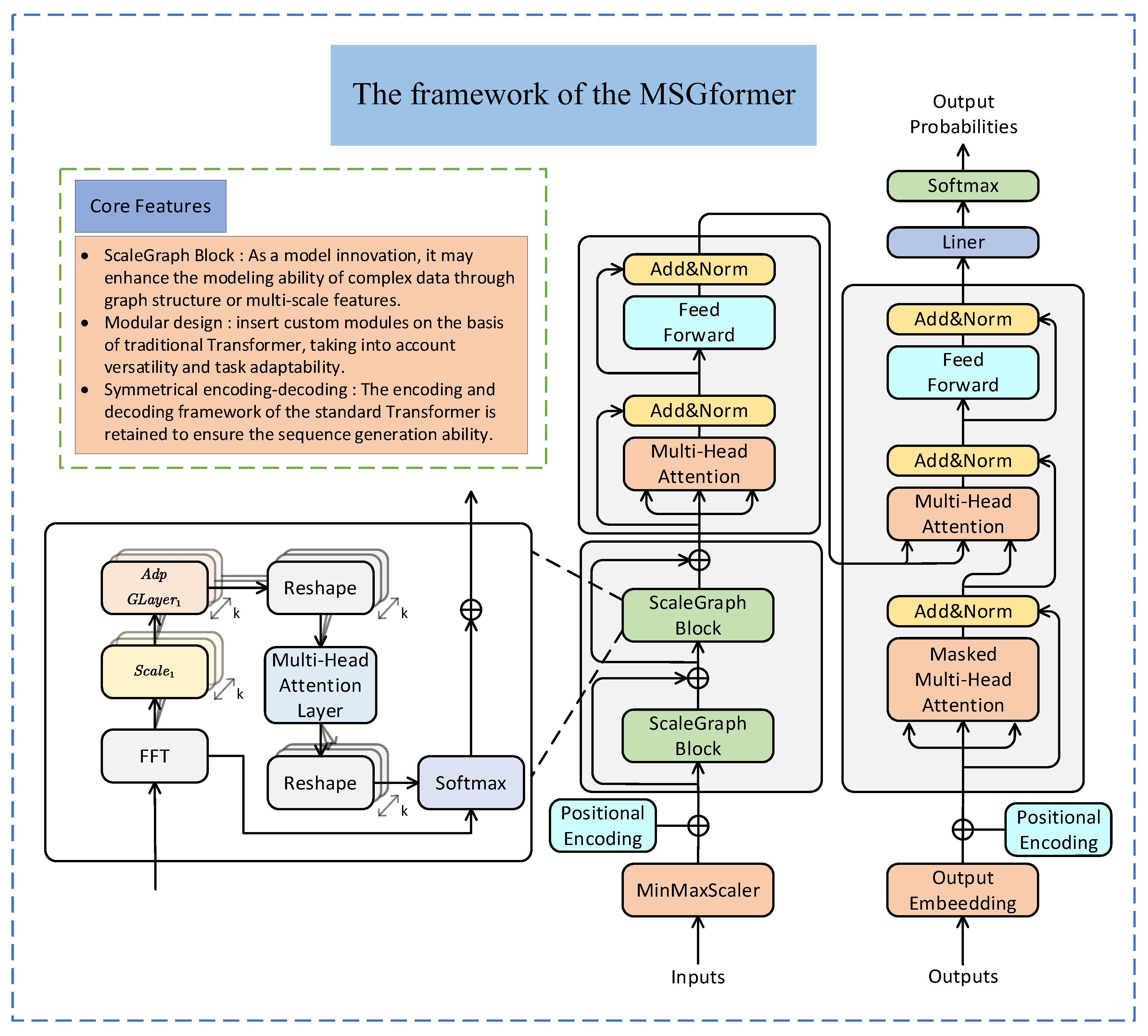
3.3. MSGformer Hybrid Model
Structure of MSGformer
4. Experiments
4.1. Data Processing
4.2. Evaluation Criteria
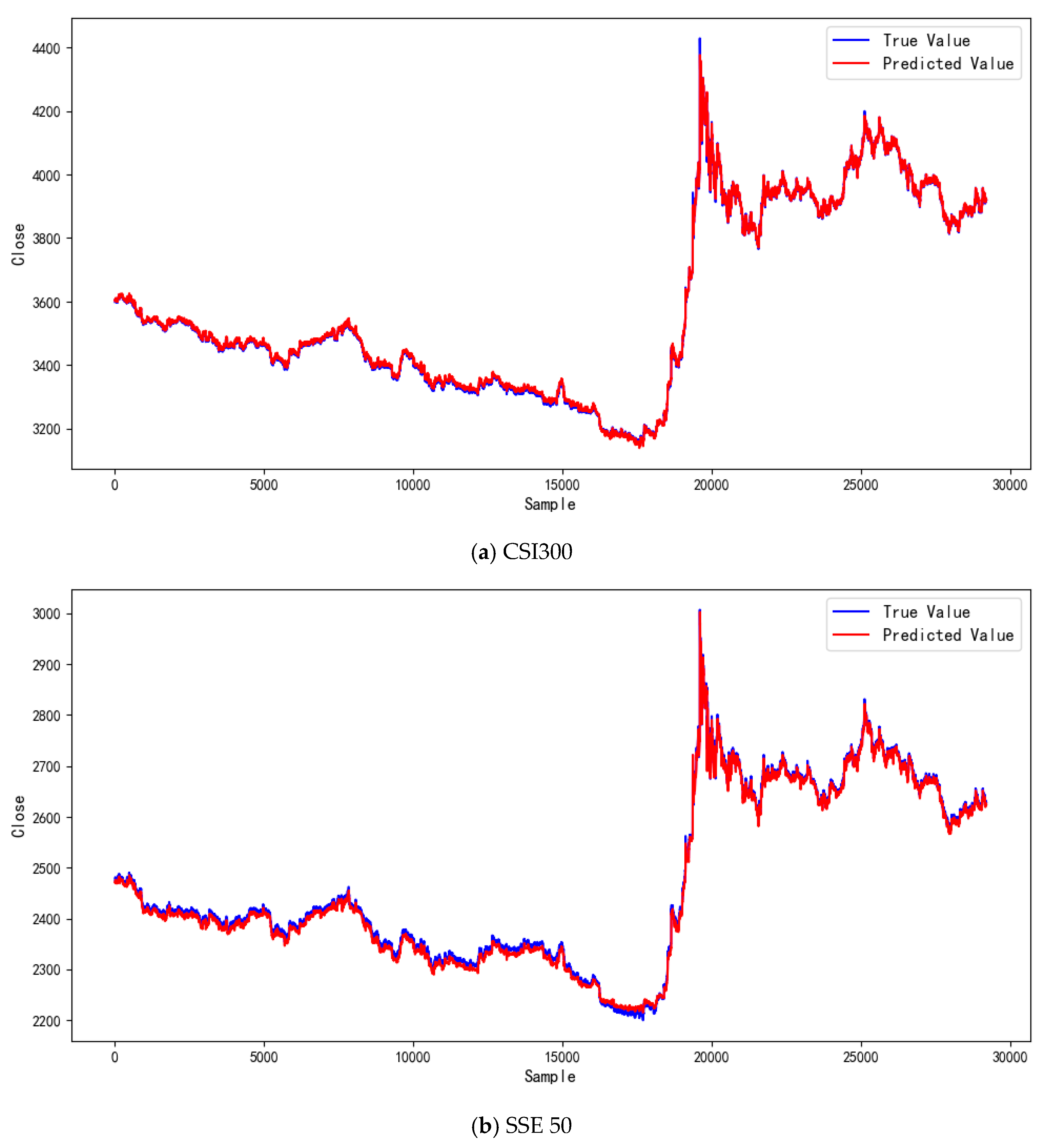
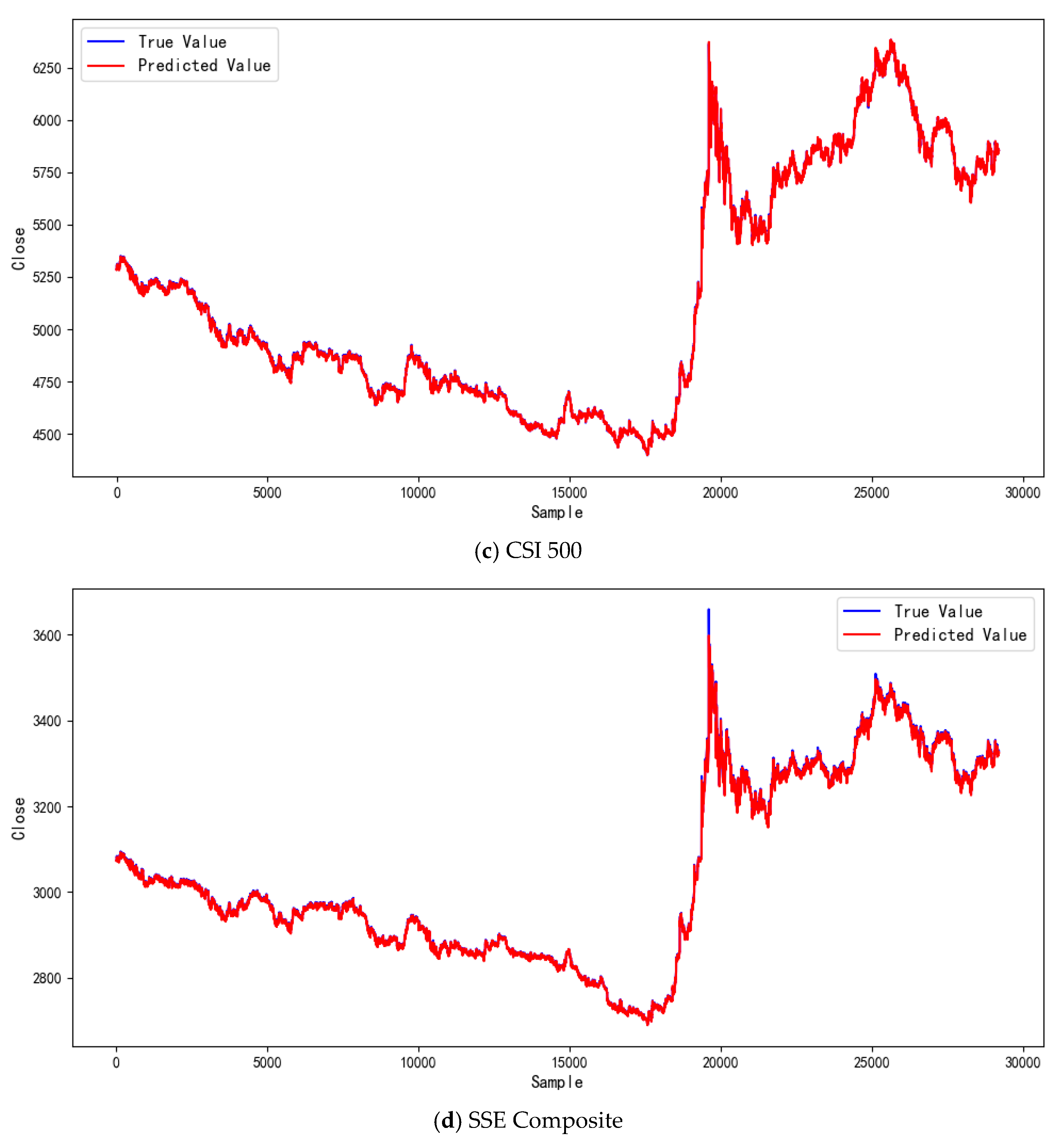
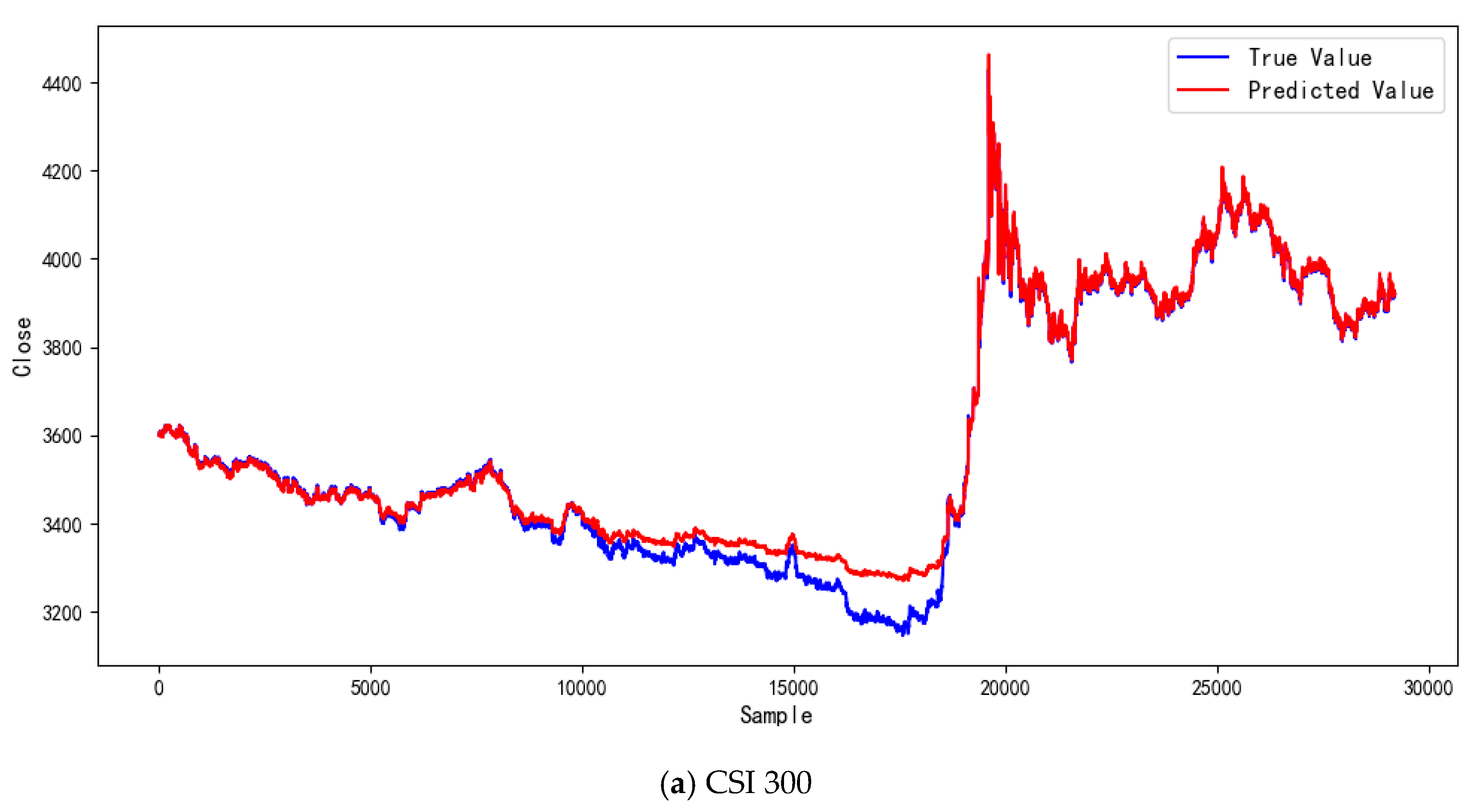
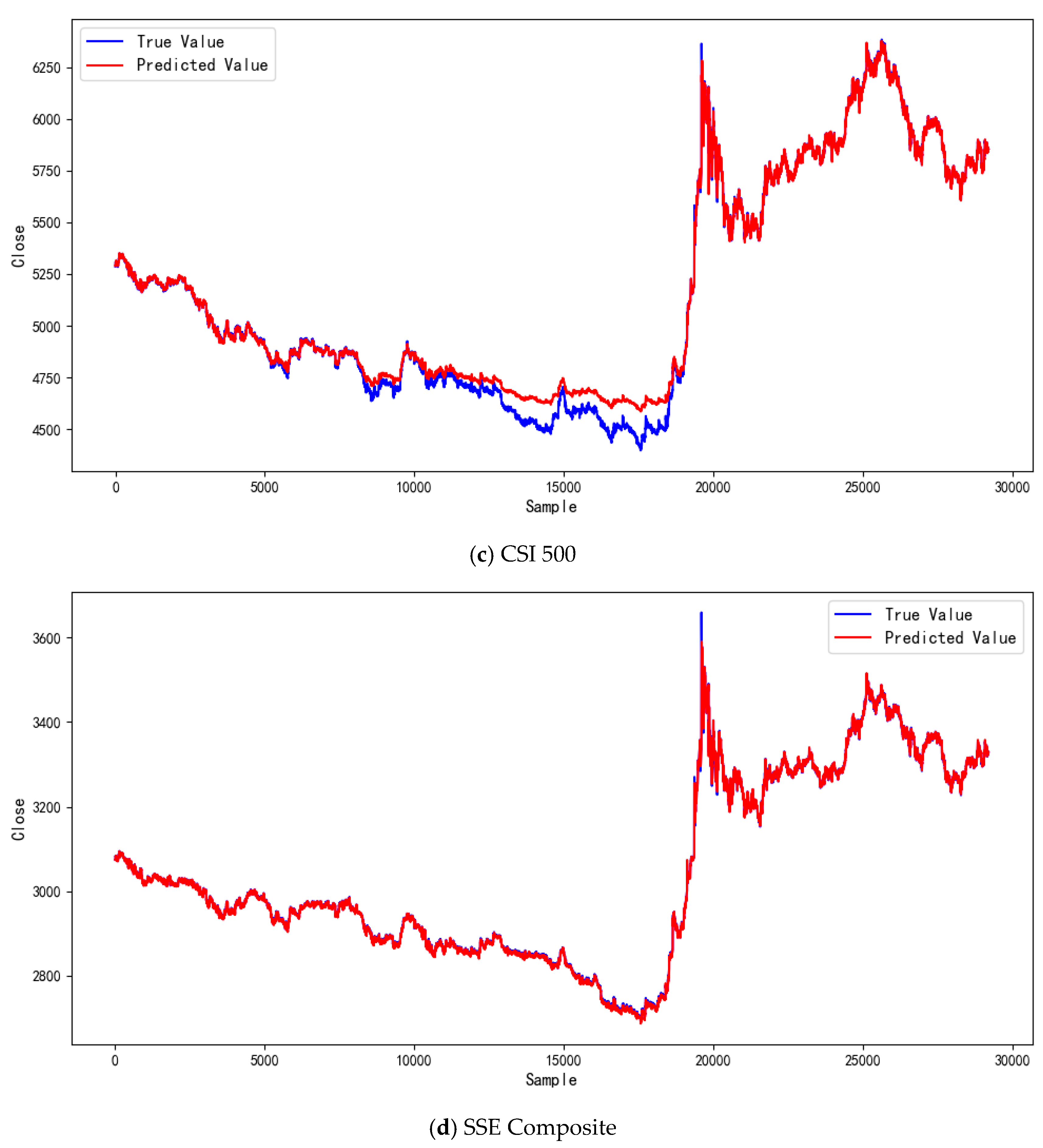
4.3. Comparative Experiments and Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fama, E.F. Efficient capital markets. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Roll, R. Volatility, correlation, and diversification in a multi-factor world. J. Portf. Manag. 2013, 39, 11–18. [Google Scholar] [CrossRef]
- Ongan, S.; Gocer, I. Testing the causalities between economic policy uncertainty and the US stock indices: Applications of linear and nonlinear approaches. Ann. Financ. Econ. 2017, 12, 1750016. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Franses, P.H.; Van Dijk, D. Non-Linear Time Series Models in Empirical Finance; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Elizar, E.; Zulkifley, M.A.; Muharar, R.; Zaman, M.H.M.; Mustaza, S.M. A Review on Multiscale-Deep-Learning Applications. Sensors 2022, 22, 7384. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Supervised Sequence Labelling; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–13. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Dosovitskiy, A.; Fischer, P.; Springenberg, J.T.; Riedmiller, M.; Brox, T. Discriminative unsupervised feature learning with convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Zhang, L.; Radke, R.J. A Multi-Stream Recurrent Neural Network for Social Role Detection in Multiparty Interactions. IEEE J. Sel. Top. Signal Process. 2020, 14, 554–567. [Google Scholar] [CrossRef]
- Keneshloo, Y.; Shi, T.; Ramakrishnan, N.; Reddy, C.K. Deep Reinforcement Learning for Sequence-to-Sequence Models. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2469–2489. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 11121–11128. [Google Scholar] [CrossRef]
- Nie, Y.; Kong, Y.; Dong, X.; Mulvey, J.M.; Poor, H.V.; Wen, Q.; Zohren, S. A survey of large language models for financial applications: Progress, prospects and challenges. arXiv 2024, arXiv:2406.11903. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Cheng, W.K.; Bea, K.T.; Leow, S.M.H.; Chan, J.Y.-L.; Hong, Z.-W.; Chen, Y.-L. A Review of Sentiment, Semantic and Event-Extraction-Based Approaches in Stock Forecasting. Mathematics 2022, 10, 2437. [Google Scholar] [CrossRef]
- Li, W.; Law, K.L.E. Deep Learning Models for Time Series Forecasting: A Review. IEEE Access 2024, 12, 92306–92327. [Google Scholar] [CrossRef]
- Cai, W.; Liang, Y.; Liu, X.; Feng, J.; Wu, Y. MSGNet: Learning Multi-Scale Inter-series Correlations for Multivariate Time Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2024, 38, 11141–11149. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis; University of Cambridge: Cambridge, UK, 1995; Volume 9514, pp. 370–413. [Google Scholar]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econ. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Ghysels, E.; Santa-Clara, P.; Valkanov, R. Predicting volatility: Getting the most out of return data sampled at different frequencies. J. Econ. 2006, 131, 59–95. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, H.; Yang, Z.; Wang, J.; Zhang, S.; Sun, Y.; Yang, L. A hybrid model based on neural networks for biomedical relation extraction. J. Biomed. Inform. 2018, 81, 83–92. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock and stock price index movement using Trend Deterministic Data Preparation and machine learning techniques. Expert Syst. Appl. 2015, 42, 259–268. [Google Scholar] [CrossRef]
- Atsalakis, G.S.; Valavanis, K.P. Surveying stock market forecasting techniques—Part II: Soft computing methods. Expert Syst. Appl. 2009, 36, 5932–5941. [Google Scholar] [CrossRef]
- Bao, W.; Yue, J.; Rao, Y.; Podobnik, B. A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PLoS ONE 2017, 12, e0180944. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Wang, J.-J.; Zhang, Z.-G.; Guo, S.-P. Forecasting stock indices with back propagation neural network. Expert Syst. Appl. 2011, 38, 14346–14355. [Google Scholar] [CrossRef]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. Efficient Stock-Market Prediction Using Ensemble Support Vector Machine. Open Comput. Sci. 2020, 10, 153–163. [Google Scholar] [CrossRef]
- Tsantekidis, A.; Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Forecasting Stock Prices from the Limit Order Book Using Convolutional Neural Networks. In Proceedings of the 2017 IEEE 19th Conference on Business Informatics (CBI), Thessaloniki, Greece, 24–27 July 2017; Volume 1, pp. 7–12. [Google Scholar] [CrossRef]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, Y.; Dai, F. A LSTM-based method for stock returns prediction: A case study of China stock market. In Proceedings of the IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 2823–2824. [Google Scholar]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Nelson, D.M.Q.; Pereira, A.C.M.; de Oliveira, R.A. Stock market’s price movement prediction with LSTM neural networks. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1419–1426. [Google Scholar]
- Wan, A.; Chang, Q.; Al-Bukhaiti, K.; He, J. Short-term power load forecasting for combined heat and power using CNN-LSTM enhanced by attention mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar] [CrossRef]
- Huang, X.; Tang, J.; Shen, Y. Long time series of ocean wave prediction based on PatchTST model. Ocean Eng. 2024, 301, 117572. [Google Scholar] [CrossRef]
- Woo, G.; Liu, C.; Sahoo, D.; Kumar, A.; Hoi, S. Etsformer: Exponential smoothing transformers for time-series forecasting. arXiv 2022, arXiv:2202.01381. [Google Scholar] [CrossRef]






| Configuration | |
|---|---|
| CPU | Intel Core i7-10700K (Intel Corp., Santa Clara, CA, USA) |
| GPU | NVIDIA GeForce RTX 4060 Ti (NVIDIA Corp., Santa Clara, CA, USA) |
| CUDA | CUDA 12.4 (NVIDIA Corp., Santa Clara, CA, USA) |
| Python version | Python 3.9 (Python Software Foundation, Wilmington, DE, USA) |
| Memory | 32 GB RAM |
| System | Windows (Microsoft Corp., Redmond, WA, USA) |
| Index | Models | MAE | RMSE | MAPE | |
|---|---|---|---|---|---|
| CSI 300 | Transformer | 0.9905 | 10.8179 | 13.3415 | 0.0038 |
| Pathformer | 0.9894 | 11.3875 | 12.9232 | 0.0031 | |
| Autoformer | 0.9849 | 13.2042 | 17.0685 | 0.0061 | |
| MSGformer | 0.9941 | 10.2282 | 12.6522 | 0.0024 | |
| SSE 50 | Transformer | 0.9985 | 9.2220 | 9.8891 | 0.0021 |
| Pathformer | 0.9981 | 9.4156 | 8.3423 | 0.0026 | |
| Autoformer | 0.9982 | 8.1590 | 7.8891 | 0.0025 | |
| MSGformer | 0.9987 | 7.8576 | 6.8296 | 0.0016 | |
| CSI 500 | Transformer | 0.9844 | 11.8954 | 11.7771 | 0.0035 |
| Pathformer | 0.9951 | 8.3648 | 9.5604 | 0.0047 | |
| Autoformer | 0.9836 | 15.6371 | 13.8985 | 0.0054 | |
| MSGformer | 0.9971 | 6.4520 | 7.5604 | 0.0018 | |
| SSE Composite | Transformer | 0.9913 | 2.5685 | 4.1778 | 0.0013 |
| Pathformer | 0.9954 | 2.5081 | 3.9778 | 0.0009 | |
| Autoformer | 0.9924 | 2. 9687 | 4.9367 | 0.0011 | |
| MSGformer | 0.9996 | 2.2553 | 3.9267 | 0.0007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Qi, H.; Ni, S.; Liu, Y. MSGformer: A Hybrid Multi-Scale Graph–Transformer Architecture for Unified Short- and Long-Term Financial Time Series Forecasting. Electronics 2025, 14, 2457. https://doi.org/10.3390/electronics14122457
Zhu M, Qi H, Ni S, Liu Y. MSGformer: A Hybrid Multi-Scale Graph–Transformer Architecture for Unified Short- and Long-Term Financial Time Series Forecasting. Electronics. 2025; 14(12):2457. https://doi.org/10.3390/electronics14122457
Chicago/Turabian StyleZhu, Mingfu, Haoran Qi, Shuiping Ni, and Yaxing Liu. 2025. "MSGformer: A Hybrid Multi-Scale Graph–Transformer Architecture for Unified Short- and Long-Term Financial Time Series Forecasting" Electronics 14, no. 12: 2457. https://doi.org/10.3390/electronics14122457
APA StyleZhu, M., Qi, H., Ni, S., & Liu, Y. (2025). MSGformer: A Hybrid Multi-Scale Graph–Transformer Architecture for Unified Short- and Long-Term Financial Time Series Forecasting. Electronics, 14(12), 2457. https://doi.org/10.3390/electronics14122457






