Frequency-Scaled Semisymbolic Analysis

Abstract

Semisymbolic analysis is one of the most valuable procedures in the automated design of circuits because it provides the poles and zeros of a transfer function. The algorithm itself consists of formulating a generalized eigenvalue problem, which is subsequently transformed into a standard one to be finally solved by the modification of a QR or QZ algorithm. Semisymbolic analysis itself has been known for a very long time, and its problems with numerical accuracy have also been known for a very long time. Since the advent of very fast circuits, this problem has heightened due to the presence of extremely small capacitances and inductances, which make the values in the matrices differ by a huge number of orders of magnitude. One option to solve this problem of numerical instability is to use more accurate arithmetics such as 128-bit numbers (and our previous works have assessed this possibility). In this article, however, we propose a more sophisticated procedure based on frequency scaling, which naturally balances the magnitudes of the matrix elements. The proposed algorithm is thoroughly verified in this study by a number of control analyses demonstrating that the use of the frequency scaling allows for accurate results to be achieved even using standard 64-bit arithmetic. Moreover, the article also shows that the implementation of frequency scaling into the subroutines for semisymbolic analysis is very easy. The overall efficiency of the newly developed algorithm is summarized in a final table that clearly shows that the number of obtained accurate and almost accurate poles and zeros increased significantly after the implementation of the suggested frequency scaling.

1. Introduction

Semisymbolic analysis is utilized in many areas of circuit design [1,2,3,4,5,6,7,8,9,10,11]. A general idea of how to use semisymbolic analysis for computing the poles and zeros of a transfer function was initially described in [12], where a very important method of utilizing the sparsity of matrices was also suggested. This procedure systematically transforms the general eigenvalue problem into the standard one that is solved by QR or QZ [13] algorithms afterward. However, for many years, several numerical problems of this procedure have been recognized with miscellaneous suggestions of ways to overcome them:

• More studies have been devoted to solving (very) large-scale problems [14,15,16,17], e.g., from both the efficiency and the accuracy points of view. Furthermore, using parallelism could also be a natural answer to this problem—in particular, contemporary versions of Fortran (2018 or 2023) are very suitable for programming these tasks [18,19].
• Some studies have worked on solving the well-known (and almost annoying) problem of the standard eigenvalue task: the accuracy of the computation of multiple or nearly multiple eigenvalues [20,21,22,23].
• Many studies have also generally focused on the frequently insufficient precision of semisymbolic analyses, which is caused by the numerical processes utilized [24,25].

Frequency scaling techniques have been successfully used in many areas of frequency planning, microwave electronics, antenna constructions, neural networks, and numerical methods in physical design [26,27,28,29,30,31], and it is not surprising that these procedures often include microwaves because there are huge differences in the values of individual circuit elements or technological parameters in the area of very high frequencies. However, we did not find any use for frequency scaling in semisymbolic analysis, i.e., in reducing the general eigenvalue problem to the standard one solved afterward via QR or QZ algorithms, which provides the poles and zeros of a transfer function of a linear or linearized circuit. For this reason, the utilization of frequency-scaled semisymbolic analysis to more accurately compute the poles and zeros of the circuit transfer function is designated as the fundamental goal of this article.

As this theme is unusual, we also demonstrate a simple method for formulating the modified system of equations for frequency-scaled semisymbolic analysis and how to determine the real poles and zeros of the transfer function corresponding to the original (unscaled) system. Moreover, the method of transforming the general eigenvalue problem into the standard one is demonstrated on an analytically solved (extraordinary) so-called dynamically degenerate circuit. Finally, the precision is increased by means of frequency-scaled semisymbolic analysis on a wide class of electrical circuits, especially microwave circuits, for which the accuracy enhancement is most necessary.

This article is organized as follows. In the beginning, there is a brief overview of the semisymbolic analysis utilized for computing the poles and zeros of linear circuits or circuits that are linearized at an operating point. The original ideas of this type of analysis can be found in [12], which is based on the fundamental theoretical article [32]. Other details are not included here because they can also be found in our previous conference paper [33] and book chapter [17]. Moreover, for a clearer understanding of how the semisymbolic analysis works without a detailed search of the literature, we included a detailed procedure of the algorithm after the initial overview, which unambiguously and completely defines the entire generalized reducing procedure of characteristic numbers to the standard form.

The method is then demonstrated using an unusual example—a dynamically degenerate circuit [34]—where a nonstandard step of the reduction procedure (in the semisymbolic analysis) must be used (This step has already been shown for a digital filter in [17]; however, here, its necessary use for an analog circuit is also shown, which is quite unusual in this area). Afterward, there is a section in which a simple method of formulating equations for frequency-scaled semisymbolic analysis is explained, as well as how the real (non-transformed) poles and zeros (and the constant of the transfer function) are obtained after it ends. Finally, the accuracy and reliability of the algorithm are verified by determining the poles and zeros of transfer functions of the following four electronic circuits that are known (and tested) for considerable numerical demands in the semisymbolic analysis:

• Low-noise antenna amplifier for a multi-constellation radio receiver for all (five) satellite navigation systems [26]—details of methods for creating the low-noise devices as well as some corresponding computer-aided design tools are described in [35,36,37,38].
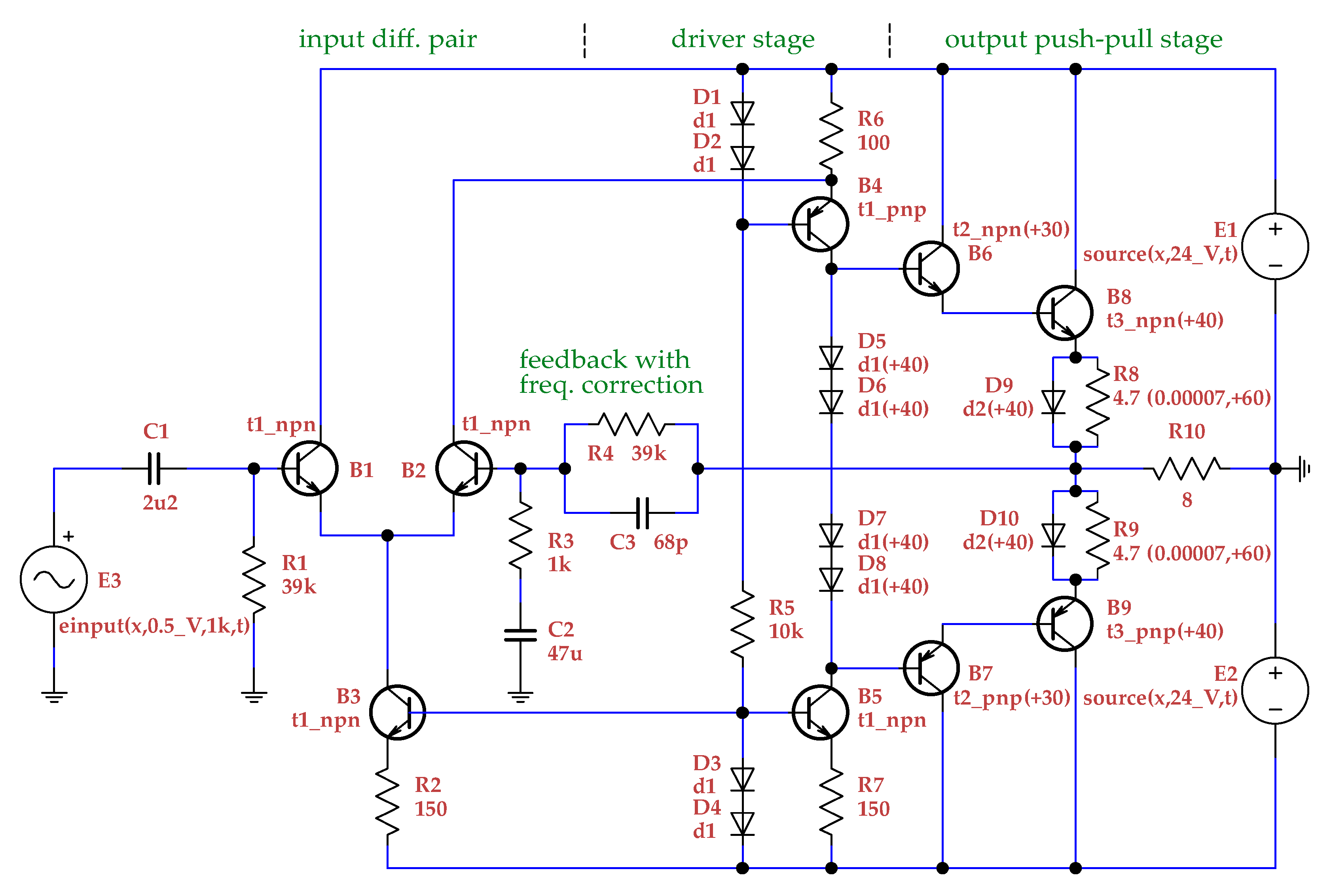
• An AB-class power amplifier [39] linearized at an operating point—more negative feedback as well as tiny capacitors of some transistors cause huge differences among the magnitudes of poles and (especially) zeros of a transfer function.
• A testbench circuit with the MDA272 operational amplifier [33,40]—as this circuit is (much more) complicated than the previous one, it also requires a more demanding test.
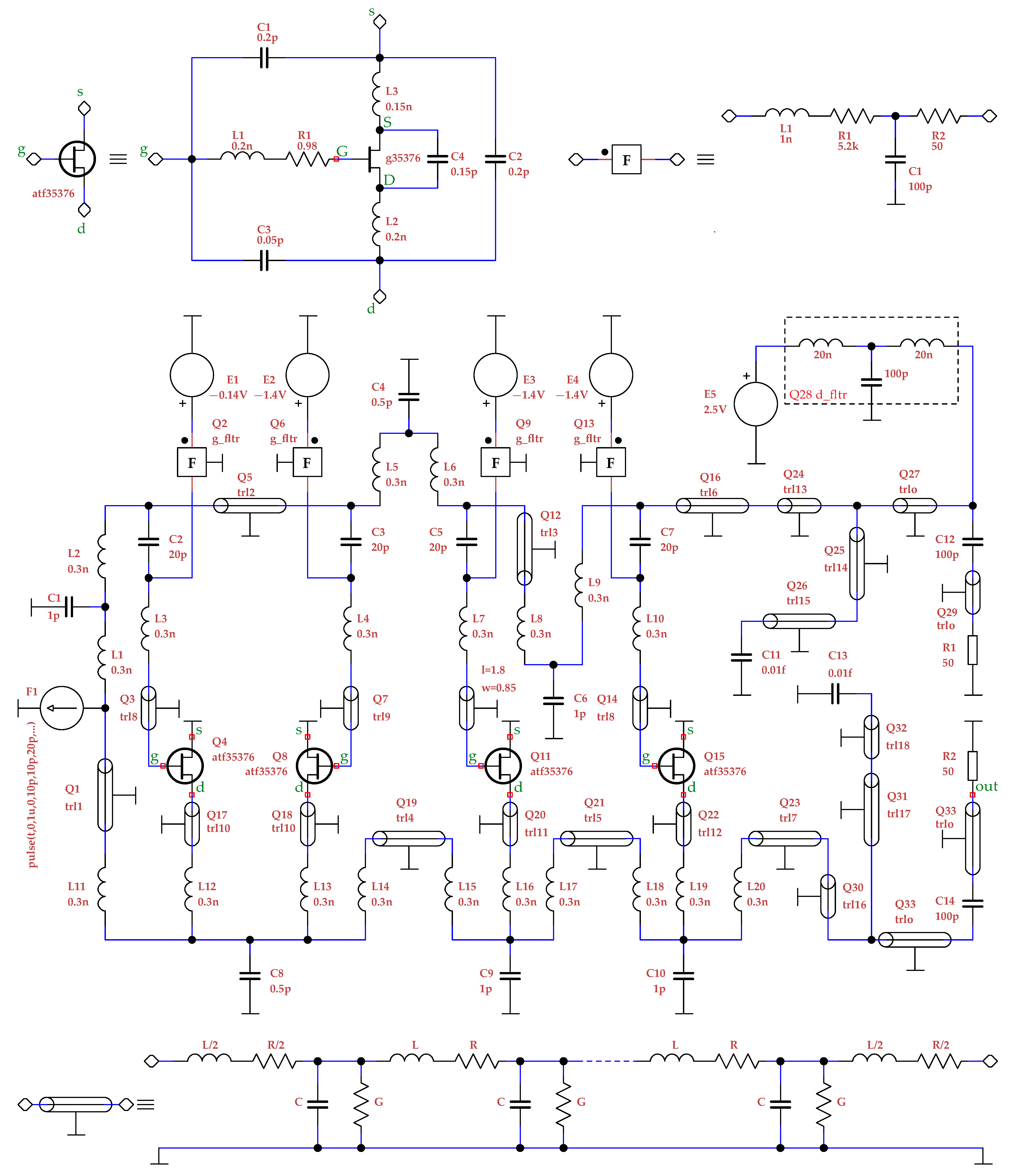
• A distributed microwave oscillator [41] represents the most demanding test—the LRCG models of microstrip lines, as well as the models of pHEMTs contain some extremely small values of parameters. Therefore, the frequency-scaled semisymbolic analysis is thoroughly verified here.

And because there is also the logical possibility of improving the numerical stability of the calculations by combining frequency scaling and 128-bit arithmetic, the benefits of this approach are demonstrated in one of the examples above. As expected, there is a further increase in the numerical robustness of the whole process in terms of choosing an accuracy parameter value. However, because this article is primarily focused on frequency-scaled semisymbolic analysis (in which all the above tasks could be managed using standard 64-bit arithmetic), we do not expand on this matter to such a level of detail in this paper (In addition, better stability of numerical calculation can obviously be expected with 128-bit arithmetic).

The purpose of the work and its significance are clear:

• First of all, this study shows that the formulation of the system of equations for frequency-scaled semisymbolic analysis is very simple, only slightly more complicated in comparison with standard (unscaled) semisymbolic analysis. Moreover, recalculation of the results of the frequency-scaled semisymbolic analysis to the actual (untransformed) values of the poles and zeros of the circuit is also very simple.
• Although the above operations (both before and after the semisymbolic analysis) are very simple to implement, they lead to a substantial accuracy improvement, which is clearly demonstrated in the four selected examples. This uncomplicated adjustment of the algorithm, leading to much more accurate results, is the main purpose of the article.

2. Brief Characteristics of Semisymbolic Analysis

In this section, we focus on the brief characteristic of semisymbolic analysis with the necessary definitions needed in the following sections. Many more details about this very useful type of analysis can be found in [1,12,13,14,15,16,17,21,22,24,33,34,39]. However, everything needed to explain the principle of frequency-scaled semisymbolic analysis is present in this section.

2.1. Reduction in Generalized Problem of Eigenvalues to Standard Problem of Eigenvalues

The system of the circuit equations of a linear circuit or a nonlinear circuit linearized at an operating point is defined by the matrix equation (see [12], e.g., and many new ones):

$$\left(s\mathit{A}+\mathit{B}\right)\mathit{v}=\mathit{e},$$

(1)

where s stands for the Laplace operator, $\mathit{A}$ and $\mathit{B}$ matrices are composed of circuit reactances and resistances depending on the method of formulating equations, and $\mathit{v}$ and $\mathit{e}$ are the Laplace images of circuit variables and input sources, respectively [14].

Poles (of all transfer functions) and zeros (of a specific transfer function) are solutions to generalized problems of eigenvalues:

$$\begin{array}{ccc}\hfill & det\left(s\mathit{A}+\mathit{B}\right)=0\hfill & \hfill \mathrm{for}\mathrm{poles},\end{array}$$

(2)

$$\begin{array}{ccc}\hfill & det\left(s{\mathit{A}}_k\left(\mathbf{0}\right)+{\mathit{B}}_k\left({\mathit{e}}_l\right)\right)=0\hfill & \hfill \mathrm{for}\mathrm{zeros},\end{array}$$

(3)

where the matrix ${\mathit{A}}_k\left(\mathbf{0}\right)$ is formed by replacing the $k$th column of $\mathit{A}$ with the column of zeros, and ${\mathit{B}}_k\left({\mathit{e}}_l\right)$ is created from $\mathit{B}$ by replacing its $k$th column with the column $\mathit{e}$, with all its elements zeroed, with the exception of one representing the $l$th source of an input signal.

It goes without saying that the solution to the generalized problem of eigenvalues is more complicated than solving the standard problem of eigenvalues $det(s\mathbf{I}-\mathit{X})=0$ (which is carefully treated in the literature and for which there are numerous software libraries). Therefore, a systematic reduction in the generalized eigenvalue problem into the standard eigenvalue problem (so-called deflation to the standard form) is performed using a sequence of operations that do not change the value of the determinant, except for its sign.

Using this systematically performed sequence (the system arrangement is described in detail, for example, in [12,34,39], etc.), the matrices in (2) and (3) are converted to the shape shown in Figure 1. The matrices ${\mathit{A}}_{\mathbf{11}}$ and ${\mathit{B}}_{\mathbf{22}}$ must always be diagonalized, and either matrix ${\mathit{B}}_{\mathbf{12}}$ or matrix ${\mathit{B}}_{\mathbf{21}}$ must be zeroed (Of course, it is possible to zero both matrices ${\mathit{B}}_{\mathbf{12}}$ and ${\mathit{B}}_{\mathbf{21}}$, but this leads to an unnecessarily large number of operations performed). Matrix ${\mathit{B}}_{\mathbf{11}}$ can have any final structure. Although the procedure resembles the Gaussian elimination method, it is a more complex process that also contains specific operations, such as the differentiation of a row described in Section 2.2.

Regarding the shape of the submatrices in Figure 1, we can simplify the calculation of the determinant in (2) (artificial multiplication using the unit matrix ${\mathit{A}}_{\mathbf{11}}{{\mathit{A}}_{\mathbf{11}}}^{-1}(=\mathbf{I})$ from the left enables transformation of the general eigenvalue problem into the standard one):

$$det\left(s\mathit{A}+\mathit{B}\right)={\left(-1\right)}^{n_{\leftrightarrow \updownarrow }}det\left[\underset{{\displaystyle =\mathbf{I}}}{\underbrace{{\mathit{A}}_{\mathbf{11}}{{\mathit{A}}_{\mathbf{11}}}^{-1}}}\left(s{\mathit{A}}_{\mathbf{11}}+{\mathit{B}}_{\mathbf{11}}\right)\right]\prod _{i=n_1+1}^{n_2}{\left({\mathit{B}}_{\mathbf{22}}\right)}_{ii}={\left(-1\right)}^{n_{\leftrightarrow \updownarrow }}\prod _{i=1}^{n_1}{\left({\mathit{A}}_{\mathbf{11}}\right)}_{ii}\prod _{i=n_1+1}^{n_2}{\left({\mathit{B}}_{\mathbf{22}}\right)}_{ii}det\left(s\mathbf{I}+{{\mathit{A}}_{\mathbf{11}}}^{-1}{\mathit{B}}_{\mathbf{11}}\right),$$

(4)

where $n_{\leftrightarrow \updownarrow }$ is the total number of column and row interchanges during the transformation.

Thus, the standard eigenvalue problem has been created, and the poles of (all) the transfer functions can be calculated as eigenvalues of the matrix $\mathit{X}=-{{\mathit{A}}_{\mathbf{11}}}^{-1}{\mathit{B}}_{\mathbf{11}}$ (The same method is applied to the general eigenvalue problem (3) for the calculation of zeros).

2.2. Extraordinary Step for Reduction in “Irreducible” Non-Diagonal Elements

The reduction process that leads to the final form on the right side of (4) seems to be a modification of the Gaussian elimination method. In certain cases, however, there is a non-diagonal element in the matrix ${\mathit{A}}_{\mathbf{11}}$ that is not reducible by any other diagonal element of this matrix. In such a case, a suitable row of the lower part of the matrix ${\mathit{B}}_{\mathbf{22}}$ is multiplied by the operator s to move this row to the left (In the time area, this operation corresponds to differentiation). Now, the originally irreducible element in the matrix ${\mathit{A}}_{\mathbf{11}}$ can be easily reduced using some element of this moved row (The description of this operation is also shown in the fourth and fifth steps of the detailed definition of the reduction procedure in Section 2.3). In [17], we demonstrated the necessity of this step using an irregular digital filter described by the $\mathcal{Z}$ transform. In this article, we show a more illustrative example based on a so-called dynamically degenerate analog circuit [34]. However, compared to this book, we introduce a significantly easier formulation of circuit equations.

2.3. Detailed Definition of Reduction Procedure

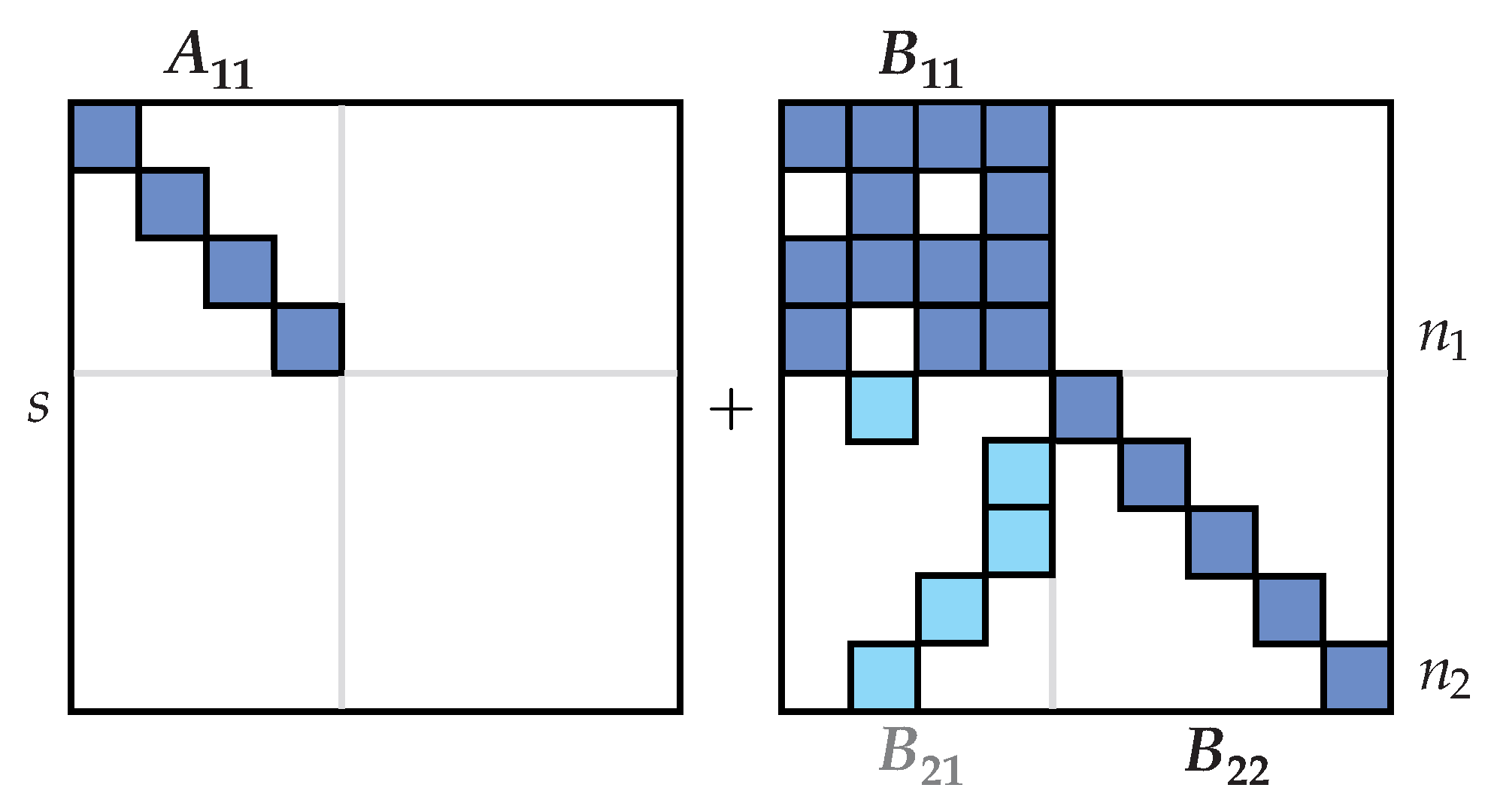
• The $\mathit{A}$ matrix is diagonalized by the sequential reduction in rows and columns with the selection of nonzero pivot elements in both columns and rows. Let us assume that the dimension of this diagonal submatrix thus created is equal to r. If $r=n_2$, then the $\mathit{A}$ matrix is nonsingular, and the procedure can be terminated.
• The final $n_2-r$ columns of the ${\mathit{B}}^{\left(2\right)}$ matrix (the ${\mathit{B}}^{\left(2\right)}$ symbol expresses that the structure of the $\mathit{B}$ matrix has changed in the meantime) are diagonalized via a backward row reduction starting from the lower right corner of this matrix. The selection of nonzero pivot elements is performed in both columns and rows of the right lower square submatrix ${\mathit{B}}^{\left(2\right)}$ of the dimension $n_2-r$ (in order to preserve the diagonal structure of ${\mathit{A}}^{\left(2\right)}$). If the number of rows q belonging to neither group of the diagonal submatrices is equal to zero, the procedure is terminated.
• A nonzero element $B_{r+q,p}^{\left(3\right)}$ is found in the $(r+q)$th row of the ${\mathit{B}}^{\left(3\right)}$ matrix, while the condition $1\leqq p\leqq r$ is fulfilled, and the $(r+q)$th column is exchanged with the $p$th column. The existence of such a nonzero element is a condition of unambiguous solvability of the task (Otherwise, the determinant is equal to zero).
• To reduce a non-diagonal element $(p,r+q)$ in the ${\mathit{A}}^{\left(4\right)}$ matrix, we multiply the $(r+q)$th row by the s (Laplace operator) multiplier (Therefore, it is necessary to later divide this row by s). This manifests itself as a horizontal shift of the $(r+q)$th row from ${\mathit{B}}^{\left(4\right)}$ to ${\mathit{A}}^{\left(4\right)}$.
• The element $(p,r+q)$ in the ${\mathit{A}}^{\left(5\right)}$ matrix is reduced by subtracting the $(r+q)$th row, and its elements are then transferred to the original location they had after Step 3 (This is the necessary division by s mentioned above).
• The $p$th row in the ${\mathit{A}}^{\left(6\right)}$ matrix is reduced by the use of the diagonal elements of this matrix.
• The non-diagonal elements in the $(r+q)$th column of the ${\mathit{B}}^{\left(7\right)}$ matrix are reduced by subtracting the $(r+q)$th row.

The whole procedure above is cyclically repeated until the condition $q=0$ is met. In each other cycle, the value of r or q drops by one. In an extreme case, the condition $q=0$ may be met at $r=0$. The system has no poles in this case. Certainly, there could be some variations of this algorithm; however, any operation must not change the value of the determinant (except for the sign).

2.4. Pivoting

Obviously, the accuracy of the process of the reduction in the generalized eigenvalue problem to the standard form is significantly influenced by the selection of pivot elements. The best results are achieved by full pivoting when the pivot elements are selected from the whole remaining submatrix. However, full pivoting is unsuitable for solving large tasks, and therefore, in this article, we only deal with partial pivoting, where the pivot elements are only selected from the respective subcolumns of the matrix (And, moreover, the partial pivoting is highly compatible with the procedures exploiting the sparsity of the matrices). The pivoting strategies are defined in a very detailed way in [39]. Here, we only describe checking the pivot element using the $ϵ$ parameter, which is also used in the examples. The $ϵ$ parameter is part of any algorithm of semisymbolic analysis. Its typical value is always related to the type of arithmetic. E.g., for 64-bit numbers, it is typically chosen as ${10}^{-16}$, as we will see in the following tables characterizing the results of these examples.

The $n$th pivot element is selected from the rest of the $n$th column of the reduced matrix:

$$A_{nn}≔\underset{n\leqq i\leqq n_2}{argmax}\left|A_{in}\right|,n=1,\dots ,n_2-1,$$

(5)

where $n_2$ is the dimension of the matrices $\mathit{A}$ and $\mathit{B}$, but this pivot element is only considered non-zero if it is not too small in comparison with the largest element in the remainder of the $n$th row:

$$\mathtt{if}\left|A_{nn}\right|\leqq ϵ\underset{n<j\leqq n_2}{max}\left|A_{nj}\right|\mathtt{then}{A}_{nn}≔0.$$

(6)

2.5. Final Form of Transfer Function

After applying the procedures described in the previous subsections for the calculations of both poles and zeros, we obtain the circuit transfer function in the form

$$c{\displaystyle \frac{{\displaystyle \prod _{i=1}^{n_{1,z}}(s-z_i)}}{{\displaystyle \prod _{i=1}^{n_1}(s-p_i)}}},$$

(7)

where c is the constant of the transfer function, which arises as a division of the expressions ${\left(-1\right)}^{n_{\leftrightarrow \updownarrow }}{\prod }_{i=1}^{n_1}{\left({\mathit{A}}_{\mathbf{11}}\right)}_{ii}{\prod }_{i=n_1+1}^{n_2}{\left({\mathit{B}}_{\mathbf{22}}\right)}_{ii}$ of (4) for the cases of the calculation of zeros and poles (Of course, the number of zeros $n_{1,z}$ may be different from the number of poles $n_1$).

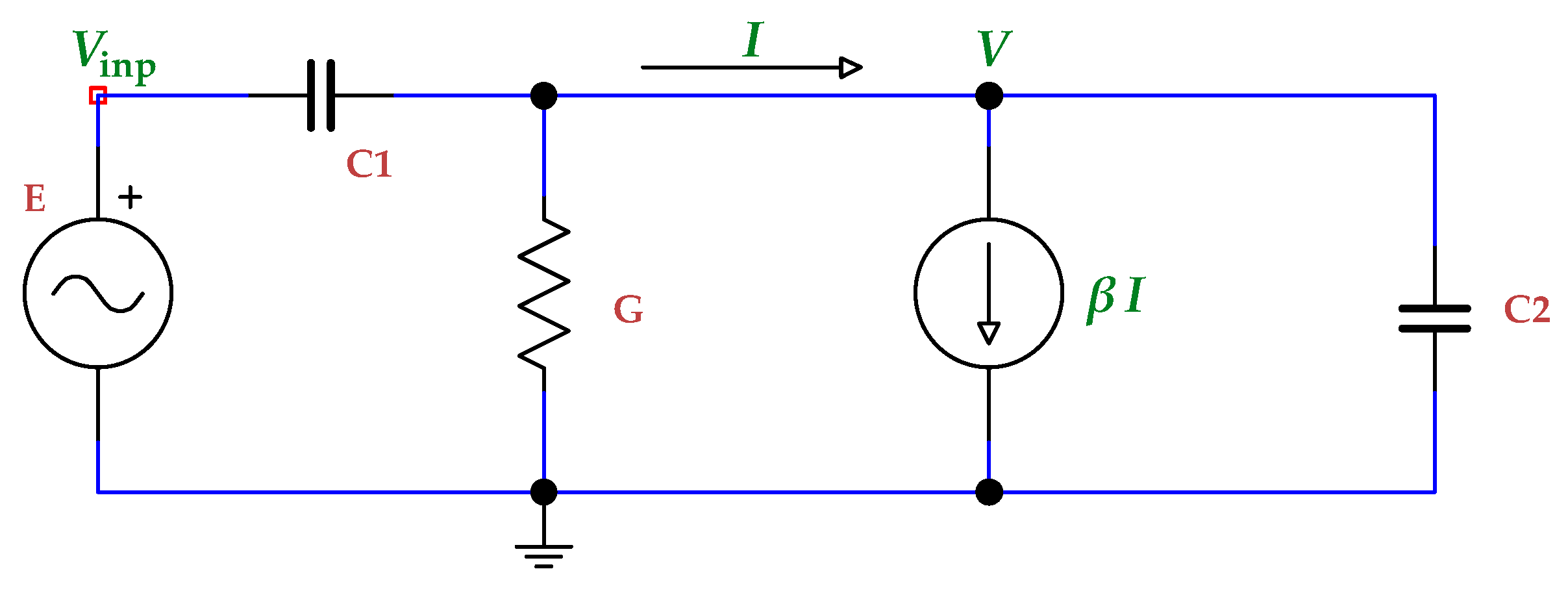
3. Analytically Solved Example of Reduction Algorithm on Dynamically Degenerate Circuit

The simple but unusual circuit in Figure 2 was used in [34] to demonstrate multiple methods. For example, it was used to demonstrate the formulation and reduction in the state equations, during which some unusual operations had to be performed due to the character of this circuit. Its unusual character is caused by the closed loop containing $C_1$, $C_2$, and E; therefore, their voltages are not independent of each other. However, the original formulation of the state equations in [34] had five equations—e.g., the current of the voltage source E was also a variable. In this section, a simpler method of formulating the system of equations containing only three variables is used. The purpose is to easily demonstrate that even for simple analog circuits, it may be necessary to use the non-standard step of the reduction procedure, which consists of the differentiation of one of the equations.

The matrix equation corresponding to the circuit in Figure 2 is as follows:

$$\left[s\left(\begin{array}{ccc}{C}_1& -C_1& \\ C_2& & \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}G& & 1\\ & & \beta -1\\ & 1& \end{array}\right)\right]\left(\begin{array}{c}V\hfill \\ V_{\mathrm{inp}}\hfill \\ I\hfill \end{array}\right)=\left(\begin{array}{c}\\ \\ E\hfill \end{array}\right).$$

(8)

For the calculation of pole(s), we start by modifying the $\mathit{A}$ and $\mathit{B}$ matrices to obtain the shapes shown in Figure 1. Initially, the first column is added to the second column:

$$s\left(\begin{array}{ccc}{C}_1& & \\ C_2& C_2& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}G& G& 1\\ & & \beta -1\\ & 1& \end{array}\right);$$

(9)

The second column is subtracted from the first column:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & C_2& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ & & \beta -1\\ -1& 1& \end{array}\right);$$

(10)

${\mathit{A}}_{\mathbf{11}}$ is now diagonalized; however, ${\mathit{B}}_{\mathbf{22}}=\mathbf{0}$. Therefore, the third row must be differentiated, i.e., moved to the left, which is the step absent in the standard Gaussian elimination:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & C_2& \\ -1& 1& \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ & & \beta -1\\ \phantom{0}& & \end{array}\right);$$

(11)

$(-C_2)$-multiple of the third row is added to the second row:

$$s\left(\begin{array}{ccc}{C}_1& & \\ C_2& & \\ -1& 1& \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ & & \beta -1\\ \phantom{0}& & \end{array}\right);$$

(12)

$\left(-{\displaystyle \frac{C_2}{C_1}}\right)$-multiple of the first row is added to the second row, and the third row is also de-differentiated (integrated), i.e., moved to the right (to the original position), as in (10):

$$s\left(\begin{array}{ccc}{C}_1& & \\ & \phantom{0}& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ & -G{\displaystyle \frac{C_2}{C_1}}& -{\displaystyle \frac{C_2}{C_1}}+\beta -1\\ -1& 1& \end{array}\right);$$

(13)

${\mathit{A}}_{\mathbf{11}}$ is now diagonalized again. As the circuit is degenerate, it only consists of one element. The second and third rows are exchanged for a future diagonalization of ${\mathit{B}}_{\mathbf{22}}$:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & \phantom{0}& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ -1& 1& \\ & -G{\displaystyle \frac{C_2}{C_1}}& -{\displaystyle \frac{C_2}{C_1}}+\beta -1\end{array}\right);$$

(14)

$\left(G{\displaystyle \frac{C_2}{C_1}}\right)$-multiple of the second row is added to the third row:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & \phantom{0}& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}& G& 1\\ -1& 1& \\ -G{\displaystyle \frac{C_2}{C_1}}& & -{\displaystyle \frac{C_2}{C_1}}+\beta -1\end{array}\right);$$

(15)

${\mathit{B}}_{\mathbf{22}}$ is now diagonalized, and we start zeroing the ${\mathit{B}}_{\mathbf{12}}$ matrix, as shown in Figure 1. $(-G)$-multiple of the second row is added to the first row:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & \phantom{0}& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}G& & 1\\ -1& 1& \\ -G{\displaystyle \frac{C_2}{C_1}}& & -{\displaystyle \frac{C_2}{C_1}}+\beta -1\end{array}\right);$$

(16)

$\left(-{\displaystyle \frac{1}{-\frac{C_2}{C_1}+\beta -1}}\right)$-multiple of the third row is added to the first row:

$$s\left(\begin{array}{ccc}{C}_1& & \\ & \phantom{0}& \\ & & \phantom{0}\end{array}\right)+\left(\begin{array}{ccc}G+{\displaystyle \frac{G\frac{C_2}{C_1}}{-\frac{C_2}{C_1}+\beta -1}}& & \\ -1& 1& \\ -G{\displaystyle \frac{C_2}{C_1}}& & -{\displaystyle \frac{C_2}{C_1}}+\beta -1\end{array}\right);$$

(17)

As ${\mathit{B}}_{\mathbf{12}}$ is now zeroed, the only pole of (all) transfer functions can be easily evaluated using the last part of (4):

$$\mathbf{I}=1,{\mathit{A}}_{\mathbf{11}}^{-1}={\displaystyle \frac{1}{C_1}},{\mathit{B}}_{\mathbf{11}}=G+{\displaystyle \frac{G\frac{C_2}{C_1}}{-\frac{C_2}{C_1}+\beta -1}},$$

(18)

therefore, the pole is the solution of the equation

$$det\left(s+{\displaystyle \frac{1}{C_1}}\left(G+{\displaystyle \frac{G\frac{C_2}{C_1}}{-\frac{C_2}{C_1}+\beta -1}}\right)\right)=0$$

(19)

and thus

$$\begin{array}{cc}\hfill p_1& =-{\displaystyle \frac{1}{C_1}}\left(G+{\displaystyle \frac{G\frac{C_2}{C_1}}{-\frac{C_2}{C_1}+\beta -1}}\right)=-{\displaystyle \frac{G}{C_1}}\left(1-{\displaystyle \frac{C_2}{C_2+C_1(1-\beta )}}\right)\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{G}{C_1}}{\displaystyle \frac{C_1(1-\beta )}{C_2+C_1(1-\beta )}}=-{\displaystyle \frac{G(1-\beta )}{C_2+C_1(1-\beta )}},\hfill \end{array}$$

(21)

which is in complete agreement with [34]. However, the procedure defined in [34] is conceived more generally and therefore uses (repeatedly in more sections) matrices $5\times 5$. Although exceptional row differentiation is also shown in [34], in our opinion, our version shown in (11) is more illustrative, and the general reduction strategy is overall clearer here due to the usage of the smaller matrices $3\times 3$.

4. Modifying Equations for Frequency-Scaled Semisymbolic Analysis

4.1. Formulating Modified System

In frequency-scaled semisymbolic analysis, the modification of (1) is controlled by a user-chosen factor $\varpi$. The choice of the value of this factor is primarily related to those elements of the circuit that cause huge differences in the magnitude of the elements in the matrix $\mathit{A}$. For example, if the source of the problem consists of extremely small capacitances of about $0.1$ pF, a reasonable choice of this factor is, say, ${10}^{13}$, as demonstrated in the following examples. However, the method is, fortunately, not very sensitive to the exact choice of this parameter, as demonstrated in Section 5.1 (And traditionally, if we obtain the same results for the program runs—which are mostly very fast—with different $\varpi$, it likely indicates the right choice).

One option is to directly modify the elements of the matrix $\mathit{A}$. However, locating these elements in memory is a bit complicated due to the efficient utilization of the sparsity of this matrix. Therefore, for simple and immediate testing of the proposed algorithm, we modifed the capacitive and inductive elements during the formulation of the equations.

Regarding the passive elements, the values of capacitors and inductors used for the formulation arise from original formulation by multiplying by $\varpi$:

$$C_{\varpi }=C\times \varpi ,L_{\varpi }=L\times \varpi .$$

(22)

Regarding the active elements, the following modified model parameters are created and used in the formulation instead of the original ones:

$$\begin{array}{cc}\hfill {\tau }_{F,\varpi }& ={\tau }_F\times \varpi (\mathrm{ideal}\mathrm{forward}\mathrm{transit}\mathrm{time});\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\tau }_{R,\varpi }& ={\tau }_R\times \varpi (\mathrm{ideal}\mathrm{reverse}\mathrm{transit}\mathrm{time});\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill C_{JE,\varpi }& =C_{JE}\times \varpi (\mathrm{zero-bias}\mathrm{base-emitter}\mathrm{depletion}\mathrm{capacitance});\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill C_{JC,\varpi }& =C_{JC}\times \varpi (\mathrm{zero-bias}\mathrm{base-collector}\mathrm{depletion}\mathrm{capacitance});\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill C_{JS,\varpi }& =C_{JS}\times \varpi (\mathrm{zero-bias}\mathrm{collector-substrate}\mathrm{depletion}\mathrm{capacitance}).\hfill \end{array}$$

(27)

for bipolar junction transistors (a definition of the entire BJT model can be found in [42], the quasi-saturation part of the model was not included because at the operating point—where the nonlinear models are linearized—transistors are far from the quasi-saturation),

$$\begin{array}{cc}\hfill {\tau }_{D,\varpi }& ={\tau }_D\times \varpi (\mathrm{transit}\mathrm{time});\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill C_{J0,\varpi }& =C_{J0}\times \varpi (\mathrm{zero-bias}\mathrm{junction}\mathrm{capacitance}).\hfill \end{array}$$

(29)

for PN-junction diodes (the whole diode model is defined in [42] as well), and

$$\begin{array}{cc}\hfill {\left(\epsilon W\right)}_{\varpi }& =\left(\epsilon W\right)\times \varpi (\mathrm{permittivity}\mathrm{width}\mathrm{product});\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill C_{JS,\varpi }& =C_{JS}\times \varpi (\mathrm{zero-bias}\mathrm{gate-source}\mathrm{junction}\mathrm{capacitance});\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill C_{JD,\varpi }& =C_{JD}\times \varpi (\mathrm{zero-bias}\mathrm{gate-drain}\mathrm{junction}\mathrm{capacitance});\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill C_{DS,\varpi }& =C_{DS}\times \varpi (\mathrm{drain-source}\mathrm{capacitance}).\hfill \end{array}$$

(33)

for pHEMTs (The original GaAs FET model is entirely defined in [43]; however, for testing, we used our original modification [44]. It has been verified that it determines the precision of standard models, e.g., see comparisons [45] for SiC MESFETs or [46] for GaN HEMTs).

It is important to note that some of the details of the models listed here are used only to illustrate the possible formulation approach; the model’s accuracy is not, of course, the topic of this article.

4.2. Determining Actual Poles, Zeros, and Constant of Transfer Function

Adjusting the formulation described in Section 4.1 will certainly change the original transfer function (7), its poles, zeros, and constant of the transfer function, i.e., we will obtain modified values $p_{i,\varpi }$, $i=1,\dots ,n_1$, $z_{i,\varpi }$, $i=1,\dots ,n_{1,z}$, and $c_{\varpi }$. The actual poles, zeros, and constant of the transfer function (7) are simply determined in the following way:

$$\begin{array}{cc}\hfill p_i& =p_{i,\varpi }\times \varpi ,i=1,\dots ,n_1,\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill z_i& =z_{i,\varpi }\times \varpi ,i=1,\dots ,n_{1,z},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill c& =c_{\varpi }\times {\varpi }^{n_1-n_{1,z}}.\hfill \end{array}$$

(36)

In other words, (34), (35), and (36) provide a solution to the original problem as if the system were unscaled.

4.3. Note About Controlling Factor

As the semisymbolic analysis—the deflation of the generalized task of characteristic values to a standard form—and subsequent determining characteristic numbers of the matrix represent a very complex numerical process, an exact determination of the factor $\varpi$ is not possible. For the vast majority of tasks, however, a rather accurate result is achieved for a fairly wide range of values of this factor, mostly even for multiple orders of $\varpi$ (This circumstance was also utilized to deal with relatively difficult test tasks in this article). However, semisymbolic analysis is a relatively rapid numerical process (unlike, e.g., optimization tasks), and hence there can always be multiple tests performed with various values of $\varpi$. Furthermore, the following is positive and very important: the inappropriate choice of $\varpi$ leads to calculating unrealistic poles and zeros (of nonsensical values like ${10}^{25}$ that cannot be caused by circuit elements), which can be easily recognized.

5. Sample Examples of Different Levels of Complexity

5.1. Antenna Low-Noise Preamplifier for Multi-Constellation Receiver of Satellite Navigation

The circuit diagram of the antenna low-noise preamplifier (for the multi-constellation receiver of satellite navigation) is shown in Figure 3. It is important to note that the accurate values of the passive elements originated from a sophisticated design via multi-objective optimization (specifically, the goal attainment method was chosen), and we directly used the output of the optimizer that gives eight significant digits.

In this case, the frequency-scaled semisymbolic analysis was able to provide accurate results, even with the standard 64-bit arithmetic. Therefore, the poles of (all) the transfer functions $-0.005093217\pm 0.5618716\mathrm{j}$, $-0.7139237$, $-0.2145403\pm 0.7367593\mathrm{j}$, $-0.5549448\pm 1.486727\mathrm{j}$, $-3.117465$, $-8.955381$, $-1.750791\pm 14.44991\mathrm{j}$, $-8.49903\pm 17.95136\mathrm{j}$, and $-20.28827$ and the zeros of the ${\displaystyle \frac{\mathrm{load}\mathrm{voltage}}{\mathrm{input}\mathrm{voltage}}}$ transfer function 0 (six-time zero), $18.70084$, and $-21.63001\pm 19.72322\mathrm{j}$ (poles/zeros written in gigahertz–GHz–units) were determined to be identical (!) by both the frequency-scaled semisymbolic analysis (64-bit compilation) and a reference semisymbolic analysis with variable-length arithmetic (2048-bit compilation). Hence, a comparison table is not necessary in this case.

In this first and simplest example, we can briefly demonstrate that the algorithm is not extremely sensitive to the new suggested factor $\varpi$. For example, for the $\varpi$ values ${10}^8$, ${10}^9$, ${10}^{10}$, ${10}^{11}$, and ${10}^{12}$, we always get exactly the same poles and zeros listed in the previous paragraph. However, for the $\varpi$ value ${10}^7$ and several other lesser ones, we only get a five-time zero instead of the correct six-time zero. Therefore, for example, the $\varpi$ value ${10}^{10}$ should be safe for analyses of this circuit.

For this “medium” $\varpi$ value (${10}^{10}$), we have also tried to examine the effect of the $ϵ$ parameter defined in (6) on the accuracy of the solution. For the $ϵ$ values ${10}^{-12}$, ${10}^{-11}$, and ${10}^{-10}$, we again obtained exactly the same poles and zeros listed above, which were also confirmed by the extremely accurate controlling analysis using the 2048-bit compilation. The $ϵ$ values ${10}^{-9}$, ${10}^{-8}$, and ${10}^{-7}$ were also usable; all the poles and zeros were again the same with the exception of one pole, which differed only in the seventh significant digit. However, the $ϵ$ values ${10}^{-14}$ and ${10}^{-13}$ only led to a four-time zero (instead of the correct six-time zero), which implies that the $ϵ$ parameter in (6) cannot be too small in some tasks. Nevertheless, it should be emphasized that a suitable $ϵ$ parameter selection must be made in every semisymbolic analysis; the only new parameter in the suggested frequency-scaled semisymbolic analysis is $\varpi$, and hence the new task here is only to determine this $\varpi$ factor.

5.2. Discrete Operational Power Amplifier Working in AB Class Mode

The circuit diagram of the power operational amplifier (with a brief description of the basic parts of the circuit) is shown in Figure 4. The amplifier is of an AB class; therefore, the poles and zeros of a transfer function can be determined at the amplifier’s operating point.

All the differing poles and zeros of the transfer function (the output is, of course, on the ungrounded contact of $R_{10}$) determined by both suggested frequency-scaled semisymbolic analysis and another extremely accurate but VERY slow analysis are shown in

Table 1. Differing poles and zeros of a transfer function of the AB-class power operational amplifier ($ϵ={10}^{-16}$ and $ϵ={10}^{-100}$ were used for analyses with 64-bit and 2048-bit precision, respectively) (There were 28 poles and 28 zeros of the calculated transfer function).

No. a	64-Bit $\mathbf{Precision},\mathit{\varpi }={10}^4$	2048-Bit $\mathbf{Precision},\mathit{\varpi }=1$
…	…	…
$28$	$-\mathrm{73,133}.1$	$-\mathrm{73,133}.0$
…	…	…
$20$	$-558.736$	$-558.735$
…	…	…
$23$	$-2425.09$	$-2425.08$
$24$	$-2429.20$	$-2429.19$
$25$	$-9295.22$	$-9294.71$
…	…	…
$27$	$-\mathrm{11,55}5.3$	$-\mathrm{11,55}6.1$
$28$	$-\mathrm{69,98}4.1$	$-\mathrm{69,98}5.6$

^a All the differing poles (upper part) and all the differing zeros (lower part) are included; they are ordered by their absolute values, and they are written in megahertz (MHz) units, e.g., the only differing pole equals approximately $-73.133$ GHz.

. This clearly confirms that 64-bit implementation is sufficient if frequency scaling is used.

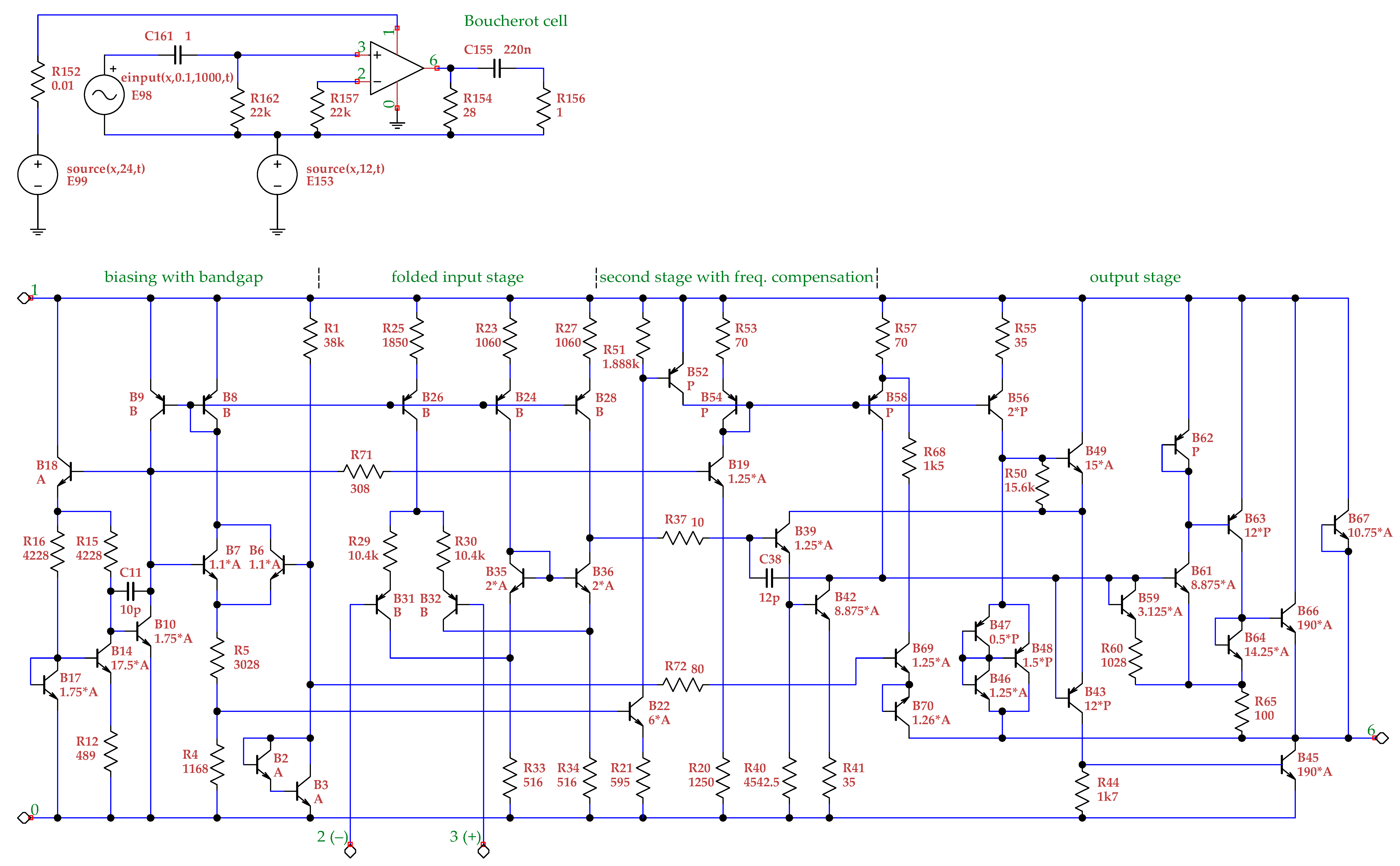
5.3. MDA 272 Integrated Operational Amplifier

The circuit diagram of the integrated operational amplifier of the 272 class is shown in Figure 5. This is a more difficult task due to the large number of bipolar junction transistors and, hence, the large total number of small capacitors, as well as the large size of the matrices in (1).

The diagram also contains a description of the basic parts of this integrated circuit, and a test-bench circuit is shown as well. Certainly, the transfer function of this circuit is much more complicated than that of the previous one (in total, both 108 poles and zeros).

In

Table 2. Differing poles and zeros of a transfer function of the MDA 272 operational amplifier ($ϵ={10}^{-100}$ was used for both analyses) (There were 108 poles and 108 zeros).

No. a	64-Bit $\mathbf{Precision},\mathit{\varpi }={10}^{12}$	2048-Bit $\mathbf{Precision},\mathit{\varpi }=1$
…	…	…
$87,88$ b	$-21,253.7\pm 403.045\mathrm{j}$	$-21,253.7\pm 403.014\mathrm{j}$
…	…	…
$107$  c	$-\mathrm{875,7}84$	$-\mathrm{875,7}75$
…	…	…
…	…	…
$2$	$-0.00000101545$	$-0.00000101546$
…	…	…
$42,43$	$-213.529\pm 1.50255\mathrm{j}$	$-213.529\pm 1.50252\mathrm{j}$
…	…	…
$64,65$	$-1755.19\pm 8.05508\mathrm{j}$	$-1755.19\pm 8.05507\mathrm{j}$
…	…	…
$71,72$	$-3131.29\pm 43.8994\mathrm{j}$	$-3131.29\pm 43.8995\mathrm{j}$
…	…	…
$100$	$-\mathrm{489,21}3$	$-\mathrm{489,21}4$
$101$	$-\mathrm{568,85}7$	$-\mathrm{568,85}8$
…	…	…
$104$	$-\mathrm{875,5}30$	$-\mathrm{875,5}14$
$105$	$-\mathrm{965,92}9$	$-\mathrm{965,92}8$
$106,107$	$-110,377\pm 1.15147\times {10}^6\mathrm{j}$	$-110,343\pm 1.15153\times {10}^6\mathrm{j}$
$108$  d	$+7.50493\times {10}^6$	$+7.50920\times {10}^6$

^a Only the most different poles (upper part) and all different zeros (lower part) are included; they are ordered by their absolute values, and they are written in megahertz (MHz) units, e.g., the last zero equals approximately $7.5$ THz (The differences between the zeros are more perceptible, and, hence, they were all included). ^b This pair of complex poles is the only one with a registerable difference in the imaginary parts, although the differences are very small because $403.045/403.014\approx 1.000077$. The differences detected in all other complex poles are less than one millionth, i.e., they are the same in at least the first six valid digits. ^c There are only eight slightly different real poles, and this one is the most different, but the difference is very small because $875,784/875,775\approx 1.00001$. The differences between the other seven ones are below one millionth. ^d Contrary to poles, zeros with positive real parts do not cause instability. This last zero is also the most different, but $7.50493/7.50920\approx 0.99943$, i.e., the difference is less than one thousandth.

, only the differing poles and zeros are shown. This comparison again clearly demonstrates that the 64-bit implementation of the frequency-scaled semisymbolic analysis is able to provide sufficient accuracy because the differences between its results and the results of the extremely accurate 2048-bit implementation are negligible: for each pole and zero, less than one thousandth.

This example emphasizes how the use of the frequency scaling suggested in this article is very important—in [17], we have shown that the 64-bit implementation of the traditional (i.e., frequency-unscaled) semisymbolic analysis practically crashed in the case of using sparse-matrix procedures (This article—as already mentioned above—is primarily focused on algorithms utilizing the sparsity of matrices that are promising for analyses of huge circuits). Another interesting matter here is that the $ϵ$ value ${10}^{-100}$ was also used for the 64-bit case, which implies that the application of (6) was probably not even necessary.

5.4. Distributed Tunable Microwave Oscillator

The circuit diagram of the distributed (tunable) microwave oscillator is shown in Figure 6, together with the schematics of models of pHEMT, filter, and microstrip line.

This is the most complicated example, (especially) due to the microstrip lines that generate a vast number of poles and zeros. Moreover, as there are many equal capacitances and inductances in these models, there exist several clusters of almost multiple eigenvalues (and calculating multiple eigenvalues traditionally represents a numerical problem). Selected poles and a zero of a transfer function are shown in

Table 3. Selected poles and a zero of the hypothetical transfer function of the distributed microwave oscillator ($ϵ={10}^{-16}$ was used for 256-bit and 2048-bit precision, ${10}^{-17}$ and ${10}^{-15}$ were also used for 64-bit precision for confirmation, and $\varpi ={10}^{13}$ was used for 256-bit and 2048-bit & 64-bit precision).

No. a	256-Bit $(\mathbf{a}.\mathbf{k}.\mathbf{a}.\mathbf{Octuple}\mathbf{Precision})$	2048-Bit and 64-Bit $\mathbf{Precision}$ b
$1$	$-1.11780$	$-1.11766$
$2$	$-1.60846$	$-1.60884$
$3$	$-1.7473$	$-1.7473$
$4$	$-1.74994$	$-1.74994$
$5$	$-24.8317$	$-24.8517$
$6$	$-31.5231$	$-31.5304$
$7$	$-32.1177$	$-32.1175$
$8$	$-32.1519$	$-32.1520$
$9,10$  c	$-32.1522$	$-32.1522$
$11,12$	$-22.4247\pm 144.110\mathrm{j}$	$-22.5129\pm 144.154\mathrm{j}$
…	…	…
$23,24$  d	$+1111.22\pm 3237.01\mathrm{j}$	$+1164.77\pm 3249.59\mathrm{j}$
…	…	…
$205,206$  e	$-81.9262\pm 54,352\mathrm{j}$	$-81.9263\pm 54,352\mathrm{j}$
…	…	…
$255$	$-725,373$	$-725,373$
$256$	$-731,586$	$-731,586$
$257$	$-738,107$	$-738,107$
$258$	$-741,167$	$-741,167$
$259,260$	$-16.2578\pm 3.56136\times {10}^6\mathrm{j}$	$-16.2578\pm 3.56136\times {10}^6\mathrm{j}$
$261,262$	$-33.9564\pm 5.74487\times {10}^6\mathrm{j}$	$-33.9564\pm 5.74487\times {10}^6\mathrm{j}$
$263$	$-6.0845\times {10}^6$	$-6.0845\times {10}^6$
$264$	$-6.98149\times {10}^6$	$-6.98149\times {10}^6$
$265$	$-6.98169\times {10}^6$	$-6.98169\times {10}^6$
$266$	$-7.01757\times {10}^6$	$-7.01757\times {10}^6$
$1$  f	$\phantom{-}0$	$-0.0000000266458$ (2048-bit)
		$-0.000000208294\phantom{0}$ (64-bit)
…	…	…

^a From a total of 266 poles, the 12 (1–12) with the smallest and the other 12 (255–266) with the biggest absolute values were included, as well as two other interesting couples (23, 24 and 205, 206) of the poles as well. Regarding zeros, only the first one (“zero at zero”) was included as an interesting test of the algorithm’s accuracy; the others do not have a physical sense. Again, all are written in megahertz (MHz) units, e.g., the last pole equals around $-7$ THz. ^b Really, all of the poles included in the table are the same for the 2048-bit and 64-bit precision (This is a remarkable result!) ^c Double (real) pole. ^d This is the smallest pole with a positive real part, and therefore, its imaginary part can be used for the estimation of the oscillation frequency (as this circuit is “weakly nonlinear”). The presumably correct period was determined by the steady-state analysis as $0.31057$ ns; hence, the oscillation frequency should be $1/(3.1057\times {10}^{-10})=3.219886$ GHz. Therefore, the errors of the estimations are only about $0.53$% and $0.92$% for the 256- and 2048- and 64-bit arithmetics, respectively! ^e This couple of poles is physically insignificant and is only included here to show the smallest poles with a difference, because all the poles, 207–266, are the same for all arithmetics, which is interesting and confirms their accuracy. ^f As there is a 100 pF capacitor in the path to the output, one zero of the transfer function should be at 0 Hz in principle, and it is called “zero at zero”. Only the 256-bit arithmetic was able to isolate the zero absolutely; however, both 2048-bit and 64-bit arithmetic were able to approximate it really well. This approximation can be improved by decreasing $ϵ$, e.g., using $ϵ={10}^{-20}$ changes it to $0.00000000426201$. However, this could be a bit risky because too small of an $ϵ$ could generate some spurious poles, although quite easily recognizable.

.

Although the oscillator itself is a nonlinear circuit, it is possible to calculate (especially for a weakly nonlinear oscillator like this one) the so-called virtual (or pseudo) operating point (with inductors replaced by a short circuit and capacitors omitted), at which the circuit can be linearized, and then the poles and zeros of transfer function can be calculated (One of the so-computed poles even allows for a relatively accurate estimate of oscillating frequency, as shown in Table 3; see footnote ^d)!

Table 3 contains only selected poles (especially the interesting ones with the smallest and the largest absolute values) and a “zero at zero,” which is also a good test of accuracy (Please see the footnotes below the table for more details). Moreover, Table 3 also contains an important couple of poles, 23 and 24, where the imaginary part can be used very well to estimate the oscillation frequency. This further confirms the meaningfulness of semisymbolic analysis for weakly nonlinear circuits (and thus for weakly nonlinear oscillators as well)! Finally, let us emphasize the remarkable result shown in Table 3: all the poles included in the table were the same (to six significant digits) for both 2048-bit and 64-bit precision. This is obviously clear evidence that, without the use of the suggested frequency scaling in 64-bit implementation (here, $\varpi ={10}^{13}$ was chosen), such an accordance would not be possible!

6. Combination of Frequency Scaling and More Accurate Arithmetic

In previous sections, we showed that frequency-scaled semisymbolic analysis provides sufficiently accurate results, even when using standard 64-bit arithmetic. This fact confirms the basic idea of the frequency scaling itself and is also very important because a number of mathematical libraries are provided in the 64-bit version (E.g., the LAPACK DLL libraries are available in 32- and 64-bit arithmetic, but not in the 80- or 128-bit version). Logically, the use of more accurate arithmetic in the frequency-scaled semisymbolic analysis will further increase the numerical stability of the whole process.

This can be clearly illustrated in the results of the low-noise antenna preamplifier described in the last paragraph of Section 5.1. When using 64-bit arithmetic and factor $\varpi$ ${10}^{10}$, the analysis provided accurate zeros of the transfer function for the values of $ϵ$ ${10}^{-10}$, ${10}^{-11}$ and ${10}^{-12}$, and inaccurate zeros for ${10}^{-13}$ and lesser. However, when using 128-bit arithmetic (and the same factor $\varpi$ ${10}^{10}$), the analysis provided accurate zeros of the transfer function for the values of $ϵ$ ${10}^{-10}$, ${10}^{-11}$,..., ${10}^{-30}$, and ${10}^{-31}$, and inaccurate zeros for ${10}^{-32}$ and lesser. In other words, the possible range of $ϵ$ in (6) is far greater for 128-bit arithmetic!

It can be noted that the response of the analyses to the $ϵ$ parameter described in the previous paragraph corresponds quite well to expectations due to the arithmetic used. The 64-bit arithmetic provides accuracy up to 17 significant digits, and the 128-bit arithmetic provides accuracy up to 34 significant digits. Therefore, the minimum applicable values of $ϵ$ ${10}^{-12}$ and ${10}^{-31}$ correspond to these accuracies quite well (The value of the $ϵ$ parameter suitable for 64-bit arithmetic is also confirmed by the results in Table 1 and Table 3, where ${10}^{-16}$ was primarily used, although there exist tasks in which no tiny element of the matrix had to be declared zero by (6), and hence ${10}^{-100}$ could be used, as seen in Table 2).

7. Another Minor but Important Improvement

In connection with the overall increase in the robustness of all subroutines for the semisymbolic analysis, we introduced an important adjustment in both new and existing procedures concerning the products ${\prod }_{i=1}^{n_1}{\left({\mathit{A}}_{\mathbf{11}}\right)}_{ii}{\prod }_{i=n_1+1}^{n_2}{\left({\mathit{B}}_{\mathbf{22}}\right)}_{ii}$ in (4). For (very) large circuits, there is a considerable risk of overflow (or underflow) in these multiplications. Therefore, we only store the logarithms of absolute values and signs during the gradual execution of these products, which turned out to be a safe solution in all the alternatives of the semisymbolic analysis. In other words, if the two numbers x and y have their signs $s_x$ and $s_y$ and logarithms (of absolute values) $l_x$ and $l_y$, respectively, and their product is determined by its sign $s_x\times s_y$ and logarithm (of absolute value) $l_x+l_y$, respectively (This is because the direct multiplication of $x\times y$ may cause overflow if the numbers x and y are too large, which is a frequent case in repeated multiplications in (4)).

8. Validation of Proposed Technique

8.1. Assessing the Effect of Accuracy of Arithmetic Used

First of all, we had to verify that for the proposed frequency-scaled semisymbolic analysis, there will be sufficient standard 64-bit arithmetic. For this verification, we used control calculations using extremely accurate 2048-bit arithmetic, as shown in the last columns of Table 1, Table 2 and Table 3. Of course, the calculations of this extremely accurate (software) 2048-bit arithmetic are almost accurate, but they last for a very long time and are hence only suitable for control purposes. And these comparisons confirmed that the proposed frequency-scaled semisymbolic analysis can be implemented in standard 64-bit arithmetic.

8.2. Comparison of Semisymbolic Analysis Results with the Results of Other Types of Analyses and the Results of Other Programs

8.2.1. Comparison of Results of Semisymbolic Analysis and Steady-State Analysis

The possibility of estimating the frequency of oscillations utilizing the layout of poles has already been presented at a local conference [47]. In addition, of course, it is also possible to determine the frequency of oscillations by analyzing a steady state, i.e., quite differently (and more precisely due to the oscillator’s nonlinearity) in the time domain, and to compare both results. A comparison of the results of both of these methods is shown in this article in Table 3, footnote ^d. We can see that the difference between the results of these two methods is less than one percent, which is undoubtedly an extremely good result (However, the oscillator is so-called weakly nonlinear, and for this class of circuits, these estimates are realistic).

We have also tried these comparisons for different gate voltages of pHEMTs of the oscillator in Figure 6. For the bias voltages $E_1$, $E_2$, $E_3$, and $E_4$ set to $-0.2$ V, $-2$ V, $-2$ V, and $-2$ V, respectively, the difference between the oscillation frequencies determined by the steady-state analysis (i.e., in the time domain) and by the location of the poles (i.e., not in the time domain) is only $1.2$% (and we obtained similar results for more bias voltages), which further validates the result of this pole in the frequency-scaled semisymbolic analysis.

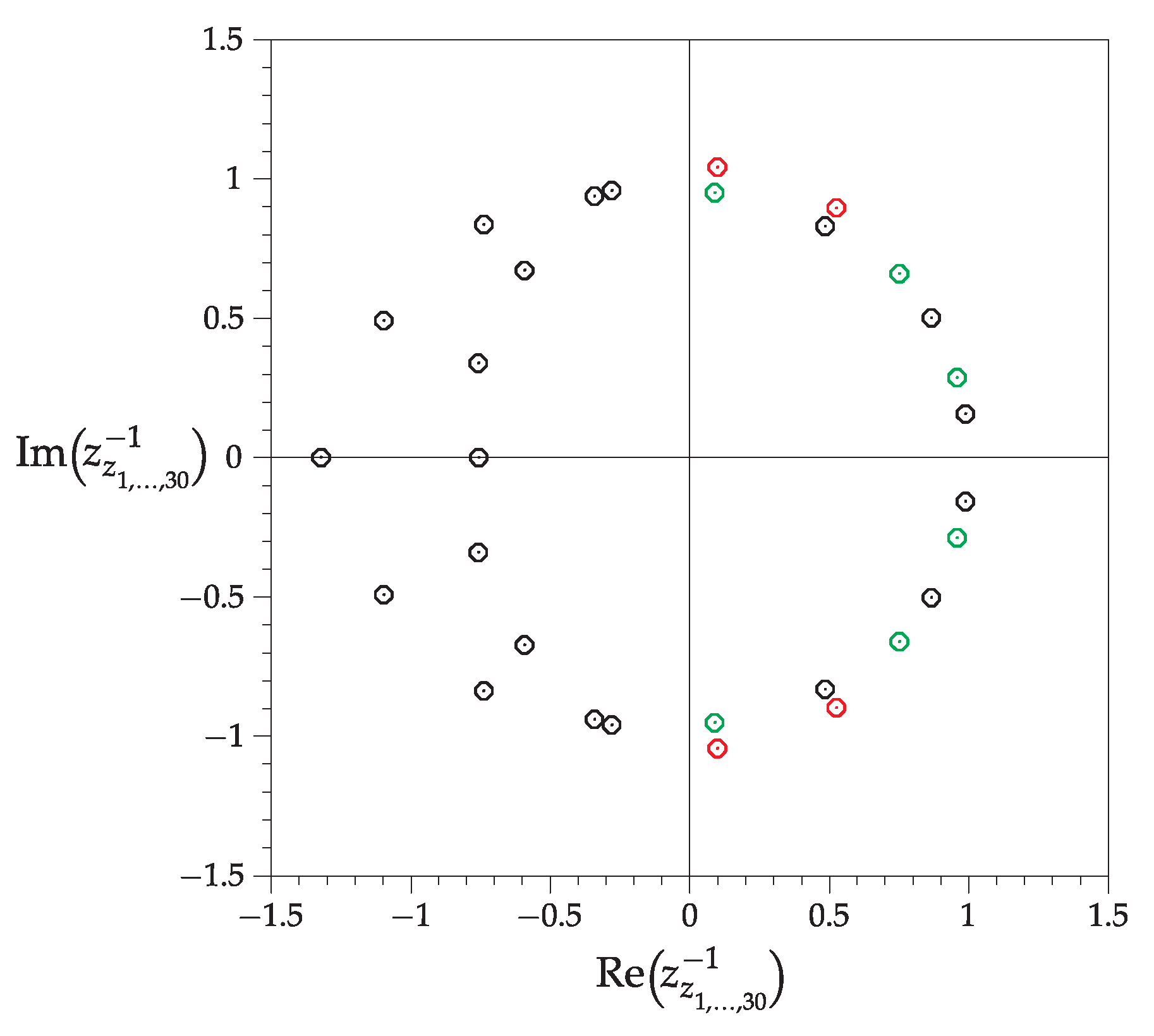
8.2.2. Comparison with Results of Another Program

In the presentation of [47], a suggestion was also made to check our algorithm of the semisymbolic analysis by means of comparison with some MATLAB (R2022a, 9.12) results. Although MATLAB itself is unable to analyze circuits of irregular structure, it can determine the poles and zeros of digital filters with a regular structure. This feature has been utilized to compare our results of the semisymbolic analysis of the digital filter shown in Figure 7 with the MATLAB ones.

Our algorithm of the semisymbolic analysis and MATLAB uncovered thirty zeros in the $z^{-1}$ plane, as shown in Figure 8, and the slight difference between them is as follows:

• Two pairs of complex zeros have the first five significant digits equal (red-colored);
• Three pairs of complex zeros have the first six significant digits equal (green-colored);
• Two real zeros and nine pairs of complex zeros have the first seven significant digits equal;

Therefore, in other words, all the zeros have at least the first five significant digits equal. This confirms the quality of the algorithm(s) quite well. And later, we performed similar tests for other even more complicated filters with similar results, confirming the algorithms.

8.3. Comparison of Frequency-Unscaled and Frequency-Scaled Semisymbolic Analyses

A key comparison between the accuracies of the frequency-unscaled and frequency-scaled semisymbolic analyses is shown in

Table 4. Comparison of the accuracy of the frequency-unscaled (i.e., classical) and frequency-scaled (i.e., proposed) analyses. The comparison is performed for 64-bit arithmetic and use of sparse matrices.

Circuit 4	Analysis	Poles			Zeros
		Accurate 1	Inaccurate 2	Incorrect 3	Accurate 1	Inaccurate 2	Incorrect 3
Low-Noise Preamplifier	Unscaled	14	0	0	1	3	5
	Scaled	14	0	0	9	0	0
AB-Class Power Amplifier	Unscaled	26	2	0	12	14	2
	Scaled	27	1	0	22	06	0
272 Operational Amplifier	Unscaled	81	27	0	41	61	6
	Scaled	105	3	0	94	14	0

¹ They have the first six significant digits equal to the reference results obtained using 2048-bit arithmetic. ² Even though they have less than the first six significant digits equal, they can be unambiguously paired with some results obtained using 2048-bit arithmetic. Their overall accuracy is still very good, as shown in Table 1 and Table 2. ³ They cannot be unambiguously paired with any result obtained by the 2048-bit arithmetic. So, they are wrong. ⁴ The frequency-unscaled semisymbolic analysis of the microwave distributed oscillator requires at least 256-bit arithmetic. Therefore, a comparison with the result of the frequency-scaled semisymbolic analysis using the 64-bit arithmetic is unavailable (The 64-bit arithmetic is fully sufficient for frequency-scaled semisymbolic analysis)!

.

The circuits in Figure 3, Figure 4 and Figure 5 were used to obtain the results in Table 4. Both frequency-unscaled (i.e., classical) and frequency-scaled (i.e., newly proposed in this article) semisymbolic analyses had the same mathematical procedure (implemented using identical arithmetic); the only difference was the frequency scaling used in the frequency-scaled semisymbolic analysis. Hence, the table clearly shows the efficiency of this procedure. In the newly suggested frequency-scaled semisymbolic analysis, no incorrect zeros were detected, and the number of precise poles and zeros increased considerably.

8.4. Note on Necessity of Accurate Calculations

The whole Section 8 primarily focuses on the discussion and verification of the accuracy of calculations. And the natural question, of course, is why the accuracy of the analyses is so important. Certainly, for normal, simple, and trouble-free technical tasks, an accuracy of, say, one percent will suffice. However, there are situations where a greater or even very high accuracy of calculations of poles and zeros is needed:

• When the poles or zeros are very close (e.g., like some in Figure 8);
• When the poles or zeros are multiple (in this case, an inaccurate calculation can cause completely incorrect information about the circuit behavior [24]);
• When the poles and zeros are optimized, e.g., in a loop of multi-objective optimization (in this case, very high accuracy is needed to ensure convergence, as shown in [48]).

9. Discussion

Although problems with the accuracy of semisymbolic analysis have been known for a long time, most of tasks can be solved using procedures programmed in the usual 64-bit arithmetic. However, we found several difficult cases in the collection of our circuits analyzed in the previous period, which could not be solved precisely even when using the latest semisymbolic analysis procedures (And some of the poles and zeros of a transfer function were determined completely incorrectly when using standard 64-bit arithmetic).

Certainly, the first method of solving this problem is to use more precise arithmetic, e.g., 80-bit or 128-bit implementations of the algorithms. We first presented using this so-called brute force at the conference [33], and an extended version of this paper was subsequently selected for publication in the book [17]. Both publications [17,33] documented the ability of the 128-bit arithmetic to improve the accuracy of the calculation of poles and zeros of a transfer function. In addition, both publications contain very illustrative solutions to tasks of the reduction in the general eigenvalue problem to the standard eigenvalue problem. In [33], the reduction for an unproblematic analog circuit was shown; however, in [17], the reduction for a much more complicated digital circuit was demonstrated in a detailed way.

In this article, a novel method based on frequency scaling was suggested. This new method represents a much more sophisticated way of solving the accuracy problem compared to the simple enlargement of the lengths of numbers in memory described in our previous work [17,33]. In addition, the implementation of the new method into existing algorithms of semisymbolic analysis is very easy (one simple method is also shown in the article), so it is a very cheap yet very effective solution.

This newly designed method does not change the reduction procedure of the generalized eigenvalue problem to the standard eigenvalue problem and its subsequent solution by a modified QR algorithm from a purely mathematical point of view. However, the primary transformation of equations to a more suitable frequency domain (via (22) to (33), e.g.), then performing a semisymbolic analysis in this new domain, and finally, the transformation of the obtained results to the original frequency domain (via (34), (35), and (36)) clearly lead to much more robust calculations. This is evident both from a comparison of the results obtained by the 64- and 2048-bit arithmetics (the latter can certainly be considered accurate) in Table 1, Table 2 and Table 3 and further comparison of the results of unscaled (i.e., original) and scaled (i.e., newly suggested) semisymbolic analysis in Table 4. Table 4 clearly confirms that for some circuits, our newly designed calculation procedure leads to a much larger number of either completely accurate or almost accurate poles and zeros. In addition, as mentioned in footnote ⁴ in this table, some circuits are now solvable in 64-bit arithmetic that were unsolvable without frequency scaling.

In addition, in this study, we mention what might be the most powerful form of a solution to the problem of accuracy: a combination of the newly suggested frequency scaling and more accurate (e.g., 128-bit) arithmetic. Of course, this solution is probably the most robust, but the main objective of this study was to check the proposed frequency scaling in standard 64-bit arithmetic (There are few compilers with 128-bit arithmetic; however, for example, Fortran/C compilers from Intel or GNU have this arithmetic implemented).

The methods described in the previous four paragraphs (i.e., the more accurate arithmetics, frequency scaling, or both) can, of course, be applied to linear circuits as well as circuits with active elements linearized at an operating point. The operating point should be selected such that the natural nonlinearity of the active element does not change it considerably, for example, with a slight change of supply voltage or temperature. This condition can be relatively easily and reliably checked via sensitivity analysis. More information about the sensitivity of operating point and other advanced sensitivity analyses is shown in [49]; however, the main modes of the sensitivity analysis are implemented in several free programs, like Micro-Cap 12.

• Other Related Topics

Another minor but valuable improvement in the implementation of the semisymbolic analysis concerning the prevention of possible overflow is shown as well.

This study also contains an illustrative example of the reduction in the general eigenvalue problem to the standard problem for a simple but extraordinary dynamically degenerate analog circuit, where the special step consisting of differentiating a row had to be used.

• Measurement

Although measurement and measuring techniques are not the topic of this article, it is appropriate to mention them as one of the ways of characterizing the overall results (Certainly, the increase in accuracy in the frequency-scaled semisymbolic analysis cannot be assessed by a measurement due to the fluctuating parameters of semiconductor elements. However, it can confirm the principal functionality of the device). The low-noise preamplifier was measured in our university and the RCD company (In addition, the amplifier was awarded by the Government Council). The AB-class power amplifier was measured in our department. The 272 OA is a standard circuit. The microwave distributed amplifier was measured in our university, and this measurement was published as well.

• Some Other Recent Works on Accuracy of Semisymbolic Analysis

Some works dealing with the accuracy of the semisymbolic analysis (in general) have been published in recent years, e.g.,

[50]: Semi-symbolic inference, a technique for executing probabilistic programs;

[51]: A neuro-semi-symbolic design;

[52]: Semi-symbolic transient analysis of circuits containing fractional-order elements;

[53]: Automated semi-symbolic state equation generation method.

However, none of them solves the problem arising from the huge difference in the magnitude of the elements in the matrices, for which we have just suggested the frequency-scaled semisymbolic analysis described in this article. Although the results described in these works do not compare well with ours, they indicate that the precision of the semisymbolic analysis is undoubtedly the subject of control in new research and publications.

10. Conclusions

The fundamental achievement described in this article consists of a newly suggested frequency scaling method in the semisymbolic analysis. This frequency-scaled semisymbolic analysis significantly improves the accuracy of the calculation of poles and zeros of the transfer function of the circuit, allowing for the analysis of even very large and otherwise problematic circuits using the standard 64-bit implementation of mathematical procedures. The proposed algorithm is particularly important for contemporary microwave circuits, for which the classical (frequency-unscaled) semisymbolic analysis leads to a huge difference in the magnitude of the matrix elements, and hence to possible numerical instability. Moreover, the implementation of frequency scaling into already existing subroutines for semisymbolic analysis is very easy, and one of the possible methods is defined in this study. The overall efficiency of the method was demonstrated during four difficult tasks, three of which were solved significantly more accurately using the standard 64-bit implementation of the newly designed frequency-scaled semisymbolic analysis. The fourth was unsolvable at all points without the frequency scaling in the 64-bit arithmetic. Thus, the proposed frequency scaling significantly increased the range of solvable circuits. Finally, a possible combination of the frequency scaling and more accurate (especially 128-bit) arithmetic is also considered.