A Cost–Benefit Analysis of Multi-Site Wafer Testing †
Abstract
1. Introduction
- Area occupation of the probe head: We explore how variations in the number of springs affect the area occupied by the probe head during testing.
- Multi-site wafer testing approach: We delve into the benefits of multi-site testing, aiming to enhance throughput and reduce overall costs.
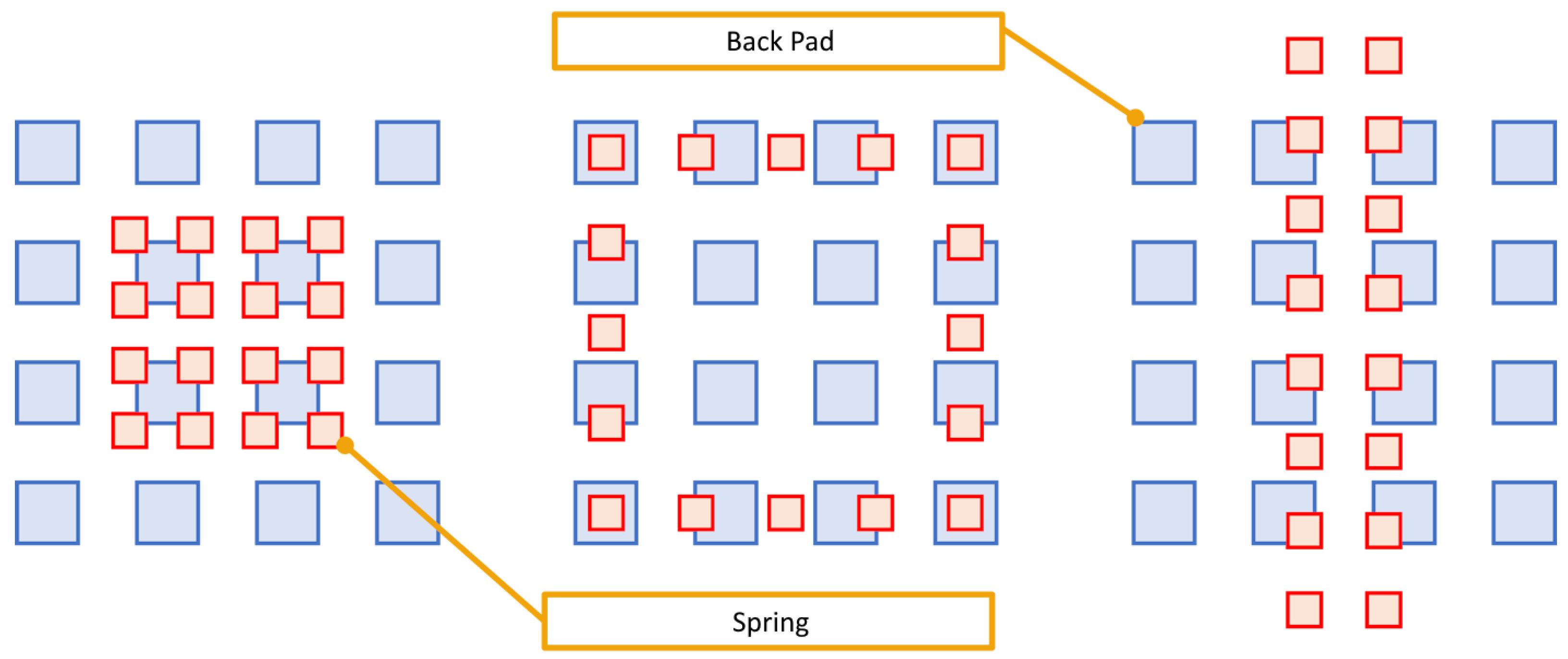
- Pad layout on a die: Considering the arrangement of pads within a die, we analyze its influence on test efficiency and cost.
2. Materials and Methods
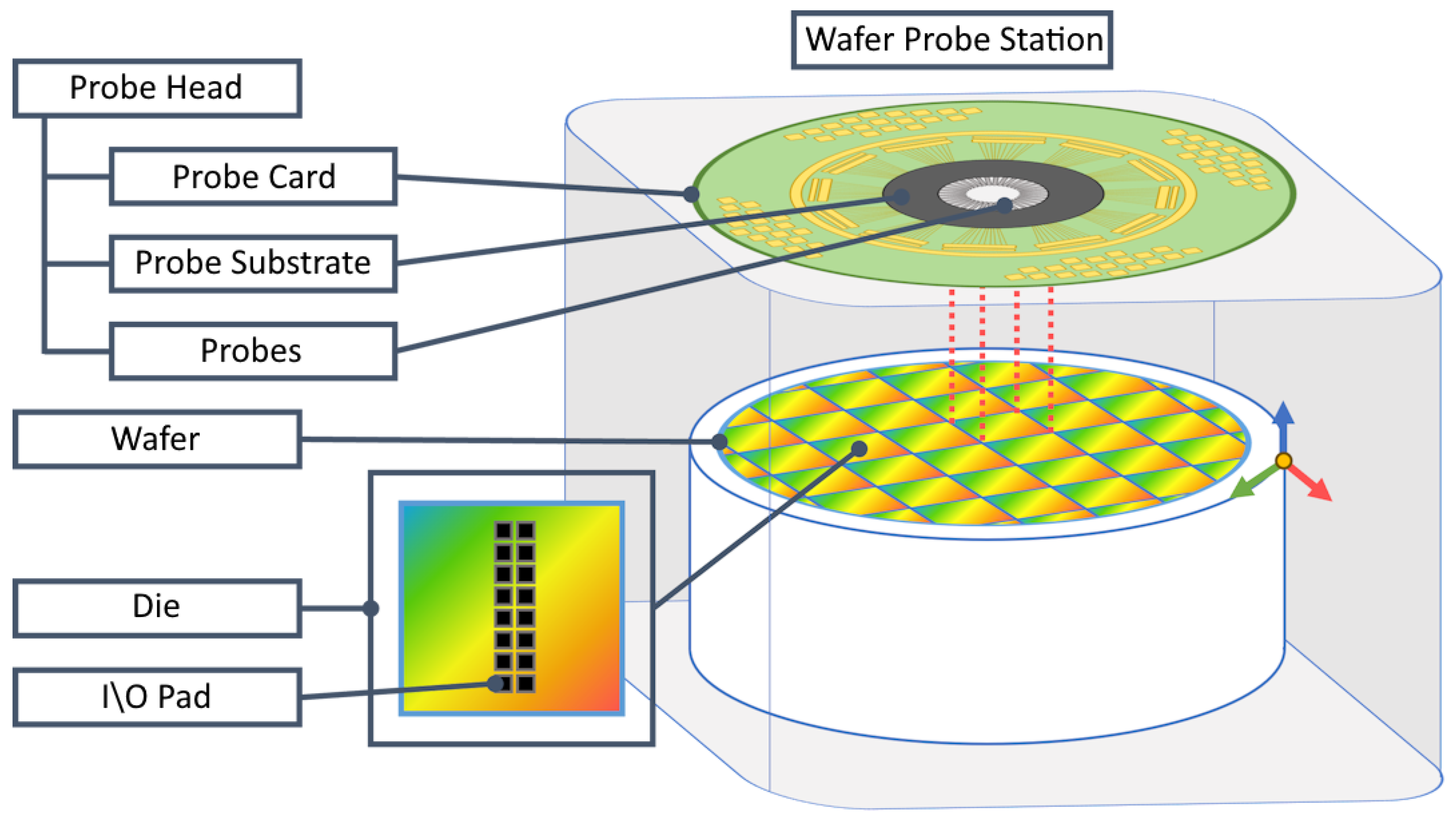
2.1. Composition and Functionality of Wafer Probe Station
2.2. Overview of Pad Layout
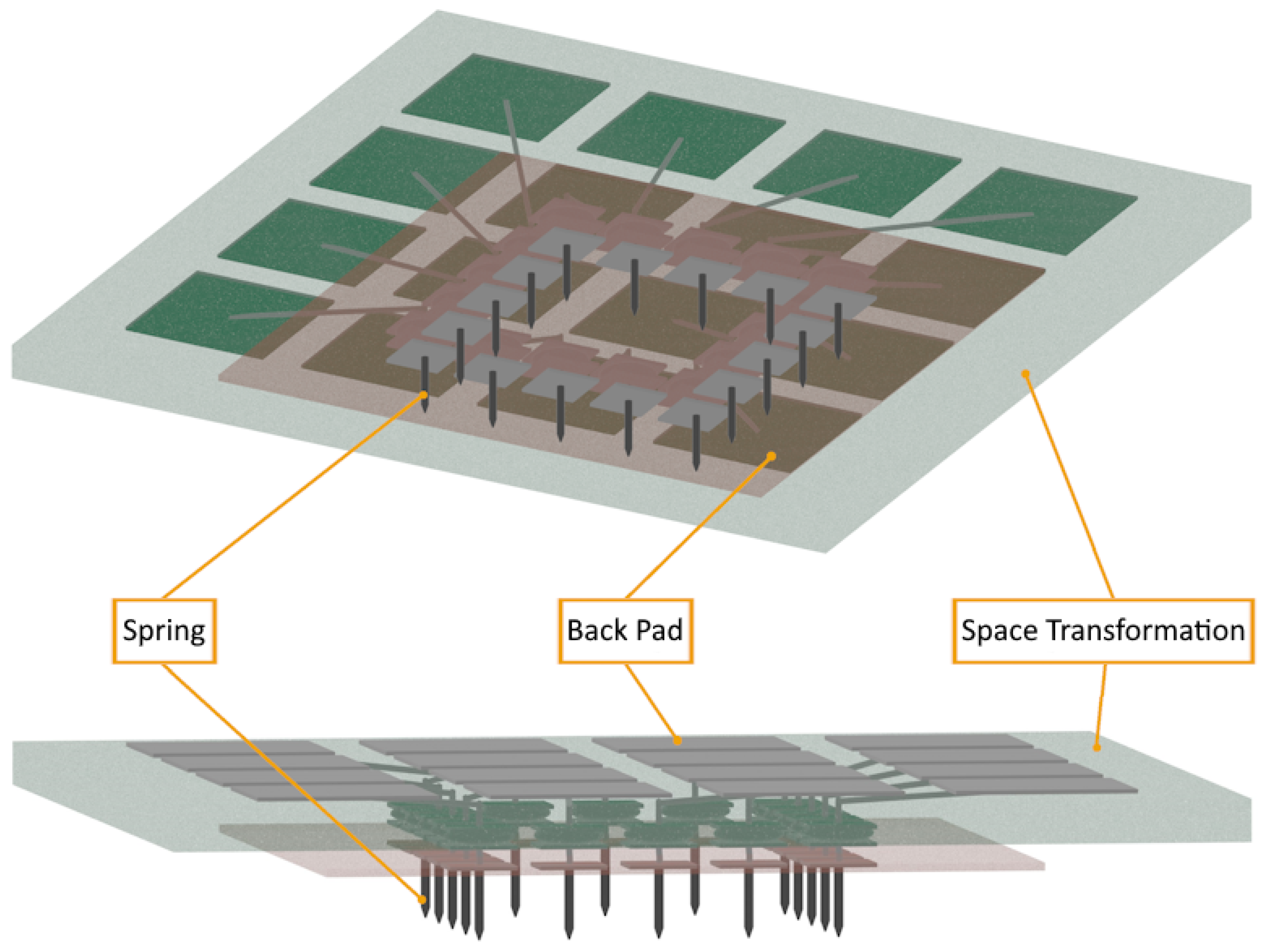
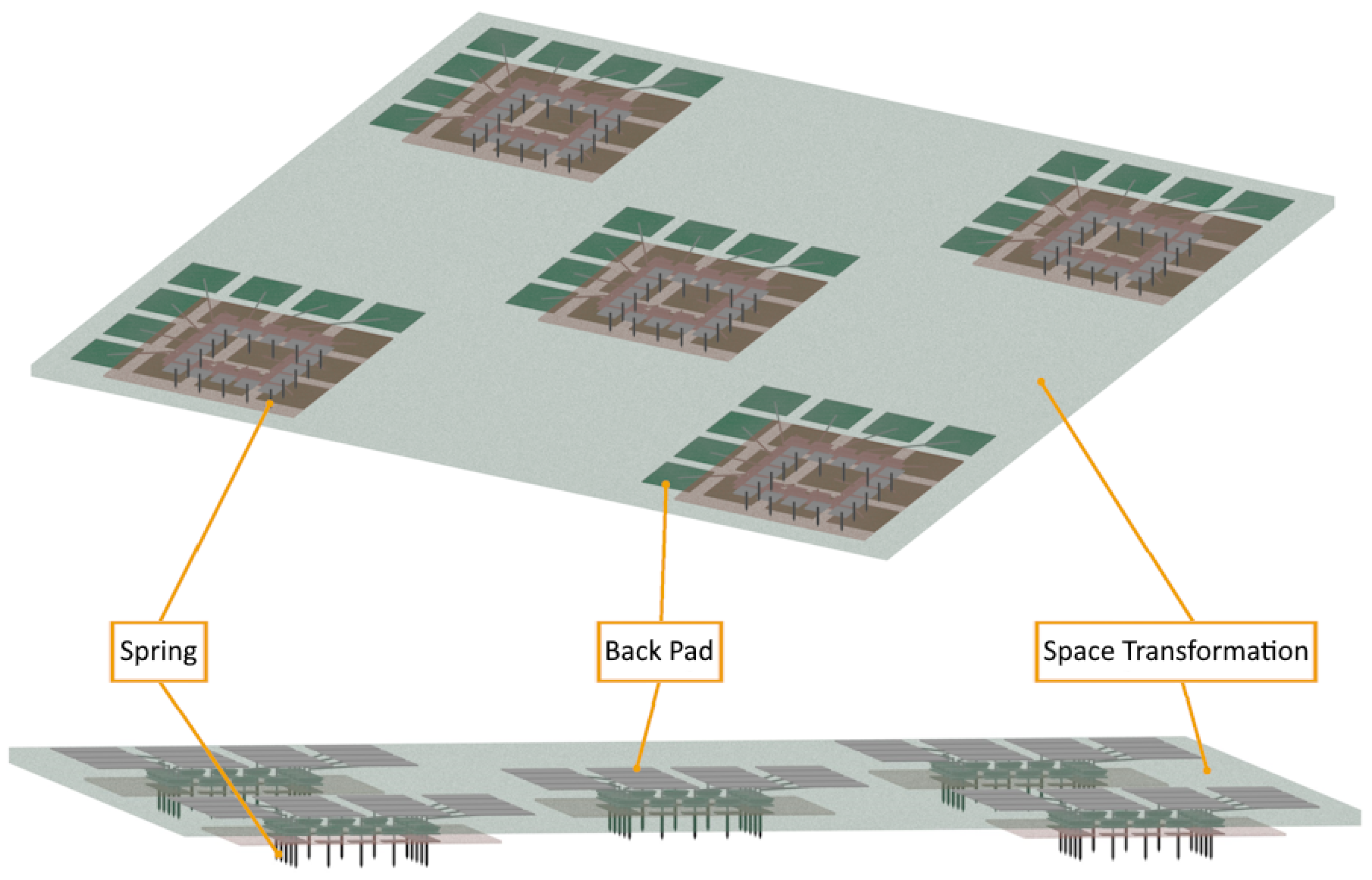
2.3. The Multi-Touch Approach
3. Results
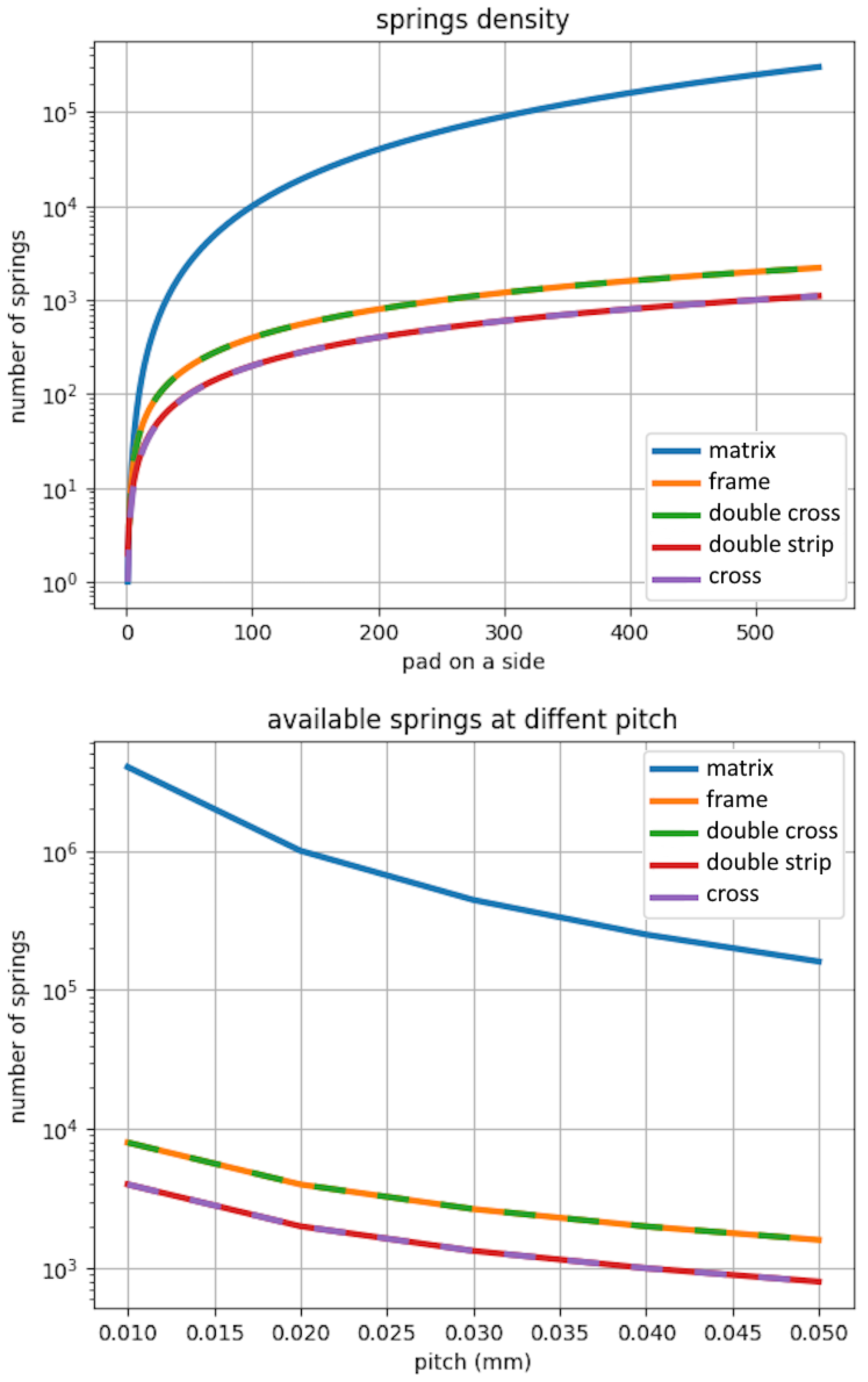
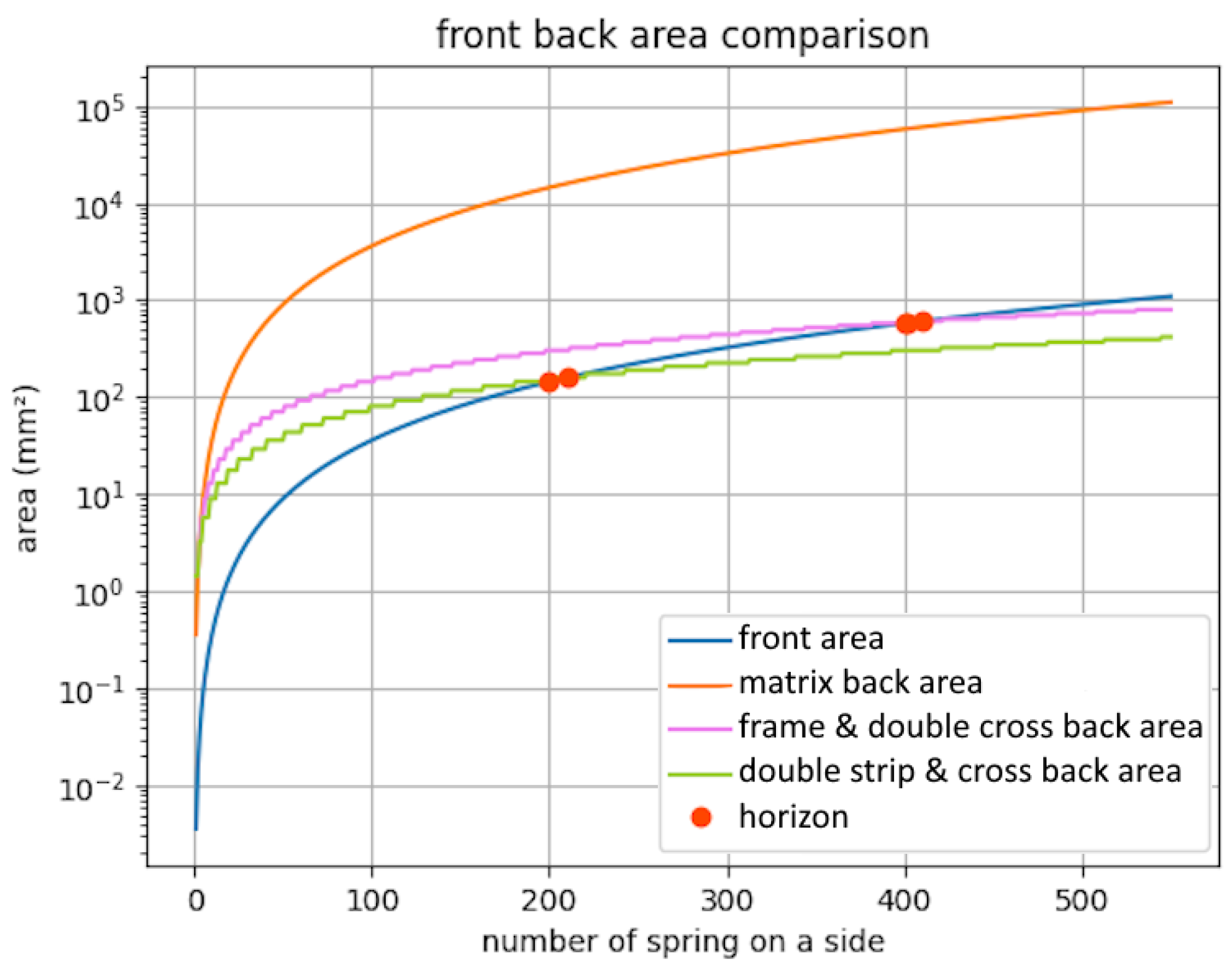
3.1. Computation of Area Occupation
- 1.
- n_springs: The number of springs that can be distributed on the desired die.
- 2.
- pitch: The distance between two test points (given in mm) and, by extension, the distance needed between two springs.
- 3.
- chip_side: The size of the die (given in mm). For simplicity’s sake, we assume the die to be squared, but the same calculations can be extended to a die of any shape.
- 4.
- fb_ratio: The ratio between the pitch and the distance between two pads on the opposite side of the space transformation device.
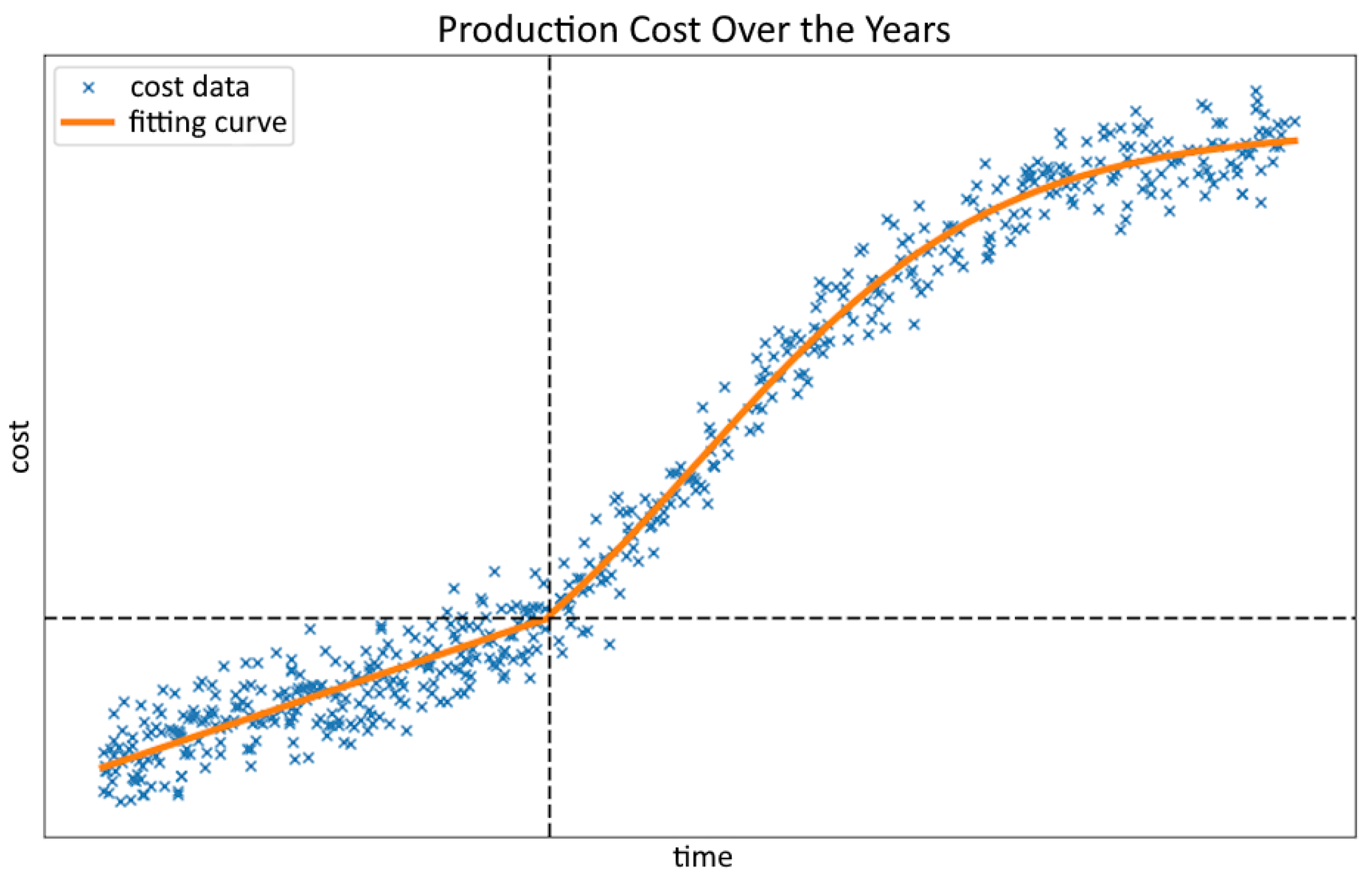
3.2. Formulation of Probe Head Cost Analysis
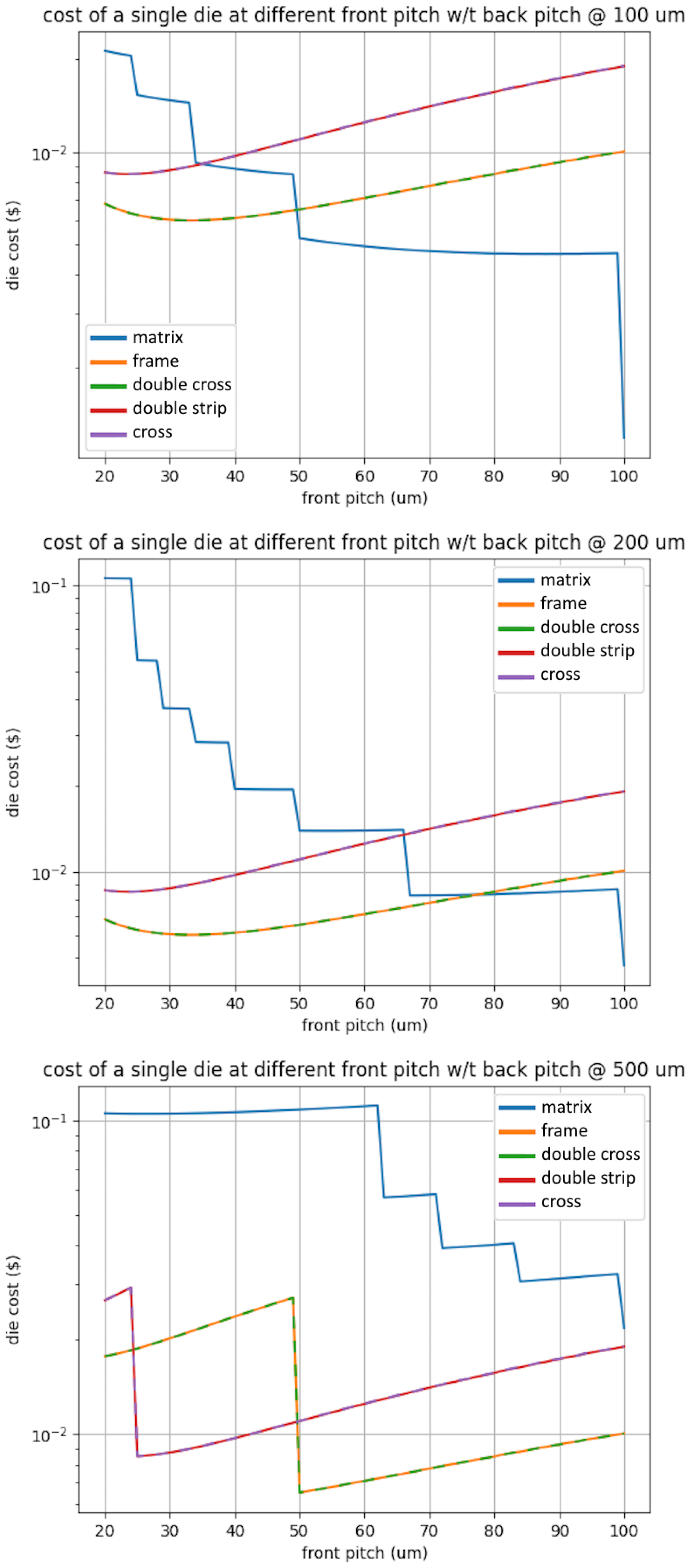
3.3. Evaluating Cost per Die
4. Discussion
4.1. Simulation of Area Computation
4.2. Experimental Evaluation of Test Cost per Die
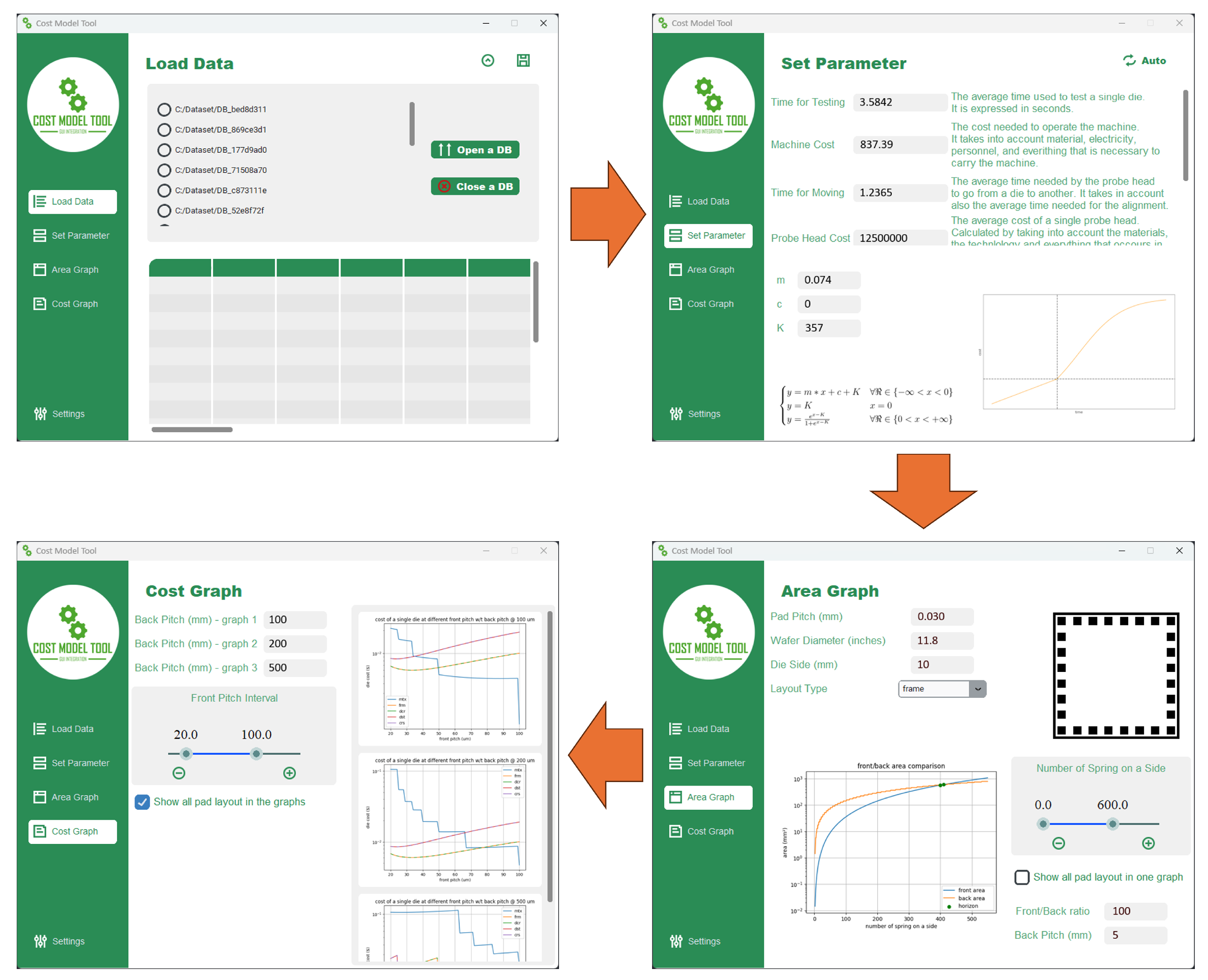
4.3. Graphical User Interface for Cost Modeling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATE | Automatic Test Equipment |
| BGA | Ball Grid Array |
| CMOS | Complementary Metal–Oxide Semiconductor |
| DB | Database |
| DIBs | Device Interface Boards |
| DPW | Dies Per Wafer |
| GUI | Graphical User Interface |
| PCB | Printed Circuit Board |
References
- Jiang, Y.; Chen, Y.; Hu, F.; Han, D.; Fang, J.; Li, G.; Ouyang, K. Solution to Optimize Warpage performance for 2.5D Fanout Packaging. In Proceedings of the 2023 24th International Conference on Electronic Packaging Technology (ICEPT), Shihezi, China, 8–11 August 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Ren, X.; Xue, K.; Jiang, F.; Wang, Q.; Ping, Y.; Pang, C.; Liu, H.; Xu, C.; Yu, D.; Shangguan, D. Design, simulation, and process development for 2.5D TSV interposer for high performance processer packaging. In Proceedings of the 2013 3rd IEEE CPMT Symposium Japan, Kyoto, Japan, 11–13 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Agrawal, M.; Chakrabarty, K. Test-Cost Modeling and Optimal Test-Flow Selection of 3-D-Stacked ICs. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2015, 34, 1523–1536. [Google Scholar] [CrossRef]
- Taouil, M.; Hamdioui, S.; Marinissen, E.J. Quality versus cost analysis for 3D Stacked ICs. In Proceedings of the 2014 IEEE 32nd VLSI Test Symposium (VTS), Napa, CA, USA, 13–17 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Stow, D.; Akgun, I.; Barnes, R.; Gu, P.; Xie, Y. Cost and Thermal Analysis of High-Performance 2.5D and 3D Integrated Circuit Design Space. In Proceedings of the 2016 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Pittsburgh, PA, USA, 11–13 July 2016; pp. 637–642. [Google Scholar] [CrossRef]
- Fukushima, T.; Sakuyama, S.; Takahashi, M.; Hashimoto, H.; Bea, J.; Marcello, T.; Kino, H.; Tanaka, T.; Koyanagi, M.; Mariappan, M. Integration of Damage-less Probe Cards Using Nano-TSV Technology for Microbumped Wafer Testing. In Proceedings of the 2021 IEEE International 3D Systems Integration Conference (3DIC), Raleigh, NC, USA, 26–29 October 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Hauck, T.; Schmadlak, I.; Argento, C.; Muller, W.H. Damage risk assessment of under-pad structures in vertical wafer probe technology. In Proceedings of the 2009 European Microelectronics and Packaging Conference, Rimini, Italy, 15–18 June 2009; pp. 1–5. [Google Scholar]
- Taouil, M.; Hamdioui, S.; Marinissen, E.J.; Bhawmik, S. Using 3D-COSTAR for 2.5D test cost optimization. In Proceedings of the 2013 IEEE International 3D Systems Integration Conference (3DIC), San Francisco, CA, USA, 2–4 October 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Sakamaki, R.; Horibe, M. Realization of Accurate On-Wafer Measurement Using Precision Probing Technique at Millimeter-Wave Frequency. IEEE Trans. Instrum. Meas. 2018, 67, 1940–1945. [Google Scholar] [CrossRef]
- Dragoi, V.; Kurz, F.; Wagenleitner, T.; Flötgen, C.; Mittendorfer, G. Wafer bonding for CMOS integration and packaging. In Proceedings of the 2012 13th International Conference on Electronic Packaging Technology & High Density Packaging, Guilin, China, 13–16 August 2012; pp. 166–170. [Google Scholar] [CrossRef]
- Maeda, Y.; Miura, T.; Matsuo, S.; Fukuda, H. Accurate Fiber Alignment using Silicon Photodiode on Grating Coupler for Wafer-Level Testing. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Dragoi, V.; Mittendorfer, G.; Flötgen, C.; Dussault, D.; Wagenleitner, T. CMOS-compatible aligned fusion wafer bonding. In Proceedings of the CAS 2011 Proceedings (2011 International Semiconductor Conference), Sinaia, Romania, 17–19 October 2011; Volume 1, pp. 141–144. [Google Scholar] [CrossRef]
- Kim, J. Active Si interposer for 3D IC integrations. In Proceedings of the 2015 International 3D Systems Integration Conference (3DIC), Sendai, Japan, 31 August–2 September 2015; pp. TS11.1.1–TS11.1.3. [Google Scholar] [CrossRef]
- Yazdani, F. A novel low cost, high performance and reliable silicon interposer. In Proceedings of the 2015 IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 28–30 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, D.X.; Pan, F.; Liu, J.H.; Xing, R.M.; Sun, R.F. Key Technologies of High-end SOC Probe Card. In Proceedings of the 2022 23rd International Conference on Electronic Packaging Technology (ICEPT), Dalian, China, 10–13 August 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Zoschke, K.; Güttler, M.; Böttcher, L.; Grübl, A.; Husmann, D.; Schemmel, J.; Meier, K.; Ehrmann, O. Full wafer redistribution and wafer embedding as key technologies for a multi-scale neuromorphic hardware cluster. In Proceedings of the 2017 IEEE 19th Electronics Packaging Technology Conference (EPTC), Singapore, 6–9 December 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Y.; Luo, X.; Xu, L.; Liu, S. Effect of die shape on die tilt in die attach process. In Proceedings of the 2013 14th International Conference on Electronic Packaging Technology, Dalian, China, 11–14 August 2013; pp. 651–655. [Google Scholar] [CrossRef]
- de Vries, D. Investigation of gross die per wafer formulas. IEEE Trans. Semicond. Manuf. 2005, 18, 136–139. [Google Scholar] [CrossRef]
- Torunbalci, M.M.; Alper, S.E.; Akin, T. Die size reduction by optimizing the dimensions of the vertical feedthrough pitch and sealing area in the advanced MEMS (aMEMS) process. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Hermann, G. Construction of a High Precision Tactile Measuring Probe. In Proceedings of the 2008 IEEE International Conference on Computational Cybernetics, Stara Lesna, Slovakia, 27–29 November 2008; pp. 219–222. [Google Scholar] [CrossRef]
- Zong, F.; Zhou, N.; Niu, J.; Sun, Z. Study on bond pad damage issue in bare Cu wire bonding on SMOS8MV wafer technology. In Proceedings of the 2015 16th International Conference on Electronic Packaging Technology (ICEPT), Changsha, China, 11–14 August 2015; pp. 108–113. [Google Scholar] [CrossRef]
- Wang, K.L.; Lin, B.Y.; Wu, C.W.; Lee, M.; Chen, H.; Lin, H.C.; Peng, C.N.; Wang, M.J. Test Cost Reduction Methodology for InFO Wafer-Level Chip-Scale Package. IEEE Des. Test 2017, 34, 50–58. [Google Scholar] [CrossRef]
- Velenis, D.; Stucchi, M.; Marinissen, E.J.; Swinnen, B.; Beyne, E. Impact of 3D design choices on manufacturing cost. In Proceedings of the 2009 IEEE International Conference on 3D System Integration, San Francisco, CA, USA, 28–30 September 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, D.; Xie, Y.; Chakrabarty, K. Cost-effective integration of three-dimensional (3D) ICs emphasizing testing cost analysis. In Proceedings of the 2010 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 7–11 November 2010; pp. 471–476. [Google Scholar] [CrossRef]
- Ferhani, F.F.; Saxena, N.R.; McCluskey, E.J.; Nigh, P. How Many Test Patterns are Useless? In Proceedings of the 26th IEEE VLSI Test Symposium (vts 2008), San Diego, CA, USA, 27 April–1 May 2008; pp. 23–28. [Google Scholar] [CrossRef]
- Lin, C.; Su, T. Rule Check of pad Placement in IC Layout With Yolo V3. In Proceedings of the 2022 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 20–21 June 2022; pp. 1–3. [Google Scholar] [CrossRef]
- Podpod; Velenis, D.; Phommahaxay, A.; Bex, P.; Fodor, F.; Marinissen, E.; Rebibis, K.; Miller, A.; Beyer, G.; Beyne, E. High Density and High Bandwidth Chip-to-Chip Connections with 20 μm Pitch Flip-Chip on Fan-Out Wafer Level Package. In Proceedings of the 2018 International Wafer Level Packaging Conference (IWLPC), San Jose, CA, USA, 23–25 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Sakamaki, R.; Horibe, M. Uncertainty Analysis Method Including Influence of Probe Alignment on On-Wafer Calibration Process. IEEE Trans. Instrum. Meas. 2019, 68, 1748–1755. [Google Scholar] [CrossRef]
- Liu, D.; Shih, M. An Experimental and Numerical Investigation Into Multilayer Probe Card Layout Design. IEEE Trans. Electron. Packag. Manuf. 2006, 29, 163–171. [Google Scholar] [CrossRef]
- Liu, D.S.; Chang, C.M.; Tu, C.Y.; Liu, A.H.; Huang, C.F.; Lee, Y.C. Optimization of Multilayer Probe Card Using Strain Energy-Based Analytical Model and Multiobjective Programming Algorithm. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 1292–1302. [Google Scholar] [CrossRef]
- Faruqi, A.; Goss, R.; Adhikari, D.; Kowtsch, T. Test Wafer Management and Automated Wafer Sorting. In Proceedings of the 2008 IEEE/SEMI Advanced Semiconductor Manufacturing Conference, Cambridge, MA, USA, 5–7 May 2008; pp. 322–326. [Google Scholar] [CrossRef]
- Kim, B.H.; Kim, J.B.; Kim, J.H. A Highly Manufacturable Large Area Array MEMS Probe Card Using Electroplating and Flipchip Bonding. IEEE Trans. Ind. Electron. 2009, 56, 1079–1085. [Google Scholar] [CrossRef]
- Brost, B.; Treibergs, V. Next generation of WLCSP contacting technologies for 250 micron pitch and below. In Proceedings of the 2018 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 11–12 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Mak, W.K.; Lin, Y.C.; Chu, C.; Wang, T.C. Pad Assignment for Die-Stacking System-in-Package Design. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2012, 31, 1711–1722. [Google Scholar] [CrossRef][Green Version]
- Müller, D.; Schäfer, J.; Massler, H.; Ohlrogge, M.; Zwick, T.; Kallfass, I. Impact of Ground Via Placement in On-Wafer Contact Pad Design up to 325 GHz. IEEE Trans. Components Packag. Manuf. Technol. 2018, 8, 1440–1450. [Google Scholar] [CrossRef]
- Williams, B.; Davis, R.; Cowell, E.W.; Yerger, J.; Greenwood, B.; Ruud, T. Source Pad Design Tradeoffs for a Power TrenchFET. IEEE Trans. Semicond. Manuf. 2022, 35, 439–445. [Google Scholar] [CrossRef]
- Tiernan, K.; Sinha, S.; Pang, L.; Williams, R.; Delling, K. How many probes is enough? A low cost method for probe card depopulation with low risk. In Proceedings of the 2015 IEEE International Test Conference (ITC), Anaheim, CA, USA, 6–8 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Ferguson, A.; Cullimore, M.; Geremia, R.; Tuohy, S.; Pelletier, E.; Braz, N.; Harris, G.; Kearsley, A.; Knowles, M.; Gaukroger, M.; et al. Recent Breakthroughs in Tight Pitch Laser Microdrilling for Mems Guide Plates. In Proceedings of the 2019 International Wafer Level Packaging Conference (IWLPC), San Jose, CA, USA, 22–24 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Iwai, H.; Nakayama, A.; Itoga, N.; Omata, K. Cantilever type probe card for at-speed memory test on wafer. In Proceedings of the 23rd IEEE VLSI Test Symposium (VTS’05), Palm Springs, CA, USA, 1–5 May 2005; pp. 85–89. [Google Scholar] [CrossRef]
- Patil, B.; Kinger, S.; Pathak, V.K. Probe station placement algorithm for probe set reduction in network fault localization. In Proceedings of the 2013 International Conference on Information Systems and Computer Networks, Mathura, India, 9–10 March 2013; pp. 164–169. [Google Scholar] [CrossRef]
- Sinhabahu, N.; Li, K.S.M.; Li, J.D.; Wang, J.; Wang, S.J. Yield-Enhanced Probe Head Cleaning with AI-Driven Image and Signal Integrity Pattern Recognition for Wafer Test. In Proceedings of the 2022 IEEE International Test Conference (ITC), Anaheim, CA, USA, 23–30 September 2022; pp. 554–558. [Google Scholar] [CrossRef]
- Gontara, S.; Boufaied, A.; Korbaa, O. A Unified approach for Selecting Probes and Probing Stations for Fault Detection and Localization in Computer Networks. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2071–2076. [Google Scholar] [CrossRef]
- Bernardi, P.; Cardone, L.; Foscale, T. Exploring trade-offs in multi-site wafer testing. In Proceedings of the 2024 IEEE 25th Latin American Test Symposium (LATS), Maceio, Brazil, 9–12 April 2024; pp. 1–4. [Google Scholar] [CrossRef]

| Die Side Length (mm) | Die Area | Dies in 6′′ Wafer | Dies in 8′′ Wafer | Dies in 12′′ Wafer | Dies in 18′′ Wafer |
|---|---|---|---|---|---|
| 1 mm | 1 mm2 | 17,366 | 31,259 | 70,008 | 157,928 |
| 2 mm | 4 mm2 | 4274 | 7724 | 17,366 | 39,278 |
| 3 mm | 9 mm2 | 1869 | 3392 | 7658 | 17,366 |
| 4 mm | 16 mm2 | 1035 | 1886 | 4274 | 9717 |
| 5 mm | 25 mm2 | 651 | 1192 | 2713 | 6187 |
| 6 mm | 36 mm2 | 445 | 818 | 1869 | 4274 |
| 7 mm | 49 mm2 | 322 | 594 | 1362 | 3123 |
| 8 mm | 64 mm2 | 242 | 449 | 1035 | 2379 |
| 9 mm | 81 mm2 | 188 | 350 | 811 | 1869 |
| 10 mm | 100 mm2 | 150 | 280 | 651 | 1506 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foscale, T.; Bernardi, P. A Cost–Benefit Analysis of Multi-Site Wafer Testing. Electronics 2025, 14, 2450. https://doi.org/10.3390/electronics14122450
Foscale T, Bernardi P. A Cost–Benefit Analysis of Multi-Site Wafer Testing. Electronics. 2025; 14(12):2450. https://doi.org/10.3390/electronics14122450
Chicago/Turabian StyleFoscale, Tommaso, and Paolo Bernardi. 2025. "A Cost–Benefit Analysis of Multi-Site Wafer Testing" Electronics 14, no. 12: 2450. https://doi.org/10.3390/electronics14122450
APA StyleFoscale, T., & Bernardi, P. (2025). A Cost–Benefit Analysis of Multi-Site Wafer Testing. Electronics, 14(12), 2450. https://doi.org/10.3390/electronics14122450







