Abstract
Secondary electron emission (SEE), a common physical phenomenon, exhibits both prominent applications in various fields and concomitant adverse impacts. Secondary electron yield (SEY) is a parameter for characterizing SEE, which determines the effect of the application and is very sensitive to the surroundings, particularly the magnetic field. Previous studies mainly focused on the influence of the magnetic field on secondary electron trajectories rather than the SEY itself. In this work, a specialized experimental platform was established to measure SEY, through which the influences caused by primary electrons and secondary electron trajectories were eliminated. The research findings demonstrate that as the magnetic field intensity increases, the SEY decreases rapidly and then gradually stabilizes. Meanwhile, a self-developed Monte Carlo simulation program was utilized to verify the above results, and it was concluded that the influence of magnetic field on SEY stems from the increased number of collisions of secondary electrons within the material. These results possess significant guiding significance and reference value for certain application scenarios where SEY suppression is required as well as for the design of multiplier devices aiming to enhance the output by utilizing magnetic fields.
1. Introduction
Secondary electron emission (SEE) is a phenomenon in which electrons escape from the surface of a material when a particle with a certain energy bombards the material [1]; this phenomenon is widely encountered and has thereby garnered extensive attention as a branch of physics. Currently, numerous precise scientific instruments and electron multiplier devices are fabricated by exploiting the SEE of a material, such as the scanning electron microscope (SEM) [2,3,4], photomultiplier tubes, and microchannel plates [5,6,7,8]. These are widely utilized in the fields of nuclear detection, aerospace, defense, and instrumentation science. Nevertheless, this phenomenon also induces many adverse effects, such as the micro-discharge effect in space high-power microwave components [9,10,11] and the electron cloud effect in particle accelerators [12,13,14]. In addition, the failure causes of Hall thrusters [15], high-voltage vacuum insulators [16,17], and vacuum electronic devices [18] are also deemed to be closely related to SEE. Consequently, SEE can impact the stable operation of the aforementioned equipment and devices. In severe circumstances, this may even result in catastrophic consequences. To achieve better application in precise scientific instruments and electron multiplier devices and circumvent the aforementioned adverse phenomena caused by SEE, an in-depth exploration of the SEE characteristics is indispensable.
The SEE characteristics of materials are measured by the secondary electron yield (SEY), which is defined as the ratio of the number of emitted electrons to the number of incident electrons [1]. Primarily, SEY is determined by the inherent properties of the materials themselves. However, it is highly sensitive to the surrounding environment, and this sensitivity can also exert an influence on the utilization of devices and equipment. As a result, it is essential to investigate the impact of the surrounding environment on it.
Magnetic field is one of the major environmental factors affecting SEY. However, the relevant studies are not sufficient.
Wang [19] observed that under magnetic field conditions, reducing the groove angle β can significantly decrease the SEY. Specifically, as β varies from 50° to 20°, the SEY drops from approximately 1.3 to 0.45. They attributed this reduction to two factors: (1) the alteration of secondary electron trajectories by the magnetic field, (2) the increased collision frequency with triangular and rectangular surface grooves. In the Hamamatsu PMT Handbook [20], it is mentioned that during the operation of photomultiplier tubes, the electron trajectories can be affected by weak magnetic fields. Especially for head-on PMT, a magnetic field of 2 mT can cause the output gain to drop sharply to near 0. Lehmann [21] concluded that in photomultiplier tubes (PMT), a smaller pore diameter exhibits stronger resistance to magnetic field interference and perform better in terms of gain and time resolution. Melikyan conducted [22] more in-depth research on the relationship between the pore diameter and the resistance to magnetic field interference in PMTs. When the magnetic field is enhanced, the radius of the Lorentz force trajectory of electrons decreases, leading to a reduction in the number of effective collisions. Therefore, the smaller the diameter, the stronger the anti-interference ability to the magnetic field. When combined with high SEY coatings on microchannel plate (MCP) pore walls, this configuration maintains elevated secondary emission efficiency during electron–wall collisions. The resulting signal attenuation thus remains minimal despite magnetic interference. Li [23] provided more systematic research conclusions on the design of photomultiplier tubes. MCP-PMTs with smaller actual apertures have a better magnetic field tolerance. When the magnetic field direction is parallel to the axial direction of the MCP channel, the gain attenuation is the fastest. Meanwhile, it was mentioned that the gain depends on the influence on the trajectory and the SEY during each collision process.
While these studies provide valuable insights for PMT applications, they primarily address trajectory effects rather than fundamental modifications to the secondary electron emission (SEE) model itself. To optimize SEE utilization and mitigate adverse effects, the dedicated investigation of magnetic field influence on the SEE model is, therefore, essential.
In this work, a dedicated SEY experimental platform was set up and relevant testing work was carried out by the authors to obtain the influence of the magnetic field on the secondary electron emission model. Furthermore, a Monte Carlo simulation code was written in Python3.8 to verify this influence and to acquire the reasons for the influence of the magnetic field on the SEE model.
2. Experimental Design
SEY serves as a metric to quantify the intensity of SEE. Consequently, in order to explore the influence of magnetic field on the SEE model, it is adequate to investigate the effect of the magnetic field on the SEY. It should be noted that, apart from affecting the SEE model, magnetic field also has an impact on the trajectory of primary electrons and the emission trajectory of secondary electrons. Consequently, in the experimental design, it is essential to ensure that the contributions of the trajectory of primary electrons and the emission trajectory of secondary electrons to the SEY results are insignificant and can be disregarded. Therefore, the sample current method [14] was chosen as the SEY measurement method under magnetic field conditions.
Based on the above method and aiming to simplify the measurement platform structure to eliminate potential confounding factors, a SEY measurement scheme was designed, as detailed in Figure 1a. The experimental apparatus is principally composed of the following components: an electron gun (Kimball Physics, FRA-2X1-2, Wilton, NH, USA) with its affiliated Faraday cup, a sample holder along with sample specimens, an adjustable voltage power supply, an electromagnet, a dual-channel picoammeter (Keithley 6482, Cleveland, OH, USA), and a computer. Figure 1b shows the experimental setup.
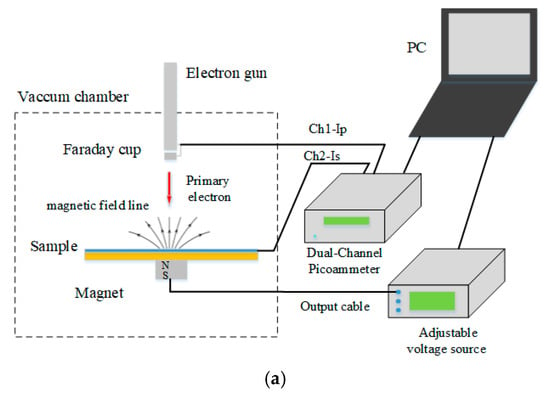

Figure 1.
(a) Experimental scheme for the SEY measurement. (b) Photograph of the experimental setup.
Among them, the electron gun is accountable for generating the primary electron beam, and the Faraday cup serves the function of receiving the primary electron current Ip. Channel 1 of the dual-channel picoammeter is assigned to measure the primary electron current Ip, whereas Channel 2 undertakes the task of measuring the sample current Is.
The electromagnet is positioned beneath the sample such that its center aligns with those of the sample and the cathode of the electron gun. By varying the current within its coil, a magnetic field with continuously adjustable intensity can be generated. When a forward current is applied, the side of the electromagnet adjacent to the sample becomes the N pole, while the opposite side (remote from the sample) becomes the S pole, as illustrated in the schematic diagram of magnetic field lines. Reversing the current flips the direction of the magnetic field. The computer receives the Ip and Is and calculates the SEY according to Formula (1):
3. Simulation
In the process of measuring the SEY based on the above experimental scheme, special caution must be exercised in choosing specific magnetic field intensities and structural parameters, especially the distance between the magnet and the electron emission plane. This is to guarantee that the impact of the magnetic field on the incident electron trajectory and the secondary electron emission trajectory is negligible for the final SEY result. To validate the appropriateness of the selected parameters, this study employs the simulation software CST Studio Suite 2024 for verification.
Firstly, the model of the magnetic field was established. Based on the actual size measurement results, the diameter and height of coils were determined (inner diameter = 15 mm, outer diameter = 18 mm, height = 10 mm). Subsequently, a Gaussmeter was employed to measure the variation trend in the magnetic field intensity with the coil current at a position 1 mm above the exact center of the sample surface. Based on these results, the number of turns of the coil, N = 1500, was determined. The comparison diagram between the simulation results of magnetic field calculation in CST and the experimental results is presented in Figure 2 (rectangles represent the experimental values, while circles represent the values calculated by CST). This ensures the equivalence between the magnetic field established in the simulation and that in the actual experiment.
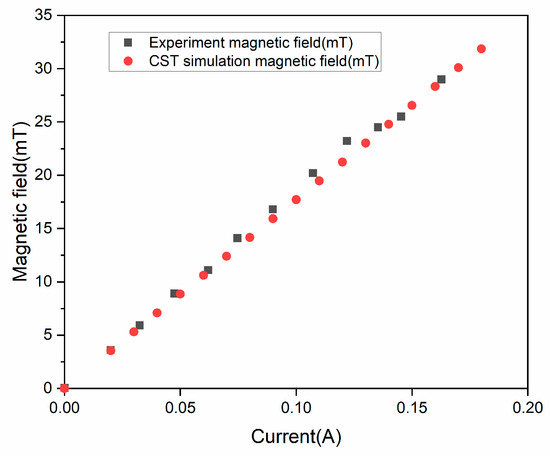
Figure 2.
Variation curve of magnetic field intensity with coil current (comparison between experiment and simulation).
Subsequently, electron trajectory modeling was carried out. The core structure of the electron gun (FRA-2X1-2)—including the cathode, grid, and anode—was preserved. Relevant structural parameters (e.g., dimensions and spacing of these core components) were input into CST to construct the electron gun geometry. In the scenario where the influence of magnetic fields was disregarded, the working distance was established as 100 mm and the electron beam energy was configured at 1000 eV. A thermionic emission model was applied during the simulation. The obtained beam spot diameter on the sample surface was 20.4 mm according to CST, which was basically consistent with the beam spot result measured by the pinhole scanning method [24]. This ensures that the incident electron trajectory in the simulation process is basically consistent with the actual situation.
In the CST simulation, two computational 2D particle monitors were configured. Monitor 1 included two virtual planes: Plane1, positioned at the anode exit (final accelerating electrode of the electron gun) to count emitted primary electrons (Num1), and Plane2, located at the sample surface to measure incident electrons (Num2). Monitor 2 consisted of two additional virtual planes: Plane3 above the sample to count escaping secondary electrons (Num3), and Plane4 to track secondary electrons returning to the surface (Num4).
The primary electron arrival ratio A is defined by Equation (2):
and the secondary electron return ratio is defined by Equation (3):
By definition, a larger value of A implies a lesser influence of the magnetic field on the incident trajectory, while a smaller η indicates a reduced impact of the magnetic field on the secondary electron trajectory. Based on the simulation results, computational analyses were performed on beam energies of 200 eV, 400 eV, 600 eV, 800 eV, and 1000 eV, with the corresponding outcomes presented in Table 1. Under the existing circumstances, when the beam energy surpasses 400 eV, the effect of the magnetic field on the trajectories of both primary and secondary electrons exerts only a negligible influence on the final SEY.

Table 1.
The values of A and η under different energy conditions.
Under the circumstance where the influence of the magnetic field on the trajectories of both primary electrons and emitted secondary electrons can be disregarded, an endeavor is made to explore the effect of the magnetic field on the internal secondary electron model. Nevertheless, neither the Furman nor the Vaughan secondary electron models available in CST are capable of accomplishing this task. These models, in particular, rely on pre-defined material parameters that cannot be adjusted to reflect magnetic field interactions. Therefore, it is essential to carry out research on the influence of the magnetic field on the internal secondary electron model of materials. The research should be grounded in the principle governing the interaction between electron beams and substances and should also incorporate a comprehensive consideration of the motion characteristics of electrons within the magnetic field. In this study, a Monte Carlo simulation program for computing SEY under magnetic field conditions has been specifically developed using the Python language. The detailed development flowchart is shown in Figure 3, and the meanings of the key parameters are illustrated in Table 2.
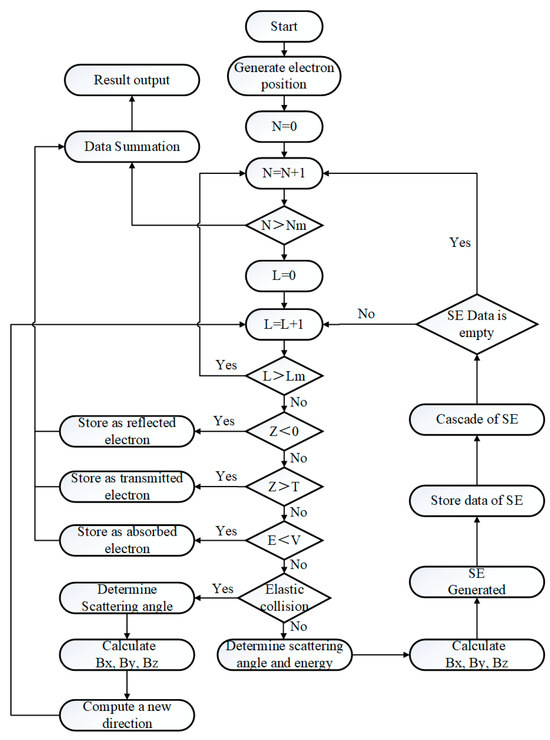
Figure 3.
Flow chart of the Monte Carlo program.

Table 2.
Monte Carlo simulation workflow variables.
In Monte Carlo simulations, the simulation of the electron transport process within the sample constitutes the core part of the entire simulation. During the simulation, the transport process can be abstracted as a series of discontinuous scattering processes, and between each scattering point, the electron flies freely. Scattering can be categorized into two distinct types, namely elastic and inelastic scattering, depending on whether there is an energy loss incurred by the electrons during the scattering process. The probabilities of the electron’s angular deflection and the magnitudes of energy loss during both elastic and inelastic scattering processes can be derived from the relevant differential scattering cross sections. In our specific simulation, the Mott cross section [25,26] is employed to characterize elastic scattering, while for inelastic scattering, the model described in reference [26] is taken into account. Based on the cross section results, the mean free paths for both elastic and inelastic scattering of electrons can be calculated, and subsequently, through these mean free paths, the probability distribution of the electron’s total free path can be determined.
1. Compared with previous Monte Carlo simulation frameworks, the authors have made improvements to the program in the following aspects to better approximate the real situation. According to the measurement results of the beam spot diameter and the characteristics of its Gaussian distribution, the electron position distribution is generated and subsequently utilized as the initial condition for incident electrons in the calculation.
2. Upon the generation of secondary electrons by the incident electrons, their energies, positions, and directions of movement are stored. Once the trajectories of the incident electrons have been computed, the stored information of these secondary electrons is retrieved and further processed as if they were incident electrons. This iterative cycle persists until all the electrons are either reflected, transmitted, or absorbed.
Based on the above, the spatial mapping of the solenoid magnetic field distribution was integrated into the simulation framework. According to the position of the electron, the three-axis directional components Bx, By, and Bz of the magnetic field in the x, y, and z directions at this position can be determined. In the calculations, it is assumed that the magnetic field has no influence on the deflection angle and the energy loss due to the collision and only affects the trajectory between the two collision events. Furthermore, the influence of the magnetic field on the free path is calculated according to its x-axis, y-axis, and z-axis components.
4. Results and Discussion
Firstly, the experimental results obtained under the condition of no coil current are compared with the simulation results to verify the credibility of the simulation program. The research is conducted by adopting the testing scheme mentioned previously and the established experimental platform, with aluminum foil (with dimensions of 100 mm × 100 mm × 50 μm) selected as the sample. In the Monte Carlo simulation, the number of incident electrons is set to 100,000, and the relationship between the SEY and the beam energy is shown in Figure 4. The rectangles denote the theoretically calculated values, while the circles represent the actual experimental values. As can be seen from the figure, the changing trends of the two are consistent. Within the energy spectrum of 0–1000 eV, the discrepancies between the simulation and experimental results remain minimal, with a discernible trend of decreasing differences as energy increases within this range.
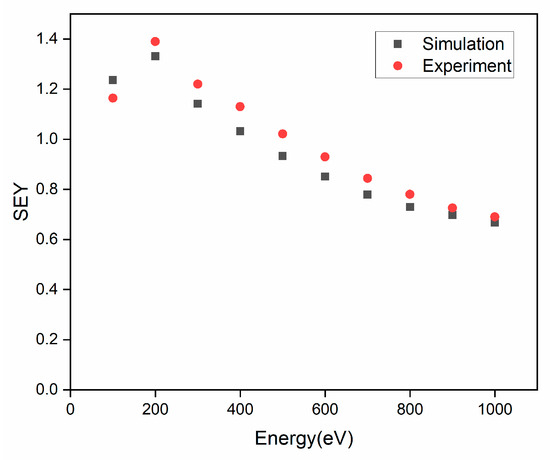
Figure 4.
The variation trend of secondary electron yield (SEY) with beam energy (comparison between experiment and simulation).
Subsequently, the experimental platform constructed was further utilized. Aluminum foil was selected as the sample, and the beam energies were set at 200 eV, 400 eV, 600 eV, 800 eV, and 1000 eV. The SEY measurements were systematically repeated five times for each experimental condition to ensure statistical reliability. The obtained data demonstrate excellent repeatability, with the maximum and minimum values of measured SEY within the same conditions not exceeding 5%. The variation trend in the SEY with the magnetic field intensity ranging from −25 mT to 25 mT (where a negative value indicates a reversed magnetic field) under each energy condition was investigated. The acquired results are presented in Figure 5. These results clearly demonstrate that the magnetic field strength initially exerts a significant impact on SEY, which declines rapidly and approaches a stable state as the magnetic field intensity increases. Secondly, after reversing the magnetic field, the SEY results are essentially consistent with those in the forward direction, indicating that the influence of the magnetic field direction on SEY is symmetrical.
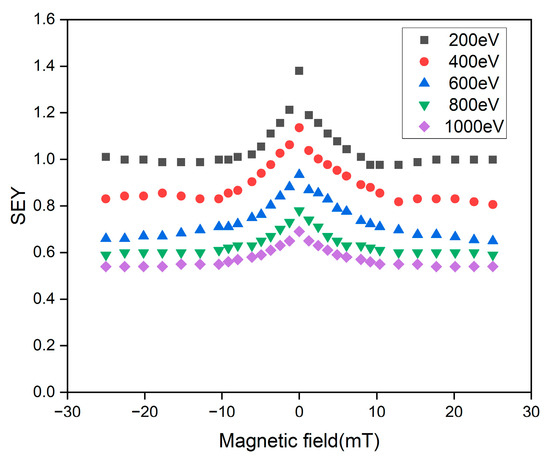
Figure 5.
Experimental results of the variation in SEY with magnetic field intensity (Beam energies = 200/400/600/800/1000 eV).
Building on this foundation, the Monte Carlo simulation program was developed to calculate the SEY under the magnetic field conditions. A comparison between the simulation outcomes and the experimental results is presented in Figure 6 (with B = 5 mT/10.4 mT/25 mT), demonstrating good consistency between the two.
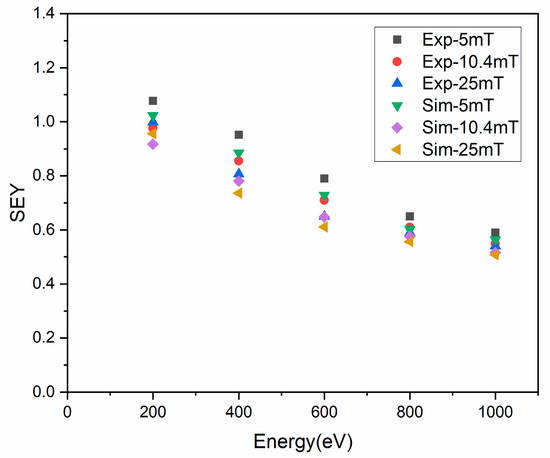
Figure 6.
Comparison between Monte Carlo simulation results and experimental results (B = 5 mT/10.4 mT/25 mT).
The analysis of Figure 5 reveals that each electron energy exhibits a distinct critical magnetic field. Below this critical value, the SEY undergoes sharp attenuation, while exceeding this threshold causes the SEY to gradually stabilize—this trend is quantitatively verified in Figure 6. Specifically, for electron energies of 800 eV and 1000 eV, the critical magnetic field strength is found to be approximately 5 mT.
Further simulations quantified the total mean free paths of electrons undergoing both elastic and inelastic collisions within the sample, confirming significant increases in both. The statistical analysis of the total counts of elastic and inelastic collisions also revealed similar growth trends. These findings elucidate the mechanism underlying the magnetic field’s influence on the secondary electron model: the applied magnetic field extends the electron trajectory length within the material, thereby increasing the collision frequency. This enhanced scattering promotes greater electron energy loss, consequently reducing the electron escape probability and ultimately reducing the measured SEY.
As illustrated in Figure 5, the symmetry of the SEY with respect to magnetic field direction is also explicable by the preceding conclusion: magnetic fields of either polarity enhance the average number of elastic and inelastic collisions of electrons within the sample, thereby resulting in a decrease in the SEY. While the reverse magnetic field alters the internal electron trajectories, the average collision frequency remains comparable to that under a forward-oriented field. This equivalence accounts for the observed symmetry.
In order to further validate the reliability of these conclusions, the increase in average collision frequency was simulated by effectively expanding both the elastic and inelastic cross sections under 0 mT conditions. Specifically, for primary electron energies of 200, 400, 600, 800, and 1000 eV, both elastic and inelastic cross sections were uniformly enlarged by a factor of 1.2. This coefficient aligns with the calculated multiple of the total increase in elastic and inelastic collision counts simulated under 25 mT conditions. The results are presented in Figure 7, where the rectangles denote the simulation data under a 25 mT magnetic field, and the circles represent simulations with enhanced cross sections under a 0 mT magnetic field. The excellent consistency between these datasets validates the conclusions.
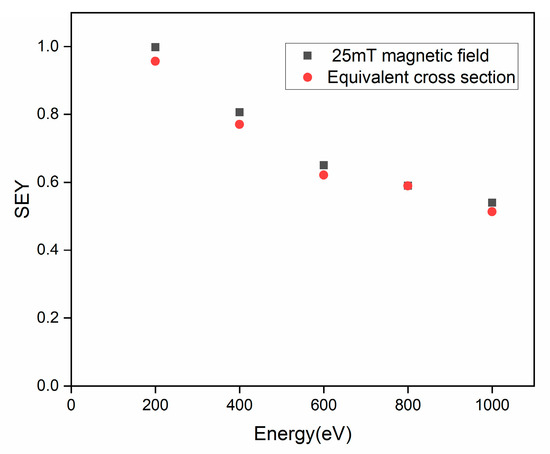
Figure 7.
Comparison of the simulation results of 25 mT and its equivalent cross section (under the condition of B = 0 mT).
5. Conclusions
In this paper, an in-depth exploration into the influence of magnetic field on secondary electron yield (SEY) is carried out, and verification is achieved through a combination of measurement and simulation. The results show that: Firstly, the magnetic field strength has a significant impact on SEY. As the magnetic field strength increases, the SEY decreases rapidly and then gradually tends to stabilize. Secondly, after reversing the magnetic field, the SEY remains basically unchanged, and the results exhibit symmetry. The influence of the magnetic field on the SEY can be attributed to its effect on the internal secondary electron emission model, which is specifically manifested in the increase in the number of elastic and inelastic collisions of secondary electrons within the material.
Based on the conclusions, in some application scenarios where SEY suppression is required, an appropriate magnetic field can be applied to significantly enhance the SEY suppression effect. On the other hand, in the design and research of multiplier devices, especially in situations where a magnetic field is utilized to increase the number of collisions between electrons and their channels, it is necessary to comprehensively take into account the influence of the magnetic field on the internal secondary electron emission model in order to achieve optimal multiplication performance.
Author Contributions
Conceptualization, C.D. and L.H.; methodology, C.D.; software, C.D. and J.H.; validation, C.D. and J.H.; formal analysis, C.D. and P.W.; investigation, C.D.; resources, L.Z.; data curation, C.D.; writing—original draft preparation, C.D.; writing—review and editing, C.D. and L.Z.; visualization, C.D., G.N. and P.W.; supervision, L.Z. and L.H.; project administration, C.D., L.Z. and L.H.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of the Ministry of Science and Technology of China, grant No. 2023YFF0719104.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to express gratitude to Shi Hongkai for his helpful discussions.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Bruining, H. Book Reviews: Physics and Applications of Secondary Electron Emission; Pergamon Press: Oxford, UK, 1955. [Google Scholar]
- Seiler, H. Secondary-Electron Emission in the Scanning Electron-Microscope. J. Appl. Phys. 1983, 54, 1–18. [Google Scholar] [CrossRef]
- Joy, D.C.; Prasad, M.S.; Meyer, H.M., III. Experimental secondary electron spectra under SEM conditions. J. Microsc. 2010, 215, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Reimer, L. Scanning Electron Microscopy: Physics of Image Formation and Microanalysis; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Yater, J.E. Secondary electron emission and vacuum electronics. J. Appl. Phys. 2023, 133, 050901. [Google Scholar] [CrossRef]
- Feller, W.B. The dynodized microchannel plate model and secondary electron emission. IEEE Trans. Electron Devices 1985, 32, 2479–2481. [Google Scholar] [CrossRef]
- Funsten, H.O.; Suszcynsky, D.M.; Harper, R.W. Mean secondary electron yield of avalanche electrons in the channels of a microchannel plate. Rev. Sci. Instrum. 1996, 67, 3478–3482. [Google Scholar] [CrossRef][Green Version]
- Tao, S.X.; Chan, H.W.; Graaf, H.V.D. Secondary Electron Emission Materials for Transmission Dynodes in Novel Photomultipliers: A Review. Materials 2016, 9, 1017. [Google Scholar] [CrossRef]
- Lau, Y.Y.; Gilgenbach, R.M.; Ang, L.K.; Kishek, R.A.; Valfells, A. Multipactor discharge on metals and dielectrics: Historical review and recent theories. Phys. Plasmas 1998, 5, 2120–2126. [Google Scholar] [CrossRef]
- Tondu, T.; Inguimbert, V.; Payan, D.; Balcon, N.; Belhaj, M. Secondary electron emission on space materials: Evaluation of the total secondary electron yield from surface potential measurements. IEEE Trans. Plasma Sci. 2012, 40, 282–290. [Google Scholar] [CrossRef]
- Yu, M.; Wang, D.; He, Y.; Li, Y.; Cui, W. Experimental Verification of Multipactor Discharge Dynamics Between Ferrite Dielectric and Metal. IEEE Trans. Electron Devices 2018, 65, 4592–4599. [Google Scholar] [CrossRef]
- Ohmi, K.; Fukuma, H.; Hiramatsu, S.; Tobiyama, M.; Flanagan, J.W.; Perevedentsev, E. Observation of Vertical Betatron Sideband due to Electron Clouds in the KEKB Low Energy Ring. Phys. Rev. Lett. 2005, 94, 054801. [Google Scholar] [CrossRef]
- Grosso, D.R.; Commisso, M.; Cimino, R.; Flammini, R.; Demma, T.; Larciprete, R.; Baglin, V. Nature of the Decrease of the Secondary-Electron Yield by Electron Bombardment and its Energy Dependence. Phys. Rev. Lett. 2012, 109, 64801. [Google Scholar] [CrossRef]
- Basovic, M. Secondary Electron Emission from Plasma Processed Accelerating Cavity Grade Niobium. Ph.D. Thesis, Old Dominion University, Norfolk, VA, USA, 2016. [Google Scholar]
- Smirnov, A.; Fisch, N.J.; Raitses, Y.; Staack, D. Measurements of secondary electron emission effects in the Hall thruster discharge. Phys. Plasmas 2006, 13, 423–430. [Google Scholar] [CrossRef]
- Anderson, R.A.; Brainard, J.P. Mechanism of pulsed surface flashover involving electron-stimulated desorption. J. Appl. Phys. 1980, 51, 1414–1421. [Google Scholar] [CrossRef]
- Chvyreva, A.; Pemen, A. Experimental investigation of electron emission from dielectric surfaces due to primary electron Beam: A review. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2274–2282. [Google Scholar] [CrossRef]
- Dickens, J.C.; Joshi, R.P.; Neuber, A.A.; Mankowski, J.; Nguyen, H.K.A. Calculations of secondary electron yield of graphene coated copper for vacuum electronic applications. AIP Adv. 2018, 8, 015325. [Google Scholar] [CrossRef]
- Munro, M.; Himel, T.; Stupakov, G.; Pivi, M.; Bane, K.; Raubenheimer, T.; Chen, C.; Wang, L. Suppression of secondary electron emission using triangular grooved surface in the ILC dipole and wiggler magnets. In Proceedings of the Particle Accelerator Conference (PAC), Albuquerque, NM, USA, 25–29 June 2007. [Google Scholar] [CrossRef][Green Version]
- PMT_handbook_v4E. Available online: https://www.hamamatsu.com.cn/content/dam/hamamatsu-photonics/sites/documents/99_SALES_LIBRARY/etd/PMT_handbook_v4E.pdf (accessed on 6 June 2025).
- Lehmann, A.; Lu, S.; Eyrich, W.; Teufel, A.; Sfienti, C.; Seitz, B.; Schepers, G.; Britting, A.; Düren, M.; Föhl, K.; et al. Performance studies of microchannel plate PMTs in high magnetic fields. Nucl. Inst. Methods Phys. Res. A 2009, 595, 173–176. [Google Scholar] [CrossRef]
- Bearden, I.; Klay, J.; Trzaska, W.; Garcia-Solis, E.; Slupecki, M.; Karavicheva, T.; Morozov, I.; Kaplin, V.; Serebryakov, D.; Melikyan, Y.; et al. Performance of the cost-effective Planacon® MCP-PMTs in strong magnetic fields. Nucl. Inst. Methods Phys. Res. A 2020, 983, 164591. [Google Scholar] [CrossRef]
- Xu, X.; Li, S.; Liu, B.; Zhang, M.; Gao, G.; Liu, H.; Gou, Y.; Qu, Y.; Xin, L.; Sai, X.; et al. Numerical Simulation on Magnetic Field Tolerance of MCP-PMTs. IEEE Trans. Nucl. Sci. 2022, 69, 850–857. [Google Scholar] [CrossRef]
- Deng, C.H.; Han, L.; Wang, Y. Design and Performance of a Miniaturized, Low-Energy, Large Beam Spot Electron Flood Gun. Electronics 2021, 10, 648. [Google Scholar] [CrossRef]
- Drouin, D.; Gauvin, R.; Joy, D.C. Computation of Polar Angle of Collisions from Partial Elastic Mott Cross-Sections. Scanning 1994, 16, 67–77. [Google Scholar] [CrossRef]
- Chang, H.Y.; Alvarado, A.; Marian, J. Calculation of secondary electron emission yields from low-energy electron deposition in tungsten surfaces. Appl. Surf. Sci. 2018, 450, 190–199. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).