Resilient Dynamic State Estimation for Power System Based on Modified Cubature Kalman Filter Against Non-Gaussian Noise and Outliers

Abstract

Accurate dynamic estimation is of vital importance for the real-time monitoring of the operating status of power systems. To address issues such as non-Gaussian noise and outlier interference, a cubature Kalman filter state estimation method based on robust functions (RF-CKF) is proposed. Firstly, based on the exponential absolute value, an estimator is established, which is represented by the exponential absolute value and quadratic functions. Secondly, the regression form of batch processing mode is established, and the estimator based on the exponential absolute value is integrated into the cubature Kalman filter framework. Finally, an example of a standard IEEE 39-bus system is used to verify the effectiveness of the proposed method. Compared with the unscented Kalman filter, cubature Kalman filter and H-infinity CKF, the proposed method has better estimation accuracy and stronger robustness in an anomaly environment.

1. Introduction

In normal operation or the electromechanical transient process of the power system, the phasor measurement unit (PMU) can realize real-time measurement of the systems state phasors, expanding the data source of the distribution system and creating better conditions for the real-time monitoring and analysis of the power system [1,2]. With the widespread development of phasor measurement units (PMUs), different types of state estimation (SE) techniques, including static SE and dynamic SE, have been developed to estimate the state information of the power grid [3]. For static SE, it is usually assumed that the power system operates under a quasi-steady state, and can monitor the bus voltage amplitude and phase angle at a certain time. Compared with static SE, dynamic SE (DSE) can monitor the dynamic changes in the system in real time [4,5]. Therefore, DSE is widely used in the implementation of electrical equipment control schemes, such as the electromechanical transient tracking of synchronous generators.

For DSE, a number of classical Kalman filters (KFs) have been proposed in recent years. For example, the extended Kalman filter (EKF) [6], unscented Kalman filter (UKF) [7], cubature Kalman filter (CKF) [8], and its modified form [9,10] are designed to dynamically estimate the state variables of the power system. Considering the bias estimation that may result from the uncertainty of non-Gaussian noise, a simplified Gaussian synthesis EKF method is proposed in reference [11] to handle nonlinear state estimation. In light of the truncation error resulting from EKF’s linearization approximation, multiple non-derivative DSE techniques have been introduced. For instance, the square root UKF can be employed along with a weighting factor applied to the measurements, and reference [12] proposes an improved method to improve numerical stability and robustness to the measured outliers. Previous work includes [13], where an adaptive UKF monitors motor transmission control inputs and status signals. Additionally, ref. [14] introduced an adaptive CKF using variable dB Bayes to model attack likelihoods, improving the detection of stochastic injection attacks. These contributions have markedly enhanced power system monitoring. However, most of the state estimation methods proposed above were developed using the objective function of the Gaussian noise distribution hypothesis; that is, they demonstrate satisfactory results exclusively under the condition that the noise in both the system and the measurements strictly conforms to Gaussian characteristics. For real-world power engineering systems, there exists certain uncertainty in the statistical characteristics of noise associated with generator modeling. For example, when the positioning system or navigation system of the PMU device is disturbed, the measurement phase angle will be biased, which will affect the statistical characteristics of the noise changes or the measurement outliers [15,16]. Therefore, in the presence of non-Gaussian noise, the estimation performance of these methods can be significantly degraded.

To alleviate the adverse impact of abnormal data in the measurement function, particularly non-Gaussian noise and load deviations [17], researchers have also proposed many improvement measures. In [18], a distributed compressive sensing-based estimation strategy was proposed. Moreover, as a local similarity measure in information-theoretic learning (ITL), entropy incorporates higher-order statistical moments of the probability distribution, demonstrating superior performance in non-Gaussian noise environments. In particular, the DSE algorithm based on the maximum entropy criterion was integrated into the standard EKF [19] and UKF [20], which effectively enhanced the robustness of the Kalman filter in non-Gaussian noise conditions. In [21], a binary random variables and image noise are used to simulate the abnormal data that must occur in the sensor. With this in mind, we designed the MC (maximum correntropy) UKF, where the criterion is no longer the minimum error but instead the maximum correlation entropy criterion, in order to obtain a more accurate result. In [22], a more expansive approach to UKF was proposed.

For power system dynamic state estimation, the uncontrollable load will inevitably lead to various situations. This method can handle the noise problem according to the general robust loss function. In [23], the authors proposed a navigation algorithm implementing an unscented Kalman filter based on Huber-M estimation, which improved the problem whereby the filtering accuracy would decrease or even diverge when the non-Gaussian noise or statistical characteristics were inaccurate. In reference [24], an adaptive adjustment strategy for Kalman filter gain is proposed based on the residual error and other characteristics. This algorithm not only improves the estimation accuracy, but also enhances the real-time and stability of the filtering process. In [25], an interpolating extended Kalman filtering algorithm is proposed. Pseudo-adaptive interpolation and strong tracking theory are introduced into the filtering process, which effectively improves the estimation accuracy and robustness to the noise of the EKF algorithm. Reference [26] proposed a generator dynamic state estimation method designed to mitigate the consequences of bad data in dynamic state estimation, and compared the forecast value with that of the generator dynamic equation to reduce the impact of bad data on filtering. An estimate based on the maximum exponential absolute value (MEAV) is proposed, with the effect of reduced outliers [27]. As demonstrated in [28], a MEAV-criteria-based distributed robust estimation scheme was developed. However, the cost functions in [27,28] are less efficient than the quadratic functions in the weighted least squares approach, particularly when the noise is low.

To solve the problems of non-Gaussian noise and outlier interference in conventional methods, this paper proposes a new cubature Kalman filter based on robust functions. The main contributions of this article are as follows:

• An estimator based on the exponential absolute value is established, which is represented by the exponential absolute value function and quadratic function.
• The regression form of batch processing mode is established, and the estimator based on the exponential absolute value is integrated into the cubature Kalman filter framework.

The remainder of this paper is structured as follows: The DSE model of the power system is established and analyzed in Section 2. Our novel robust DSE framework is introduced in Section 3. An extensive performance evaluation through IEEE 39-bus case studies is presented in Section 4, while Section 5 highlights the main findings and implications.

2. Dynamic State Estimation Model of Power System

Generally, the discrete differential equation of the actual power system consists of two time-varying discrete nonlinear functions, state variable and measured value, which are realized by the improved Euler method. The mathematical representation of the nonlinear function is given by

$$\left\{\begin{array}{l}{\mathit{x}}_{\mathit{k}}=\mathit{f}\left({\mathit{x}}_{\mathit{k}-1},{\mathit{u}}_{\mathit{k}-1}\right)+{\mathit{w}}_{\mathit{k}-1}\\ {\mathit{z}}_{\mathit{k}}=\mathit{h}\left({\mathit{x}}_{\mathit{k}},{\mathit{u}}_{\mathit{k}}\right)+{\mathit{v}}_{\mathit{k}}\end{array}\right.$$

(1)

where f(·) and h(·) represent the nonlinear state propagation and observation functions, respectively; the subscript k represents the time scale; x_k and z_k represent state variables and observation vector, respectively; u_k represents the input vector; w_k is the system noise and v_k is measurement noise; and the covariance matrices are Q_k and R_k, respectively.

As one of the key features in a power system, the accurate modeling of the synchronous generator is very important for the dynamic tracking of the power system. The proposed approach utilizes a fourth-order synchronous machine representation, offering enhanced fidelity to real-world generator dynamics over traditional second-order approximations. The state-space representation is developed as follows:

$$\left\{\begin{array}{l}\dot{\delta }=\omega -{\omega }_0\\ \dot{\omega }={\displaystyle \frac{{\omega }_0}{2T_j}}\left[T_{\mathrm{m}}-T_{\mathrm{e}}-{\displaystyle \frac{K_{\mathrm{D}}}{{\omega }_0}}\left(\omega -{\omega }_0\right)\right]\\ {\dot{e}}_q^{\prime }={\displaystyle \frac{1}{T_{d0}^{\prime }}}\left[E_{\mathrm{f}d}-e_q^{\prime }-\left(x_d-x_d^{\prime }\right)i_d\right]\\ {\dot{e}}_d^{\prime }={\displaystyle \frac{1}{T_{q0}^{\prime }}}\left[-e_d^{\prime }+\left(x_q-x_q^{\prime }\right)i_q\right]\end{array}\right.$$

(2)

where $\omega$ represents the rotor speed per unit, $\delta$ is the power angle; ${\omega }_0=2\pi f_0$ is the angular frequency rating; $T_e$ is the electromagnetic power of the generator; $T_m$ is the mechanical power; $T_j$ denotes the inertial constant, $K_D$ is the damping coefficient; $E_{fd}$ indicates the excitation voltage; $e_q^{\prime }$ is the transient potential of the $q$ axis and $e_d^{\prime }$ is the transient potential of the $d$ axis, respectively; and $x_d$ denotes synchronous reactance and $x_d^{\prime }$ denotes the transient reactance of direct axis, respectively. In addition, $x_q$ indicates synchronous reactance and $x_q^{\prime }$ stands for transient reactance of quadrature axis; $i_d$ and $i_q$ indicate the stator currents of the direct and quadrature axes, respectively; and $T_{d0}^{\prime }$ and $T_{q0}^{\prime }$ represent the open circuit transient time constants of the direct and quadrature axes of the generator, respectively.

Compared with Equation (1), the state vector is set to ${\mathit{x}}_{\mathit{k}}={[\delta \omega e_q^{\prime } e_d^{\prime }]}^T$ and the input vector is set to ${\mathit{u}}_{\mathit{k}}={[T_m E_{fd} i_R i_I]}^T$. In order to improve the estimation accuracy of the synchronous generator, this paper adopts four-dimensional measurement, and the measurement function of generator is set to ${\mathit{z}}_{\mathit{k}}={[\delta \omega e_R e_I]}^T$, where $e_R$ and $e_I$ can be expressed as follows:

$$e_R=\left(e_d^{\prime }+i_d{x}_q^{\prime }\right)\sin (\delta )+\left(e_q^{\prime }-i_d{x}_d^{\prime }\right)\cos (\delta )$$

(3)

$$e_I=\left(e_q^{\prime }-i_d{x}_d^{\prime }\right)\sin (\delta )-\left(e_d^{\prime }+i_q{x}_q^{\prime }\right)\cos (\delta )$$

(4)

Moreover, to facilitate the solution, the above formula can be reformulated in terms of state and input variables, expressed by

$$i_d=i_R\sin (\delta )-i_I\cos (\delta )$$

(5)

$$i_q=i_I\sin (\delta )+i_R\cos (\delta )$$

(6)

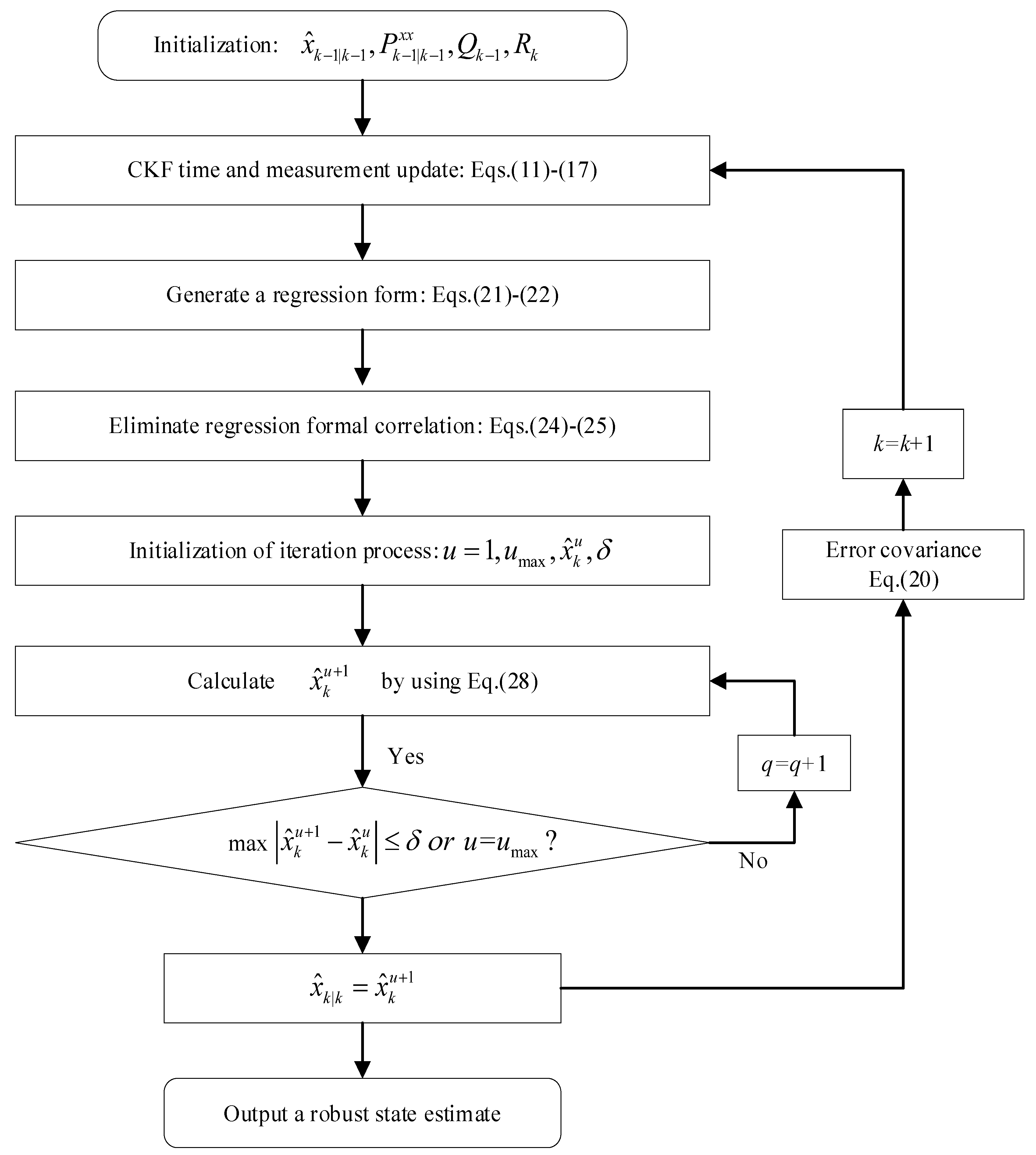
3. Proposed RF-CKF Method

Firstly, based on robust function, a novel robust estimator is proposed, and then it is combined with CKF to solve non-Gaussian noise and outlier problems.

3.1. Robust Function-Based Estimator

A robust estimator based on the MCE criterion and a quadratic function is derived. It is realized by minimizing:

$$J_p={\displaystyle \sum _{i=1}^m{\rho }_p}(r_i)$$

(7)

where ${\rho }_p$ is given by

$${\rho }_p(r_i)=\left\{\begin{array}{l}-a_i\exp (a_i+{\displaystyle \frac{r_i}{{\sigma }_i}})+{\displaystyle \frac{a_i^2}{2}}+a_i, r_i<-a_i{\sigma }_i\\ {\displaystyle \frac{r_i^2}{2{\sigma }_i^2}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left|r_i\right|\le a_i{\sigma }_i\\ -a_i\exp (a_i-{\displaystyle \frac{r_i}{{\sigma }_i}})+{\displaystyle \frac{a_i^2}{2}}+a_i, r_i>a_i{\sigma }_i\end{array}\right.$$

(8)

where $a_i$ denotes the threshold parameter that determines the transition between quadratic and robust functions. ${\sigma }_i$ represents the standard deviation of measurement noise. Quadratic functions can guarantee its stability, and robust functions are less sensitive to outliers. The combination of the two can maintain high estimation accuracy when handling normal observations, while maintaining robustness when encountering outliers. Note that (8) is continuous and differentiable.

3.2. RF-CKF Estimation Method

As a relatively new Kalman filter for nonlinear models, the main concept of a CKF is the third-order sphere-phase-diameter volume rule, which facilitates the numerical approximation of multivariate moment integrals. The above robust function is combined with the CKF, which consists of three steps: (1) state prediction; (2) measurement update; (3) linear regression model derivation.

3.2.1. State Prediction

First, we establish the initial state estimate and error covariance:

$${\hat{\mathit{x}}}_{0|0}=E\left[{\mathit{x}}_0\right]$$

(9)

$${\mathit{P}}_{0|0}=E[({\mathit{x}}_0-{\hat{\mathit{x}}}_{0|0}){({\mathit{x}}_0-{\hat{\mathit{x}}}_{0|0})}^T]$$

(10)

A series of cubature points are generated according to the spherical radial method:

$${\mathit{x}}_{i,k-1\mid k-1}={\mathit{S}}_{k-1\mid k-1}{\mathit{\xi }}_{\mathit{i}}+{\hat{\mathit{x}}}_{k-1\mid k-1},\hspace{1em}\mathrm{for} \mathit{i}=1,\dots ,2\mathit{n}$$

(11)

where ${\mathit{S}}_{\mathit{k}-1\mid \mathit{k}-1}=chol({\mathit{P}}_{\mathit{k}-1\mid \mathit{k}-1})$, and $\left\{{\xi }_i\right\}(i=1,2,\dots ,2n)$ is defined as

$${\mathit{\xi }}_{\mathit{i}}=[{\mathit{I}}_{\mathit{n}\times \mathit{n}},-{\mathit{I}}_{\mathit{n}\times \mathit{n}}]$$

(12)

The calculation of the propagated cubature points can be derived by

$${\mathit{x}}_{i,k|k-1}^{*}=\mathit{f}\left({\mathit{x}}_{i,k-1|k-1},{\mathit{u}}_k\right)$$

(13)

Calculate the predicted value of the state ${\hat{\mathit{x}}}_{k|k-1}$ at time instant $k$ and the corresponding error covariance ${\mathit{P}}_{k|k-1}$

$$\left\{\begin{array}{l}{\hat{\mathit{x}}}_{k|k-1}={\displaystyle \frac{1}{2n}}{\displaystyle \sum _{i=1}^{2n}{\mathit{x}}_{i,k|k-1}^{*}}\\ {\mathit{P}}_{k|k-1}={\displaystyle \frac{1}{2n}}{\displaystyle \sum _{i=1}^{2n}{\mathit{x}}_{i,k|k-1}^{*}}{({\mathit{x}}_{i,k|k-1}^{*})}^T-{\hat{\mathit{x}}}_{k|k-1}{\hat{\mathit{x}}}_{k|k-1}^T+{\mathit{Q}}_{k-1}\end{array}\right.$$

(14)

3.2.2. Measurement Update

A set of cubature points ${\mathit{x}}_{i,k|k-1}$ are generated based on the state prediction

$${\mathit{x}}_{i,k\mid k-1}={\mathit{S}}_{k|k-1}{\xi }_i+{\hat{\mathit{x}}}_{k|k-1}, \mathrm{for} i=1,\dots ,2n$$

(15)

The measurement equation $\mathit{h}(\cdot )$ is utilized to derive the predicted value of the sampling point through propagation

$${\mathit{Z}}_{i,k|k-1}=\mathit{h}({\mathit{x}}_{i,k|k-1},{\mathit{u}}_k)$$

(16)

Following that, the computation of the mean values ${\hat{\mathit{z}}}_{\mathit{k}\mid \mathit{k}-1}$, prediction error covariance of measurement ${\mathit{P}}_{k|k-1}^{\mathrm{zz}}$, and cross-covariance ${\mathit{P}}_{k|k-1}^{xz}$ for measurements can be further refined as follows

$$\left\{\begin{array}{l}{\hat{\mathit{z}}}_{k\mid k-1}={\displaystyle \frac{1}{2n}}{\displaystyle \sum _{i=1}^{2n}{\mathit{Z}}_{i,k\mid k-1}}\\ {\mathit{P}}_{k\mid k-1}^{zz}={\displaystyle \frac{1}{2n}}{\displaystyle \sum _{i=1}^{2n}{\mathit{Z}}_{i,k\mid k-1}{\mathit{Z}}_{i,k\mid k-1}^T-{\hat{\mathit{z}}}_{k\mid k-1}{\hat{\mathit{z}}}_{k\mid k-1}^T+{\mathit{R}}_k}\\ {\mathit{P}}_{k\mid k-1}^{xz}={\displaystyle \frac{1}{2n}}{\displaystyle \sum _{i=1}^{2n}{\mathit{x}}_{i,k\mid k-1}}{\mathit{Z}}_{i,k\mid k-1}^T-{\hat{\mathit{x}}}_{k\mid k-1}{\hat{\mathit{z}}}_{k\mid k-1}^T\end{array}\right.$$

(17)

3.2.3. State Update

Calculate the Kalman filter gain:

$${\mathit{K}}_k={\mathit{P}}_{k|k-1}^{xz}{{\mathit{P}}_{k|k-1}^{zz}}^{-1}$$

(18)

By using the deviation between the measured value and the predicted value of the measured quantity, the predicted value of the generator state quantity is filtered by the Kalman filter gain, and the estimated value of the state quantity of the generator state quantity is finally obtained:

$${\hat{\mathit{x}}}_{k|k}={\hat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k({\mathit{z}}_k-{\hat{\mathit{z}}}_{k|k-1})$$

(19)

Calculate the error covariance matrix:

$${\mathit{P}}_{k|k}={\mathit{P}}_{k|k-1}-{\mathit{K}}_k{\mathit{P}}_{k|k-1}^{zz}{\mathit{K}}_k^T$$

(20)

3.2.4. Linear Regression Model Derivation

In order to facilitate matrix solving, statistical regression matrix is defined as ${\mathit{H}}_k={({\mathit{P}}_{k|k-1}^{-1}{\mathit{P}}_{xz,k|k-1})}^T$. The nonlinear measurement equation is linearized as follows:

$${\mathit{Z}}_k=h({\hat{\mathit{x}}}_{k|k-1})+{\mathit{H}}_k({\mathit{x}}_k-{\hat{\mathit{x}}}_{k|k-1})+{\mathit{v}}_k$$

(21)

Robust functions are integrated into the CKF through linear regression models. The regression form is obtained by state prediction and the measurements:

$$\left[\begin{array}{c}{\mathit{Z}}_k+{\mathit{H}}_k{\hat{\mathit{x}}}_{k|k-1}-h({\hat{\mathit{x}}}_{k|k-1})\\ {\hat{\mathit{x}}}_{k|k-1}\end{array}\right]=\left[\begin{array}{l}{\mathit{H}}_k\\ {\mathit{I}}_k\end{array}\right]{\mathit{x}}_k+\left[\begin{array}{l}{\mathit{v}}_k\\ -{\mathit{e}}_k\end{array}\right]$$

(22)

Let ${\left[{\mathit{v}}_k -{\mathit{e}}_k\right]}^T$ be denoted as ${\xi }_k$, then

$$E\left[{\xi }_k{\xi }_k^T\right]=\left[\begin{array}{ll}{\mathit{R}}_k& 0\\ 0& {\mathit{P}}_{k|k-1}\end{array}\right]={\mathit{\epsilon }}_k{\mathit{\epsilon }}_k^T$$

(23)

where ${\mathit{\epsilon }}_k$ is the Cholesky decomposition factor.

To optimize the solving process, Equation (19) is transformed by multiplying both sides with ${\mathit{\epsilon }}_k^{-1}$ to eliminate the correlation between the state vector and the measurement vector.

$${\mathit{\epsilon }}_k^{-1}\left[\begin{array}{c}{\mathit{Z}}_k+{\mathit{H}}_k{\hat{\mathit{x}}}_{k|k-1}-h({\hat{\mathit{x}}}_{k|k-1})\\ {\hat{\mathit{x}}}_{k|k-1}\end{array}\right]={\mathit{\epsilon }}_k^{-1}\left[\begin{array}{l}{\mathit{H}}_k\\ {\mathit{I}}_k\end{array}\right]{\mathit{x}}_k+{\mathit{\epsilon }}_k^{-1}\left[\begin{array}{l}{\mathit{v}}_k\\ -{\mathit{e}}_k\end{array}\right]$$

(24)

which can be condensed as

$${\mathit{D}}_k={\mathit{B}}_k{\mathit{x}}_k+{\mathit{\gamma }}_k$$

(25)

where $E\left[{\mathit{\gamma }}_k{\mathit{\gamma }}_k^T\right]=I$, and the derivation process is as follows:

$$\begin{array}{ll}E\left[{\mathit{\gamma }}_k{\mathit{\gamma }}_k^T\right]& =E\left[{\mathit{\epsilon }}_k^{-1}{\xi }_k{\xi }_k^T{({\mathit{\epsilon }}_k^{-1})}^T\right]\\ & =E\left[{\mathit{\epsilon }}_k^{-1}{\mathit{\epsilon }}_k{\mathit{\epsilon }}_k^T{({\mathit{\epsilon }}_k^{-1})}^T\right]=E\left[I\right]=I\end{array}$$

(26)

By substituting the residual ${\gamma }_k$ into (7), we get the cost function

$$J_p={\displaystyle \sum _{i=1}^m{\rho }_p}(r_{i,k})$$

(27)

where $r_{i,k}=D_{i,k}-b_i^T{\hat{x}}_k$ is the i-th residual at time k, and $b_i^T$ is the i-th row vector of $B_k$.

Minimize the above cost function and, according to mathematical theory, take the partial derivative of (24) with respect to $x_k$ and make it equal to 0:

$$\begin{array}{ll}{\displaystyle \frac{\partial J}{\partial {\hat{x}}_k}}& ={\displaystyle \frac{\partial J}{\partial r_{i,k}}}{\displaystyle \frac{\partial r_{i,k}}{\partial {\hat{x}}_k}}\\ & ={\displaystyle \sum _{i=1}^m\frac{\partial \rho (r_{i,k})}{\partial r_{i,k}}\frac{1}{r_{i,k}}{r}_{i,k}\frac{\partial r_{i,k}}{\partial {\hat{x}}_k}}\\ & =-{\displaystyle \sum _{i=1}^m{q}_{i,k}}{r}_{i,k}{b}_i^T\\ & =-B_k^{T}Q{\overline{r}}_k\end{array}$$

(28)

where ${\overline{r}}_k={[r_{1,k},r_{2,k}\cdots ,r_{m,k}]}^T$ and $Q_k=diag(q_{1,k},$$q_{2,k},\cdots q_{m,k})$. The factor expression of weighting matrix $Q$ is as follows:

$$\begin{array}{ll}{q}_{i,k}& ={\displaystyle \frac{\partial \rho (r_{i,k})}{\partial r_{i,k}}}{\displaystyle \frac{1}{r_{i,k}}}\\ & =\left\{\begin{array}{l}{\displaystyle \frac{-a_i\exp (a_i+\frac{r_{i,k}}{s_i})}{s_i{r}_{i,k}}}, r_i<-a_i{s}_i\\ {\displaystyle \frac{1}{s_i^2}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \left|r_i\right|\le a_i{s}_i\\ {\displaystyle \frac{a_i\exp (a_i-\frac{r_{i,k}}{s_i})}{s_i{r}_{i,k}}}, r_i>a_i{s}_i\end{array}\right.\end{array}$$

(29)

Given that the threshold parameter $a_i$ is bounded within the interval [1.5,3] and noise ${\gamma }_k$ in the regression model, then $a_i$ is set to 3 and $s_i$ is set to 1 for simplicity [29].

The iterative form of the state ${\hat{x}}_k^{u+1}$ and the updated form of the error covariance $P_{k|k}$ are given as follows:

$${\hat{x}}_k^{u+1}={\hat{x}}_k^u+{(B_k^T{Q}_k^u{B}_k)}^{-1}(B_k^T{Q}_k^u{D}_k)$$

(30)

For clarity, the generator DSE method RF-CKF proposed in this paper is summarized in Figure 1.

4. Simulation Results

In order to verify the effectiveness of our proposed method RF-CKF, this section conducts extensive simulations on an IEEE 39-bus system, including normal Gaussian noise, non-Gaussian noise, and outlier disturbance mountain scenes, to illustrate the performance of the proposed method in resolving anomalies. In addition, for the analysis, comparisons were made with the UKF, CKF, and HCKF methods, proposed in recent years.

Test Systems: In the actual power engineering, the equipment will inevitably experience interference and noise in the transmission process, so in the test system, we listed the ideal situation, non-Gaussian noise, and outlier interference as three conditions. The IEEE 39-bus test system is adopted, and its detailed parameters and the connection relationship between each bus are described in [30]. PSCAD/EMTDC V5 software is used to generate the real turntable and the measured values of the system to simulate the transient stability data of the power system. In addition, the control input variables of the generator model are known. At 0.5 s, a three-phase metal short circuit fault is set at the bus 16–21 line outlet and cleared 0.2 s later. Set the total simulation time to 10 s and the PMU sampling rate to 50 samples per second. Due to page limitations, the estimated results of generator 8 (G8) are used as an example. It should be noted that the implementation of the methods discussed was executed within the MATLAB 2024a framework using a computer equipped with an Intel Core CPU i5-7200U processor (Intel, Santa Clara, CA, USA), 2.5 GHz, and 8 GB RAM.

Case 1: In the test, we postulate that the noise statistics of the synchronous generator model follow a normal Gaussian distribution with a mean of zero. The status of the generator is tracked by using the UKF, CKF, and HCKF methods and the proposed RF-CKF method.

Case 2: Considering that in the actual system there will inevitably be noise and external interference in the measuring equipment, resulting in a serious deviation of the measurement noise from the assumed Gaussian distribution. To validate the efficacy of the proposed approach under these conditions, the measurement noise is modeled as a zero-mean non-Gaussian process following both heavy-tailed bimodal Gaussian mixture distributions.

Case 3: Considering the limitations of measurement synchronization and the inherent saturation problem of the current transformer for measurement, the observed signals collected by the PMU may not change over time. In terms of the test condition setting, it is assumed that the observed quantity data is not updated during the period from 0.8 s to 1.1 s, and none of the four measurement variables change over time during this 0.3 s period.

Furthermore, to ensure a rigorous comparative analysis, we employ the root-mean-square error (RMSE) metric to quantitatively assess the performance of all considered methodologies across diverse case scenarios, as defined below:

$$\mathit{RMSE}=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{k=1}^n{({\hat{\mathit{x}}}_k-{\mathit{x}}_k)}^2}}{n}}}$$

(31)

where $n$ represents the total step size, $k$ is the time instant, $\mathit{x}=[\delta \omega e_q^{\prime } e_d^{\prime }]$, ${\hat{\mathit{x}}}_k$ is the estimated value, and ${\mathit{x}}_k$ is the truth value.

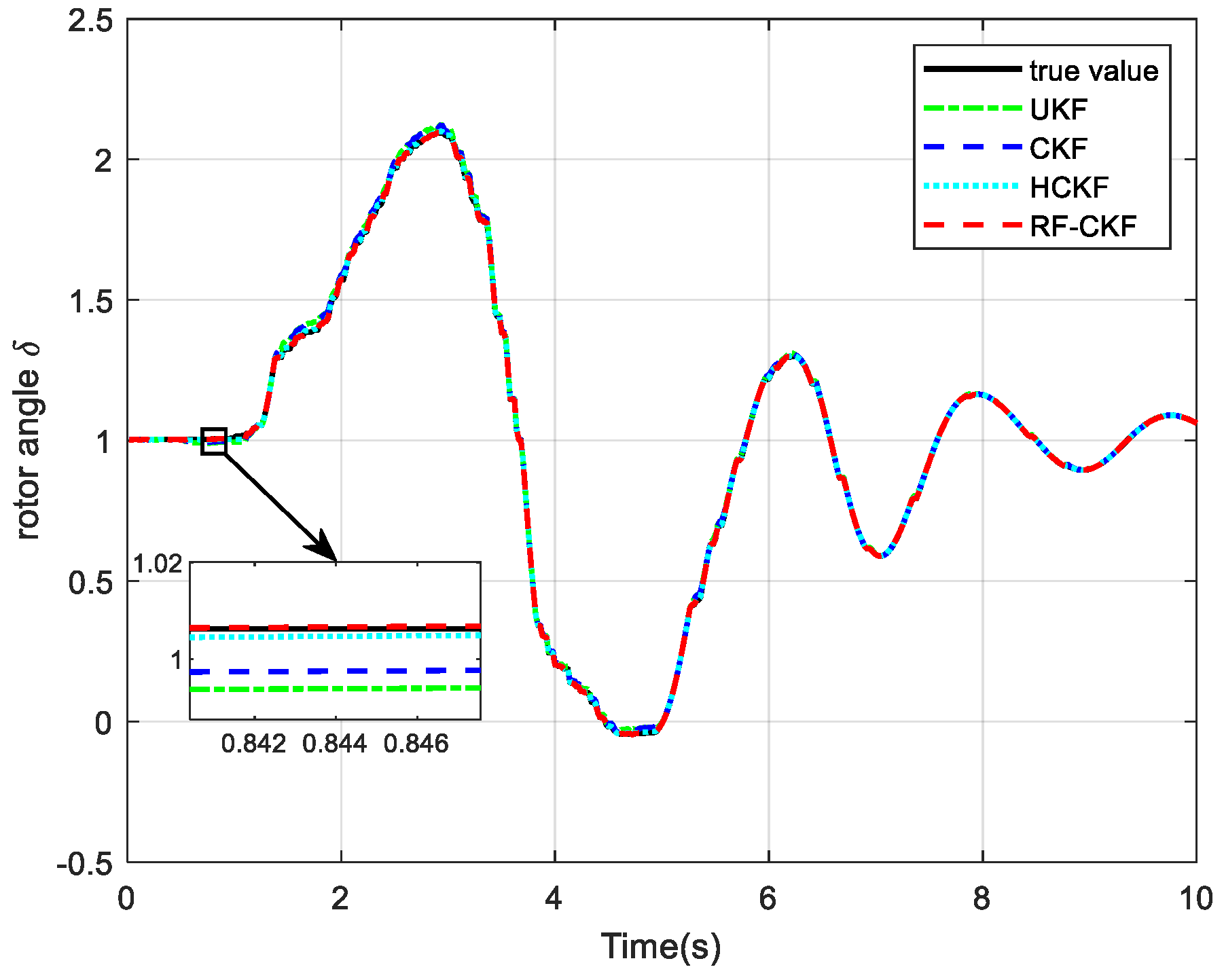
4.1. Case 1: Gaussian Noise Test

In this subsection, the noise characteristics of the synchronous generator model are assumed to adhere to a Gaussian distribution with zero mean, state noise covariance and measurement noise variance are set as $Q_k={10}^{-6}I$ and $R_k={10}^{-5}I$, respectively. The initial value of the state error covariance is set to ${10}^{-5}I$, the threshold parameter $a_i$ is set to 3, and $s_i$ is set to 1.

The UKF, CKF, and HCKF methods and the proposed RF-CKF approach are implemented to track the states of generators. The comparative performance levels of the evaluated methodologies are illustrated in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

The experimental findings demonstrate substantial deviations between the UKF estimates and the ground truth values. The CKF is less sensitive to parameter selection, so it can achieve better estimation results than the UKF. Furthermore, since the HCKF integrates robust control theory, it can dynamically adjust the system and measure noise parameters, thereby improving its accuracy. The developed RF-CKF, due to the introduction of a robust function and regression model, can be combined with the CKF to achieve stable tracking.

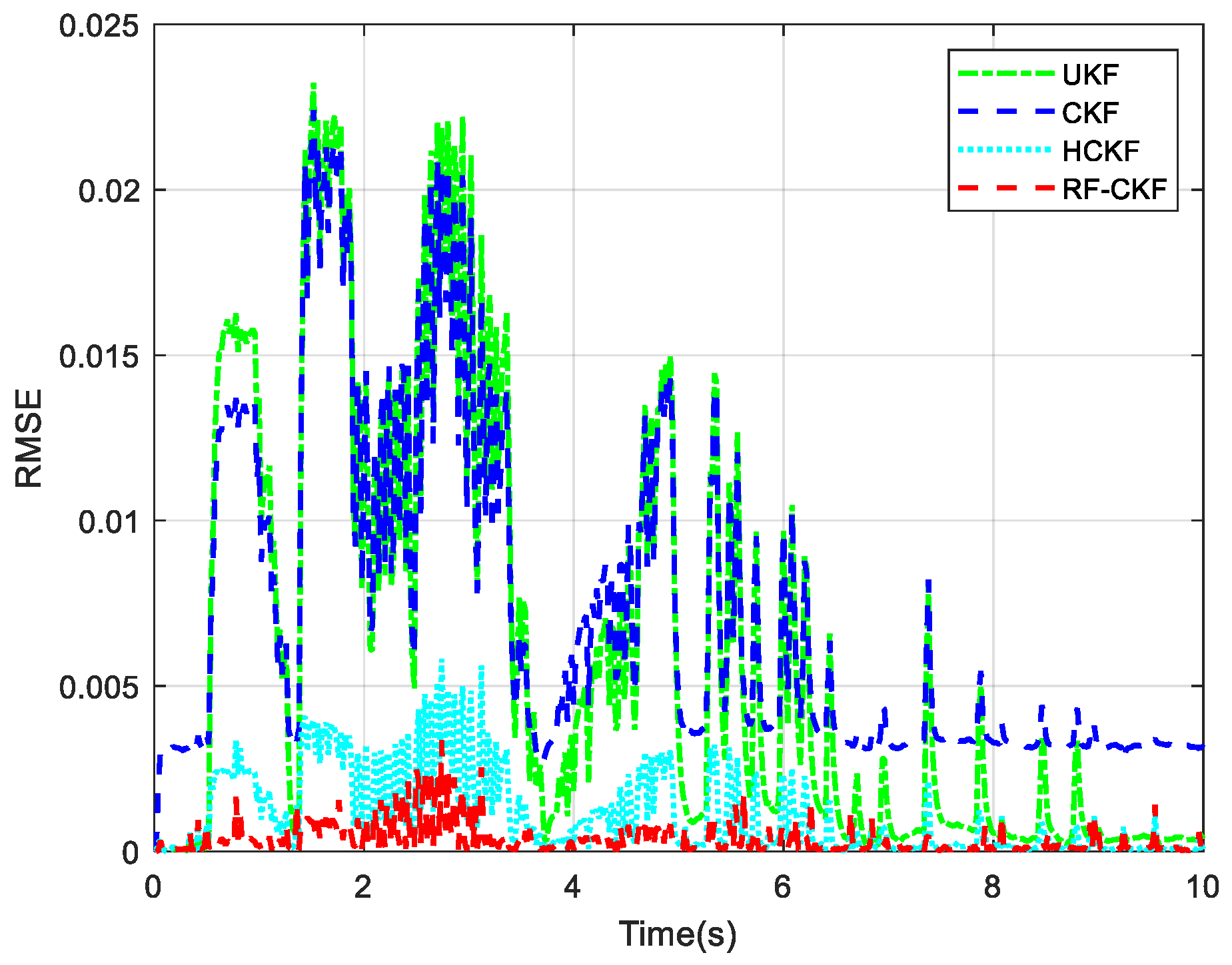
4.2. Case 2: Non-Gaussian Noise Test

In the real system, the measurement equipment will inevitably have noise and external disturbances, which leads to the measurement noise seriously deviating from the assumed Gaussian distribution. To rigorously evaluate the proposed method’s performance under these operational conditions, we model the measurement noise as a zero-mean non-Gaussian distribution characterized by a heavy-tailed bimodal Gaussian mixture, and the covariance is set to $v_1={10}^{-5}$ and $v_2={10}^{-6}$, respectively. Set the degree of the mixture to 0.1. The mathematical expression can be expressed as

$$r_k\sim (1-a)N(0,v_1^2)+aN(0,v_2^2)$$

(32)

Under this condition, the performance of the three methods in iteration is compared, as shown in Figure 7, Figure 8, Figure 9 and Figure 10, and the results of error index RMSE of each method are shown in Figure 11.

It is clear that under heavy-tail noise conditions, the UKF shows significantly poor estimation ability due to its severe parameter dependence, followed by the CKF. Both methods deviate from the true state value in their estimated results. The relatively new method HCKF utilizes the H-infinity theory and is superior to the UKF and CKF to a certain extent. However, the RF-CKF method outperforms them by better matching the trajectory of the real state and achieving minimal estimation errors. This is due to the derivation of robust functions that can effectively handle noise. It helps to reduce the estimation error and improve the accuracy of state estimation. This method can better handle the nonlinear, non-gaussian, and other complex cases of complex systems, so as to obtain more reliable state estimation results. Therefore, compared with other methods, the RF-CKF method has higher filtering accuracy and robustness.

In addition, Figure 11 and

Table 1. Performance comparison.

Metric	UKF	CKF	HCKF	RF-CKF
$\delta$	0.0116	0.0110	0.0020	0.0004
$\omega$	0.1606	0.1603	0.0246	0.0028
$e_q^{\prime }$	0.0055	0.0053	0.0017	0.0010
$e_d^{\prime }$	0.0124	0.0127	0.0021	0.0005

comprehensively represent the RMSE (root mean square error) index of various methods under non-Gaussian noise conditions. It can be seen that the UKF has numerical instability, causing its error to be the highest among the compared methods. The CKF followed suit. Combining robust control theory into the CKF significantly reduces these errors, thereby improving the estimation accuracy. Especially in the presence of system uncertainties and interferences, the HCKF shows stronger robustness and reliability. In addition, the RF-CKF is the most efficient and accurate estimation method among the methods discussed.

4.3. Case 3: Observation Outliers Conditions

Due to constraints in measurement synchronization and the intrinsic saturation characteristics of current transformers, PMU-acquired signals may exhibit temporal invariance [31].

To rigorously assess the estimation capability of the proposed methodology, we consider the PMU-acquired data is not updated during the period of 0.8 s to 1.1 s, and the four measurements do not change during this period of 0.3 s. Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 show the tracing results of different methods. Due to the influence of outliers, the state estimation performance of the UKF and CKF methods will be significantly degraded. Although the HCKF can still approximately track the generator state, the tracking speed, convergence speed, and estimation accuracy cannot meet the requirements. In contrast, the RF-CKF method maintains better estimation results in this operation scenario. This is because the RF-CKF method introduces a robust function that can maintain the outliers, thereby reducing the error.

In order to more intuitively compare the state estimation results and performance of the UKF, CKF, HCKF, and RF-CKF methods,

Table 2. Performance comparison.

Metric	UKF	CKF	HCKF	RF-CKF
$\delta$	0.0119	0.0112	0.0026	0.0016
$\omega$	0.1539	0.1537	0.1172	0.1148
$e_q^{\prime }$	0.0052	0.0051	0.0021	0.0018
$e_d^{\prime }$	0.0123	0.0126	0.0023	0.0015

further gives the error scatter plot and RMS error values of the different methods. Compared with the three other methods, the RF-CKF method error is still the smallest within 0.3 s when the observed value does not change.

It can be seen that there is a large deviation between the UKF, CKF, and HCKF methods. During the period of 0.8–1.1 s, the RF-CKF method can effectively alleviate the destructive influence of outliers in the observed data, although the measured value is not updated, indicating that the combination of robust function and the CKF can effectively improve performance.

5. Conclusions

For the safe and reliable operation of the power system, real-time and accurate state estimation is of vital importance. In response to this demand, this paper proposes a dynamic state estimation method for synchronous generators based on robust functions and the CKF, which is mainly used to solve the problem of abnormal measurement data. Through the analysis of the experimental results, the following conclusions can be drawn:

(1)

The established robust estimator, represented by the exponential absolute value function and the quadratic function, can integrate stability and sensitivity to abnormal measurements to solve the problem of poor estimation accuracy caused by abnormal measurements.

(2)

The RF-CKF method proposed in this paper can effectively handle non-Gaussian noise by using robust functions, better match the trajectories of real states, achieve the minimum estimation error, and improve the accuracy of state estimation.

(3)

After applying the research method of this study, the batch processing regression form utilizes more measurement data, which can effectively alleviate the destructive impact of outliers in the observed data, ensure its stability, and thereby reduce errors.

The simulation results show that, compared with the traditional UKF and CKF methods and the HCKF method proposed in recent years, the estimation error of the proposed method can be reduced by nearly one order of magnitude.

For future work, we put forward the following suggestions: (1) Adjust the algorithm to enhance its adaptability to various measurement data anomalies and system configurations. (2) Subsequently, the impact of parameter selection on the performance of the method can be further studied, and an adaptive parameter adjustment strategy can be developed to enhance the robustness of the method.