iTransformer-FFC: A Frequency-Aware Transformer Framework for Multi-Scale Time Series Forecasting
Abstract
1. Introduction
- Hierarchical temporal modeling: iTransformer-FFC integrates Inception-style convolution and factorized attention to jointly capture short-term and long-term temporal dependencies with reduced computational cost.
- Frequency-aware feature enhancement: The model employs Fast Fourier Convolution (FFC) to extract dominant periodic components and suppress high-frequency noise, improving robustness to non-stationarity.
- Improved long-horizon forecasting: Through multi-scale fusion and efficient attention, the model achieves superior accuracy and stability over extended prediction windows.
2. Related Work
3. Methodology
3.1. Problem Formulation
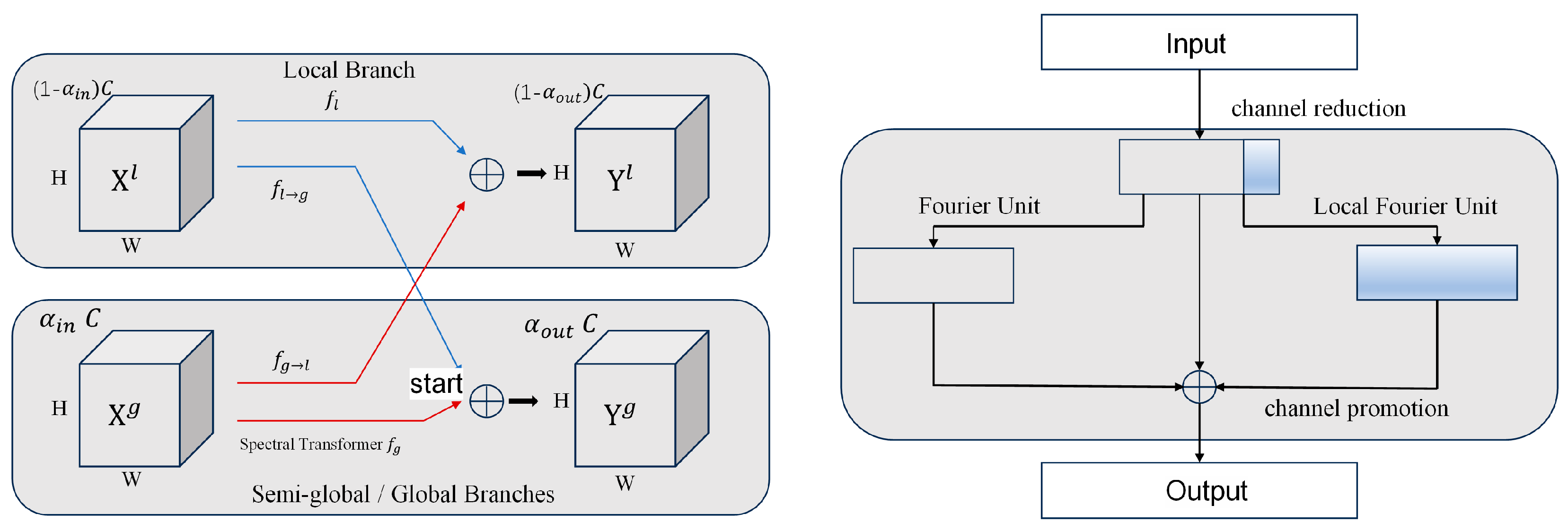
3.2. Fast Fourier Convolution (FFC)
3.2.1. FFC Architectural Design
3.2.2. Spectral Transformer
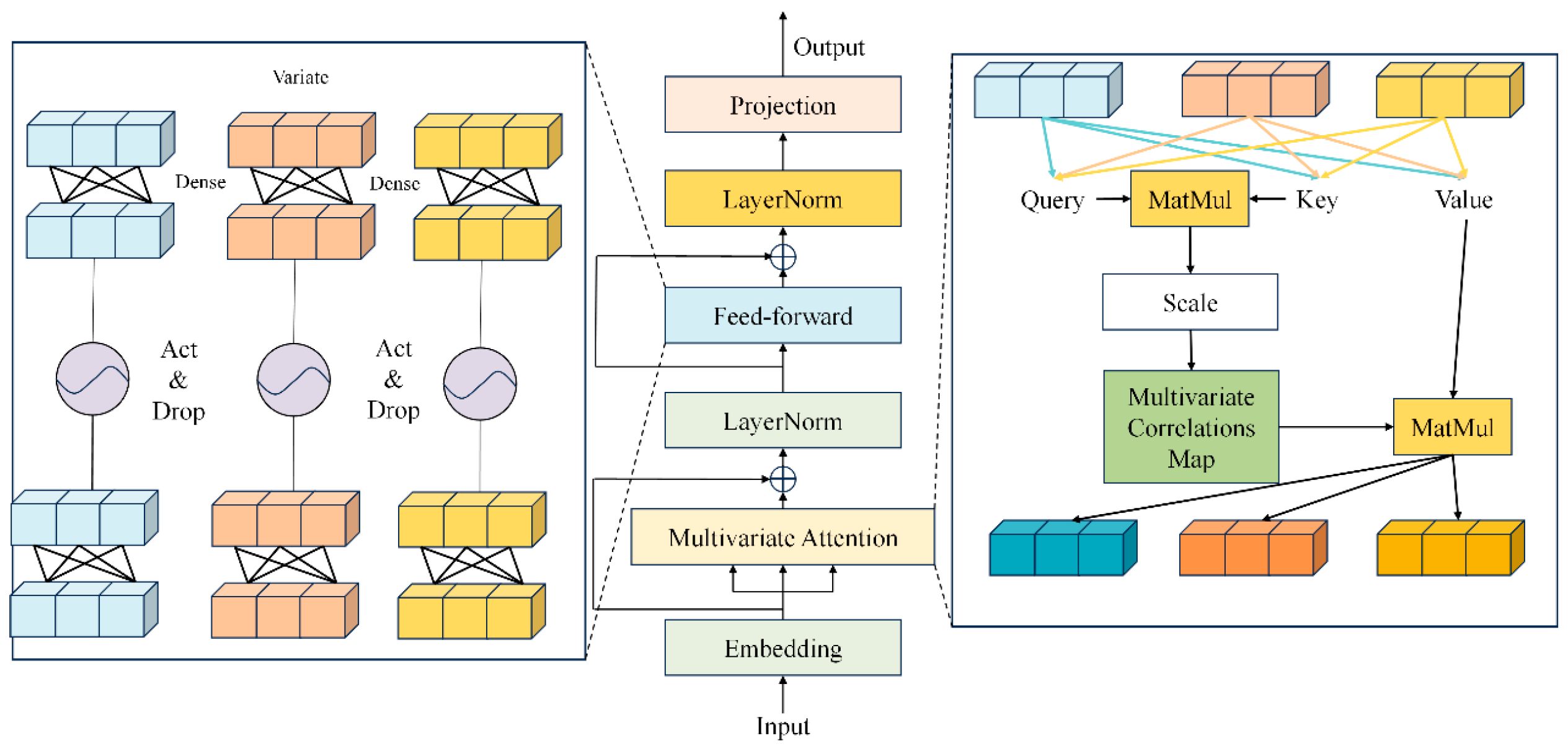
3.3. Itransformer
3.4. Model Architecture of iTransformer-FFC
4. Experiments
4.1. Data
4.2. Evaluation Criteria
4.3. Results
4.4. Experimental Analysis
4.4.1. Architectural Design
4.4.2. Robustness and Statistical Significance Analysis
4.4.3. Training and Inference Efficiency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Nelson, D.M.Q.; Pereira, A.C.M.; De Oliveira, R.A. Stock market’s price movement prediction with LSTM neural networks. In Proceedings of the2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1419–1426. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica J. Econom. Soc. 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Laptev, N.; Yosinski, J.; Li, L.E.; Smyl, S. Time-series extreme event forecasting with neural networks at Uber. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; PMLR: Sydney, Australia, 2017; pp. 1–5. [Google Scholar]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Wen, R.; Torkkola, K.; Narayanaswamy, B.; Madeka, D. A multi-horizon quantile recurrent forecaster. arXiv 2017, arXiv:1711.11053. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Tonekaboni, S.; Eytan, D.; Goldenberg, A. Unsupervised representation learning for time series with temporal neighborhood coding. arXiv 2021, arXiv:2106.00750. [Google Scholar]
- Fortuin, V.; Hüser, M.; Locatello, F.; Strathmann, H.; Rätsch, G. Som-vae: Interpretable discrete representation learning on time series. arXiv 2018, arXiv:1806.02199. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Alharthi, M.; Mahmood, A. xlstmtime: Long-term time series forecasting with xlstm. AI 2024, 5, 1482–1495. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. (NeurIPS) 2017, 30, 5998–6008. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Choromanski, K.; Likhosherstov, V.; Dohan, D.; Song, X.; Gane, A.; Sarlos, T.; Hawkins, P.; Davis, J.; Mohiuddin, A.; Kaiser, L.; et al. Rethinking attention with performers. arXiv 2020, arXiv:2009.14794. [Google Scholar]
- Yi, K.; Zhang, Q.; Cao, L.; Wang, S.; Long, G.; Hu, L.; He, H.; Niu, Z.; Fan, W.; Xiong, H. A survey on deep learning based time series analysis with frequency transformation. arXiv 2023, arXiv:2302.02173. [Google Scholar]
- Kang, B.G.; Lee, D.; Kim, H.; Chung, D.; Yoon, S. Introducing Spectral Attention for Long-Range Dependency in Time Series Forecasting. arXiv 2024, arXiv:2410.20772. [Google Scholar]
- Wu, M.; Gao, Z.; Huang, Y.; Xiao, Z.; Ng, D.W.K.; Zhang, Z. Deep learning-based rate-splitting multiple access for reconfigurable intelligent surface-aided tera-hertz massive MIMO. IEEE J. Sel. Areas Commun. 2023, 41, 1431–1451. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Lwin, T.C.; Zin, T.T.; Tin, P. Predicting Calving Time of Dairy Cows by Exponential Smoothing Models. In Proceedings of the 2020 IEEE 9th Global Conference on Consumer Electronics (GCCE), Kobe, Japan, 13–16 October 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Ajiga, D.I.; Adeleye, R.A.; Tubokirifuruar, T.S.; Bello, B.G.; Ndubuisi, N.L.; Asuzu, O.F.; Owolabi, O.R. Machine learning for stock market forecasting: A review of models and accuracy. Financ. Account. Res. J. 2024, 6, 112–124. [Google Scholar]
- Miotto, R.; Wang, F.; Wang, S.; Jiang, X.; Dudley, J.T. Deep learning for healthcare: Review, opportunities and challenges. Brief. Bioinform. 2018, 19, 1236–1246. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef]
- Choi, E.; Bahadori, M.T.; Schuetz, A.; Stewart, W.F.; Sun, J. Doctor AI: Predicting Clinical Events via Recurrent Neural Networks. In Proceedings of the Machine Learning for Healthcare Conference (MLHC), PMLR, Los Angeles, CA, USA, 19–20 August 2016; Volume 56, pp. 301–318. [Google Scholar]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. New Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef]
- Razzak, M.I.; Imran, M.; Xu, G. Big data analytics for preventive medicine. Neural Comput. Appl. 2020, 32, 4417–4451. [Google Scholar] [CrossRef]
- Darapaneni, N.; Paduri, A.R.; Sharma, H.; Manjrekar, M.; Hindlekar, N.; Bhagat, P.; Aiyer, U.; Agarwal, Y. Stock price prediction using sentiment analysis and deep learning for Indian markets. arXiv 2022, arXiv:2204.05783. [Google Scholar]
- Goh, A.T.C. Modeling soil correlations using neural networks. J. Comput. Civ. Eng. 1995, 9, 275–278. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Pmlr, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Sepp, H.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Bao, W.; Yue, J.; Rao, Y. A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PLoS ONE 2017, 12, e0180944. [Google Scholar] [CrossRef] [PubMed]
- Kai, C.; Zhou, Y.; Dai, F. An LSTM-Based Method for Stock Returns Prediction: A Case Study of the China Stock Market. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2823–2830. [Google Scholar]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient transformers: A survey. ACM Comput. Surv. 2022, 55, 1–28. [Google Scholar] [CrossRef]
- Xinhe, L.; Wang, W. Deep time series forecasting models: A comprehensive survey. Mathematics 2024, 12, 1504. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023. [Google Scholar]







| Datasets | Exchange | ETTh1 | ETTm1 | ETTh2 | ETTm2 |
|---|---|---|---|---|---|
| Variables | 8 | 7 | 7 | 7 | 7 |
| Timesteps | 5120 | 17,420 | 69,680 | 17,420 | 69,680 |
| Frequencies | Daily | 1 h | 15 min | 1 h | 15 min |
| Datasets | Mean | Median | Maximum | Minimum | MAD |
|---|---|---|---|---|---|
| Exchange | 0.65441 | 0.66918 | 0.8823 | 0.3931 | 0.0953 |
| ETTh1 | 13.3246 | 11.3959 | 47.0068 | −4.0799 | 6.7493 |
| ETTm1 | 13.3206 | 11.3959 | 46.0069 | −4.2210 | 6.7476 |
| ETTh2 | 13.3247 | 11.3960 | 46.0070 | −4.0800 | 6.7494 |
| ETTm2 | 26.6097 | 26.5769 | 58.8769 | −2.6465 | 10.010 |
| Parameters | Value |
|---|---|
| batch size | 64 |
| pred length | 1 |
| learning rate | 0.001 |
| d_model | 64 |
| Index | Models | MAE | MSE | R2 |
|---|---|---|---|---|
| Exchange | iTransformer-FFC | 0.003806 | 0.000028 | 0.994 |
| iTransformer | 0.003843 | 0.000029 | 0.994 | |
| Transformer | 0.004089 | 0.000033 | 0.993 | |
| PatchTST | 0.004806 | 0.000037 | 0.992 | |
| ETTh1 | iTransformer-FFC | 0.475 | 0.455 | 0.961 |
| iTransformer | 0.599 | 0.734 | 0.938 | |
| Transformer | 0.524 | 0.569 | 0.951 | |
| PatchTST | 0.560 | 0.633 | 0.946 | |
| ETTm1 | iTransformer-FFC | 0.228 | 0.114 | 0.990 |
| iTransformer | 0.236 | 0.122 | 0.989 | |
| Transformer | 0.238 | 0.124 | 0.989 | |
| PatchTST | 0.228 | 0.114 | 0.990 | |
| ETTh2 | iTransformer-FFC | 0.884 | 0.782 | 0.993 |
| iTransformer | 0.891 | 0.816 | 0.992 | |
| Transformer | 1.035 | 2.28 | 0.980 | |
| PatchTST | 0.987 | 2.31 | 0.984 | |
| ETTm2 | iTransformer-FFC | 0.196 | 0.078 | 0.999 |
| iTransformer | 0.217 | 0.096 | 0.997 | |
| Transformer | 0.237 | 0.104 | 0.994 | |
| PatchTST | 0.279 | 0.157 | 0.995 |
| Index | Models | MAE | MSE | R2 |
|---|---|---|---|---|
| ETTh1 | iTransformer-FFC | 0.675 | 0.455 | 0.961 |
| No-FFC | 0.604 | 0.798 | 0.931 | |
| No-FSA | 0.512 | 0.590 | 0.948 | |
| No-MSF | 0.541 | 0.625 | 0.940 | |
| ETTh2 | iTransformer-FFC | 0.884 | 0.782 | 0.993 |
| No-FFC | 0.840 | 0.969 | 0.982 | |
| No-FSA | 1.010 | 2.112 | 0.973 | |
| No-MSF | 0.963 | 1.908 | 0.976 |
| Comparison | Metric | Mean Difference | t-Value | p-Value | Significance |
|---|---|---|---|---|---|
| iTransformer-FFC vs. iTransformer | MAE | −0.024 | 4.51 | 0.0012 | Yes (p < 0.01) |
| iTransformer-FFC vs. PatchTST | MAE | −0.019 | 3.12 | 0.0068 | Yes (p < 0.01) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Cai, Z. iTransformer-FFC: A Frequency-Aware Transformer Framework for Multi-Scale Time Series Forecasting. Electronics 2025, 14, 2378. https://doi.org/10.3390/electronics14122378
Tang Y, Cai Z. iTransformer-FFC: A Frequency-Aware Transformer Framework for Multi-Scale Time Series Forecasting. Electronics. 2025; 14(12):2378. https://doi.org/10.3390/electronics14122378
Chicago/Turabian StyleTang, Yongli, and Zhongqi Cai. 2025. "iTransformer-FFC: A Frequency-Aware Transformer Framework for Multi-Scale Time Series Forecasting" Electronics 14, no. 12: 2378. https://doi.org/10.3390/electronics14122378
APA StyleTang, Y., & Cai, Z. (2025). iTransformer-FFC: A Frequency-Aware Transformer Framework for Multi-Scale Time Series Forecasting. Electronics, 14(12), 2378. https://doi.org/10.3390/electronics14122378






