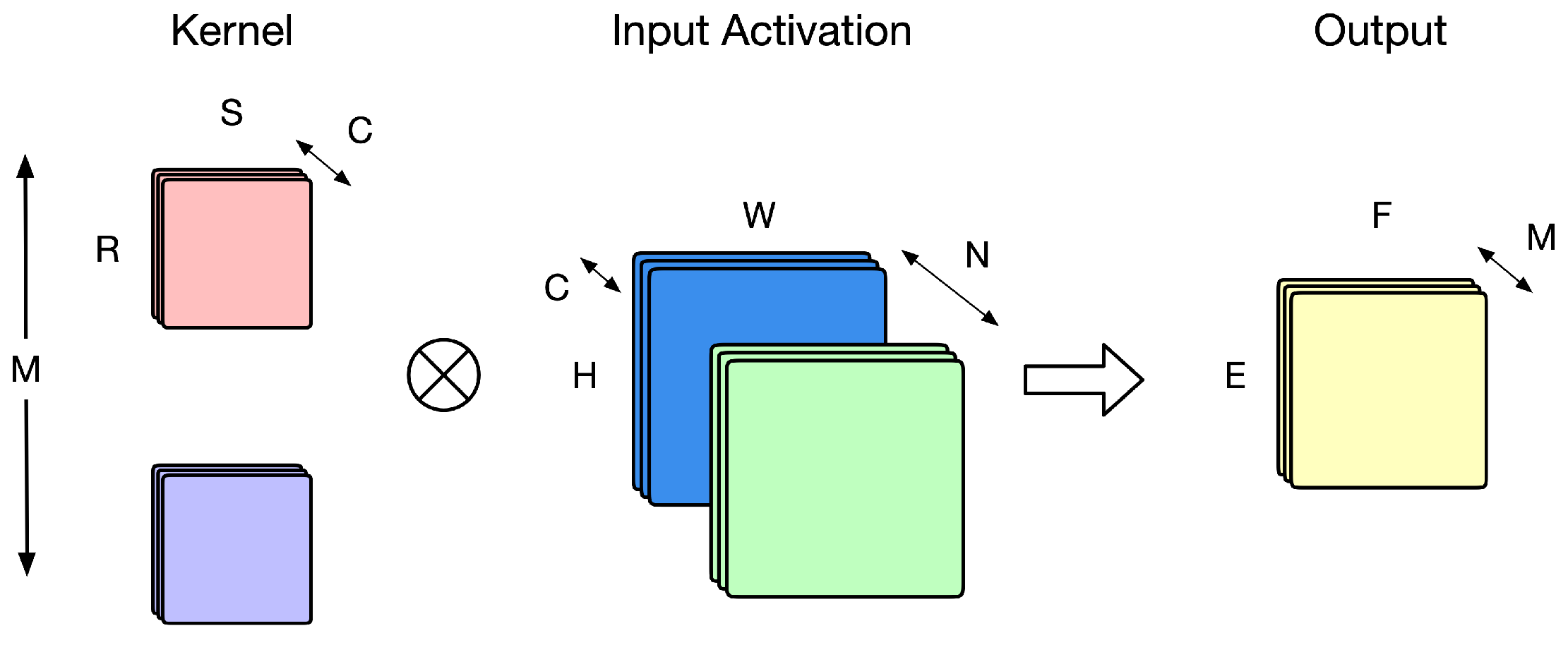
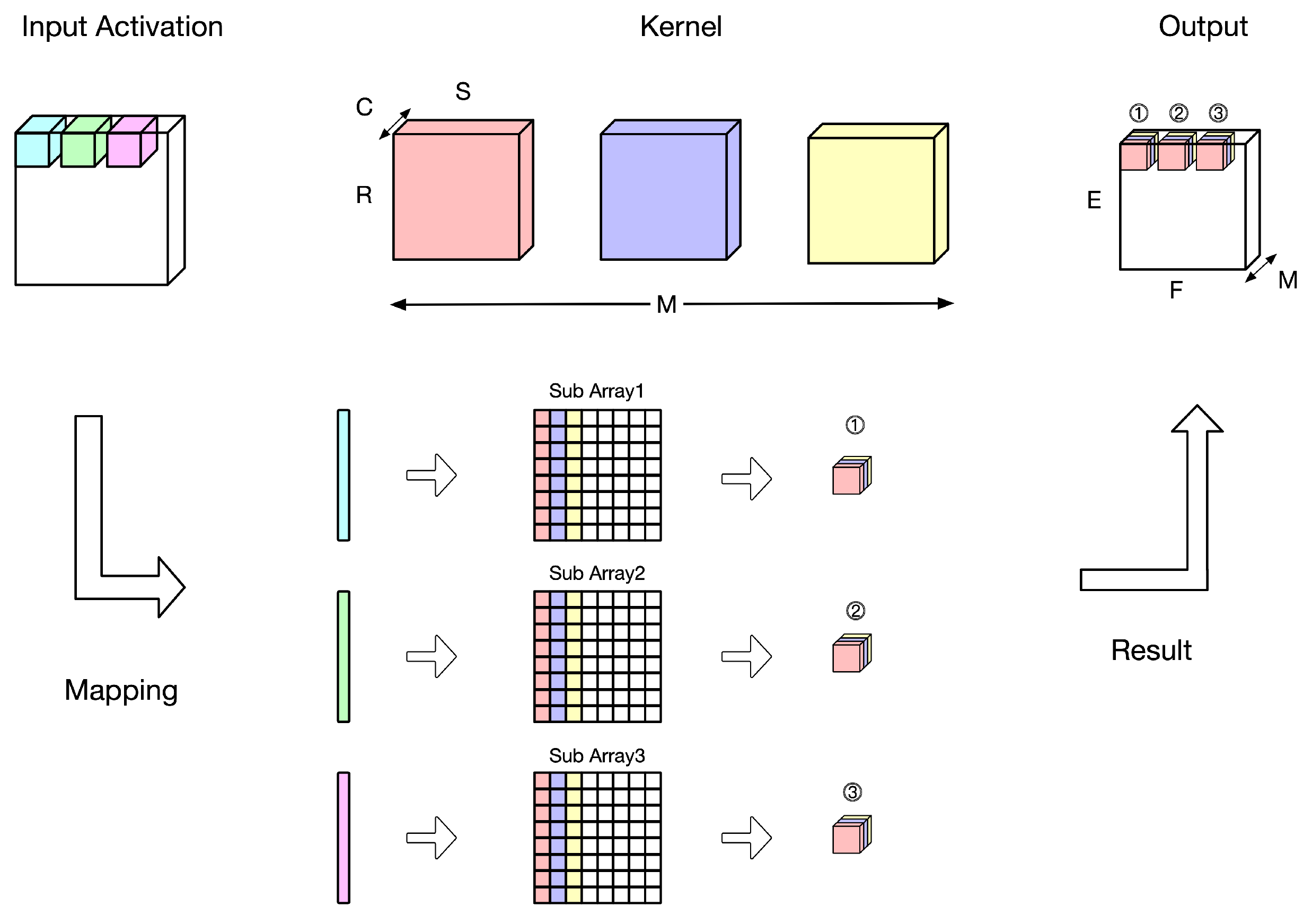
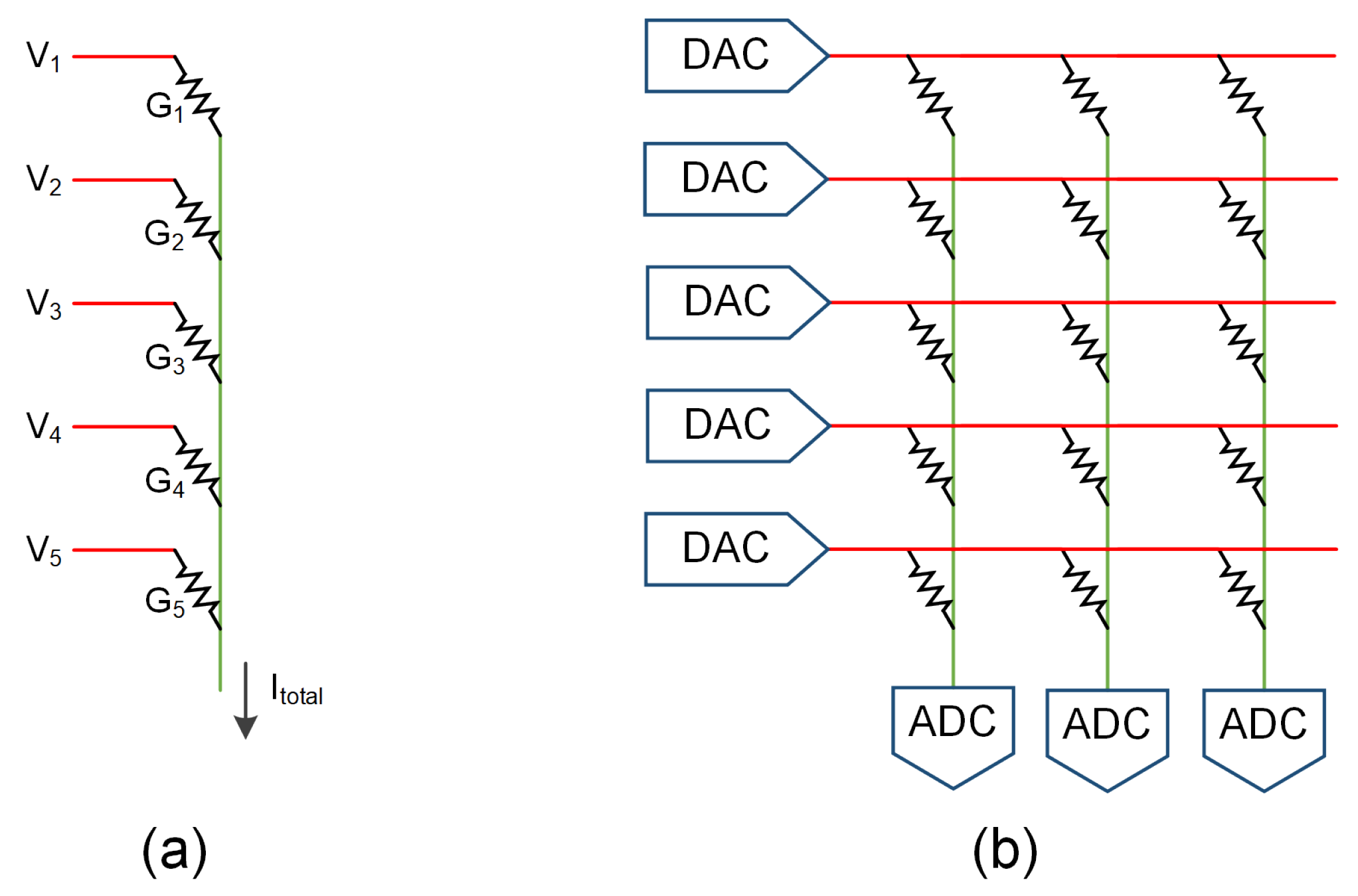
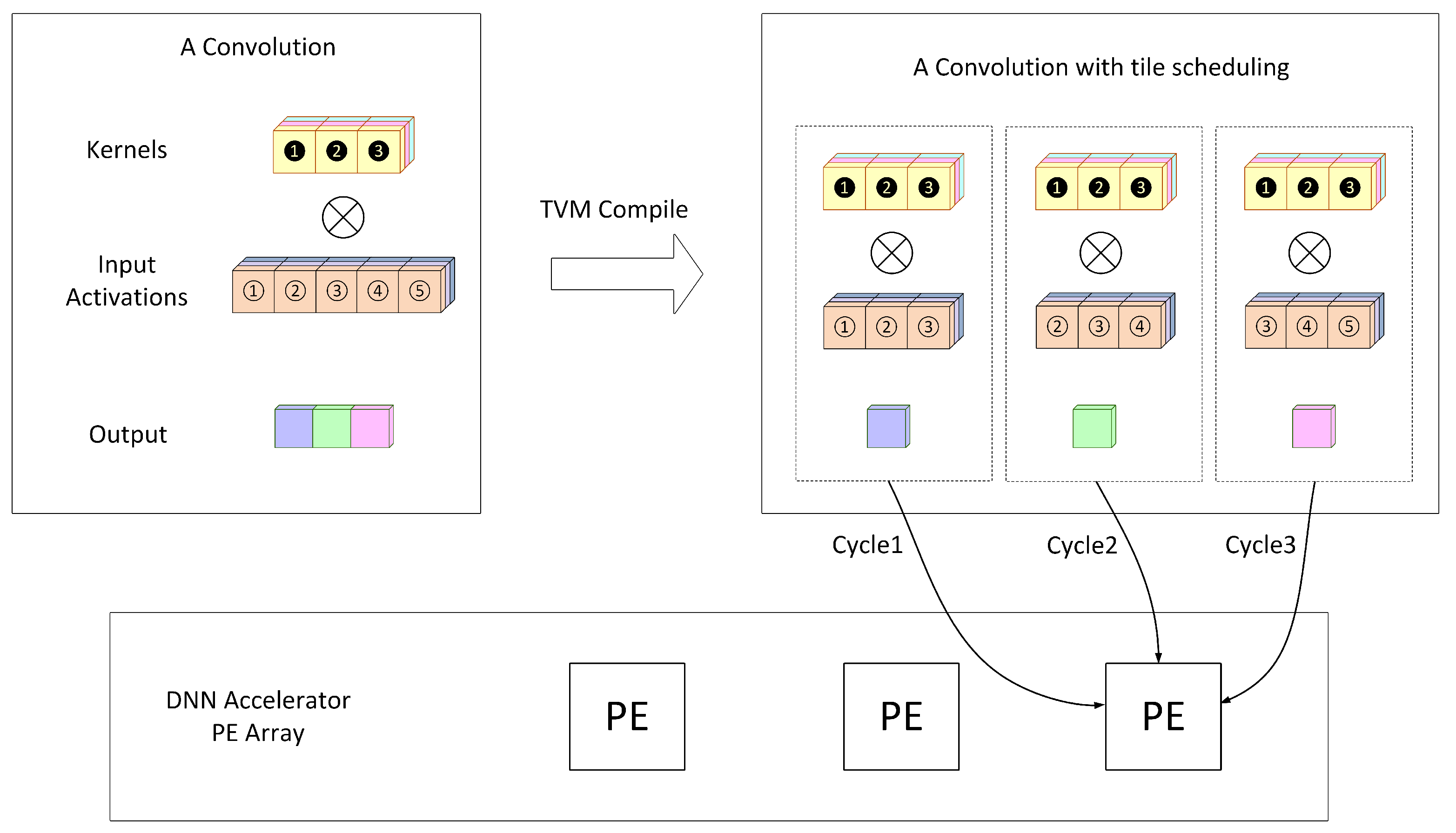
1. Introduction
In recent years, artificial intelligence (AI) has been widely applied in fields such as healthcare, computer vision, and natural language processing. To address various data characteristics, numerous deep neural network (DNN) models have been developed to process and analyze large volumes of data, for instance, convolutional neural networks (CNNs), which are primarily employed in image processing and computer vision. To improve performance, many CNN architectures have been proposed [
1,
2,
3,
4,
5,
6,
7]. As CNN scales up rapidly, their architectures have become increasingly complex. Since CNN comprises multiple convolutional layers, each requiring extensive computations, enhancing computational efficiency has become paramount.
To enable developers to efficiently construct, train, and deploy DNN models while optimizing computational performance and resource utilization, several widely adopted deep learning frameworks have been introduced, including PyTorch [
8], TensorFlow [
9], MXNet [
10], and Caffe [
11]. However, deploying models created with different frameworks onto target hardware platforms still requires substantial effort. In particular, to satisfy real-time constraints such as low latency and high throughput, a range of DNN accelerators, including GPUs, Google’s TPU [
12], Nvidia Jetson, FPGAs, and various ASICs, are commonly employed. Although these DNN accelerators can greatly enhance the performance of neural network computations, effectively mapping models onto diverse hardware platforms also necessitates the use of efficient and adaptable compilers.
Foundational studies and overviews of classical optimization methods can be found in [
13,
14]. Deep learning frameworks typically incorporate a variety of general-purpose libraries that assist developers in building and optimizing DNN models. For example, convolution operations can be reformulated as matrix vector multiplications (MVMs) using basic linear algebra subprograms (BLAS), enabling efficient execution through the general matrix multiplication (GEMM) functions provided by these libraries. In addition to general-purpose solutions, many neural network accelerator vendors offer specialized libraries tailored for DNN workloads: TensorRT, for example, supports graph-level optimizations and low-precision quantization, while other libraries [
15,
16] target specific accelerator architectures. However, the rapid pace of innovation in deep learning has made it challenging for library development to keep up with the evolving demands of DNN accelerator users.
To alleviate the burden of manually optimizing neural network models for each DNN accelerator, several deep learning compilers, such as Glow [
17], nGraph [
18], and TVM [
19], have been introduced. These compilers accept models defined in deep learning frameworks and apply optimizations tailored to both the model characteristics and the target hardware architecture, ultimately generating code that executes efficiently on a variety of DNN accelerators. Moreover, many of these compilers are built on top of well-established tool chains from general-purpose compilers, such as LLVM [
20], which further enhances their portability across different accelerator platforms.
While deep learning compilers streamline the deployment of DNN models onto hardware accelerators, their optimizations are largely software-centric, leaving significant opportunities to enhance hardware utilization. Given that storage space in each processing element (PE) is a critical hardware constraint, this paper focuses on optimizing on-chip data storage usage and addresses two key issues:
Layer Fusion: If a PE has sufficient storage space to hold the data required for two or more layers, we use layer fusion to make full use of its storage capacity.
Model Partitioning: If a PE’s storage space is insufficient to accommodate the data required by a single layer, we partition the computations of that layer and distribute them across multiple PEs for concurrent execution.
On the other hand, there have also been several advances in DNN accelerator design in recent years. In general, most DNN accelerators have focused on architectural improvements in three main directions: systolic arrays [
21,
22,
23], network-on-chip (NoC) designs [
24,
25,
26], and reduced tree structures [
27]. Furthermore, some research has explored specialized architectural designs; for example, Ref. [
28] proposes methods that simplify computation and reduce latency, while [
29,
30] utilize compression techniques to save memory. Other studies have introduced techniques such as optimizing activation functions [
31] to reduce processing latency in DNN accelerators. However, these hardware designs still follow the von Neumann architecture, which suffers from performance bottlenecks as a result of heavy data transfer. Although various approaches have been proposed to mitigate these bottlenecks, such as analyzing dataflows to minimize data transfers [
32,
33,
34] or employing approximate computing to reduce power consumption and data traffic [
35,
36,
37,
38], they remain constrained by the fundamental limitations of the von Neumann architecture and do not fully resolve the issue of data transfer.
In-memory computing has gained wide recognition as a promising strategy for addressing the von Neumann bottleneck. In particular, previous work [
39,
40] introduced pioneering memristor-based DNN accelerators that significantly reduce both data movement and power consumption during neural network computations. Unlike conventional von Neumann architectures that separate computation and data storage, these accelerators execute MVMs directly in memory, thereby enhancing energy efficiency. In this architecture, input activations are first converted into analog signals, while weights are stored within memory cells; the dot product is performed in situ, substantially minimizing data transfer. As shown in [
41], metal–oxide resistive RAM (ReRAM) can be assembled into crossbar arrays to efficiently handle MVM operations in both convolutional and fully connected layers. Furthermore, due to their multilevel storage capabilities, compact area footprint, and low read/write latencies, ReRAM-based memory arrays have emerged as one of the most effective hardware solutions for DNN acceleration [
42,
43,
44,
45,
46]. Several tools have been introduced to facilitate high-level design for ReRAM-based DNN accelerators. For example, Ref. [
47] examines the weight mapping and data flow within these accelerators, while [
48] simulates the hardware behavior of the nonlinear characteristics of ReRAM in the high-level design stage. However, the development of deep learning compilers specifically tailored for ReRAM-based DNN accelerators remains largely unexplored.
In this paper, we present a deep learning compiler specifically tailored for ReRAM-based DNN accelerators, based on the open-source TVM framework [
19]. Our primary objective is to optimize the usage of data storage. To achieve this, our core contribution is an approach that determines the optimal mapping strategy by jointly applying layer fusion and model partitioning, while accounting for the storage constraints of each PE. By integrating these two techniques, we reduce the data transfer overhead between off-chip and on-chip memory, thereby enhancing the execution efficiency of neural network models on ReRAM-based DNN accelerators. The experimental results show that our compiler effectively optimizes data storage under a variety of hardware configurations, allowing designers to accurately evaluate DNN models at an early stage in the design process.
The contributions of this paper are elaborated as follows:
We present the first approach to integrate layer fusion and model partitioning into TVM’s graph-level compilation stage.
Building on this integration, we propose an algorithm that tailors data storage optimization to multiple objectives.
The remainder of this paper is organized as follows.
Section 2 introduces the background materials, and
Section 3 discusses our motivation.
Section 4 presents the proposed algorithm, which combines layer fusion and model partitioning.
Section 5 provides the experimental results. Finally,
Section 6 offers concluding remarks.
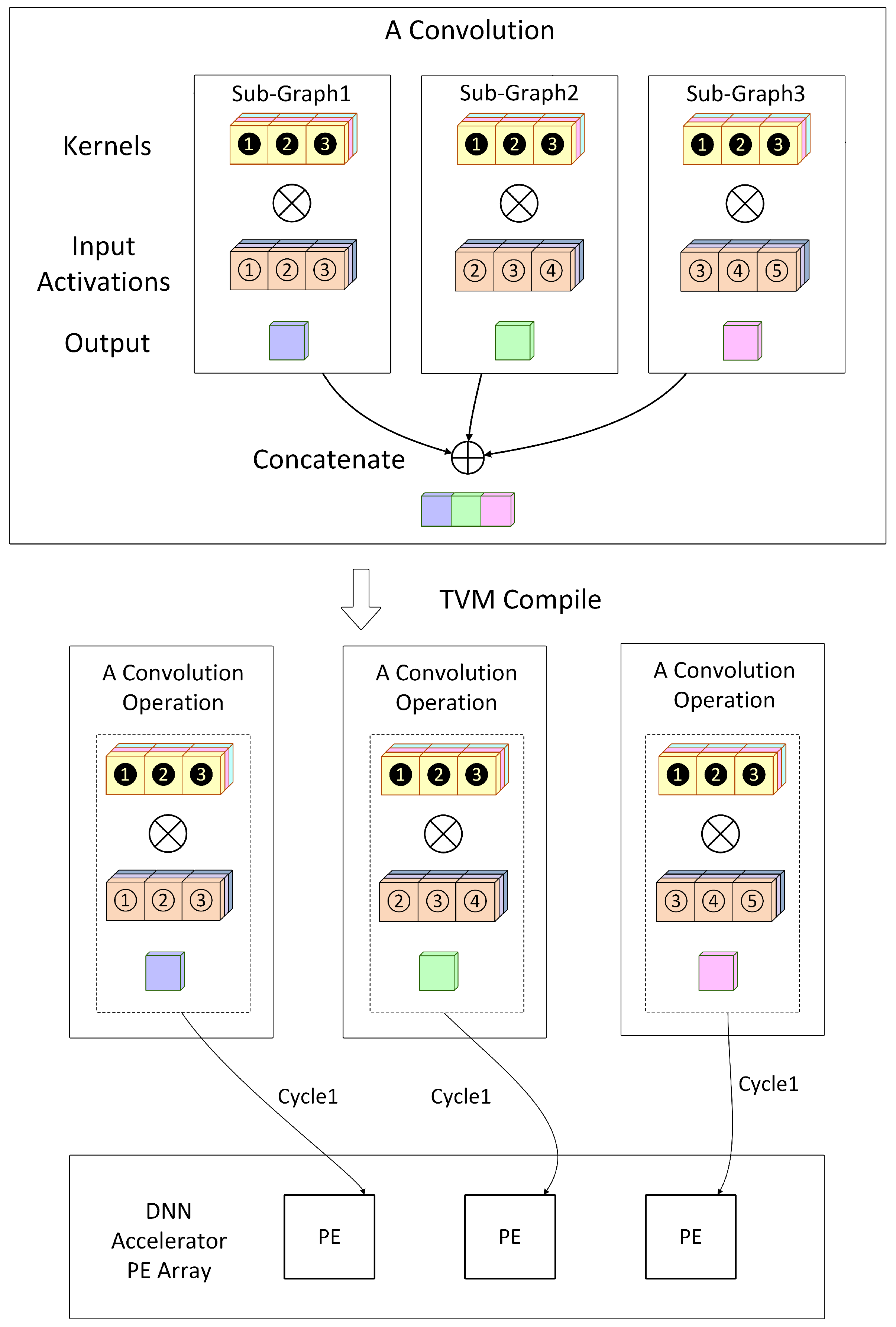
4. The Proposed Approach
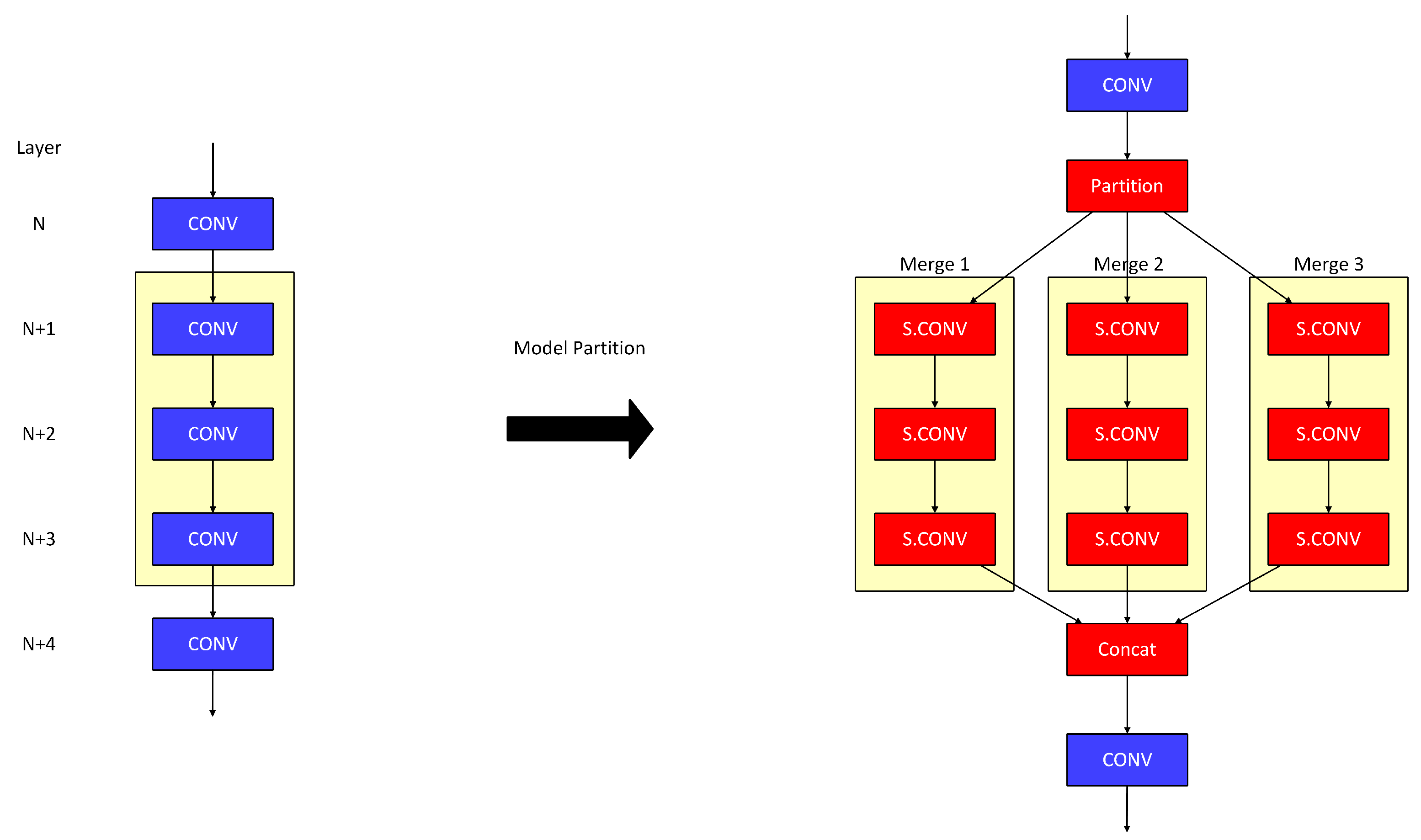
In our approach, we combine the advantages of layer fusion and model partitioning. When on-chip storage exceeds the requirements for a single stage, layer fusion merges multiple layers to reduce data transfers. In contrast, when on-chip storage is insufficient for a fused stage, the layers are partitioned into subgroups to lessen the storage demand. As illustrated in
Figure 9, the left side shows the original model with five convolutional layers, while the right side demonstrates the model after the combined application of layer fusion and model partitioning.
In
Figure 9, we fuse three layers of the model to reduce communication costs between off-chip memory and on-chip storage. However, this fused model requires a larger on-chip storage capacity. To address this issue, we partition the fused layers into three subgroups, as shown on the right side of
Figure 9 (highlighted by yellow boxes). Converting the fused layers into smaller subgroups significantly reduces the total storage required per PE. In this figure, each subgroup (i.e., partitioned fused layers) is labeled for clearer distinction, using the names Merge1, Merge2, and Merge3.
The proposed approach is based on TVM. From
Figure 5, we see that when a model is input into TVM, the parser transforms it into relay IR modules. Each module comprises a series of operations supported by TVM, with every operation represented using an abstract syntax tree (AST) structure. TVM then applies a series of optimization passes over the entire tree to enhance performance. In our proposed approach, we concentrate on the stage from the frontend to the relay IR modules, with a focus on the graph level. Using the AST structure and the optimization passes in TVM, we implement a combination of model partitioning and layer fusion to achieve efficient model transformation and optimization.
Given a sub-model executed on a PE, it is essential to calculate the storage space required by that PE. Notably, due to layer fusion, a sub-model may consist of a single layer or a set of fused layers. Additionally, with model partitioning considered, a sub-model may represent a partitioned single layer or a partitioned set of fused layers. Algorithm 1 computes the storage space needed to execute a sub-model on a PE. The input is a sub-model, and the output is the storage space required by a PE to execute the sub-model.
In the first line of Algorithm 1, we define a
BackTrace function. This function uses the input dimension of the current layer, together with the stride, kernel size, and padding of the preceding layer, to compute the input dimension that the preceding layer must have to produce the output required by the current layer. The notations
,
,
denote the stride, kernel size, and padding of layer
i. The formula used by this function to calculate the input dimension of the preceding layer can be derived from the equations given in the literature [
51].
We use the LeNet model as an example to illustrate the concept of function
BackTrace in Algorithm 1. The LeNet model consists of five layers in total, with a batch size of 1. The input size of the fifth layer is (16, 5, 5), which implies that the output size of the fourth layer is also (16, 5, 5). In the fourth layer, both the stride and kernel size are (2, 2), and the padding is set to 0. Given this information, the function
BackTrace can be used to compute that the height and width of the input activation to the fourth layer are both
.
| Algorithm 1: Calculate The Required Storage Space of a Sub-Model |
![Electronics 14 02352 i001]() |
In Algorithm 1, we use the function Calculate_Storage to compute the required storage space. The variable ActivationStorage represents the storage size required for input activations. The variable WeightStorage represents the storage size required for the weights. The variable TotalStorage represents the total storage size, which includes both input activations and weights. The notation represents the number of channels in the layer i.
For a given sub-model, starting from the output feature map of its last layer, denoted as , we apply the function BackTrace to traverse the network layer by layer and calculate the storage needed for the input activations of each layer. Note that because the output of the preceding layer serves as the input to the current layer, they are able to share the same memory space. Since memory space can be shared across different layers during execution, we only need to allocate the maximum storage space required among these layers.
Finally, we compute the storage space required for the weight parameters. Unlike input activations, weights cannot be shared between layers; therefore, the weight parameters of all layers must be stored in memory. In Algorithm 1, we calculate the total weight storage by summing the storage requirements of each layer’s weight parameters. Note that denotes the number of kernels.
In Algorithm 2, given a DNN, our objective is to compute the minimum storage space required for every possible sub-model within the DNN. We consider two scenarios separately: one where only layer fusion is applied and another where both layer fusion and model partitioning are used.
Only Layer Fusion: If a DNN has
n layers, there are
potential points at which layer fusion can be applied. The total number of candidate solutions is given by the following equation:
A layer, or a fused layer, is referred to as a sub-model. Each candidate solution is composed of sub-models. Procedure identifies the storage required for each possible sub-model. The notation represents a sub-model formed by applying layer fusion from layer i to layer j. We use the procedure from Algorithm 1 to compute the minimum storage space required for each sub-model . The notation denotes the storage space available to each PE. The notation denotes the required storage size. If the minimum storage space required by a sub-model exceeds the storage capacity provided by a PE, we consider the storage requirement of that sub-model to be infinite (i.e., the sub-model is not selected for use).
Layer Fusion and Model Partitioning: Considering model partitioning, we use the notation to denote the maximum number of allowable partitions for sub-model , a parameter that can be specified by the user. Under this constraint, the procedure evaluates the storage requirements for all feasible combinations of layer fusion and model partitioning strategies. Within this procedure, we use the notation to represent a partition of sub-model when it is divided into k partitions.
If a DNN has n layers, then in the case of layer fusion only, each candidate solution contains at most n sub-models. Suppose that the maximum number of allowable partitions for each sub-model is t, where t is a constant. Therefore, when model partitioning is applied, a candidate solution originally derived from layer fusion may lead to O() candidate solutions. Since layer fusion alone can generate candidate solutions, combining layer fusion and model partitioning results in O() candidate solutions. Because t is a constant, the total number of candidate solutions in the combined approach can be expressed as O(). Note that the run time of the proposed approach scales proportionally with the number of candidate solutions.
Dividing a sub-model into multiple sub-models allows those partitions to run concurrently. However, the DNN accelerator must have a sufficient number of PEs to support simultaneous execution. Therefore, for each sub-model, the maximum allowable number of partitions can be set equal to the number of PEs in the accelerator.
| Algorithm 2: Compute The Minimum Storage Space Required for Possible Sub-Models |
![Electronics 14 02352 i002]() |
Algorithm 2 computes the minimum storage space required for all possible sub-models, where each partition resulting from model partitioning is also considered a sub-model. The computed results are stored in a database called , enabling efficient retrieval of the required storage space for any sub-model via the query .
Algorithm 1 mainly calculates the storage space required for a sub-model. If we want to calculate the data transfer required for a sub-model instead, this algorithm needs to be slightly modified. To compute the data transfer for a sub-model, for input activations, we only need to consider the input activations required by the first layer, i.e., . The input activations for the subsequent layers do not require data transfer (because they are shared internally within the PE memory). Algorithm 3 is the algorithm used to calculate the data transfer required for a sub-model. In Algorithm 3, the variable TotalTransfer represents the total amount of data transfer, including both input activations and weights.
Similarly, we compute the data transfer required for all possible sub-models, treating each partition generated through model partitioning as an individual sub-model. The computed results are stored in a database, called
Data_Transfer, enabling efficient retrieval of the required data transfer for any given sub-model SM via the query
Data_Transfer(SM). Algorithm 4, which is a slight modification of Algorithm 2, describes the method for computing the data transfer required for all possible sub-models.
| Algorithm 3: Calculate The Required Total Data Transfer of a Sub-Model |
![Electronics 14 02352 i003]() |
| Algorithm 4: Compute The Data Transfer Required for Possible Sub-Models |
![Electronics 14 02352 i004]() |
Algorithm 5 aims to determine the optimal solution for the simultaneous application of layer fusion and model partitioning to a given DNN. To support different design objectives, we provide two distinct procedures: one that minimizes the storage space required for executing the DNN (that is, procedure
) and another that minimizes the amount of data transfer during execution (that is, procedure
). For a given DNN, all candidate solutions arising from the joint application of layer fusion and model partitioning can be exhaustively enumerated. The two procedures in Algorithm 5 carry out an exhaustive search over the design space to identify the optimal solution based on their respective optimization objectives. The notation
denotes the maximum memory storage required among all sub-models in the candidate solution
. The notation
denotes the total amount of data transferred among all sub-models in the candidate solution
. The notation
refers to the optimal solution.
| Algorithm 5: Determine the Optimal Solution for the Execution of a DNN |
![Electronics 14 02352 i005]() |
The procedure is formulated to identify the minimum storage solution. For each candidate solution, this procedure first derives all associated sub-models and then determines the storage space required for each. The storage requirement of a candidate solution is defined as the maximum storage demand among its sub-models. The candidate exhibiting the lowest storage requirement is selected as the optimal solution.
The procedure is designed to identify the solution that minimizes data transfer. For each candidate solution, this procedure first derives all associated sub-models and then calculates the data transfer required for each. The total data transfer of a candidate solution is defined as the sum of the data transfer requirements across all its sub-models. The candidate solution with the lowest total data transfer is selected as the optimal solution.
Note that in Algorithm 5, we utilize the database , constructed by Algorithm 2, and the database , constructed by Algorithm 4. For any sub-model , the query returns its corresponding storage space requirement. Using this database, users can invoke the procedure to obtain the minimum storage solution. Similarly, for any sub-model , the query returns its corresponding data transfer requirement. Using this database, users can invoke the procedure to identify the minimum data transfer solution.