Adaptation of Fuzzy Systems Based on Ordered Fuzzy Numbers: A Review of Applications and Development Prospects
Abstract
1. Introduction
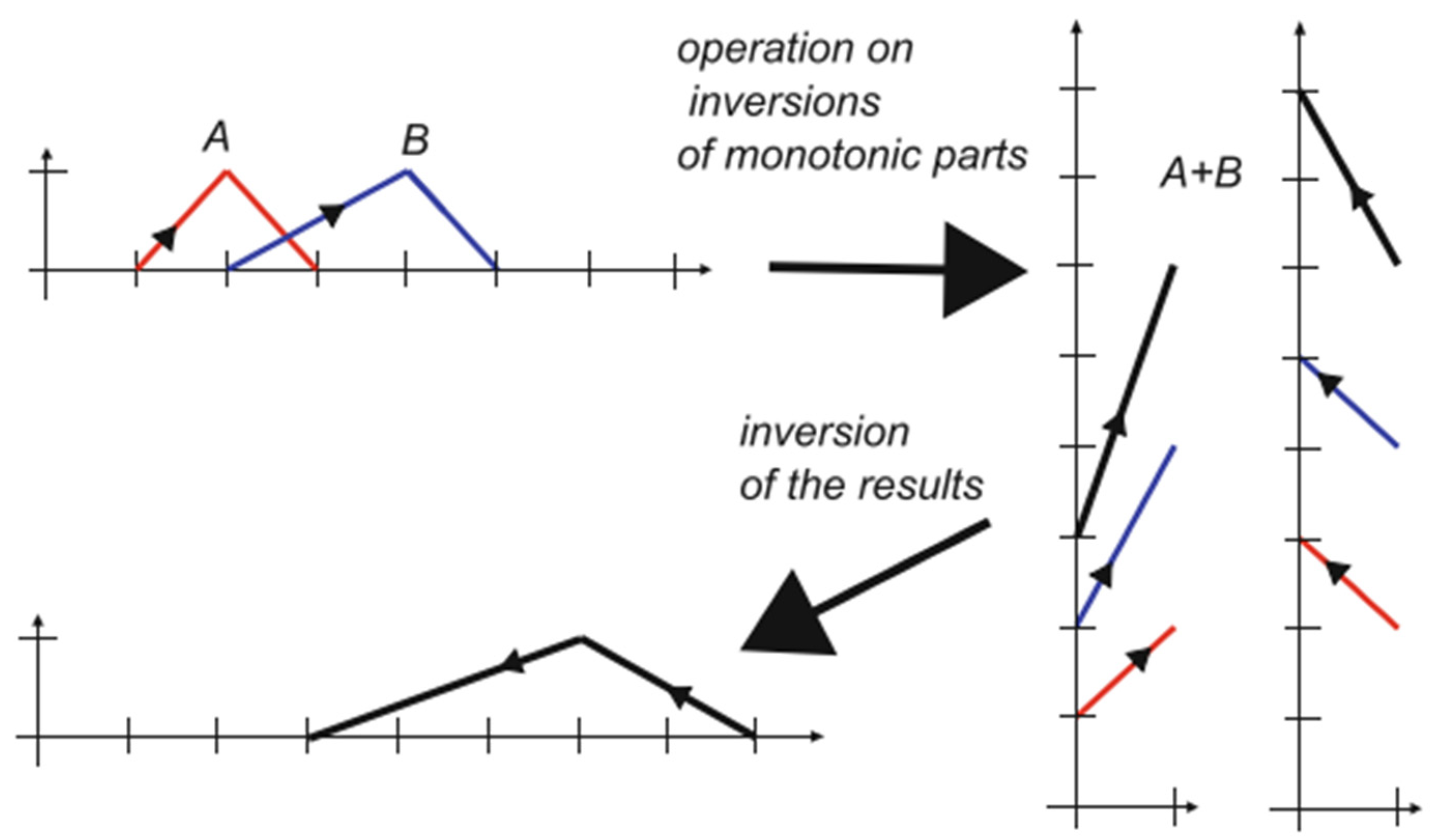
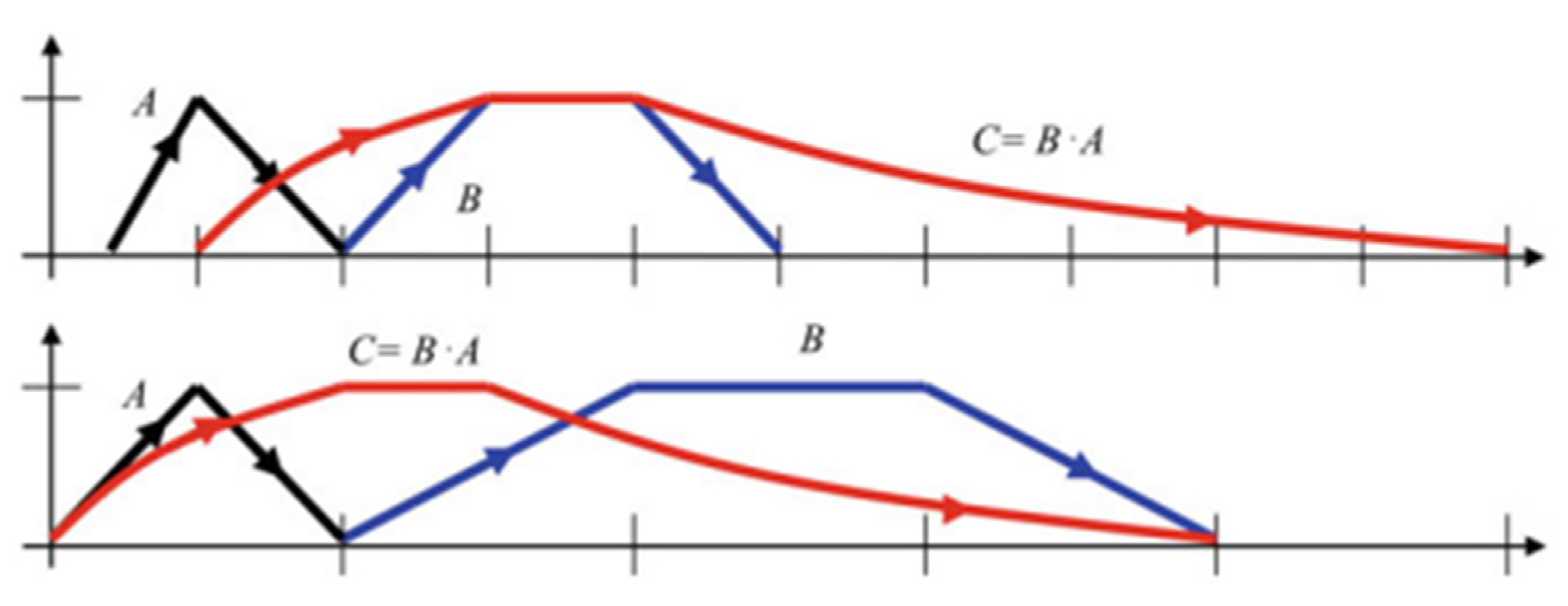
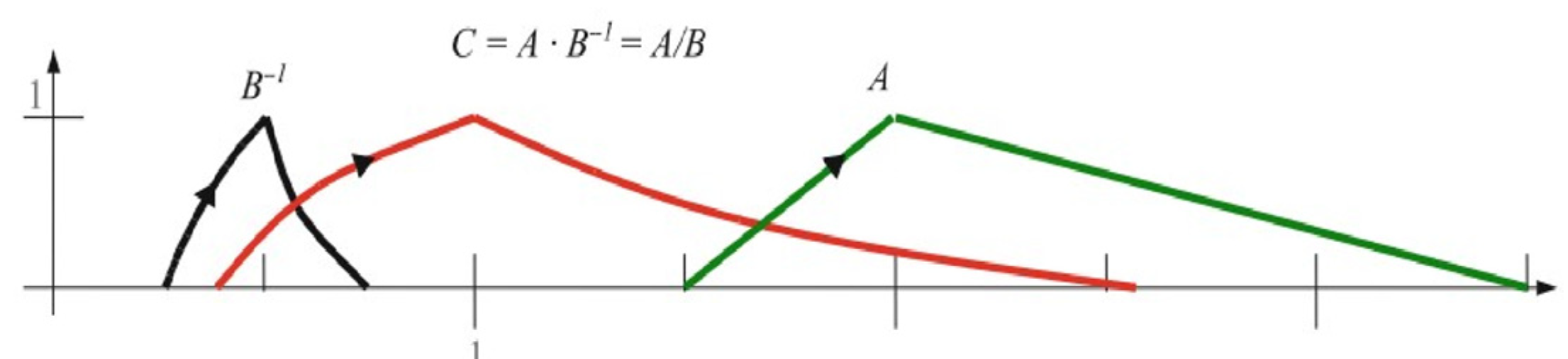
2. Ordered Fuzzy Numbers
2.1. Definition of OFNs and Arithmetic Properties
- f (increasing part) represents the up-part of the fuzzy number;
- (a)
- shows an Ordered Fuzzy Number, where the functions f and g represent, respectively, the upper (UP) and lower (DOWN) parts of the fuzzy number. The axes denote the variables x and y, and the lines represent the ranges of these functions.
- (b)
- represents fuzzy numbers in the classical sense, where the functions f−1 and g−1 invert the original relationships. An additional interval (marked with a horizontal line) illustrates the difference between the ordered representation and the classical approach.
- (c)
- Simplistically denotes the order of the inverse functions with bold arrows, emphasizing that we are dealing with an ordered pair of functions.
2.2. The Role of OFNs
2.3. Challanges
2.4. Development Prospects
2.4.1. Theoretical Developments
2.4.2. Practical Implementations
2.5. Adaptation Methods
2.5.1. Genetic Algorithms
2.5.2. Evolutionary Programming
2.5.3. Learning Algorithms
- (a)
- y—predicted value (dependent variable);
- x—independent variable (feature);
- β0, β1—parameters of the linear regression model;
- —random error component;
- E(y)—expected value of y, this is most commonly interpreted as the predicted probability of an event occurring y = 1;
- x′β—represents the scalar product of the transpose vector x and the parameter vector β;
- xT—transposed feature vector.
- (b)
- β—weight (parameter) vector;
- —slack variable (SVM);
- C—regularization parameter (SVM);
- N—number of samples;
- yi—class label for sample ii;
- pi—proportion of class i in a node (Decision Trees);
- c—number of classes;
- J—objective function (K-Means);
- rnk—assignment of point n o cluster k;
- xn—data point;
- —centroid of cluster k;
- K—number of clusters.
- (c)
- Advanced algorithm—The last group includes algorithms based on neural networks, which are more complex and used in dynamic environments or when processing large data sets. An example of such an algorithm is the neural network, whose core formula is a = f(Wp + b), where:
- neuron activation;
- f—activation function;
- Wp—weight of the connection in a neural network;
- bias;
2.5.4. Reinforcement Learning
- (a)
- The environment—This is the task or simulation with which the algorithm (also called the agent or player) interacts. The goal of RL is to maximize the reward provided by the environment, i.e., to train the agent to achieve the maximum outcome in the environment, e.g., winning the most games or achieving the highest reward.
- (b)
- Agent—This is the element that interacts with the environment. The goal of the agent is to maximize the reward, i.e., to learn the most beneficial interaction with the environment. The agent’s behavior is determined by a so-called policy or function that is designed to return an appropriate action. Most commonly, a neural network is used as a policy.
- (c)
- Buffer—This is a data store that holds information collected by the agent during learning, which is then used to train the agent.
- v*(s) is the maximum expected value that can be obtained starting from state s and making optimal decisions;
- s—is the current state;
- a—the action taken in state s;
- A(s))—the set of all possible actions in state s;
- s′—the next state after performing the action a (next state);
- r—the reward received after moving to state s′ (reward);
- —probability that after performing action a in state s in order to move to state s′ and receive reward r (transition probability);
- —discount factor, a number between 0 and 1, which determines how much future rewards count (discount factor) [83].
- Q (s, a)—Q-value for state s and action a;
- α—learning rate;
- R—reward;
- —discount factor;
- s, s′—current and next state;
- a, a′—current and next action.
2.5.5. Online Adaptation
2.5.6. Critical Comparison of Adaptation Approaches
2.6. Tools and Resources for OFN Systems
2.7. Evolution of the OFN Model—Overview of Development Stages
3. Discussion
- OFNs offer a nuanced extension of fuzzy numbers that preserves the order and direction of the trend, making them suitable for applications where directional uncertainty matters (e.g., dynamic systems, economics).
- Type-1 fuzzy sets are the basis of fuzzy logic, valued for their simplicity and efficiency, but limited in handling complex or vague uncertainty.
- Type-2 fuzzy sets introduce a higher order of flexibility and are efficient in uncertain environments, but their computational cost limits practical applications.
- Intuitionistic fuzzy sets are excellent at modeling fluctuations and dual perspectives (membership vs. non-membership)and are well suited for decision-making and human-centered systems.
3.1. Limitations of the Study
3.2. Key Directions for Future Research
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kosiński, W.; Prokopowicz, P.; Ślęzak, D. Ordered fuzzy numbers. Bull. Pol. Acad. Sci. 2003, 51, 327–339. [Google Scholar]
- Piasecki, K. Revision of the Kosiński’s Theory of Ordered Fuzzy Numbers. Axioms 2018, 7, 16. [Google Scholar] [CrossRef]
- Marszałek, A.; Burczyński, T. Modeling of limit order book data with ordered fuzzy numbers. Appl. Soft Comput. 2024, 158, 111555. [Google Scholar] [CrossRef]
- Pisz, I.; Chwastyk, A.; Łapuńka, I. Assessing the profitability of investment projects using ordered fuzzy numbers. Log Forum 2019, 15, 6. [Google Scholar] [CrossRef]
- Roszkowska, E. O możliwościach wykorzystania skierowanych liczb rozmytych do podejmowania decyzji wielokryterialnych. Przegląd Stat. Stat. Rev. 2017, 64, 373–398. [Google Scholar] [CrossRef]
- Roszkowska, E.; Kacprzak, D. The fuzzy SAW and fuzzy TOPSIS procedures based on ordered fuzzy numbers. Inf. Sci. 2016, 369, 564–584. [Google Scholar] [CrossRef]
- Contieri, P.; Guilherme, S.; Rosley, A.; Luis, A.; De, S.-E. Industry 4.0 enabling technologies in manufacturing: Implementation priorities and difficulties in an emerging country. Technol. Anal. Strateg. Manag. 2022, 34, 489–503. [Google Scholar] [CrossRef]
- Apiecionek, Ł.; Moś, R.; Ewald, D. Fuzzy Neural Network with Ordered Fuzzy Numbers for Life Quality Technologies. Appl. Sci. 2023, 13, 3487. [Google Scholar] [CrossRef]
- Apiecionek, Ł.; Dobrosielski, W.; Ewald, D. Ordered Fuzzy Numbers for IoT Smart Home Solution. In Advances and New Developments in Fuzzy Logic and Technology; Atanassov, K.T., Atanassova, V., Kacprzyk, J., Kałuszko, A., Krawczak, M., Owsiński, J.W., Sotirov, S.S., Sotirova, E., Szmidt, E., Zadrożny, S., Eds.; Springer: Cham, Switzerland, 2021; pp. 302–310. [Google Scholar] [CrossRef]
- Rudnik, K.; Chwastyk, A.; Pisz, I. Approach Based on the Ordered Fuzzy Decision Making System Dedicated to Supplier Evaluation in Supply Chain Management. Entropy 2024, 26, 860. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Czerniak, J.; Mikołajewski, D.; Apiecionek, Ł.; Ślęzak, D. (Eds.) Theory and Applications of Ordered Fuzzy Numbers: A Tribute to Professor Witold Kosiński. In Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2017; Volume 356. [Google Scholar] [CrossRef]
- Chwastyk, A. Applications of Ordered Fuzzy Numbers in Medicine. In Uncertainty and Imprecision in Decision Making and Decision Support: New Challenges, Solutions and Perspectives. Selected Papers from BOS-2018, held on September 24-26, 2018, and IWIFSGN-2018, held on September 27-28, 2018 in Warsaw, Poland; Atanassov, K.T., Atanassova, V., Kacprzyk, J., Kaluszko, A., Krawczak, M., Owsinski, J.W., Sotirov, S., Sotirova, E., Szmidt, E., Zadrozny, S., et al., Eds.; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1081, pp. 103–112. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Singpurwalla, N.D.; Booker, J.M. Membership Functions and Probability Measures of Fuzzy Sets. J. Am. Stat. Assoc. 2004, 99, 867–877. [Google Scholar] [CrossRef]
- Kosinski, W.; Prokopowicz, P.; Ślęzak, D. Calculus with Fuzzy Numbers. InIntelligent Media Technology for Communicative Intelligence; Springer: Berlin/Heidelberg, Germany, 2004; pp. 21–28. [Google Scholar]
- Kacprzak, D. Skierowane liczby rozmyte w modelowaniu ekonomicznym. Optim. Stud. Ekon. 2010, 3, 263–281. [Google Scholar]
- Koleśnik, R.; Kosiński, W.; Prokopowicz, P.; Frischmuth, K. On algebra of ordered fuzzy numbers. In Soft Computing—Foundations and Theoretical Aspects; Atanassov, K.T., Hryniewicz, O., Kacprzyk, J., Eds.; Akademicka Oficyna Wydawnicza EXIT: Warszawa, Poland, 2004; pp. 291–302. [Google Scholar]
- Yang, C.; Zhang, X. Adaptive Fuzzy Control for Fractional-Order Networked Control Systems with Input Time Delay and Data Loss. J. Nonlinear Math. Phys. 2024, 31, 35. [Google Scholar] [CrossRef]
- Sun, J.; Yan, Y.; Yu, S. Adaptive Fuzzy Control for T-S Fuzzy Fractional Order Nonautonomous Systems Based on Q-learning. IEEE Trans. Fuzzy Syst. 2024, 32, 388–397. [Google Scholar] [CrossRef]
- Mirzajani, S.; Aghababa, M.P.; Heydari, A. Adaptive control of nonlinear fractional-order systems using T–S fuzzy method. Int. J. Mach. Learn. Cybern. 2019, 10, 527–540. [Google Scholar] [CrossRef]
- Marszałek, A.; Burczyński, T. Modeling and forecasting financial time series with ordered fuzzy candlesticks. Inf. Sci. 2014, 273, 144–155. [Google Scholar] [CrossRef]
- Gould, M.D.; Porter, M.A.; Williams, S.; McDonald, M.; Fenn, D.J.; Howison, S.D. Limit order books. Quant. Financ. 2013, 13, 1709–1742. [Google Scholar] [CrossRef]
- Lucas, P.; Orang, O.; Silva, P.; Mendes, E.; Guimarães, F. A Tutorial on Fuzzy Time Series Forecasting Models: Recent Advances and Challenges. Learn. Nonlinear Models 2022, 19, 29–50. [Google Scholar] [CrossRef]
- Abdullah, L. High Order Fuzzy Time Series for Exchange Rates Forecasting. In Proceedings of the 2011 3rd Conference on Data Mining and Optimization (DMO), Putrajaya, Malaysia, 28–29 June 2011. [Google Scholar]
- Rudnik, K.; Chwastyk, A. Inference Mechanism Based on Ordered Fuzzy Rules. In Proceedings of the 2023 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Incheon, Republic of Korea, 13–17 August 2023; IEEE: Incheon, Republic of Korea, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Czerniak, J.M.; Dobrosielski, W.; Angryk, R.A. Comparison of two kinds of fuzzy arithmetic, LR and OFN, applied to fuzzy observation of the cofferdam water level. Comput. Sci. 2013, 14, 443–458. [Google Scholar] [CrossRef]
- Rudnik, K.; Chwastyk, A.; Pisz, I.; Bocewicz, G. Ordered fuzzy rules generation based on incremental dataset. In Proceedings of the 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Luxembourg, 11–14 July 2021; IEEE: Luxembourg, 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Piasecki, K. Relation “Greater than or Equal to” between Ordered Fuzzy Numbers. Appl. Syst. Innov. 2019, 2, 26. [Google Scholar] [CrossRef]
- Łyczkowska-Hanćkowiak, A.; Wójcicka-Wójtowicz, A. On Portfolio Analysis Using Oriented Fuzzy Numbers for the Trade-Related Sector of the Warsaw Stock Exchange. Oper. Res. Decis. 2023, 33, 155–170. [Google Scholar] [CrossRef]
- Prokopowicz, P. Adaptation of rules in the fuzzy control system using the arithmetic of ordered fuzzy numbers. In Proceedings of the Artificial Intelligence and Soft Computing—ICAISC 2008, Zakopane, Poland, 22–26 June 2008; Rutkowski, L., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2008; Volume 5097. [Google Scholar] [CrossRef]
- Bocewicz, G.; Banaszak, Z.A.; Rudnik, K.; Witczak, M.; Smutnicki, C.; Wikarek, J. Milk-run Routing and Scheduling Subject to Fuzzy Pickup and Delivery Time Constraints: An Ordered Fuzzy Numbers Approach. In Proceedings of the 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Kacprzak, D. Fuzzy topsis method for group decision making. Mult. Criteria Decis. Mak. 2019, 13, 116–132. [Google Scholar] [CrossRef]
- Pacana, A.; Siwiec, D. Pro-Quality Choice a Machine by Using Ordered Fuzzy Numbers Model. Conf. Qual. Prod. Improv. CQPI 2020, 2, 180–187. [Google Scholar]
- Małolepsza, O. Metody adaptacji systemów wiedzy opartej na zbiorach rozmytych. Stud. I Mater. Inform. Stosowanej 2023, 15, 11–20. [Google Scholar]
- Apiecionek, Ł. Fully Scalable Fuzzy Neural Network for Data Processing. Sensors 2024, 24, 5169. [Google Scholar] [CrossRef] [PubMed]
- Pei, S.; Zhang, H.; Zhu, Y.; Hu, C. Lightweight transmission line defect identification method based on OFN network and distillation method. IET Image Process. 2024, 18, 3518–3529. [Google Scholar] [CrossRef]
- Ewald, D.; Zarzycki, H.; Apiecionek, L.; Czerniak, J. Ordered Fuzzy Numbers Applied in Bee Swarm Optimization Systems. JUCS J. Univers. Comput. Sci. 2020, 26, 1475–1494. [Google Scholar] [CrossRef]
- Kosiński, W.K.; Kosiński, W.; Kościeński, K. Ordered Fuzzy Numbers Approach to an Investment Project Evaluation. Manag. Prod. Eng. Rev. 2013, 4, 50–62. [Google Scholar] [CrossRef]
- Castellano, G.; Scaringi, R.; Vessio, G.; Zaza, G. Integrating Graph Neural Networks and Fuzzy Logic to Enhance Deep Learning Interpretability. In Proceedings of the Fourth International Workshop on Multilingual Semantic Web (MSW 2024), Paris, France, 11–13 December 2024; 2024. [Google Scholar]
- Pekaslan, D.; Chen, C.; Wagner, C.; Garibaldi, J.M. Performance and Interpretability in Fuzzy Logic Systems—Can We Have Both. In Proceedings of the Information Processing and Management of Uncertainty in Knowledge-Based Systems. IPMU 2020, Lisbon, Portugal, 15–19 June 2020; Lesot, M.-J., Zighed, D.A., Ali, M., Bouchon-Meunier, B., Eds.; Communications in Computer and Information Science. Springer: Cham, Switzerland, 2020; Volume 1237, pp. 553–566. [Google Scholar] [CrossRef]
- Voskoglou, M.G. Uncertainty, Fuzzy Sets and Related Theories. Orient. J. Phys. Sci. 2019, 4, 1–3. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Type-2 Fuzzy Logic: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Lima, J.F.; Patiño-León, A.; Orellana, M.; Zambrano-Martinez, J.L. Evaluating the Impact of Membership Functions and Defuzzification Methods in a Fuzzy System: Case of Air Quality Levels. Appl. Sci. 2025, 15, 1934. [Google Scholar] [CrossRef]
- Halkiopoulos, C.; Gkintoni, E. Leveraging AI in E-Learning: Personalized Learning and Adaptive Assessment through Cognitive Neuropsychology—A Systematic Analysis. Electronics 2024, 13, 3762. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, Q.; Hu, Y.; Wu, B. Design of fuzzy system-fuzzy neural network-backstepping control for complex robot system. Inf. Sci. 2021, 546, 1230–1255. [Google Scholar] [CrossRef]
- Torres, A.; Nieto, J.J. Fuzzy logic in medicine and bioinformatics. J. Biotechnol. Biomed. 2006, 2006, 91908. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, L. A Novel Underlying Algorithm for Reducing Uncertainty in Process Industry Risk Assessment. Processes 2024, 12, 1292. [Google Scholar] [CrossRef]
- Mortaji, S.T.H.; Noori, S.; Bagherpour, M. Directed earned value management based on ordered fuzzy numbers. J. Intell. Fuzzy Syst. 2021, 40, 10183–10196. [Google Scholar] [CrossRef]
- Pérez-Gaspar, M.; Gomez, J.; Bárcenas, E.; Garcia, F. A Fuzzy Description Logic Based IoT Framework: Formal Verification and End User Programming. PLoS ONE 2024, 19, e0296655. [Google Scholar] [CrossRef]
- Devikala, S.; Rabi, J.; Murugan, V.P.; Raj, J.S.C.M.; Sundaram, K.M.; Sivakumar, K. Development of Fuzzy Logic Controller in Automatic Vehicle Navigation Using IoT. J. Electr. Syst. 2024, 20, 114–121. [Google Scholar] [CrossRef]
- Małolepsza, O.; Mikołajewski, D.; Prokopowicz, P. Using Fuzzy Logic to Analyse Weather Conditions. Electronics 2025, 14, 85. [Google Scholar] [CrossRef]
- Rachmad, Y.E. Adaptive Learning Theory. In La Paz Costanera Publicaciones Internacionales, Edición Especial; OSF: El Paso, IL, USA, 2022. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. In Physica A: Statistical Mechanics and its Applications; Elsevier: Amsterdam, Netherlands, 2011. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Kaya, Y.; Uyar, M.; Tekin, R. A Novel Crossover Operator for Genetic Algorithms: Ring Crossover. arXiv 2011, arXiv:1105.0355. [Google Scholar]
- Winiczenko, R. Algorytmy genetyczne i ich zastosowania. In Postępy Techniki Przetwórstwa Spożywczego; SGGW Press: Warsaw, Poland, 2008. [Google Scholar]
- Cox, E. Fuzzy Modeling and Genetic Algorithms for Data Mining and Exploration; Morgan Kaufmann: Burlington, MA, USA, 2005. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Wang, W.; Jing, Z.; Zhao, S.; Lu, Z.; Xing, Z.; Guo, S. Intelligent Height Adjustment Method of Shearer Drum Based on Rough Set Significance Reduction and Fuzzy Rough Radial Basis Function Neural Network. Appl. Sci. 2023, 13, 2877. [Google Scholar] [CrossRef]
- Hassan, H.E.; Ibrahiem, K.H.; Madian, A.H. Optimizing multiprocessor performance in real-time systems using an innovative genetic algorithm approach. Sci. Rep. 2025, 15, 3842. [Google Scholar] [CrossRef] [PubMed]
- García-Valdez, M.; Mancilla, A.; Castillo, O.; Merelo-Guervós, J.J. Distributed and Asynchronous Population-Based Optimization Applied to the Optimal Design of Fuzzy Controllers. Symmetry 2023, 15, 467. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.; Chen, Y. Implementation of evolutionary fuzzy systems. IEEE Trans. Fuzzy Syst. 1999, 7, 109–119. [Google Scholar] [CrossRef]
- Fogel, D.B. Evolutionary programming: An introduction and some current directions. Stat. Comput. 1994, 4, 113–129. [Google Scholar] [CrossRef]
- Li, H.; Gupta, M.M. Fuzzy Logic and Inteligent Systems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Houghten, S.; Banik, S. Effective decoders for DNA codes. BioSystems 2022, 211, 104583. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Lu, J.; Ma, G.; Zhang, G. Fuzzy Machine Learning: A Comprehensive Framework and Systematic Review. IEEE Trans. Fuzzy Syst. 2024, 32, 3861–3878. [Google Scholar] [CrossRef]
- Wiktorowicz, K. Uczący się regulator rozmyty z modelem odniesienia. In Pomiary Automatyka Kontrola; Stowarzyszenie Inżynierów i Techników Mechaników Polskich SIMP: Warszawa, Poland, 2008; p. 12. [Google Scholar]
- Rusiecki, A. Algorytmy Uczenia Sieci Neuronowych Odporne Na Błędy W Danych; Politechnika Wrocławska: Wrocław, Poland, 2007. [Google Scholar]
- Smola, A.; Vishwanathan, S.V.N. Introduction to Machine Learning; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zander, E.; van Oostendorp, B.; Bede, B. Reinforcement learning with Takagi-Sugeno-Kang fuzzy systems. Complex Eng. Syst. 2023, 3, 9. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Daniya, T.; Geetha, M.; Kumar, K.S. Classification and regression trees with gini index. Adv. Math. Sci. J. 2020, 9, 1857–8438. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Yue, H.; Xia, J. Reinforcement learning-based optimal adaptive fuzzy control for nonlinear multi-agent systems with prescribed performance. Complex Eng. Syst. 2023, 3, 19. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Yasami, A.; Volos, C.; Bekiros, S.; Jahanshahi, H. A New Fuzzy Reinforcement Learning Method for Effective Chemotherapy. Mathematics 2023, 11, 477. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Bingham, E. Reinforcement learning in neurofuzzy traffic signal control. Eur. J. Oper. Res. 2001, 131, 232–241. [Google Scholar] [CrossRef]
- Liu, Q.; Mu, X.; Huang, W.; Fu, Q.; Zhang, Y. A Sarsa(λ) Algorithm Based on Double-Layer Fuzzy Reasoning. Math. Probl. Eng. 2013, 561026. [Google Scholar] [CrossRef]
- Horbowska, J. Ethical Competencies in Machine Learning from a Communicational Perspective in Educational Process. Kwart. Nauk. Fides Et Ratio 2024, 58, 38–45. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018; pp. 74–75. [Google Scholar]
- Fikri, N.; Rida, M.; Abghour, N.; Moussaid, K.; El Omri, A. An adaptive and real-time based architecture for financial data integration. J. Big Data 2019, 6, 97. [Google Scholar] [CrossRef]
- Abernethy, J.; Kale, S. Adaptive Market Making via Online Learning. In Proceedings of the NIPS, Lake Tahoe, NV, USA, 5–10 December 2013. [Google Scholar]
- Tsuchiya, Y.; Balch, T.; Drews, P.; Rosman, G. Online Adaptation of Learned Vehicle Dynamics Model with Meta-Learning Approach. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024. [Google Scholar]
- Khati, H.; Talem, H.; Touat, M.A.; Mellah, R.; Guermah, S. Online Adaptation of a Compensatory Neuro-Fuzzy Controller Parameters Using the Extended Kalman Filter: Application on an Inverted Pendulum. Eng. Proc. 2022, 14, 11. [Google Scholar]
- Cara, A.B.; Lendek, Z.; Babuska, R.; Pomares, H.; Rojas, I. Online self-organizing adaptive fuzzy controller: Application to a nonlinear servo system. In Proceedings of the FUZZ-IEEE 2010, IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July2010. [Google Scholar]
- Kasabov, N. Evolving fuzzy neural networks for supervised/unsupervised online knowledge-based learning. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2001, 31, 902–918. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing-A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Prokopowicz, P.; Mikołajewski, D.; Mikołajewska, E.; Tyburek, K. Modeling Trends in the Hierarchical Fuzzy System for Multi-Criteria Evaluation of Medical Data. InAdvances in Fuzzy Logic and Technology 2017. EUSFLAT IWIFSGN 2017 2017. Advances in Intelligent Systems and Computing; Kacprzyk, J., Szmidt, E., Zadrożny, S., Atanassov, K., Krawczak, M., Eds.; Springer: Cham, Germany, 2018; Volume 643. [Google Scholar] [CrossRef]
- Cingolani, P.; Alcala-Fdez, J. jFuzzyLogic: A Java Library to Design Fuzzy Logic Controllers According to the Standard for Fuzzy Control Programming. Int. J. Comput. Intell. Syst. 2013, 6, 61–75. [Google Scholar] [CrossRef]
- Peneva, V.; Popchev, I. Aggregation of fuzzy preference relations to multicriteria decision making. Fuzzy Optim Decis Mak. 2007, 6, 351–365. [Google Scholar] [CrossRef]
- Gast, C.; Traylor, R. On Ordered Fuzzy Numbers Generated By Time Series. arXiv 2020. [Google Scholar] [CrossRef]
- Sagias, V.D.; Zacharia, P.; Tempeloudis, A.; Stergiou, C. Adaptive Neuro-Fuzzy Inference System-Based Predictive Modeling of Mechanical Properties in Additive Manufacturing. Machines 2024, 12, 523. [Google Scholar] [CrossRef]
- Kushal, A. Quantum model regression for generating fuzzy numbers in adiabatic quantum computing. Inf. Sci. 2024, 678, 121018. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy Set Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Dilimulati, B.; Bruha, I. Genetic Algorithms in a dynamically changing environment. WIT Trans. Inf. Commun. Technol. 2007, 38, 65–73. [Google Scholar] [CrossRef]
- Fogel, D.B. A Comparison of Evolutionary Programming and Genetic Algorithms on Selected Constrained Optimization Problems. SIMULATION 1995, 64, 397–404. [Google Scholar] [CrossRef]


| Algorithm | Core Formula | Purpose |
|---|---|---|
| Linear Regression | Predict continuous values | |
| Logistic Regression | Binary classification |
| Algorithm | Core Formula | Purpose |
|---|---|---|
| SVM | Primal: Subject to: | Finding optional decision boundaries |
| Decision Trees | Creating decision hierarchies | |
| K-Means | Discovering data clusters |
| Years | Key Developments |
|---|---|
| 2002–2006 | Conceptual phase and first implementations |
| 2007–2014 | Development of methods and new applications |
| 2015–2020 | Advanced trend processing and algorithm refinement |
| 2021–present | New directions and broad applications |
| Method | Feature | Application | Advantages | Limitations |
|---|---|---|---|---|
| Genetic algorithms | Automatic adaptation of parameters (e.g., crossover and mutation rates) based on population information. | Parameter optimization, adaptation of fuzzy systems to achieve optimal solutions, parameterization of membership functions | Global search of the solution space, flexibility to adapt to change. | High computational complexity, slow convergence in large spaces. |
| Evolutionary programming | It is based on mutation as the main operator. | Search for optimal solutions, used to optimize parameters, improve system performance | Efficacy in continuous environments, no recombination required. | Slower convergence than GAs in some tasks. |
| Learning algorithms | Dynamic update of learning rate and model parameters | Classification, pattern recognition, data analysis | Effectiveness in environments with unstructured data. | Dependence on quality of input data, risk of overfitting. |
| Reinforcement learning | Reward/punishment-based learning from environment. | Adaptation of fuzzy system parameters and rules, optimization of fuzzy systems in dynamic and uncertain environments, decision making | Adaptation to unknown conditions, long-term optimization. | Requires big data resources, convergence problems in non-stationary environments. |
| Online adaptation | Fast adjustment of parameters without re-training | Monitoring systems, dynamic and changing environment | Computational efficiency, millisecond response. | Requires an initial training phase, instability in highly dynamic environments. |
| Method | Application Area |
|---|---|
| Variants of error propagation in neural networks with OFN | Learning neural networks, prediction |
| Adaptation of rules in control systems | Control of industrial processes |
| Adaptation of OFN discretization parameters | Calculation optimization, process modeling |
| Adjustment of cost thresholds in the LOB to OFN transformation | Analysis of stock market data, predictive systems |
| Adaptation of neural network architecture | Neuro-fuzzy network design |
| Gradient learning in OFN space | Machine learning, optimization |
| Context-dependent arithmetic (directional) | Simulation of dynamic systems, control |
| Aspect | OFNs | Type-1 Fuzzy Sets | Type-2 Fuzzy Sets | Intuitionistic Fuzzy Sets |
|---|---|---|---|---|
| Definition | Fuzzy numbers with explicit order and directionality | Standard fuzzy sets with a single membership function | Fuzzy sets where membership is another fuzzy set | Fuzzy sets with membership and non-membership function |
| Mathematical complexity | Moderate | Low | High | Moderate |
| Membership function | Describes both value and its orientation (increasing/decreasing) | Fixed membership function | Fluctuating Fuzzy membership | Membership + non-membership ≤ 1 |
| Representative of uncertainty | Directional uncertainty (increasing/decreasing trends) | Limited to membership degree | Handles both value and uncertainty in membership function | Captures hesitation margin |
| Arithmetic operations | Well suited, flexible, preserves order and direction in computations | Simple but can lose details in complex operations | Complex but accurate in modeling uncertainty | Requires more complex arithmetic than Type-1 fuzzy sets |
| Interpretability | Medium, depending on the context of the data due to directional features | High: easy to understand and interpret | Low due to complex interpretation and implementation | Medium: requires understanding of hesitation degree |
| Advantages | Effectively models order, direction and uncertainty | Simple, easy to interpret and implement | Flexible, comprehensively captures uncertainty | Captures hesitation and dual uncertainty |
| Limitations | Less intuitive than Type-1 fuzzy sets | Cannot represent higher-order uncertainty | High computational demands | Can be hard to elicit both membership and non-membership data |
| Standardization | Still evolving in theory and applications | Standardized | Standardized but less implemented due to complexity | Less standardized—it varies across application domain |
| Adaptation | Emerging, increasingly used | Most widely used | Growing interest in high-uncertainty environments | Increasing use in certain applications (e.g., cognitive modeling) |
| Application(s) | Engineering, economics, decision making, trend modeling | Control systems, pattern recognition, classification | Control and decision making in highly uncertain environments | Medical diagnosis, human-related patterns recognition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Małolepsza, O.; Mikołajewski, D.; Prokopowicz, P. Adaptation of Fuzzy Systems Based on Ordered Fuzzy Numbers: A Review of Applications and Development Prospects. Electronics 2025, 14, 2341. https://doi.org/10.3390/electronics14122341
Małolepsza O, Mikołajewski D, Prokopowicz P. Adaptation of Fuzzy Systems Based on Ordered Fuzzy Numbers: A Review of Applications and Development Prospects. Electronics. 2025; 14(12):2341. https://doi.org/10.3390/electronics14122341
Chicago/Turabian StyleMałolepsza, Olga, Dariusz Mikołajewski, and Piotr Prokopowicz. 2025. "Adaptation of Fuzzy Systems Based on Ordered Fuzzy Numbers: A Review of Applications and Development Prospects" Electronics 14, no. 12: 2341. https://doi.org/10.3390/electronics14122341
APA StyleMałolepsza, O., Mikołajewski, D., & Prokopowicz, P. (2025). Adaptation of Fuzzy Systems Based on Ordered Fuzzy Numbers: A Review of Applications and Development Prospects. Electronics, 14(12), 2341. https://doi.org/10.3390/electronics14122341






