Abstract
To make predictions, one can use machine learning and/or knowledge-based approaches. Knowledge-based approaches focus on developing systems with reasoning capabilities to solve application problems. Traditionally, statistical techniques have been used, while more recently, machine learning techniques have been used to make predictions. Both types of techniques are based almost exclusively on the analysis of historical data. This paper proposes a model that combines knowledge engineering and intelligent data analysis, leveraging the causal relationship between a past event and its known consequences. By determining the similarity between a current analogous situation and the past event, the model infers what the consequences of the current situation might be. The main contribution is the combination of various knowledge engineering techniques to improve the prediction outcomes for certain events. The present approach not only relies on analysing historical data but also integrates smart data utilization, the identification of the most similar past event, and the prediction or definition of cause–effect rules based on causal inference. One use case is presented: predicting the percentage of students who are promoted to the next grade with all subjects passed over the four years of middle school. Applying statistical regression techniques, a predicted value of 68.67% was obtained. Applying the proposed model, a value of 62.85% was obtained. The actual value published by the Spanish Department of Education for the 2021–2022 school year was 63.95%. The prediction using statistical techniques deviated 7.3% from the actual value. The proposed method deviated only 1.7% from the actual value. The proposed method improved the prediction compared to the value obtained using statistical techniques.
1. Introduction
Knowledge engineering is a discipline that captures, models and uses expert knowledge for decision making, complex problem solving and making predictions. In the context of predictions, it extracts and structures relevant information, allowing the generation of models capable of anticipating future events.
1.1. Literature Review
Salatino et al. [1] propose an innovative framework that uses a large-scale knowledge graph, based on Computer Science Ontology (CSO), to detect, analyze and predict emerging research topics. Traditionally, this analysis has relied on bibliometric methods that may not capture complex dynamics or predict the evolution of emerging topics. The lack of a formal and structured representation of research topics makes detection difficult. The new approach uses statistical techniques, such as trend analysis, to obtain better results than bibliometric methods. Gu et al. [2] addresses the challenge that exponential growth in scientific publications represents for researchers. This increase makes it difficult to identify research ideas. The authors developed an evolving knowledge graph, built from more than 21 million scientific articles. This graph combines a semantic network, created from the content of the articles, and an impact network, based on the historical citations of the articles. Using machine learning techniques, they trained the model. Krenn et al. [3] develops a benchmark based on real data to predict the future of artificial intelligence research. Through a knowledge graph containing more than 100,000 articles and 64,000 concepts, various methodologies are used, from statistics to machine learning, to anticipate new research directions in the field of AI. Zeineddine, H. et al. [4] seeks to develop a predictive model that identifies students at greatest risk of academic failure from the moment of admission, using only data from before the start of their university studies. This would allow educational institutions to implement early interventions to improve student retention and performance. The accuracy in identifying students at high risk of academic failure was 75.9%. Chen, Y. et al. [5] the study seeks to develop a predictive and visual analysis method that, using academic data prior to graduation, allows students to anticipate their first academic or work destination. A visual analysis system based on the CIRF-MLP model, called CausalCareerVis, was developed to analyze the causality and correlation between academic performance and the first destination of graduates, as well as to predict the latter. In Kitto, K. et al. [6], the main objective is to demonstrate how causal models, specifically directed acyclic graphs (DAGs), can serve as a tool to formalize educational theories and link them with data collected through educational technologies. Causal models were applied to two educational settings: self-regulated learning and reflective writing. In both cases, the DAGs helped identify causal relationships and generate predictions that can be tested with real-world data. In Cao, C. et al. [7], the main objective is to develop a system that uses large-scale language models (such as GPT-4) to transform abstract STEM concepts into understandable metaphors. These metaphors are then converted into visual representations, such as storyboards and animated videos, to facilitate student comprehension and retention of knowledge. Preliminary tests yielded promising results in terms of content generation and potential educational effectiveness.
Table 1 shows the papers reviewed, the techniques used, and their strengths and weaknesses:

Table 1.
Comparative literature review.
1.2. Context
Statistical techniques and machine learning techniques are used to make predictions. Statistical techniques can reduce the uncertainty of what will happen in the future. Machine learning techniques identify non-trivial patterns in the data. Both statistical and machine learning techniques rely on analyzing historical data. When other factors apart from historical data are involved in the prediction, statistical techniques and machine learning techniques are not sufficient. The goal of standard statistical analysis is to estimate whether the experimental conditions do not change (Pearl J. [8]). On the other hand, machine learning models have some problems; they work well for the kind of event they have been trained on [9].
The proposed model aims to go beyond extrapolations based solely on historical data or the discovery of patterns from historical data, incorporating expert and contextual knowledge specific to the domain being predicted. First, historical data is collected and organized to provide an empirical foundation reflecting past behaviour. However, relying solely on experience can be limiting as it does not account for the dynamic and evolving nature of the context. The integration of additional specific knowledge involves incorporating expert information and inference rules not directly derived from historical data. This knowledge enables the representation of causal relationships and relevant contextual factors.
Prediction can be categorized by four scenarios: near-certainty scenario, trend continuation scenario, random scenario and uncertainty scenario. The near-certainty scenario is based on highly reliable datasets, strong historical evidence, and patterns that show a high probability of recurring. It involves analyzing past trends and patterns observed in the behavior of studied events, providing a nearly certain basis for inferring future behavior. The trend continuation scenario assumes that observed past trends and patterns will continue unchanged into the future. The likelihood of these predictions is lower than the near-certainty scenario, but the historical trend is expected to persist. The underlying hypothesis is that the factors influencing the event’s behaviour in the past will remain the same in the future. A random scenario assumes that future outcomes are unpredictable and determined by random events or causes. There are no identifiable patterns or trends in historical data, and future outcomes are completely independent of past results. An uncertainty scenario is characterized by incomplete information, making predictions challenging. Factors contributing to uncertainty include:
- Lack of quality data (unknown, incomplete, or inaccurate information);
- Unpredictable changes in relevant causes (unexpected events, political decisions, technological advances, or external factors);
- The presence of multiple alternative possibilities.
The proposed model focuses on the uncertainty scenario. Despite the advantages of integrating additional knowledge into the prediction process, this approach is complex. Acquiring and representing expert knowledge, as well as combining historical data with additional knowledge, increases the difficulty of making accurate predictions.
1.3. General Objective and Contribution
The objective is to propose a method based on knowledge engineering that improves the predictive performance of statistical techniques and machine learning methods to predict certain complex events. To achieve this, the approach employs several techniques: reasoning by analogy, smart data analysis, and causal inference.
- Perform smart data analysis: Dashboards for data selection, transformation, and integration will be developed to extract insights from the data. This will provide empirical knowledge of how the event to be predicted has behaved in the past and will uncover new non-trivial knowledge about the event.
- Apply reasoning by analogy: An analogy-based reasoning approach will be developed to relate past and present events with similar characteristics and shared contexts. This method will facilitate the identification of analogies, and the most similar past event will serve as a basis for predicting the new event.
- Integration of causal relationships: Causal relationships extracted from smart data analysis and expert knowledge will be incorporated into the prediction process.
- Finally, the validation of the results of the proposed method with the Pearson chi-square test of independence and MAE (mean absolute error).
The advantages of using reasoning by similarity and causal relationships are that it allows for handling uncertainty or incomplete data. Similarity reasoning explains what has happened previously in similar cases. Causal relationships explain why an event occurred. The intelligent data analysis technique exploits large volumes of structured data, supporting the two previous techniques by extracting non-obvious knowledge from the data. Using these three techniques together to make predictions is better suited to different contexts than using only one of them. The main contribution is the combination of various knowledge engineering techniques to improve prediction results for certain events. This approach is not only based on the analysis of historical data, but also integrates intelligent data utilization, identification of the most similar past event, and prediction or definition of cause–effect rules.
1.4. Structure of This Paper
The subsequent sections of this document are structured as follows. Section 2, which explains the proposed model is explained, consists of three parts: the materials in which the elements of the proposed model are defined; the method that explains the tasks to be performed, and the validation in which the results obtained by the proposed model are compared with the real results using the Pearson chi square test and MAE. In Section 3, The proposed model is applied to predict the percentage of students who were promoted to the next grade with all subjects passed across the four years of middle school for the 2021–2022 academic year. To do this, the data from the 2010–2011 to 2020–2021 school years are analysed, considering key factors, such as the ratio of teachers per student, the economic expenditure per student and the ratio of students repeating a grade per total number of students. To make the final prediction, the following specific factors are considered: the average mortgage by state, the percentage of single-parent and two-parent families by state and the increase in the CPI by state. Section 4 presents the discussion and conclusions.
2. Materials and Methods
The proposed model employs three techniques: reasoning by analogy using a distance function to identify previous events similar to the event to be predicted, smart data analysis through the development of dashboards (Qlikview v.12) to extract knowledge from data, and causal relationships to predict and/or generalize knowledge through defined relationships.
This section is divided into three parts:
- Materials: This defines the model’s elements, with the two main objects being the most similar previous event and the event to be predicted, their relationship and cause–effect relationship.
- Methods: This specifies the phases and tasks to standardize and systematize the process by employing reasoning by analogy, smart data analysis, and the definition of cause–effect rules.
- Validation: To validate the results of the proposed model, the Pearson chi-square test of independence is used. This is a statistical procedure used to determine whether there is a significant relationship between two variables, specifically, the most similar previous event and the event to be predicted.
2.1. Materials
The model (Figure 1) consists of the most similar previous event (Ev) and the event to be predicted (Ev′). A previous event (Ev) is defined as a set of common causes (C) that produce certain effects (E). Common causes are those shared by both the previous events and the event to be predicted.
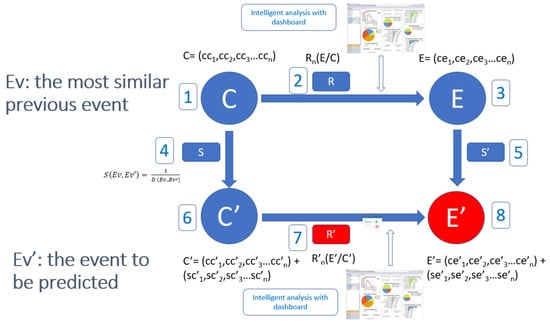
Figure 1.
Proposed model.
Explanation of Figure 1.
- Number 1. Causes of the most similar previous event (C).
- Number 2. Cause-effect relationship of the most similar previous event (R).
- Number 3. Effects of the most similar previous event (E).
- Number 4. Similarity between the causes of the most similar previous event and the event to be predicted (S).
- Number 5. Similarity between the effects of the most similar previous event and the effects of the event to be predicted (S′)
- Number 6. Causes of the event to be predicted (C′)
- Number 7. Cause-effect relationship of the event to be predicted (R′)
- Number 8. Effects of the event to be predicted (E′)
Table 2 provides descriptions of the most important variables of the proposed model.

Table 2.
Most important variables of the proposed model.
The event to be predicted (Ev′) is a set of common causes from the most similar previous event (C), plus a set of specific causes (C′) that produce effects E′ (Formula (1)):
The causes of the most similar previous event are defined as a set of common causes as follows C (cc1, cc2, cc3, …, ccn). A cause is represented as a vector composed of (Id, Den, Val).
Intra-event relationships between the most similar previous event (Ev) and the event to be predicted (Ev′) are defined through the similarity function (S). The function S determines how similar a previous event is to the event to be predicted based on common causes. Initially, a database of previous events, defined by a set of common causes, is established. Applying the similarity function between previous events and the event to be predicted identifies the most similar previous event.
The similarity function S is defined as the inverse of the distance between the common causes of previous events and the common causes of the event to be predicted (Formula (2)). The previous event with the smallest distance to the event to be predicted is called the most similar previous event (Ev).
To calculate the distance between two vectors, the Manhattan distance or Euclidean distance can be used (Formula (3)). The Manhattan distance is the sum of the absolute differences between the common causes of the most similar previous event (Ev) and the event to be predicted (Ev′). The Euclidean distance is the square root of the sum of the differences between the common causes squared of the most similar previous event (Ev) and the event to be predicted (Ev′).
In the most similar previous event (Ev), the inter-event relationship R is defined. The effects (E) of the most similar previous event are represented as a set of effects (ce1, ce2, ce3, …, cen), where each effect is described as a vector composed of (Id, Den, Val).
The proposed model is based on the hypothesis that
- If some causes (C) of the most similar previous event (Ev) produce specific effects (E), and;
- There is a certain degree of similarity between the common causes (C) of the event to be predicted (Ev′);
- Then, there will also be a certain degree of similarity between the effects (E) of the most similar previous event (Ev) and the effects (E′) of the event to be predicted (Ev′).
The effects (E) of the previous event (Ev) and the effects (E′) of the event to be predicted (Ev′) are connected via the similarity function S′. Just as S relates the common causes (C) of the previous event (Ev) to those of the event to be predicted (Ev′), the similarity function S′ relates the effects (E) of the previous event (Ev) to the hypothetical effects (E′) of the event to be predict (Ev′).
In the event to be predicted, the combination of common causes (cc1, cc2, cc3, …, ccn) and specific causes (sc1, sc2, sc3, …, scn) produces effects (E′). The effects of the event to be predicted consist of:
- Common effects (ce1, ce2, ce3, …, cen) from the most similar previous event;
- Specific effects (se1, se2, se3, …, sen) are unique to the event to be predicted.
Specific causes and effects are related through confounding variables. A confounding variable (Vcf) is defined as a vector composed of (Id, Den, Val).
The intelligent analysis of data through dashboards allows for understanding and modelling causal relationships in both the most similar previous event (Ev) and the event to be predicted (Ev′). Key techniques include:
- Identifying Relevant Causes and Effects: Detect patterns in large datasets, distinguishing between common and specific causes while reducing noise.
- Expanding Expert Knowledge: Recognize complex, non-trivial patterns.
- Evaluating Causal Relationships: Assess whether causal relationships are valid or spurious by controlling for confounding variables.
- Discovering Causal Rules: Automate knowledge generalization into IF…THEN rules.
- Predicting Future Effects: Analyze historical patterns to extrapolate how identified causes will affect future events.
The most similar previous event is related to the event to be predicted through a hierarchical relationship between common causes (Figure 2).
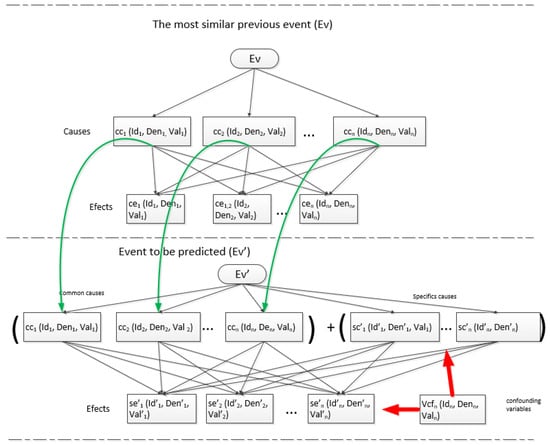
Figure 2.
Relationship between the most similar previous event and the event to be predicted.
- Most Similar Previous Event (Ev): The root represents the event, intermediate levels represent common causes (C), and the leaves represent common effects (E).
- Event to Be Predicted (Ev′): The root represents the event, intermediate levels include common causes (C) from the most similar previous event and specific causes (C′) of the event to be predicted, while the leaves represent specific effects (E′).
Confounding variables are related to the causes and effects of the event to be predicted, influencing the result of the prediction.
In Figure 2, the green arrows indicate the relationship of common causes between the most similar previous event and the predicted event. The red arrows indicate the relationship between confounding variables and the specific causes and effects of the predicted event.
The hypothetical effects (E′) of the new event (Ev′) are the result of the common causes of the most similar previous event in the event to be predicted (E′/C), plus the specific causes of the event to be predicted (E′/C′) (Formula (4)) as follows:
Effects (Ev′) = EffectsEv′ (E′/C) + EffectsEv′ (E′/C′)
- EffectsEv′ (E′/C) is the EffectEv (E/C) of the most similar previous event, adjusted proportionally based on the result of the similarity function S through the similarity function S′ (Formula (5)).Effects Ev′ (E′/C) = f (EffectsEv (E/C), Similarity FunctionS′)
- EffectsEv′ (E′/C′): The specific causes (C′) of the new event (Ev′) are derived from expert knowledge extracted through the intelligent utilization of large datasets using dashboards (Formula (6)).EffectsEv′ (E′/C′) = f (Intelligent analysis of big data)
2.2. Methods
The phases and tasks are defined by applying the definitions from the previous section. The process consists of three phases: smart data analysis, reasoning by analogy, and cause–effect relationships. Figure 3 indicates the set of tasks to be performed in each phase.
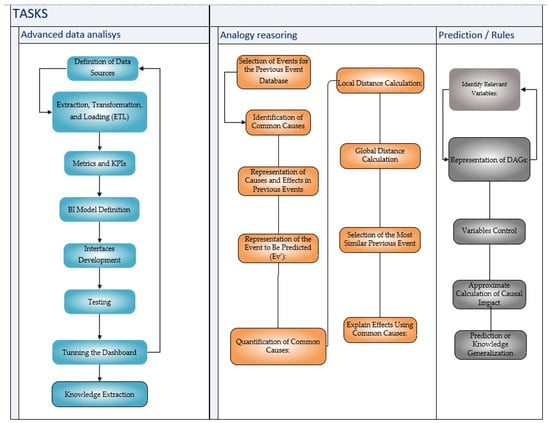
Figure 3.
Proposed method: Phases and task.
- Smart data analysis
Dashboards are developed to perform an intelligent analysis of data from both previous events and the event to be predicted. This activity is essential as it enables not only a static (descriptive) view of the data but also a dynamic (causal) perspective. It comprises the following tasks:
- Definition of Data Sources:
- ∘
- Data Definition: Identify the data required to develop the dashboard. Describe the obtained data, the meaning of attributes, and their format. Descriptive statistics techniques can be applied to explore the data.
- ∘
- Define Data Sources: Determine the origin of each dataset.
- ∘
- Establish Dimensional and Fact Entities: Dimensions categorize and describe factors, while factors are numerical or quantitative measures that represent key metrics for analysis.
- Extraction, Transformation, and Loading (ETL):This process cleans and transforms the data into a suitable format for analysis and storage in a centralized repository (data lake):
- ∘
- Extraction: Gather data from multiple sources, such as databases, flat files, online applications, and event logs. All relevant data for analysis is collected.
- ∘
- Transformation: Perform operations to clean, structure, and prepare the data for analysis.
- ∘
- Loading: Load the transformed data into a centralized repository (e.g., data warehouse or analytical database).
- Metrics and KPIs:
- ∘
- Metrics are quantitative values that measure a specific aspect of an event. They are quantitative (always expressed in numerical terms), specific (related to a particular aspect of the event) and comparable (allow for analysis across different periods or contexts).
- ∘
- Key Performance Indicators (KPIs) are strategically selected metrics used to assess whether an organization is meeting its key objectives. They are more specific and directly linked to the event’s strategic goals. They are characterized by relevant (aligned with the event’s strategic) and contextualized (their value has meaning within a context).
- BI Model Definition:The model is constructed by relating entities based on the characteristics stored in dimensional and fact entities:
- ∘
- Identify Key Attributes: Abstract and select attributes to serve as primary and foreign keys, establishing connections between factors and dimensions.
- ∘
- Define a Star Schema: Create relationships between entities. In the star schema, fact entities act as the central core connecting the dimensions that contextualize the data.
- Interface Development:Information is grouped into sections, defining what data will be displayed in each dashboard section.
- Testing:Execute the model and verify that the metrics and indicators displayed on the dashboard match those calculated from the data sources.
- Tuning the Dashboard:Developing the dashboard for knowledge extraction is an iterative process. Necessary adjustments are made to ETL processes and the user interface until non-trivial expert knowledge that meets the dashboard’s objectives is uncovered.
- Knowledge Extraction:Interpret the obtained results, focusing on how various dashboard selections translate into knowledge and uncover hidden information. Identify the causes and variables relevant to the event to be predicted.
- Reasoning by Analogy
The objective is to identify the previous event most similar to the event to be predicted. This involves analysing previous events that share characteristics and patterns with the event to be predicted, leveraging historical data to understand and forecast possible outcomes. The process includes the following tasks:
- Selection of Events for the Previous Event Database:Select representative previous events based on their relevance and similarity to the event to be predicted.
- Identification of Common Causes:Identify common causes through the smart data analysis described earlier or by consulting domain experts to determine influential causes.
- Representation of Causes and Effects in Previous Events:Represent previous events using vectors that include relevant causes and their corresponding effects.
- Representation of the Event to Be Predicted (Ev′):Similar to previous events, represent the event to be predicted as a collection of common causes (C).
- Quantification of Common Causes:Quantify the common causes of previous events (Ev) and the event to be predicted (Ev′) based on knowledge derived from smart data analysis.
- Local Distance Calculation:Use a local distance function to measure similarity between individual causes of previous events and the event to be predicted, identifying the most similar previous event.
- Global Distance Calculation:Calculate the global distance to assess the overall similarity of the event to be predicted (Ev′) relative to the entire database of previous events.
- Selection of the Most Similar Previous Event:Evaluate the local distance function to compare each common cause of previous events with the corresponding cause in the event to be predicted. The previous event with the smallest distance is identified as the most similar previous event.
- Explain Effects Using Common Causes:If the common causes (C) of the most similar previous event (Ev) are similar to the common causes (C′) of the event to be predicted (Ev′), it can be inferred that their effects (E and E′) will also be similar.
- Prediction or Generalization of Knowledge
Knowledge extracted through smart data analysis can infer relationships between causes, effects, and confounding variables. To achieve this, the model uses Directed Acyclic Graphs (DAGs) and removes the undesired effects of confounding variables on causes and effects.
- Identify Relevant Variables:Determine independent variables (causes), dependent variables (effects), and confounding variables.
- Representation of DAGs:Create a DAG comprising causes, effects, and confounding variables. In a DAG, causes are nodes, and causal relationships are arrows pointing from causes to effects.
- Variable Control:Include confounding variables in the model to eliminate their biasing effects. Confounding variables often create “backdoor effects”. Steps to mitigate this include:
- ∘
- Identifying variables through smart data analysis.
- ∘
- Including them as control variables in the model.
- ∘
- Evaluating whether the influence of causes on effects changes significantly.
- Approximate Calculation of Causal Impact:Understand how independent variables influence dependent variables using techniques such as regression discontinuity, matching, or a difference-in-differences (DiD) design.
- Prediction or Knowledge Generalization:
- ∘
- Prediction: Use the most similar previous event and its effects as a baseline to model the influence of specific causes on the new event’s effects.
- ∘
- Definition of Rules: Define cause–effect rules as conditional statements linking antecedents (“IF”) to consequences (“THEN”).
2.3. Validation
Validation allows measuring the accuracy of the results obtained from the proposed predictive model. Common validation metrics used for event prediction (e.g., precision, recall, F1 score) are not applicable to this model, as it relies not only on historical data analysis but also on causality and reasoning by analogy. It is essential to consider that, in the proposed predictive model, past events and the event to be predicted are not identical, with the differentiating factor being the specific causes of the event to be predicted compared to past events. In the event to be predicted, causality generates different effects from those in past events.
The Pearson chi-squared (Chi2) test will be used after the event to be predicted has occurred, comparing actual results to predicted results. The Chi2 test will provide an approximation of the goodness of fit for the proposed improved predictive model.
The Chi2 test is a statistical procedure used to determine whether there are significant differences between the actual results and those predicted by the model. The basic idea of the test is to compare the values of the observed data with what would be expected if the initial hypothesis were true. The Chi2 independence test will be used to determine whether the two variables (observed and expected) are independent or related (Formula (7)).
Chi2 = ∑(Observed data − predicted data)2/predicted data
Key elements of the chi-squared test:
- Null Hypothesis (H0): Assumes no significant differences between observed and expected values; both follow a similar pattern.
- Alternative Hypothesis (H1): Opposes the null hypothesis, indicating significant differences between the two variables. The expected data do not align with the observed data.
- Degree of Freedom: Depends on the number of sample values and is used to consult Chi2 tables. It is calculated as (Formula (8)):
- Significance Level or Critical Value (α): Represents the probability that the null hypothesis is true.
- Decision Criterion:
- ∘
- Reject H0 when Chi2 >= Chi2t (r − 1) × (k − 1). If the calculated Chi2 value is greater than or equal to the critical value, the null hypothesis is rejected, indicating no significant relationship between the two categorical variables.
- ∘
- Fail to reject H0 when Chi2 < Chi2t (r − 1) × (k − 1). If the calculated Chi2 value is less than the critical value, the null hypothesis cannot be rejected, indicating a significant relationship between the hypothetical and observed values.
Interpreting chi-squared results:
- The larger the Chi2 value, the less likely the initial hypothesis is true.
- The closer Chi2 is to zero, the more aligned the observed and predicted distributions are.
Another validation method to be used is the MAE (mean absolute error), a measure of the difference between two continuous variables. Considering two data series (some calculated and some observed) relating to the same event, the mean absolute error is used to quantify the accuracy of a prediction technique. It is calculated as the sum of the absolute value between the calculated value and the observed value divided by the number of values (n), Formula (9). A low MAE indicates that the model’s predictions are, on average, close to the actual values.
MAE = ∑|Observed data − predicted data|/n
3. Prediction of the Percentage of Students Who Promote to the Next Grade with All Subjects Passed in the Four Years of Middle School for the 2021–2022 School Year in Spain
Middle school in Spain is a fundamental stage in the educational system, as it marks the transition from primary education to higher levels of academic training. It lasts four years, generally from ages 12 to 16. The reason why middle school was chosen is that it is the last educational level that is compulsory; that is, all boys and girls must complete it, with the results being more representative than other non-compulsory educational levels (High School, university, etc.).
The objective is to apply the proposed model to predict the percentage of students who are promoted to the next grade with all subjects passed in the four years of middle school for the 2021–2022 school year, considering some social, educational and economic factors. Smart data analysis will be conducted using data from the 2011–2012 to 2020–2021 school years to identify common causes, specific causes, and patterns for prediction and knowledge generalization.
Machine learning techniques, such as neural networks, or statistical techniques, can be used to make the prediction. Some studies in the scientific literature use machine learning methods:
- Junemann, M.AP. et al. [10]: Implemented neural networks to predict the academic performance of 15-year-old students in reading, mathematics, and science based on familial, social, and economic factors.
- Wang, T. et al. [11]: Used neural networks to calculate the number of errors a student might make while solving a problem. This prediction was based on the problem’s specific attributes and the student’s skills. The method was applied to optimize problem selection in a final assessment process.
- Cripps, A. [12]: Focused on university students, examining demographic characteristics, such as age, gender, and race, along with college entrance test results. Neural networks were used to predict a student’s ability to complete a course and their final grade.
- Buenaño-Fernandez, D. et al. [13]: Applied machine learning techniques to predict final grades of computer engineering students in Ecuador. This prediction was based on the students’ performance history across 68 courses in the program, using decision trees.
- Moscoso-Zea, O. et al. [14]: Analyzed student data to predict graduation rates based on characteristics of enrolled students. The prediction enabled early corrective measures to improve the admission process.
- Sheel, S. J. et al. [15]: Compared the use of neural networks with traditional statistical models to classify students into two groups based on the results of a single math-level test.
- Kalles, D. et al. [16] and Kotsiantis, S. et al. [17]: Used data from distance education to predict success or failure in final exams through various techniques, including neural networks. These datasets included demographic information, individual assignment grades, and virtual class attendance levels.
Studies based on machine learning techniques are not very accurate because they only consider historical data to make predictions. Regarding statistical techniques, regression analysis is particularly popular for making predictions, and it models the relationship between independent variables and dependent variables. Linear regression will be used to predict the statistical percentage of students who will be promoted with all middle school subjects passed during the 2021–2022 school year [18]. Table 3 presents the percentage of students promoted with all subjects passed in middle school from the 2011–2012 to 2020–2021 school years:

Table 3.
School years and percentage of students promoted.
In the following bar chart (Figure 4), the data from the previous table is represented, and the trend line (in blue) is calculated using linear regression:
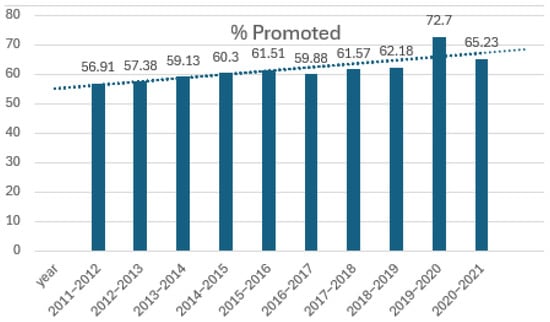
Figure 4.
Percentage of students promoted: trend line by school years.
The equation defining the trend line is y = 1.285·x − 2529.6, with a correlation coefficient (R2) of 0.6767. Using this equation to calculate the value for the 2021–2022 school year, it is determined that 68.67% of middle school students will be promoted with all subjects passed.
Other types of regression can also be applied to predict the percentage of students who will be promoted in the 2021−2022 school year, yielding the following equations:
- Logarithmic Regression: The function equation is y = 6.209·ln (x) + 50.812;
- Second-Degree Polynomial Regression: The function equation is y = 0.0632·x2 − 253.49·x + 254.35;
- Power Regression: The function equation is y = 8·10 − 136·x41.42.
In all cases, the result is approximately 68%. Following the trend observed in the results from the 2011–2012 to 2020–2021 period and applying the regression, the percentage of students who are promoted to the next grade with all subjects passed in the 2021–2022 school year is expected to range between 67% and 69%. We will now apply the proposed method to predict the percentage of students who are promoted to the next grade with all subjects passed in the 2021–2022 school year.
- Smart data analysis
An intelligent analysis will be conducted to correlate the percentage of students who are promoted with all subjects passed in each year of middle school, taking into account educational and economic factors. The goal is to uncover non-obvious relationships in the data. Common causes values (expenditure per student, teacher ratio, repeater ratio) and specifics causes values (GDP per capita, single-parent household ratio, average mortgage cost) are expressed in different orders of magnitude: units, tens, and hundreds. To perform the various calculations, values have been normalized between 0 and 1 with the max–min method. However, in certain parts of the paper, the values are shown in their original order of magnitude to facilitate understanding.
- Data Sources
The following datasets were downloaded from the open data and statistical portal web of the Department of Education of Spain:
- Number of students who are promoted in middle school [19]
- Total number of enrolled students in middle school [20]
- Total expenditure (€) on middle school [21]
- Total number of teachers in middle school [22]
- Total number of repeating students in middle school [23]
A data lake with a centralized, flat storage structure was created to store the raw datasets. Each dataset was uniquely identified and tagged with metadata (source URL, description, download date). The purpose of the data lake is to provide accessible data for large-scale analysis.
- Data Extraction, Transformation, and Loading (ETL)
The focus of the intelligent analysis is the percentage of students who are promoted with all subjects passed in middle school, calculated using Formula (10):
Number of students who pass all subjects in middle school × 100/Number of students enrolled in middle school
Each dataset was segmented using the following criteria:
School years: 2011–2012, 2012–2013, 2013–2014, 2014–2015, 2015–2016, 2016–2017, 2017–2018, 2018–2019, 2019–2020, and 2020–2021.
- Promoted type: All subjects passed;
- States: Each of Spain’s 17 states and two autonomous cities, total 19 states;
- Grade: First, second, third and fourth grades of middle school.
- Metrics and KPIs
Using the processed datasets, a dashboard was developed to conduct smart data analysis, generating the following KPIs (Figure 3):
- Expenditure (€) per student who advances to the next grade with all subjects passed in middle school, segmented by school year and state (Formula (11)):Total expenditure (€)/Number of students enrolled in middle school
- Percentage of teachers in middle school relative to the number of enrolled students in middle school, segmented by school year and state (Formula (12)):Total number of teachers × 100/Number of students enrolled in middle school
- Percentage of repeating students in middle school relative to the number of enrolled students in middle school, segmented by school year and state (Formula (13)):Total number of repeating students × 100/Number of students enrolled in middle school
- BI Model Definition
A structured and simplified representation of the data is created to facilitate the analysis and understanding of the dashboard’s objective. Entities and fields that connect the various entities are defined.
The fact entity consists of states grouped into states and school years, from 2011–2012 to 2020–2021 (Figure 5). The dimension entities are the study characteristics:
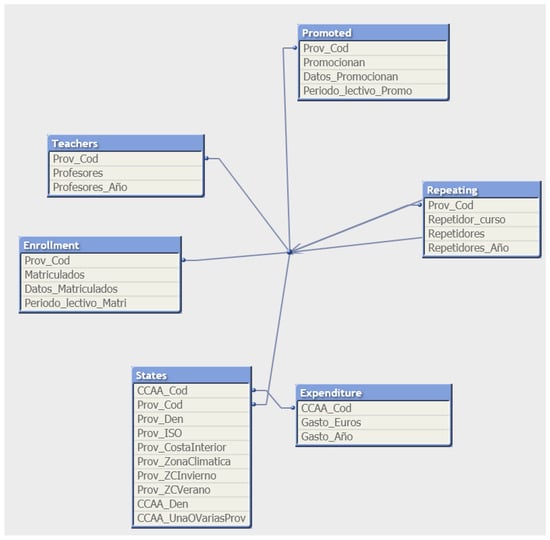
Figure 5.
Percentage of students who are promoted to the next grade: data model.
- Teacher–student ratio;
- The average expenditure per student;
- Ratio of repeating students.
- Interface Development
In the dashboard, each KPI (percentage of teachers to enrolled students, expenditure per enrolled student, and percentage of repeating students to enrolled students) is compared with the percentage of students who are promoted with all subjects passed in each state (Figure 6):
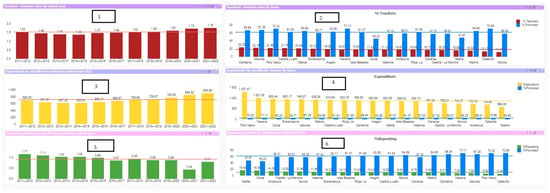
Figure 6.
Educational KPIs regarding the percentage of students promoted from 2011–2012 to 2020–2021.
- Explanation of the graphics in Figure 6:
- Graphic 1. Teachers- students ratio by school year (colour red).
- Graphic 2. Teachers-students ratio by State. Compare, by State, the teacher-student ratio (red) with the promoted student ratio (blue).
- Graphic 3. Expenditure by enrolment student by school year (colour yellow)
- Graphic 4. Expenditure by enrolment student by State. Compare, by State, expenditure by enrolment student (colour yellow) with the promoted student ratio (blue).
- Graphic 5. Repeating student by enrolment student by school year (colour green).
- Graphic 6. Repeating student by enrolment student by State. Compare, by State, Repeating student by enrolment student (colour green) with the promoted student ratio (blue).
- Knowledge Extraction
The KPIs are analyzed in relation to the percentage of students who are promoted by state. Regarding the expenditure per student KPI, typical cases are the following:
- Below-average expenditure per student: Generally, the percentage of students who are promoted to the next grade is below average in the Balearic Islands, Valencia, Canary Islands, Castilla-La Mancha, Murcia, and Andalusia.
- Above-average expenditure per student: Typically, the percentage of students promoted to the next grade is above average in the Basque Country, Navarre, Asturias, Galicia, Castilla y León, La Rioja, Cantabria, and Aragón.
Atypical cases:
- States with a below-average expenditure per student but an above-average student promotion rate are Madrid and Catalonia.
- States with an above-average expenditure per student but a below-average student promotion rate are Ceuta, Extremadura, and Melilla.
Teacher–student ratio
For the percentage of teachers to total student KPI, typical cases are the following:
- Below-average teacher–student ratio: The percentage of students who are promoted to the next grade is below average in Ceuta, Valencia, Andalusia, Castilla-La Mancha, Melilla, Canary Islands, Extremadura, and Murcia.
- Above-average teacher–student ratio: The percentage of students who are promoted to the next grade is above average in Cantabria, Asturias, Basque Country, Castilla y León, Galicia, Aragón, and Navarre.
Atypical cases:
- A below-average teacher–student ratio and an above-average student promotion rate are found in La Rioja, Madrid, and Catalonia.
- An above-average teacher–student ratio and a below-average student promotion rate are found in Extremadura and the Balearic Islands.
Repeating student ratio:
For the percentage of repeating students to total student KPI, the typical cases are as follows:
- Below-average repeating student ratio: Typically, the percentage of students who are promoted to the next grade is above average in Galicia, Madrid, Cantabria, Navarre, Asturias, the Basque Country, and Catalonia.
- Above-average repeating student ratio: Generally, the percentage of students who are promoted to the next grade is below average in Melilla, Ceuta, Andalusia, Castilla-La Mancha, Murcia, Valencia, Extremadura, and the Balearic Islands.
Atypical cases:
- Below-average repeating student ratio and a below-average student promotion rate: Canary Islands.
- Above-average repeating student ratio and an above-average student promotion rate: La Rioja, Aragón, and Castilla y León.
New knowledge has been discovered from Intelligent Educational Data Analysis. Intelligent analysis of educational data has revealed the following non-trivial relationships:
- States with a lower-than-average investment per student and a lower-than-average teacher–student ratio have a higher-than-average rate of students promoted to the next grade (Madrid and Catalonia).
- States that have a below-average percentage of teachers, an above-average percentage of repeating students per total number of enrolled students, and their students are promoted to the next grade above the average (La Rioja).
- States whose investment per student is above average, with the percentage of teachers below average, and students promoted to the next grade below average (Ceuta, Melilla and Extremadura).
Table 4 provides a summary relating the percentage of students who are promoted to the next grade above and below average in each autonomous community (2011–2012 to 2020–2021) to the percentage of teachers per student, expenditure per student, and percentage of repeating students to total enrolled students.

Table 4.
Smart data analysis: percentage of students promoted to the next grade from 2011–2012 to 2020–2021 by state.
In Table 4, for each row, cells with a green background indicate better outliers. Cells with a red background indicate worse outliers. And cells with a white background indicate normal values.
The intelligent analysis of the data will lead to the rules that will be used to predict the percentage of students who will be promoted to the next grade after passing all subjects in the 2021–2022 school year.
- Reasoning by Analogy
- Selection of Events in the Database of Previous Events
The database of previous events consists of the percentage of students who are promoted to the next grade with all subjects passed during the 2011–2012 to 2020–2021 school years.
Previous events are defined as the percentage of middle school students who are promoted to the next grade in the 2011–2012 to 2020–2021 school years. The event to be predicted is the percentage of middle school students who will be promoted to the next grade in the 2021–2022 school year. The prediction is based on similarity relationships, identifying the school year most similar to the 2021–2022 school year.
The educational factors discussed earlier are transformed into common causes in the proposed model (expenditure per student, the percentage of teachers per student, and the percentage of repeating students). Socioeconomic factors (e.g., consumer price index CPI, average mortgage costs, and percentage of single-parent households in Spain) are treated as specific causes in the model. The prediction starts with the school year in which the percentage of students who are promoted to the next grade with all subjects passed is most similar to 2021–2022 and adjusts the prediction based on specific causes.
The final prediction for the total percentage of students who are promoted to the next grade in 2021–2022 is calculated as the average percentage of students who are promoted to the next grade in each state of Spain during that school year, considering the results of the intelligent analysis of educational factors.
- Identification of Common Causes
From the smart data analysis, the following common causes were identified:
- Teacher-to-student ratio;
- Expenditure per student;
- Percentage of repeating students to total enrolled students.
These three factors will represent both previous events and the event to be predicted, forming the foundation for identifying the school year most similar to 2021–2022.
- Representation of Causes and Effects in Previous Events
To identify the most similar previous event, a database of previous events is constructed, represented as vectors in the format cause → effect, with the following structure:
(school year, region, expenditure per student, % teachers, % repeating students) → (students promoted with all subjects passed).
Examples include:
- For the 2011–2012 school year in Andalusia:
- ∘
- (2011–2012; Andalusia; 640.29€; 1.53; 1.75) → (57.18%).
- For other states:
- ∘
- (2011–2012; Aragón; 740.80€; 1.74; 1.11) → (56.99%);
- ∘
- (2011–2012; Asturias; 920.02€; 2.01; 0.89) → (62.02%);
- ∘
- …;
- ∘
- (2020–2021; Basque Country; 1370.80€; 2.15; 0.39) → (72.62%);
- ∘
- (2020–2021; La Rioja; 950.65€; 1.69; 0.39) → (64.21%);
- ∘
- (2020–2021; Valencian Region; 900.59€; 1.89; 0.42) → (61.99%).
For each school year, the data can also be represented as a vector for aggregated KPIs:
(school year, % teachers, expenditure per student, % repeating Students) → (students promoted with all subjects passed).
- Examples include:
- (2011–2012; 1.52%; 690.80€; 1.17%) → (56.91%);
- (2012–2013; 1.45%; 640.16€; 1.11%) → (57.38%);
- …;
- (2019–2020; 1.63%; 780.46€; 0.89%) → (73.69%);
- (2020–2021; 1.73%; 850.45€; 0.44%) → (65.74%).
- Representation of the Event to Be Predicted (Ev′)
The event to be predicted is represented similarly to previous events using common causes:
(school year, region, expenditure per student, % teachers, % repeating students).
Examples for 2021–2022:
- (2021–2022; Andalusia; 840.85€; 1.71%; 1.12%);
- (2021–2022; Aragon; 960.73€; 2.13%; 0.86%);
- (2021–2022; Asturias; 990.93€; 2.18%; 0.60%).
For aggregated data:
(2021–2022; 1.76%; 900.49€; 0.81%).
- Quantifying Common Causes for Previous Events and the Event to Be Predicted
A software application was developed to process vectors of causes and effects from previous events and the common causes of the event to be predicted. Figure 7 shows the wireframe of the application:

Figure 7.
Wireframe for calculating the most similar previous event.
Figure 8 shows an overview of the developed application. The objective is to identify the previous event most similar to the one being predicted:
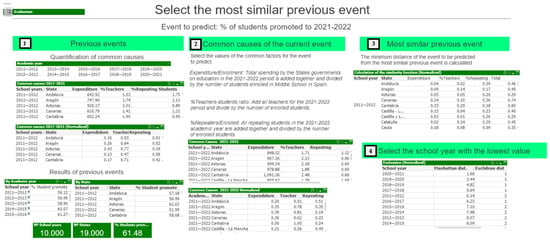
Figure 8.
Application overview for calculating the most similar previous event.
- Section 1: Quantifies the academic periods from 2011–2012 to 2020–2021 based on common causes. Results for previous events are displayed by school year and state.
- Section 2: Quantifies the common causes for the event to be predicted.
- Section 3: Calculate distance from previous events to the event to be predicted based on common causes.
- Section 4: Selects the most similar previous event, detailed in the next section.
- Local Distance Calculation
In Section 3 of Figure 8, the Manhattan distance function is applied. This function calculates the sum of the absolute difference between the common causes of the 2021–2022 school year and the common causes of each year in the database of previous events (Formula (14)) as follows:
Manhattan distance = ∑ abs (% Teachers for the 2021–2022 school year − % Teachers from 2011–2012 to 2020–2021 school years) + abs (Expenditure per Student for the 2021–2022 school year − Expenditure per Student from 2011–2012 to 2020–2021 school years) + abs (% Repeating Students for the 2021–2022 school year − % Repeating Students from 2011–2012 to 2020–2021 school years)
In Section 3 of Figure 8, the Ecuclidian distance function is applied. This function calculates the square root of the sum of the differences between the common causes of the 2021–2022 school year and the common causes of each year in the database of previous events (Formula (15)) as follows:
Euclidean distance = sqrt root (∑(% Teachers for the 2021–2022 school year − % Teachers from 2011–2012 to 2020–2021 school years)2 + (Expenditure per Student for the 2021–2022 school year − Expenditure per Student from 2011–2012 to 2020–2021 school years)2 + (% Repeating Students for the 2021–2022 school year − % Repeating Students from 2011–2012 to 2020–2021 school years)2)
This method identifies the previous event most similar to the event to be predicted. The previous event with the smallest distance is the most similar to the event to be predicted (Section 4, Figure 8).
- Global Distance Calculation
Global distance quantifies the overall similarity between the event to be predicted and previous events. It assesses how similar or different the event to be predicted is compared to events stored in the database, considering common causes.
To calculate the global distance, the average expenditure per student, teacher-to-student ratio, and repeating student-to-student ratio of their normalized values will be used: Average (expenditure, % teachers, % repeating students) → (0.34; 0.41; 0.66), as shown in Table 5.

Table 5.
Average of common causes to calculate global distance (normalized).
For the event to be predicted, the common causes normalized are (2021–2022; 1.00; 1.00; 0.68%). The global distance is calculated as the mean of the common causes:
- Average common causes of previous events: 0.43;
- Average common causes of the event to be predicted: 0.84.
The mean of the event to be predicted is nearly 92% higher than the average of previous events, indicating that the new event is significantly different from the previous ones.
- Selecting the Most Similar Previous Event
The event most similar to the percentage of students who advanced to the next grade in all middle school grades during the 2021–2022 school year is the 2020–2021 school year, with a Manhattan distance of 1.66 points and a Euclidean distance of 1.51 points (Figure 8, Section 4). Table 6 calculates the local distance from the school years 2010–2011 to 2020–2021 with respect to the school year 2020–2022, according to common causes.

Table 6.
Local distance calculation for the percentage of students promoted in 2021–2022 (normalized).
The 2020–2021 school year is the most similar to the predicted 2021–2022 school year. In the most similar previous event (2020–2021), 65.23% of students advanced to the next grade with all subjects passed, serving as the baseline for the final prediction.
- Prediction and/or Generalization of Knowledge
- Identifying Relevant Variables
There are numerous variables that significantly influence and predict academic performance, such as parental education level, ethnicity, and the type of housing where students live (e.g., number of rooms, city area, housing price). Collecting data on these variables and correlating them with the percentage of middle school students who are promoted with all subjects passed for each state and school year is a complex task.
As such, the selected variables are as follows:
- Expenditure per student;
- Teacher-to-student ratio;
- Repeating student ratio.
These variables, grouped by year and state, are available on the websites of Spain’s National Institute of Statistics (INE) and the Department of Education of Spain.
- Directed Acyclic Graphs (DAGs)
From smart data analysis, three types of factors are identified:
- Economic factors
- Educational resources
- Educational system efficiency
The percentage of students who are promoted is determined by average expenditure per student, the teacher–student ratio, and the repeating student-to-student ratio (Figure 9). These causes are interrelated (some influencing others), ultimately affecting the percentage of students who are promoted.
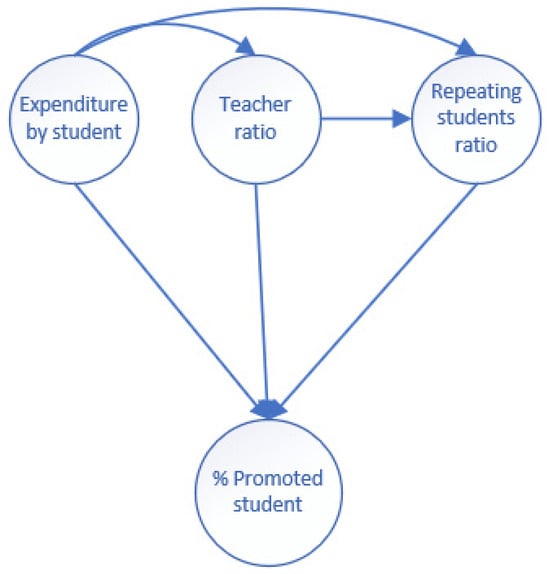
Figure 9.
Percentage of students promoted in 2021–2022: related variables.
- The expenditure per student impacts the teacher ratio and repeating student ratio: a higher expenditure leads to more teachers and fewer repeating students.
- The teacher ratio also affects the repeating student ratio: more teachers result in smaller class sizes, which in turn reduces the number of repeating students.
Expert elicitation algorithm (IC) is a process by which expert knowledge in a specific domain is collected and formalized to build or refine causal models. In contexts where data is limited, incomplete, or expensive to obtain, expert elicitation allows for the following:
- Identifying relevant variables and plausible causal relationships.
- Establishing assumptions about the direction of causal relationships.
- Validating or adjusting causal structures proposed by algorithms, such as CI.
By applying expert elicitation (IC), the dates and the direction are consistent. For example, the expenditure per student not only affects the percentage of students promoted but also influences the teacher ratio and the percentage of students who repeat. The teacher ratio directly influences the percentage of students promoted, as well as the percentage of students who repeat. The more teachers per student, the fewer repeaters.
- Variable Control
Controlling variables simplifies graph interpretation by isolating direct causal relationships. The analysis includes independent variables (expenditure per student, teacher ratio, and repeating student ratio) that influence the outcome (percentage of students who are promoted with all subjects passed). Three backdoor paths are identified in DAG:
- Backdoor path 1: Teacher ratio ← expenditure per student → percentage of students promoted, i.e., spending per student affects both the teacher ratio and the percentage of students promoted.
- Backdoor path 2: Repeating student ratio ← expenditure per student → percentage of students promoted, i.e., spending per student affects both the repeating student ratio and the percentage of students promoted.
- Backdoor path 3: Teacher ratio ← expenditure per student → repeating student ratio → percentage of students promoted, i.e., spending per student affects both the teacher ratio and the repeating student ratio, and the repeating student ratio affects the percentage of students promoted.
To eliminate the blockage of the three backdoors, the expenditure per student must be adjusted. Neither the teacher ratio nor the repeating student ratio should be adjusted because this would disrupt the estimated effect (Figure 10).
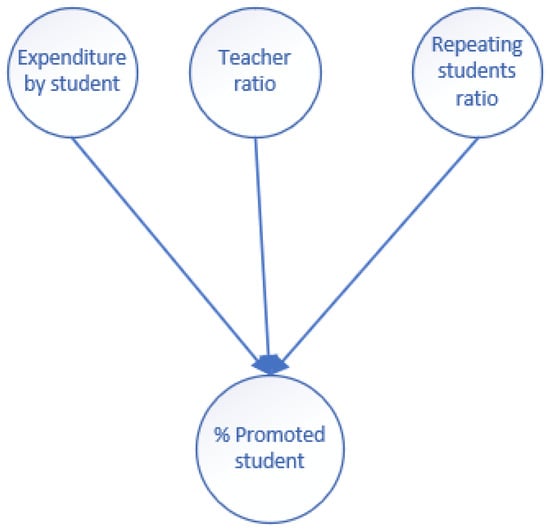
Figure 10.
Percentage of students promoted in 2021–2022: direct relationships among variables.
- Atypical case: 2019–2020 school year
During the 2016–2017 to 2018–2019 and 2020–2021 school years, the percentage of students who advanced to the next grade with all subjects passed was between 60% and 65% (Table 7).

Table 7.
Percentage of students promoted to the next grade (2016–2017 to 2020–2021).
However, during the 2019–2020 school year, there was a notable increase in the percentage of students who were promoted to the next grade: 72.70%. This can be attributed to a combination of factors stemming from the COVID-19 pandemic:
- Relaxation of assessment and promotion criteria: The Department of Education of Spain and the states agreed that grade repetition would be an exceptional measure, allowing most students to progress to the next educational level, even with outstanding subjects.
- Reduction in academic demands: The abrupt transition to online learning led to an overall decrease in the academic load and assessment requirements, making it easier for more students to meet the passing criteria.
- Decrease in the repetition rate: Official statistics show that the rate of repeating students in compulsory secondary education has decreased significantly.
- Adaptation of final assessments: Final exams and assessments were modified to adapt to the new educational reality, in many cases increasing the optionality and reducing the difficulty.
- Family support during lockdown: The teleworking of many parents, especially mothers, allowed for greater supervision and support in their children’s educational process, which had a positive impact on their academic performance.
- Focus on students’ emotional well-being: Educational authorities prioritized students’ emotional well-being during the pandemic, leading to greater understanding and flexibility on the part of teachers in assessing academic performance.
- Reduction of academic pressure: The elimination of in-person exams and the adaptation of assessments reduced pressure on students, allowing them to perform better in a less stressful environment.
- Institutional awareness of educational inequalities: The pandemic highlighted inequalities in access to education, leading institutions to take steps to ensure all students had the opportunity to advance their education, regardless of their circumstances.
- Faculty commitment: Faculty quickly adapted their teaching and assessment methods to continue the educational process online, showing great dedication to ensuring students could successfully complete the course.
- Approximate Causal Impact Calculation
Causal impact is analyzed using multiple regression. Independent variables (causes) include expenditure per student, the teacher ratio, and the repeating student ratio
The regression models the relationship between independent variables and the dependent variable (percentage of students who are promoted), in Formula (16) as follows:
% students promote = β0 + β1 × expenditure per student + β2 × ratio of teachers + β3 × ratio of repeating students
- Expenditure per student, teacher ratio, and repeating student ratio are the independent variables;
- β0, β1, β2, β3 are the regression coefficients representing the impact of each independent variable on the percentage of students who are promoted.
The coefficients (β0, β1, β2, β3) are estimated to determine the causal impact of the independent variables on the percentage of students who will be promoted. A table is created (Table 8) with the independent variables (expenditure per student, teacher ratio, repeating student ratio) and the dependent variable (percent of student promoted):

Table 8.
Input table with the independent and dependent variables for calculating multiple regression (normalized).
The multiple correlation coefficient is 0.9539 and the coefficient of determination R2 → 0.9100 and adjusted R2 → 0.6401. This means that the three independent variables are highly correlated with the dependent variable. The mutiple regression Formula (17) (β0, β1, β2, β3) is as follows:
%Student promoted = 38.71 + 109.0046 × Expenditure per student − 67.2252 × Teachers ratio + 22.3770 × Repeating student ratio
In Table 9, for each school year, the actual value of the percentage of promoted students is compared with the value obtained by the regression formula.

Table 9.
Comparison of real promotion vs regression calculation.
By applying multiple regression, the percentage of students who are promoted to the next grade from the 2016–2017 to 2020–2021 school years has shown a consistent increase in relation to the expenditure per student, the teacher ratio and the repeating student ratio.
- Prediction and Rules
To identify the specific causes related to the percentage of students who advanced a grade with all subjects passed, various studies were used, showing a direct relationship between family economic situation, family structure, and academic performance. The work by Considine, G. et al. [24] indicates that low socioeconomic status directly affects academic performance. In this study, the economic aspect of families is reflected in the evolution of the consumer price index (CPI) (an increase in the CPI indicates families have less money for other expenses) and the cost of housing mortgages (the primary expense for most families).
Regarding family structure, the study considers whether a family has a single parent or two parents. Various studies associate two-parent families with greater emotional stability and more appropriate behavior in children, resulting in better academic performance (Wallerstein, J. [25]; Niemeyer, T. D. et al. [26]; Ram, B. et al. [27]; White, L. et al. [28]). Conversely, single-parent families negatively influence academic performance for several reasons:
- Single-parent families have fewer economic resources since they rely solely on the income of one parent and, at best, partial support from the other parent.
- They have a reduced ability to provide more effective parenting, as responsibilities cannot be shared equally between two parents.
- A single parent lacks the support of another adult to address challenges and difficulties related to educating children.
- The parent has reduced emotional stability caused by the absence of support from a second parent.
- Data Sources
The following datasets were downloaded from Spain’s National Institute of Statistics (INE):
- CPI evolution by month and state [29];
- Number of single-parent households by year and CC.AA. [30];
- Number of two-parent households by year and CC.AA. [30];
- Number of mortgages constituted by month and CC.AA. [31];
- Total amount of mortgages constituted by month and CC.AA. [31].
- Prediction Application Overview
Figure 11 shows the wireframe for the software application used for prediction.
Figure 11.
Wireframe of the prediction application.
Figure 12 shows the general interface of the software application used for prediction, incorporating the most similar previous event and adjustments for specific causes. It consists of the following parts:
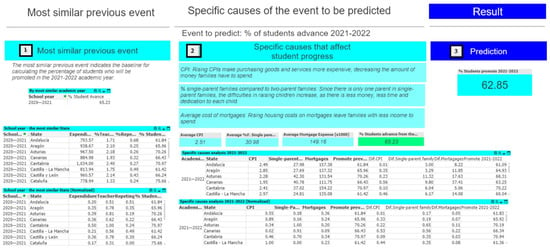
Figure 12.
Percentage of students promoted in 2021–2022: specific causes and prediction.
- Section 1: Displays the values of common causes and the results of the most similar previous event (2020–2021 school year).
- Section 2: Evaluates the specific causes for the event to be predicted (2021–2022 school year).
- Section 3: Produces the final prediction, accounting for the effect of the most similar previous event and adjustments for the specific causes of the event to be predicted.
- Specific causes and prediction
The variables CPI, single-parent household, and average mortgage cost have increased in recent years, negatively impacting academic performance.
The prediction for the percentage of students who are promoted in the 2021–2022 school year by CC.AA. is calculated as the sum of the absolute differences between each variable and the respective average for that variable (Formula (18)), as follows:
∑ abs (Average CPI − Event to predict CPI by state) + abs (Average of single-parent families − Event to predict single-parent families by state) − abs (Average mortgages − Event to predict mortgages by state)
The predicted percentage for the 2021–2022 school year is 62.85%.
- Results and Validation
- Results
From the intelligent analysis of educational data, the following rules were derived:
- IF the state expenditure by student is above the average
- ∘
- IF the teacher ratio is above the average
- ▪
- IF the repeating student ratio is below the average
- ▪
- IF the percentage of students who are promoted to the next grade is above the average: Asturias, Cantabría, Galicia, Basque Country.
- ▪
- OTHERWISE
- ▪
- IF the percentage of students who are promoted to the next grade is above the average: Aragón, Castilla-León
- ▪
- OTHERWISE Extremadura
- ∘
- OTHERWISE
- ▪
- IF the repeating student ratio is below the average THEN
- ▪
- IF the percentage of students who are promoted to the next grade is above the average: La Rioja
- ▪
- OTHERWISE
- ▪
- IF the percentage of students who are promoted to the next grade is below the average: Ceuta, Melilla
- OTHERWISE
- ∘
- IF the teacher ratio is above the average
- ▪
- IF the repeating student ratio is above the average THEN
- ▪
- IF the percentage of students who are promoted to the next grade is above the average: Balearic Island
- ∘
- OTHERWISE
- ▪
- IF the repeating student ratio is below the average THEN
- ▪
- IF the percentage of students who are promoted to the next grade is above the average: Canary Island
- ▪
- OTHERWISE Madrid, Catalonia
- ▪
- OTHERWISE
- ▪
- IF the percentage of students who are promoted to the next grade is below the average: Andalusia, Castilla- La Mancha, Valencian Region, Region of Murcia.
The percentage of students who are promoted to the next grade in the 2021–2022 school year was predicted as the average across all 19 states (Formula (19)):
Average (percentage of students who will be promoted to the next grade in the 2021–2022 school year by state)
The predicted percentage of students who are promoted to the next grade in the 2021–2022 school year is 62.85%.
- Validation
In December 2023, the Department of Education of Spain published the students who were promoted for the 2021–2022 school year [32]. The actual percentage of students who are promoted to the next grade in all four middle school grades, with all subjects passed, by CC.AA. was calculated as 63.94%, using the criteria shown in Figure 13.
Figure 13.
Percentage of students promoted to the next grade in 2021–2022: Criteria for calculating the actual percentage of students promoted to the next grade in middle school.
Once the above data has been downloaded, the average for each state and the total for the four grades is calculated, obtaining a value of 63.94% (Table 10).

Table 10.
Percentage of students promoted to the next grade in 2021–2022: Calculation of the actual percentage of students.
- Table 10 columns:
1st Grade→ First Grade.
2nd Grade → Second Grade
3rd Grade → Third Grade
4th Grade → Fourth Grade
Real Promot. → The real % of students who have been promoted in the 2021–2022 school year
To validate the accuracy of the proposed improved prediction method, the chi-square (χ2) function is used. For each state, the percentage of students who were promoted to the next grade with all subjects passed during the 2021–2022 school year (the actual event result) is compared with the value predicted by the proposed method. In Table 11, the columns are as follows:

Table 11.
Percentage of students promoted to the next grade in 2021–2022: Pearson Chi2 and MAE calculations.
- “Real Average” Column: The actual average percentage, for each state, of students who were promoted to the next grade with all subjects passed across the four middle school grades during the 2021–2022 school year.
- “Predicted Average” Column: The percentage predicted by the proposed method, for each CC.AA., of students who are promoted to the next grade with all subjects passed across the four ESO grades during the 2021–2022 school year.
- “Chi2” Column: X2 = ∑(<State>% promoted to the next grade 2021/2022 − <State>% promoted to the next grade proposed method 2021/2022)2/(<State> % promoted to the next grade proposed method 2021/2022).
- MAE column: (1/n) × ∑(<State>% promoted to the next grade 2021/2022 − <State>% promoted to the next grade proposed method 2021/2022)2, been n the number of states.
The calculated Chi2 value is 18.88, with a significance level (α) of 5% (0.05) and 19 degrees of freedom (19 states). From the Chi2 table, the critical value at 19 degrees of freedom and α = 0.05 is 30.1.
Since 18.88 < 30.1, the null hypothesis is accepted: the predicted and actual percentages of students who are promoted to the next grade are significantly related.
Regarding the MAE calculation, Ceuta and Melilla skew the data, as their values are in the tens, while the rest of the states have values in units. Excluding the states of Ceuta and Melilla, the sum of the absolute value of the difference between the observed value and the predicted value is 33.83. This sum is divided by the number of values, which is 17, yielding a result of 1.99. This value is relatively low compared to the individual values. The average distance between the observed and predicted values is small, validating the predicted results.
4. Discussion and Conclusions
Knowledge engineering can use statistical techniques and machine learning techniques to make predictions. These types of techniques can be useful in scenarios with stable and well-structured data; however, in dynamic and uncertain contexts, such as educational performance, their validity is limited. Statistical and machine learning techniques for making predictions present several problems:
- They require complete and representative data to perform. In contexts where information is partial, these techniques can generate biased or unreliable results.
- Statistical models, such as linear regression, assume that past trends will continue in the future, which is not always true where political, economic and social factors influence in an unpredictable way.
- Neural networks and other machine learning models are effective when there are clear and repetitive patterns in the data. However, the relationships between variables are not always linear or constant, which limits their predictive capacity.
- Techniques such as neural networks present a “black box effect”, which makes it difficult to understand how and why certain predictions are generated.
- Regarding the influence of non-quantifiable external factors, aspects such as student motivation, teaching quality or family influence are difficult to quantify and, therefore, difficult to model with statistical or machine learning approaches.
- Prediction models are often trained on historical data, which makes them less flexible when faced with changing conditions. Factors such as new educational policies or economic crises can drastically change the rate of school promotion, something that these models cannot accurately predict.
Since statistical and machine learning techniques have these limitations, we propose a hybrid model that combines three techniques: intelligent data analysis, similarity reasoning, and causal relationships. Each technique complements the others. Specifically,
- Intelligent data analysis provides an empirical basis for the model, identifying trends and patterns in historical data as well as identifying relevant variables. It is estimated to contribute 60% to the model.
- Similarity reasoning establishes a baseline from which to predict the new event based on analogy with similar previous cases. It is estimated to contribute 25% to the model.
- Causal relationships allow us to understand the cause–effect relationships between variables, beyond correlations, improving the ability to generalize knowledge. It is estimated to contribute 15% to the model.
This predictive approach integrates historical data with expert knowledge to enhance accuracy in uncertain scenarios. The model establishes a database of prior events, each characterized by specific causes and effects, forming a set of cause–effect rules. Both past events and the target event are represented as vectors, facilitating comparison through a distance function to identify the most similar prior event. Shared causes between the events enable this comparison, while the target event also includes unique causes. In the most similar past event, both causes and effects are known; in the target event, only the causes are known, and the effects are to be predicted. The model operates on the premise that the effects of similar events are likely to be analogous. Throughout the process, intelligent data analysis is employed to discern common and specific causes, as well as the effects of the most similar prior event.
The proposed model has been applied to a use case: predicting the percentage of students who were promoted with all subjects passed in middle school in the school year 2021–2022 in Spain. Prior to applying the proposed model, and taking into account the results of the school years from 2010–2011 to 2020–2021, the statistical regression technique was applied, obtaining a value of 68.67%.
Applying the proposed model, an intelligent analysis of the data has been carried out and the ratio of teachers per student, the expenditure per student and the number of repeating students per school year have been related. Interesting results are obtained. The following are atypical cases:
- The teacher–student ratio is below the average and the number of students who are promoted is above the average: La Rioja, Madrid and Catalonia.
- The expenditure per student is below the average and the number of students who are promoted to the next grade is above the average: Madrid and Catalonia.
- The repeating student ratio is higher than the average and the number of students is above the average: La Rioja, Aragón and Castilla and León.
Vice versa:
- States with an expenditure above average, have a below-average percentage of students promoted: Extremadura and Balearic Island.
- States with an above-average teacher ratio have a below-average percentage of students promoted: Ceuta, Extremadura and Melilla.
- States with a lower rate of repeaters have a below-average percentage of students promoted: Canary Island.
This non-obvious knowledge that we discovered can be used to study success and failure cases to determine which educational policies to implement, and which not, based on the experiences of different states.
Subsequently, reasoning by analogy is performed. To do this, the database of previous events is defined with the percentage of students who are promoted to the next grade with all subjects passed from the 2010–2011 to 2020–2021 school years. Using the defined distance function, it is found that the most similar previous event is the 2020–2021 school year, with a result of 62.85%. Finally, the defined acyclic graphs are used to establish the relationships between the common causes and the result, eliminating derived relationships.
The specific causes of the event to be predicted are defined: the value of the CPI, the percentage of single-parent and bi-parent families and the average value of the mortgage. Taking into account the intelligent analysis of the data, reasoning by analogy and the cause–effect relationships, the proposed model predicts a value of 62.85%. If statistical techniques had been applied, 68.67% of students would have been promoted in the 2021–2022 school year. In December 2023, the Spanish Department of Education published the percentage of students promoted with all subjects passed in middle school in the 2021–2022 school year at 63.94%, which is validated by the Pearson chi-square test and MAE metric. After applying the Pearson test and MAE metric, a value is obtained that confirms the result obtained by the proposed model.
This paper is useful because the Spanish Department of Education publishes the percentage of students who advance to the next grade with all subjects passed, almost one year later. The objectives of predicting the percentage of students who advance to the next grade with all subjects passed before the official results are published are several:
- Detecting academic failure early in order to intervene as quickly as possible.
- Optimizing the planning of educational resources, e.g., increasing investment per student, increasing the number of teachers, reducing the number of students per class, etc.
- If a low passing rate is predicted, strategies can be designed to change the pedagogical approach.
- Showing predictive evidence to support improvements in educational investments. Measuring the impact of educational policies, e.g., scholarships, reinforcement programs, curricular changes, etc.
Finally, future studies could include the following
- Integrating new educational, social, and economic factors.
- Applying the model to different educational levels (high school, university, etc.) and countries would test its generalization and adaptability. Such expansion could reveal new patterns.
- Train and compare at least two state-of-the-art algorithms (e.g., Random Forest, Gradient Boosting Machines) using the same features, and report comparative metrics (MAE, RMSE) alongside the hybrid model.
- Developing intuitive dashboards and visualization tools would make the model’s information more accessible to educators and policymakers, facilitating data-driven decision-making.
Future research could refine the hybrid predictive model, making it a more comprehensive and versatile tool for enhancing educational outcomes in dynamic and uncertain environments.
Author Contributions
Conceptualization, A.L. and J.A.O.; methodology, A.L. and J.A.O.; software, A.L.; validation, J.A.O., J.S.-G. and F.P.R.; formal analysis, A.L.; investigation, A.L.; resources, A.L. and J.A.O.; data curation, A.L.; writing—original draft preparation, A.L.; writing—review and editing, A.L. and J.A.O.; visualization, A.L.; supervision, J.A.O., J.S.-G. and F.P.R.; project administration, J.A.O., J.S.-G. and J.S.-G.; funding acquisition, J.A.O. All authors have read and agreed to the published version of the manuscript.
Funding
The Spanish Government has partially supported this work under the grant SAFER: PID2019-104735RB-C42 (ERA/ERDF, EU), and project PLEC2021-007681 funded by MCIN/AEI/10.13039/501100011033 and the European Union Next Generation EU/PRTR.
Data Availability Statement
Publicly available datasets were analyzed in this study. See the references.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Salatino, A.A.; Mannocci, A.; Osborne, F. Detection, analysis, and prediction of research topics with scientific knowledge graphs. In Predicting the Dynamics of Research Impact; Springer: Cham, Switzerland, 2021; pp. 225–252. [Google Scholar]
- Gu, X.; Krenn, M. Forecasting high-impact research topics via machine learning on evolving knowledge graphs. arXiv 2024, arXiv:2402.08640. [Google Scholar] [CrossRef]
- Krenn, M.; Buffoni, L.; Coutinho, B.; Eppel, S.; Foster, J.G.; Gritsevskiy, A.; Kopp, M. Predicting the Future of AI with AI: High-quality link prediction in an exponentially growing knowledge network. arXiv 2022, arXiv:2210.00881. [Google Scholar]
- Zeineddine, H.; Braendle, U.; Farah, A. Enhancing prediction of student success: Automated machine learning approach. Comput. Electr. Eng. 2021, 89, 106903. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, W.; Wang, L.; Dong, Y.; Liang, C.J. Where do they go next? Causal inference-based prediction and visual analysis of graduates’ first destination. J. Vis. 2024, 27, 885–908. [Google Scholar] [CrossRef]
- Kitto, K.; Hicks, B.; Buckingham Shum, S. Using causal models to bridge the divide between big data and educational theory. Br. J. Educ. Technol. 2023, 54, 1095–1124. [Google Scholar] [CrossRef]
- Cao, C.; Ding, Z.; Lee, G.G.; Jiao, J.; Lin, J.; Zhai, X. Elucidating stem concepts through generative ai: A multi-modal exploration of analogical reasoning. arXiv 2023, arXiv:2308.10454. [Google Scholar]
- Pearl, J. Causal inference. In Causality: Objectives and Assessment; PMLR: Cambridge, MA, USA, 2010; pp. 39–58. [Google Scholar]
- Loyola-Gonzalez, O. Black-box vs. white-box: Understanding their advantages and weaknesses from a practical point of view. IEEE Access 2019, 7, 154096–154113. [Google Scholar] [CrossRef]
- Junemann, M.A.P.; Lagos, P.A.S.; Arriagada, R.C. Neural Networks to Predict Schooling Failure/Success. Comput. Sci. 2007, 4528, 571–579. [Google Scholar]
- Wang, T.; Mitrovic, A. Using neural networks to predict student’s performance. In Proceedings of the International Conference on Computers in Education, Auckland, New Zealand, 3–6 December 2002; pp. 969–973. [Google Scholar]
- Cripps, A. Using artificial neural networks to predict academic performance. In Proceedings of the ACM Symposium on Applied Computing, Philadelphia, PA, USA, 17–19 February 1996; pp. 33–37. [Google Scholar]
- Buenaño-Fernández, D.; Gil, D.; Luján-Mora, S. Application of Machine Learning in Predicting Performance for Computer Engineering Students: A Case Study. Sustainability 2019, 11, 2833. [Google Scholar] [CrossRef]
- Moscoso-Zea, O.; Saa, P.; Luján-Mora, S. Evaluation of algorithms to predict graduation rate in higher education institutions by applying educational data mining. Australas. J. Eng. Educ. 2019, 24, 4–13. [Google Scholar] [CrossRef]
- Sheel, S.J.; Vrooman, D.; Renner, R.S.; Dawsey, S.K. A Comparison of Neural Networks and Classical Discriminant Analysis in Predicting Students’ Mathematics Placement Examination Scores. Comput. Sci. 2001, 2074, 952–957. [Google Scholar]
- Kalles, D.; Pierrakeas, C. Analyzing student performance in distance learning with genetic algorithms and decision trees. Appl. Artif. Intell. 2006, 20, 655–674. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Pierrakeas, C.; Pintelas, P. Predicting students’ performance in distance learning using machine learning techniques. Appl. Artif. Intell. 2004, 18, 411–426. [Google Scholar] [CrossRef]
- % of Middle School Students who Promoted to the Next Grade with All Subjects Passed in the 2020–2021 School Years. Department of Education of Spain. Statistics on Non-University Education. Available online: https://estadisticas.educacion.gob.es/EducaJaxiPx/Tabla.htm?path=/no-universitaria/alumnado/matriculado/2020-2021-rd/gen-eso/l0/&file=eso_01.px&L=0 (accessed on 1 January 2024).
- Number of Students Who Promoted to the Next Grade in Middle School from 2011–2012 to 2020–2021 School Years. Available online: https://www.educacionfpydeportes.gob.es/servicios-al-ciudadano/estadisticas/no-universitaria/alumnado/resultados.html (accessed on 1 January 2024).
- Number of Students Enrolled in Middle School from 2011–2012 to 2020–2021 School Years. Available online: https://www.educacionfpydeportes.gob.es/servicios-al-ciudadano/estadisticas/no-universitaria/alumnado/matriculado.html (accessed on 1 January 2024).
- Total Expenditure (€) per Student in Middel School from 2011–2012 to 2020–2021. Available online: https://www.educacionfpydeportes.gob.es/servicios-al-ciudadano/estadisticas/economicas/gasto.html (accessed on 1 January 2024).
- Number of Teachers at the Middle School from 2011–2012 to 2020–2021 School Years. Available online: https://www.educacionfpydeportes.gob.es/servicios-al-ciudadano/estadisticas/no-universitaria/profesorado/estadistica.html (accessed on 1 January 2024).
- Number of Repeating Students in Middle School from 2021-2012 to 2020-2021. Available online: https://estadisticas.educacion.gob.es/EducaJaxiPx/Tabla.htm?path=/no-universitaria/alumnado/matriculado/2020-2021-rd/gen-eso/l0/&file=eso_04.px&L=0 (accessed on 1 January 2024).
- Considine, G.; Zappalà, G. The influence of social and economic disadvantage in the academic performance of school students in Australia. J. Sociol. 2002, 38, 129–148. [Google Scholar] [CrossRef]
- Wallerstein, J. Children of Divorce: Stress and Developmental Task; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Niemeyer, T.D.; Torres, M.I.V. Percepción materna del ajuste socioemocional de sus hijos preescolares: Estudio descriptivo y comparativo de familias separadas e intactas con alto y bajo nivel de ajuste marital. Revista de Psicología 2000, 9, 29–44. [Google Scholar] [CrossRef][Green Version]
- Ram, B.; Feng, H. Changes in family structure and child outcomes: Roles of economic and familiar resources. Policy Stud. J. 2003, 31, 309–330. [Google Scholar] [CrossRef]
- White, L.; Rogers, S.J. Economic circumstances and family outcomes: A review of the 1990s. J. Marriage Fam. 2000, 62, 1035–1051. [Google Scholar] [CrossRef]
- Evolution of the Consumer Price Index (CPI) by Month and State. Available online: https://www.ine.es/jaxiT3/Tabla.htm?t=50918 (accessed on 1 January 2024).
- The Number of Single-Parent and Two-Parent Households by Year and State. Available online: https://www.ine.es/jaxi/Tabla.htm?path=/t20/p274/serie/prov/p02/l0/&file=02001.px&L=0 (accessed on 1 January 2024).
- The Number and Amount of Mortgages Signed per Month and State. Available online: https://www.ine.es/jaxiT3/Tabla.htm?t=3200&L=0 (accessed on 1 January 2024).
- Data for Calculating the % of Students who Promote to the Next Grade at Middel School with All Subjects Passed for the 2021–2022 School Year. Available online: https://estadisticas.educacion.gob.es/EducaJaxiPx/Tabla.htm?path=/no-universitaria/alumnado/resultados/2021-2022-rd/reggen/l0/&file=reggen_3_03.px (accessed on 1 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).