Parallel Ant Colony Algorithm for Sunway Many-Core Processors

Abstract

Ant colony optimization (ACO) has garnered significant attention because of its wide application in route planning problems. Nevertheless, ACO requires a long time to calculate when tackling complex issues. Parallelization emerges as an effective strategy to improve algorithm execution efficiency, and especially in large-scale computations, parallelization technology can significantly reduce execution time. In this study, we propose an ant colony algorithm (Sunway ant colony optimization, SWACO) based on a second-level parallel strategy and tailored to the hardware characteristics of Sunway many-core processors. The first level involves process-level parallelism, in which the initial ant colony is divided into multiple child ant colonies according to the number of processors, with each child ant colony independently performing computations on each island. The second level is thread-level parallelism, utilizing the computing power of the slave core to accelerate path selection and pheromone updates of the ants, thereby effectively improving algorithm execution efficiency. The experimental results demonstrate that, across multiple TSP datasets, the SWACO algorithm significantly reduces computation time, achieving an overall speedup ratio by 3–6 times, and maintains the gap within 5%. A substantial acceleration effect was achieved.

1. Introduction

The ant colony algorithm, inspired by natural foraging behavior, is an excellent strategy for solving optimization problems [1]. DORIGO et al. [2] proposed that the ant colony algorithm simulates the foraging behavior of ants, finding the optimal solution through the dissemination and updating of pheromones. This design makes it particularly suitable for combinatorial optimization problems, such as route planning and the Traveling Salesman Problem (TSP). Compared with other algorithms, ACO exhibits inherent advantages in solving the TSP, due to its unique group collaboration strategy and positive feedback mechanism [3]: it simulates collective behavior to gradually approach the optimal path, demonstrating strong global search capability. During the search process, ants utilize local information and dynamic feedback from global pheromone trails to effectively avoid local optima, continuously approaching the global optimum. Additionally, ACO features distributed computation and good robustness, enabling it to adapt to complex and large-scale problem-solving. However, because the movement of ants is random, once the population size reaches a certain level, it can take a long time for the ant colony algorithm to find a better solution. This is particularly evident in complex or large-scale problems, in which the local search efficiency of the algorithm is low, leading to prolonged computation times and a failure to converge to the global optimal solution within a reasonable timeframe. Therefore, accelerating the convergence process of the algorithm and improving its efficiency in solving large-scale problems have become important research directions.

To address these challenges, researchers have proposed various optimization strategies, such as improving the pheromone update mechanism and adopting an adaptive adjustment strategies. For example, Ronghua Meng [4] proposed an improved smoothing ant colony optimization algorithm. Yu et al. [5] introduced a dual ant colony optimization algorithm that incorporates dynamic differentiation and neighborhood induction mechanisms. Wu Qinghong et al. [6] proposed applying mutation mechanisms to the ant colony algorithm to improve its convergence rate. Wang Ying et al. [7] proposed an adaptive adjustment of parameters to address the challenge of obtaining the global optimum. Additionally, Li et al. [8] utilized the feature that the ant colony algorithm can be easily combined with other methods. By integrating it with the particle swarm algorithm, it improves the pheromone update strategy and achieves performance enhancement.

However, as the complexity of the problem to be solved increases, the dimension of individual solutions grows, and the search space of feasible solutions expands exponentially. To ensure that either the optimal solution or a better solution for the specific problem can be obtained, the population size and the number of iterations are typically set larger, resulting in increased time consumption for the algorithm. Under such circumstances, accelerating the solution speed of the ant colony algorithm has become a new research hotspot.

With the rapid development of parallel computers, their application alongside corresponding parallel frameworks provides practical solutions for large-scale problems and has gradually become a research focus for scholars worldwide. For instance, Gao et al. [9] proposed a GPU-based parallel ACO algorithm. Zeng et al. [10] introduced a fast CUDA-based fully parallel ant colony optimization algorithm for the TSP, achieving promising results. Huang Zhenhua et al. [11] aimed to address the drawback of long running times in large-scale and multi-iteration problems of the max–min ant colony algorithm. Based on a parallel strategy, they implemented MMAS concurrency on a CPU-GPU cooperative heterogeneous computing environment platform. Zhang Ying et al. [12] studied an ant colony algorithm based on the Spark framework to address the capacity constraint in the Vehicle Routing Problem (VRP). Baydogmus et al. [13] explored an improved method for solving the TSP/mTSP by combining parallel clustering with an elite ant colony algorithm. By introducing clustering and elite strategies, the global search capability of the algorithm was further enhanced, improving both solution quality and solving speed. Le et al. [14] applied a parallel Max–Min Ant System algorithm to optimize the bidder selection problem in multi-round procurement for software project management, thereby improving resource utilization and project management efficiency via optimized bidder selection.

Although progress has been made in the ant colony algorithm using parallel computing frameworks such as GPU parallelism and CUDA, practical application scenarios remain limited due to the constraints of data dimensionality during parallel implementation. In various contexts, such as path planning [15], optimization problems like clustering are widespread [16]. In recent years, numerous efficient methods have emerged in the field of evolutionary algorithms. For example, Differential Evolution (DE) has shown excellent performance in continuous space optimization. However, the mutation and crossover operations of DE require redesigned encoding schemes when applied to discrete combinatorial optimization problems such as the TSP, and its population diversity tends to decline in high-dimensional spaces. In contrast, through a self-learning strategy, the ant colony algorithm can use part of the information for reasoning, making it suitable for solving complex optimization problems. Due to the strong data independence among individuals in the ant colony algorithm and its inherent parallelism, it is well-suited for implementation on a massively parallel platform. Unlike traditional homogeneous CPU/GPU systems, the Sunway 26010 many-core processor, with its unique heterogeneous architecture and supporting software environment, provides strong support for the parallel acceleration of ant colony algorithms. Its hierarchical MPE-CPE structure, local memory equipped on each CPE, and efficient DMA mechanism not only meet the frequent data access and computation-intensive characteristics of ant colony algorithms during iterations but also significantly reduce communication overhead and latency. Therefore, this work leverages the Sunway many-core processor to investigate the heterogeneous parallelism of the ant colony algorithm within the Sunway many-core architecture, combining the algorithm characteristics with those of the processor architecture to propose a parallelizing algorithm based on the Sunway processor, referred to as the ant colony algorithm (SWACO). Building on this platform, this work designs a second-level parallelization of the typical ant colony algorithm, combining the MPI [17] and Athread [18] (the SW26010 dedicated accelerated thread library), which is implemented in two programming models. The main contributions of this work can be summarized as follows:

• This paper proposes a secondary parallel ant colony algorithm based on the Sunway many-core processors. In consideration of the hardware characteristics of the Sunway many-core processors, an ant colony algorithm (SWACO) with a two-level parallel strategy combining process-level and thread-level parallelism is designed.
• The island model is proposed for process-level parallelism. In process-level parallelism, the initial ant colony is divided into multiple sub-colonies using the island model. Each sub-colony independently executes on different computing units, effectively distributing the computational tasks and improving the parallel efficiency of the algorithm.
• By solving the Traveling Salesman Problem (TSP), a comparative experiment was conducted between serial ACO and parallel ACO. The results show that SWACO achieved a maximum speedup of 5.72 times, while keeping the gap under 5%.

The structure of the rest of this paper is as follows. Section 2 introduces the background of the SW26010 processor and the ACO algorithm. Section 3 details the implementation of SWACO. Section 4 presents the experimental evaluation results. Section 5 concludes the paper.

2. Related Work

2.1. Sunway 26010 Processor

“Sunway TaihuLight” is China’s first supercomputer that completely uses domestic processors, which won first place in the top 500 supercomputers four times between 2016 and 2017 [19]. Its core component, the SW26010 processor, adopts a heterogeneous many-core architecture. Each processor has 260 cores and is divided into four core groups. The core groups are interconnected through a network-on-chip (NOC) and integrate a system interface (SI) bus, which connects to standard PCIe interfaces for direct connection and interconnection between chips [20,21]. Each core group comprises a management processing element (MPE), a memory controller unit (MC), 8 GB of memory, and 64 computation processing element cores (computing processing elements, CPEs) arranged in an 8 × 8 array. The MPE is primarily responsible for task management and scheduling, whereas the CPEs perform intensive computing tasks [22]. Each SW26010 processor is equipped with 32 GB of memory, with each core group containing 8 GB of memory [23]. Each slave core has 64 KB of local data memory (LDM) [24] that functions as a user-controlled cache. The slave core can be executed by the global load/store instructions (gld/gst) [25] and use direct memory access (DMA) to access the main memory [26]. This special design improves performance but also poses programming challenges. Effectively dividing tasks and data to fully utilize the computational efficiency of slave cores is the key to improving performance.

2.2. ACO Algorithm

ACO is a probabilistic path optimization algorithm inspired by the collective behavior of ants, which transfer information via pheromones to find the shortest path. Ants in ant colonies transfer information by releasing pheromones and tend to follow paths with relatively high pheromone concentrations. Each ant then strengthens the pheromones on these paths when passing by, forming a positive feedback mechanism. Eventually, the entire ant colony converges on the shortest path. The algorithm is characterized by distributed computation, positive feedback, and heuristic search, making it a heuristic method for global optimization [27].

The state transition probability and pheromone update formulas of the ant colony algorithm are shown in the following:

a. Path selection probability formula

In the ant colony algorithm, the probability that ant k moves from city i to city j is expressed in the following formula:

$$p_{ij}^k=\left\{\begin{array}{cc}{\displaystyle \frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }\times {\left[{\mu }_{ij}\left(t\right)\right]}^{\beta }}{{\displaystyle \sum _{j\in {\mathrm{allow}}_k}}{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }\times {\left[{\mu }_{ij}\left(t\right)\right]}^{\beta }}}\hfill & j\in {\mathrm{allow}}_k\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

where ${\tau }_{ij}\left(t\right)$ represents the pheromone concentration on path i to j during time t, and ${\mu }_{ij}\left(t\right)={\displaystyle \frac{1}{d_{ij}}}$ represents the visibility from city i to city j, that is, the reciprocal of the distance. $\alpha$ is a pheromone-inspired factor, $\beta$ is the expectation heuristic factor, and ${\mathrm{allow}}_k$ is the set of cities that ant k has not yet visited.

b. Visibility formula

Visibility ${\mu }_{ij}$ is defined as the reciprocal of the distance between city i and city j as follows:

$${\mu }_{ij}={\displaystyle \frac{1}{d_{ij}}}j\in {\mathrm{allow}}_k$$

(2)

$d_{ij}\left(t\right)$ is the Euclidean distance from city i to city j and can be expressed as follows:

$$d_{ij}\left(t\right)=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}$$

(3)

where $(x_i,y_i)$ and $(x_j,y_j)$ are the coordinates of city i and city j, respectively.

c. Pheromone update formula

The pheromone is updated via the following formula after each iteration:

$${\tau }_{ij}(t+1)=(1-\rho )\times {\tau }_{ij}\left(t\right)+\Delta {\tau }_{ij}\left(t\right)$$

(4)

where $\rho$ is the pheromone volatilization coefficient, and $\Delta {\tau }_{ij}\left(t\right)$ is the amount of pheromone increased by ants on the path, which is defined as follows:

$$\Delta {\tau }_{ij}\left(t\right)=\sum _{k=1}^m\Delta {\tau }_{ij}^k\left(t\right)$$

(5)

where $\Delta {\tau }_{ij}^k\left(t\right)$ is the contribution of the k-th ant on path i to j, expressed as follows:

$$\Delta {\tau }_{ij}^k\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{Q}{l_k}}\hfill & \mathrm{if}\mathrm{the}\mathrm{ant}k\mathrm{walks}\mathrm{the}\mathrm{path}(i,j)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

where Q is a constant that represents the amount of pheromone released by each ant, and $l_k$ is the path length of ant k.

3. Design and Implementation of the Parallel ACO Algorithm

The distinctive master–slave core architecture of the Sunway many-core processor provides an ideal platform to implement highly parallelized algorithms. Therefore, this study designs a second-level parallel model based on the physical architecture of the Sunway processor. The first level is process-level parallelism, which implements parallelism between the main cores and employs the MPI for interprocess communication and task allocation.

The second level pertains to thread-level parallelism. The accelerated thread library (Athread library) of the Sunway processor is a program acceleration library designed for the two-level parallel programming model (master–slave accelerated programming model) to enhance user convenience and speed. It flexibly controls and schedules the threads within the core group to improve the acceleration performance of the concurrent execution across multiple cores in the core group. The parallelism among the slave cores is achieved through the unique thread library of the Sunway processor, which fully leverages the acceleration capabilities of the slave cores and enables the hybrid parallelism of the ant colony algorithm. The secondary parallel master core and the slave core use the MPI+Athread hybrid programming model.

Figure 1 illustrates the mapping scheme of the ant colony algorithm on the SW26010 processor utilizing the island master–slave mode, where p1, p2, p3, and p4 denote the four subpopulations. Each subpopulation is an island, and the islands evolve in parallel according to the coarse-grained model. Each subpopulation is divided into n groups according to the number of slave cores allocated, except for the last one. Each group, except for the last, contains the same number of individuals, and the number of groups n does not exceed N (where N is the number of slave cores in each core group, which is 64). The individuals in each group are calculated in parallel according to the master–slave model. The initialization and selection of the optimal solution are executed in the master core, whereas the path calculation and pheromone updates are performed in the slave cores. Each subpopulation in the ant colony algorithm is mapped to the master core of the core group, and the individuals in the subpopulation are mapped to the slave cores of the core group. The parallelism between core groups is executed in coarse-grained mode, whereas the master–slave mode is used within the core group. This arrangement achieves two-level parallelism between groups and within a population to enhance the convergence speed and solution quality of the algorithm.

3.1. Level-1 Parallel Mode

Within one-level parallelism mode, the main core executes parallel tasks, whereas the MPI facilitates interprocess communication. A master core-based parallel ACO (parallel ant colony optimization, PACO) was designed as shown in Algorithm 1. Each MPI process controls a subset of ant colonies, with the number of ants typically evenly distributed among each processing core. Each process runs independently and executes its own ant colony search task in parallel, periodically exchanging pheromone information through MPI communication to prevent any single process from becoming trapped in a local optimal solution. Specifically, each process maintains an independent pheromone matrix. After each iteration, each process sends the locally discovered optimal solution to the main process, which then broadcasts the optimal solution after comparison to guide the update of the global pheromones. Figure 2 illustrates the specific execution workflow of PACO.

Algorithm 1 One level of parallelism is shown below

1: # Initialize the MPI environment   2: MPI_Init (&argc, &argv)   3: # Obtain the total number of processes and the current process ID   4: MPI_Comm_size (MPI_COMM_WORLD, &procs)   5: MPI_Comm_rank (MPI_COMM_WORLD, &rank)   6: # Record the start time   7: start_time = MPI_Wtime()   8: if rank == 0: then           ▹ Main process operations   9:     ACO_Load_cities(argv[1])           ▹ Load city data 10:     # Broadcast city data to all processes 11:     MPI_Bcast (city, NUM_CITIES, MPI_CITY, 0, MPI_COMM_WORLD) 12:     # Establish city connection and initialize ant state 13:     ACO_Link_cities() 14:     ACO_Reset_ants() 15: end if 16: # Perform multiple communication cycles 17: for i in range (NUM_COMMS) do 18:     # Multiple tours, each ant moves on the graph 19:     for j in range (NUM_TOURS * NUM_CITIES) do 20:         ACO_Step_ants() # Ants move forward 21:         if j % NUM_CITIES == 0 and j!= 0 then 22:            ACO_Update_pheromone() # Update pheromone 23:            ACO_Update_best() # Update the best path 24:            ACO_Reset_ants() # Reset the state of ants 25:         end if 26:     end for 27: end for 28: #Collect the best path to the main process 29: MPI_Gather(&best, 1, MPI_BEST, all_best, 1, MPI_BEST, 0, MPI_COMM_WORLD) 30: if rank == 0: # The main process chooses the global optimal path then 31:     best = find_global_best_path (all_best) 32:     #Record the end time 33:     end_time = MPI_Wtime() 34: end if 35: if rank == 0 then           ▹ The main process prints the final result 36:     # End the MPI environment 37:     MPI_Finalize() 38: end if

3.2. Second-Stage Parallel Mode

Within the secondary parallel mode, the Sunway many-core processors adopt the island master–slave mode, which relies on the cooperation between the master core and the slave cores to execute computational tasks. Under this paradigm, the ant colony is partitioned into several subpopulations, with each subpopulation corresponding to an “island”, where the master–slave acceleration parallel mode paradigm is applied. In this structure, the master core is responsible for processing the portion of the task that cannot be executed in parallel by the slave cores, including control and communication operations, whereas the slave cores perform specific computational tasks. While a slave core is executing the computational task, the master core remains in a waiting state, as shown in Figure 3.

The core concept entails partitioning the ant colony into four smaller ant colonies on the SW26010 processor and then distributing these colonies to four core groups for parallel processing. Within each core group, the slave cores compare their respective computation results, select the optimal solution, and send it to the master core. The master core collects the optimal solutions from all four core groups, determines the best solution among them, and broadcasts this solution to all the core groups. Each core group subsequently updates its pheromone matrix on the basis of the received optimal solution and the pheromones from the previous generation. Using these methods, the parallel Sunway ant colony optimization (SWACO) algorithm based on the Sunway processor was designed, as shown in Algorithm 2. Figure 4 illustrates the specific execution process.

Algorithm 2 Second level of parallelism is as follows

1: # Initialize the MPI and Athread environments   2: MPI_Init (&argc, &argv)   3: athread_init()   4: # Obtain the total number of processes and the current process ID   5: MPI_Comm_size (MPI_COMM_WORLD, &procs)   6: MPI_Comm_rank (MPI_COMM_WORLD, &rank)   7: # Record the start time   8: start_time = MPI_Wtime()   9: if rank == 0 then           ▹ Main process operations 10:       ACO_Load_cities(argv[1]) # Load city data 11:       # Broadcast city data to all processes 12:       MPI_Bcast (city, NUM_CITIES * NUM_CITIES, MPI_INT, 0, MPI_COMM_WORLD) 13:       # Establish city connection and initialize ant state 14:       ACO_Link_cities() 15:       ACO_Reset_ants() 16: end if 17: # Perform multiple communication cycles 18: for i in range (NUM_COMMS) do 19:       # Schedule the slave cores for ant mobile computing 20:       athread_spawn (Slave_Step_ants, NULL) 21:       athread_join() 22:       # Collect path information calculated from the core 23:       MPI_Gather(&local_best_path, 1, MPI_PATH, all_paths, 1, MPI_PATH, 0, MPI_COMM_WORLD) 24:       # The main process updates the optimal path 25:       best = ACO_Update_best (all_paths) 26:       MPI_Bcast(&best, 1, MPI_BEST, 0, MPI_COMM_WORLD) # Synchronize best path information 27:       if i % NUM_CITIES == 0 then 28:             # Determine whether to update the pheromone 29:             # Call to update pheromone from nucleus 30:             athread_spawn (Slave_Update_pheromone, NULL) 31:             athread_join() 32:       end if 33: end for 34: # Record the end time 35: end_time = MPI_Wtime() 36: # The main process prints the final result 37: # Clean up and end the environment 38: athread_halt() 39: MPI_Finalize()

4. Experiment and Analysis

4.1. Experimental Parameters

In this work, the TSP instance from the public calculation example TSPLIB was employed to conduct experiments. The experimental environment comprises an SW26010 processor with 3.4 GB of MPES memory and 28.0 GB of CEPS memory. Each processor incorporates four core groups, with each core group containing 1 MPE+64 CPEs for experimental analysis. During the process, the importance of pheromones was set to 1, the importance of heuristic factors was set to 5, the evaporation coefficient of pheromones was set to 0.1, and the coefficient of pheromone increase intensity was set to 100. These values were fine-tuned based on the relevant literature [28] and validated through experiments.

Table 1. Experimental parameters.

Module	Parameters
MPE	2 GHz, 64-KB L1 D-cache, 512-KB L2 cache
CPE	2 GHz, 128 KB
CG	1 MPE + 64 CPEs

lists the details of the experimental environments used.

4.2. Performance Test of the Serial Ant Colony Algorithm

In this section, the ACO algorithm is tested on the SW26010 processor using the Eli76, Bier127, Ts225, Pr226, and Pr439 datasets. The number of ant colonies was set equal to the number of cities. Each test was conducted over 100 iterations, with all results derived from 10 independent executions. In all tables of the experimental results, the optimal solution, average solution, average time length, and gap are expressed as Best, Avg, Avg Time, and Gap, respectively. The gap is calculated using the formula (Avg-Hbest)/Hbest, where Hbest represents the optimal solution for the corresponding dataset. The results are shown in

Table 2. Running results of the serial ACO.

Dataset	Hbest	Best	Avg	AvgTime (s)	Gap (%)
Eli76	538	566	577	7.42	7.40
Bier127	118,282	125,945	126,994	47.42	7.36
Ts225	126,643	131,748	132,367	397.78	4.03
Pr226	80,369	86,040	87,199	403.25	8.49
Pr439	107,217	122,536	123,367	5089.03	15.06

.

Table 2 shows that as the size of the dataset increases, the running time increases significantly. The Eli76 dataset required the least amount of time at 7.42 s, whereas the largest Pr439 dataset required as much as 5089.03 s. As the size of the dataset increased, the gap also increased. Particularly for large datasets, the ACO algorithm encounters the following problems: Due to limited computing resources, ACO cannot perform enough iterations on large-scale datasets, resulting in an incomplete exploration of the solution search space. In addition, the positive feedback mechanism of pheromones makes the algorithm more prone to getting stuck in local optimal solutions, which further exacerbates the increase in the gap. For instance, the gap of the Ts225 dataset was low, whereas the larger Pr439 dataset exhibited a significant increase in gap to 15.06%, indicating that the ACO algorithm faces greater optimization challenges on large-scale datasets. Therefore, parallel processing was employed to address these challenges.

4.3. Performance Testing of the PACO Algorithm

In this section, the PACO algorithm is tested on the four main cores of the SW26010 processor using the Eli76, Bier127, Ts225, Pr226, and Pr439 datasets. The number of ant colonies was configured to match the number of cities. Each test was performed for 100 iterations. All test results were based on 10 independent runs.

Table 3. PACO runs the results on small-scale datasets.

Dataset	Hbest	Best	Avg	AvgTime (s)	Gap (%)
Eli76	538	540	551	2.32	2.42
Bier127	118,282	119,845	122,764	14.82	3.79
Ts225	126,643	130,148	131,552	124.31	3.88
Pr226	80,369	84,981	86,148	126.02	7.19
Pr439	107,217	115,304	116,127	1562.14	8.31

lists the running results.

According to the comparison of the data in Table 2 and Table 3, when the amount of data is small, the serial ACO and PACO do not significantly differ. As dataset size increases, PACO demonstrates significant advantages over serial ACO in terms of execution time, solution quality, and gap. The solution quality also approaches the historical optimal solution (Hbest). For all datasets, PACO outperforms serial ACO, with the maximum speedup ratio reaching 3.26 and the accuracy rate increasing by a maximum of 6.75%. This not only greatly improves computational efficiency but also effectively improves the accuracy of understanding. In summary, PACO fully leverages parallel computing to significantly optimize the overall performance of the algorithm when processing large-scale datasets.

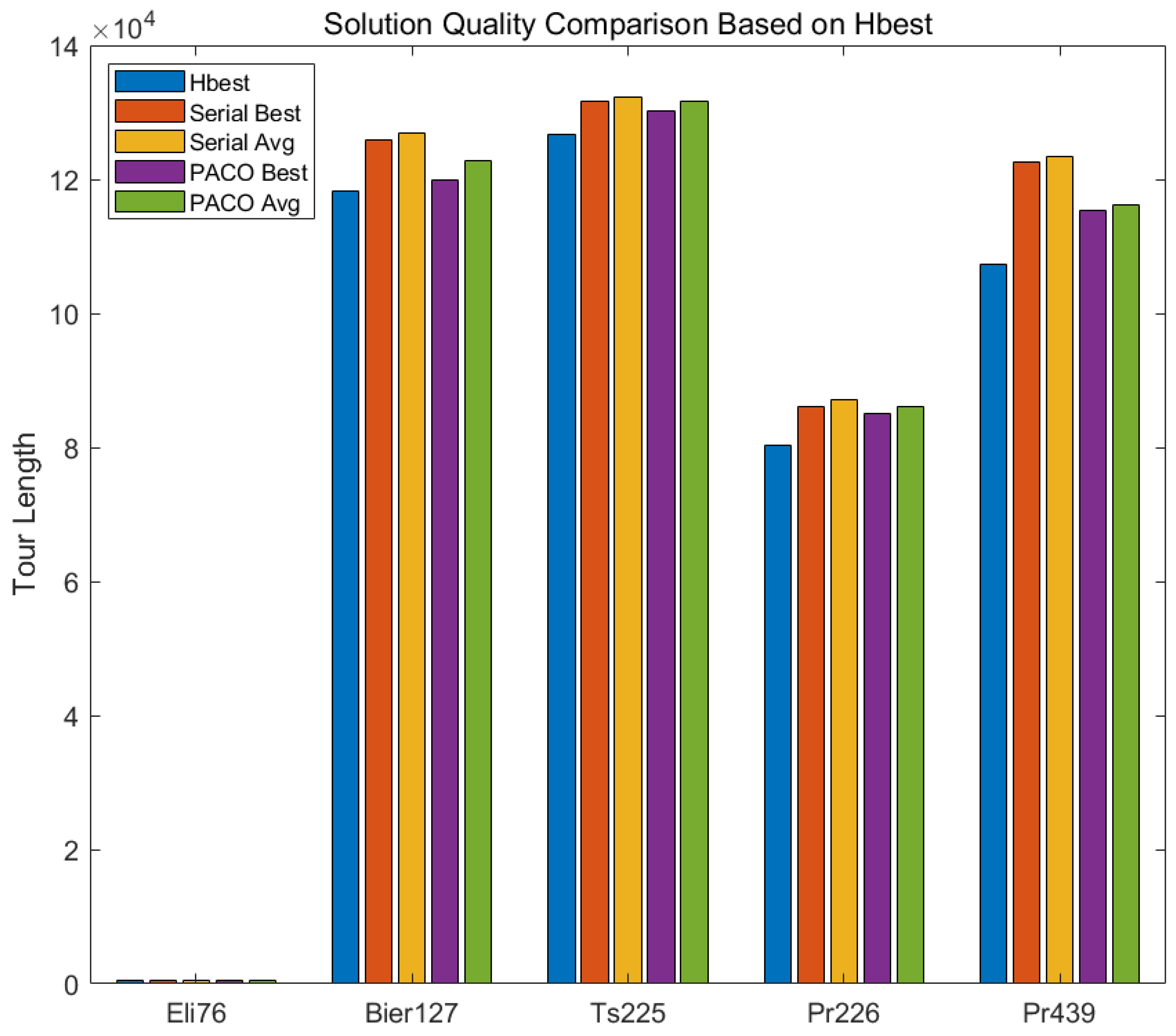
Figure 5 presents a comparison of solution quality between the serial ant colony algorithm (ACO) and the parallel ant colony optimization (PACO) across five TSP datasets: Eli76, Bier127, Ts225, Pr226, and Pr439. The blue bars represent the theoretical optimal solutions (Hbest) and serve as reference benchmarks. The orange and yellow bars correspond to the best and average solutions obtained by the serial ACO, while the purple and green bars represent the best and average solutions achieved by PACO. As shown in the figure, for the small-scale dataset Eli76, both algorithms yield solutions close to Hbest. However, as the problem scale increases—such as in the Bier127 and Ts225 datasets—the best and average solutions from the serial ACO begin to deviate from Hbest, indicating a decline in its search performance. In contrast, PACO maintains smaller deviations and more stable solutions for these medium-sized problems.The difference becomes even more pronounced in the larger datasets Pr226 and Pr439. The serial ACO shows significantly higher deviation from Hbest, while PACO consistently produces solutions that are much closer to the theoretical optimum. Especially in large-scale scenarios, PACO not only improves solution quality but also significantly reduces computation time.

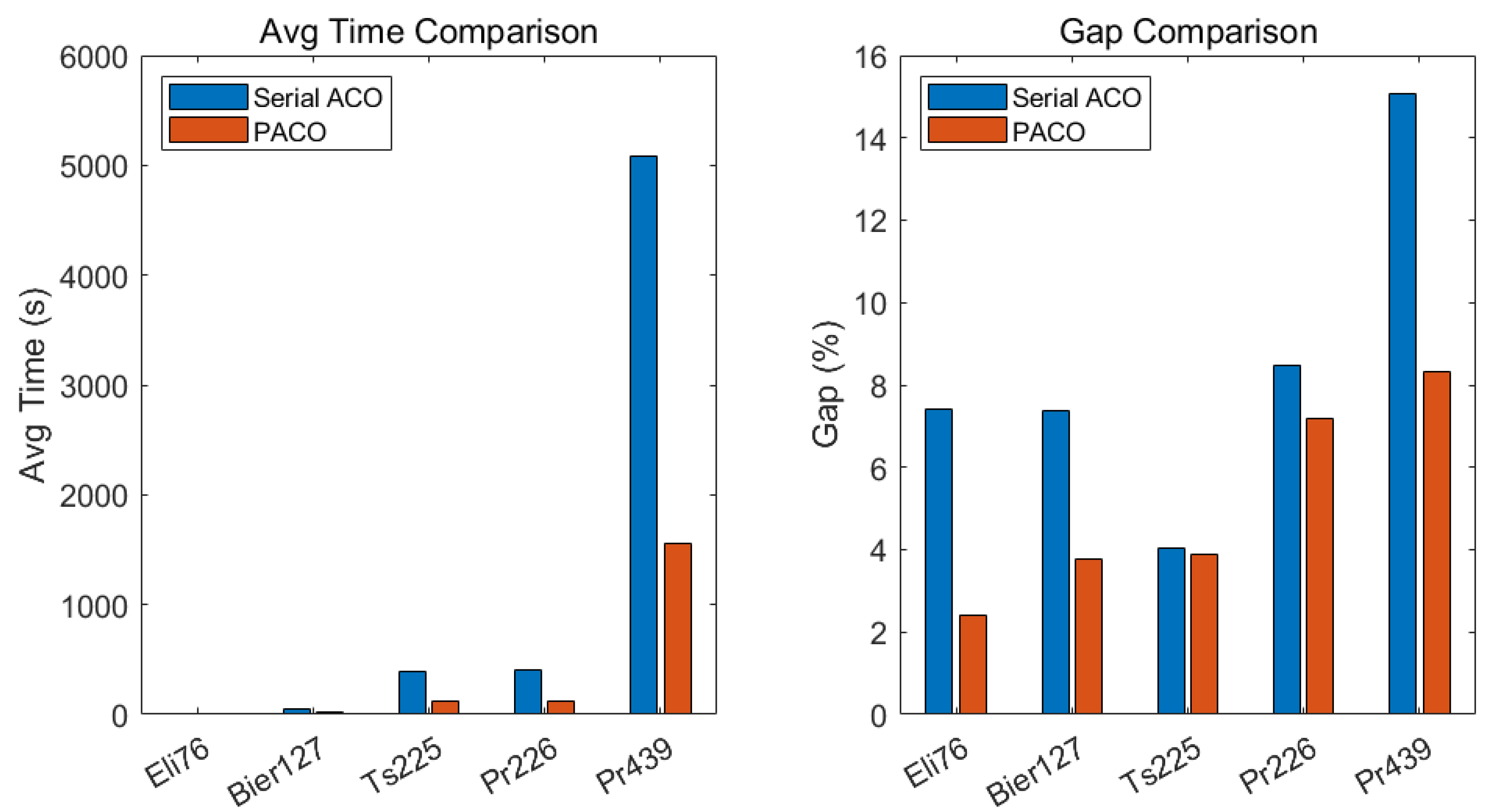
Figure 6 shows a comparison of the average time and gap between ACO and PACO under identical experimental conditions. Compared with the serial ant colony algorithm, the ACO algorithm using MPI parallelism exhibited a more significant trend in running time, and the quality of the solution was higher. The running time is significantly reduced on large-scale datasets, with an average increase of approximately 3 times. In addition, the solution quality is improved, and the gap is significantly reduced. Particularly on larger datasets, such as Pr439, PACO demonstrated a stronger advantage.

In addition, tests were conducted on the Pr439, Pr1002, Pla7397, Fnl4461, Brd14051, D18512, Pla33810, and Pla85900 large-scale datasets, which produced favorable outcomes.

Table 4. PACO runs the results on large-scale datasets.

Dataset	Hbest	Best	Avg	AvgTime (s)	Gap (%)
Pr1002	259,045	270,702	278,934	31.72	7.68
Pla7397	23,260,728	24,307,460	24,873,241	636.19	6.93
Brd14051	469,385	490,507	540,523	1665.56	15.16
Fnl4461	182,566	190,781	206,789	1738.99	13.27
D18512	645,238	674,274	733,000	2518.72	13.60
Pla33810	66,048,945	69,021,148	73,500,234	6216.81	11.28
Pla85900	142,382,641	148,789,860	157,832,450	25,176.51	10.85

lists the run results of these tests.

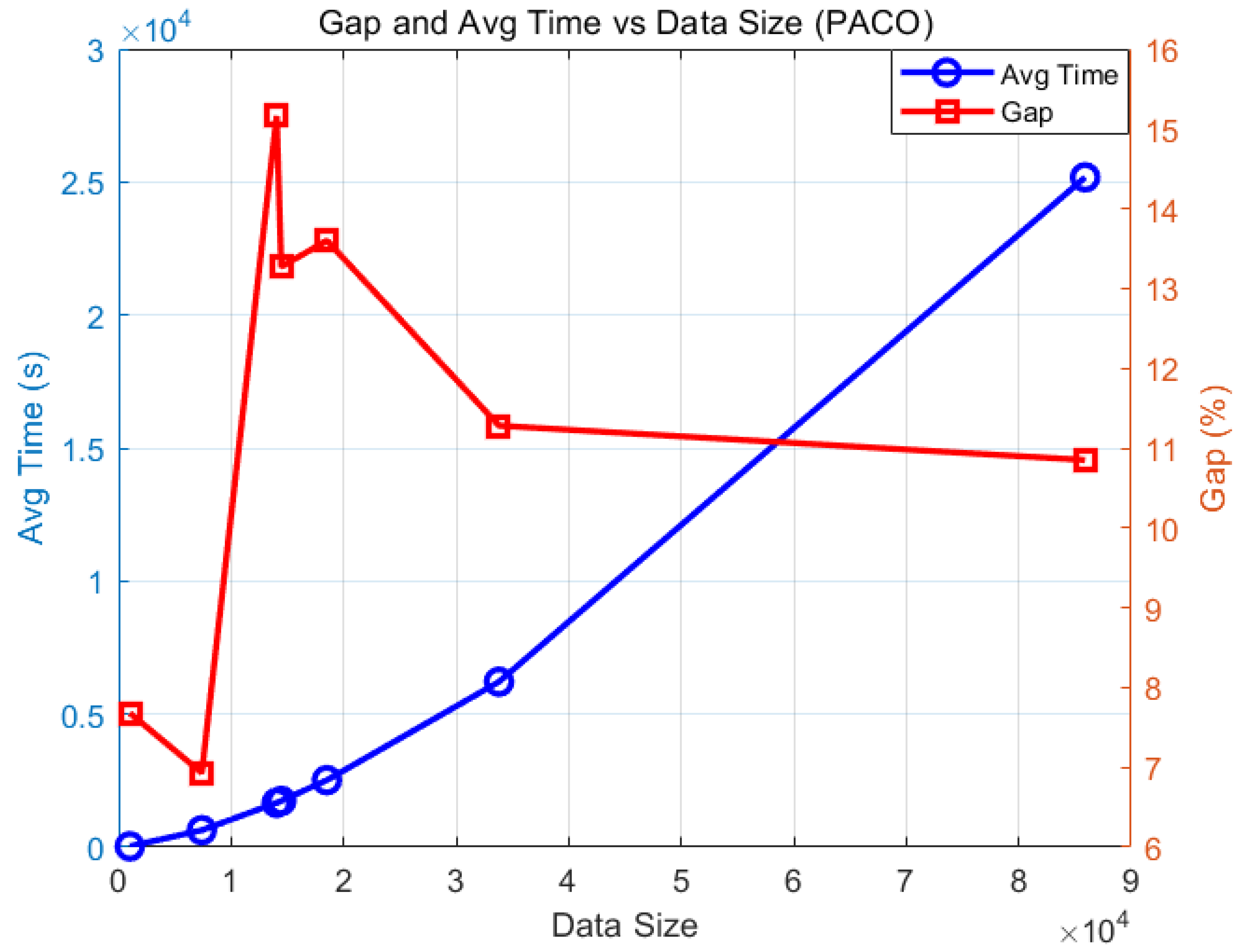
Table 4 shows that as the amount of data increases, the quality of the PACO algorithm’s solution significantly decreases, whereas the running time gradually increases. For the very large-scale datasets, Pla7397, D18512, Pla33810, and Pla85900, the gap between the solution quality of the PACO algorithm and the historical optimal solution (the difference between Avg and Hbest) became more pronounced. For large-scale datasets, such as Pla33810 and Pla85900, the running time of the PACO algorithm approaches two hours or even longer. In particular, for the Brd14051 and Fnl4461 datasets, the gap reached 15.16% and 13.27%, respectively.

As shown in Figure 7, as the amount of data increases, the gap of PACO exhibits a fluctuating trend. The gap showed an upward trend when the dataset size was small, then decreased after reaching a certain size; however, it always remained above 10% and exhibited large fluctuations. This is particularly evident in the Brd14051 dataset, where the gap reaches 15.16%. Due to the ultra-large scale and asymmetric structure of the dataset, the stability of the algorithm’s performance is affected, resulting in a sharp increase in the solution gap and noticeable fluctuations. In contrast, the gaps in the Pr1002 and Pla7397 datasets are relatively low, at 7.68% and 6.93%, respectively, indicating better stability of the algorithm on medium-scale symmetric problems. For the Fnl4461 and D18512 datasets, the gap rises to around 13%, reflecting a decline in solution quality as the problem scale increases. However, in the ultra-large-scale symmetric datasets Pla33810 and Pla85900, the gap drops back to around 11%, suggesting that PACO still maintains a certain level of robustness in large-scale problems with regular structure.

Overall, as the dataset size increases, the PACO algorithm faces growing challenges in maintaining high solution quality, especially in large-scale or asymmetric instances where performance tends to fluctuate more significantly. Concurrently, the running time significantly increases with larger dataset sizes, and the general trend is positively correlated with the amount of data. For instance, when the dataset increased from 1002 to 7397, the running time increased by approximately 1905.64%, and when the dataset increased from 7397 to 14,051, the running time increased by approximately 161.80%. Although the increase was only 4.41% for some medium-sized datasets (such as 14,051–14,461), the running time increased significantly again for larger-scale datasets (such as 33,810–855,900), with an increase of approximately 304.97%.

These findings demonstrate that pure MPI parallelism can no longer effectively solve the dual problems of computational efficiency and solution quality. The scalability of the PACO algorithm is limited when handling large-scale problems. To enhance its performance on large-scale datasets, this work introduces a hybrid parallelism mode aimed at optimizing algorithm efficiency and solution quality, thereby improving its capacity to address the challenges posed by large-scale data.

4.4. Performance Testing of the SWACO Algorithm

In this section, the performance test of the SWACO algorithm on the four cores of the SW26010 processor is compared with that of the previous PACO algorithm. The test datasets used include Pr1002, Pla7397, Fnl4461, Brd14051, D18512, Pla33810, and Pla85900, which further evaluate the performance of the algorithm on large-scale problems.

Table 5. Results of SWACO operation.

Dataset	Hbest	Best	Avg	AvgTime (s)	Gap (%)
Pr1002	259,045	26,8420	269,895	27.42	4.19
Pla7397	23,260,728	23,975,600	24,098,012	111.50	3.60
Brd14051	469,385	482,301	484,530	291.90	3.22
Fnl4461	182,566	189,032	190,014	304.77	4.08
D18512	645,238	663,640	667,121	441.43	3.39
Pla33810	66,048,945	67,543,212	67,901,234	1089.54	2.80
Pla85900	142,382,641	145,983,210	147,401,032	4412.32	3.52

lists the run results.

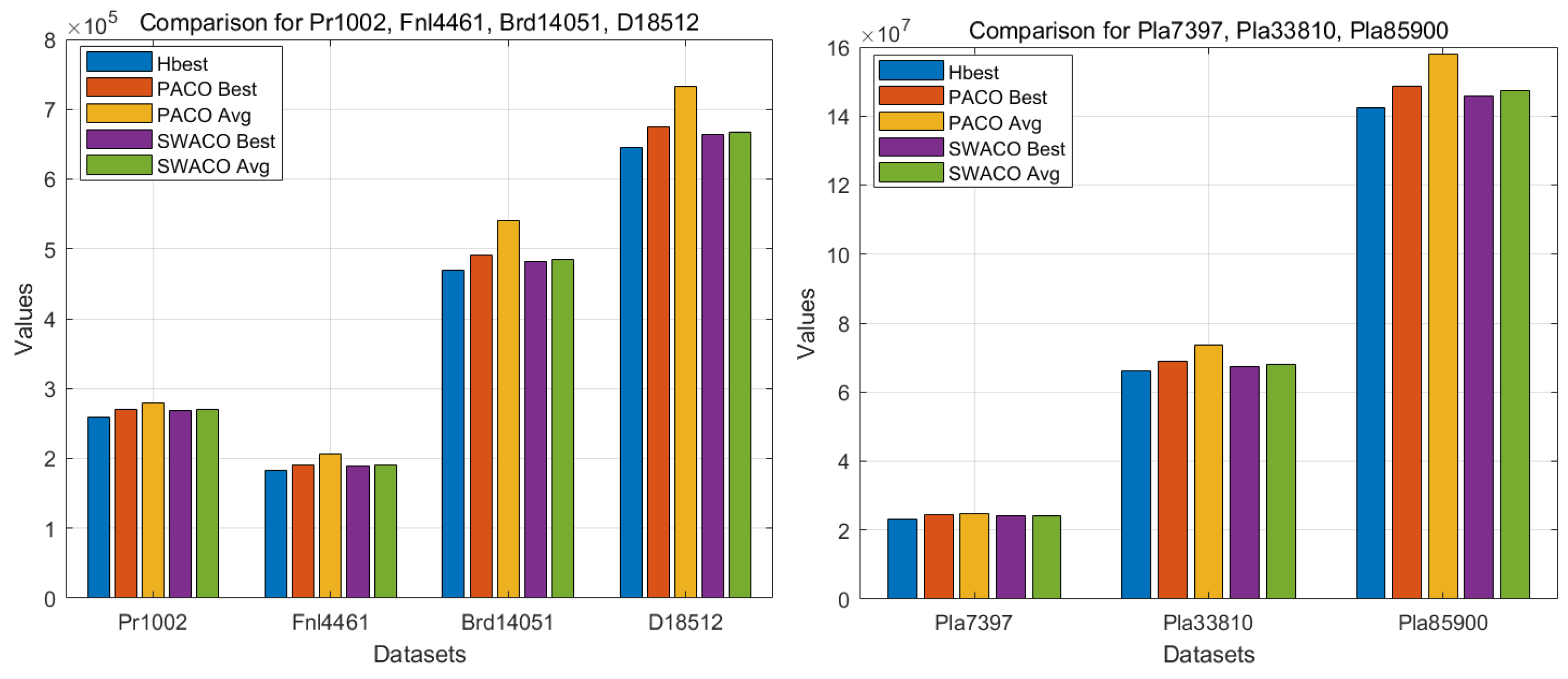
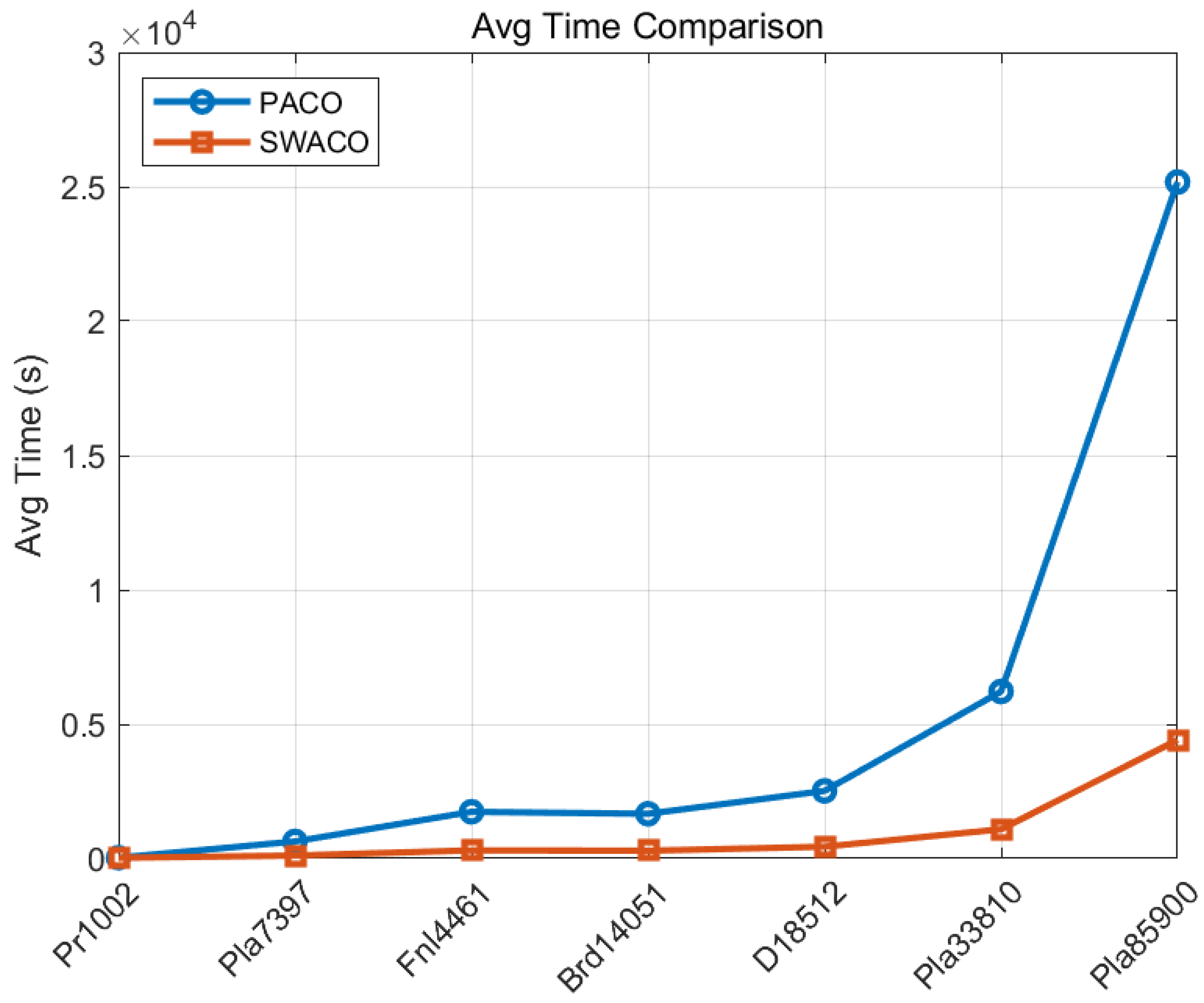
Table 4 and Table 5 indicate that, across all datasets, SWACO’s best solution outperforms PACO’s, exhibits a faster convergence speed, and significantly reduces the gap. As the dataset size increases, the advantages of the SWACO algorithm become more evident. In particular, when processing the Pla33810 and Pla85900 datasets, the running time is significantly reduced, and the solution quality is improved compared with that of the PACO algorithm.

Since the results of the Pr1002, Fnl4461, Brd14051, and D18512 datasets are not on the same scale as those of the other three datasets, the comparison of the Best and AVG values of the PACO and SWACO algorithms will be presented using two separate bar charts. A comparison of the results in Figure 8 shows that, compared with the PACO algorithm, the SWACO algorithm demonstrates higher solution quality, especially in a multicore environment. The SWACO algorithm can make full use of the advantages of multicore parallel computing to improve the efficiency of large-scale problems.

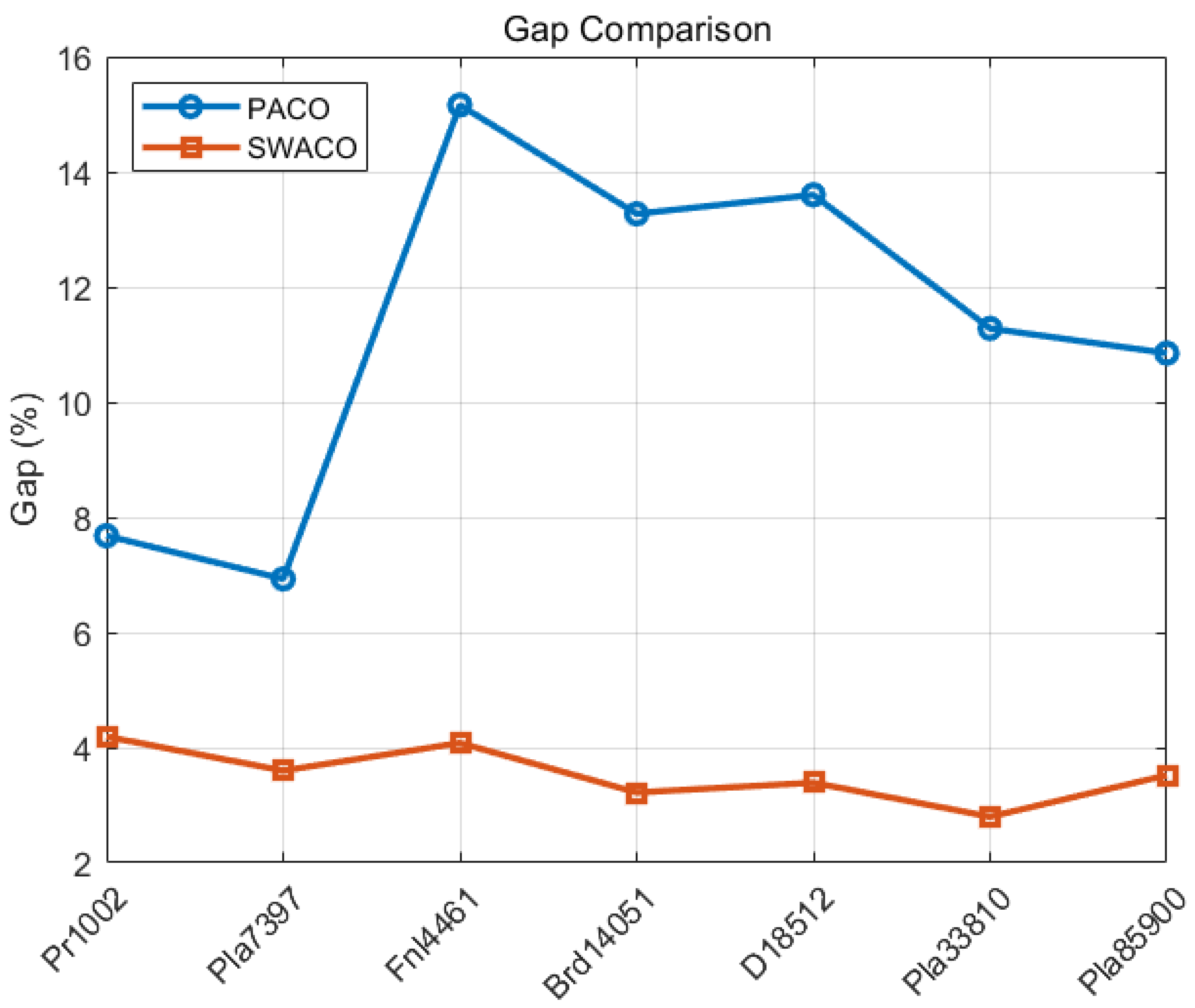
As shown in Figure 9, the quality of the optimal solution using the hybrid model on large datasets is far greater than that of PACO, with the average errors all within 5%. This difference becomes increasingly obvious as the scale expands. As shown in Figure 10, the algorithm using the second level of parallelism demonstrates excellent performance. Compared with the traditional algorithm that uses only the first level of parallelism, the use of Athread to accelerate the fitness calculation results in a maximum increase in a running time of 5.72 times. The algorithm achieves better acceleration performance.

The abovementioned experimental findings indicate that by using multistrategy parallelism in path calculation and pheromone updates, the SWACO algorithm demonstrates its superiority in solving large-scale problems. Relative to the serial ACO and PACO algorithms, the SWACO algorithm showed better solving ability on large-scale datasets, further validating the advantages of the multistrategy parallel adaptive method in a massively parallel computing environment.

4.5. Comparative Experiment of SWACO and Other Algorithms

To further demonstrate the effectiveness of the SWACO algorithm, this section compares it with the Genetic Algorithm (GA) and Simulated Annealing Algorithm (SA), which are widely used in solving the Traveling Salesman Problem (TSP), as well as with the ACO-ABC [29] and PACO-3Opt [30] algorithms reported in the other literature.The parameter settings for the GA and SA in the experiments were based on References [31,32]. The specific experimental results are shown in

Table 6. Comparison of numerical experimental results between SWACO and other algorithms.

Algorithm	Matrix	Eil51	Berlin52	Eil76	KroA100	Pr226
SWACO	Avg	426.2	7542	539.1	21,309.3	81,022
	Best	426	7542	538	21,282	80,732
	${\mathrm{Gap}}_{\mathrm{avg}}$(%)	0.04	0	0.20	0.13	0.81
GA	Avg	591	10172	649	38,981	404,120
	Best	483	8951	599	31,985	359,198
	${\mathrm{Gap}}_{\mathrm{avg}}$(%)	38.73	34.87	20.63	83.16	402.83
SA	Avg	535	9695	751	38,620	415,250
	Best	493	8745	701	33,969	375,992
	${\mathrm{Gap}}_{\mathrm{avg}}$(%)	25.59	28.55	39.59	81.47	416.68
ACO-ABC	Avg	443.4	7544.4	558.0	22,435.3	-
	Best	-	-	-	-	-
	${\mathrm{Gap}}_{\mathrm{avg}}$(%)	4.08	0.03	3.17	5.42	-
PACO-3opt	Avg	426.3	7542	539.8	21,326.7	-
	Best	426	7542	538	21,282	-
	${\mathrm{Gap}}_{\mathrm{avg}}$(%)	0.08	0	0.34	0.21	-

.

From Table 6, it can be seen that the SWACO algorithm demonstrates the best solution quality and stability across various TSP instances. Its average gap (${\mathrm{Gap}}_{\mathrm{avg}}$) is the lowest among all the compared data, such as 0% for Berlin52, and 0.04% and 0.13% for Eil51 and KroA100, respectively. The optimal solutions often coincide with theoretical values, indicating that its solutions are very close to the optimum. In contrast, the GA and SA perform poorly, with significantly higher average gaps, especially on Pr226, where they reach 402.83% and 416.68%, respectively. They also show instability on other dataset scales, reflecting poorer solution quality and robustness compared to SWACO. The ACO-ABC algorithm performs well on the Berlin52 dataset with an average gap of 0.03%, close to SWACO’s level, but its overall results are relatively higher. Although PACO-3Opt achieves better optimal solutions on Eil51 and Berlin52, the gap between average and optimal solutions is large; for example, the average gap is 0.34% on Eil76 and 0.21% on KroA100, showing less stability. In summary, SWACO not only outperforms other algorithms comprehensively in solution quality and stability but also achieves optimal or near-optimal levels on multiple datasets.

5. Conclusions

In this work, on the basis of the SW26010 processor, the first-level PACO and the second-level parallel ant colony algorithm (SWACO) are designed and implemented. By fully leveraging the advantages of the heterogeneous many-core structure, this work investigates the parallelized design of the ant colony algorithm for large-scale complex problems, verifying the performance of the algorithm with multiple TSP datasets. The SWACO algorithm achieves multithreaded acceleration of path calculation and pheromone updates through a hybrid parallel model based on an MPI and Athread. The experimental results show that, when addressing large-scale optimization problems, the SWACO algorithm has a significant performance advantage over the traditional serial ACO and one-level parallel PACO algorithms. Specifically, for the small- and medium-scale datasets, the maximum speedup ratio of the PACO algorithm reached 3.26 times that of the serial ACO algorithm, with an accuracy increase of up to 6.75%. For large-scale datasets, the running time of the SWACO algorithm was significantly shorter than that of the PACO algorithm, achieving a maximum speedup of 5.72 times. Additionally, the quality of the solution was closer to the optimal solution, with the error consistently within 5%, indicating a substantial performance advantage.

The SWACO algorithm proposed in this paper mainly targets static TSP instances, while its robustness and real-time update capabilities in dynamic environments (such as traffic navigation and logistics scheduling) have not been fully explored. In addition, as the problem scale expands to millions of nodes, the communication overhead and load balancing bottlenecks of the two-level parallel strategy may limit performance improvements. Future work will focus on optimizing algorithm details and hardware architecture adaptability, as well as integrating with other algorithms to further enhance the SWACO algorithm and better exploit the performance potential of heterogeneous many-core processors.