Figure 1.
Dumper vehicle studied in the present work and used in the real mining environment.
Figure 1.
Dumper vehicle studied in the present work and used in the real mining environment.
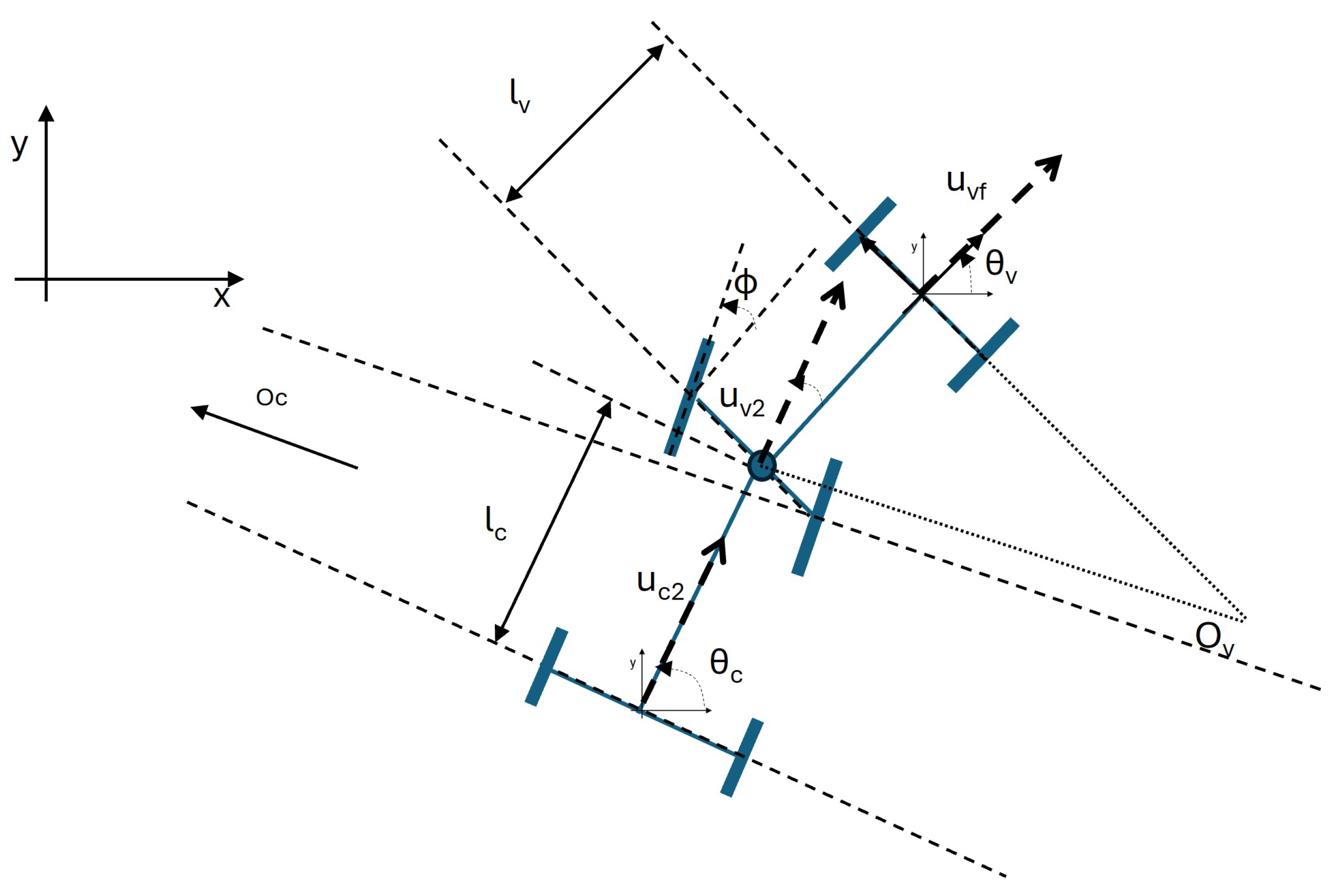
Figure 2.
Schematic of the vehicle showing the main parameters involved. and are the instantaneous centers of rotation for the vehicle and the trailer, respectively (the arrows show the positive sense of the angle).
Figure 2.
Schematic of the vehicle showing the main parameters involved. and are the instantaneous centers of rotation for the vehicle and the trailer, respectively (the arrows show the positive sense of the angle).
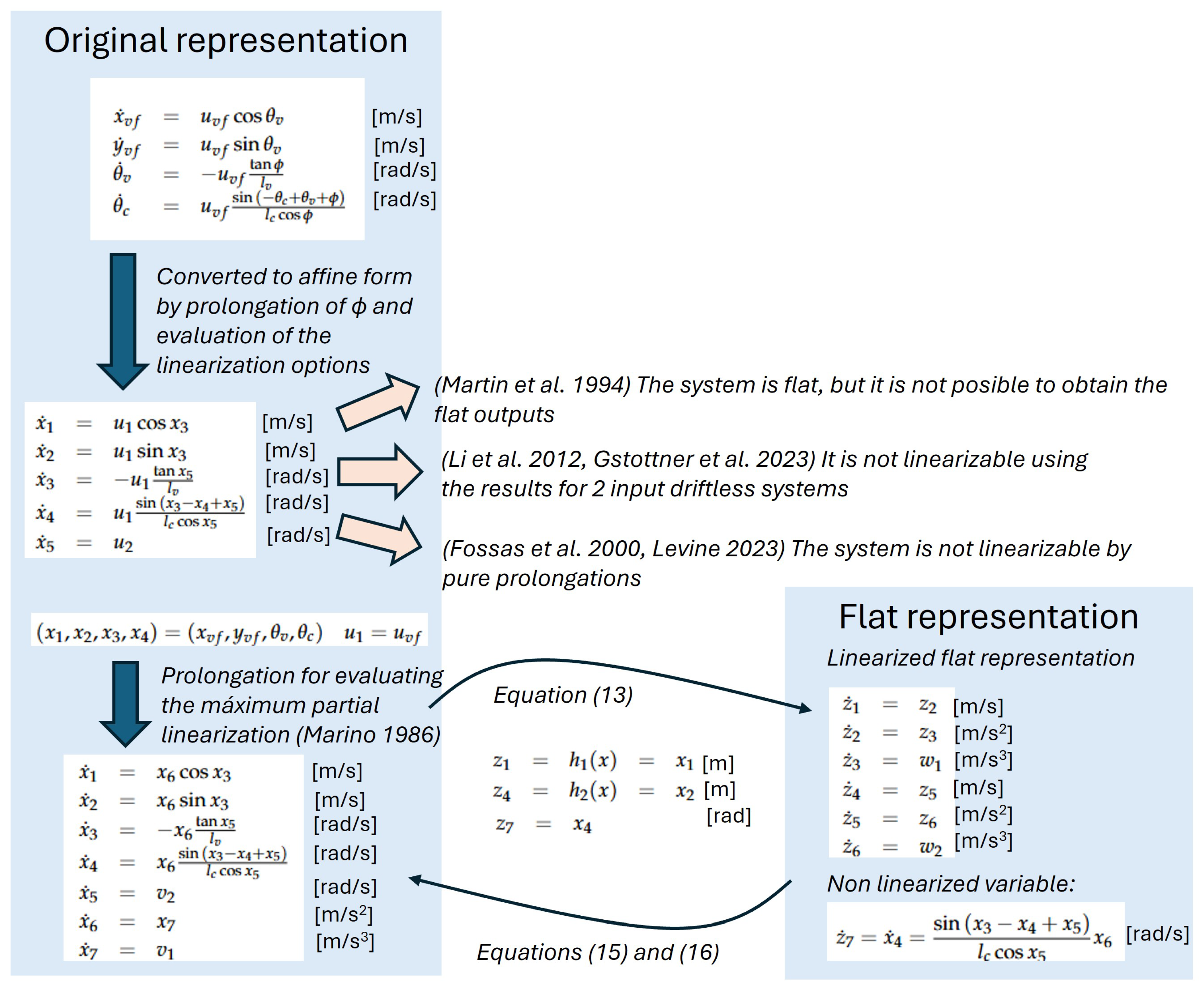
Figure 3.
Summary of the linearization process and the change of variables. The evaluation of the differential flatness is done according to Martin et al. 1994 [
22]. The obtainment of the flat outputs is first evaluated by using the results from Li et al. 2012 [
23] and Gstottner et al. 2023 [
24] for 2 input driftless systems, and the results from Fossas et al. 2000 [
25] and Levine 2023 [
26] by using prolongations. None of these approaches worked, and it is finally decided to solve the problem by using the partial linearization described in Marino 1986 [
20].
Figure 3.
Summary of the linearization process and the change of variables. The evaluation of the differential flatness is done according to Martin et al. 1994 [
22]. The obtainment of the flat outputs is first evaluated by using the results from Li et al. 2012 [
23] and Gstottner et al. 2023 [
24] for 2 input driftless systems, and the results from Fossas et al. 2000 [
25] and Levine 2023 [
26] by using prolongations. None of these approaches worked, and it is finally decided to solve the problem by using the partial linearization described in Marino 1986 [
20].
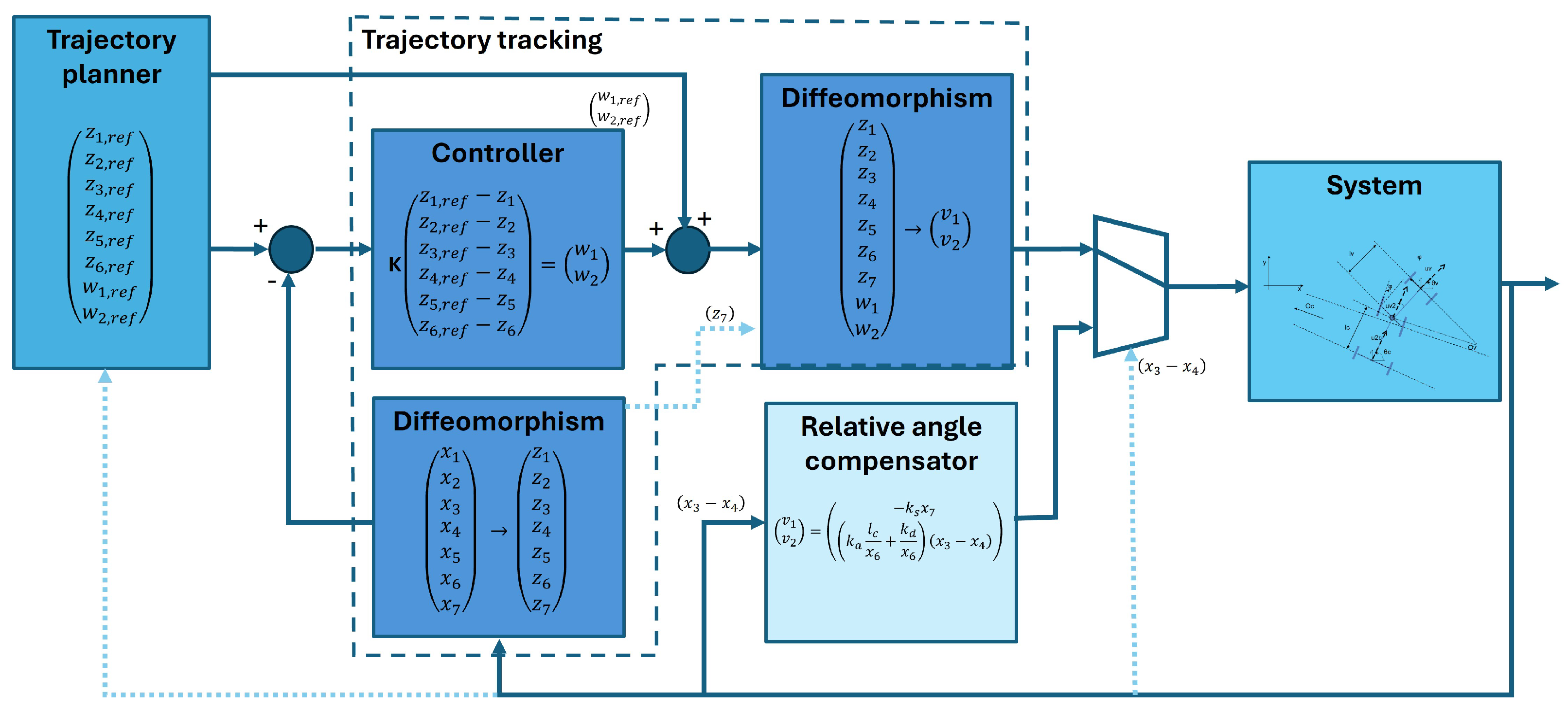
Figure 4.
Description of the control loop.
Figure 4.
Description of the control loop.
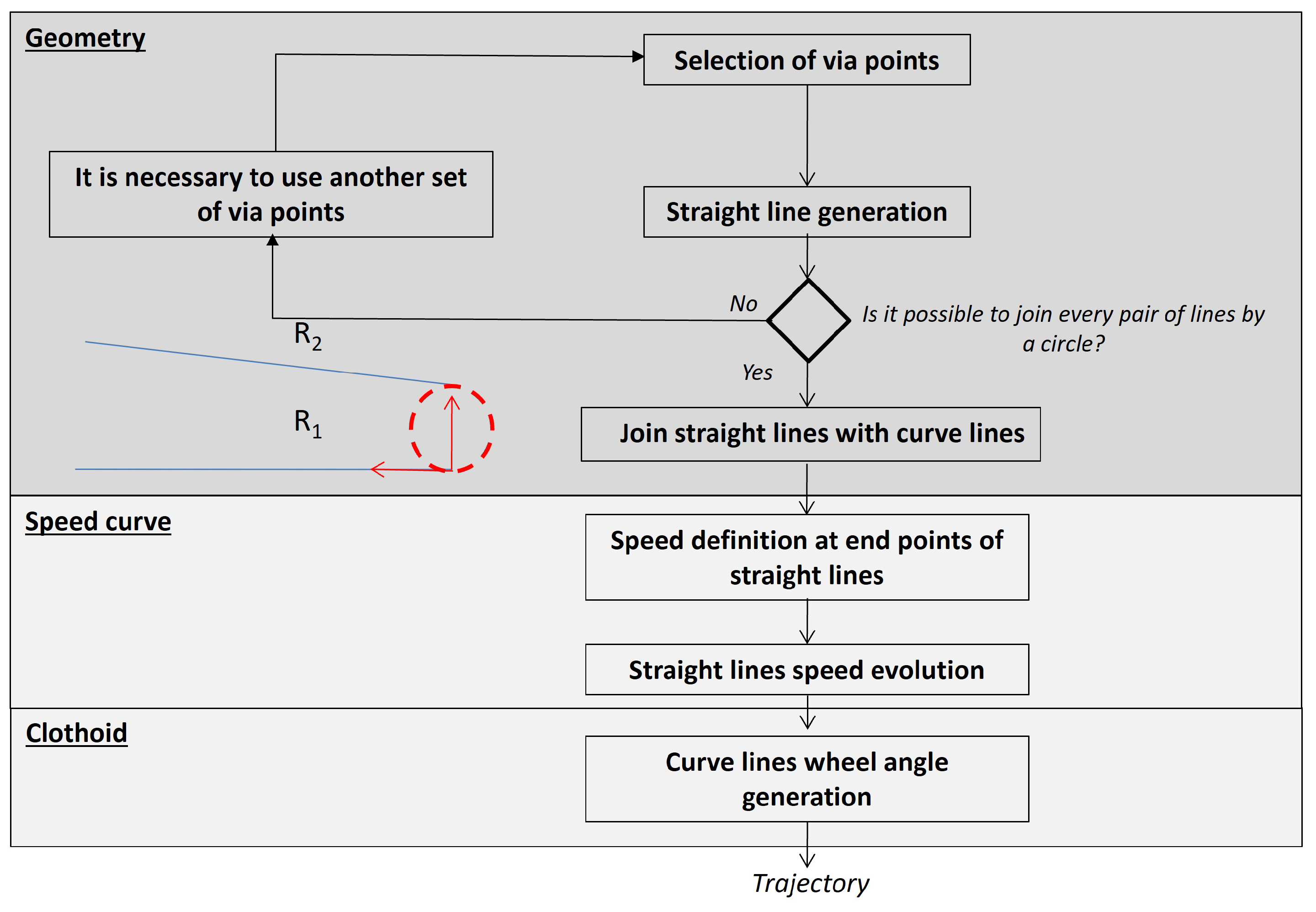
Figure 5.
Algorithm for generating the trajectory.
Figure 5.
Algorithm for generating the trajectory.
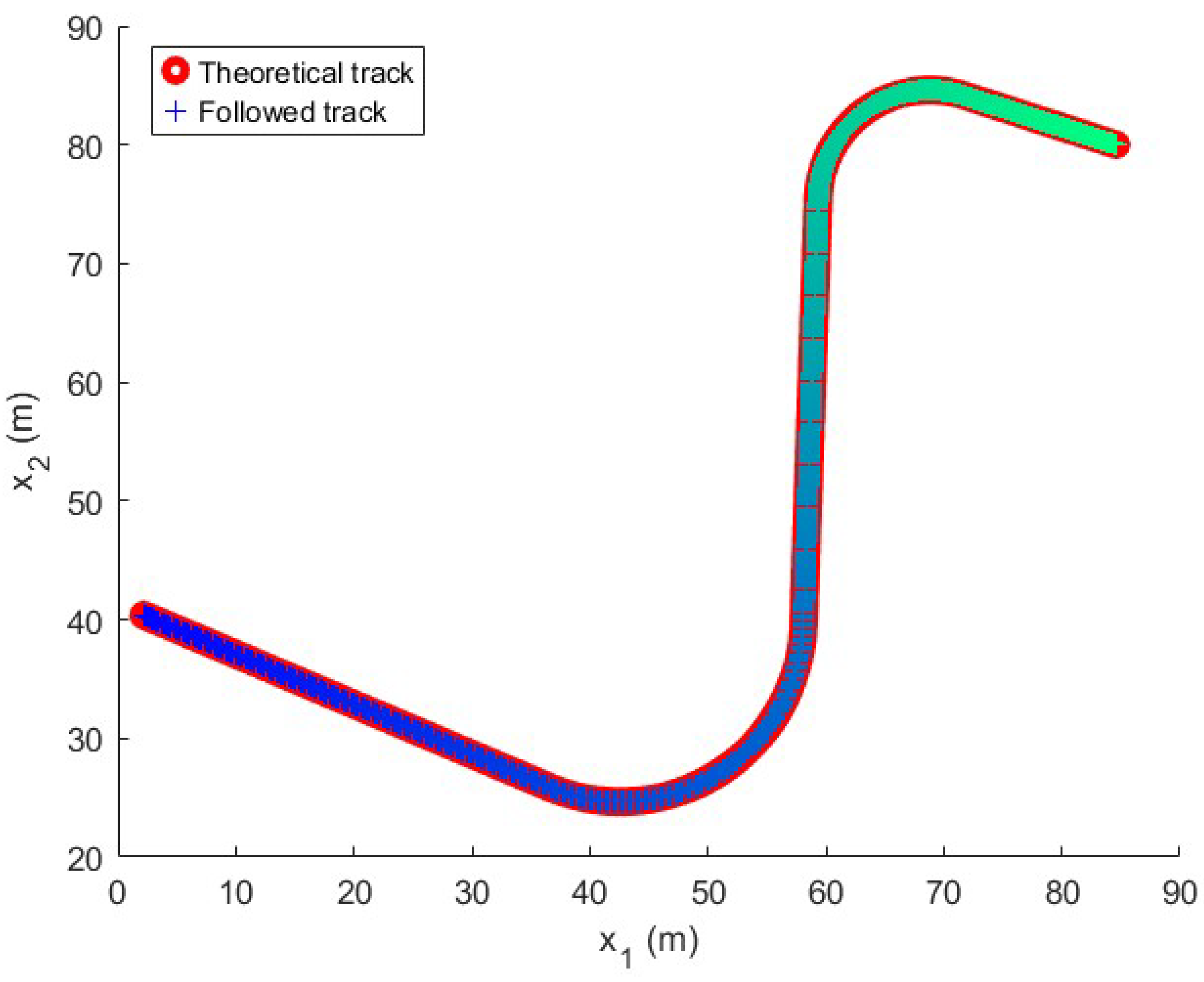
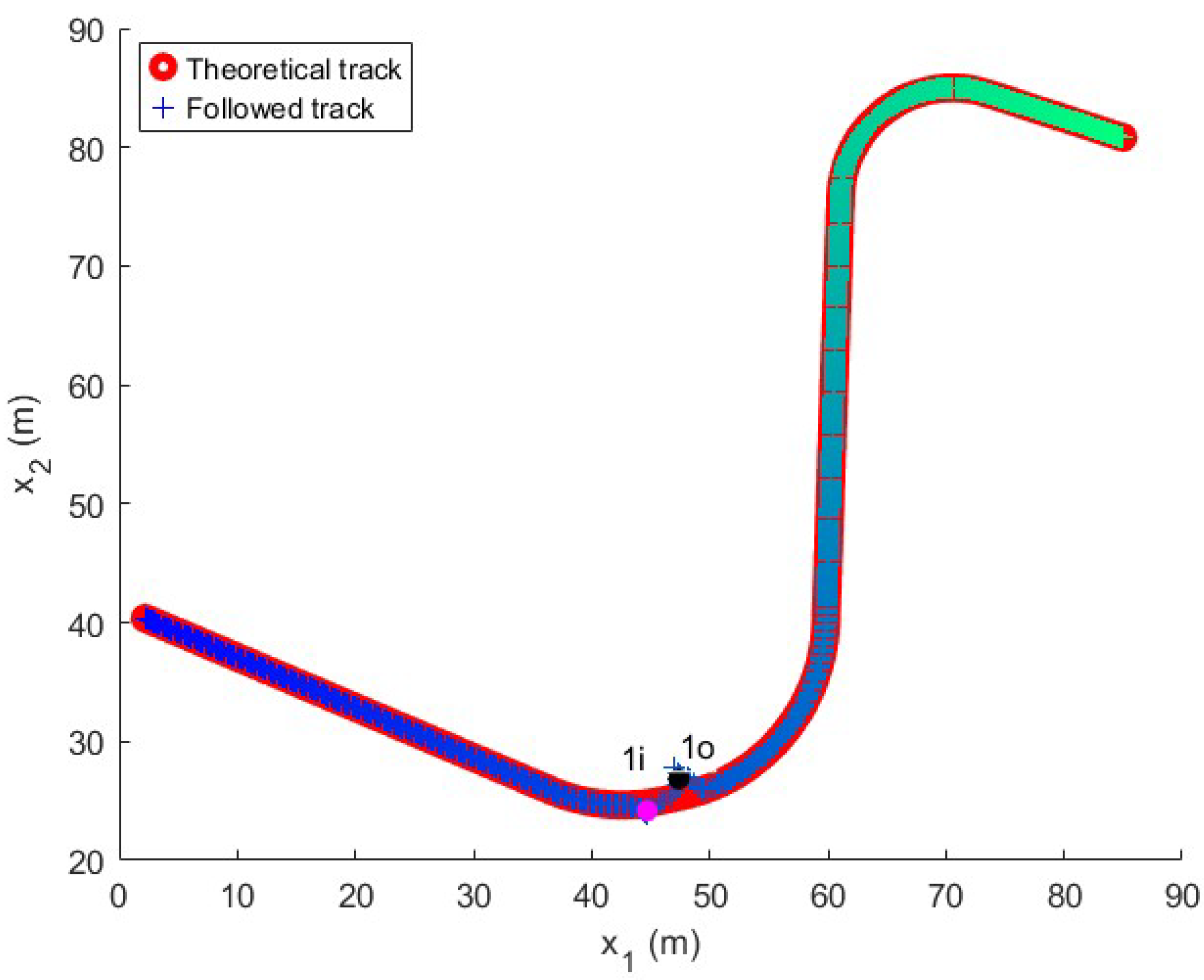
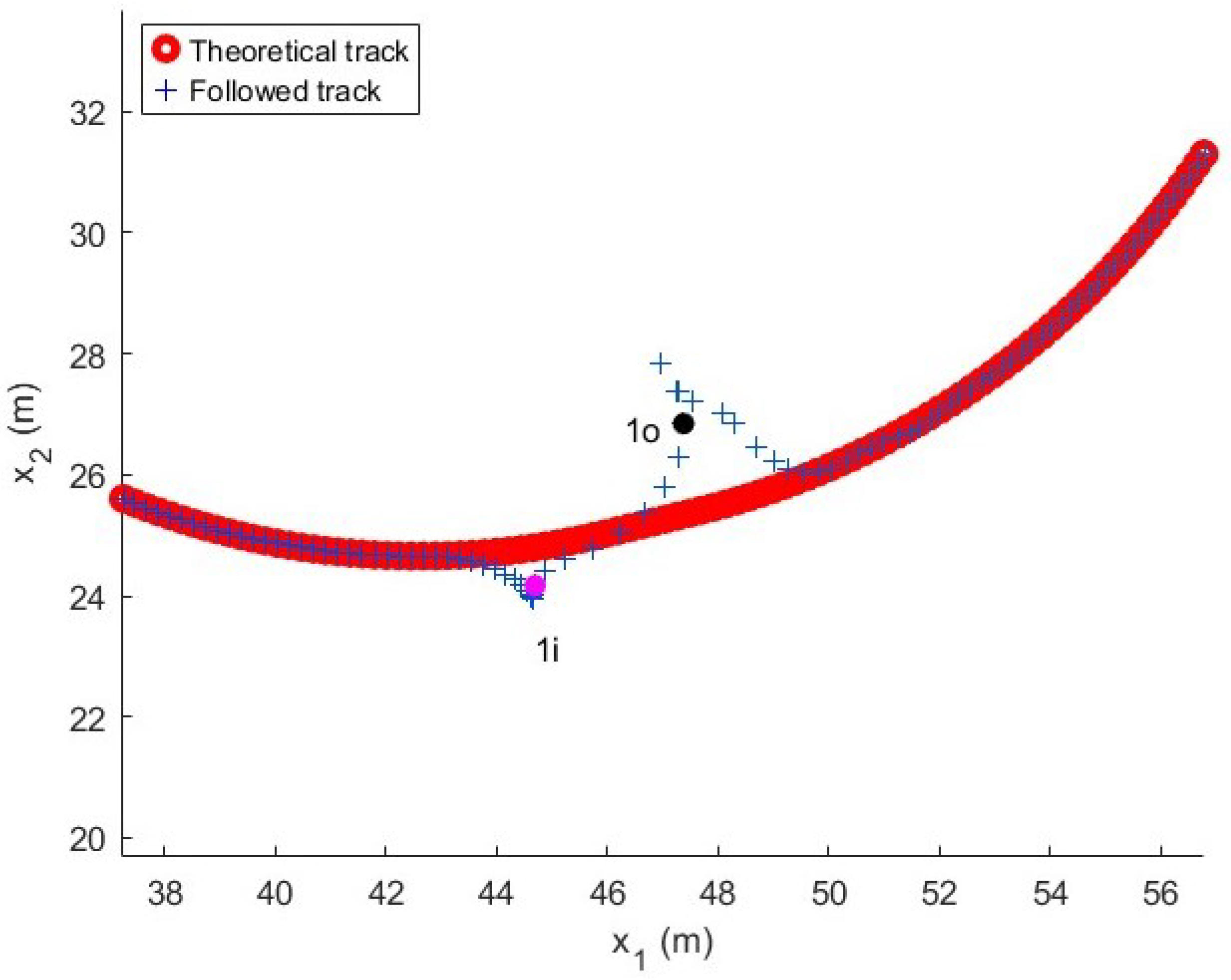
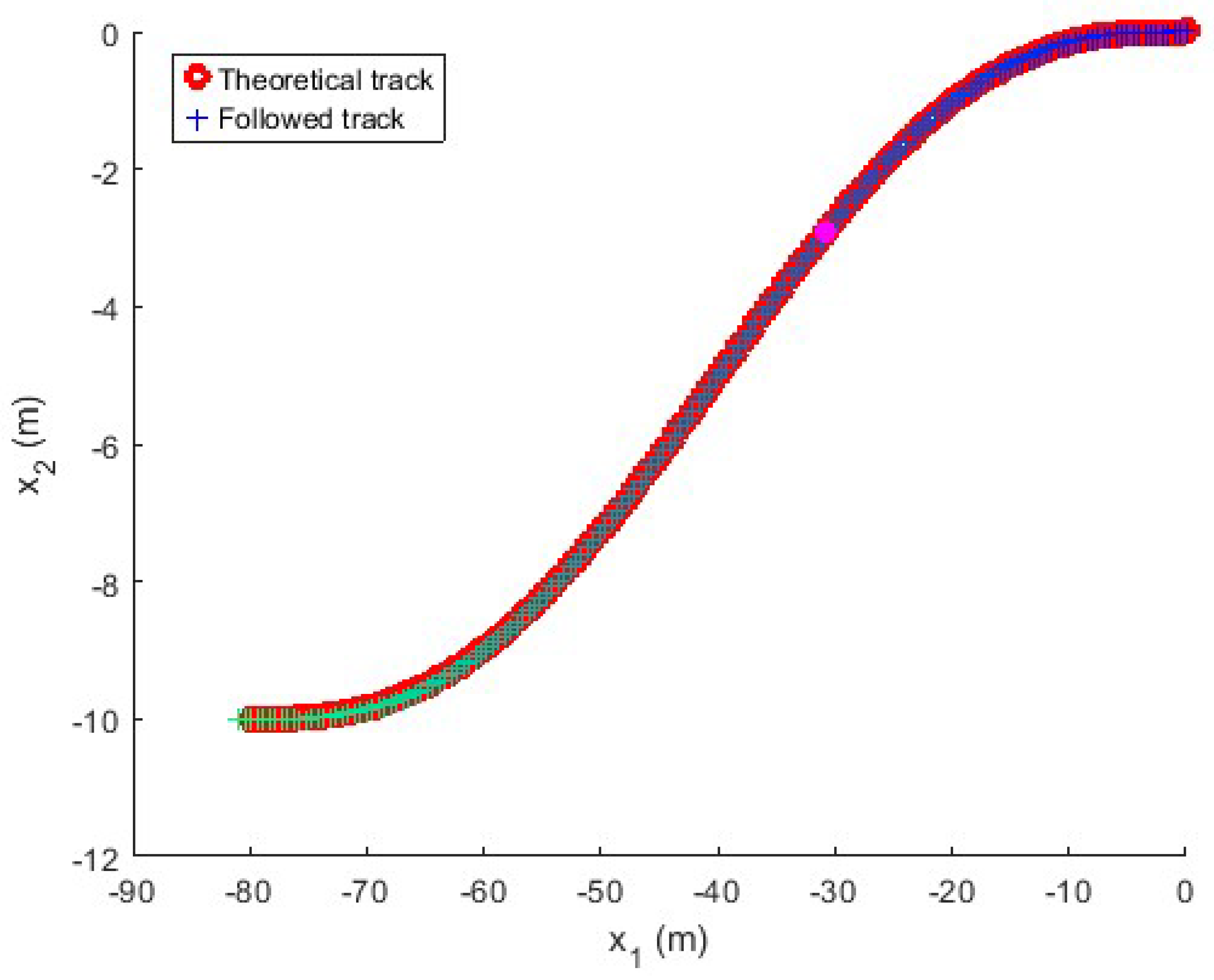
Figure 6.
Followed trajectory in the long maneuver test. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern.
Figure 6.
Followed trajectory in the long maneuver test. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern.
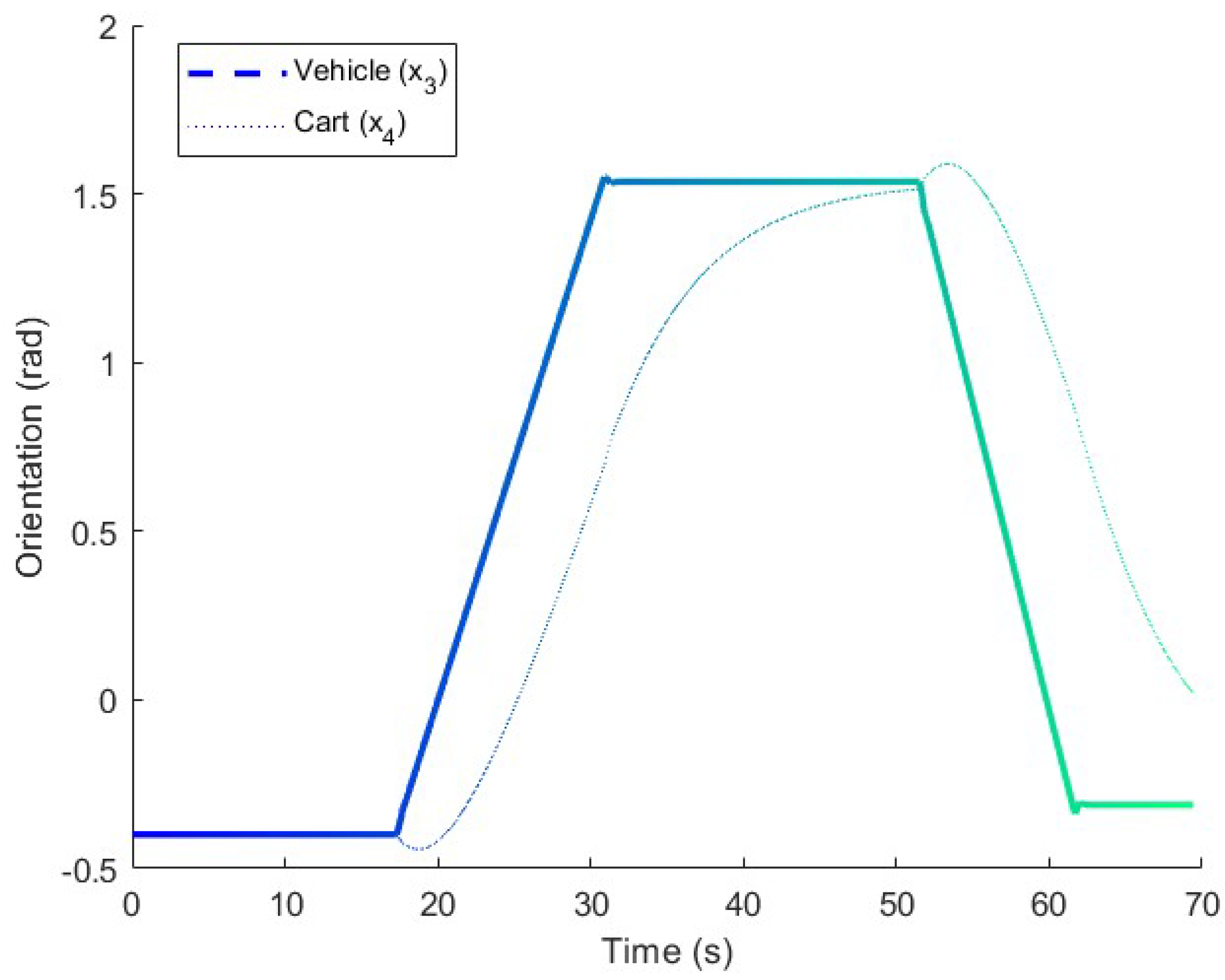
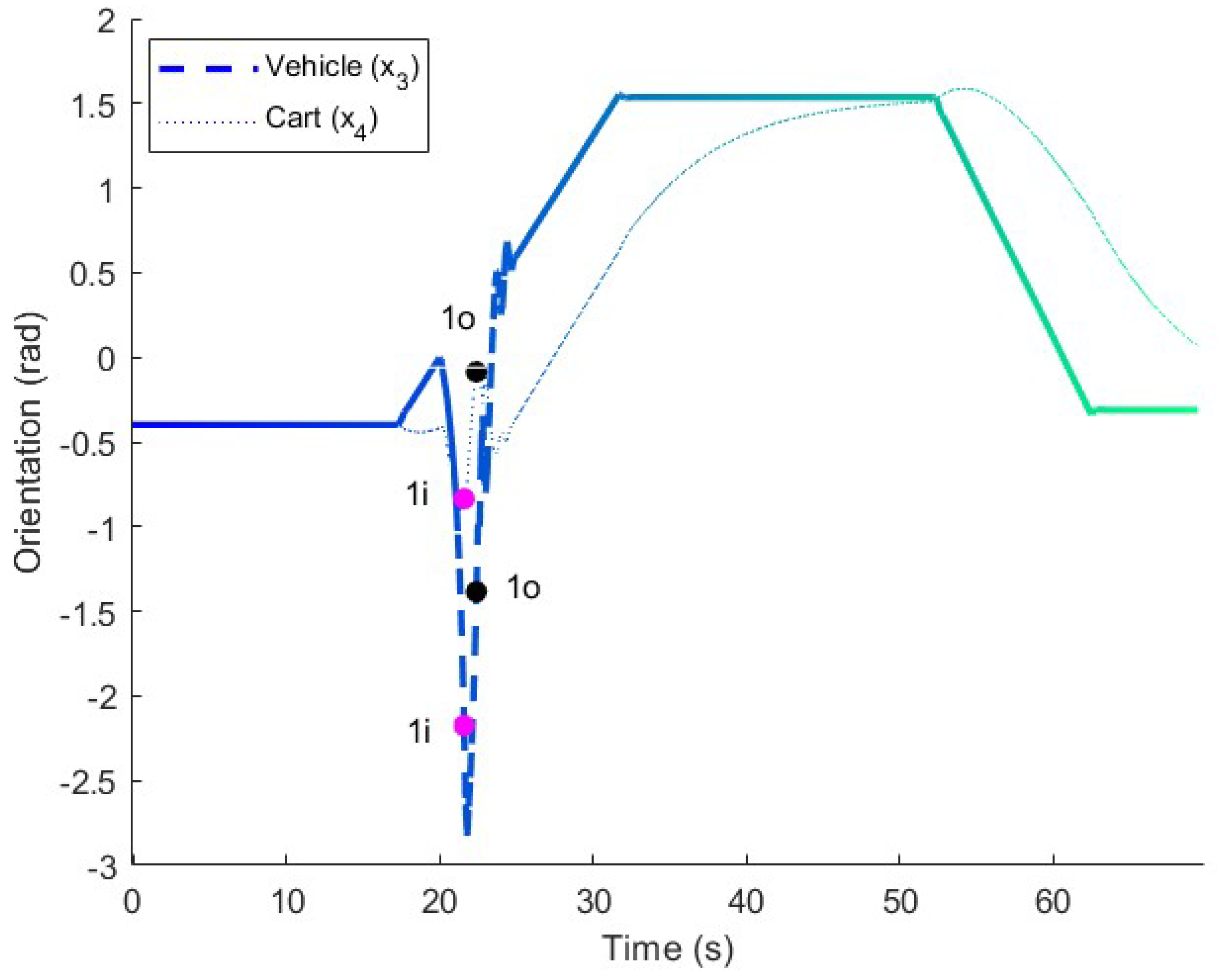
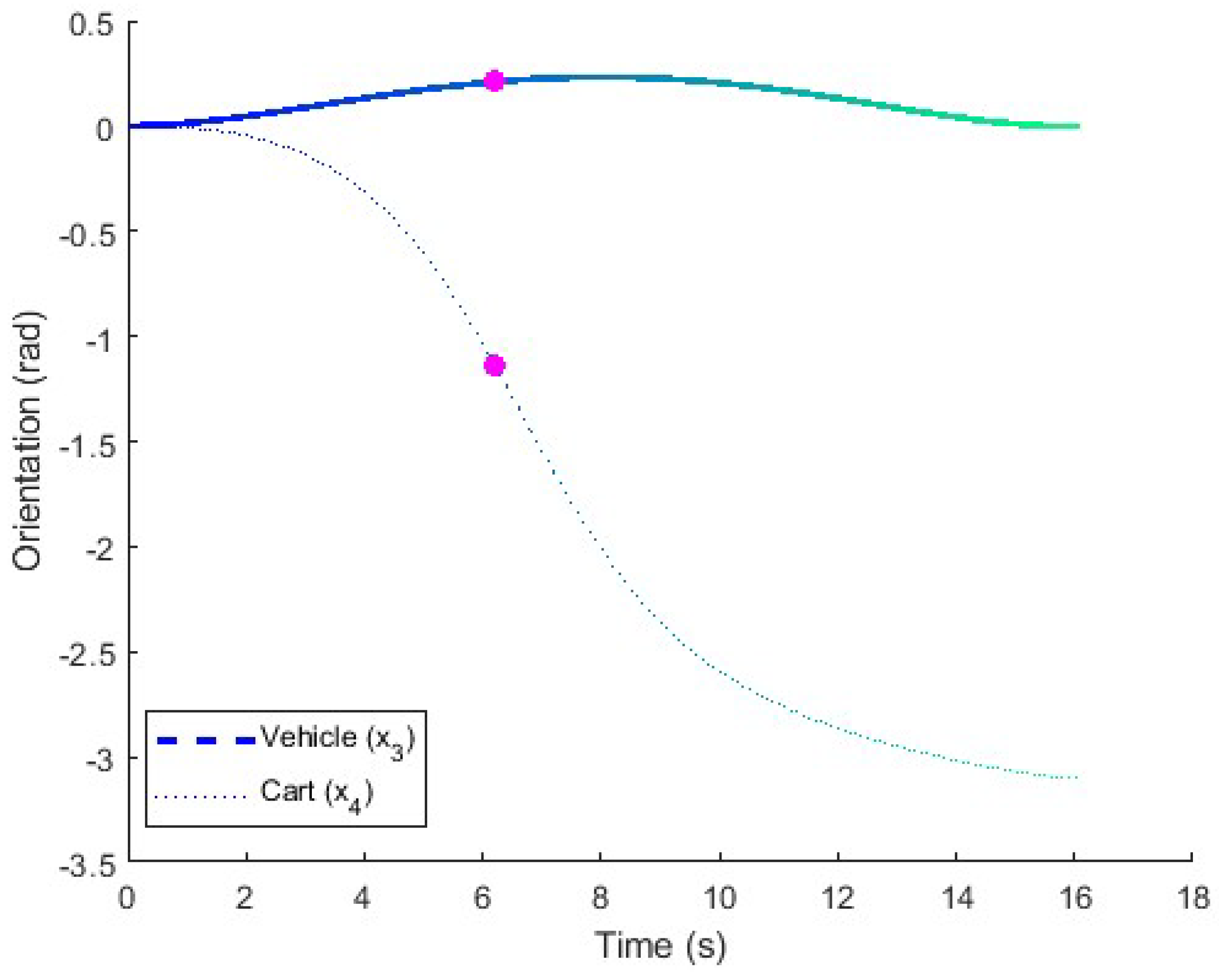
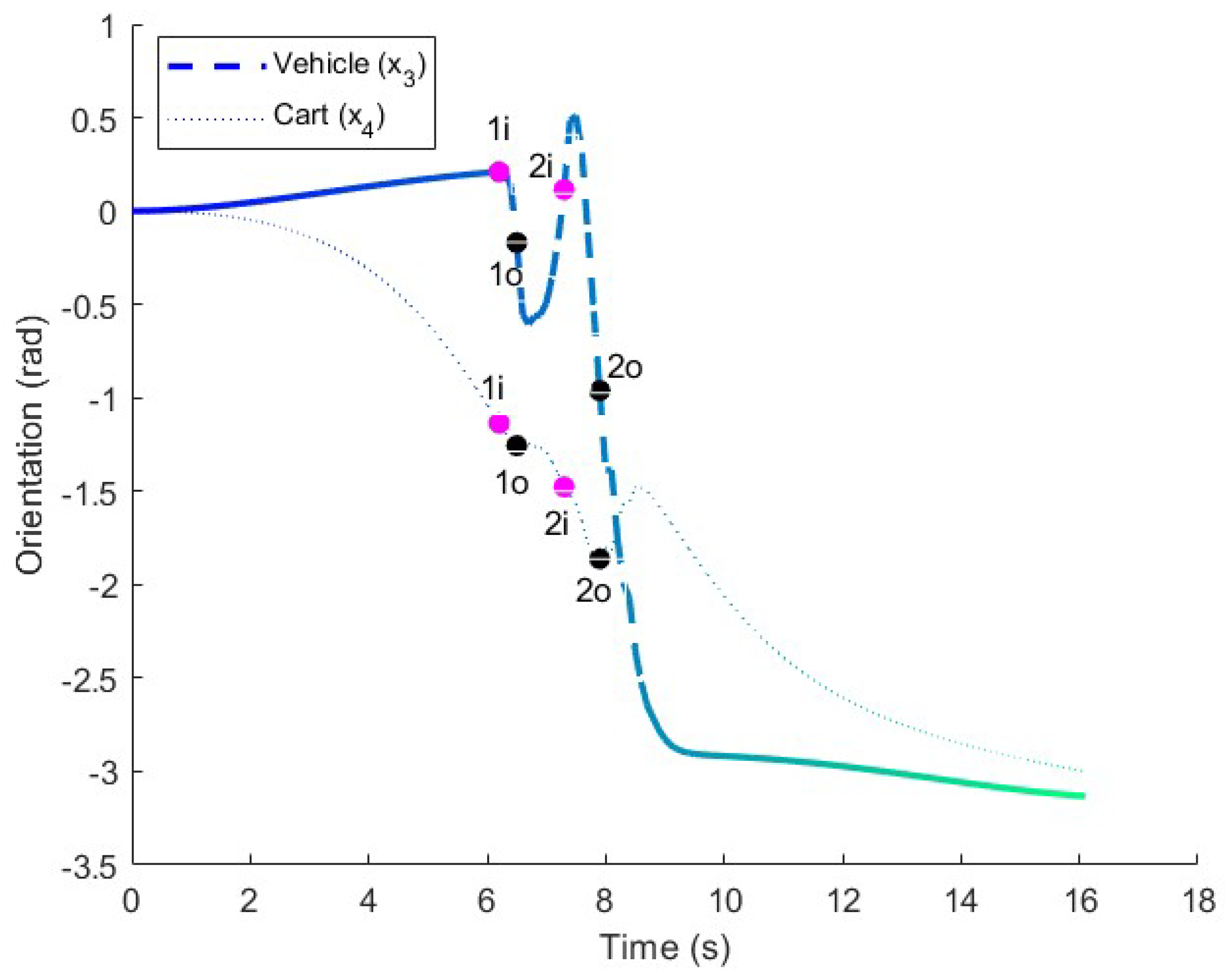
Figure 7.
Orientation in the long maneuver test. The orientations of the vehicle and cart are represented in the figure for comparison.
Figure 7.
Orientation in the long maneuver test. The orientations of the vehicle and cart are represented in the figure for comparison.
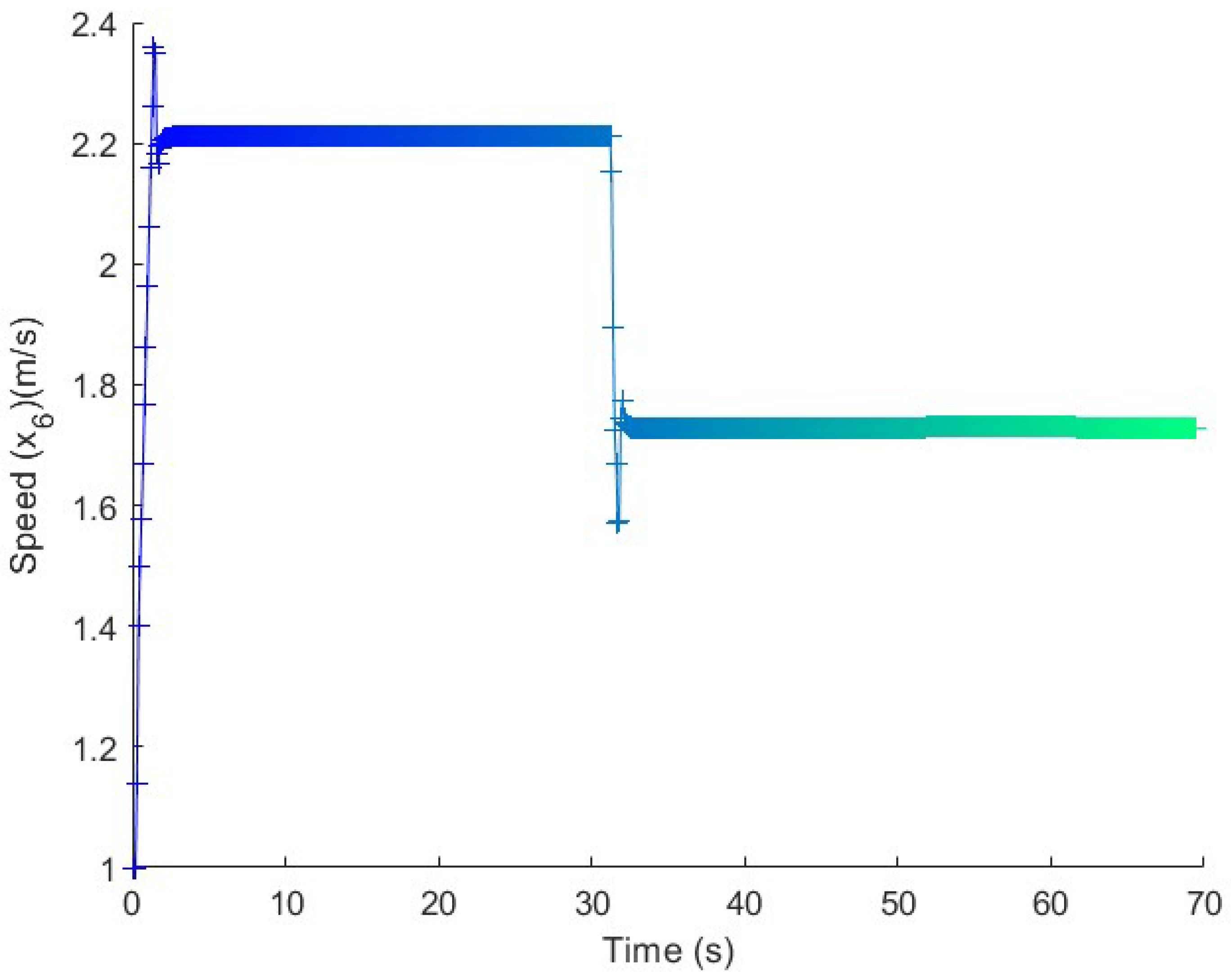
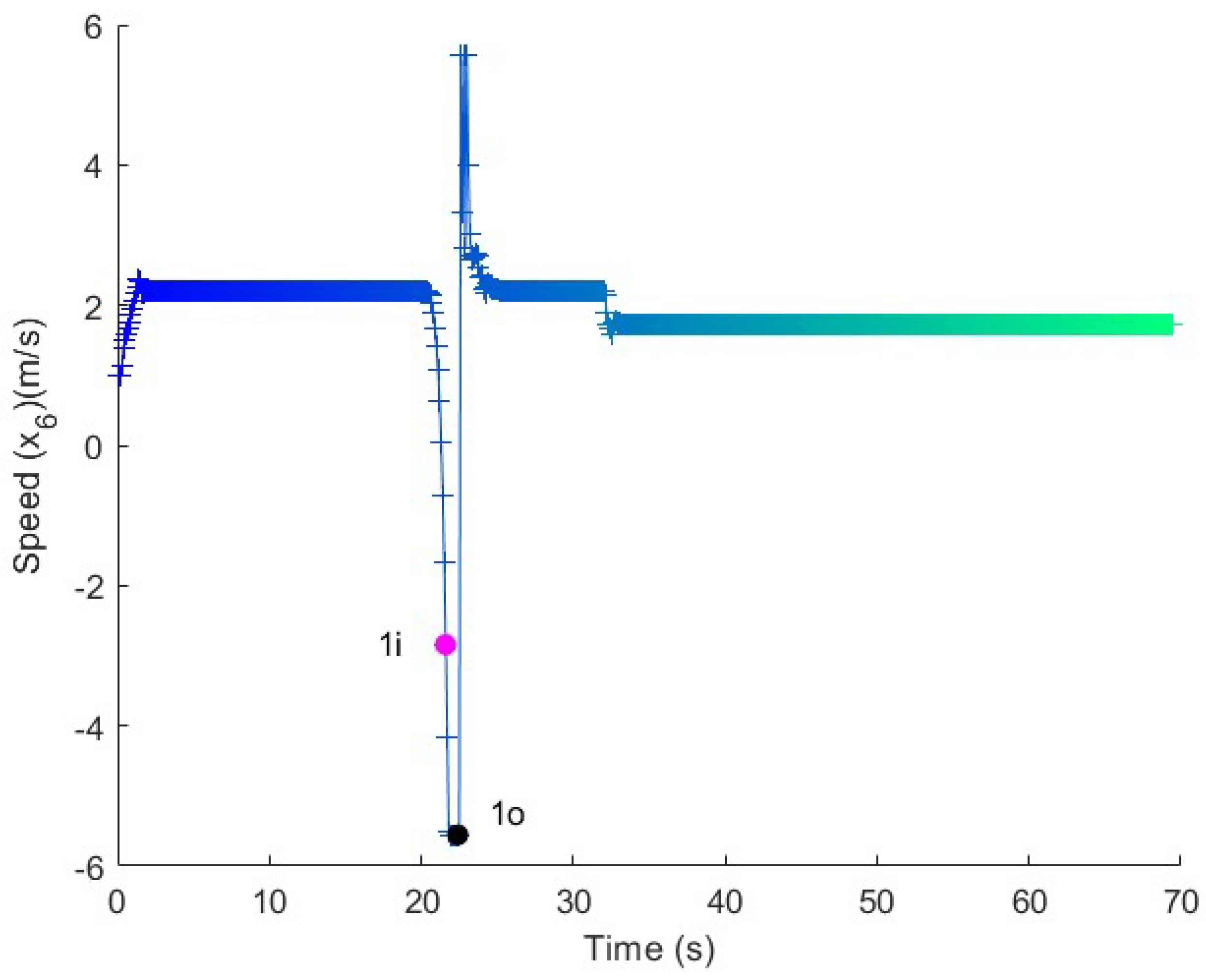
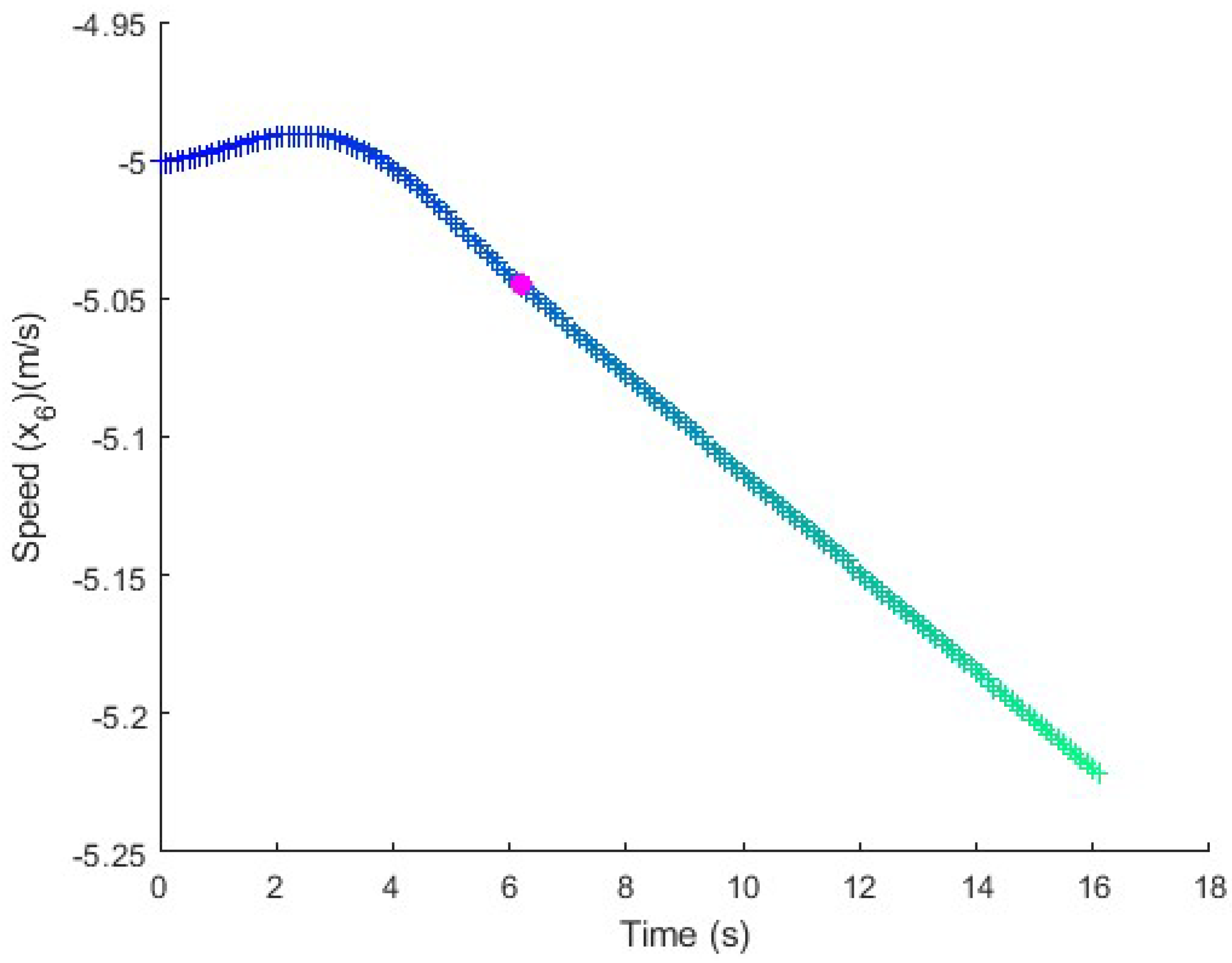
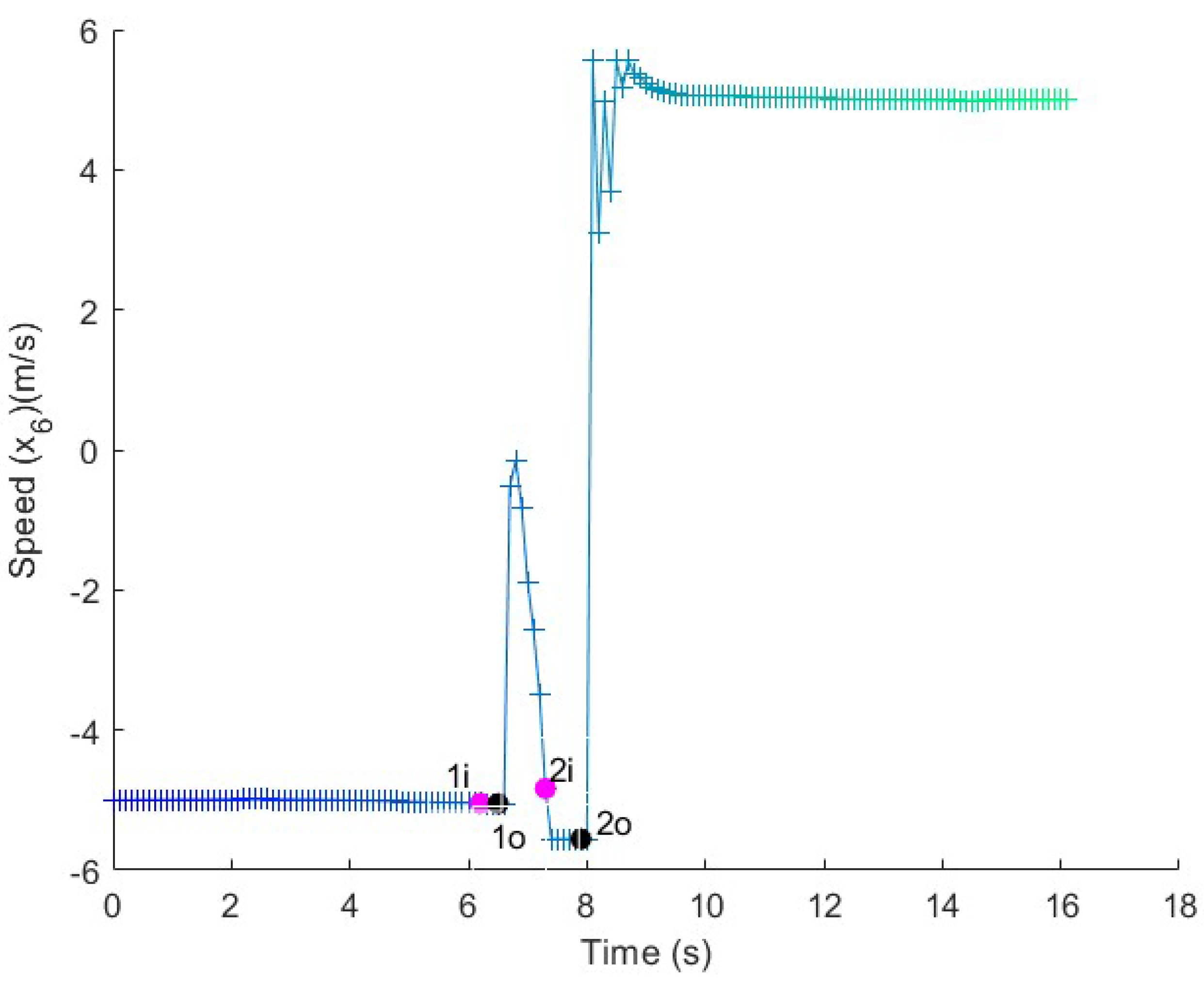
Figure 8.
Speed in the long maneuver test. The speed is adapted along the straight lines and kept constant in the turns.
Figure 8.
Speed in the long maneuver test. The speed is adapted along the straight lines and kept constant in the turns.
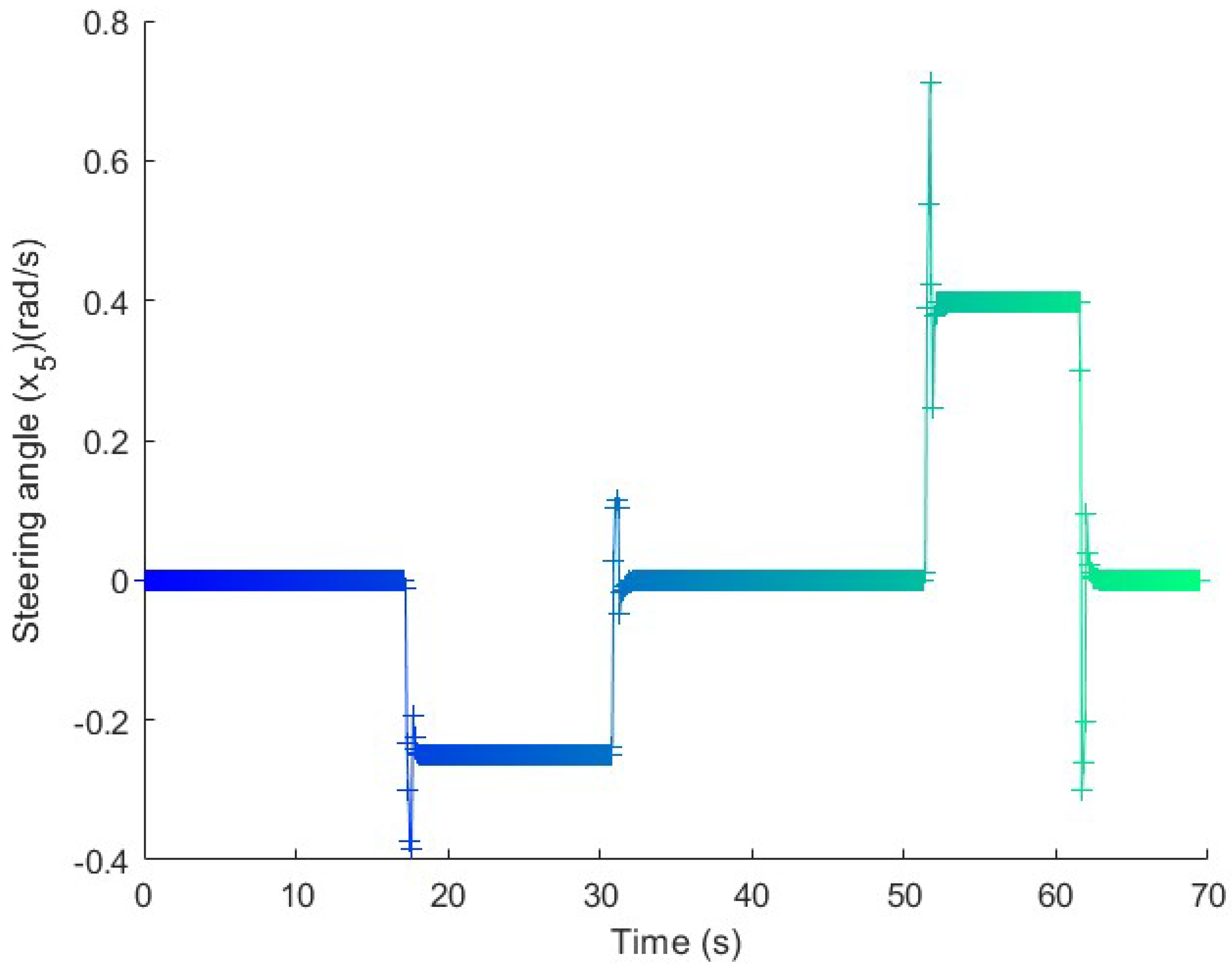
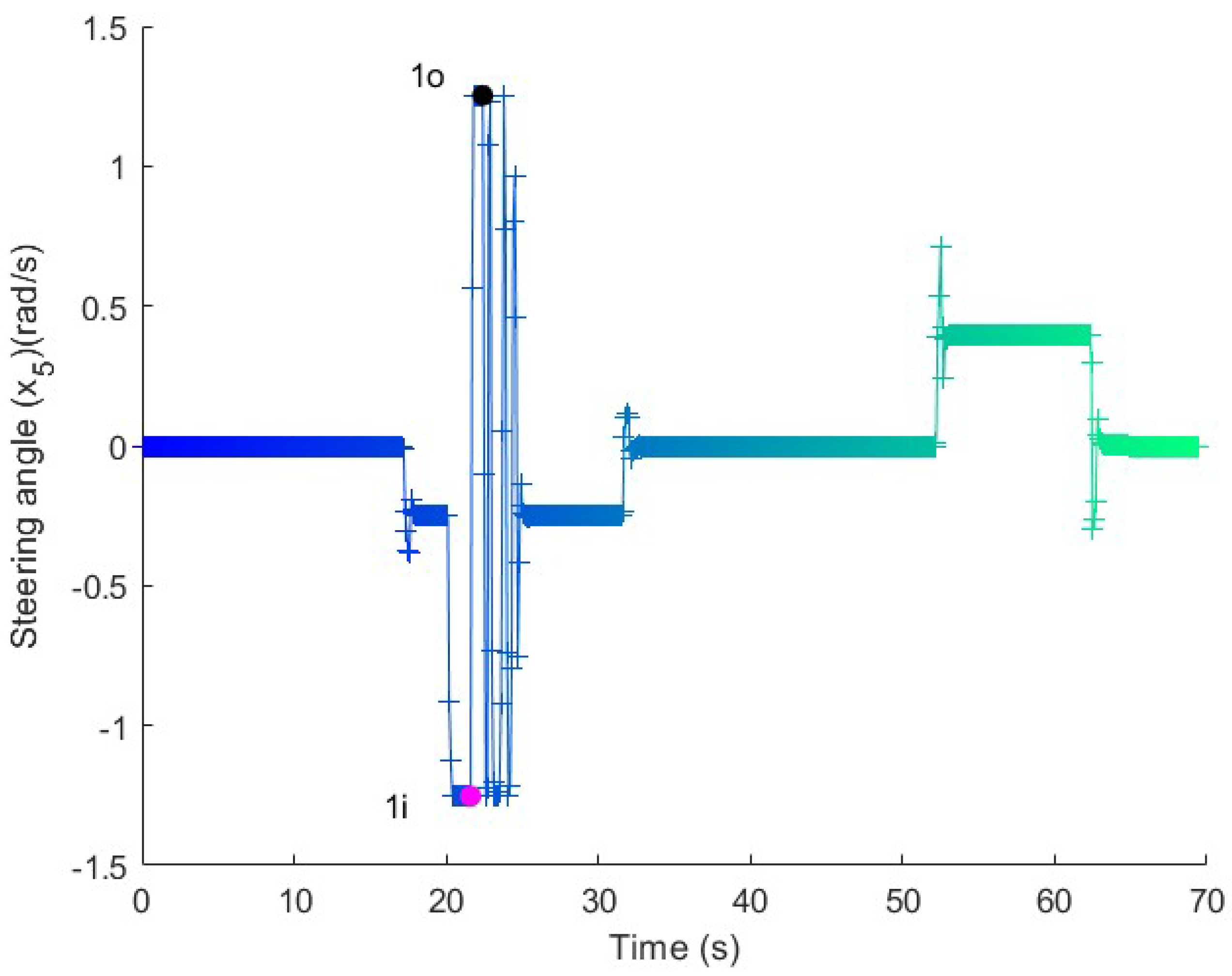
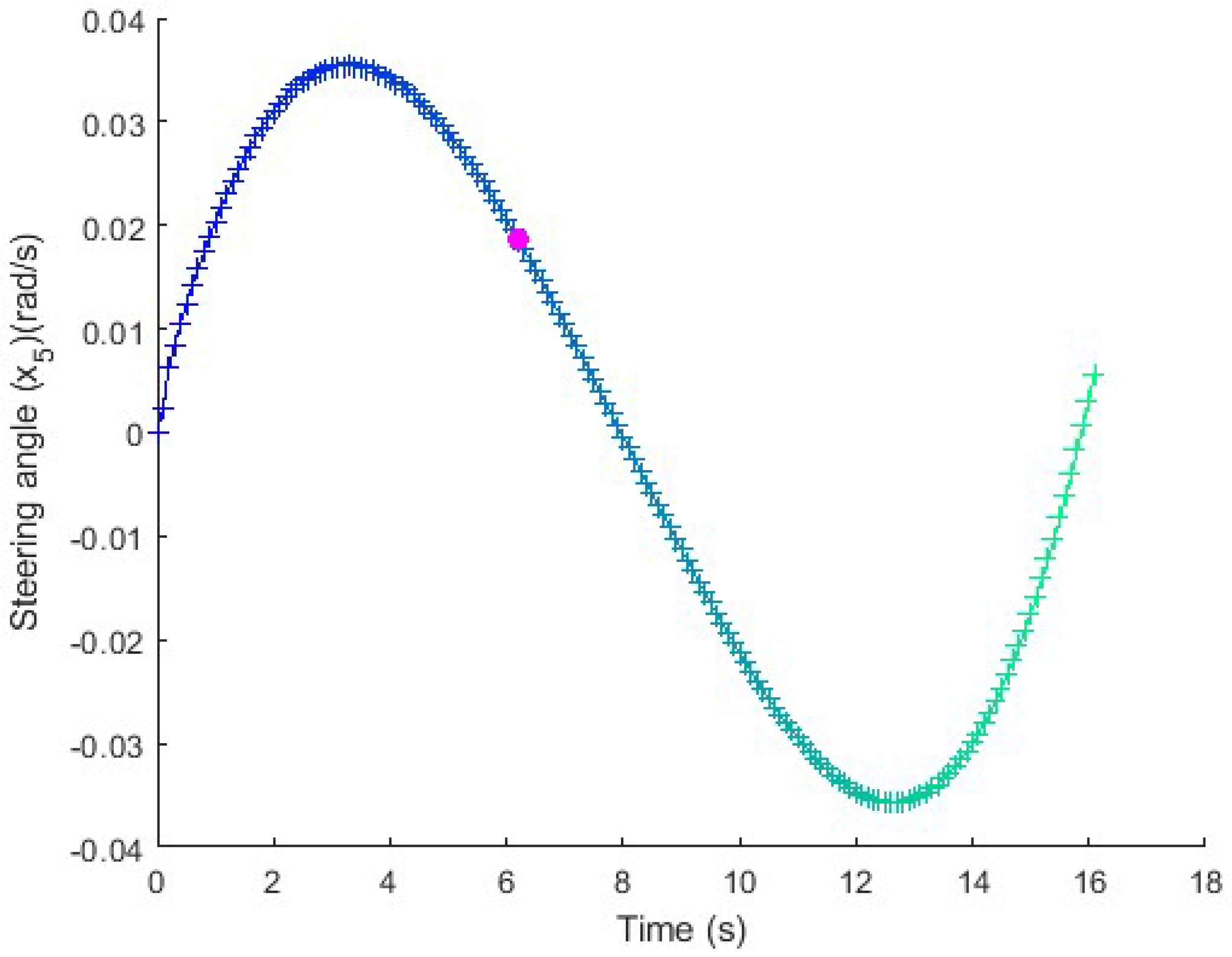
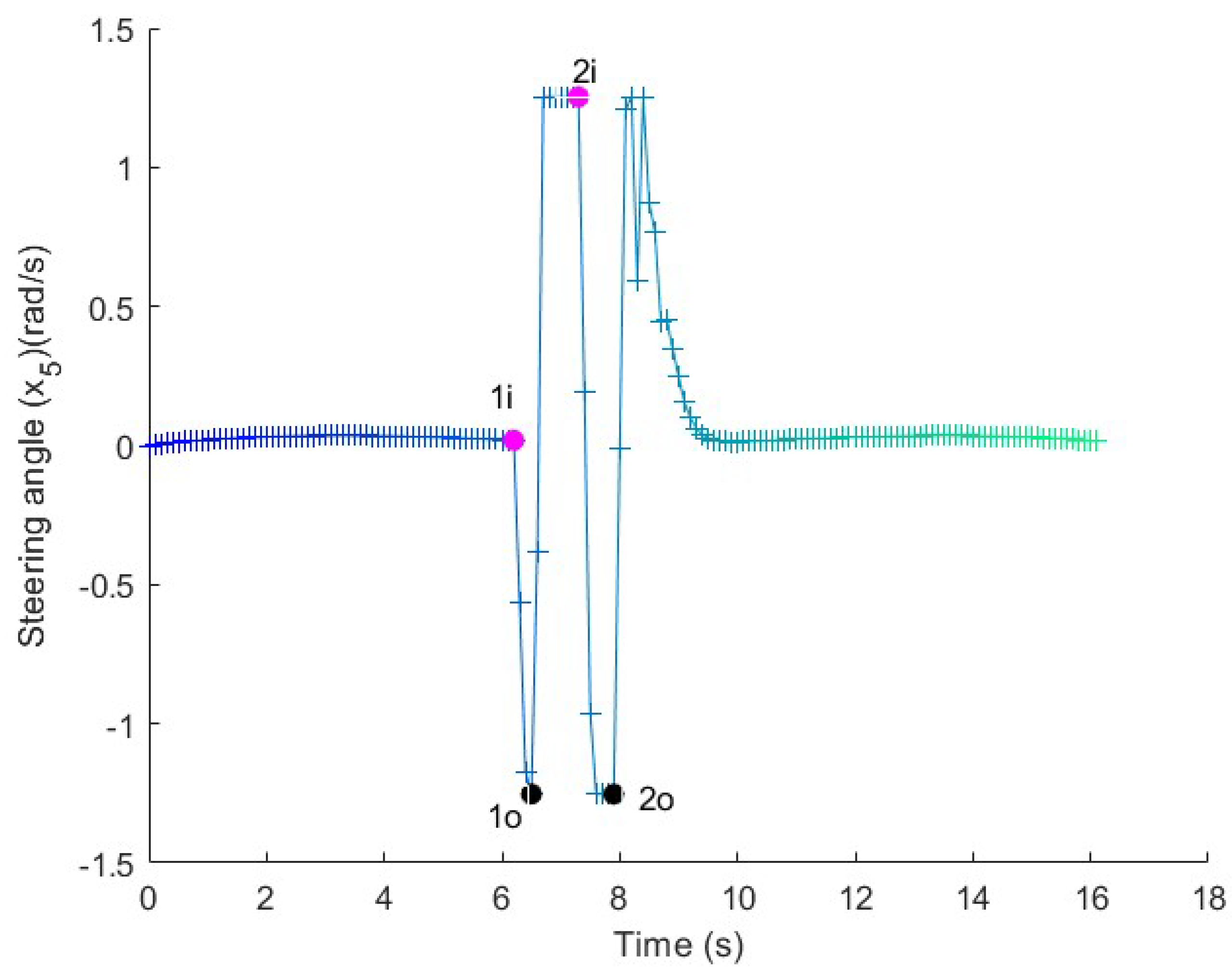
Figure 9.
Steering in the long maneuver test. The angle is kept constant along the straight line and the curves, with an adaptation range at the beginning of the turn.
Figure 9.
Steering in the long maneuver test. The angle is kept constant along the straight line and the curves, with an adaptation range at the beginning of the turn.
Figure 10.
Followed trajectory in the long maneuver test without a compensator. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 10.
Followed trajectory in the long maneuver test without a compensator. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 11.
Orientation in the long maneuver test without a compensator. In the absence of the relative angle compensator, the vehicle and trailer exceed the rad relative angle, which is physically impossible. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 11.
Orientation in the long maneuver test without a compensator. In the absence of the relative angle compensator, the vehicle and trailer exceed the rad relative angle, which is physically impossible. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 12.
Speed in the long maneuver test without a compensator. Between 21 s and 27 s, the vehicle speed is high, and it takes a long time to recover from the perturbation.The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 12.
Speed in the long maneuver test without a compensator. Between 21 s and 27 s, the vehicle speed is high, and it takes a long time to recover from the perturbation.The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 13.
Steering in the long maneuver test without a compensator. The steering command is much less smooth than the one without perturbation. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
Figure 13.
Steering in the long maneuver test without a compensator. The steering command is much less smooth than the one without perturbation. The pink and black dots represents the instants at which the relative angle compensator would have been activated and deactivated, respectively, if it were in operation.
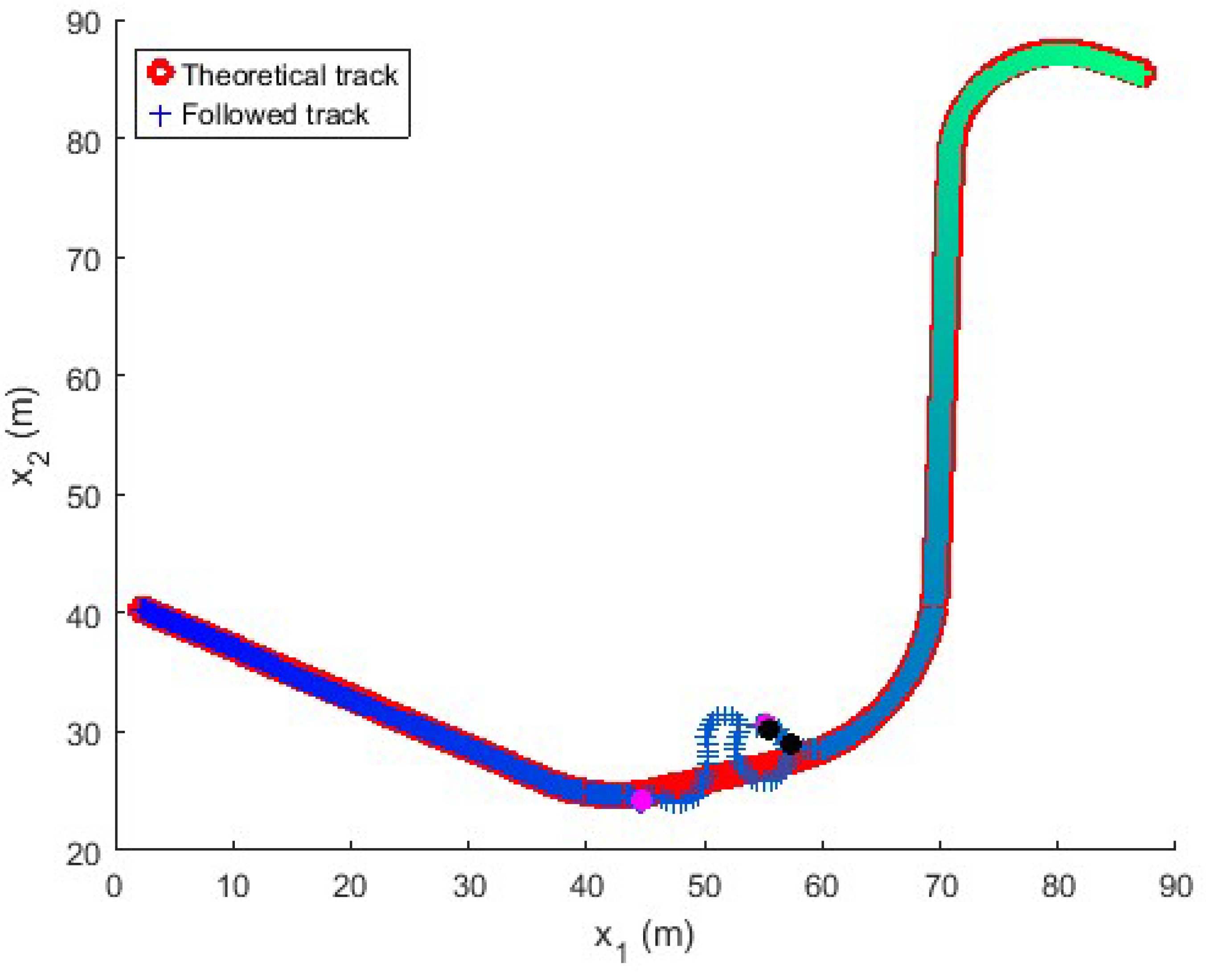
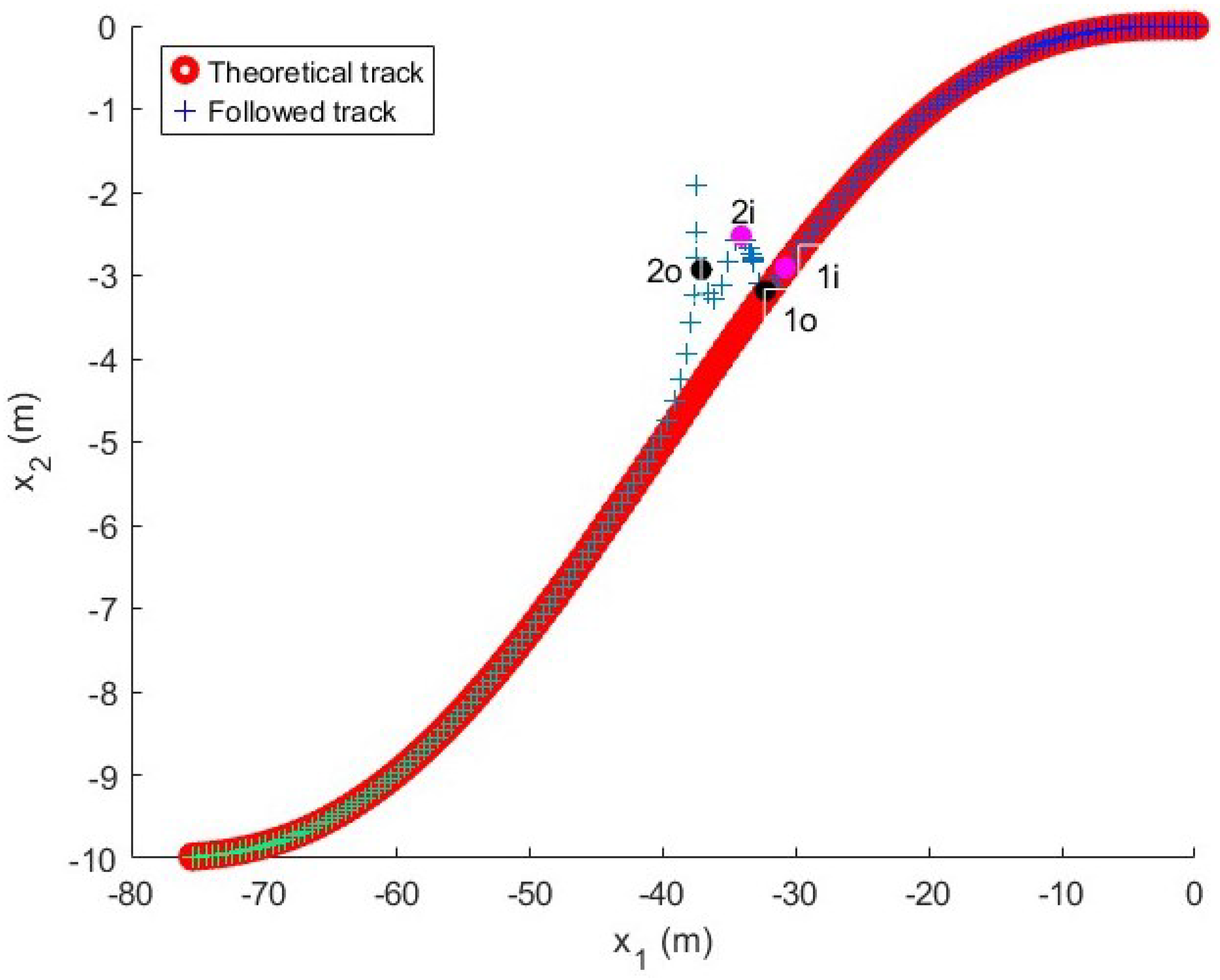
Figure 14.
Followed trajectory in the long maneuver test with perturbation. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern. (pink dot) and (black dot) represent the points at which the relative angle compensator starts and stops.
Figure 14.
Followed trajectory in the long maneuver test with perturbation. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern. (pink dot) and (black dot) represent the points at which the relative angle compensator starts and stops.
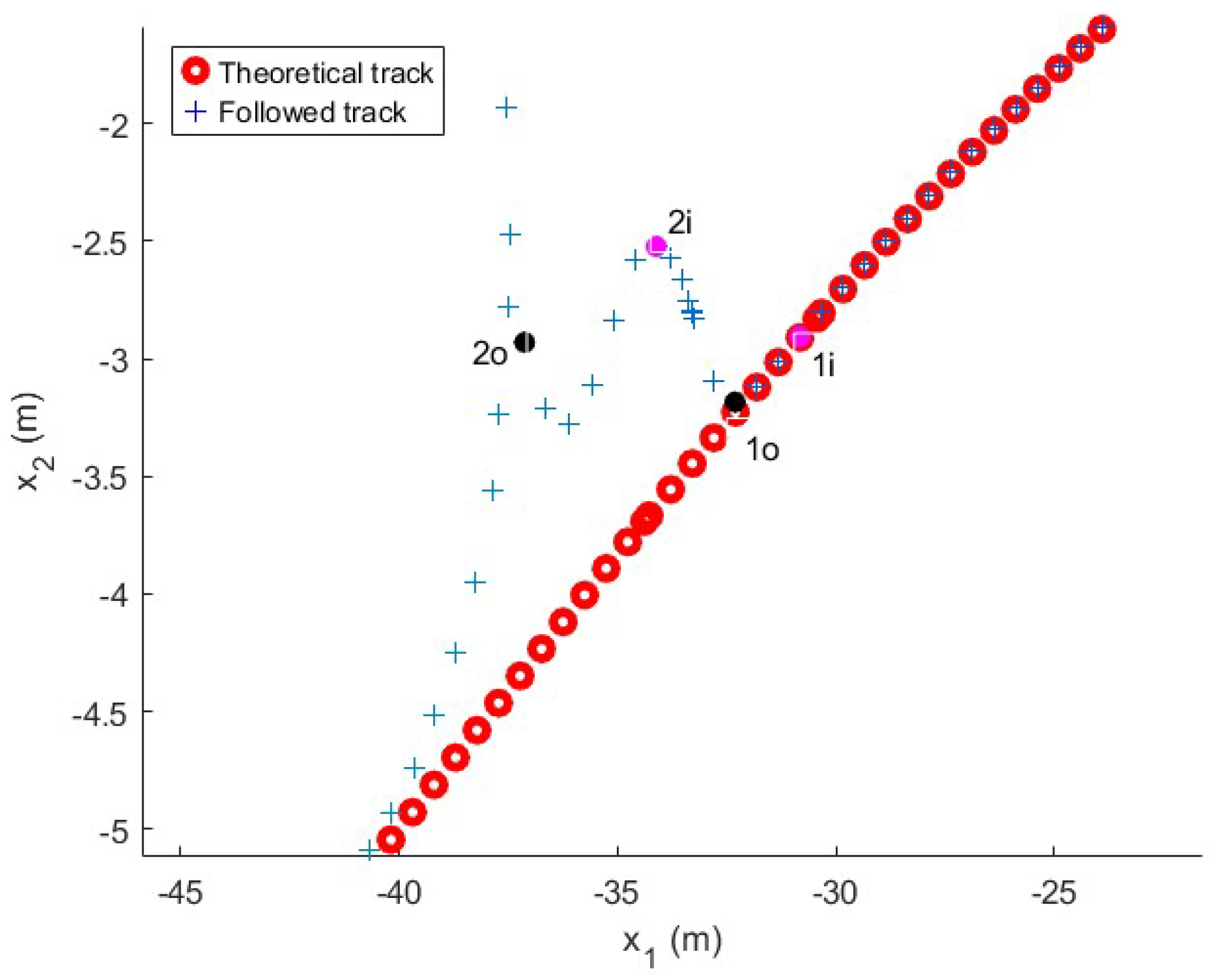
Figure 15.
Detail of the followed trajectory in the long maneuver test with perturbation. Point (pink dot) shows that before the relative angle compensator starts, the vehicle has already deviated from its trajectory due to the movement of the trailer. Point (black dot) shows the moment at which the relative angle compensator returns control to the trajectory follower.
Figure 15.
Detail of the followed trajectory in the long maneuver test with perturbation. Point (pink dot) shows that before the relative angle compensator starts, the vehicle has already deviated from its trajectory due to the movement of the trailer. Point (black dot) shows the moment at which the relative angle compensator returns control to the trajectory follower.
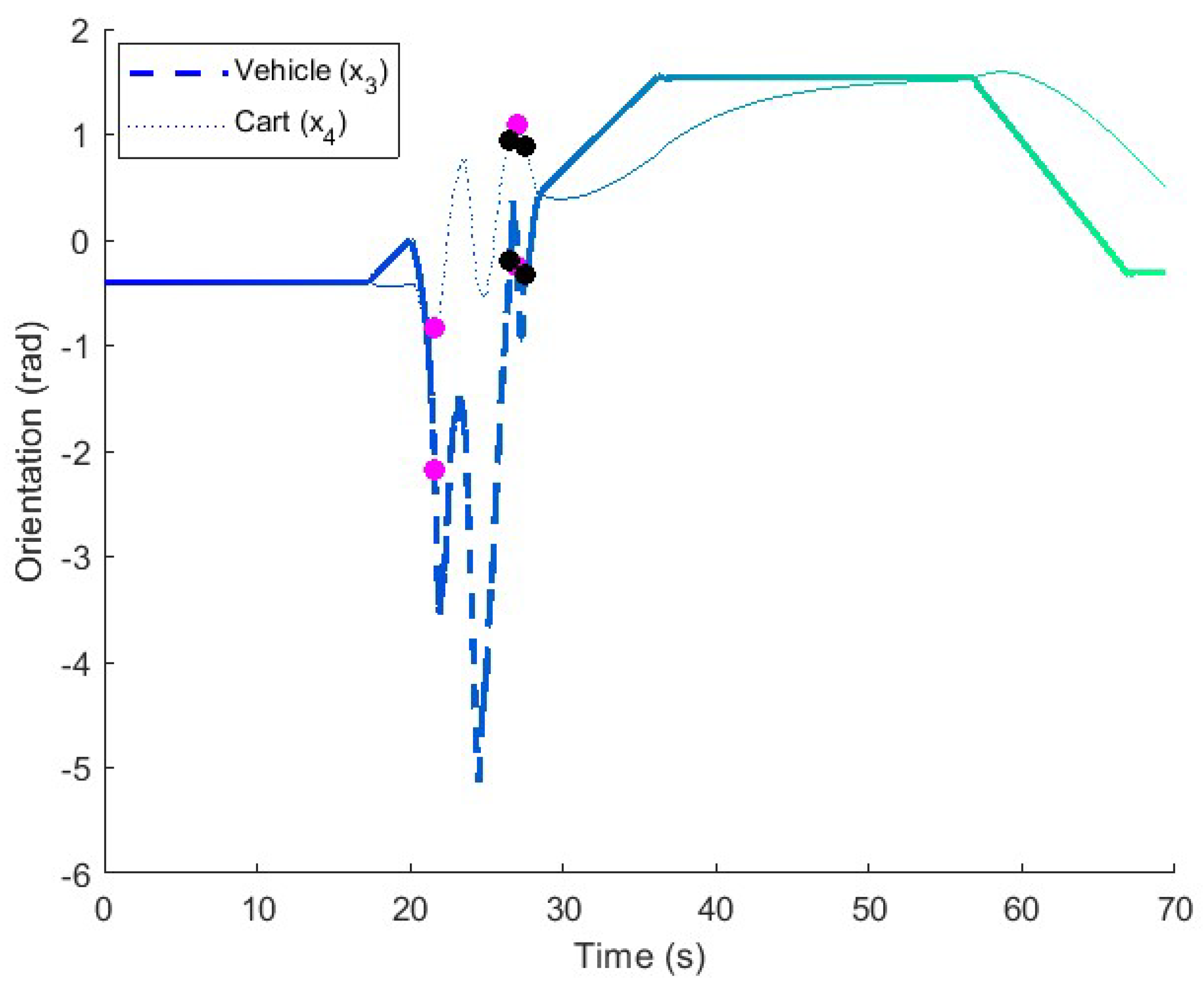
Figure 16.
Orientation in the long maneuver test with perturbation. Points and show the start and stop moments of the relative angle compensator in the orientation of the trailer and the vehicle. The relative angle is reduced during the compensation maneuver. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 16.
Orientation in the long maneuver test with perturbation. Points and show the start and stop moments of the relative angle compensator in the orientation of the trailer and the vehicle. The relative angle is reduced during the compensation maneuver. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
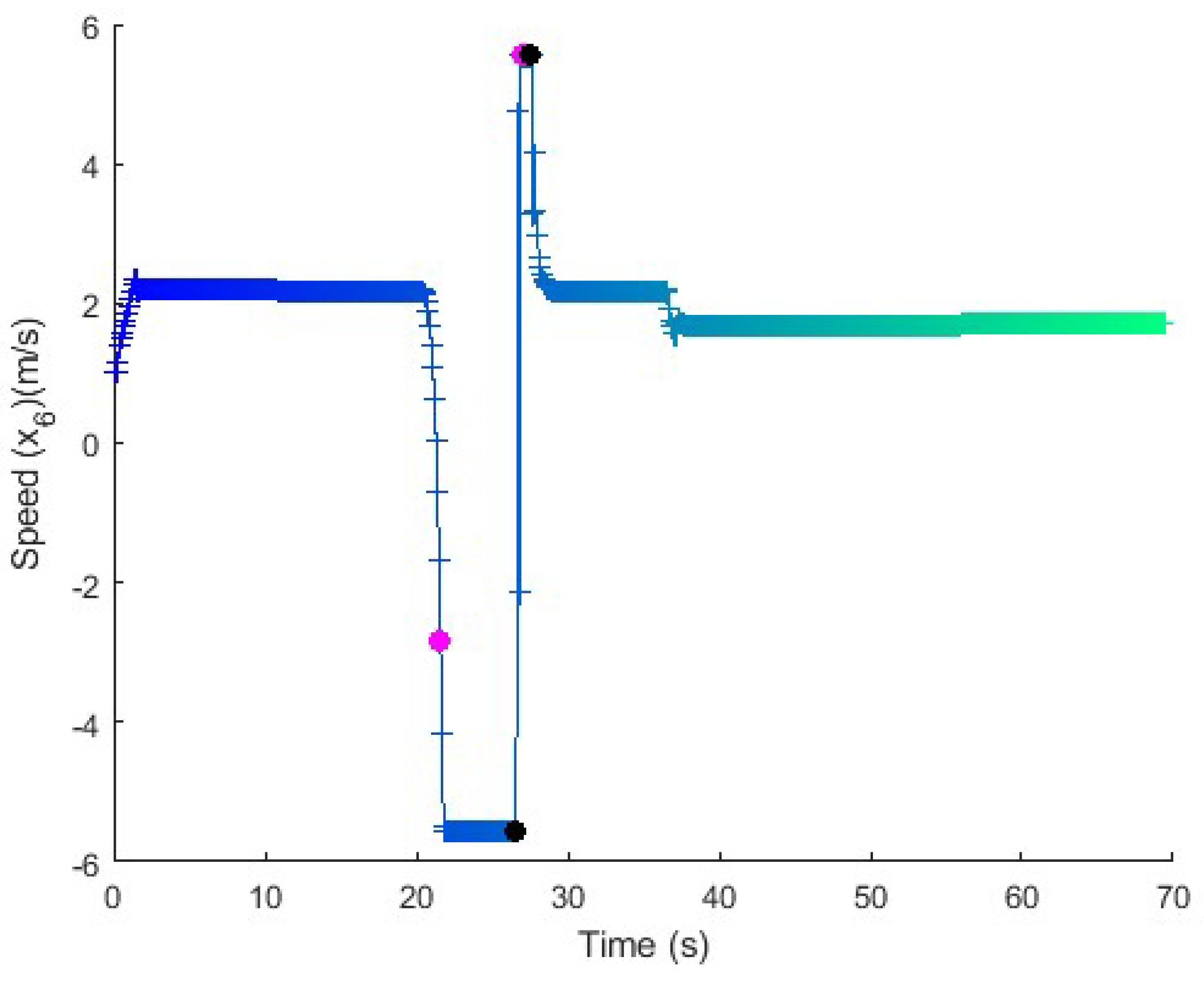
Figure 17.
Speed in the long maneuver test with perturbation. Once the relative angle compensator starts, the speed tends toward a constant value. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 17.
Speed in the long maneuver test with perturbation. Once the relative angle compensator starts, the speed tends toward a constant value. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
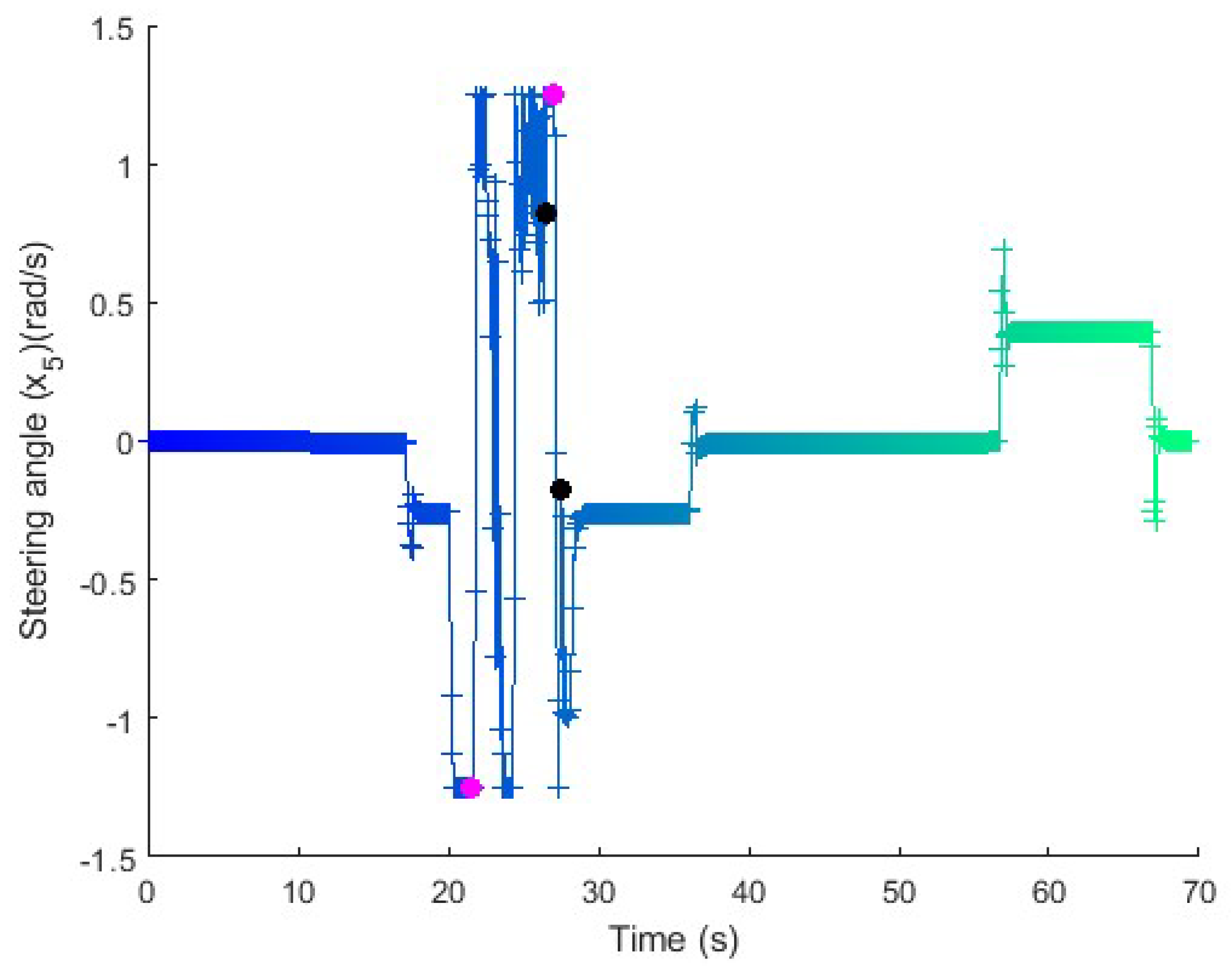
Figure 18.
Steering in the long maneuver test with perturbation. The relative angle compensator tends to counter maneuver the steering wheel to reduce the relative angle. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 18.
Steering in the long maneuver test with perturbation. The relative angle compensator tends to counter maneuver the steering wheel to reduce the relative angle. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
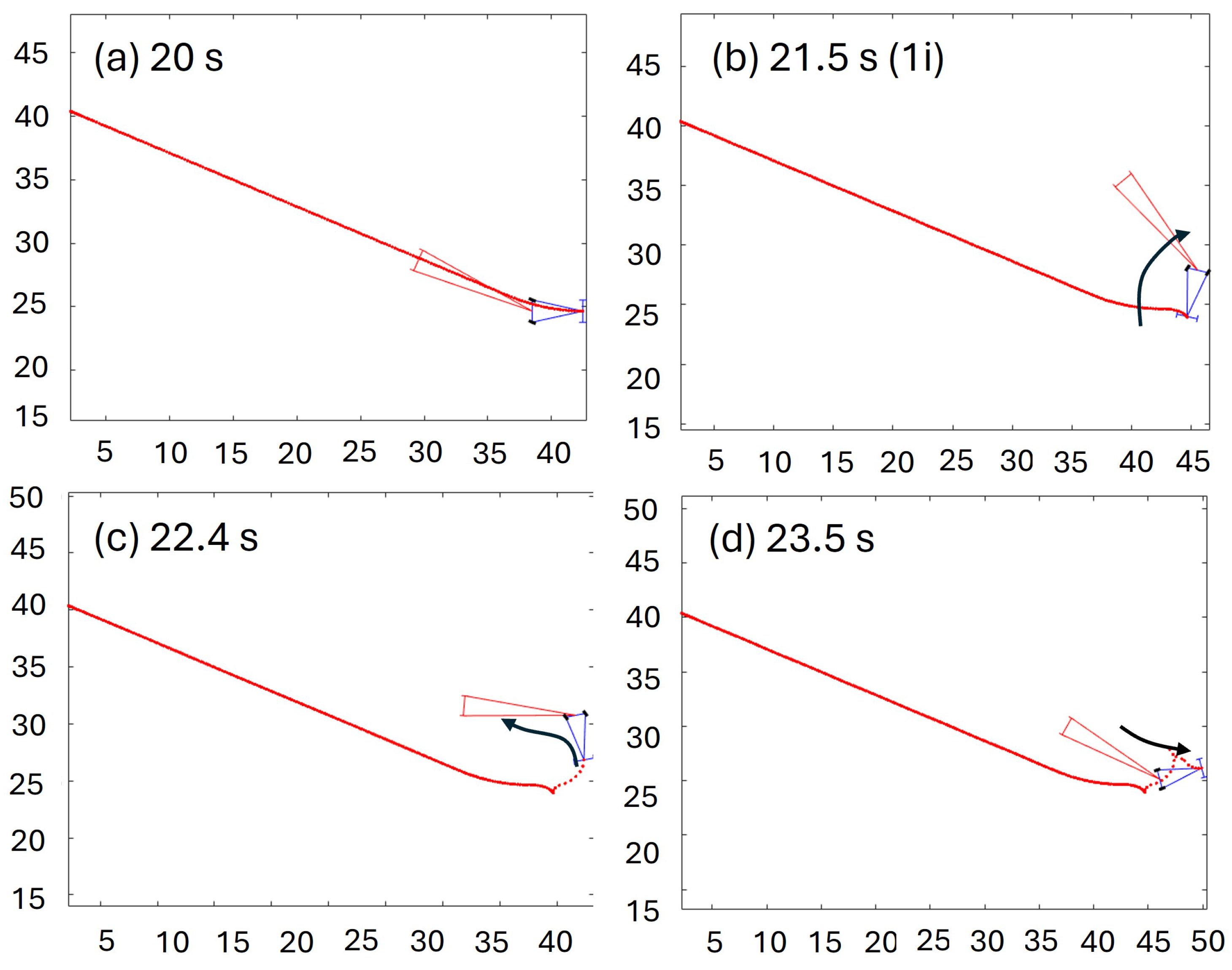
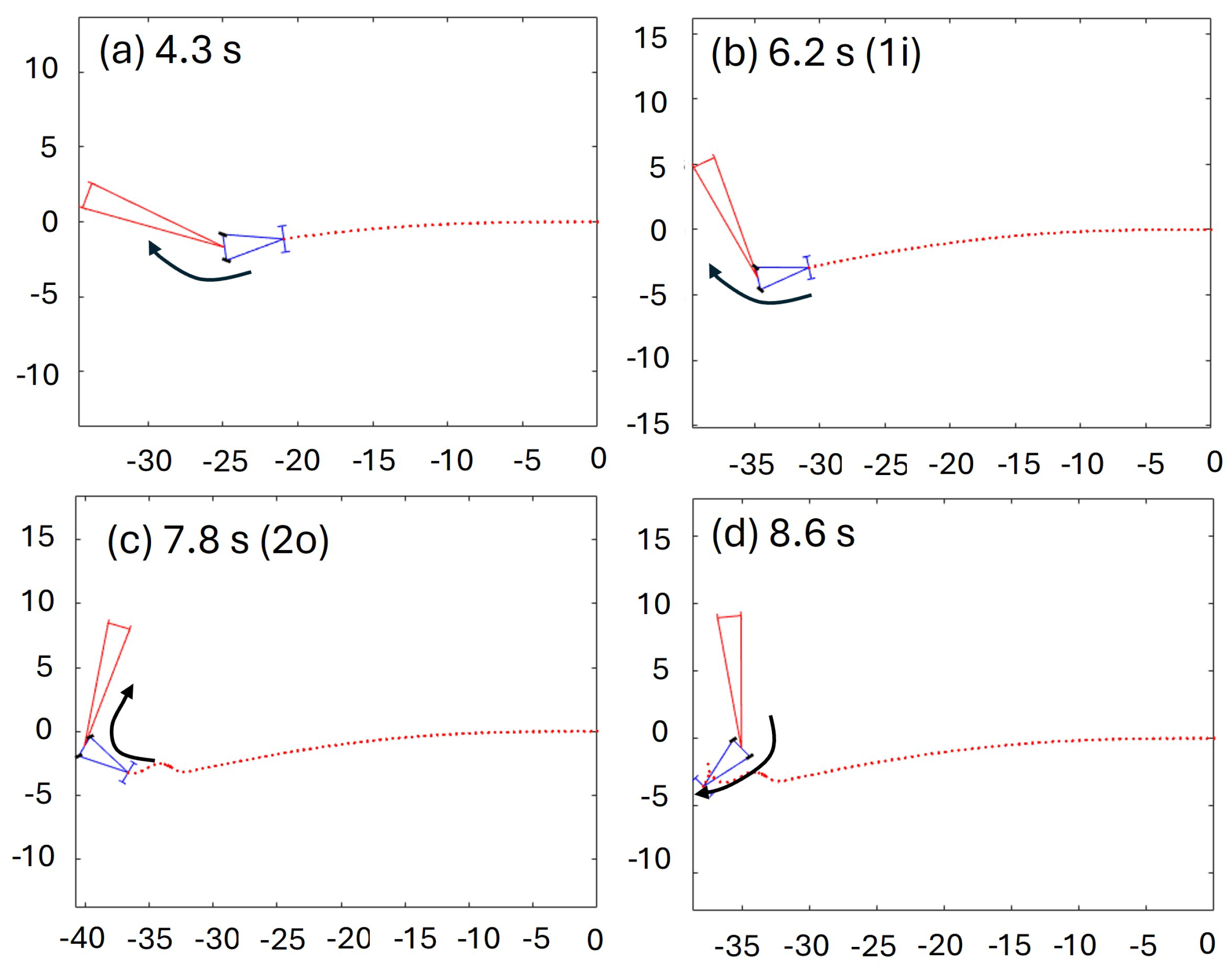
Figure 19.
Detailed representation of the maneuver in the long maneuver test with perturbation (vehicle in blue and trailer in red). (a) The vehicle follows the trajectory with a small relative angle between the vehicle and trailer; (b) the compensator activates at 21.5 s due to the perturbation; (c) the compensator moves the vehicle backwards to compensate for the angle; (d) once the vehicle and trailer are aligned, the vehicle restarts movement in the forward sense.
Figure 19.
Detailed representation of the maneuver in the long maneuver test with perturbation (vehicle in blue and trailer in red). (a) The vehicle follows the trajectory with a small relative angle between the vehicle and trailer; (b) the compensator activates at 21.5 s due to the perturbation; (c) the compensator moves the vehicle backwards to compensate for the angle; (d) once the vehicle and trailer are aligned, the vehicle restarts movement in the forward sense.
Figure 20.
Followed trajectory in the long maneuver test without a compensator. The pink dot shows that the relative angle compensator would have started operation very early during trajectory tracking.
Figure 20.
Followed trajectory in the long maneuver test without a compensator. The pink dot shows that the relative angle compensator would have started operation very early during trajectory tracking.
Figure 21.
Orientation in the long maneuver test without a compensator. The difference between the two curves shows a relative angle of almost rad during most of the trajectory, which implies a collision between the vehicle and trailer. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 21.
Orientation in the long maneuver test without a compensator. The difference between the two curves shows a relative angle of almost rad during most of the trajectory, which implies a collision between the vehicle and trailer. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 22.
Speed in the long maneuver test without a compensator. The speed evolution shows a very constant tendency along the whole trajectory because the controller does not try to compensate for the relative angle at any moment, which results in the collision between the vehicle and trailer. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 22.
Speed in the long maneuver test without a compensator. The speed evolution shows a very constant tendency along the whole trajectory because the controller does not try to compensate for the relative angle at any moment, which results in the collision between the vehicle and trailer. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 23.
Steering in the long maneuver test without a compensator. The steering evolution does not show any countermeasure to compensating for the excessive relative angle. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 23.
Steering in the long maneuver test without a compensator. The steering evolution does not show any countermeasure to compensating for the excessive relative angle. The pink dot shows the instant at which the relative angle compensator would have started operation if it would be present.
Figure 24.
Followed trajectory in the backward maneuver test. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern. In this case, the relative angle compensator is activated and deactivated twice, at (pink dots) and (black dots), respectively.
Figure 24.
Followed trajectory in the backward maneuver test. The figure shows the reference in red and the followed path with a color pattern that evolves over time to relate the track point to the variable evolution in the following figures, which maintain the same color pattern. In this case, the relative angle compensator is activated and deactivated twice, at (pink dots) and (black dots), respectively.
Figure 25.
Detail of the followed trajectory in the forward maneuver test. The first activation () is a short compensation with a minimal effect on the trajectory. The second one () shows a more drastic tracking error caused by the relative angle. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 25.
Detail of the followed trajectory in the forward maneuver test. The first activation () is a short compensation with a minimal effect on the trajectory. The second one () shows a more drastic tracking error caused by the relative angle. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 26.
Orientation in the backward maneuver test. The difference between the angles of the trailer and vehicle is lower after the actuation of the relative angle compensator, as can be seen in at points compared with . The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 26.
Orientation in the backward maneuver test. The difference between the angles of the trailer and vehicle is lower after the actuation of the relative angle compensator, as can be seen in at points compared with . The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 27.
Speed in the backward maneuver test. After the second actuation of the relative angle compensator (), the trajectory tracker changes the speed. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 27.
Speed in the backward maneuver test. After the second actuation of the relative angle compensator (), the trajectory tracker changes the speed. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 28.
Steering in the backward maneuver test. The first actuation of the relative angle compensator at shows a short actuation of the steering wheel, but the second one at results in a much larger counter-maneuver, with the steering wheel turning the complete range. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 28.
Steering in the backward maneuver test. The first actuation of the relative angle compensator at shows a short actuation of the steering wheel, but the second one at results in a much larger counter-maneuver, with the steering wheel turning the complete range. The pink and black dots represents the instants at which the relative angle compensator have been activated and deactivated, respectively.
Figure 29.
Detail of the maneuver in the backward maneuver test (vehicle in blue and trailer in red). (a) From the very beginning, the trailer tends to swing with respect to the vehicle; (b) at , the relative angle is large; (c) at , the relative angle compensator turns the vehicle to align the vehicle and cart; (d) once aligned, the vehicle continues in the forward direction.
Figure 29.
Detail of the maneuver in the backward maneuver test (vehicle in blue and trailer in red). (a) From the very beginning, the trailer tends to swing with respect to the vehicle; (b) at , the relative angle is large; (c) at , the relative angle compensator turns the vehicle to align the vehicle and cart; (d) once aligned, the vehicle continues in the forward direction.
Table 1.
Main dimensions of the vehicle and trailer.
Table 1.
Main dimensions of the vehicle and trailer.
| Vehicle length | 3.98 m |
| Vehicle width | 1.75 m |
| Vehicle weight | 1800 kg |
| Trailer length | 4.90 m |
| Trailer width | 1.86 m |
| Trailer weight | 480 kg |
Table 2.
Sizing procedure for the relative angle compensator.
Table 2.
Sizing procedure for the relative angle compensator.
| Gain | Equation |
|---|
| Response time of the speed controller (28) |
| Stability of the relative angle compensator (21) |
| Response time of the relative angle compensator (27) |
Table 3.
Comparison of the evolution with and without a relative angle compensator. The maximum error is the longest distance between the vehicle reference point in the middle of the front axle and the theoretical trajectory, the maximum angle is the greatest difference between the vehicle and trailer orientation, and the time delay is the increased duration of the test with respect to the reference case.
Table 3.
Comparison of the evolution with and without a relative angle compensator. The maximum error is the longest distance between the vehicle reference point in the middle of the front axle and the theoretical trajectory, the maximum angle is the greatest difference between the vehicle and trailer orientation, and the time delay is the increased duration of the test with respect to the reference case.
| Test | Max. Error | Max. Angle | Time Delay |
|---|
| Forward without compensator | m | rad | s |
| Forward with compensator | m | rad | s |
| Backward without compensator | m | rad | s |
| Backward with compensator | m | rad | s |