GenDRA: Generative Data Reconstruction Attacks on Federated Edge Learning and Countermeasures

Abstract

Federated edge learning (FEL) unites the decentralized training capabilities of multiple edge nodes to allow model gradient sharing and parameter aggregation across a peer-to-peer network. However, many intrinsic policy conflicts still exist in FEL, for example, the open accessibility of gradients will lead to the privacy leakage risk during the federal aggregation process. In this paper, we first identify that malicious users weaponized with generative artificial intelligence (GenAI) can generate fake samples that are almost identical to FEL participants’ training data. By analyzing how different configurations of GenAI affect attack effectiveness, we find that an adversary with strong patchwork and reconstruction capabilities can stealthily steal diverse training data from nearly all FEL participants. To thwart such a generative data reconstruction attack (GenDRA) scheme, we propose a novel target semantic dissolution (TSD) mechanism for enhancing the privacy-preserving ability of FEL, which encrypts only a very small number (≤10%) of gradient values in each training round that have a significant impact on human visual formation using format-preserving encryption. With TSD, the speculator cannot obtain a fake sample that is visually similar to the training sample because real gradients are actively concealed. Extensive experiments based on four benchmark datasets are performed to demonstrate the huge threat of GenAI and the effectiveness of TSD in all aspects: compelling accuracy performance, strong visual privacy guarantee, and low computing overhead.

1. Introduction

Federated edge learning (FEL) intelligently analyzes decentralized data that are aggregated from various sensors at edge servers in the Internet of things (IoT). From the perspective of collaborative intelligence, the FEL system mainly solves the problem of distributed data utilization, feature sharing, and global model aggregation [1]. On the one hand, IoT operators often prohibit user data from leaving their local network domains. Thus, FEL provides a data processing paradigm, executing learning procedures locally [2]. On the other hand, to achieve a global decision-making model, FEL allows distributed nodes to share model parameters with each other and then generate a global learning model [3]. 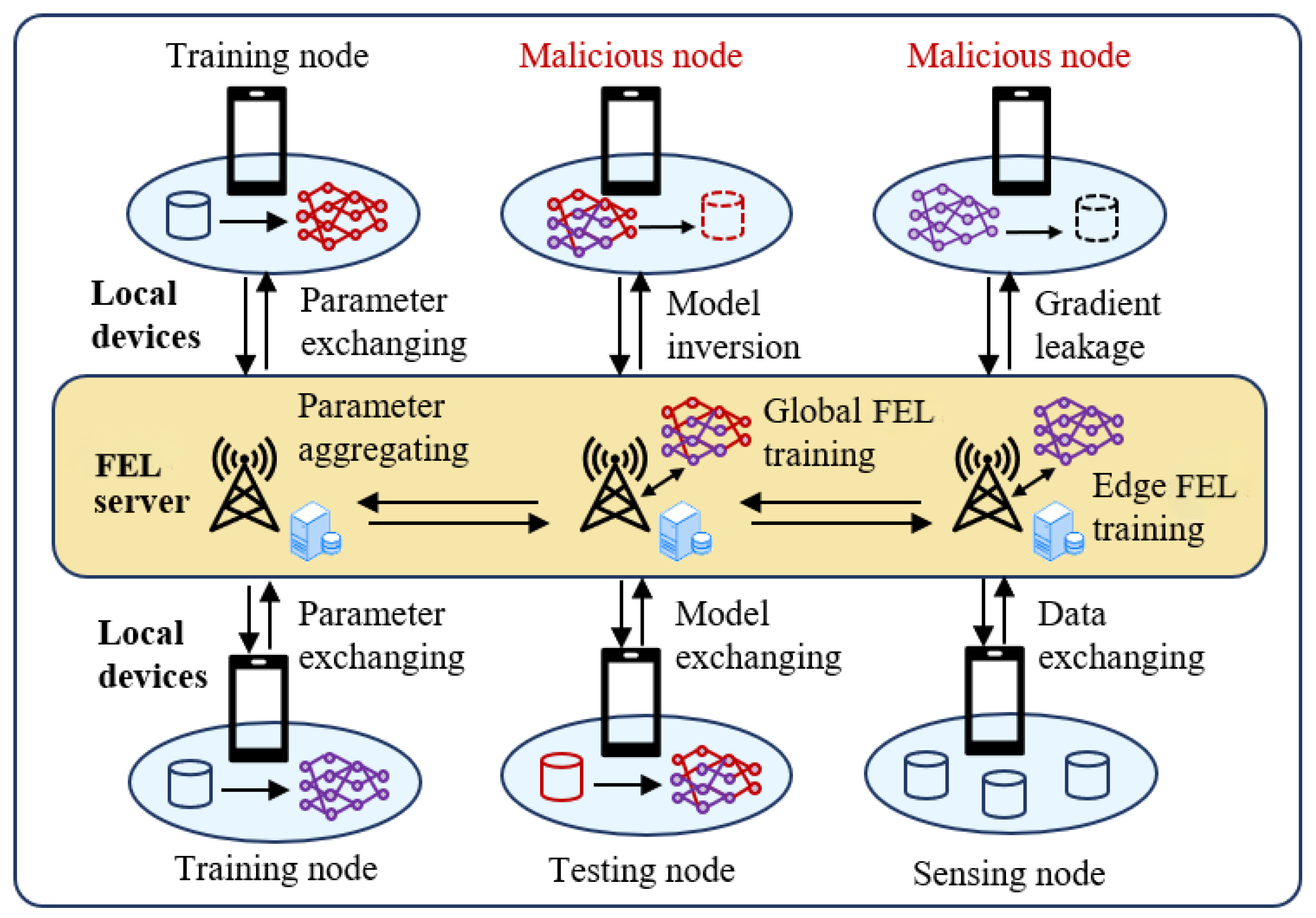As illustrated in Figure 1, a typical FEL system includes one central server, several local devices, and multiple data sensors. Each local device updates its local learning model using on-device data and submits the resulting model parameters for global aggregation. After each training round, each local device will receive an updated global learning model. FEL makes it possible to process massive IoT data in a distributed way and generates better decisions using the global learning model. Updating the global learning model in FEL can be periodic or triggered. Due to its inherent privacy-reserving and mobility support ability, FEL is perceived to have great potential in various industries like unmanned aerial vehicles (UAV) and financial payments.

However, recent studies show that FEL faces significant privacy leakage threats [4]. According to the difference in attack periods, privacy leakage threats in FEL can be mainly divided into two categories: (1) gradient leakage attacks, which aim to reconstruct the training data in the current training round based on submitted gradients [5,6,7]; (2) model inversion attacks, which focus on reconstructing all training samples from a pretrained model [8,9,10]. The former will recurrently produce dummy data and enforce the dummy gradient to approximate the ground-truth gradient shared between parameter servers and local devices. The latter tends to utilize the generative adversarial network (GAN) to improve the quality of reconstructed data [11]. However, existing privacy leakage threats often rely on overly strict or impractical assumptions. For example, the success rate of gradient leakage attacks drops significantly when the batch size exceeds one or when the FEL model has undergone multiple training rounds. In practice, it is almost impossible for local devices to feed only one sample in each training round due to the limitation of communication resources and computing resources. Model inversion attack cannot obtain high-quality reconstruction data without all model parameters and a large number of iterations. Since both gradient leakage attack and model inversion attack are not tightly coupled with each other, it is difficult to reconstruct fresh training data.

In this paper, we first verify our hypothesis that the adversary can implement a unified attack on FEL by combining the above two kinds of attacks to reconstruct fresh training data. In the unified attack, we use the derivative function of the similarity between dummy gradients and real gradients as one signal to update a generator and additionally take the derivative function of the similarity between dummy labels and real labels as another signal to update the same generator. After being attacked, it can be found that the adversary obtains a generator that can reconstruct dummy data similar to fresh training data. Furthermore, it also can be found that the unified attack has greater configurability and interpretability in FEL due to the strong bondability between the participating node and the generator.

To mitigate this unified attack, we propose to use format-preserving encryption to convert partial bits of real gradients into uniformly distributed noises, which prevents the adversary from capturing real gradients. With our defense, the objective function of the adversary will be changed because the submitted real gradients will be replaced with perturbed gradients. Different from existing defense methods, our defense almost has no effect on the convergence of the training process for most perturbed gradients belonging to endogenous heavy-tailed gradient noises, and only partial bits of the gradient values are encrypted. The main contributions are summarized as follows:

• A unified formulation of different privacy leakage variants is established, which focuses on reconstructing the fresh training data in FEL. The unified attack consists of two stages: (1) the free-riding stage and (2) the data reconstruction stage. In the free-riding stage, the dummy data obtained from the generator activate local devices to retrain the global FEL model, which creates an opportunity for the adversary to capture gradient information automatically. In the data reconstruction stage, the adversary jointly optimizes gradient similarity and prediction similarity through a max–min adversarial objective to update the generator.
• A novel privacy leakage mitigation (PLM) framework is proposed based on format-preserving encryption, which effectively hides the correlation between private information and gradients. With PLM, attackers cannot reconstruct fresh training data clearly without significant accuracy reductions. Moreover, the PLM incurs less computational cost, for it only encrypts fewer bits of endogenous heavy-tailed gradient noise.
• Extensive experiments are implemented to validate the effectiveness of the proposed attack and defense methods. The results demonstrate that privacy leakage threats on FEL can be significantly mitigated with our methods.

The rest of this paper is organized as follows. Section 2 discusses the related work. Section 3 instantiates the system model. Section 4 introduces the overview and workflow of the proposed PLM scheme. Extensive evaluations are conducted in Section 5. Finally, Section 6 summarizes our work.

2. Related Work

2.1. Federated Edge Learning

FEL is an application fusion of mobile edge computing and federated learning under the IoT scenario [12,13]. It realizes a collaborative learning paradigm by distributing learning tasks to network edges. The life cycle of FEL models usually includes six stages: local data collection, data pre-processing, local model training, parameter aggregation, global model inference, and global model distribution. The FEL server usually performs operations such as parameter aggregation, global model inference, and global model distribution. The local client performs operations such as local data collection, data pre-processing, and local model training.

Although keeping data local provides a certain level of security, FEL still faces many privacy leakage threats [14]. On the one hand, the untrusted parameter server may reconstruct training data from the gradients submitted by each local device using the privacy leakage algorithms proposed in [6]. On the other hand, the adversary can also reconstruct the training set based on model inversion [15]. The common feature of privacy leakage threat is to generate dummy samples that can approximate real gradients, predictions, and weight parameters of the learning model. A privacy-preserving FEL model should achieve self-immunity against different privacy leakage threats.

2.2. Privacy Leakage Mitigation in FEL

Many privacy leakage mitigation countermeasures have been studied in recent years, which can be divided into two branches: (1) cryptography-based gradient hiding and (2) sparsity-based gradient hiding. The former aims at preventing untrusted servers from accessing real gradients during the FEL training process. Encrypting these gradients before being outsourced to the FEL server using homomorphic encryption is helpful for ensuring the availability, integrity, and confidentiality of gradients [16,17]. However, this method requires redundant encryption and decryption processes during each training round, resulting in too high communication and computational costs in real scenarios. In a small network with only several local devices, it is uneconomic to add a specific key server separated from the parameter server to maintain the complex homomorphic encryption process. The latter aims to make attackers unable to reconstruct training data without sacrificing any model accuracy. The implementation of sparsity-oriented gradient hiding includes gradient pruning and differential privacy, which can be directly applied in the distributed training process without any prior knowledge. Therein, the differential privacy method can add Gaussian noises into any position of the input layer, hidden layer, and output layer [18,19,20]. Different from differential privacy, gradient pruning effectively suppresses the shortcut phenomenon in the stochastic gradient descent (SGD) process, which can also be used to optimize the communication cost of FEL [21,22,23]. However, the performance of gradient pruning and differential privacy closely depends on the resemblance between the dummy gradient and the real gradient. When the resemblance is low enough, the model accuracy will be significantly reduced. Moreover, Li et al. [7] found that leveraging the latent space of generative adversarial networks (GANs) trained on public image datasets as a prior can compensate for information loss during gradient matching, thereby enabling the reconstruction of higher-quality data.

Motivated by these challenges, in this paper, we first establish a unified formulation for different variants of privacy leakage threats. Unlike existing methods that can only reconstruct samples that participated in the initial few epochs of each training round, our method combines model inversion attacks and gradient leakage attacks to jointly reconstruct fresh training data reliably. To counter this generative, versatile, and powerful attack at low cost, we propose a novel privacy leakage mitigation (PLM) scheme by introducing format-preserving encryption, which can induce attackers to reconstruct data with high background noise rather than real fresh training data.

3. System Model

3.1. FEL System Model

A typical FEL system often consists of one parameter server and M local clients. Each local client $C^m$ has one well-marked dataset $D^m=(X^m,Y^m)$, where $m\in 1,2,\dots ,M$, $X^m={\left\{x_i\right\}}_{i=1}^{N^m}$, and $Y^m={\left\{y_i\right\}}_{i=1}^{N^m}$, in which $N={\sum }_m^M{N}^m$ denotes the total sample number in the FEL. A federal classification task aims to learn a non-linear function f parameterized by ${\left\{W^m\right\}}_{m=1}^M\in \mathrm{𝒲}$ by optimizing the following objective function:

$$\mathcal{L}=\sum _{m=1}^M{\lambda }^m{\mathcal{L}}^m(f^m(X^m,W^m),Y^m),$$

(1)

where ${\mathcal{L}}^m$, which denotes that the loss at client m is often implemented by cross-entropy loss.

The most popular gradient aggregation algorithm for federated learning is FederatedAveraging [24]. During the model training procedure, stochastic gradient descent (SGD) technology is utilized to minimize Equation (1). The objective of multiple training rounds is to learn the optimized $\widehat{W}$ that can minimize $\mathcal{L}$:

$$\widehat{W}=\underset{W}{arg min} \mathcal{L}=\underset{W}{arg min}\sum _{m=1}^M{\displaystyle \frac{N^m}{N}}{\mathcal{L}}^m.$$

(2)

In each training round t of mobile federated learning, each client will train a local learning model using local data $D^m$ and then send model gradients $\Delta W_t^m$ to the parameter server to update the global model parameter $W_t$ as $W_{t+1}$. The parameter server aggregates model gradients collected from each client using the FederatedAveraging algorithm and distributes an updated global model $W_{t+1}$ to each client. The training process in each client and parameter server is formulated as follows:

$$\begin{array}{cc}Client:\hfill & \left(1\right) W_{t+1}^m=W_t^m-\sum _i^I\sum _b^B\eta \nabla {\mathcal{L}}^m(f;b),\hfill \\ \hfill & \left(2\right) \Delta W_{t+1}^m=W_{t+1}^m-W_t^m,\hfill \end{array}$$

(3)

$$\begin{array}{cc}Server:\hfill & \left(1\right) W_{t+1}=W^t+\sum _{m\in M}{\displaystyle \frac{N^m}{N}}\Delta W_{t+1}^m,\hfill \end{array}$$

(4)

where $\eta$ denotes the learning rate, and b denotes the training batch. Furthermore, $W_{t+1}^m$ represents the local model parameters after the training round t, and $W_{t+1}$ stands for the updated global model after the training round t. In practice, not all clients will be specified to participate in gradient aggregation at round t.

3.2. Unified Attack Model

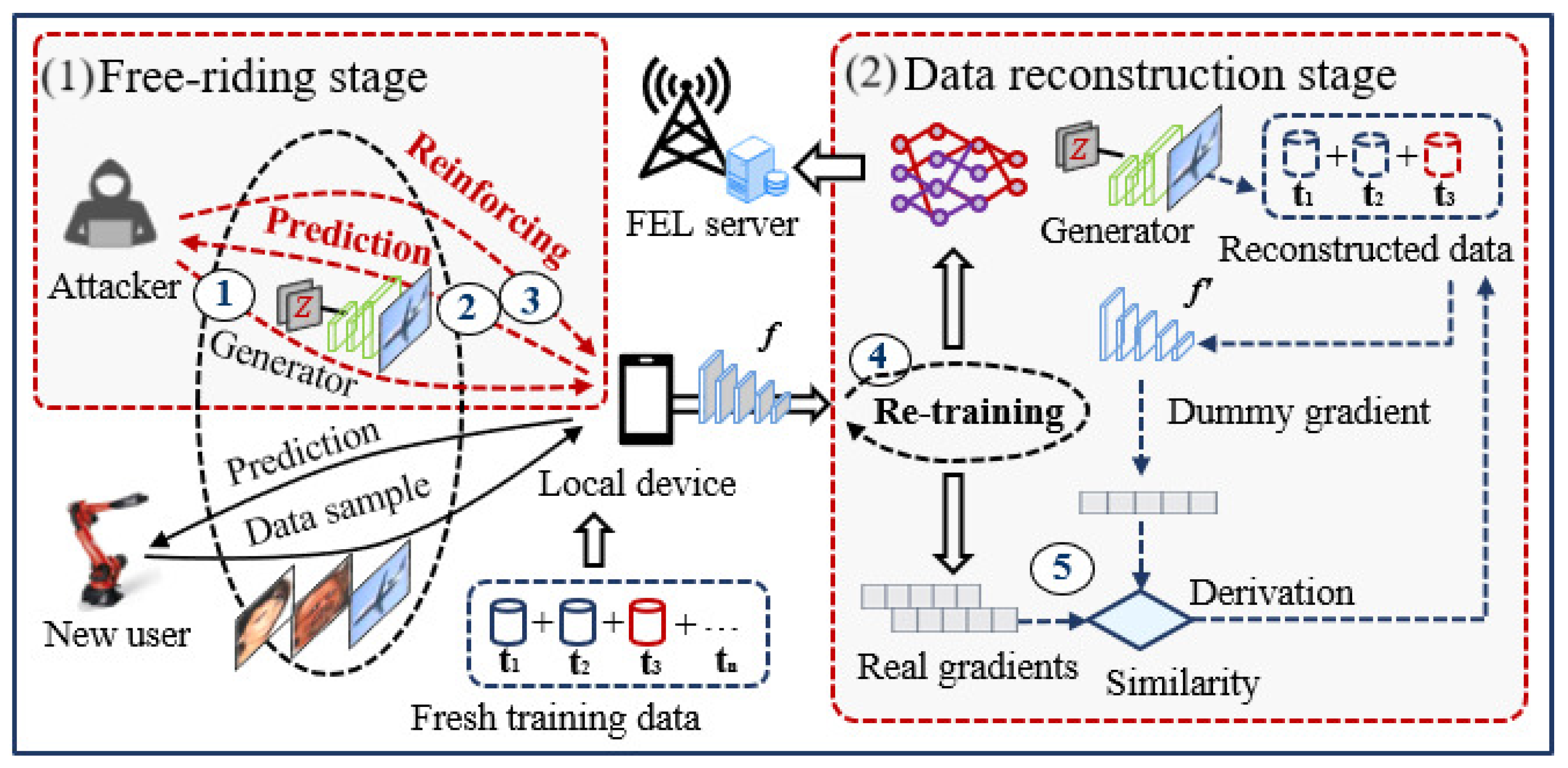
The proposed unified attack model takes full advantage of FEL’s characteristics on distributed training, as illustrated in Figure 2. Specifically, our unified attack model consists of two core stages: (1) in the free-riding stage, the adversary impersonates a legitimate participant to obtain access to the FEL model. (2) In the data reconstruction stage, the adversary trains a generator under the supervision of a pretrained FEL model to produce dummy data. These dummy samples are then repeatedly queried against the model to generate dummy gradients that align with the captured ones. At this point, due to the semantic gap between the dummy and real data, the model’s accuracy degrades. Once the local device detects that the model accuracy falls below a predefined threshold, it will trigger a retraining process for the FEL model. Therefore, fresh training data on each local device will participate in the FEL model training process. In the later stage, the adversary needs to solve an adversarial max–min optimization problem to inversely generate dummy data that approximate fresh training data. Note that dummy data obtained by the existing model inversion attack are similar to history training data, while dummy data obtained by the proposed unified attack are similar to the fresh training data.

3.2.1. Free-Riding Stage

The unified attack model can automatically activate the FEL system to make the adversary participate in the local model training process and the global model aggregation process, acting as a free rider. The first attack round launched to activate the FEL mainly consists of three steps. First, the adversary randomly specifies the labels of the private data to be reconstructed, samples the noises from the uniform distribution, and inputs the noises into the generator. Secondly, a set of low-quality dummy data can be generated, which can be mixed with real data to repeatedly query the pretrained model. At this time, the accuracy of the pretraining model on dummy data and fresh training data is low. To enhance the model accuracy on these data, the global FEL model needs to be retrained. Thirdly, once the model retraining process of FEL is activated, the fresh training data will be used as a training set to participate in local training and model aggregation. Meanwhile, the adversary can participate in the retraining process and obtain gradient information.

3.2.2. Data Reconstruction Stage

For standard FEL, each client randomly selects a mini-batch of samples $B^m(x_t^m,y_t^m)$ from their own local dataset to calculate local gradients in the training round t:

$${\nabla }_{W}F\left(x_t^m\right)={\displaystyle \frac{\partial \mathcal{L}(F,x_t^m,y_t^m)}{\partial W_t}}.$$

(5)

Given gradients ${\nabla }_{W}F\left(x_t^m\right)$, the adversary can recover training data $(x_t^i,y_t^i)$. A detailed reconstruction process can be divided into three steps: (a) generate dummy data, (b) compute dummy gradients and dummy labels, and (c) compute the similarity loss and update the dummy data. Dummy gradients denoted via ${\nabla }_W\widehat{F}\left({\widehat{x}}_t^m\right)$ are generated by feeding the dummy data ${\widehat{x}}_t^m$ and the dummy label ${\widehat{y}}_t^m$:

$${\nabla }_W\widehat{F}\left({\widehat{x}}_t^m\right)={\displaystyle \frac{\partial \mathcal{L}(F,{\widehat{x}}_t^m,{\widehat{y}}_t^m)}{\partial W_t}}.$$

(6)

For natural images, the gradient is unique for mapping inputs onto labels. To reconstruct high-quality inputs, a KL-divergence loss is defined to implement the attack:

$${\widehat{x}}_t^{m\ast },{\widehat{y}}_t^{m\ast }=\underset{{\widehat{x}}_t^m,{\widehat{y}}_t^m}{argmin}{\displaystyle \frac{{\nabla }_W\widehat{F}\left({\widehat{x}}_t^m\right)\ast {\nabla }_{W}F\left(x_t^m\right)}{\left|\right|{\nabla }_W\widehat{F}\left({\widehat{x}}_t^m\right)\left|\right|\ast \left|\right|{\nabla }_{W}F\left(x_t^m\right)\left|\right|}}.$$

(7)

Since dummy samples in the unified attack model are generated by the generator, the ultimate goal is the following:

$$\widehat{G}{\left(z\right)}_t^{m\ast },{\widehat{y}}_t^{m\ast }=\underset{\widehat{G}{\left(z\right)}_t^m,{\widehat{y}}_t^m}{argmin}{\displaystyle \frac{{\nabla }_W\widehat{F}(\widehat{G}{\left(z\right)}_t^m)\ast {\nabla }_{W}F\left(x_t^m\right)}{||{\nabla }_W\widehat{F}(\widehat{G}{\left(z\right)}_t^m)||\ast ||{\nabla }_{W}F\left(x_t^m\right)||}}.$$

(8)

According to [25], label details can be analytically reconstructed from leaked gradients of each client model. Based on the known label information, we find that attackers can persistently reconstruct fresh training data from leaked gradients. The whole workflow of the unified attack can be formulated using Algorithm 1.

Algorithm 1: Unified attack.

3.3. Comparison with Existing Attacks

Compared to traditional DLG attacks, unified attacks benefit from the joint supervision of the pretrained model and the generator, leading to faster and more stable convergence. Both differential privacy and gradient pruning make it difficult to resist unified attacks because the attack success rate is closely bound to the accuracy of the pretrained FEL model. Considering the memory of neural networks, a high-accuracy pretrained FEL model will guide the generator to learn more prior knowledge from the neural memory, which assists the generator in generating higher-quality dummy data.

Different from existing model inversion attacks, the unified attack process does not care about historic training samples of the pretrained FEL model but focuses on reconstructing fresh training data in the current training round. Once the adversary implants the generator on the local device, fresh training data can be stolen by attackers at any time. It can be seen that the unified attack is a fully new attack model, which has a profound impact on FEL security. Furthermore, in the unified attack model, the adversary has stronger concealment because of acting as a free rider.

4. Proposed PLM Framework

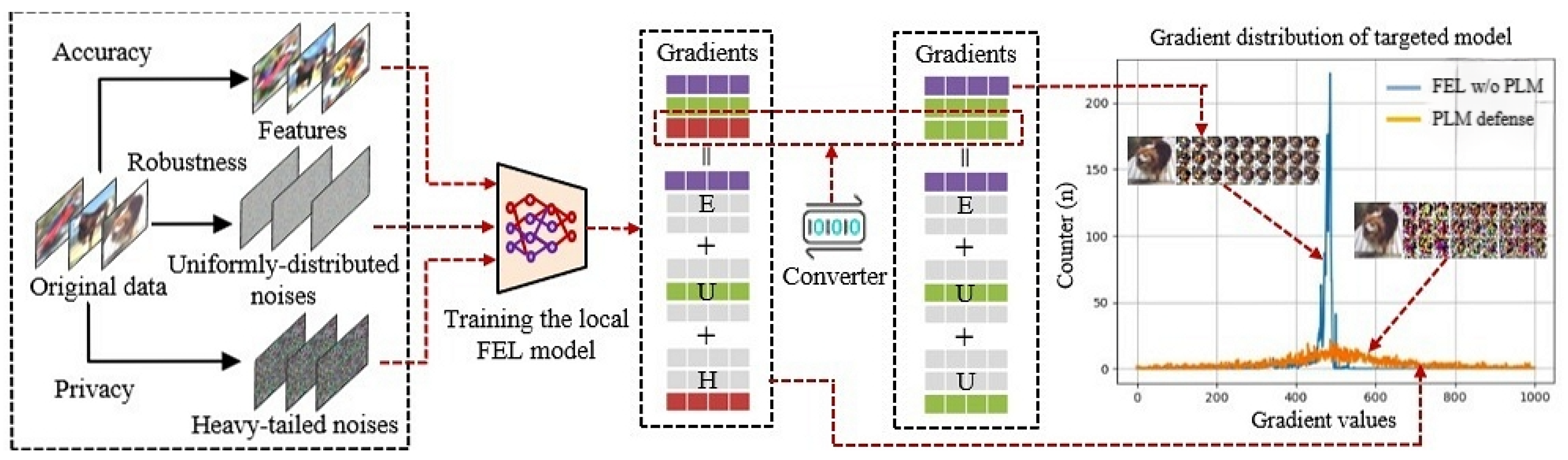
In this section, we propose a privacy leakage mitigation (PLM) framework, which fixes the disadvantages of existing privacy-enhancing methods and greatly improves defense efficiency. To defend against unified attacks, we actively convert heavy-tailed noises into uniformly distributed noises using the format-preserving encryption algorithm, which can confuse the human eye by damaging background pixels but provide good learning performance. The training dataset in our PLM framework is modeled in three parts: (1) features, (2) uniformly distributed noise, and (3) heavy-tailed noise. The learning process based on “trial and error" is treated as end-to-end feature fixing. Once the learning model extracts enough necessary features that can prove that all training data belong to the corresponding ground-truth labels, the model training process is completed. However, different kinds of noises (i.e., hidden in the inputs or produced in the phases of stochastic gradient descent and back-propagation) have different impacts on the learning process. On the one hand, filtering some noises on the inputs can accelerate the convergence of neural networks [26]. On the other hand, adding some noises can improve the robustness of neural networks [27]. Furthermore, using specially designed noises, malicious users can implement highly converted adversarial example attacks [28], data poisoning attacks [29], and backdoor attacks [30].

4.1. Motivation and Overview of PLM

Both encryption-based gradient hiding and sparsity-driven gradient hiding have problems when applied in FEL scenarios. These methods inherited from traditional federated learning suffer from several serious drawbacks as follows: (1) the defender was assumed to have sufficient computation resources in the past to encrypt all gradients during each training round, but this is almost impossible when the size of the targeted FL model is deployed in mobile edge computing scenarios; (2) the gradient noises will also be pre-processed (e.g., encrypted or pruned) together with predicted gradient values, which significantly hurts the learning convergence; (3) the interpretability of existing defenses is too low to treat every gradient value indiscriminately.

Intuitively, inspired by gradient pruning, each FEL client can pre-process its local gradients before submitting them to the server. Instead of directly zeroing out large gradients, we randomly map heavy-tailed values into a uniform distribution. An overview of the proposed scheme is illustrated in Figure 3. Specifically, PLM consists of two key components to realize this randomized defense process:

• A heavy-tailed gradient noise converter is proposed for each FEL client to prevent gradient leakage attacks;
• A model training strategy via PLM is designated to attentively adjust the trade-off between privacy budget and accuracy.

Figure 3. Overview of the proposed PLM framework. Different from existing defense methods, PLM prevents unified attacks by retrofitting internal hidden gradient noises, which allows PLM to obtain a higher defense effect with a very small computing cost and accuracy loss.

Figure 3. Overview of the proposed PLM framework. Different from existing defense methods, PLM prevents unified attacks by retrofitting internal hidden gradient noises, which allows PLM to obtain a higher defense effect with a very small computing cost and accuracy loss.

Note that we do not add any additional noises but make full use of internal gradient noises, which minimizes the defense cost against differential privacy [19].

To build a secure FEL that can be immune to more serious privacy leakage threats, the PLM framework is proposed in this paper, which selectively encrypts a few parts of endogenous heavy-tailed gradient noises using the format-reserved encryption algorithm. The strengths of this paper against existing studies includes three aspects: (1) gradients are encrypted as ciphertext locally before submitting them to the FEL server, and this ciphertext also participates in the model aggregation process for the format of the encrypted gradient. Based on this, the quality of reconstructed data is damaged for these ciphertext acts as uniform noises are added into real gradients; (2) the global model can achieve a high privacy-preserving ability with a low computing cost as only a few parts of heavy-tailed gradient noises are encrypted; (3) PLM makes the privacy leakage threat controllable for the learner due to the flexibility of the encryption rate. To the best of our knowledge, this is the first work to study unified attacks and their countermeasures.

4.2. Gradient Noises in FEL

If a random layer is not added to the neural network and each training round uses the entire dataset, the trained neural network is deterministic and will not introduce any gradient noises. But, in practice, as shown in Equations (3) and (4), we randomly sample b samples as a batch from the dataset at training round t (with or without replacement) and then estimate the gradient on this batch. The gradient noise is expressed as the bias of the gradient on the batch from the average value (if the gradient is an unbiased estimation, the average value is the true value); that is, there are many gradient noises in each training round:

$$\begin{array}{cc}{\mathcal{U}}^m\hfill & \triangleq \nabla {\widehat{\mathcal{L}}}^m(F;b)-\nabla {\mathcal{L}}^m(F;D),\hfill \end{array}$$

(9)

where $\nabla {\widehat{\mathcal{L}}}^m(F;b)$ represents practical gradients, and $\nabla {\mathcal{L}}^m(F;D)$ denotes ideal gradients. The traditional view is that gradient noise conforms to the uniform distribution. With many experimental observations and theoretical derivations, S. Umut et al. [31] found that there are defects in fitting gradient noise via uniform distribution, and the distribution of gradient noise is more in line with the heavy-tailed distribution. Therefore, the real updating of FEL models in FEL should be rewritten as follows:

$$\begin{array}{cc}{W}_{t+1}^m\hfill & =W_t^m-\sum _i^I\sum _b^B\eta \nabla {\mathcal{L}}^m(F;b)+\eta {\sigma }^{\frac{1}{\alpha }}{\mathrm{𝒮}}_t,\hfill \end{array}$$

(10)

where $\sigma$ is constant variance, and $\alpha \in (0,2]$ denotes the scaling factor (when $\alpha =2$, it will be fitted as a uniform distribution).

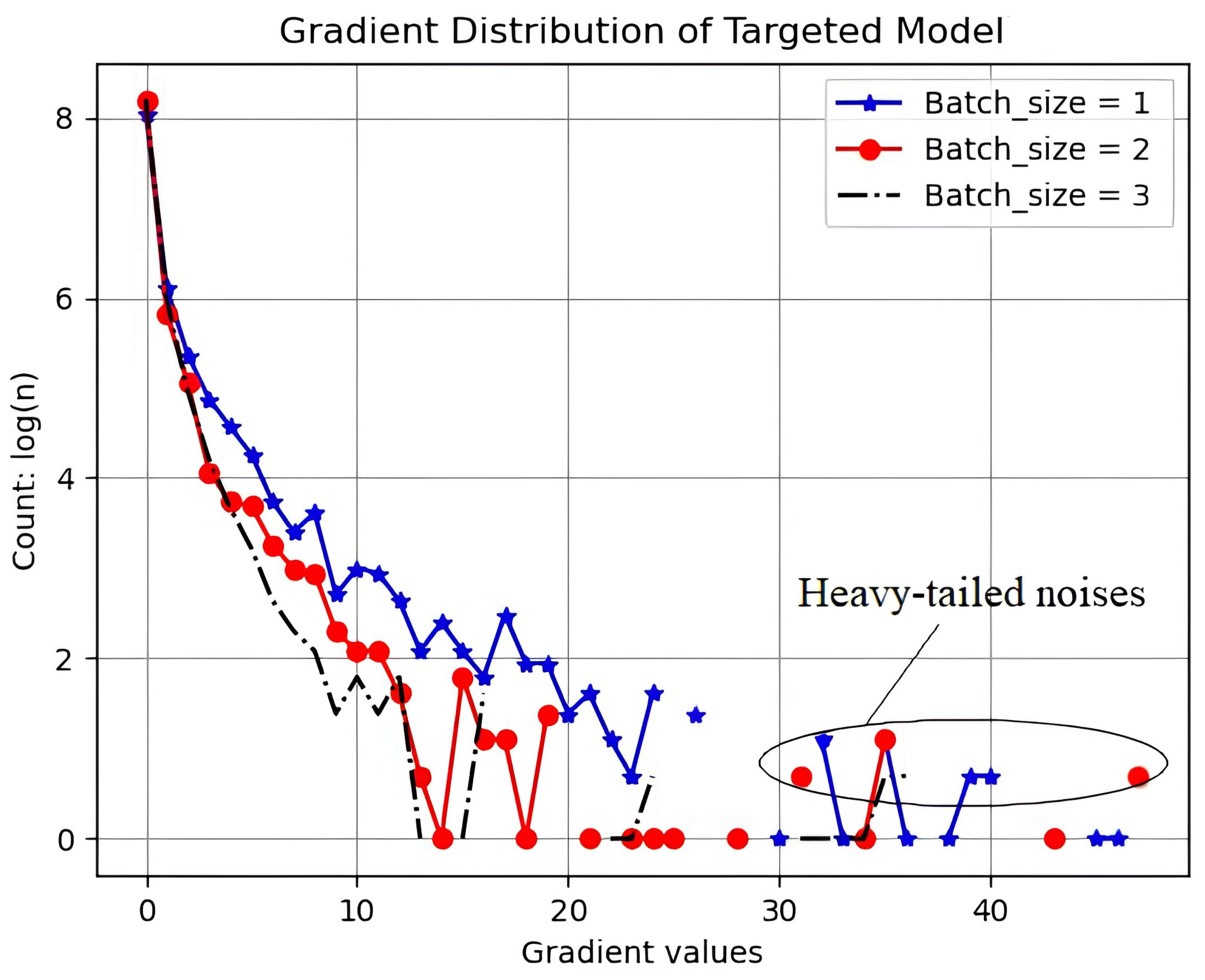
Furthermore, as network depth and width increase, the tail of the gradient noise distribution becomes heavier, indicating that SGD may unintentionally guide the training process toward undesired shortcuts [32]. Since the batch size is inversely proportional to the size of heavy-tailed noise and the attack success rate is inversely proportional to the batch size, we can boldly guess that less heavy-tailed noises result in a lower success rate of unified attacks. As illustrated in Figure 4, an FEL model with many heavy-tailed noises means that larger gradient values account for a large proportion.

In this paper, we propose the PLM framework against unified attacks. As introduced in Section 3, training an FEL system includes two steps: (1) training the local model at local devices according to Equation (3); (2) aggregating gradients into the server and updating the global FEL model according to Equation (4). In the first step, due to the existence of gradient noises, the local FEL model is updated according to Equation (10) rather than Equation (3). Therefore, the practical gradient that the adversary can obtain will contain two parts: (1) gradient noises: $-\eta {\sigma }^{\frac{1}{\alpha }{\mathrm{𝒮}}_t}$; (2) real gradients: $\nabla W_t^m$. Then, we need to solve the following problem: the fundamental reason why the adversary can successfully reconstruct the training data is that the optimization target in Equation (8) can be easily achieved by iteratively approaching real gradients as well as gradient noises.

4.3. Heavy-Tailed Gradient Noise Converter

As the most important component in the PLM framework, the gradient noise converter is implemented through cryptographic primitives. The gradient operation in the gradient noise converter is mainly divided into two stages: (1) gradient noise selection and (2) gradient noise conversion.

4.3.1. Gradient Noise Selection

Unlike traditional differential privacy methods that inject uniform noise into all gradients, PLM applies fine-grained format-preserving encryption to selectively perturb parts of gradient values. This raises the key challenge of determining which gradients should be encrypted.

Given the large number of parameters in deep neural networks, encrypting all gradients would incur substantial computational costs and degrade model accuracy. To balance efficiency and utility, PLM targets heavy-tailed gradients and transforms them into uniformly distributed noise, thereby retaining most of the informative gradient components while mitigating the risk of gradient leakage.

• The strategy of DLG attacks and unified attacks is to reduce the similarity between predicted gradients and ground truth gradients. As the gap between encrypted gradients and original gradients increases during the training process, the difficulty for the adversary to reconstruct private data will increase. Also, the most effective method to increase the gap is to encrypt the highest non-zero bit of the original gradients with larger absolute values.
• If the gradient value is small and extremely similar, it means that the model parameter may be close to the local minimum point, and if the gradient is encrypted with a large relative change, it may cause the model parameter to deviate from the point and thus affect the convergence speed of the model. The parameter with a large gradient value would have significant updates in the next several training rounds, so some changes to its values will likely be “corrected” in future training.

To bring out the trailed gradient value selection mechanism, we denote the gradient value that the adversary can obtain as $\nabla W_t^m=\{\nabla W_t^m\left(h\right),\nabla W_t^m\left(e\right)\}$, where $W_t^m\left(h\right)$ represents for the integer section and $W_t^m\left(e\right)$ represents for the decimal section. As seen in Figure 4, the gradient distribution of the targeted FEL model is similar to the heavy-tailed distribution. To fix the heavy-tailed distribution as the uniform distribution, some larger values will be selected from the gradients for conversion.

Combining the above motivations, we formulate a novel gradient value selection algorithm as follows:

• $\nabla W_t^m$ are the observed gradients of neural networks;
• Calculate the absolute values of $\nabla W_t^m$ as $abs(\nabla W_t^m)$;
• Calculate the average of $abs(\nabla W_t^m)$ as $\overline{abs}(\nabla W_t^m)$;
• Select the tailed gradients whose absolute values are greater than $r\ast \overline{abs}(\nabla W_t^m)$, where r is a specific ratio, and denote them as $G_{tail}\in \nabla W_t^m$.

4.3.2. Gradient Noise Conversion

For a non-zero real number $\mathcal{A}$, we can approximate it by the k-decimal: $\mathcal{A}={\alpha }_m{\alpha }_{m-1}\dots {\alpha }_1{\alpha }_0.{\alpha }_{-1}\dots a_{-l}$; that is, $\mathcal{A}={\sum }_{-l\le i\le m}{a}_i{k}^i$. In order to make the scale of the replaced number comparable to that of the original number, and taking the computing cost into consideration, we can generate a cipher key to reflect $a_m$, the highest-bit number of ${\alpha }_m$, to another number ${\alpha }_i$, where the cipher key will be a randomly specified permutation. Using this method, we can convert the highest bit number of $W_t^m\left(h\right)$ as the other number of $W_t^m\left(e\right)$. Thus, the converted gradient is $\nabla {\overline{W}}_t^m=\{\nabla W_t^m\left(e\right),\nabla W_t^m\left(h\right)\}$. Since higher bits have a greater impact on the data distribution than lowest bits, the uniform distribution of $\nabla W_t^m\left(e\right)$ after conversion is greater than the original gradients.

To analyze the effectiveness of conversion, we decompose the gradient observed by the adversary into two components: the ground-truth gradient $\nabla W_t^m\left(g\right)$ and the deviation gradient $\nabla W_t^m\left(d\right)$. In the deviation gradient, the uniform distribution section is expressed as $\nabla W_t^m\left(d_g\right)$, and the heavy-tailed distribution section is expressed as $\nabla W_t^m\left(d_h\right)$. The threat model can be changed as follows:

$${\widehat{x}}_t^{m\ast },{\widehat{y}}_t^{m\ast }=\underset{{\widehat{x}}_t^m}{arg} \underset{{\widehat{y}}_t^m}{min} \left|\right|\nabla {\widehat{W}}_t^m-(\nabla W_t^m\left(g\right)+\nabla W_t^m\left(d_h\right))|{|}^2.$$

(11)

After we execute the tailed gradient value conversion process, the gradients that the adversary can obtain will be changed as follows:

$${\widehat{x}}_t^{m\ast },{\widehat{y}}_t^{m\ast }=\underset{{\widehat{x}}_t^m}{arg} \underset{{\widehat{y}}_t^m}{min} \left|\right|\nabla {\widehat{W}}_t^m-(\nabla W_t^m\left(g\right)+\nabla W_t^m\left(d_g\right))|{|}^2.$$

(12)

Comparing $\nabla W_t^m\left(d_h\right)$ with $\nabla W_t^m\left(d_g\right)$, the biggest difference is located at the tail of gradient values. Considering that the neural network is often modeled as a weighted function $y=F(Wx,b)=F({\sum }_{i=1}^n{W}_i{x}_i,b)$, when the heavy-tail noise in the gradient is converted into uniform noise, the data reconstructed by the attacker will also contain uniform noise, which means the adversary can not reconstruct the original data if there are sufficient uniform noises.

The workflow of the gradient noise converter used in practice is shown in Algorithm 2. The difference between theoretical analysis and practical engineering is that only the highest-bit number of the larger gradient value is encrypted as the number at the other bits rather than all bits of integer sections to minimize the impact on the model accuracy. Note that $sign(·)$ represents the sign function: $sign\left(g\right)=\left|g\right|/g$, in which g is non-zero.

Algorithm 2: Gradient noise converter.

4.4. Model Training Strategy via PLM

For the reader’s convenience, we consider fully connected neural networks (FCNs) with the SiLU activation function, in which the loss function is implemented as the cross-entropy between the real label y and the “soft-maxed” output $\widehat{y}$. For FCNs with H layers, the mathematical process of the prediction can be represented as follows:

$$F\left(X\right)=W_H{D}_H{W}_{H-1}\dots W_1{D}_1{W}_{0}X,$$

(13)

where $W_h$ is the known weight of the h-th layer, and the activation pattern $D_h\left(z_h\right)=SiLU\left(z_h\right)=diag(z_{hk}\{z_{hk}>0\}$, …, $0\{z_{hk}<0\})$, which can be deduced from the shared gradients [33]. For each layer $h\in [0,H-1]$, we have the following gradient:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{L}}{\partial W_h}}=& \sum _k^K[{\displaystyle \frac{\partial \mathcal{L}}{\partial F_k}}\left(D_h{W}_{h-1}\dots W_{0}X\right)\hfill \\ \hfill & ({\left[W_H\right]}_k^T{D}_H\dots W_{h+1}{D}_{h+1})],\hfill \end{array}$$

(14)

where $\mathcal{L}$ stands for the loss function, and $f_c$ is the k-th output value of the FCN, which can also be treated as the known information [33].

We observe that on the right side of Equation (12), for each $h\in \{0,1,2,\cdots ,H-1\}$, the matrix $\left(D_h{W}_{h-1}\dots W_{0}X\right)$ is actually a column vector, and the remaining part of the right side is a row vector. Thus, it can be inferred that the rows or columns of the matrix ${\displaystyle \frac{\partial \mathcal{L}}{\partial W_h}}$ are proportional. Therefore, artificially changing some gradient values would disrupt the proportional relationships of columns or rows of matrix ${\displaystyle \frac{\partial \mathcal{L}}{\partial W_h}}$, and this means that there are no solutions to Equation (14). Consequently, the DLG attack is reduced to a regression problem over encrypted gradients. By carefully designing the encryption strategy, the minimizer, i.e., the dummy input that minimizes the objective, can be forced to deviate significantly from the ground-truth input, thereby obstructing accurate reconstruction. The overall training process with PLM is summarized in Algorithm 3.

Algorithm 3: Model training strategy with PLM.

5. Experimental Results and Discussions

In this section, we first conduct the DLG attack and gradient pruning-based defense on the FEL as the baseline. Then, the unified attack is implemented to demonstrate the identified threat. To validate the feasibility and interpretability of the proposed PLM, we also design extensive comparison experiments and abbreviation experiments. Finally, visual experimental results for the interpretability of unified attack and PLM are provided in detail.

5.1. Experimental Setup

In the experiment, an FEL system with one FEL server and several FEL clients is considered to solve the image classification problem. The number of FEL clients can be dynamically configured to simulate different application scenarios. At the FEL client, we use LeNet via three convolution layers and one fully connected layer as the local classification model. The parameters of each LeNet model can be updated once the retraining process is activated. The learning rate of each classification model is set to 0.01.

The used generative network includes three convolution blocks, and each convolution block consists of a convolution layer, a BatchNorm layer, and an activation layer. Except for the last convolution block that uses the Sigmoid function, the other convolution blocks use the SiLU function for activation. The hardware server is configured with Dell T7920 workstation 64G memory and two NVIDIA Tesla V100 GPUs.

5.2. DLG Attack and Defense

5.2.1. DLG Attack Setup

For the related DLG attack model, we follow the settings introduced in [25]. Each attack model will carry out 20,000 optimization loops during the training process. As the most famous gradient leakage attack, the DLG has achieved a very high attack success rate. However, most existing studies focus on simulated attacks that train an initialized model on a single sample and attempt to reconstruct that sample. When applied to FEL, such settings introduce practical issues. First, using only one sample in model training makes the measured attack success rate (ASR) less credible, as the reconstruction performance of DLG attacks also depends on the initial state of the model. On the other hand, samples participating in FEL training may have defects, occlusions, etc., in the actual environment, which may also affect the ASR of the DLG.

In our experiment, we attempt to discuss the possibility of using a DLG attack in the practical FEL training process, i.e., the attack target is not an initialized learning model but a pretraining model under complex application scenarios. First, we divided the CIFAR10 and MNIST data involved in model training into two groups: one contains clean images, and the other contains occluded images. The sample that will be fed into the learning model for training is selected randomly from the above two groups. Therein, the size of the occluded area in CIFAR10 is $12\times 12$, while in MNIST, it is $7\times 7$. Furthermore, it is very difficult to successfully implement DLG attacks on pretrained models. When the attacker wants to attack a pretrained model, the attack success rate of DLG is very low. To validate this weakness of the DLG attack, we provide extensive experiments with different network structures and try to deploy the DLG attack on different training epochs.

5.2.2. DLG Attack Results

When we simulate the DLG attack on FEL, we find that the convergence speed of DLG attacks on clean images and occluded images are similar, which means that the occlusion of sensitive parts of samples participating in model training can play a certain role in privacy protection, and a DLG attack alone cannot reconstruct sensitive areas that are occluded.

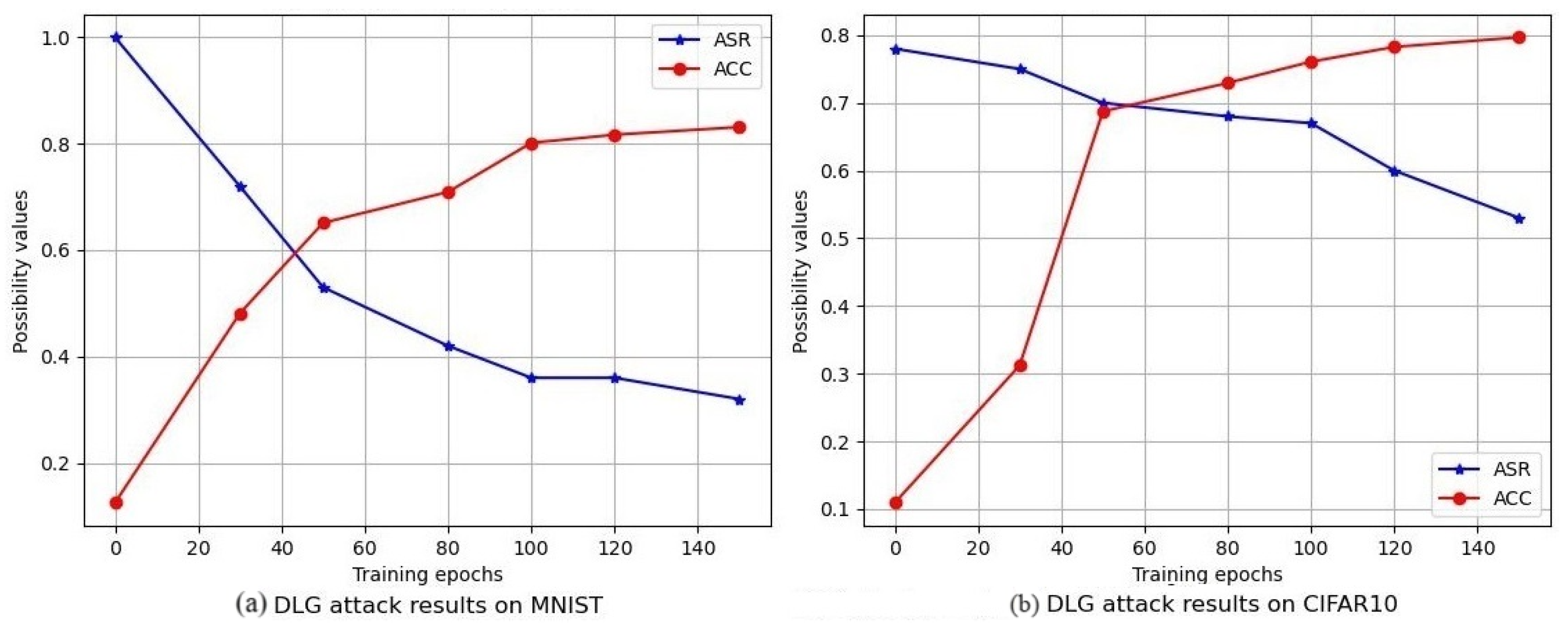
From Figure 5, we can find that DLG attacks are becoming much more difficult to achieve along with the rise of the training epoch. The specific reason is that in the later stage of training, the model has a certain ability to classify samples. At this time, a training epoch requires a little modification to the learning model, i.e., the gradient is generally very small. Under this condition, it is difficult for attackers to find key features through such small gradients and then steal the training samples. Therefore, in the later stage of training, the success rate of DLG attacks is greatly reduced. We looked at the gradient data and found that the gradient of the model in the training process was much smaller than that of the initialized model, which confirms our idea.

5.2.3. DLG Defense Results

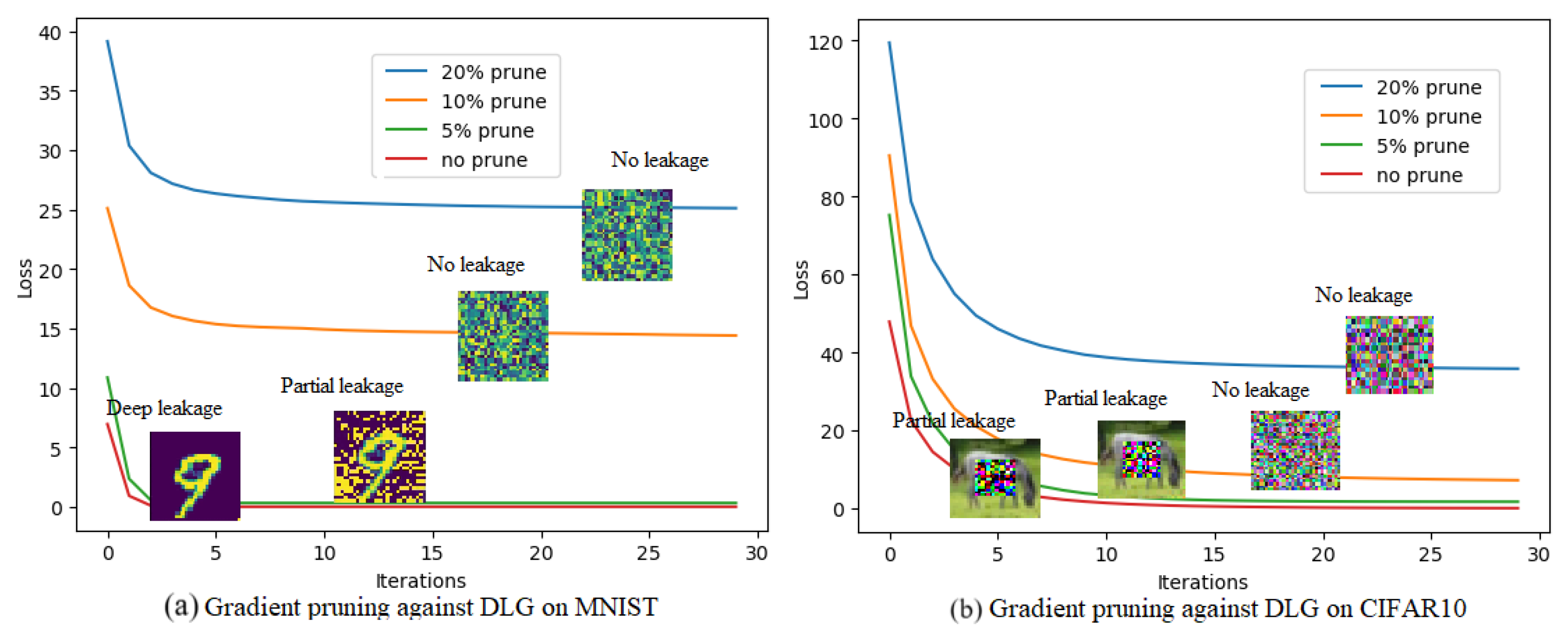
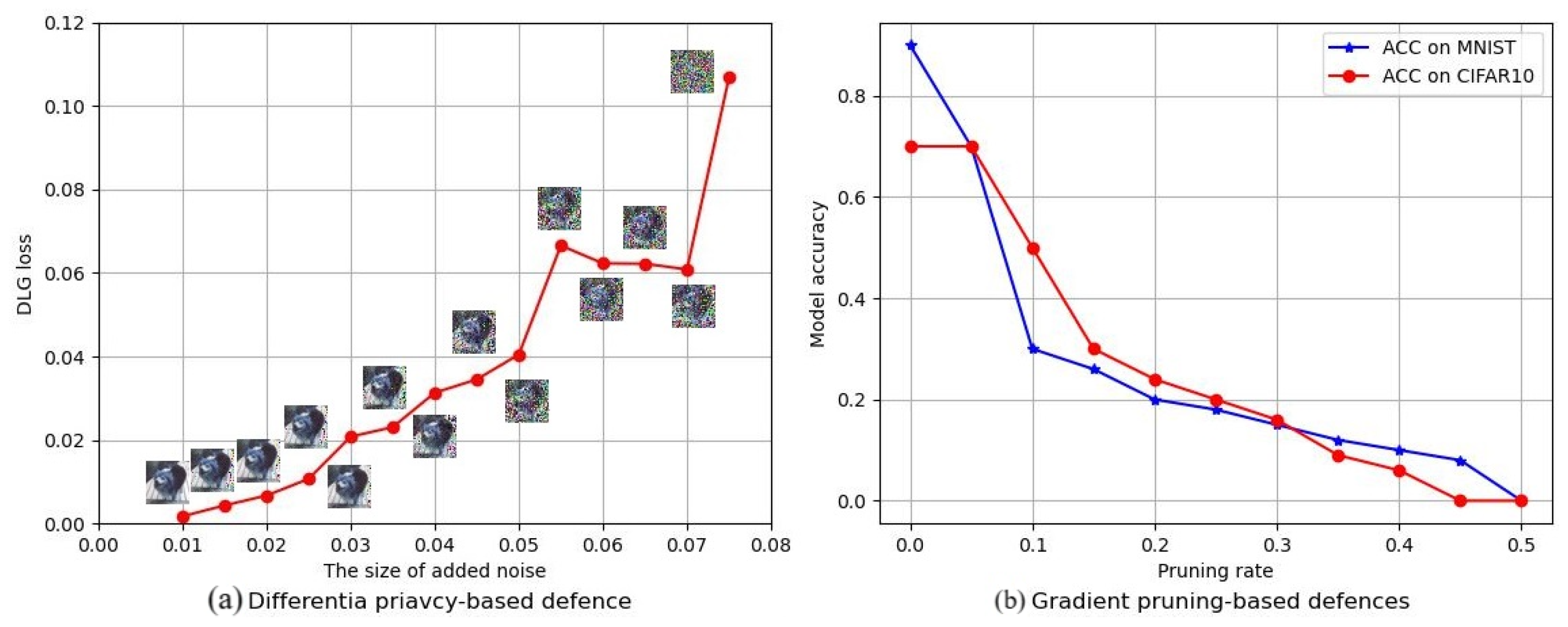
In this section, we first observe the performance of gradient pruning-based defense methods. As described in [6], gradient pruning is the most significant defense method, which is implemented by proportionally presetting partial gradients to zero. Therefore, we select the gradient pruning method as one of the comparison technologies. Figure 6 shows gradient pruning against DLG attacks on the MNIST dataset and CIFAR10 dataset. We can find that as the pruning rate increases, the effect of the DLG attack decreases sharply. Experimental results show that 10% of gradient information needs to be pruned to achieve high defense interpretability for MNIST and CIFAR10. It means that the convergence of DLG attacks is sensitive to gradient pruning.

Different from the gradient pruning method, differential privacy (DP) technology advocates the addition of uniformly distributed noises into the gradients. The essence of differential privacy is to interfere with the objective function of DLG attacks so that the privacy reconstruction process is destroyed. However, since the effects of added uniformly distributed noises on key features and common features are equivalent, better defense performance usually needs a lot of uniformly distributed noises, which may reduce the model accuracy of FEL. We recorded and listed the model accuracy under different defense settings in Figure 7.

5.2.4. Discussion

Similar to the uninterpretability of deep learning, reconstructing data from gradients is also highly uninterpretable. Experimental results about the DLG attack effect and the performance of related defense methods provide strong support for further analysis. The following conclusions can be drawn from the above experiments: (1) DLG attacks are indeed able to reconstruct training samples with high confidence when the training batch is small; (2) there are great challenges in defending DLG attacks without affecting model accuracy. X. Pan et al. [33] started from the fact that the size of the training batch has a great influence on the attack success rate of DLG attacks and established a neuron exclusivity-based theoretical analysis method for this issue, in which a training batch with more exclusively activated neurons is more vulnerable to DLG attacks. Building on this, they further proposed a deterministic attack algorithm and a defense strategy based on exclusivity reduction. In contrast, the unified attack extends the original DLG objective by incorporating a generator into the privacy reconstruction process, enabling class-specific fitting of diverse samples. The unified attack cleverly avoids the neuron exclusivity that arises when multiple samples want to activate the same neuron. The proposed PLM enhances the aliasing between training samples by transforming endogenous heavy-tailed gradient noises into uniformly distributed noises, thereby achieving a low-cost and efficient defense effect.

5.3. Unified Attack and PLM Defense

5.3.1. Unified Attack Setup

For the unified attack model, the adversary will make 4000 optimization loops, which is less than 20,000, for this attack model has a faster convergence speed. For comparison, we first implement the unified attack using only one sample. Then, we extend the unified attack to the scenario of Batch_size > 1. All other settings are consistent with the DLG attack.

5.3.2. Unified Attack Results

We randomly select multiple samples from the dataset as fresh training data to participate in the retraining process. Therefore, the objective of the generator is to reconstruct dummy data that are similar to fresh training data. The available prior data are memorized in the pretraining FEL model. The latter stage is to update the generator to persistently reconstruct the dummy data that are similar to fresh training data under the supervision of Equation (8). In the experiment, we set the Batch_size = 1, Batch_size = 2, and Batch_size = 3 scenarios separately to evaluate the performance of the unified attack. In the scenario with multiple samples, it is necessary to initialize the generator with multiple uniformly distributed noises with different centers. Figure 8 illustrates the unified attack results when the Batch_size is set as 3. Compared with traditional DLG attacks, our unified attack demonstrates a significant improvement in reconstructing multiple training samples simultaneously. This advantage highlights the enhanced scalability and reconstruction fidelity achieved by leveraging both gradient and prediction supervision.

5.4. Interpretability of the Proposed Unified Attack

Unlike traditional model inversion or DLG attacks, which often focus on reconstructing individual samples or rely on fixed initialization, the unified attack aims to reconstruct “fresh training data” with enhanced adaptability and stealth. By introducing a generator into the DLG pipeline, the solution space is extended from a fixed point to a distribution, allowing broader representation capacity through upsampling, downsampling, and transformation. The proposed generator addresses two fundamental questions: (1) how to generate plausible data samples and (2) how to ensure that their distribution matches that of true training data. To jointly optimize these objectives, we employ four loss terms:

$$L_r={\displaystyle \frac{1}{n}}\sum _{i=1}^{N}MSE(F\left(G\left(z_i\right)\right),y_i),$$

(15)

$$L_s={\displaystyle \frac{1}{n}}\sum _{i=1}^{N}MSE(F\left(G\left(z_i\right)\right),y_i^t),$$

(16)

$$L_a=-{\displaystyle \frac{1}{n}}\sum _{i=1}^N\left|\right|F\left(G\left(z_i\right)\right){\left|\right|}_1,$$

(17)

$$L_g={\displaystyle \frac{1}{n}}\sum _{i=1}^{N}KL({\nabla }_{w}F\left(G\left(z_i\right)\right),{\nabla }_{w}F\left(x_i\right)).$$

(18)

Here, $L_r$ enforces alignment between the model’s prediction and the real label, assuming the FEL model has sufficient discriminative power. $L_s$ reflects target distribution alignment, assuming the adversary can estimate target labels. $L_a$ ensures high activation responses, increasing confidence in reconstructed features. $L_g$ enforces gradient similarity with real training samples. Collectively, these losses enable the generator to generalize across affine transformations and semantic variations, improving attack success rates and robustness.

5.4.1. PLM’s Results

We choose training and testing data from MNIST, F-MNIST, CIFAR10, and SVHN, respectively. Furthermore, we train a classifier model for each dataset. In the first group, the classifier is trained without any defenses, and the training iterations, training loss, and model accuracy are recorded. In the second group, the classifier is trained with encrypted gradients, where $k=16$ and $r=8$. We trained all the classifiers for 4000 epochs and repeated that 10 times. The average training time in the first group, $t_1$, and that in the second group, $t_2$, can be found in

Table 1. Comparison of average training times.

Dataset	Training Time ${\mathit{t}}_1/\mathbf{s}$	Training Time ${\mathit{t}}_2/\mathbf{s}$	${\mathit{t}}_2/{\mathit{t}}_1$
MNIST	21.164 (0.114)	29.811 (0.355)	1.408
F-MNIST	28.756 (0.187)	45.135 (1.015)	1.570
SVHN	60.057 (0.966)	78.194 (0.264)	1.302
CIFAR-10	63.021 (0.102)	88.706 (0.772)	1.407

, with standard deviations in parentheses. It is shown that the overhead for different models is very different. Note that the classifier we created for the MNIST dataset has several additional fully connected layers, which could lead to more extra training time than the other three classifiers. The overhead brought by PLM is about 0.4 times the original training time, which is relatively acceptable.

In addition, we also evaluate the influence of the PLM on model accuracy. For 10 repetitions, we also present the average and standard deviation of the accuracy in

Table 2. Model accuracy (%) under different datasets with or without the PLM.

Dataset	${\mathit{A}}_1$-Training a	${\mathit{A}}_2$-Training a	${\mathit{A}}_1$-Test	${\mathit{A}}_2$-Test
MNIST	99.25 (0.14)	99.24 (0.11)	98.40 (0.16)	98.36 (0.16)
F-MNIST	96.87 (0.40)	96.72 (0.43)	90.96 (0.22)	90.70 (0.20)
SVHN	98.56 (0.13)	98.71 (0.16)	92.70 (0.18)	92.72 (0.15)
CIFAR-10	98.72 (0.31)	98.73 (0.20)	83.68 (0.39)	83.78 (0.34)

^a $A_1$ stands for the accuracy of the model trained normally, while $A_2$ stands for that of the model trained with the PLM. Then, “training” refers to the rates coming from the training sets.

. Comparing the learning accuracy of normally trained models and PLM models, we can determine that, for the training dataset, there is almost no decline in the learning accuracy if the PLM is added. For the testing dataset, the decline of learning accuracy is less than 0.3%, which is much less than the $30\sim 50\%$ decline in gradient pruning, as illustrated in Table 2. Therefore, the effect of the PLM on model accuracy is also pretty slight.

We further evaluate the effectiveness of the TSD defense on the CIFAR-10 dataset in terms of attack success rate and convergence efficiency. As shown in

Table 3. Evaluation of GenDRA under CIFAR-10: Attack effectiveness and convergence with/without TSD.

Defense	Conv. Time (s)	Iterations	PSNR	SSIM
w/o TSD	5.29	149	21.78	0.88
			22.20	0.93
			22.92	0.85
with TSD	None	None	6.28	0.11
			6.86	0.20
			6.28	0.12

, when no defense is applied, GenDRA converges in 5.29 seconds (149 iterations) and reconstructs high-fidelity images with PSNR values above 21 and SSIM scores above 0.84. However, when TSD is applied, the attack fails to converge, and the perceptual quality of the reconstructed images drops sharply (e.g., PSNR around 6 and SSIM below 0.21). These results confirm that TSD not only delays or blocks convergence but also severely reduces the visual similarity between reconstructed and ground-truth samples.

5.4.2. Limitations of Prior Attacks and Practical Advantages of GenDRA

Label-based model inversion attacks such as GMI [9] and IF-GMI [11] require explicit access to class labels and rely on pretrained GANs from public datasets. These assumptions are impractical in federated edge learning (FEL), where labels are hidden, and data distributions across clients are often heterogeneous. Moreover, such methods are sensitive to label coverage; if the target class is underrepresented in GAN training, inversion may fail entirely.

In contrast, GenDRA is a label-free, gradient-supervised attack that exploits only shared gradients during training. It supports batch-wise inversion and adapts well to unseen data without requiring external priors, making it more realistic and deployable in FEL environments.

Unlike DLG [33], which is non-persistent and restarts upon interruption, GenDRA accumulates knowledge through a generator, enabling more efficient and flexible attacks. Furthermore, our PLM defense perturbs only a small fraction of visually sensitive gradients, preserving model accuracy while effectively reducing reconstruction fidelity.

6. Conclusions

This paper introduces GenDRA, a unified generative data reconstruction attack tailored to federated edge learning (FEL), which leverages batch-wise gradients to reconstruct training data without requiring label access or external priors. Compared to traditional gradient leakage attacks such as DLG, GenDRA significantly improves reconstruction quality, especially when the batch size exceeds one. For example, on CIFAR-10, GenDRA achieves reconstruction results with PSNR over 22 and SSIM above 0.88. To mitigate this threat, we propose a lightweight and effective defense mechanism, target semantic dissolution (TSD), which selectively encrypts visually critical gradient components while preserving model accuracy and training convergence. Experimental results show that with TSD enabled, the attack fails to converge and reconstructed images degrade significantly (e.g., PSNR drops to around 6 and SSIM below 0.20). Meanwhile, the model accuracy decline is less than 0.3%, indicating that TSD maintains task performance while effectively resisting reconstruction. Extensive experiments demonstrate that our method generalizes well across datasets and architectures, offering a practical framework for both exposing and mitigating privacy risks in FEL.

Limitations and Future Challenges

While GenDRA achieves notable improvements over existing methods, several limitations remain. On the attacker side, GenDRA may experience convergence instability under strong gradient perturbations or in deep models with high gradient compression. Additionally, the current framework does not incorporate any auxiliary prior (e.g., public datasets or synthetic data), which may restrict its effectiveness in extremely noisy or sparse gradient settings. Future extensions may explore hybrid strategies that combine gradient inversion with weak priors to further enhance reconstruction fidelity. In addition, we plan to extend our framework beyond the image domain, including text and speech data, where modality-specific challenges such as discrete token recovery and temporal alignment must be addressed.

From the defense perspective, TSD may be vulnerable to adaptive adversaries who craft gradient updates to circumvent the encrypted subset or embed backdoor triggers that survive perturbation. Moreover, in scenarios where the semantic signal is widely diffused across the gradient space, targeting a small encrypted portion may not suffice. Future research may explore combining TSD with differentially private noise injection, certified robustness bounds, or dynamic gradient masking to strengthen its generalization and adaptability against evolving threats.