Review of Intelligent Motor Controller Parameter Self-Tuning Technology
Abstract
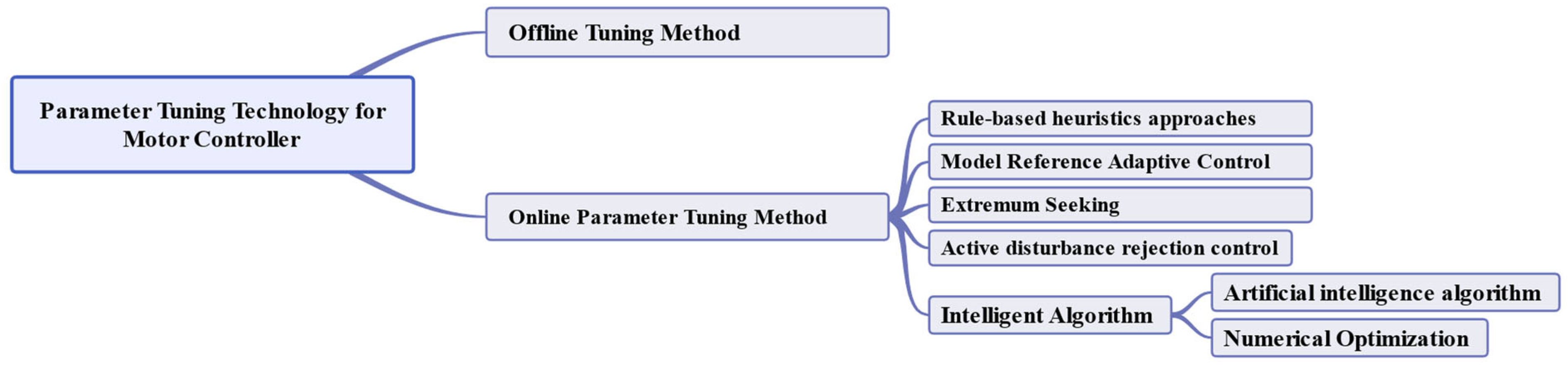
1. Introduction
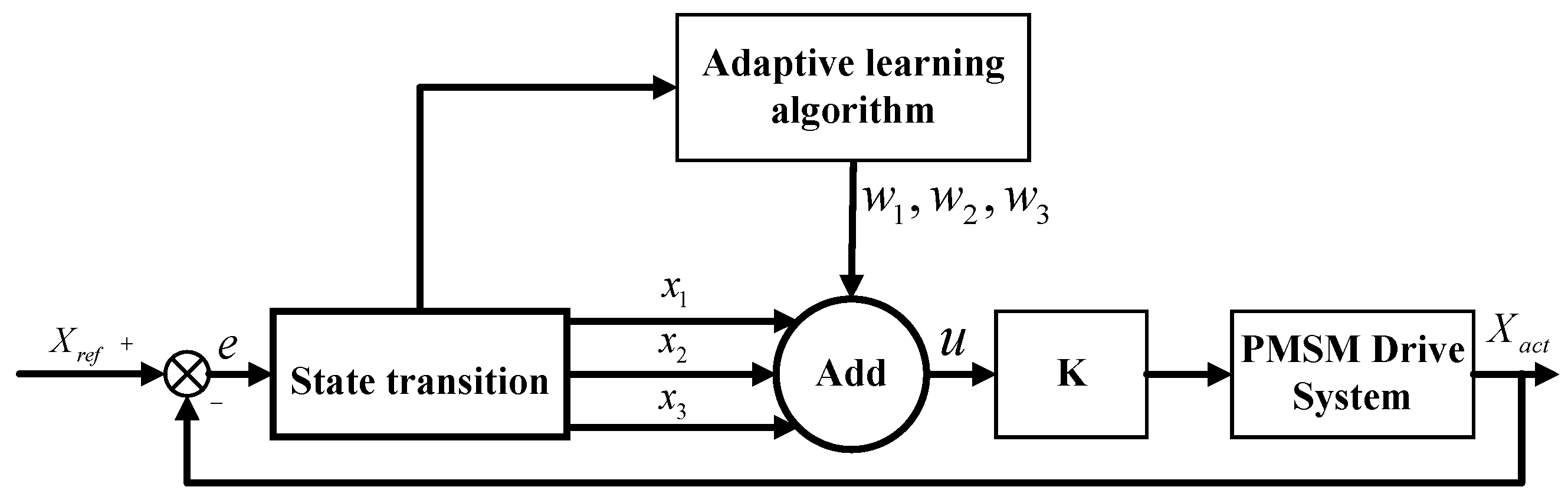
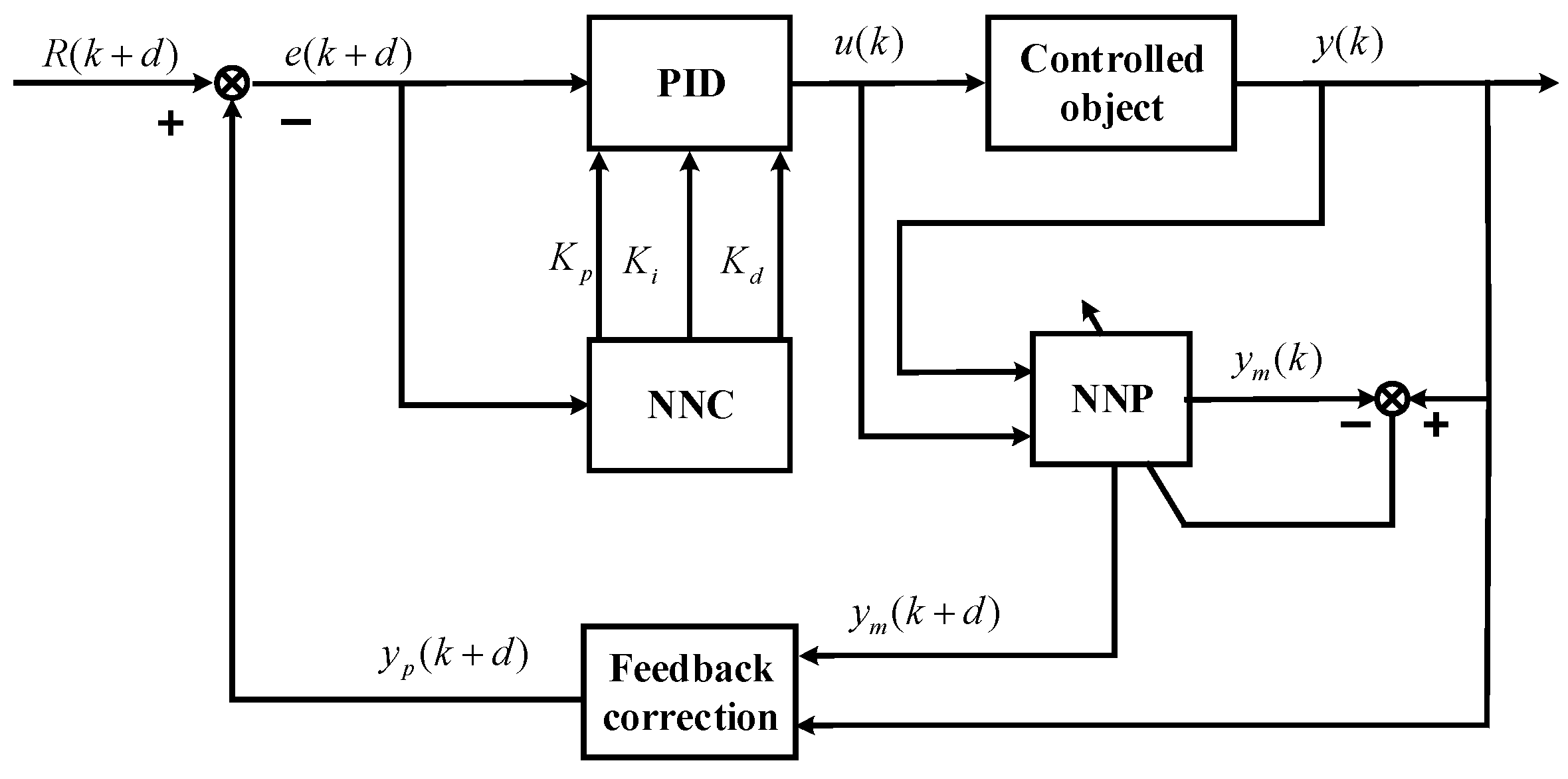
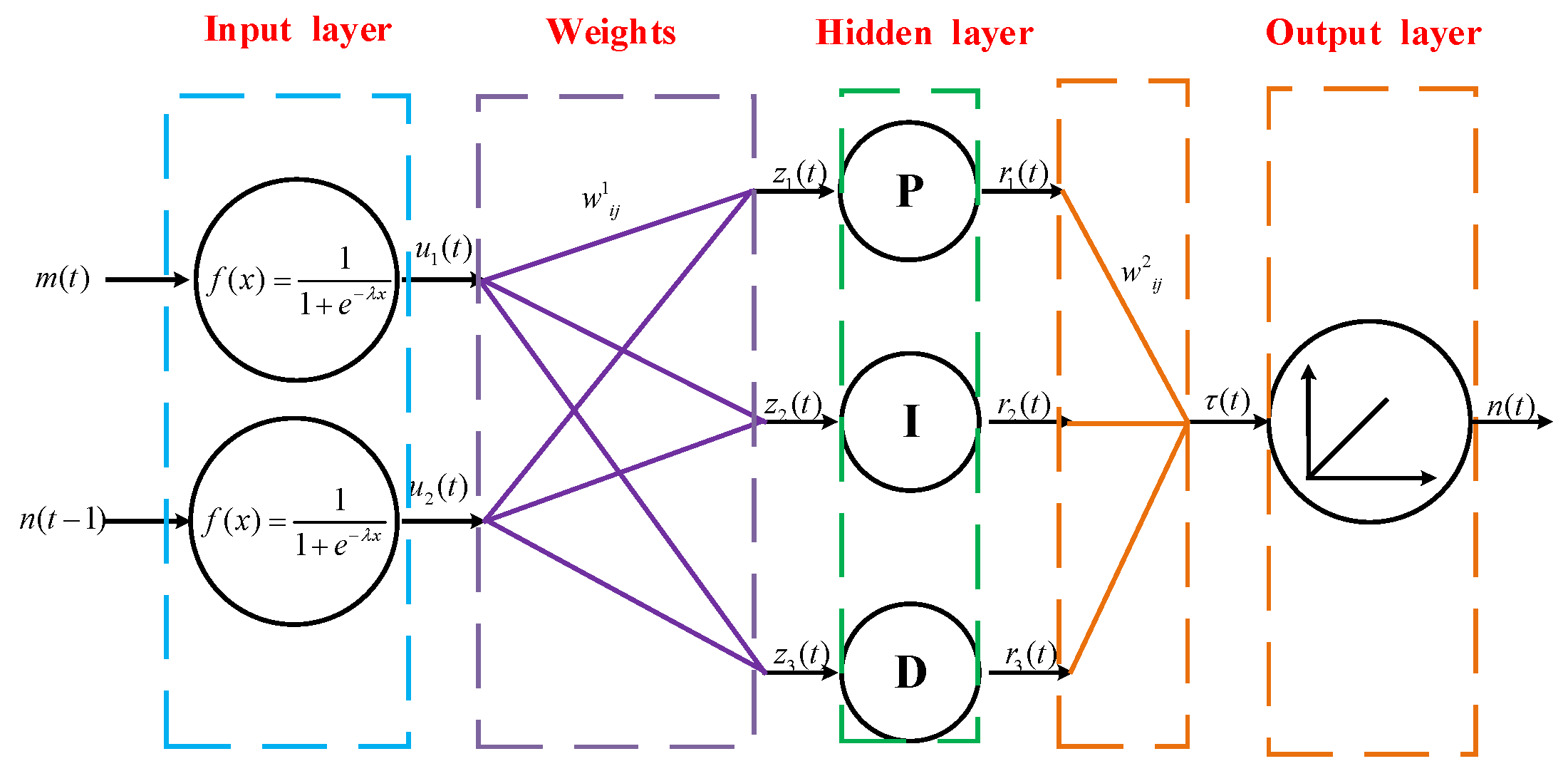
2. Single-Neuron PID Controller
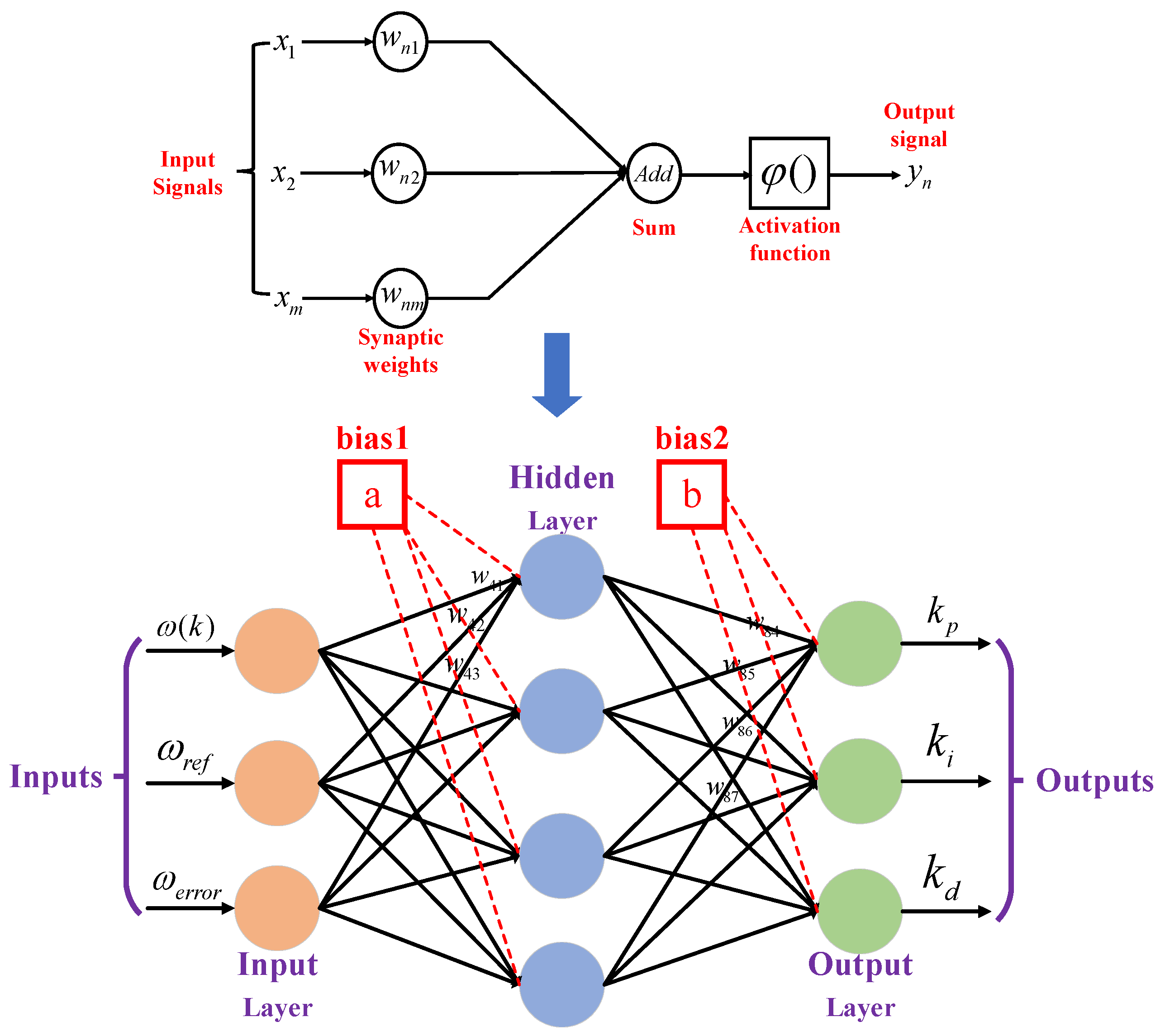
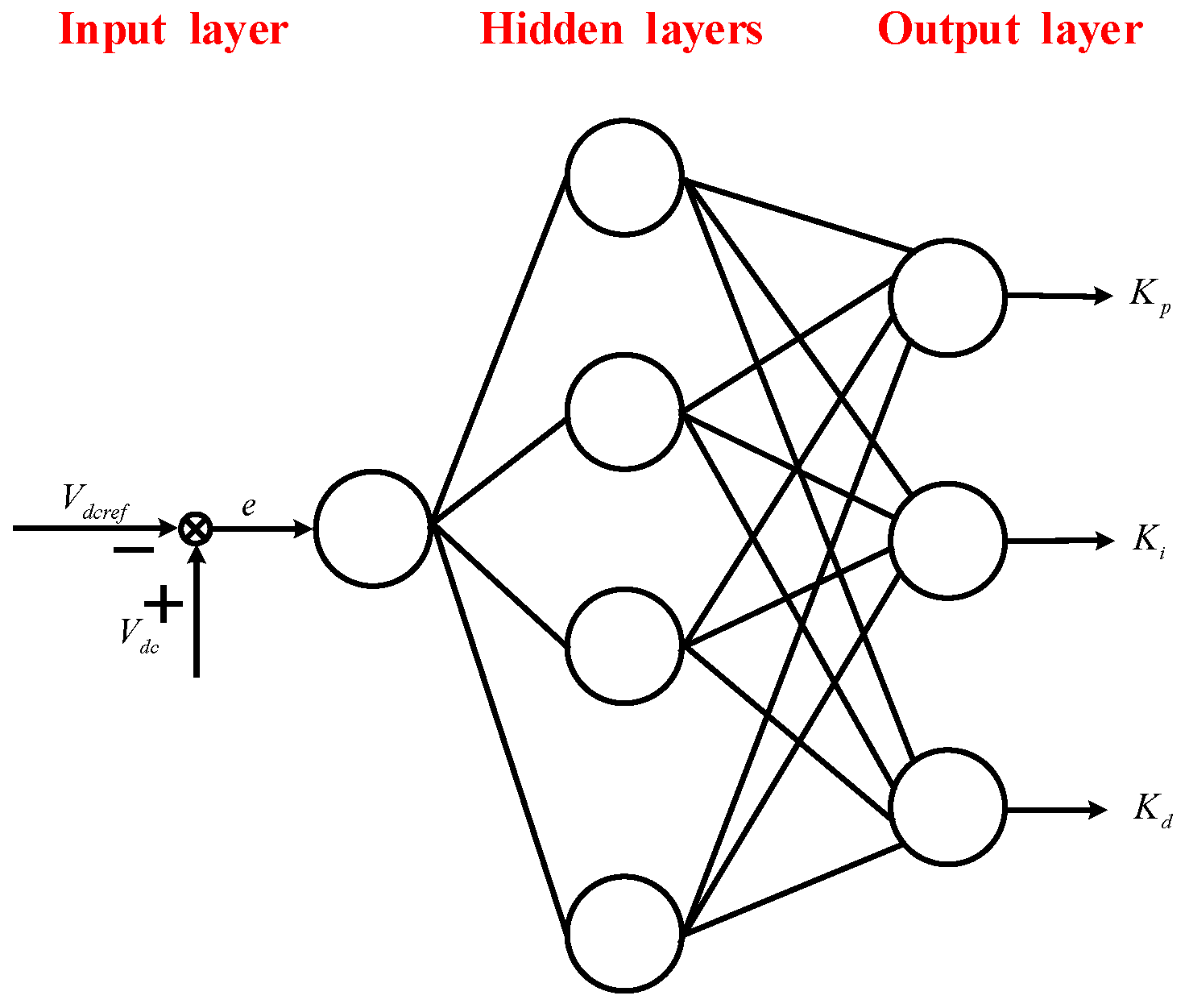
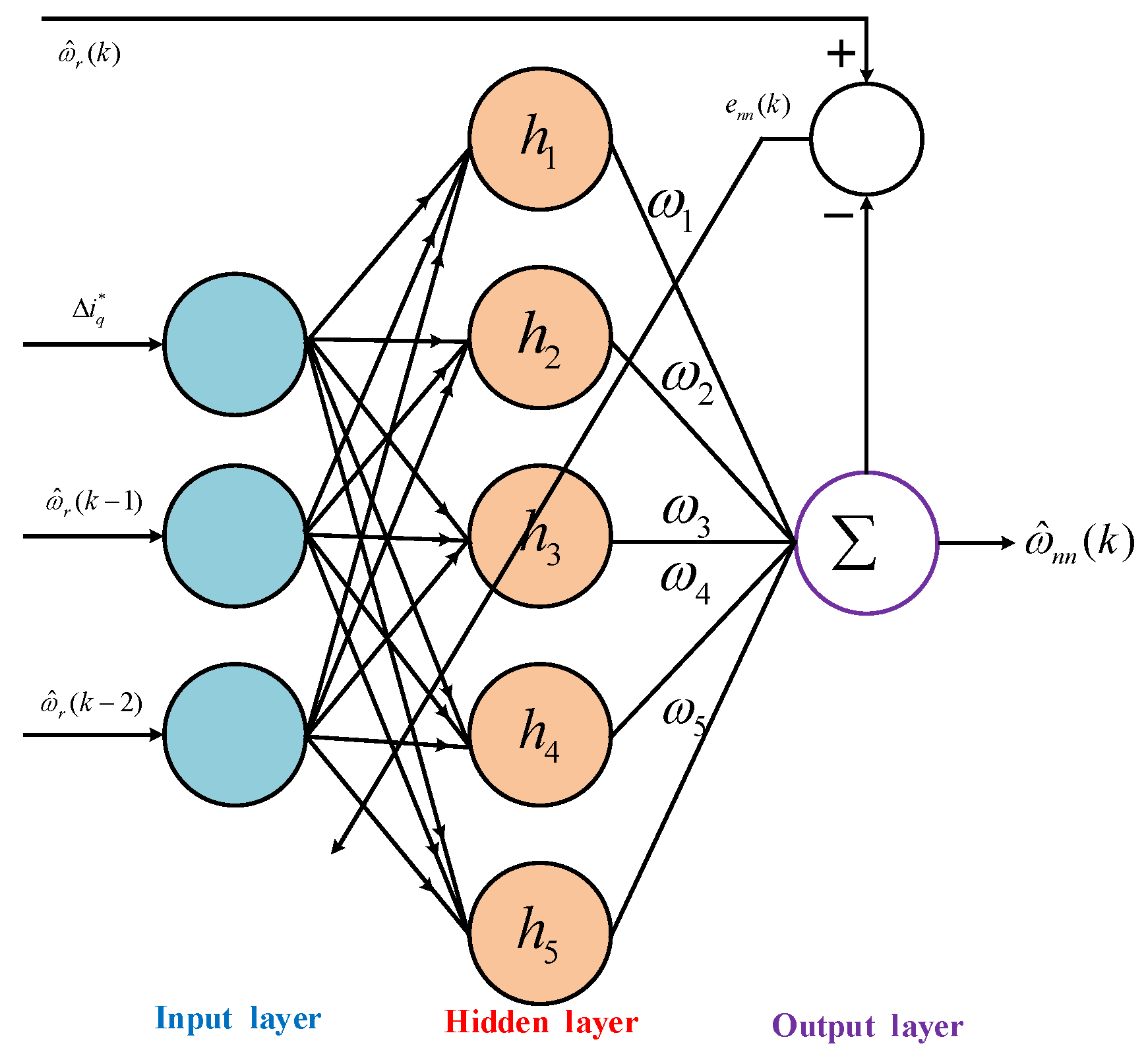
3. Neural-Network-Based PID Controller
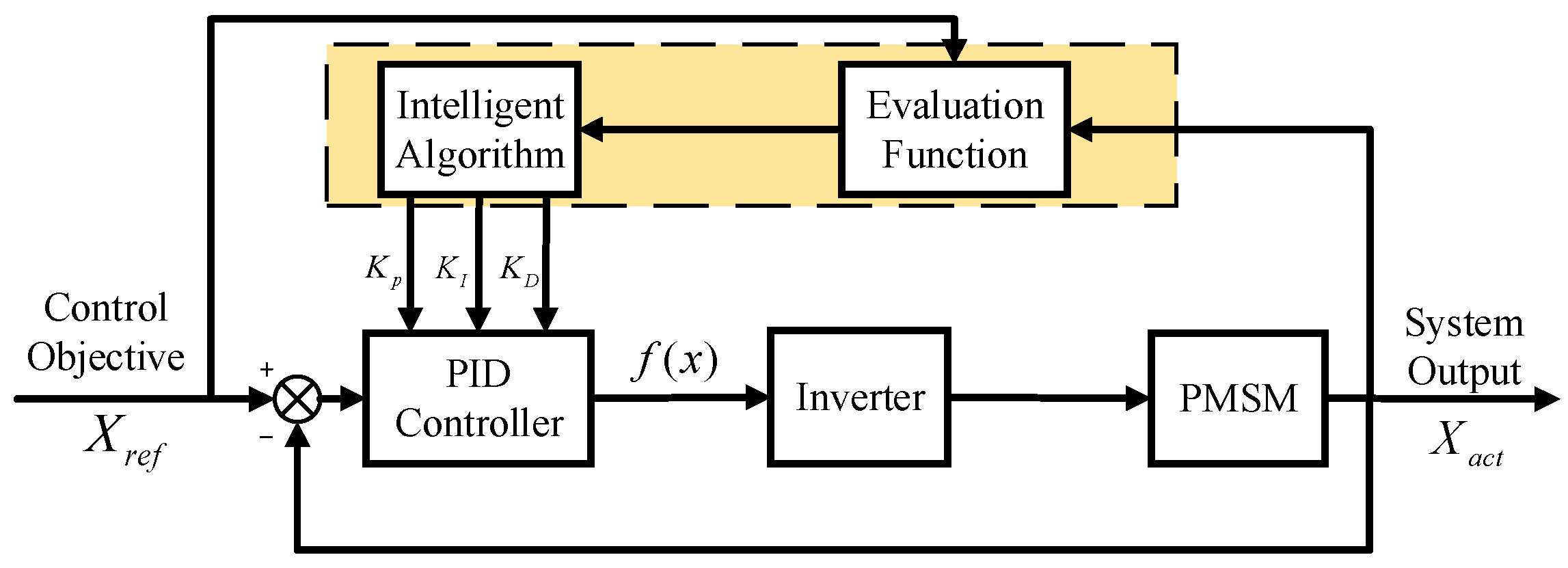
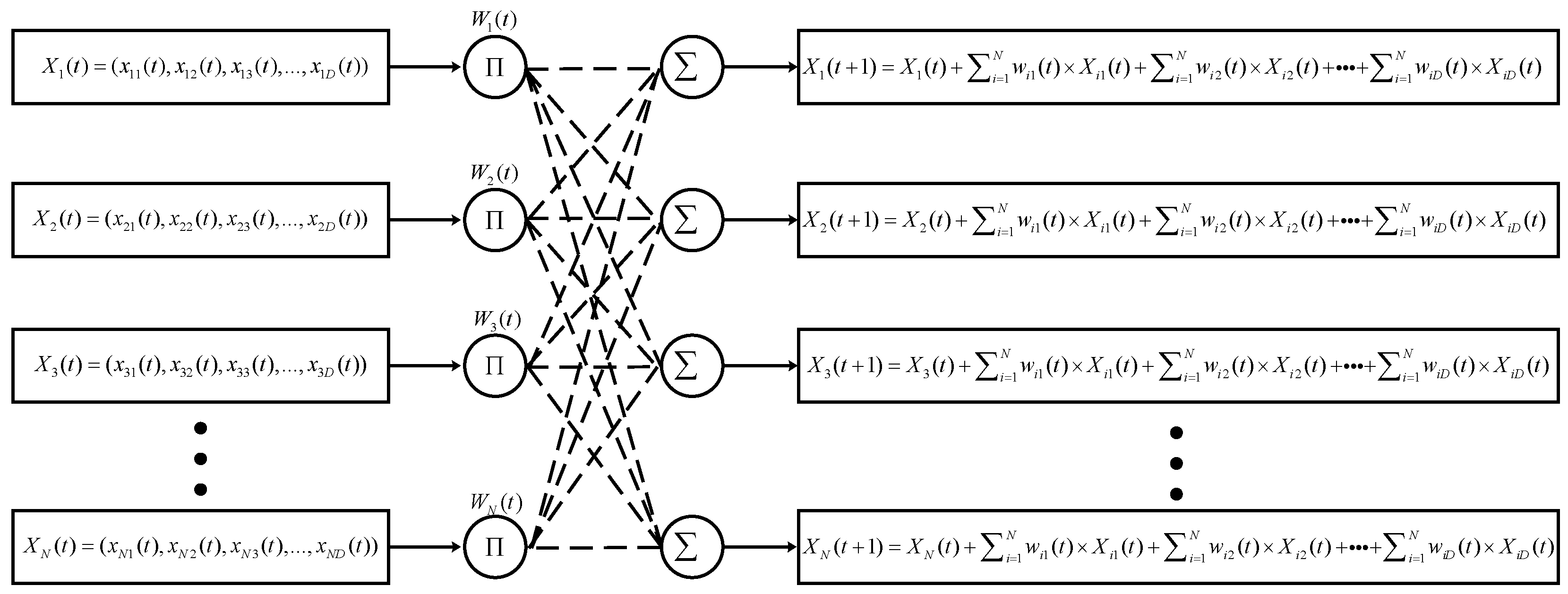
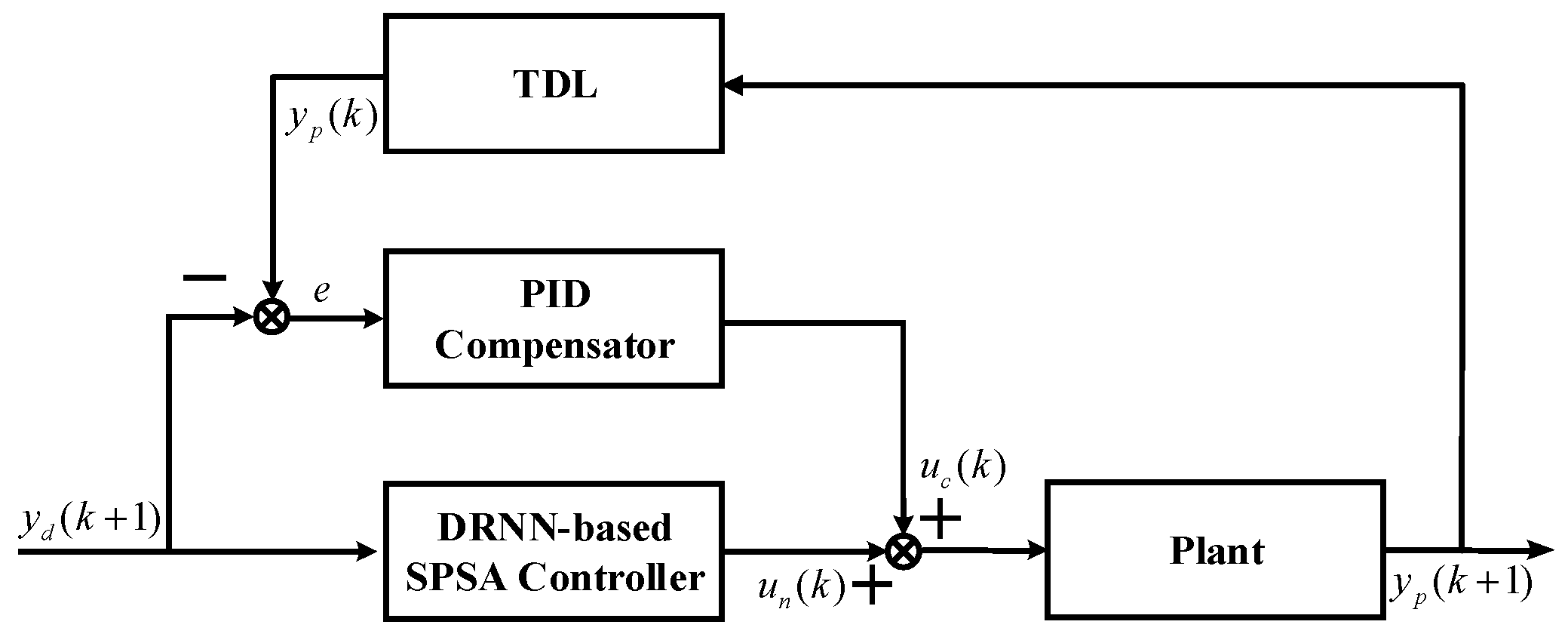
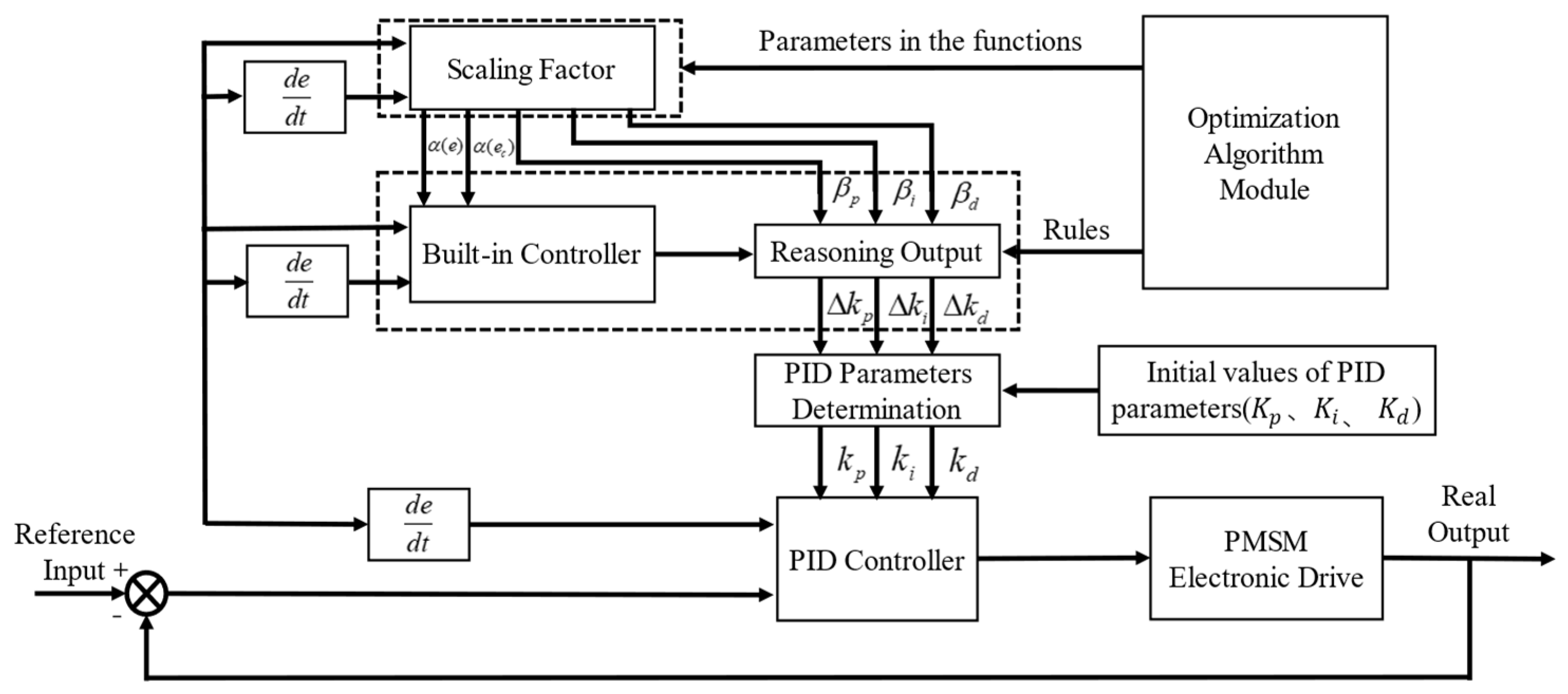
4. PID Controller Utilizing a Numerical Optimization Algorithm
5. Simulation Experiment
5.1. Data Collection Process
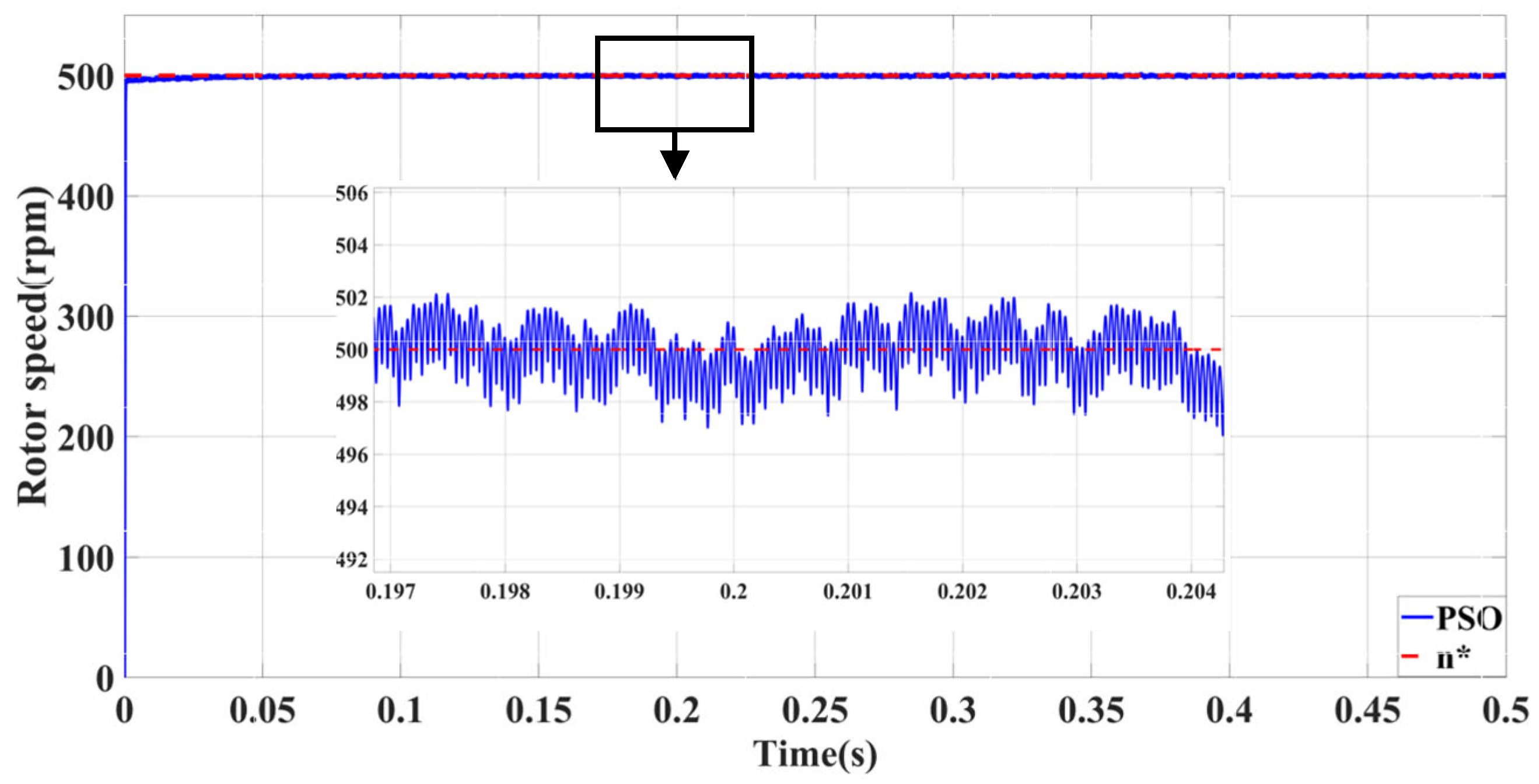
5.2. Simulation Results
5.3. Analysis of the Limitations of the Intelligent Self-Tuning Method
6. Primary Research Challenges Discussion
- (1)
- Nonlinearity and Coupling in PMSM Control Systems
- (2)
- Computational Complexity of PID Parameter Self-Tuning Algorithms
- (3)
- Robustness and Adaptability
- (4)
- Multi-Objective Optimization Requirements
- (5)
- Experimental validation and hardware performance evaluation
- (6)
- Insufficient integration with traditional control methodologies
7. Conclusions
- (1)
- Enhanced control accuracy: By employing more optimized control methods and advanced control parameter self-tuning algorithms, the tracking precision, response speed, and computational efficiency of the control system can be further improved.
- (2)
- Greater algorithm and framework integration: A hybrid control parameter self-tuning method that combines numerical optimization algorithms, neural networks, and single-neuron approaches is proposed to leverage the strengths of different algorithms across various application scenarios. The neural network weights are optimized using the application of a numerical optimization algorithm. A hybrid control parameter self-tuning framework that integrates intelligent algorithms with traditional frequency domain analysis and state observers can effectively leverage the strengths of various control parameter self-tuning methods, thereby achieving superior tuning performance.
- (3)
- Improved adaptability: Advanced control theory and optimization algorithms are utilized to balance multiple performance indices, ensuring that the servo system operates at maximum efficiency while achieving high performance.
- (4)
- Increased specificity: A targeted controller parameter self-tuning method is developed based on the specific requirements and characteristics of actual system operating conditions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PID | proportional–integral–derivative |
| PSO | particle swarm optimized |
| AWPSO | adaptive weighted particle swarm optimization |
| PMSM | permanent magnet synchronous motor |
| GA | genetic algorithm |
| BPNN | backpropagation neural network |
| ANN | artificial neural network |
| MPC | model predictive control |
| RBFNN | radial basis function neural network |
| Adam | adaptive moment estimation |
| FPGA | field-programmable gate array |
| HASS | home assistant |
| SSA | sparse search algorithm |
| DE | differential evolution |
| IMM-MADRL | improved monkey multiagent deep reinforcement learning |
| VRFT | virtual reference feedback tuning |
| VCAC | vector-based constant amplitude control |
| GABS | genetic algorithm based on the state space |
| NT | non-singular terminal sliding variable |
| GABS | genetic algorithm based on the state-space |
| NDX | normal distribution crossover |
| MOSTA | multi-objective state transition algorithm |
| VNS | variable neighborhood search |
| DTC | direct torque control |
| ASIC | application-specific integrated circuit |
| HDL | hardware description language |
| PLC | programmable logic controller |
| AABC-FL | adaptive artificial bee colony fuzzy logic |
| OPC | OLE for process control |
| UA | unified architecture |
| DRL | deep reinforcement learning |
| MICNN | multi-input convolutional neural network |
| CNN | convolutional neural network |
| ALBP | adaptive local binary pattern |
References
- Skowron, M.; Krzysztofiak, M. Permanent Magnet Synchronous Motor Stator and Rotor Fault Detection Using Transfer Learning and Field-Circuit Model. IEEE Access 2025, 13, 74555–74566. [Google Scholar] [CrossRef]
- Yu, K.; Li, S.; Zhu, W.; Wang, Z. Sensorless Control Scheme for PMSM Drive via Generalized Proportional Integral Observers and Kalman Filter. IEEE Trans. Power Electron. 2025, 40, 4020–4033. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, J.; Jiang, Z.; Tang, T.; Tang, H.; Shi, L. PID Adaptive Feedback Motor System Based on Neural Network. IEEE Access 2024, 12, 60149–60154. [Google Scholar] [CrossRef]
- Assani, N.; Matić, P. Evaluating the ANN Model Performance for PID Controller Tuning in Flow Process Control: A Comparative Study. IEEE Access 2025, 13, 88499–88508. [Google Scholar] [CrossRef]
- Moučka, M.; Hofreiter, M. PID Controller with an Autotuning Function. IEEE Access 2024, 12, 136202–136221. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y.; Gan, H.; Liu, Y.; Chen, Y. A Current- and Speed-Loop Decoupling Controller for SPMSM Under Periodic Disturbances. IEEE Trans. Power Electron. 2024, 39, 6889–6902. [Google Scholar] [CrossRef]
- Altınkaya, H.; Ekmekci, D. Tuning of PID Controller in PLC-Based Automatic Voltage Regulator System Using Adaptive Artificial Bee Colony–Fuzzy Logic Algorithm. Electronics 2024, 13, 5039. [Google Scholar] [CrossRef]
- Elhawat, M.; Altınkaya, H. Frequency Regulation of Stand-Alone Synchronous Generator via Induction Motor Speed Control Using a PSO-Fuzzy PID Controller. Appl. Sci. 2025, 15, 3634. [Google Scholar] [CrossRef]
- Maarouf, A.; Bin Salamah, Y.; Ahmad, I. Decentralized Control Framework for Optimal Platoon Spacing and Energy Efficiency. Electronics 2025, 14, 169. [Google Scholar] [CrossRef]
- Mahmoud, A.; Bajodah, A.H. Performance Enhancement of MRAC via Generalized Dynamic Inversion. Actuators 2025, 14, 18. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Q.; Zhou, X.; Sun, L.; Gao, D.; Lu, H. Current Control Method of Vehicle Permanent Magnet Synchronous Motor Based on Active Disturbance Rejection Control. World Electr. Veh. J. 2023, 14, 2. [Google Scholar] [CrossRef]
- Song, Y.; Wan, W.; Zhu, L.; Song, A. Modeling and Control Design for a Musculoskeletal Robot via Adaptive Dynamic Programming. IEEE Trans. Autom. Sci. Eng. 2025, 22, 14843–14854. [Google Scholar] [CrossRef]
- Massoud, M.M.; Alves, P.H.T.F.; Libby, J. Enhancing Dual-Loop Pressure Control in Pneumatic Soft Robotics with a Comparison of Evolutionary Algorithms for PID & FOPID Controller Tuning. IEEE Robot. Autom. Lett. 2025, 10, 6119–6126. [Google Scholar] [CrossRef]
- Hou, L.; Zhao, X.; Chen, T.; Zhang, Y.; Ling, Q.; Tao, B. A Sensing Strategy Combining Kinematic Model with FBG Sensors for Continuum Robots. IEEE Trans. Instrum. Meas. 2025, 74, 7506911. [Google Scholar] [CrossRef]
- Bi, Q.; Ji, W.; Yi, J.; Zhan, H.; Xia, G.-S. Cross-Level Multi-Instance Distillation for Self-Supervised Fine-Grained Visual Categorization. IEEE Trans. Image Process. 2025, 34, 2954–2969. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H. Study on the Optimization for Reactive Power Regulation of Synchronous Condenser Based on Single Neuron Adaptive PID*. Chin. J. Electr. Eng. 2025, 11, 184–193. [Google Scholar] [CrossRef]
- Ajith, N.; Rajendran, A.; Naldi, G.; D’Angelo, E.; Diwakar, S. An Equivalent Single Spiking Neuron Model of the Working Memory. In Proceedings of the 2025 International Conference on Cognitive Computing in Engineering, Communications, Sciences and Biomedical Health Informatics (IC3ECSBHI), Greater Noida, India, 16–18 January 2025; pp. 570–574. [Google Scholar] [CrossRef]
- Wu, C.; Wang, X.; Yang, L. Research on Simulation of Temperature Control System for Gyro Based on Single Neuron PID. In Proceedings of the 2010 International Conference on Machine Vision and Human-Machine Interface, Kaifeng, China, 24–25 April 2010; pp. 381–384. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Lu, X. Temperature control based on a single neuron PID algorithm for a blackbody radiation source. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 220–225. [Google Scholar] [CrossRef]
- El Zoghby, H.M.; Samir, A.S.; Bendary, A.F.; Hazem, A.; Ramadan, H.S.; Elmesalawy, M.M.; Afia, R.S.A. Islanded Microgrids Frequency Support Using Green Hydrogen Energy Storage with AI-Based Controllers. IEEE Access 2024, 12, 128129–128140. [Google Scholar] [CrossRef]
- Ma, F.; Lu, J.; Liu, L.; He, Y. Application of Improved Single Neuron Adaptive PID Control Method in the Angle Predefined Loop of Active Radar Seeker for Anti-radiation Missile. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 2160–2164. [Google Scholar] [CrossRef]
- Jiao, J.; Chen, J.; Qiao, Y.; Wang, W.; Wang, C.; Gu, L. Single Neuron PID Control of Agricultural Robot Steering System Based on Online Identification. In Proceedings of the 2018 IEEE Fourth International Conference on Big Data Computing Service and Applications (BigDataService), Bamberg, Germany, 26–29 March 2018; pp. 193–199. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, H.; Liu, Z.; Liu, Y.; Zhu, Y.; Zhao, J. Real-Time Kinematic Control for Redundant Manipulators in a Time-Varying Environment: Multiple-Dynamic Obstacle Avoidance and Fast Tracking of a Moving Object. IEEE Trans. Ind. Inform. 2020, 16, 28–41. [Google Scholar] [CrossRef]
- Xu, S.; Shi, S.; Jiang, W.; Hashimoto, S. Cooperative Control of Recurrent Neural Network for PID-Based Single Phase Hotplate Temperature Control Systems. IEEE Access 2023, 11, 105557–105569. [Google Scholar] [CrossRef]
- Cao, H.; Li, X. Thermal Management-Oriented Multivariable Robust Control of a kW-Scale Solid Oxide Fuel Cell Stand-Alone System. IEEE Trans. Energy Convers. 2016, 31, 596–605. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Luo, X.; Li, Y.; Qin, B. Neural Dynamics for Cooperative Control of Redundant Robot Manipulators. IEEE Trans. Ind. Inform. 2018, 14, 3812–3821. [Google Scholar] [CrossRef]
- Karlsson, V.; Kämäräinen, J. Neural Code Translation with LIF Neuron Microcircuits. Neural Comput. 2025, 37, 1124–1153. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhou, Q.; Xie, B. Application Research of Intelligent PID Parameter Optimization Algorithm for XY Linear Motor Motion Platform in Wire Bonder. In Proceedings of the 2024 25th International Conference on Electronic Packaging Technology (ICEPT), Tianjin, China, 7–9 August 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, G.; Yan, Q. Error Tracking-Based Neuro-Adaptive Learning Control for Pneumatic Artificial Muscle Systems with Output Constraint. IEEE Access 2023, 11, 127479–127491. [Google Scholar] [CrossRef]
- Al-Saoudi, A.F.; Al-Aubidy, K.M.; Al-Mahasneh, A.J. Comparison of PID, Fuzzy Logic, ANFIS and Model Predictive Controllers for Cruise Control System. In Proceedings of the 2024 21st International Multi-Conference on Systems, Signals & Devices (SSD), Erbil, Iraq, 22–25 April 2024; pp. 263–265. [Google Scholar] [CrossRef]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Effective Nonlinear Model Predictive Control Scheme Tuned by Improved NN for Robotic Manipulators. IEEE Access 2021, 9, 64278–64290. [Google Scholar] [CrossRef]
- Xiong, N. Research on Adaptive Decoupling Control Algorithm Based on Optimal Parameter Identification. In Proceedings of the 2024 IEEE 6th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 26–28 July 2024; pp. 977–982. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Guan, X.; Ma, Z.; Tang, P.; Zheng, C. Precise Docking Control of AUV Based on Neural Network Adaptive Controller. In Proceedings of the 2018 IEEE 8th International Conference on Underwater System Technology: Theory and Applications (USYS), Wuhan, China, 1–3 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gueye, D.; Ndiaye, A.; Diao, A. Adaptive Controller Based on Neural Network Artificial to Improve Three-phase Inverter Connected to the Grid. In Proceedings of the 2020 9th International Conference on Renewable Energy Research and Application (ICRERA), Glasgow, UK, 27–30 September 2020; pp. 72–77. [Google Scholar] [CrossRef]
- Kasprzyk, K.; Gałuszka, A. Energy savings possibilities gained from neural network application in compressed air supervisory control systems. In Proceedings of the 2023 27th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 22–25 August 2023; pp. 279–285. [Google Scholar] [CrossRef]
- Rezaei, A.; Talaeizadeh, A.; Alasty, A. Self-Tuning PID Controller for an Arm-Angle Adjustable Quadrotor Using an Actor-Critic-Based Neural Network. In Proceedings of the 2024 19th Iranian Conference on Intelligent Systems (ICIS), Sirjan, Iran, 23–24 October 2024; pp. 205–210. [Google Scholar] [CrossRef]
- Himavathi, S.; Anitha, D.; Muthuramalingam, A. Feedforward Neural Network Implementation in FPGA Using Layer Multiplexing for Effective Resource Utilization. IEEE Trans. Neural Netw. 2007, 18, 880–888. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q. Hysteresis Model of Magnetically Controlled Shape Memory Alloy Based on a PID Neural Network. IEEE Trans. Magn. 2015, 51, 7301504. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Q.; Wang, Y.; Dong, Q. Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform. Electronics 2022, 11, 4162. [Google Scholar] [CrossRef]
- Hoai, H.-K.; Than, H. Realization of the Sensor-less Permanent Magnet Synchronous Motor Drive Control System with an Intelligent Controller. Electronics 2020, 9, 365. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Wang, P.; Cai, S.; Xu, C.; Chu, J. Output Feedback-Based Continuous-Time Distributed PID Optimization Algorithms. IEEE Trans. Netw. Sci. Eng. 2025, 12, 955–969. [Google Scholar] [CrossRef]
- Neath, M.J.; Swain, A.K.; Madawala, U.K.; Thrimawithana, D.J. An Optimal PID Controller for a Bidirectional Inductive Power Transfer System Using Multiobjective Genetic Algorithm. IEEE Trans. Power Electron. 2014, 29, 1523–1531. [Google Scholar] [CrossRef]
- Wang, H.; Xu, S.; Hu, H. PID Controller for PMSM Speed Control Based on Improved Quantum Genetic Algorithm Optimization. IEEE Access 2023, 11, 61091–61102. [Google Scholar] [CrossRef]
- Fan, X.; Bai, X.; Jiang, Z.; Zhang, S. An Optimization Method of Attitude Control Parameters Based on Genetic Algorithm for the Boost-Glide Rocket. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4356–4376. [Google Scholar] [CrossRef]
- Tan, V.V.; Tu, D.T.; Vinh, N.V.; Thang, P.T.; Mihaly, A.; Gaspar, P. Optimizing a Hybrid Controller for Automotive Active Suspension System by Using Genetic Algorithms with Two High Level Parameters. IEEE Access 2024, 12, 172451–172464. [Google Scholar] [CrossRef]
- Hasanien, H.M. Design Optimization of PID Controller in Automatic Voltage Regulator System Using Taguchi Combined Genetic Algorithm Method. IEEE Syst. J. 2013, 7, 825–831. [Google Scholar] [CrossRef]
- Li, J.; Li, W. On-Line PID Parameters Optimization Control for Wind Power Generation System Based on Genetic Algorithm. IEEE Access 2020, 8, 137094–137100. [Google Scholar] [CrossRef]
- Zhang, H.; Assawinchaichote, W.; Shi, Y. New PID Parameter Autotuning for Nonlinear Systems Based on a Modified Monkey–Multiagent DRL Algorithm. IEEE Access 2021, 9, 78799–78811. [Google Scholar] [CrossRef]
- Wan, J.; He, B.; Wang, D.; Yan, T.; Shen, Y. Fractional-Order PID Motion Control for AUV Using Cloud-Model-Based Quantum Genetic Algorithm. IEEE Access 2019, 7, 124828–124843. [Google Scholar] [CrossRef]
- Tayarani-N, M.-H.; Yao, X.; Xu, H. Meta-Heuristic Algorithms in Car Engine Design: A Literature Survey. IEEE Trans. Evol. Comput. 2015, 19, 609–629. [Google Scholar] [CrossRef]
- Serradilla, F.; Cañas, N.; Naranjo, J.E. Optimization of the Energy Consumption of Electric Motors through Metaheuristics and PID Controllers. Electronics 2020, 9, 1842. [Google Scholar] [CrossRef]
- Juang, J.-G.; Huang, M.-T.; Liu, W.-K. PID Control Using Presearched Genetic Algorithms for a MIMO System. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 716–727. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, Z.P.; Wan, Z.C.; Wan, G.C.; Tong, M.S. Fast Braking of Segmented Electro-Pneumatic Braking System by Using Variable-Universe Fuzzy-PID Controller Optimized by Genetic Algorithm. IEEE Trans. Veh. Technol. 2025, 74, 2610–2619. [Google Scholar] [CrossRef]
- Jin, K.; Xiao, P.; Yang, D.; Fang, Z.; Zhang, R.; Yang, A. Research on Steering-by-Wire System Motor Control Based on an Improved Sparrow Search Proportional–Integral–Derivative Algorithm. Electronics 2024, 13, 4553. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, X.; Zhang, F.; Gu, Y.; Deng, K.; Xu, Y.; Xie, T.; Song, Y. Adaptive Weighted Particle Swarm Optimization for Controlling Multiple Switched Reluctance Motors with Enhanced Deviatoric Coupling Control. Electronics 2024, 13, 4320. [Google Scholar] [CrossRef]
- Ma, C.; Huang, B.; Basher, M.K.; Rob, M.A.; Jiang, Y. Fuzzy PID Control Design of Mining Electric Locomotive Based on Permanent Magnet Synchronous Motor. Electronics 2024, 13, 1855. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; El-Sousy, F.F.M.; Ali, M.M. A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor. Electronics 2023, 12, 4955. [Google Scholar] [CrossRef]
- Singh, N.; Sharma, A.K.; Tiwari, M.; Jasiński, M.; Leonowicz, Z.; Rusek, S.; Gono, R. Robust Control of SEDCM by Fuzzy-PSO. Electronics 2023, 12, 335. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, R.; Zhou, S.; Liu, Z. Design and Analysis of a Drive System for a Series Manipulator Based on Orthogonal-Fuzzy PID Control. Electronics 2019, 8, 1051. [Google Scholar] [CrossRef]
- Bao, L.; Peng, F.; Huang, Y.; Du, Y. An Online Auto-Tuning Method for PID Controllers Based on Back Propagation Neural Network. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024; pp. 657–663. [Google Scholar] [CrossRef]
- Mei, J.; Yuan, H.; Chu, X.; Ding, L. Efficient Optimization Method of the Meshed Return Plane Through Fusion of Convolutional Neural Network and Improved Particle Swarm Optimization. Electronics 2025, 14, 1035. [Google Scholar] [CrossRef]
- Kaur, R.; Asad, A.; Al Abdul Wahid, S.; Mohammadi, F. A Survey of Advancements in Scheduling Techniques for Efficient Deep Learning Computations on GPUs. Electronics 2025, 14, 1048. [Google Scholar] [CrossRef]
- Moin, H.; Shah, U.H.; Khan, M.J.; Sajid, H. Fine-Tuning Quadcopter Control Parameters via Deep Actor-Critic Learning Framework: An Exploration of Nonlinear Stability Analysis and Intelligent Gain Tuning. IEEE Access 2024, 12, 173462–173474. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, S.; Lu, E.; Wei, Q.; Yang, Z. Study on Cross-Coupling Synchronous Control Strategy of Dual-Motor Based on Improved Active Disturbance Rejection Control–Nonsingular Fast Terminal Sliding Mode Control Strategy. Electronics 2025, 14, 526. [Google Scholar] [CrossRef]
- Liu, L.; Liu, C.; Che, C.; Wu, Y.; Zhao, Q. Research on the Coordinated Control of Mining Multi-PMSM Systems Based on an Improved Active Disturbance Rejection Controller. Electronics 2025, 14, 477. [Google Scholar] [CrossRef]
- Ma, S.; Zhao, J.; Xiong, Y.; Wang, H.; Yao, X. Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law. Electronics 2024, 13, 2352. [Google Scholar] [CrossRef]
- Ye, S.; Long, Z.; Ju, J.; Peng, T.; Yin, J.; Zhao, H. Toward Ultrasonic Wire Bonding for High Power Device: A Vector Based Resonant Frequency Tracking and Constant Amplitude Control. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1337–1348. [Google Scholar] [CrossRef]
- Wen, C.; Li, S.; Wang, P.; Li, J. An Input-Series Output-Parallel DC–DC Converter Based on Fuzzy PID Three-Loop Control Strategy. Electronics 2024, 13, 2342. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, A.; Cao, Y. Optimal PID Parameter Tuning Method of First-Order Time-Lag System Based on BP Neural Network. In Proceedings of the 2024 IEEE 6th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 26–28 July 2024; pp. 1001–1006. [Google Scholar] [CrossRef]
- Sun, G. Optimal Tuning of Dominate Parameters of Complex Electromechanical System Based on Fuzzy PID Control. In Proceedings of the 2023 International Conference on Telecommunications, Electronics and Informatics (ICTEI), Lisbon, Portugal, 11–13 September 2023; pp. 18–22. [Google Scholar] [CrossRef]
- Behnamgol, V.; Asadi, M.; Aphale, S.S.; Sohani, B. Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation. Electronics 2025, 14, 1455. [Google Scholar] [CrossRef]
- Feng, T.; Deng, S.; Chen, X.; Zhang, C.; Mao, Y. A Generalized Type-2 Fuzzy-Based Analog Memristive Controller. Electronics 2025, 14, 1178. [Google Scholar] [CrossRef]
- Alshireedah, A.; Yusupov, Z.; Rahebi, J. Optimizing Solar Water-Pumping Systems Using PID-Jellyfish Controller with ANN Integration. Electronics 2025, 14, 1172. [Google Scholar] [CrossRef]
- Wang, M.; Zeng, S.; He, Y.; Su, S.; Liu, P. Multi-Objective Optimization of a Fractional-Order Control System for an EMS-Type Maglev Model. IEEE Trans. Veh. Technol. 2024, 73, 12652–12667. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Q.; Wang, Y.; Jin, Q. A novel design method of multi-objective robust PID controller for industrial process. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 242–246. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, J.; Yang, C.; Gui, W. Set-Point Tracking and Multi-Objective Optimization-Based PID Control for the Goethite Process. IEEE Access 2018, 6, 36683–36698. [Google Scholar] [CrossRef]
- Silva, G.; Silva, P.; Santos, V.; Segundo, A.; Luz, E.; Moreira, G. A VNS Algorithm for PID Controller: Hardware-In-The-Loop Approach. IEEE Lat. Am. Trans. 2021, 19, 1502–1510. [Google Scholar] [CrossRef]
- Chai, T.; Zhou, Z.; Cheng, S.; Jia, Y.; Song, Y. Industrial Metaverse-Based Intelligent PID Optimal Tuning System for Complex Industrial Processes. IEEE Trans. Cybern. 2024, 54, 6458–6470. [Google Scholar] [CrossRef]
- Ghenna, S.; Giraud, F.; Giraud-Audine, C.; Amberg, M. Vector Control of Piezoelectric Transducers and Ultrasonic Actuators. IEEE Trans. Ind. Electron. 2018, 65, 4880–4888. [Google Scholar] [CrossRef]
- Sung, G.-M.; Tung, L.-F.; Huang, C.-C.; Huang, H.-Y. Modified Predictive Direct Torque Control ASIC with Multistage Hysteresis and Fuzzy Controller for a Three-Phase Induction Motor Drive. Electronics 2022, 11, 1802. [Google Scholar] [CrossRef]
- Ren, J.; Teoh, S.S. A Hybrid Adaptive Fusion Deep Learning Model for Fault Diagnosis of Rotating Machinery Under Noisy Conditions. IEEE Access 2025. [Google Scholar] [CrossRef]
- Lai, Z.; Peng, W.; Feng, G.; Pan, M. Bayesian Deep Learning for Fault Diagnosis of Induction Motors with Reduced Data Reliance and Improved Interpretability. IEEE Trans. Energy Convers. 2025. [Google Scholar] [CrossRef]
- Geraei, H.; Rodriguez, E.A.V.; Majma, E.; Habibi, S.; Al-Ani, D. A Noise Invariant Method for Bearing Fault Detection and Diagnosis Using Adapted Local Binary Pattern (ALBP) and Short-Time Fourier Transform (STFT). IEEE Access 2024, 12, 107247–107260. [Google Scholar] [CrossRef]


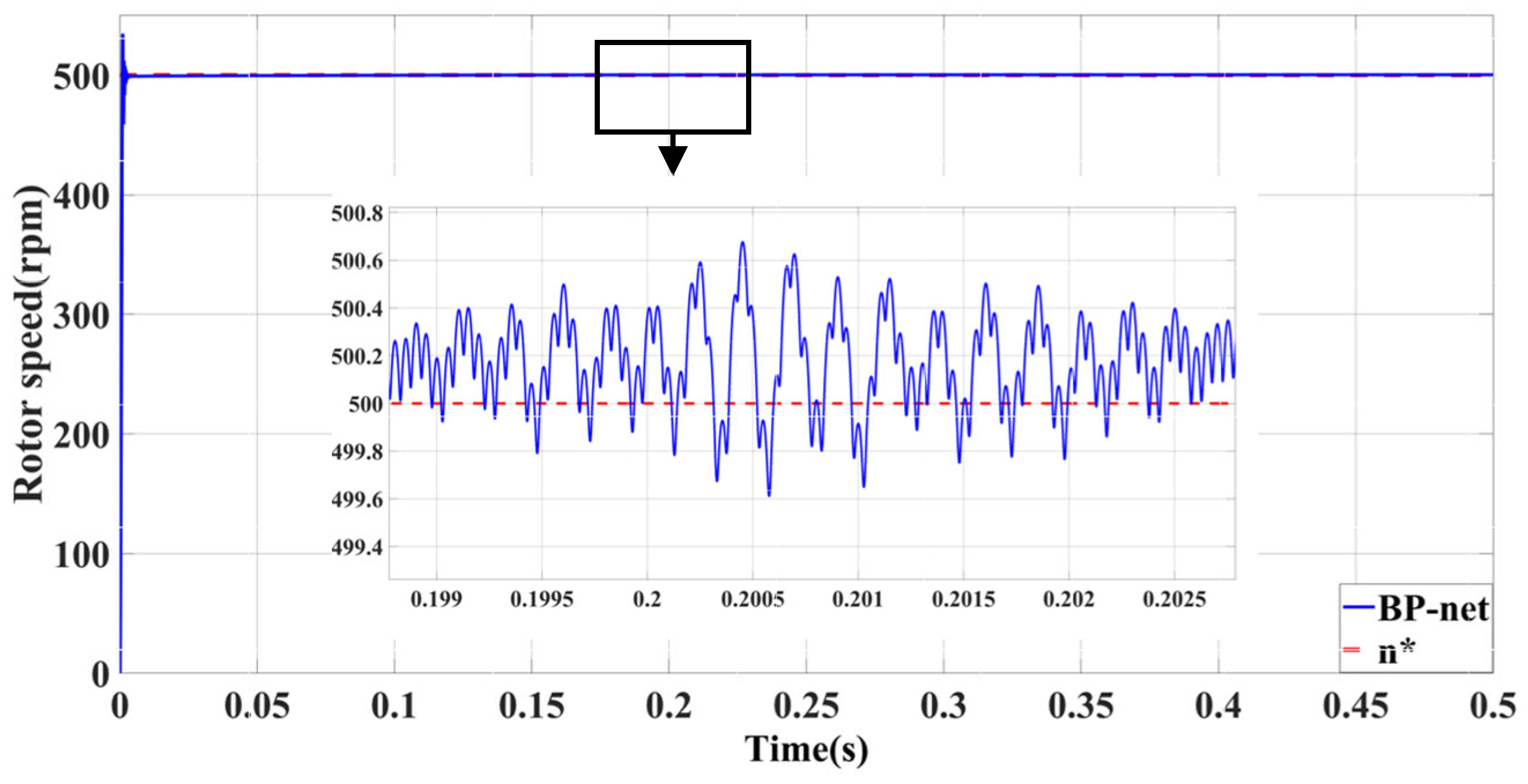
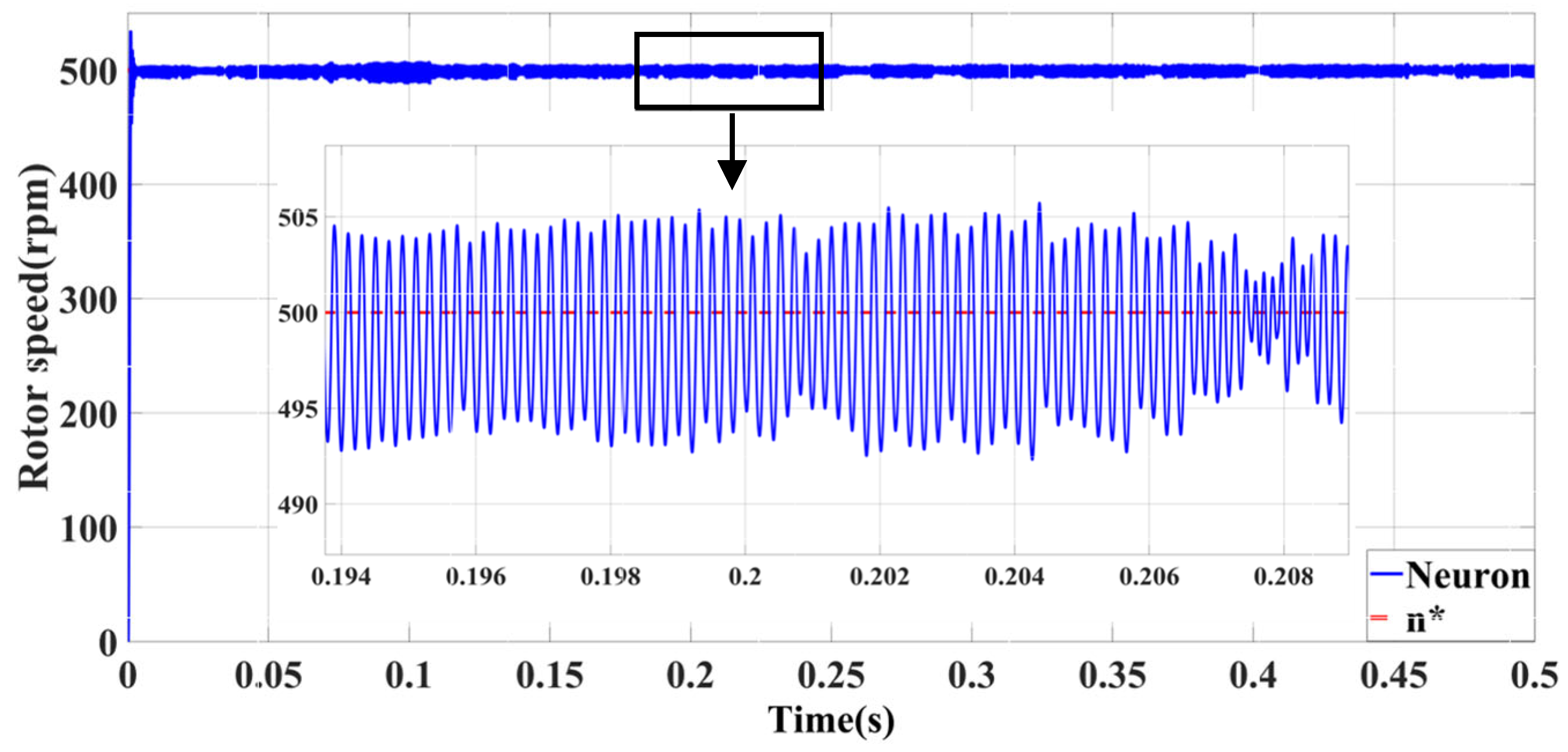
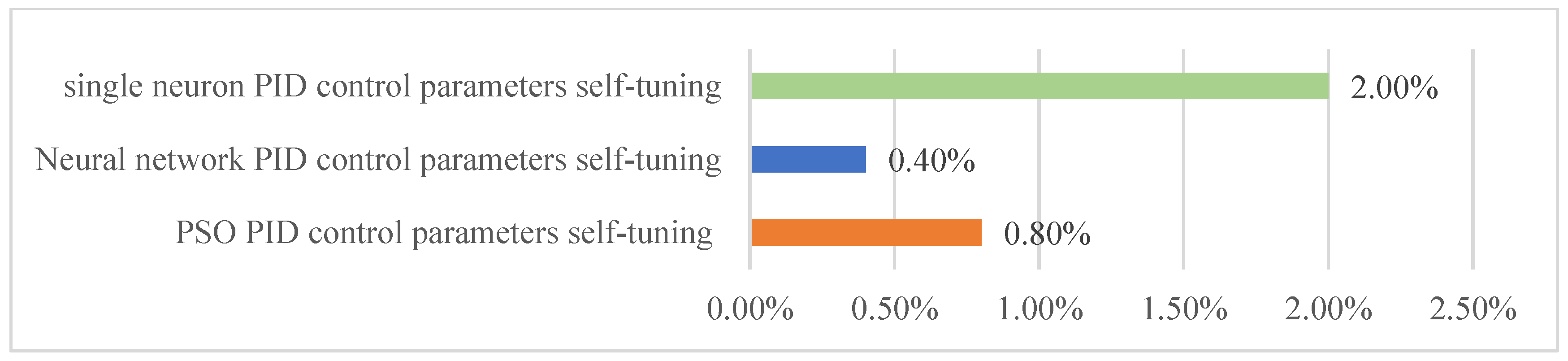
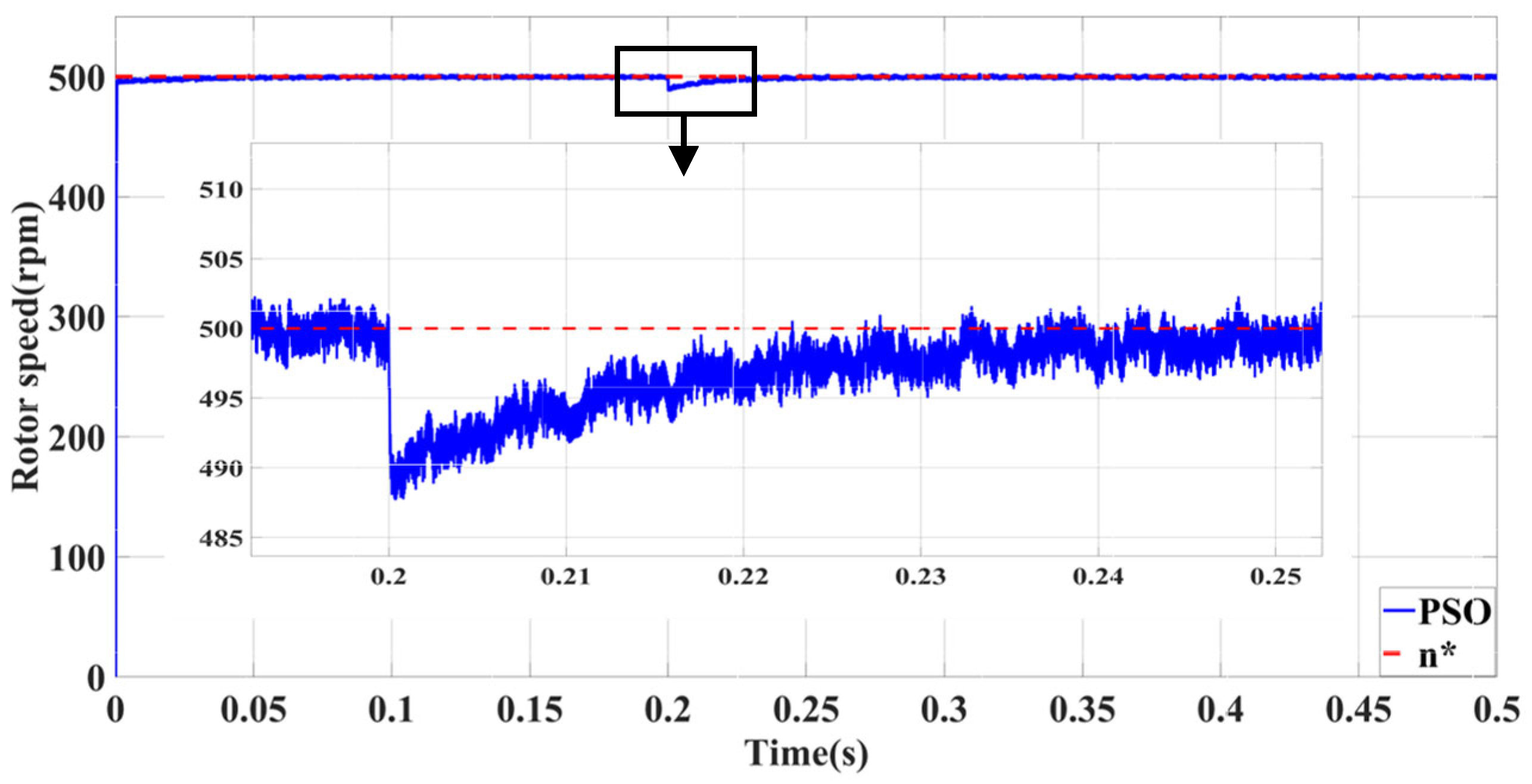

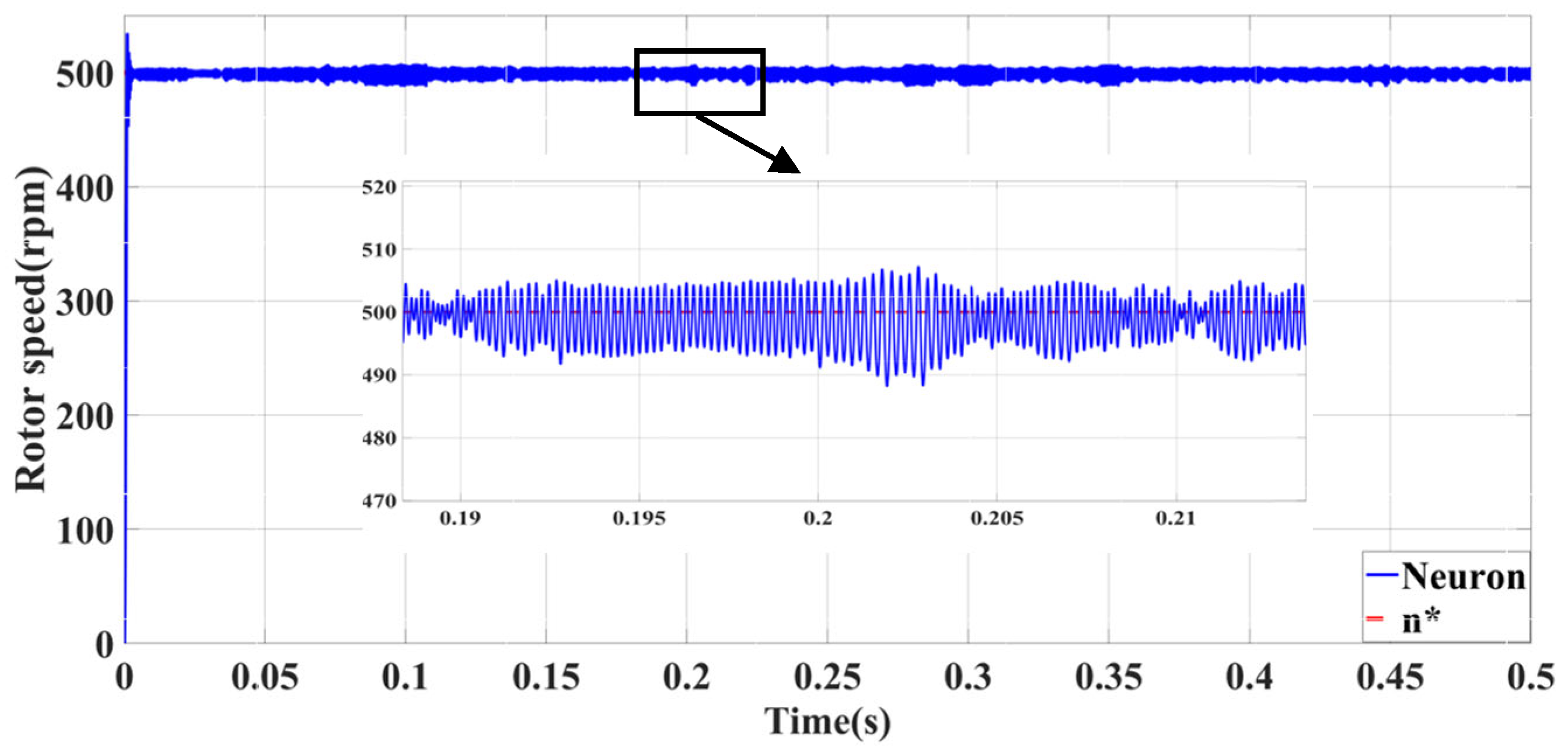
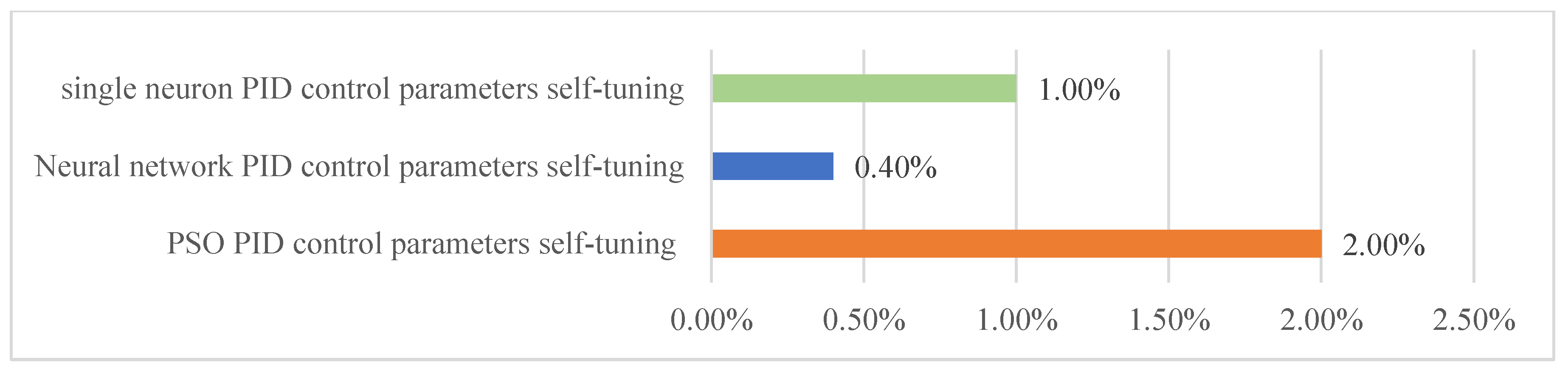
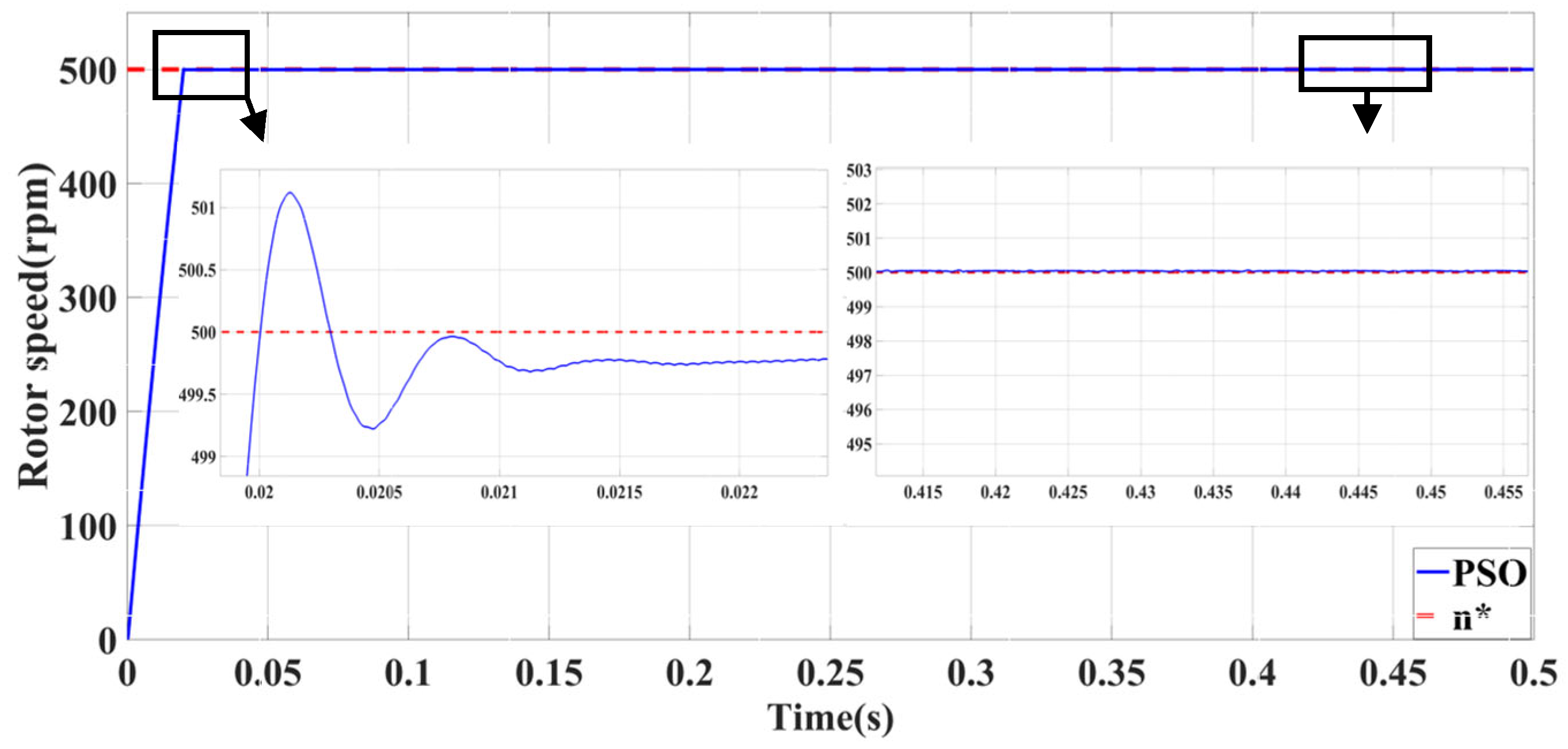
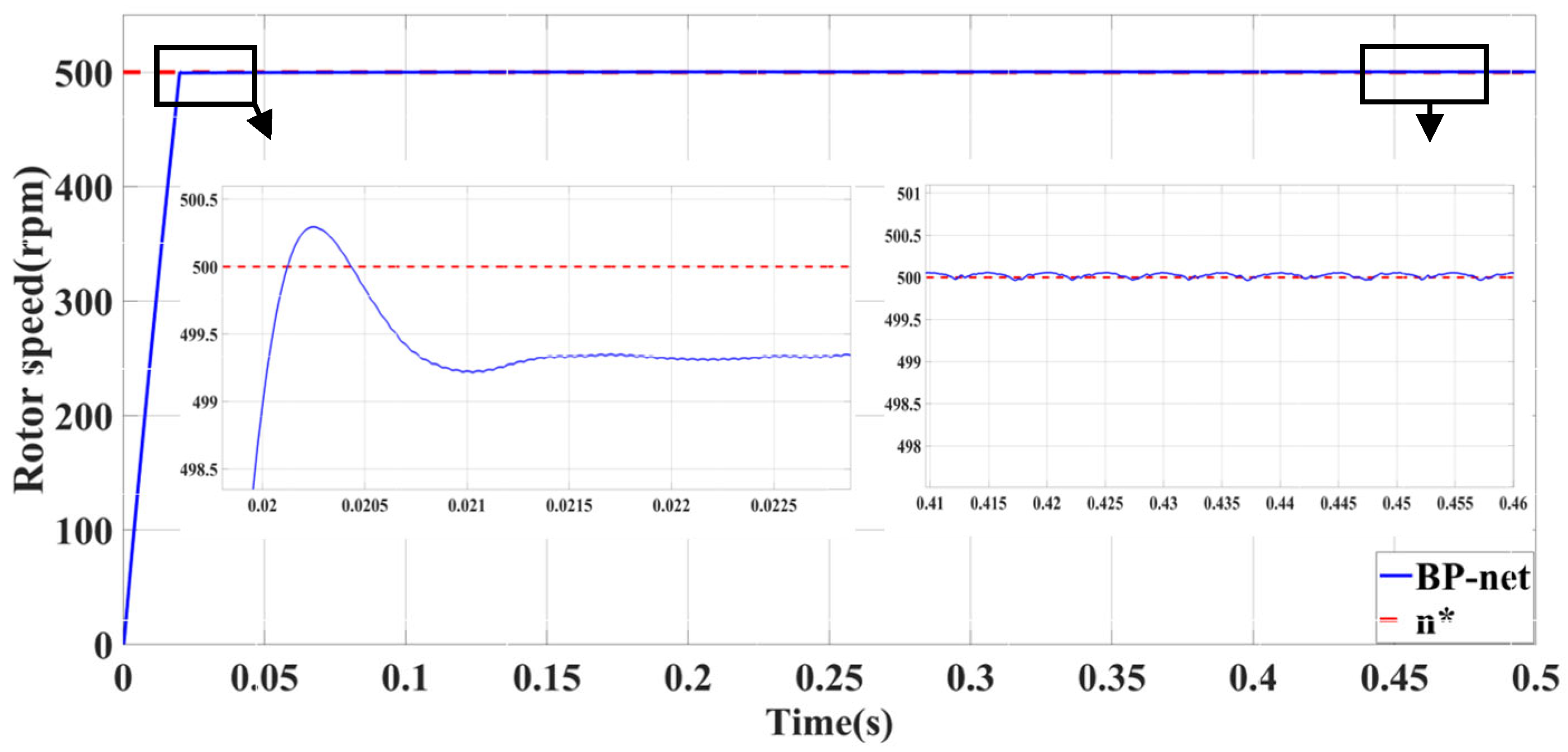
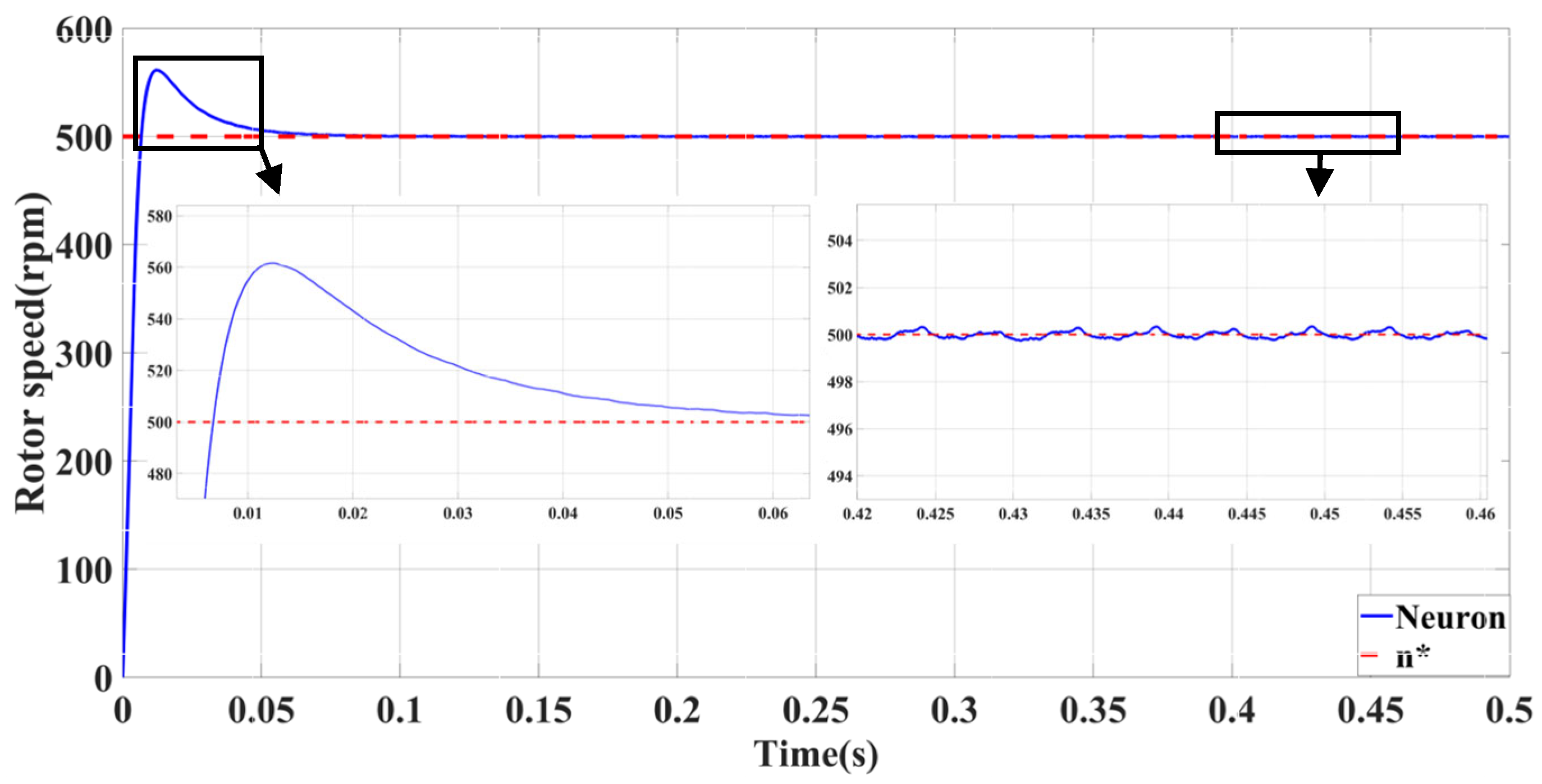
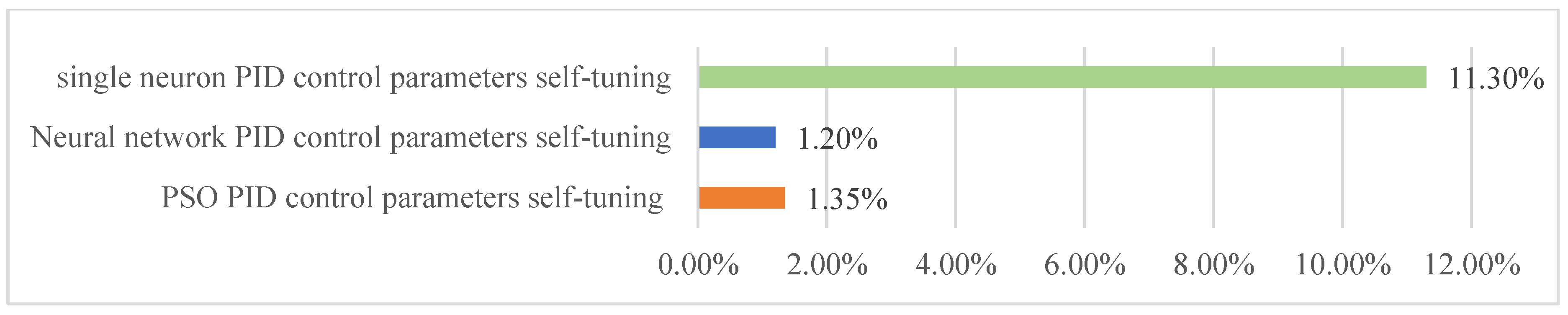
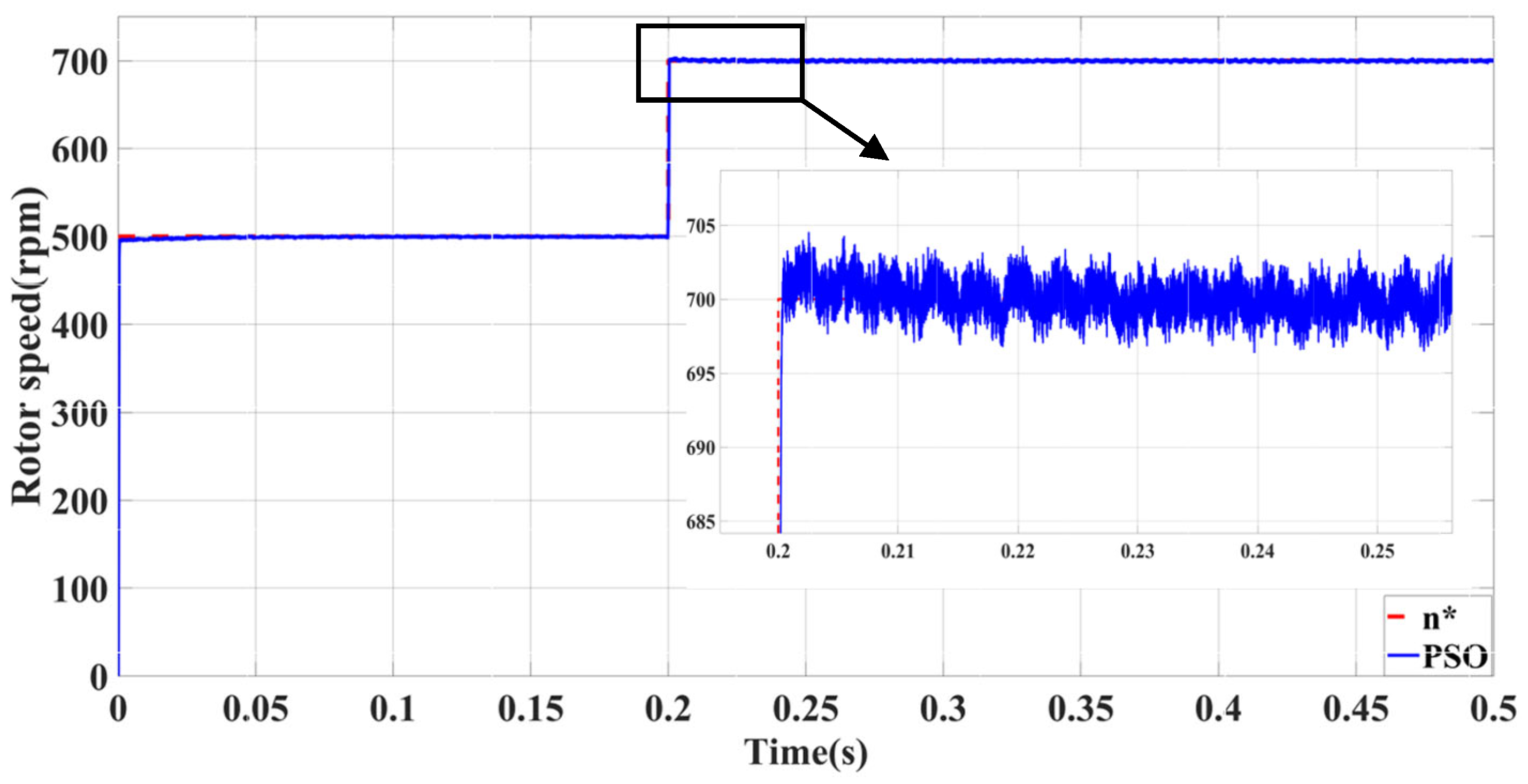
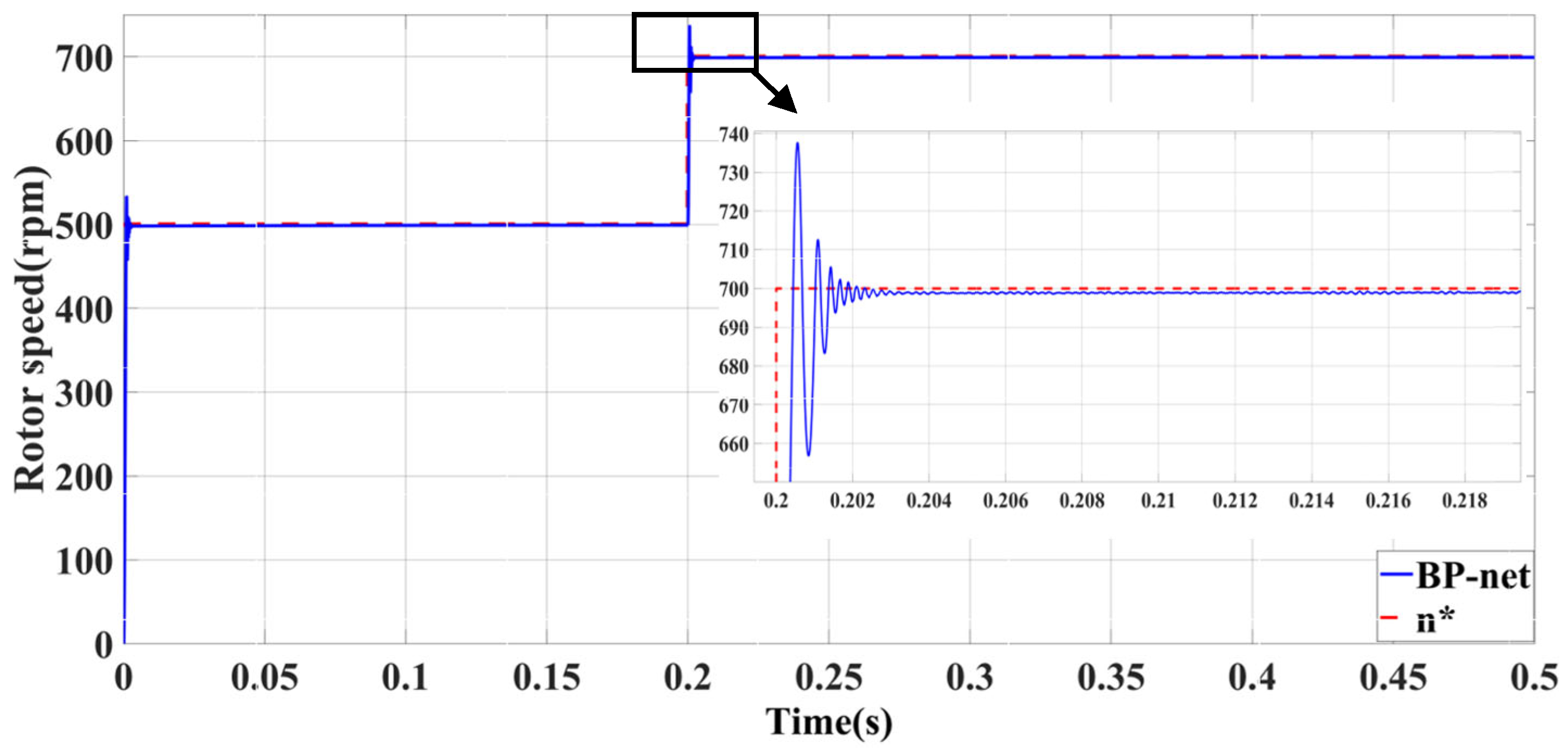
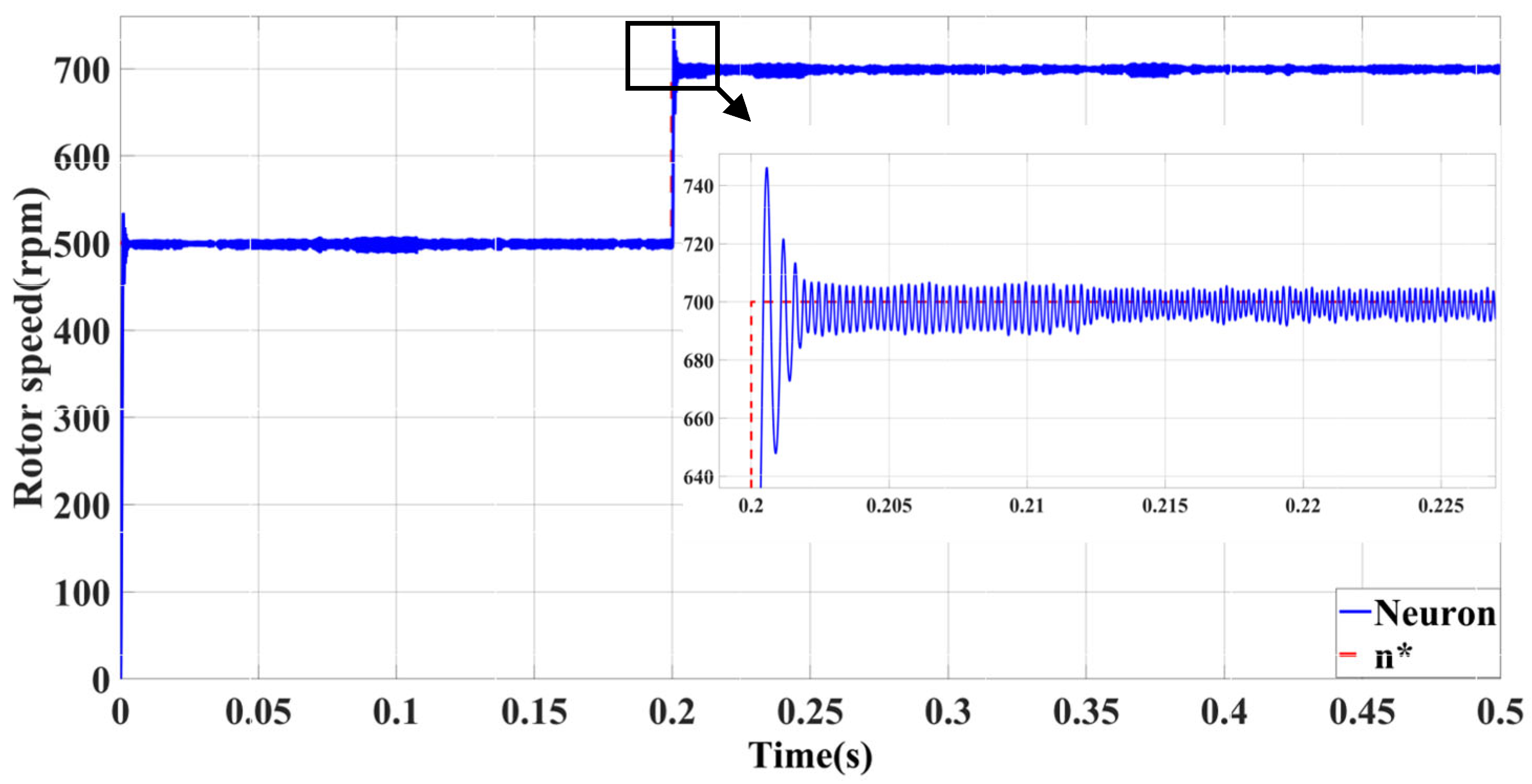

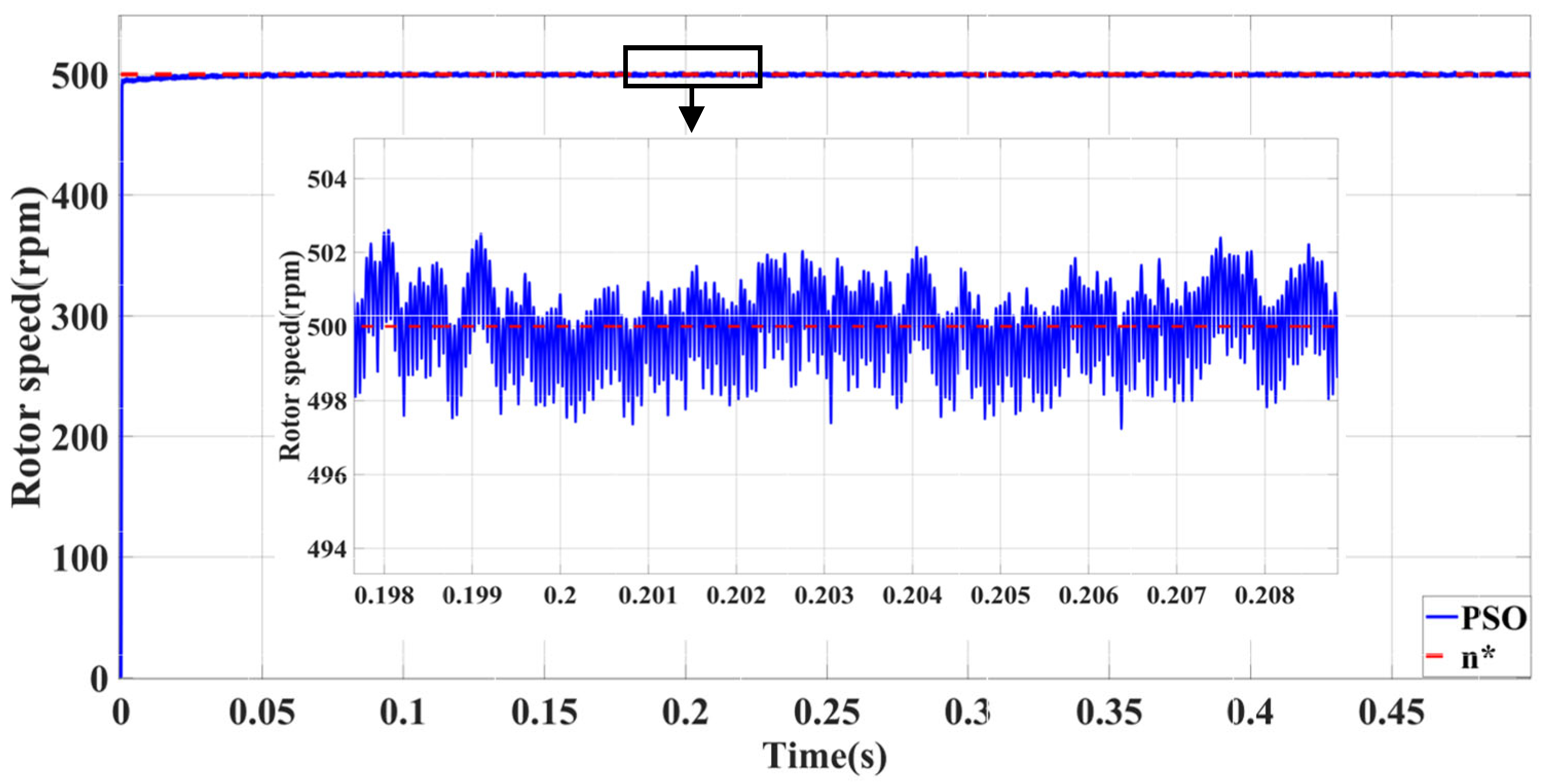
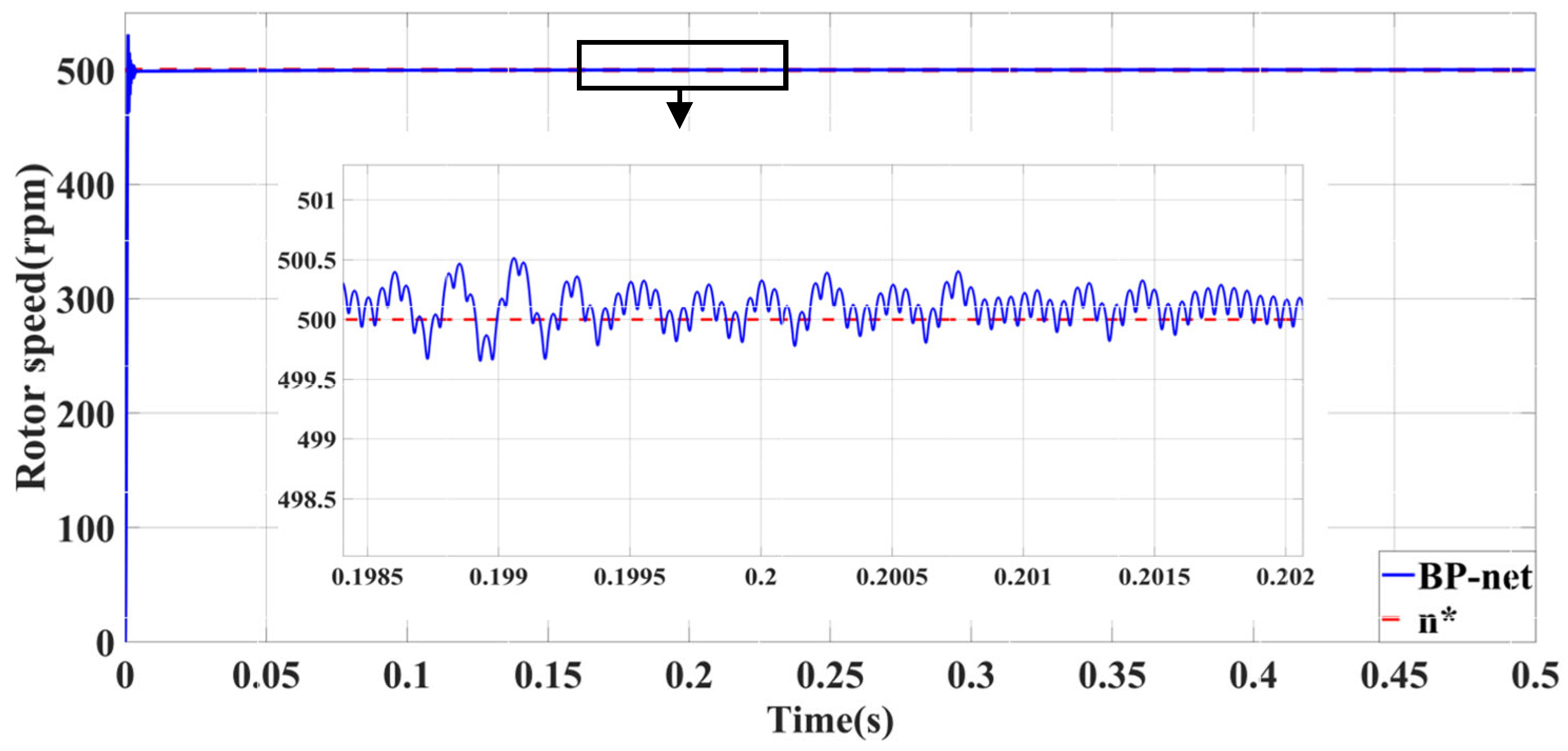
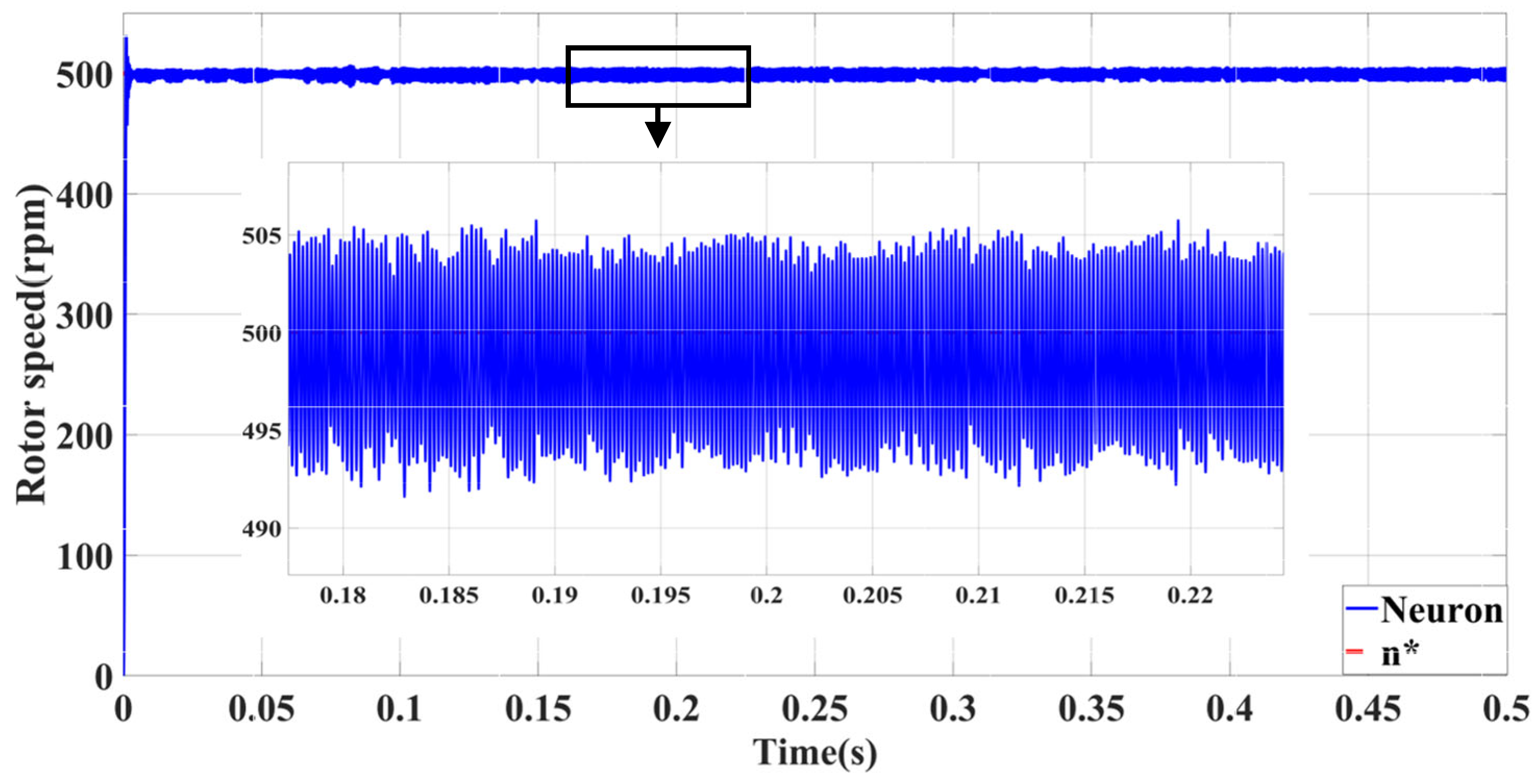

| Self-Tuning Method for Control Parameters | Enhanced Methods | Key Features |
|---|---|---|
| Single-neuron PID controller | Sum of squares in weighting calculation | Enhanced efficiency |
| Optimization of fixed learning rate | Enhanced self-tuning property | |
| Quadratic performance-based exponential learning algorithm | Enhanced adaptability and anti-jamming capabilities | |
| Optimization of GA | Enhanced robustness | |
| Compound control model | Avoid local optimal solution | |
| RBFNN state identification | Improved control performance | |
| Hebbian computational methodology | Self-tuning speed increased | |
| Stochastic optimization of adaptive momentum | Withstand coupling and nonlinearity | |
| Implement of feedforward control structure | Combination of robust, PID control |
| Self-Tuning Method for Control Parameters | Enhanced Methods | Key Features |
|---|---|---|
| Neural network-based PID controller | Determine the initial values of weights | Enhanced efficiency |
| Feedforward control approach | Streamline the calculation process | |
| Fuzzy logic algorithm | Acceleration of weight iteration | |
| Cuckoo search algorithm | Enhanced robustness | |
| Diagonally recursive optimization algorithm | Streamline the calculation process | |
| Adaptive compensator | Enhance overall accuracy | |
| Improved ANN | Enhanced efficiency | |
| Improved MPC | Enhanced dynamic performance | |
| Reinforcement learning with actor–critic methods | maneuverability and stability | |
| Optimize architecture of hidden layers | Optimization of hardware utilization | |
| Incorporate nonlinear computational factor | Enhanced dynamic performance |
| Self-Tuning Method for Control Parameters | Enhanced Methods | Key Features |
|---|---|---|
| Numerical optimization algorithm | Derivative-free optimization method | Enhanced efficiency |
| Enhanced algorithm for quantum property analysis | Avoid local optimal solution | |
| Nonlinear dynamic model | Avoid local optimal solution | |
| Inference algorithms for large-scale models | Minimize nonlinear disturbances | |
| Combination of PSO and GA | Enhanced step response speed | |
| Comprehensive anti-saturation strategy | Mitigate harmonic components | |
| Apply IMM-MADRL algorithm | Improved overall performance | |
| Quantum-inspired GA | Enhanced search efficiency | |
| Metaheuristic algorithm | Better resilience against disturbances | |
| Theory for multiple input–output systems | Multiple parameters self-tuning | |
| Fuzzy inference system | Enhanced system performance |
| Motor Specifications | Numerical Data |
|---|---|
| Resistance of the motor stator | 2.2 |
| Motor direct axis inductance | 3.95 |
| Motor quadrature axis inductance | 3.95 |
| Number of motor poles | 4 |
| Flux of the permanent magnet motor | 0.1827 |
| Initial specified velocity | 500 |
| Moment of inertia () | 0.00011 |
| Coefficient of viscous damping () | 0.0012 |
| Rated torque of the motor () | 1.3 |
| Self-Tuning Method for Control Parameters | Advantages | Limitations | Shared Characteristics |
|---|---|---|---|
| Neuron-PID | Minimal influence of abrupt load torque | Significant no-load following error | Minimal influence of viscous friction coefficient |
| Minimal impact of sudden speed signal | Significant overshoot with large load | ||
| BPNN-PID | Minimal no-load following error | Significant influence of abrupt load torque | |
| Superior performance with large load | Significant impact of sudden speed signal | ||
| PSO-PID | Minimal no-load following error | Significant influence of abrupt load torque | |
| Superior performance with large load | Significant impact of sudden speed signal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Huang, Y. Review of Intelligent Motor Controller Parameter Self-Tuning Technology. Electronics 2025, 14, 2229. https://doi.org/10.3390/electronics14112229
Song Z, Huang Y. Review of Intelligent Motor Controller Parameter Self-Tuning Technology. Electronics. 2025; 14(11):2229. https://doi.org/10.3390/electronics14112229
Chicago/Turabian StyleSong, Zhiru, and Yunkai Huang. 2025. "Review of Intelligent Motor Controller Parameter Self-Tuning Technology" Electronics 14, no. 11: 2229. https://doi.org/10.3390/electronics14112229
APA StyleSong, Z., & Huang, Y. (2025). Review of Intelligent Motor Controller Parameter Self-Tuning Technology. Electronics, 14(11), 2229. https://doi.org/10.3390/electronics14112229







