Prediction of the Probability of IC Failure and Validation of Stochastic EM-Fields Coupling into PCB Traces Using a Bespoke RF IC Detector
Abstract
1. Introduction
2. Methodology to Predict the Probability of the Susceptibility of ICs
2.1. Numerical Method Based on Monte Carlo
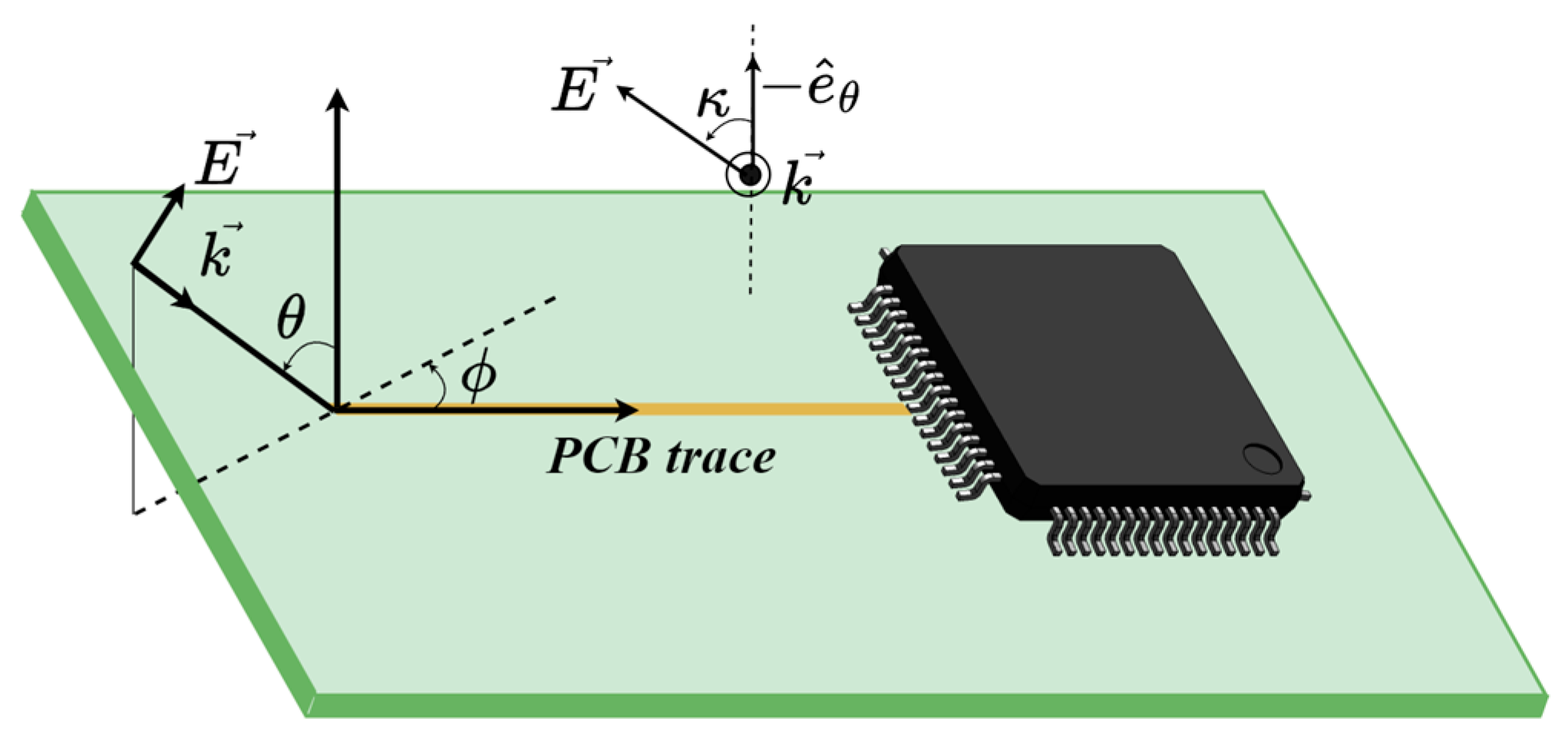
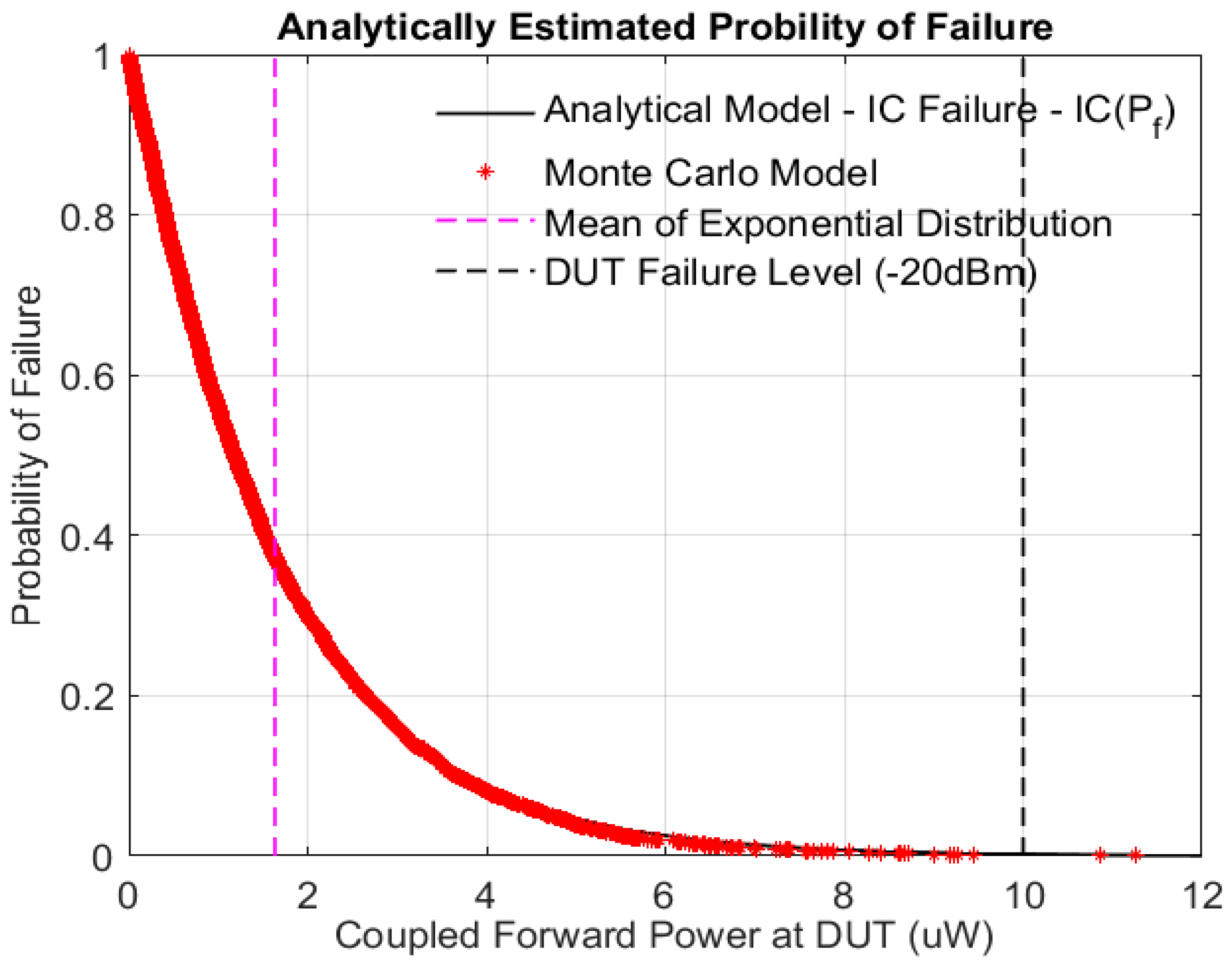
2.2. Analytical Methodology to Predict the Probability of the Susceptibility of ICs
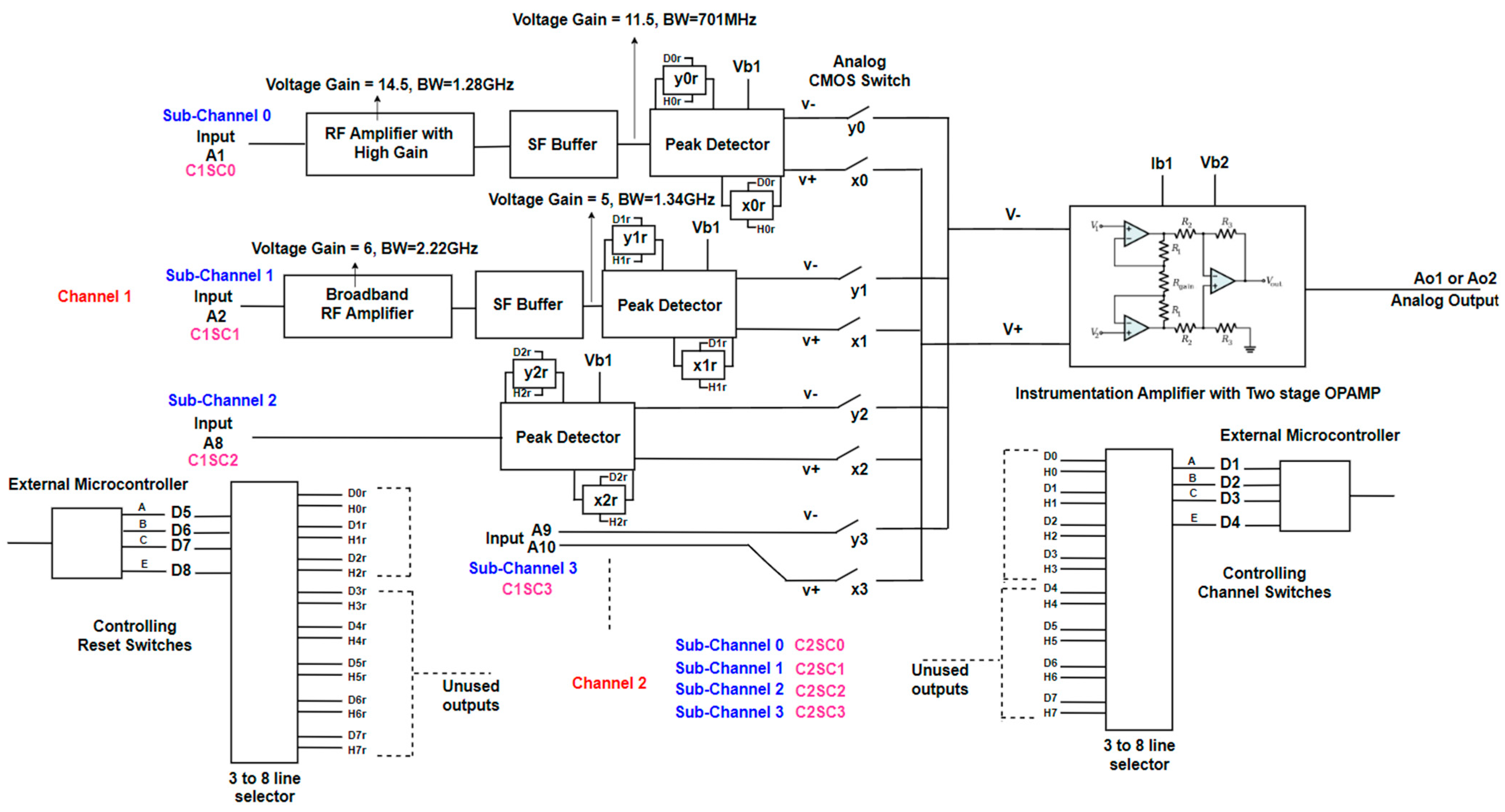
3. Custom RF IC Detector
3.1. Introduction and Working Principles of the RF IC Detector
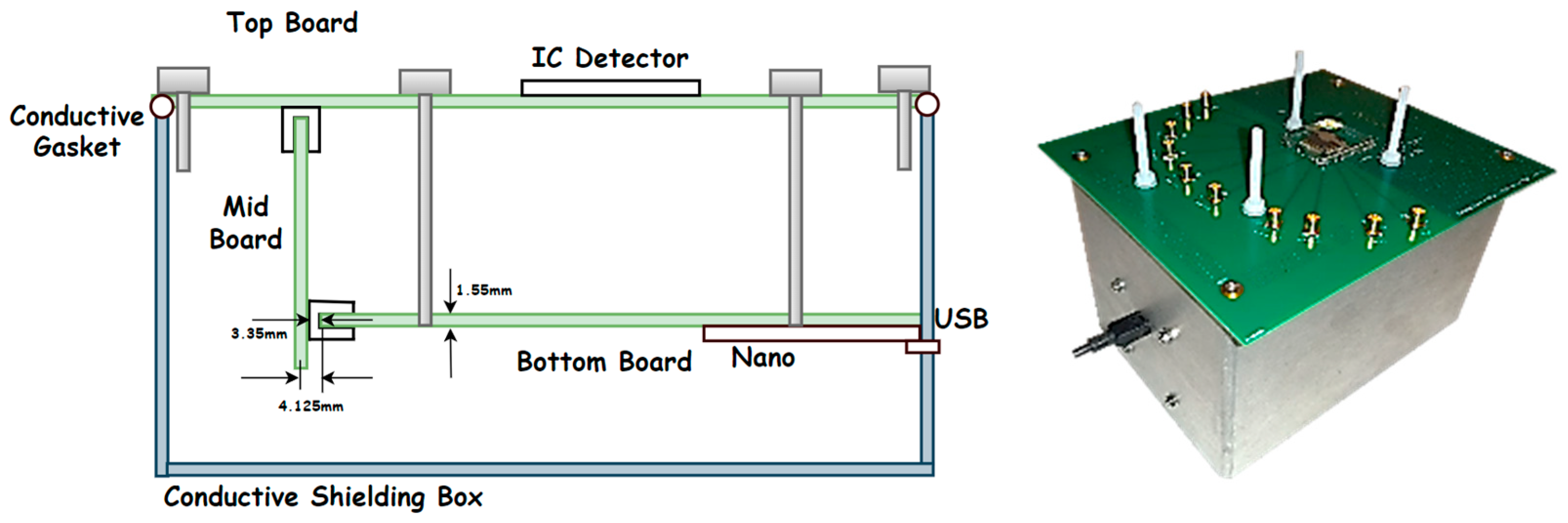
3.2. PCB Test Bench for RF IC Detector Characterization
3.3. Radiated Susceptibility of the PCB Test Bench
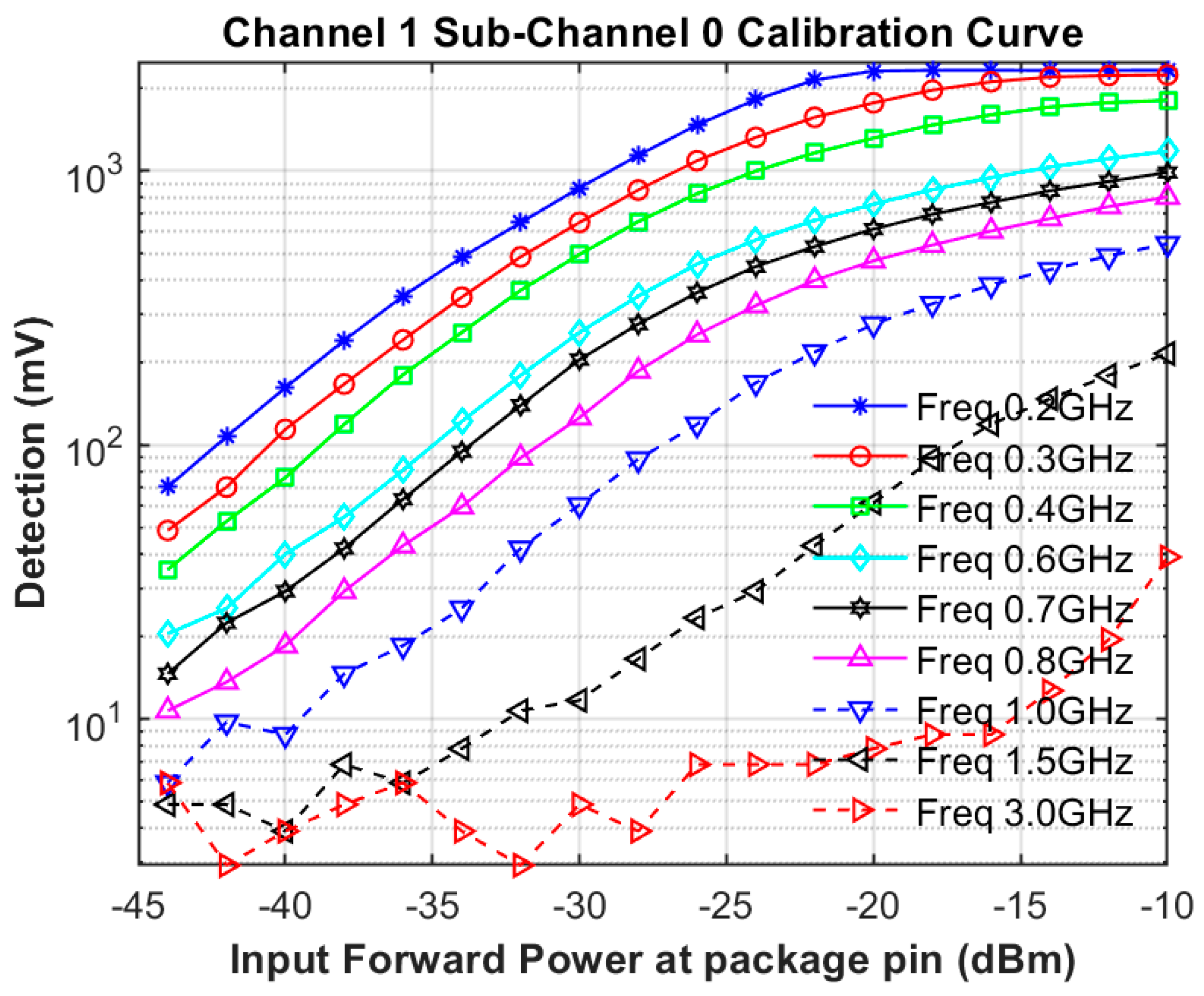
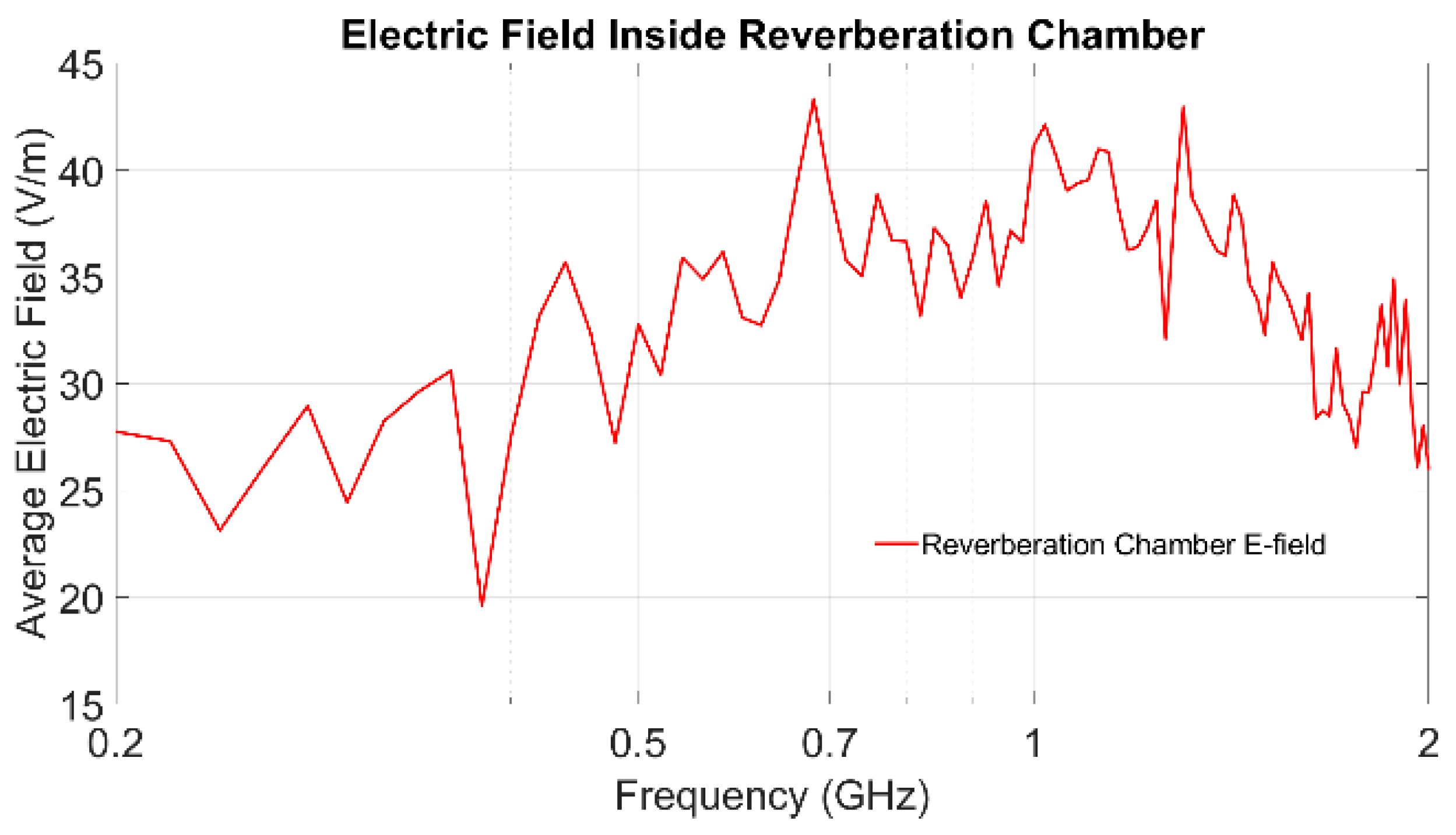
3.4. Calibration of the RF IC Detector Test Bench for Radiated Measurements
4. Experimental Validation of Stochastic EM-Field Coupling into PCB Traces
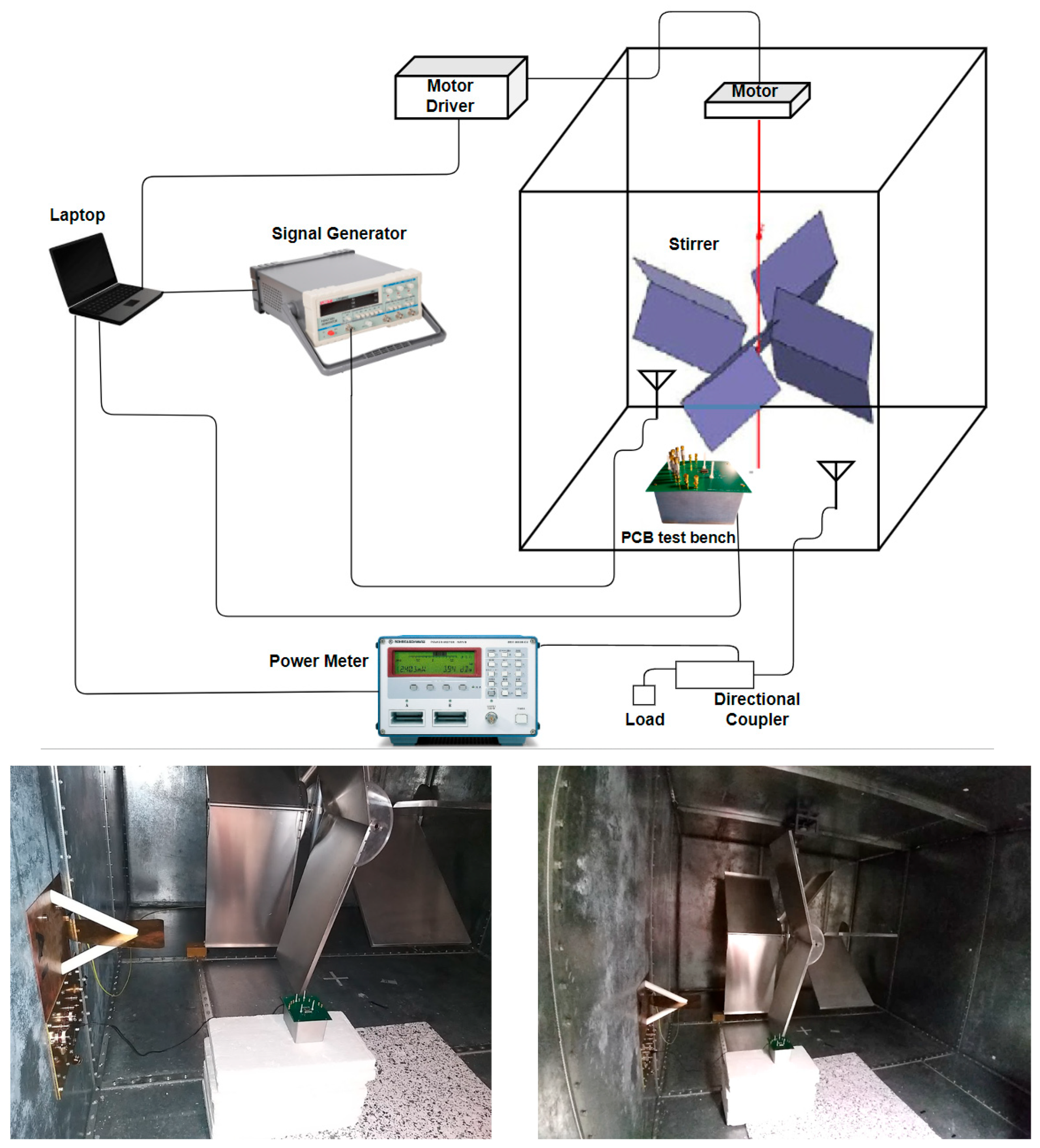
4.1. Measurement Setup
4.2. Coupled Forward Power at the Package Pin
Average Coupled Forward Power at the Package Pin
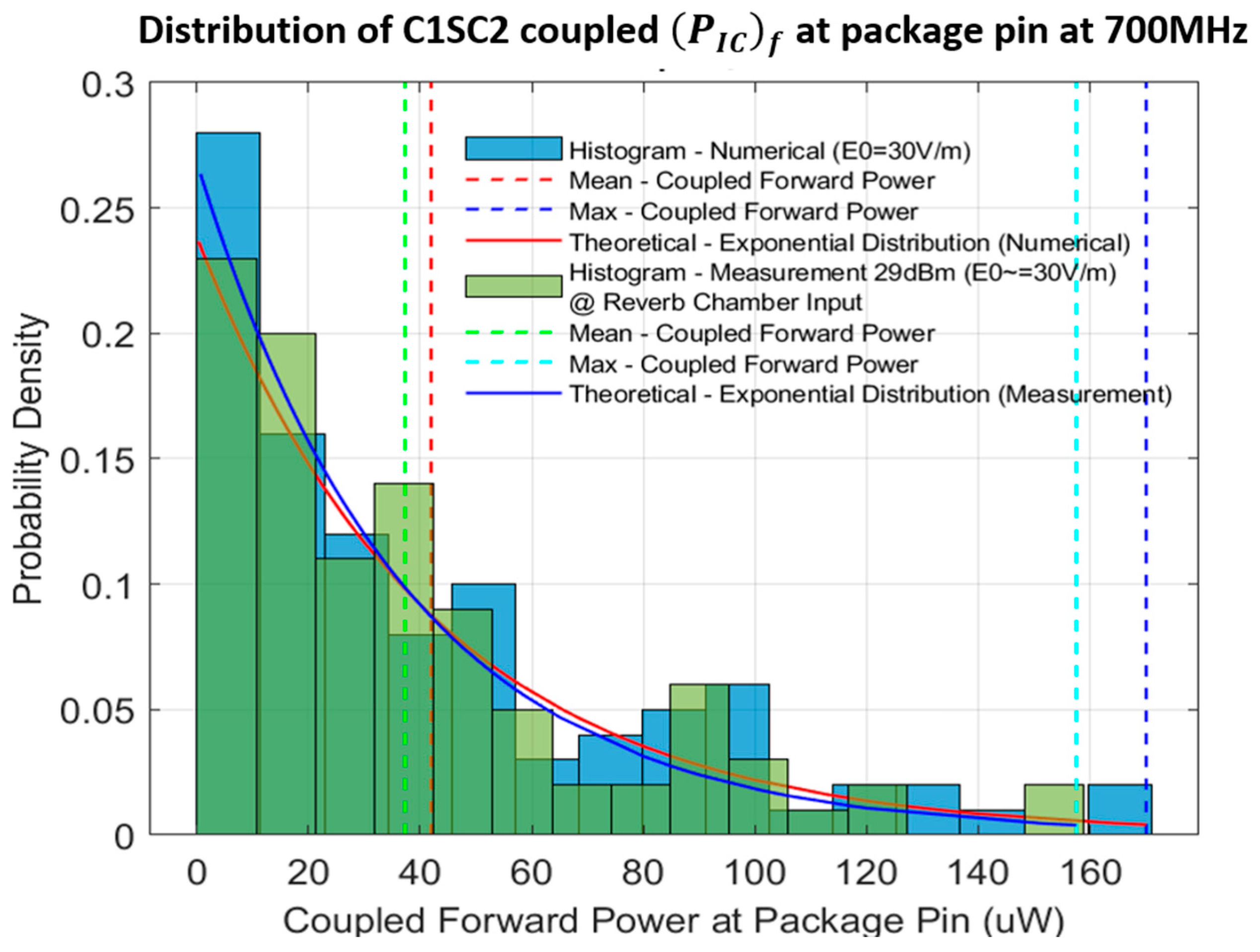
4.3. Coupled Forward Power Distribution at the Package Pin
5. Correlating Prediction Models with Practical Applications
5.1. Correlating with Test Specifications of EMC Limits for Automotive ICs
5.2. Correlating with Everyday Electronic Appliances
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AACS | Average Absorption Cross-Section |
| BLT | Baum–Liu–Tesche |
| CDF | Cumulative Distribution Function |
| C1SC2 | Channel 1 Sub-channel 2 |
| DAC | Digital-to-Analog Converter |
| DPI | Direct Power Injection |
| DUT | Device Under Test |
| EM | Electromagnetic |
| EMC | Electromagnetic Compatibility |
| EMI | Electromagnetic Interference |
| EUT | Equipment Under Test |
| GTEM | Gigahertz Transverse Electromagnetic |
| IC | Integrated Circuits |
| MC | Monte Carlo |
| PCB | Printed Circuit Board |
| RF IC | Radio Frequency Integrated Circuit |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
| TRL/M | Through-Reflect-Line/Match |
| UoY | University of York |
| VNA | Vector Network Analyzer |
References
- Konefal, T.; Marvin, A.C.; Dawson, J.F.; Robinson, M.P. A Statistical Model to Estimate an Upper Bound on the Probability of Failure of a System Installed on an Irradiated Vehicle. IEEE Trans. Electromagn. Compat. 2007, 49, 840–848. [Google Scholar] [CrossRef]
- Mehri, M.; Masoumi, N. Statistical Prediction and Quantification of Radiated Susceptibility for Electronic Systems PCB in Electromagnetic Polluted Environments. IEEE Trans. Electromagn. Compat. 2017, 59, 498–508. [Google Scholar] [CrossRef]
- Perdriau, R.; Ramdani, M.; Maurice, O.; Dubois, S.; Sicard, E. Assessment of the Radiated Immunity of Integrated Circuits in the 3–40 GHz Range. In Proceedings of the 2011 8th Workshop on Electromagnetic Compatibility of Integrated Circuits, Dubrovnik, Croatia, 6–9 November 2011; pp. 18–23. [Google Scholar]
- Heinrich, R.; Bechly, R.; Deutschmann, B. Radiated Immunity Testing of Integrated Circuits in Reverberation Chambers. In Proceedings of the International Symposium on Electromagnetic Compatibility—EMC EUROPE, Rome, Italy, 17–21 September 2012; pp. 1–4. [Google Scholar]
- BS EN 61000-4-21; Testing and Measurement Techniques—Reverberation Chamber Test Methods. BSI Standards Publication: London, UK, 2011.
- Hwang, J.; Han, Y.; Park, H.; Nah, W.; Kim, S. Radiated Electromagnetic Immunity Analysis of VCO Using IC Stripline Method. In Proceedings of the 2015 10th International Workshop on the Electromagnetic Compatibility of Integrated Circuits (EMC Compo), Edinburgh, UK, 10–13 November 2015; pp. 147–151. [Google Scholar]
- Boyer, A.; Nolhier, N.; Caignet, F.; Dhia, S.B. Correlation between Near-Field Scan Immunity and Radiated Susceptibility at Integrated Circuit Level. In Proceedings of the 2022 International Symposium on Electromagnetic Compatibility—EMC Europe, Gothenburg, Sweden, 5–8 September 2022; pp. 120–125. [Google Scholar]
- Koohestani, M.; Perdriau, R.; Ramdani, M. An Effective Approach to Mitigate IC Radiated Susceptibility in EM Far-Field Region. In Proceedings of the 2019 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Barcelona, Spain, 2–6 September 2019; pp. 144–148. [Google Scholar]
- Xie, H.; Dawson, J.F.; Yan, J.; Marvin, A.C.; Robinson, M.P. Numerical and Analytical Analysis of Stochastic Electromagnetic Fields Coupling to a Printed Circuit Board Trace. IEEE Trans. Electromagn. Compat. 2020, 62, 1128–1135. [Google Scholar] [CrossRef]
- Venkateshaiah, A.H.; Xie, H.; Dawson, J.F.; Marvin, A.C.; Dawson, L.; Robinson, M.P. Coupling of Energy Into PCB Traces in a Reverberant Environment: Absorption Cross-section and Probability of Susceptibility. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar]
- Tang, H.H.; Venkateshaiah, A.F.; Dawson, J.F.; Marvin, A.C.; Robinson, M.P.; Ge, J. Analysis and Estimation of Electromagnetic Energy Coupled into IC packages. In Proceedings of the 2021 Joint IEEE International Symposium on Electromagnetic Compatibility, Signal and Power Integrity, EMC Europe, Raleigh, NC, USA, 26 July–13 August 2021. [Google Scholar]
- Tesche, F.M.; Butler, C.M. On the addition of EM field propagation and coupling effects in the BLT equation. Interact. Notes 2003, 588, 1–43. [Google Scholar]
- Tesche, F.M.; Ianoz, M.; Karlsson, T. EMC Analysis Methods and Computational Models; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Hall, S.; Pytel, S.G.; Huray, P.G.; Hua, D.; Moonshiram, A.; Brist, G.A.; Sijercic, E. Multigigahertz Causal Transmission Line Modeling Methodology Using a 3-D Hemispherical Surface Roughness Approach. IEEE Trans. Microw. Theory Tech. 2007, 55, 2614–2624. [Google Scholar] [CrossRef]
- Zhang, J.; Koledintseva, M.Y.; Drewniak, J.L.; Pommerenke, D.J.; DuBroff, R.E.; Yang, Z.; Cheng, W.; Rozanov, K.N.; Antonini, G.; Orlandi, A. Reconstruction of Dispersive Dielectric Properties for PCB Substrates Using a Genetic Algorithm. IEEE Trans. Electromagn. Compat. 2008, 50, 704–714. [Google Scholar] [CrossRef]
- IS400, FR4. Substrate, Eurocircuits. Available online: https://www.isola-group.com/wp-content/uploads/data-sheets/is400-laminate-and-prepreg-isola-group.pdf?t=1822223916 (accessed on 25 May 2025).
- Koledintseva, M.Y.; Rozanov, K.N.; Orlandi, A.; Drewniak, J.L. Extraction of Lorentzian and Debye Parameters of Dielectric and Magnetic Dispersive Materials for FDTD Modeling. J. Electr. Eng. 2002, 53, 97–100. [Google Scholar]
- Sohn, Y.-S.; Lee, J.-C.; Park, H.-J.; Cho, S.-I. Empirical equations on electrical parameters of coupled microstrip lines for crosstalk estimation in printed circuit board. IEEE Trans. Adv. Packag. 2001, 24, 521–527. [Google Scholar] [CrossRef]
- Leone, M.; Singer, H.L. On the coupling of an external electromagnetic field to a printed circuit board trace. IEEE Trans. Electromagn. Compat. 1999, 41, 418–424. [Google Scholar] [CrossRef]
- Magdowski, M.; Tkachenko, S.V.; Vick, R. Coupling of Stochastic Electromagnetic Fields to a Transmission Line in a Reverberation Chamber. IEEE Trans. Electromagn. Compat. 2011, 53, 308–317. [Google Scholar] [CrossRef]
- BS EN 62132-4; Integrated Circuits—Measurement of Electromagnetic Immunity 150 kHz to 1 GHz Part 4, Direct RF Power Injection Method. BSI Standards Publication: London, UK, 2006.
- Hill, D.A. Plane Wave Integral Representation for Fields in Reverberation Chambers. IEEE Trans. Electromagn. Compat. 1998, 40, 209–217. [Google Scholar] [CrossRef]
- Wellander, N.; Lunden, O.; Backstrom, M. The Maximum Value Distribution in a Reverberation Chamber. In Proceedings of the 2001 IEEE EMC International Symposium. Symposium Record. International Symposium on Electromagnetic Compatibility (Cat. No. 01CH37161), Montreal, QC, Canada, 13–17 August 2001; Volume 2, pp. 2751–2756. [Google Scholar]
- Arduino Nano (V2.3) User Manual. 2008. Available online: https://www.arduino.cc/en/uploads/Main/ArduinoNanoManual23.pdf (accessed on 25 May 2025).
- Elektroindustrei, Z.D. Generic IC EMC Test Specification; Version 2.1; ZVEI—German Electrical and Electronic Manufacturers’ Association: Frankfurt am Main, Germany, 2017; Available online: https://www.zvei.org/presse-medien/publikationen/leitfaden-generic-ic-emc-test-specification-version-21 (accessed on 25 May 2025).
- Klotz, F. EMC Test Specification for Integrated Circuits. In Proceedings of the 2007 18th International Zurich Symposium on Electromagnetic Compatibility, Munich, Germany, 24–28 September 2007; pp. 73–78. [Google Scholar]
- FCC Part 15, U.S. EMC Standard. Available online: https://www.academyofemc.com/emc-standards (accessed on 25 May 2025).








| Parameter Name | Radiated Board |
|---|---|
| Number of Layers | 4 |
| RF PCB track width (w) | 0.48 mm |
| RF PCB track thickness (t) | 18 μm |
| Substrate height from ground plane for RF PCB tracks (h) | 1.43 mm |
| Characteristic Impedance of the RF PCB Track | 115 Ω |
| Board Dimension | 180 × 153 mm2 |
| Coefficient for the Roughness Effect () [Calculated using Equation (5)] | 2.2 @700 MHz |
| Dielectric Constant (Dk)/Relative Permittivity () | (FR4-improved, IS400) [16] 4.0 @100 MHz 3.9 @500 MHz |
| Diffraction Factor (Df)/Loss Tangent () | 0.020 @100 MHz 0.022 @500 MHz |
| Local Pin C1SC2 at 700 MHz for 400 V/m | ||
|---|---|---|
| If the IC Under Testing Belongs to the Class | Then the Probability of IC Failure Is | |
| Class | Limit Lines | |
| I | 0 dBm | 88.00% |
| II | 6 dBm | 59.97% |
| III | 12 dBm | 12.96% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunasanahalli Venkateshaiah, A.; Dawson, J.F.; Trefzer, M.A.; Xie, H.; Bale, S.J.; Marvin, A.C.; Robinson, M.P. Prediction of the Probability of IC Failure and Validation of Stochastic EM-Fields Coupling into PCB Traces Using a Bespoke RF IC Detector. Electronics 2025, 14, 2187. https://doi.org/10.3390/electronics14112187
Hunasanahalli Venkateshaiah A, Dawson JF, Trefzer MA, Xie H, Bale SJ, Marvin AC, Robinson MP. Prediction of the Probability of IC Failure and Validation of Stochastic EM-Fields Coupling into PCB Traces Using a Bespoke RF IC Detector. Electronics. 2025; 14(11):2187. https://doi.org/10.3390/electronics14112187
Chicago/Turabian StyleHunasanahalli Venkateshaiah, Arunkumar, John F. Dawson, Martin A. Trefzer, Haiyan Xie, Simon J. Bale, Andrew C. Marvin, and Martin P. Robinson. 2025. "Prediction of the Probability of IC Failure and Validation of Stochastic EM-Fields Coupling into PCB Traces Using a Bespoke RF IC Detector" Electronics 14, no. 11: 2187. https://doi.org/10.3390/electronics14112187
APA StyleHunasanahalli Venkateshaiah, A., Dawson, J. F., Trefzer, M. A., Xie, H., Bale, S. J., Marvin, A. C., & Robinson, M. P. (2025). Prediction of the Probability of IC Failure and Validation of Stochastic EM-Fields Coupling into PCB Traces Using a Bespoke RF IC Detector. Electronics, 14(11), 2187. https://doi.org/10.3390/electronics14112187







