A Unified and Resource-Aware Framework for Adaptive Inference Acceleration on Edge and Embedded Platforms
Abstract
1. Introduction
- A unified inference optimization framework is presented that systematically integrates mixed-precision quantization, heterogeneous sparse attention, and dynamic expert routing. This framework is tailored for edge deployment scenarios and jointly addresses computational, memory, and adaptability challenges. Unlike prior approaches that focus on isolated optimization aspects, this work demonstrates the synergistic benefits of combining these strategies within a coherent architecture.
- A token-aware adaptive execution strategy is introduced within the unified framework, enabling dynamic adjustment of bit-width, attention sparsity, and expert activation based on token complexity or generation stage. This mechanism supports fine-grained control of inference cost and allows flexible trade-offs between latency and output quality across diverse tasks and hardware profiles.
- The proposed approach is implemented and validated across both autoregressive and diffusion-based generative models on real-world platforms. Experimental results show that the method achieves up to 2.4× end-to-end speed-up and 1.8× memory reduction on devices such as NVIDIA A100 and NVIDIA Jetson AGX Orin, with generation quality comparable to or better than full-precision baselines.
2. Related Work
2.1. Model Compression and Static Optimizations
2.2. Efficient Architectures and Dynamic Execution Approaches
2.3. System-Level Optimizations for Edge AI
3. Materials and Methods
3.1. System Architecture
- Precision Optimization Stage: Model weights, activations, and KV caches are quantized in a layer-wise manner, guided by sensitivity profiling to preserve generation quality while reducing memory and computation cost.
- Computation Reduction Stage: Sparse attention modules with heterogeneous masking strategies are applied to reduce attention overhead. This step dynamically adjusts the attention pattern per head or layer, depending on task type and sequence length.
- Computation Allocation Stage: A capacity-aware expert routing mechanism is introduced to adaptively activate experts based on token-level or timestep-level complexity, enabling input-aware computation balancing.
3.2. Mixed-Precision Quantization with Layer-Wise Sensitivity
3.2.1. Layer-Wise Sensitivity Profiling
- Static profiling, where calibration is performed on a representative validation set using post-training quantization (PTQ).
- Dynamic profiling, where layer sensitivity is inferred online during training or fine-tuning by monitoring quantization-induced degradation in intermediate outputs or end-task accuracy.
- Non-critical layers (e.g., intermediate feed-forward blocks) can be quantized to 2.8-bit or 3.6-bit using logarithmic or non-uniform quantization grids.
- High-impact layers (e.g., embedding layers, layer norms, and output heads) retain 8-bit or mixed FP16 precision.
3.2.2. Weight and Activation Quantization
3.2.3. Deployment and Compatibility
3.3. Sparse Attention with Adaptive Heterogeneous Masking
3.3.1. Adaptive Sparse Mask Generation
- Local attention heads, which apply sparse attention within a predefined sliding window, significantly reducing complexity, typically set as = 8 or = 16 depending on sequence length:
- Sparse global heads (top-k routing), which selectively attend to global context via learned sparse patterns, ensuring long-range dependency modeling. In the following formula, the selects the top-k attention scores for each query . In our experiments, we set = 16 as a default value.
- Dense heads, reserved for layers or tasks requiring high precision, fully attending to the entire input sequence, which is used for critical layers or final stages requiring a full information context.
3.3.2. Masking Strategy and Learning Mechanism
- Rule-based construction: Masks are defined using deterministic heuristics, such as fixed sliding windows or block-wise patterns, providing predictable latency and efficiency gains.
- Learnable gating mechanism: Attention sparsity is learned dynamically during fine-tuning via a small auxiliary network that predicts mask patterns, allowing the model to adapt attention sparsity to input content dynamically.
3.3.3. Implementation and Compatibility
| Algorithm 1 The pseudo-code of the Adaptive Sparse Attention Algorithm. |
| Initialization: Set attention type ∈ {Local, Sparse_Global, Dense}, Set , Upon Receiving Inputs : 1. Calculate raw attention scores: 2. Generate mask based on :
3. Apply mask to scores: 4. Compute attention probabilities: 5. Compute output: Output: Return |
3.4. Dynamic Expert Routing with Capacity-Aware Scheduling
3.4.1. Design Principles and Motivation
- Complexity-Aware Expert Assignment: Tokens are routed dynamically based on their learned complexity profiles, rather than static gating probabilities alone. This complexity estimation incorporates contextual embeddings, enabling intelligent selection of experts aligned with actual token complexity.
- Global Capacity Scheduling: We introduce a global scheduling constraint, termed the capacity predictor, that dynamically monitors and balances the total computational load across experts. Unlike traditional gating, which operates purely at the individual token level, our global capacity predictor ensures balanced expert utilization and prevents computational hotspots or overloads.
- Adaptive Runtime Optimization: The routing strategy dynamically interacts with the mixed-precision quantization and adaptive sparse-attention strategies outlined earlier. This integrative design allows for real-time joint optimization of expert selection, precision configuration, and attention sparsity, significantly enhancing inference flexibility and efficiency.
3.4.2. Routing Module and Capacity Predictor
3.4.3. Implementation and Technical Novelty
3.5. Integrated Framework and Execution Strategy
3.5.1. Coordinated Three-Stage Architecture
- Precision Assignment: Prior to deployment, sensitivity profiling assigns optimal bit-widths to individual layers, yielding a quantized model with minimal quality degradation. These configurations are exported using formats such as ONNX and TensorRT for cross-platform deployment.
- Sparse Computation: During inference, attention modules select heterogeneous sparse masking patterns based on token context and model precision settings, enabling dynamic trade-offs between computation, memory, and accuracy.
- Dynamic Routing: Input tokens are routed through expert modules based on real-time complexity scores and global capacity constraints. Lightweight routing heads ensure balanced expert utilization without introducing significant overheads.
3.5.2. Adaptive Inference Flow
3.5.3. Innovation and Impact
3.6. Complexity Analysis and Theoretical Efficiency Gains
3.6.1. Complexity Analysis for Mixed-Precision Quantization
3.6.2. Complexity Reduction from Adaptive Sparse Attention
3.6.3. Complexity Benefits of Dynamic Expert Routing
3.6.4. Integrated Complexity and Efficiency Gains
4. Experimental Results and Discussion
4.1. Experimental Setting
4.2. Datasets and Models
4.3. Ablation Study
4.4. Comparison with Existing Methods
4.5. Generalization Across Hardware Platforms
4.6. Qualitative Case Studies
4.7. Robustness, Adaptivity, and Stability
4.7.1. Adaptivity Under Resource Fluctuation
4.7.2. Robustness to Input Perturbation
- Text perturbation: introducing irrelevant clauses, numerical distractors, or reordering tokens in arithmetic questions.
- Image prompt degradation: low-resolution blur, occlusion masks, and mismatched conditioning embeddings.
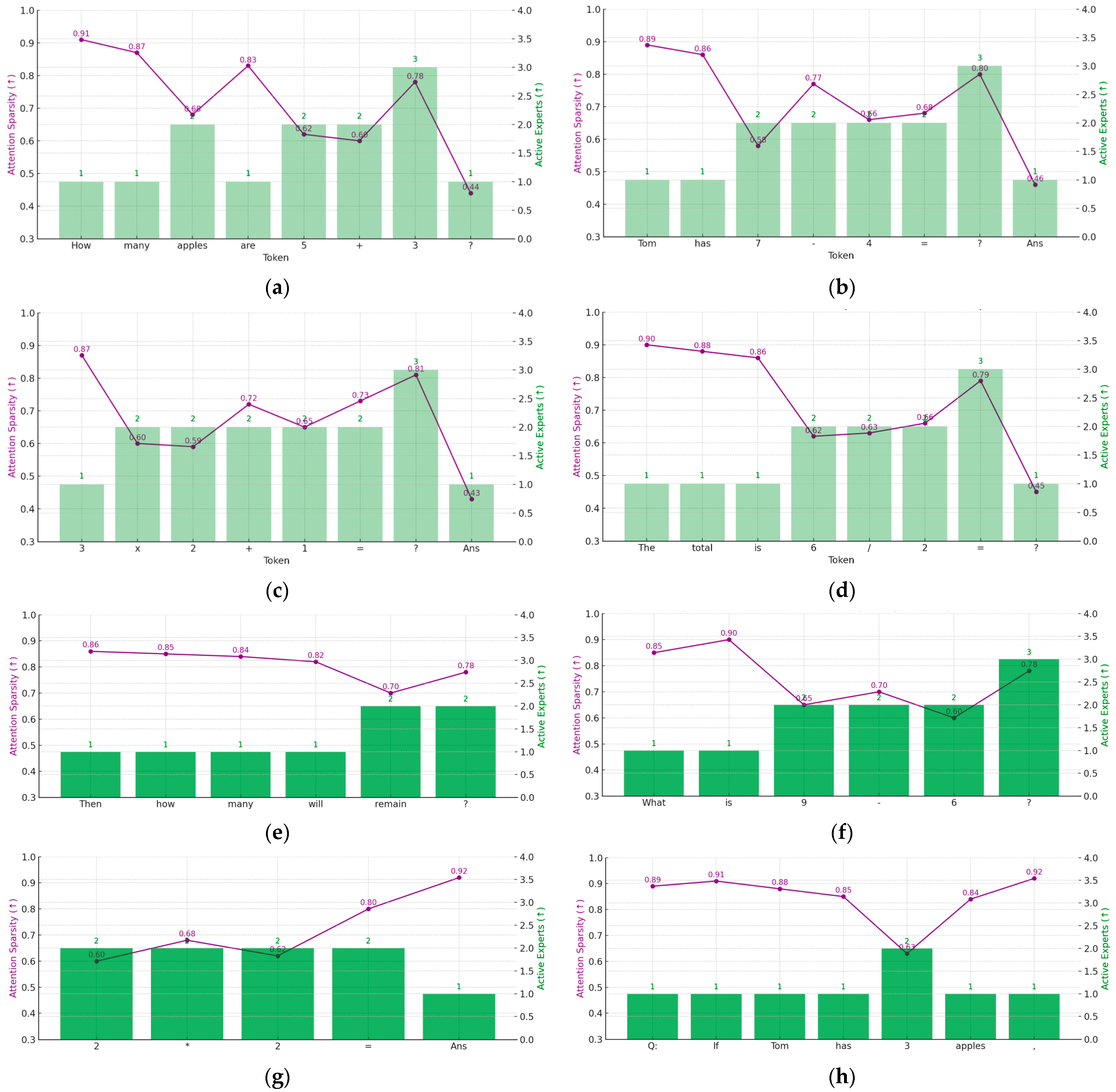
4.7.3. Token-Level Stability Visualization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FID | Fréchet Inception Distance |
| GPTQ | Post-Training Quantization for Generative Pre-trained Transformers |
| CLIP | Contrastive Language-Image Pre-Training |
| DPO | Direct Preference Optimization |
| KV cache | Key-Value cache |
| LLM | Large Language Model |
Appendix A
Practical Deployment of Custom Sub-Byte Quantization and Modules
| Algorithm A1. Conceptual N-bit Sub-byte Dequantization. |
| Input: packed_int8_data: Byte array containing packed N-bit integer values. scales: Array of floating-point scale factors (per-tensor or per-channel). zero_points: Array of integer zero-points (for asymmetric quantization, per-tensor or per-channel). num_total_elements: Integer, total number of N-bit elements to dequantize. N: Integer, the bit-width of the sub-byte elements (e.g., 3 for 2.8-bit, 4 for 3.6-bit). Output: dequantized_fp_data: Floating-point array to store dequantized elements. Procedure Dequantize_SubByte_Elements(packed_int8_data, scales, zero_points, dequantized_fp_data, num_total_elements, N): element_idx = 0 BITS_PER_BYTE = 8 for byte_pos from 0 to (length of packed_int8_data) − 1: current_byte = packed_int8_data[byte_pos] num_elements_in_this_byte = BITS_PER_BYTE / N // Assuming N divides 8 for simplicity for k from 0 to num_elements_in_this_byte − 1: if element_idx >= num_total_elements: return // All elements processed //1. Extract the k-th N-bit integer value from current_byte. //This requires bitwise shift and mask operations. //Example: shift = N × k; mask = (1 << N) − 1; //(Actual extraction order depends on LSB/MSB packing convention) n_bit_integer = (current_byte >> (BITS_PER_BYTE-(k + 1) × N)) & ((1 << N) − 1) //2. Interpret the N-bit integer (e.g., map to signed range if necessary). //Example for signed: if n_bit_integer >= (1 << (N − 1)): //effective_int_value = n_bit_integer-(1 << N) //else: effective_int_value = n_bit_integer effective_int_value = interpret_N_bit_value(n_bit_integer, N) // Placeholder for interpretation logic //3. Apply dequantization formula (affine example). //For non-linear (e.g., log): effective_float_value = apply_inverse_log_map(effective_int_value) //current_scale and current_zp might be indexed if per-channel. current_scale = scales[get_scale_index_for_element(element_idx)] current_zp = zero_points[get_zp_index_for_element(element_idx)] dequantized_fp_data[element_idx] = current_scale × (float(effective_int_value)-float(current_zp)) element_idx = element_idx + 1 |
References
- Balaji, Y.; Nah, S.; Huang, X.; Vahdat, A.; Song, J.; Kreis, K.; Aittala, M.; Aila, T.; Laine, S.; Catanzaro, B.; et al. ediffi: Text-to-image diffusion models with an ensemble of expert denoisers. arXiv 2022, arXiv:2211.01324. [Google Scholar]
- Zhang, S.; Roller, S.; Goyal, N.; Artetxe, M.; Chen, M.; Chen, S.; Dewan, C.; Diab, M.; Li, X.; Lin, X.V.; et al. Opt: Open pre-trained transformer language models. arXiv 2022, arXiv:2205.01068. [Google Scholar]
- Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.; Choi, S.; Teh, Y.W. Set transformer: A framework for attention-based permutationinvariant neural networks. in International conference on machine learning. In In Proceedings of the 36th International Conference on Machine Learning, PMLR 97, Long Beach, CA, USA, 9–15 June 2019; pp. 3744–3753. [Google Scholar]
- Chang, H.; Zhang, H.; Barber, J.; Maschinot, A.; Lezama, J.; Jiang, L.; Yang, M.-H.; Murphy, K.P.; Freeman, W.T.; Rubinstein, M.; et al. Muse: Textto-image generation via masked generative transformers. In Proceedings of the 40th International Conference on Machine Learning, ICML, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Esser, P.; Chiu, J.; Atighehchian, P.; Germanidis, A. Structure and content-guided video synthesis with diffusion models. In Proceedings of the 2023 CVPR, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Karras, T.; Aittala, M.; Aila, T.; Laine, S. Elucidating the design space of diffusion-based generative models. In Proceedings of the 2022 NeurIPS, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. LLaMA: Open and Efficient Foundation Language Models. arXiv 2023, arXiv:2302.13971. [Google Scholar] [CrossRef]
- OpenAI. GPT-4 Technical Report. arXiv 2023, arXiv:2303.08774. [Google Scholar] [CrossRef]
- Fang, G.; Ma, X.; Wang, X. Structural pruning for diffusion models. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Li, S.; Ning, X.; Hong, K.; Liu, T.; Wang, L.; Li, X.; Zhong, K.; Dai, G.; Yang, H.; Wang, Y. Llm-mq: Mixed-Precision Quantization for Efficient llm Deployment. In Proceedings of the NeurIPS 2023 Efficient Natural Language and Speech Processing Workshop, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Jiang, H.; Wu, Q.; Lin, C.-Y.; Yang, Y.; Qiu, L. Llmlingua:Compressing prompts for accelerated inference of large language models. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, Singapore, 6–10 December 2023. [Google Scholar]
- Griggs, T.; Liu, X.; Yu, J.; Kim, D.; Chiang, W.-L.; Cheung, A.; Stoica, I. Mélange: Cost Efficient Large Language Model Serving by Exploiting GPU Heterogeneity. arXiv 2024, arXiv:2404.14527. [Google Scholar]
- Dao, T.; Fu, D.; Ermon, S.; Rudra, A.; Re, C. Flashattention: Fast and memory-efficient exact attention with io-awareness. Adv. Neural Inf. Process. Syst. 2022, 35, 16.344–16.359. [Google Scholar]
- He, Y.; Liu, L.; Liu, J.; Wu, W.; Zhou, H.; Zhuang, B. Ptqd: Accurate post-training quantization for diffusion models. arXiv 2023, arXiv:2305.10657. [Google Scholar]
- Hessel, J.; Holtzman, A.; Forbes, M.; Le Bras, R.; Choi, Y. Clipscore: A reference-free evaluation metric for image captioning. arXiv 2021, arXiv:2104.08718. [Google Scholar]
- Chevalier, A.; Wettig, A.; Ajith, A.; Chen, D. Adapting language models to compress contexts. arXiv 2023, arXiv:2305.14788. [Google Scholar]
- Li, L.; Li, H.; Zheng, X.; Wu, J.; Xiao, X.; Zheng, M.; Pan, X.; Chao, F.; Ji, R. Autodiffusion: Training-free optimization of time steps and architectures for automated diffusion model acceleration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 7105–7114. [Google Scholar]
- Li, Y.; Wang, H.; Jin, Q.; Hu, J.; Chemerys, P.; Fu, Y.; Wang, Y.; Tulyakov, S.; Ren, J. Snapfusion: Text-to-image diffusion model on mobile devices within two seconds. arXiv 2023, arXiv:2306.00980. [Google Scholar]
- Wingate, D.; Shoeybi, M.; Sorensen, T. Prompt compression and contrastive conditioning for controllability and toxicity reduction in language models. arXiv 2022, arXiv:2210.03162. [Google Scholar]
- Wang, X.; Zheng, Y.; Wan, Z.; Zhang, M. Svd-llm: Truncationaware singular value decomposition for large language model compression. arXiv 2024, arXiv:2403.07378. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 10684–10695. [Google Scholar] [CrossRef]
- Lyu, Z.; Xu, X.; Yang, C.; Lin, D.; Dai, B. Accelerating diffusion models via early stop of the diffusion process. arXiv 2022, arXiv:2205.12524. [Google Scholar]
- Li, S.; Ning, X.; Wang, Y.; Lin, Z. LLM-MQ: Mixed-Precision Quantization for Efficient LLM Deployment. Available online: https://nicsefc.ee.tsinghua.edu.cn/nics_file/pdf/5c805adc-b555-499f-9882-5ca35ce674b5.pdf (accessed on 25 May 2025).
- Zhao, T.; Ning, X.; Fang, T.; Liu, E.; Huang, G.; Lin, Z.; Yan, S.; Dai, G.; Wang, Y. MixDQ: Memory-Efficient Few-Step Text-to-Image Diffusion Models with Metric-Decoupled Mixed Precision Quantization. arXiv 2024, arXiv:2405.17873. [Google Scholar] [CrossRef]
- Mu, J.; Li, X.L.; Goodman, N. Learning to compress prompts with gist tokens. arXiv 2023, arXiv:2304.08467. [Google Scholar]
- Yuan, Z.; Lu, P.; Zhang, H.; Ning, X. DiTFastAttn: Attention Compression for Diffusion Transformer Models. arXiv 2024, arXiv:2406.08552. [Google Scholar] [CrossRef]
- Fu, T.; Huang, H.; Ning, X.; Zhang, G.; Chen, B.; Wu, T.; Wang, H.; Huang, Z.; Li, S.; Yan, S.; et al. MoA: Mixture of Sparse Attention for Automatic Large Language Model Compression. arXiv 2024, arXiv:2406.14909. [Google Scholar] [CrossRef]
- Chiang, W.-L.; Li, Z.; Lin, Z.; Sheng, Y.; Wu, Z.; Zhang, H.; Zheng, L.; Zhuang, S.; Zhuang, Y.; Gonzalez, J.E.; et al. Vicuna: An Opensource Chatbot Impressing gpt-4 with 90%* Chatgpt Quality. 2023. Available online: https://vicuna.lmsys.org (accessed on 14 April 2023).
- Lepikhin, D.; Lee, H.; Xu, Y.; Chen, Z.; Firat, O.; Huang, Y.; Krikun, M.; Shazeer, N. GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding. arXiv 2020, arXiv:2006.16668. [Google Scholar] [CrossRef]
- Shang, Y.; Yuan, Z.; Xie, B.; Wu, B.; Yan, Y. Post-training quantization on diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1972–1981. [Google Scholar]
- Xia, H.; Yang, Z.; Dong, Q.; Wang, P.; Li, Y.; Ge, T.; Liu, T.; Li, W.; Sui, Z. Unlocking Efficiency in Large Language Model Inference: A Comprehensive Survey of Speculative Decoding. arXiv 2024, arXiv:2401.07851. [Google Scholar] [CrossRef]
- Liang, C.; Zuo, S.; Zhang, Q.; He, P.; Chen, W.; Zhao, T. Less is more: Task-aware layer-wise distillation for language model compression. in International Conference on Machine Learning. In Proceedings of the 40th International Conference on Machine Learning, PMLR, 2023, Honolulu, HI, USA, 23–29 July 2023; pp. 20.852–20.867. [Google Scholar]
- Xu, J.; Tan, X.; Luo, R.; Song, K.; Li, J.; Qin, T.; Liu, T.-Y. Nasbert: Task-agnostic and adaptive-size bert compression with neural architecture search. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 1933–1943. [Google Scholar]
- Gao, Z.-F.; Liu, P.; Zhao, W.X.; Lu, Z.-Y.; Wen, J.-R. Parameterefficient mixture-of-experts architecture for pre-trained language models. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 3263–3273. [Google Scholar]
- Zoph, B.; Bello, I.; Kumar, S.; Du, N.; Huang, Y.; Dean, J.; Shazeer, N.; Fedus, W. St-moe: Designing stable and transferable sparse expert models. arXiv 2022, arXiv:2202.08906. [Google Scholar]
- Du, N.; Huang, Y.; Dai, A.M.; Tong, S.; Lepikhin, D.; Xu, Y.; Krikun, M.; Zhou, Y.; Yu, A.W.; Firat, O.; et al. Glam: Efficient scaling of language models with mixture-of-experts. in International Conference on Machine Learning. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 5547–5569. [Google Scholar]
- Hwang, C.; Cui, W.; Xiong, Y.; Yang, Z.; Liu, Z.; Hu, H.; Wang, Z.; Salas, R.; Jose, J.; Ram, P.; et al. Tutel: Adaptive mixture-of-experts at scale. Proc. Mach. Learn. Syst. 2023, 5, 269–287. [Google Scholar]
- Jiang, A.Q.; Sablayrolles, A.; Roux, A.; Mensch, A.; Savary, B.; Chaplot, D.S.; Casas, D.D.L.; Hanna, E.B.; Bressand, F.; Lengyel, G. Mixtral of experts. arXiv 2024, arXiv:2401.04088. [Google Scholar]
- Kong, J.; Wang, J.; Yu, L.-C.; Zhang, X. Accelerating inference for pretrained language models by unified multi-perspective early exiting. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 4677–4686. [Google Scholar]
- Yao, J.; Yang, B.; Wang, X. Reconstruction vs. Generation: Taming Optimization Dilemma in Latent Diffusion Models. arXiv 2024, arXiv:2501.01423. [Google Scholar] [CrossRef]
- Roy, A.; Saffar, M.; Vaswani, A.; Grangier, D. Efficient contentbased sparse attention with routing transformers. Trans. Assoc. Comput. Linguist. 2021, 9, 53–68. [Google Scholar] [CrossRef]
- Agrawal, A.; Kedia, N.; Panwar, A.; Mohan, J.; Kwatra, N.; Gulavani, B.; Tumanov, A.; Ramjee, R. Taming Throughput-Latency Tradeoff in LLM Inference with Sarathi-Serve. In Proceedings of the 18th USENIX Symposium on Operating Systems Design and Implementation (OSDI 24), Santa Clara, CA, USA, 10–12 July 2024; pp. 117–134. Available online: https://www.usenix.org/conference/osdi24/presentation/agrawal (accessed on 25 May 2025).
- Frantar, E.; Alistarh, D. Sparsegpt: Massive language models can be accurately pruned in one-shot. arXiv 2023, arXiv:2301.00774. [Google Scholar]
- Wei, X.; Zhang, Y.; Li, Y.; Zhang, X.; Gong, R.; Guo, J.; Liu, X. Outlier suppression+: Accurate quantization of large language models by equivalent and optimal shifting and scaling. arXiv 2023, arXiv:2304.09145. [Google Scholar]
- Kurtic, E.; Campos, D.; Nguyen, T.; Frantar, E.; Kurtz, M.; Fineran, B.; Goin, M.; Alistarh, D. The optimal bert surgeon: Scalable and accurate second-order pruning for large language models. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, Abu Dhabi, United Arab Emirates, 7–11 December 2022; pp. 4163–4181. [Google Scholar]
- Zhou, Z.; Ning, X.; Hong, K.; Lin, Z.; Wang, J.; Han, H.; Liu, J.; Yang, D. A Survey on Efficient Inference for Large Language Models. arXiv 2024, arXiv:2404.14294. [Google Scholar] [CrossRef]
- Yin, T.; Gharbi, M.; Zhang, R.; Sinha, U.; Puri, R.; Anandkumar, A.; Vincent, P. One-step Diffusion with Distribution Matching Distillation. arXiv 2023, arXiv:2311.18828. [Google Scholar] [CrossRef]
- Ma, X.; Fang, G.; Wang, X. DeepCache: Accelerating Diffusion Models for Free. arXiv 2023, arXiv:2312.00858. [Google Scholar] [CrossRef]
- Yuan, X.; Qiao, Y. Diffusion-TS: Interpretable Diffusion for General Time Series Generation. arXiv 2024, arXiv:2403.01742. [Google Scholar] [CrossRef]
- Shi, M.; Yuan, Z.; Yang, H.; Wang, X.; Zheng, M.; Tao, X.; Zhao, W.; Zheng, W.; Zhou, J.; Lu, J.; et al. DiffMoE: Dynamic Token Selection for Scalable Diffusion Transformers. arXiv 2025, arXiv:2503.14487. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.; Zhang, P.; Wei, J.; Zhu, J.; Chen, J. SageAttention2: Efficient Attention with Thorough Outlier Smoothing and Per-thread INT4 Quantization. arXiv 2024, arXiv:2411.10958. [Google Scholar] [CrossRef]
- Prabhu, R.; Nayak, A.; Mohan, J.; Ramjee, R.; Panwar, A. vAttention: Dynamic Memory Management for Serving LLMs without PagedAttention. In Proceedings of the 29th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ‘25), Rotterdam, The Netherlands, 30 March–3 April 2025. [Google Scholar] [CrossRef]
- Liu, A.; Bai, H.; Lu, Z.; Sun, Y.; Kong, X.; Wang, S.; Shan, J.; Jose, A.M.; Liu, X.; Wen, L.; et al. TIS-DPO: Token-Level Importance Sampling for Direct Preference Optimization with Estimated Weights. arXiv 2024, arXiv:2410.04350. [Google Scholar] [CrossRef]
- Sun, Z.; Zang, X.; Zheng, K.; Xu, J.; Zhang, X.; Yu, W.; Song, Y.; Li, H. ReDeEP: Detecting Hallucination in Retrieval-Augmented Generation via Mechanistic Interpretability. arXiv 2024, arXiv:2410.11414. [Google Scholar] [CrossRef]
- Zheng, K.; Ye, Q.; Chi, K.; Liu, X.; Saad, A.; Yu, K. Minimization of Task Completion Time in Wireless Powered Mobile Edge–Cloud Computing Networks. IEEE Internet Things J. 2024, 11, 38068–38085. [Google Scholar] [CrossRef]
- Zheng, K.; Jiang, G.; Liu, X.; Chi, K.; Yao, X.; Liu, J. DRL-Based Offloading for Computation Delay Minimization in Wireless-Powered Multi-Access Edge Computing. IEEE Trans. Commun. 2023, 71, 1755–1770. [Google Scholar] [CrossRef]
- Zheng, K.; Luo, R.; Liu, X.; Qiu, J.; Liu, J. Distributed DDPG-Based Resource Allocation for Age of Information Minimization in Mobile Wireless-Powered Internet of Things. IEEE Internet Things J. 2024, 11, 29102–29115. [Google Scholar] [CrossRef]
- Mai do, H.; Tran, T.P.; Yoo, M. Quality of Experience Optimization for AR Service in an MEC Federation System. IEEE Access 2025, 13, 69821–69839. [Google Scholar] [CrossRef]
- Frantar, E.; Ashkboos, S.; Hoefler, T.; Alistarh, D. GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. arXiv 2022, arXiv:2210.17323. [Google Scholar]
- Dao, T.; Fu, D.Y.; Ermon, S.; Rudra, A.; Ré, C. FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness. arXiv 2022, arXiv:2205.14135. [Google Scholar]

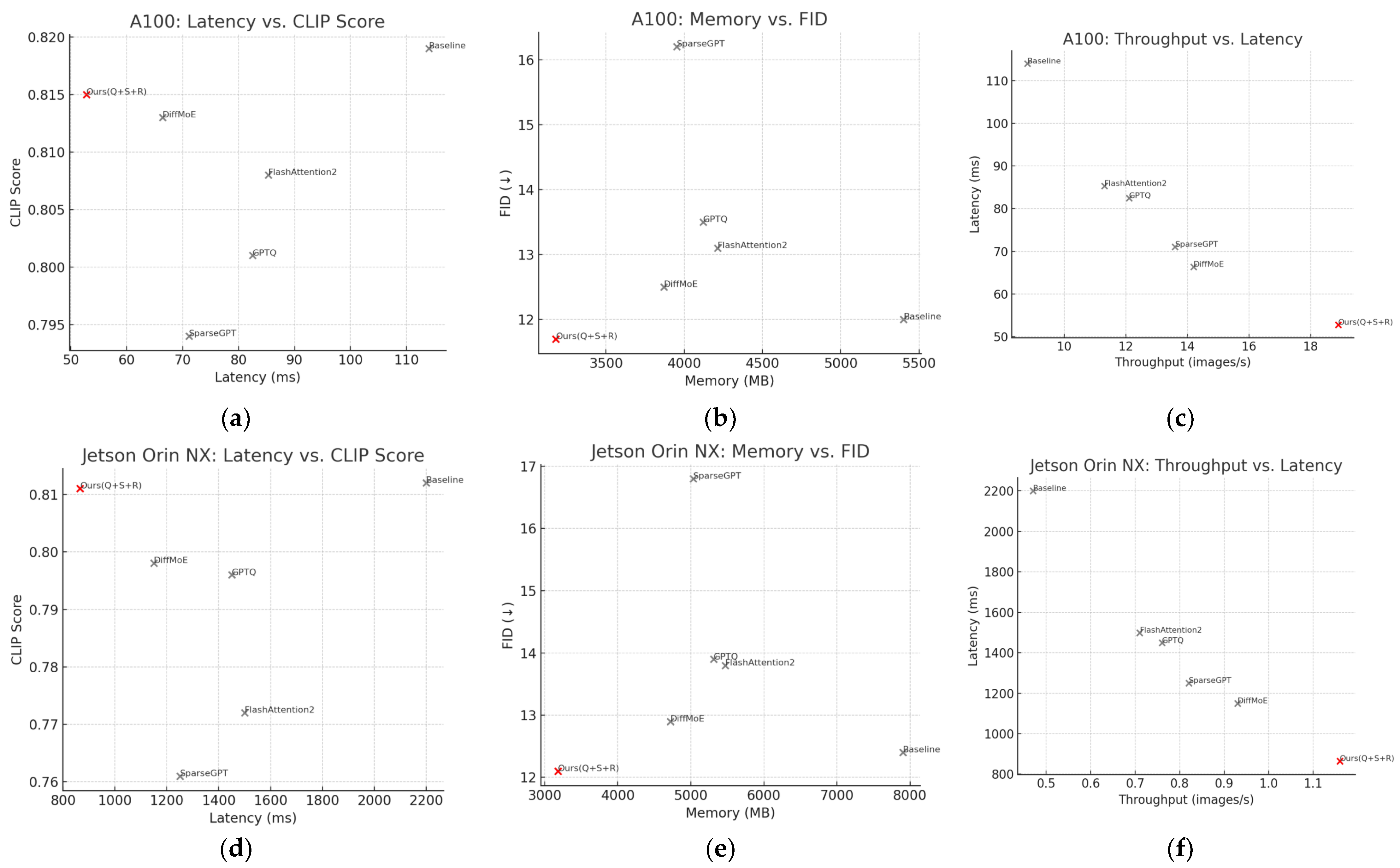



| Configuration (LLaMA-7B) | Quantization (Q) | Sparse Attention (S) | Routing (R) | Latency (ms) A100 | Memory (MB) A100 | Accuracy (%) A100 | Latency (ms) Jetson Orin NX | Memory (MB) Jetson Orin NX | Accuracy (%) Jetson Orin NX |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | × | × | × | 100.0 | 9119 | 87.2 | 85.0 | 7902 | 87.0 |
| Q | √ | × | × | 72.0 (↓28.0%) | 6218 (↓31.8%) | 86.8 (↓0.5%) | 61.5 (↓27.6%) | 5314 (↓32.8%) | 86.7 (↓0.3%) |
| S | × | √ | × | 78.5 (↓21.5%) | 7125 (↓21.9%) | 86.9 (↓0.3%) | 66.2 (↓22.1%) | 6116 (↓22.6%) | 86.8 (↓0.2%) |
| R | × | × | √ | 80.0 (↓20.0%) | 7073 (↓22.4%) | 87.1 (↓0.1%) | 67.5 (↓20.6%) | 6153 (↓22.1%) | 86.9 (↓0.1%) |
| Q + S | √ | √ | × | 56.2 (↓43.8%) | 5210 (↓42.9%) | 86.5 (↓0.8%) | 49.0 (↓42.4%) | 4147 (↓47.5%) | 86.3 (↓0.8%) |
| Q + R | √ | × | √ | 54.1 (↓45.9%) | 5012 (↓45.0%) | 86.7 (↓0.6%) | 47.8 (↓43.8%) | 4057 (↓48.7%) | 86.6 (↓0.5%) |
| S + R | × | √ | √ | 53.8 (↓46.2%) | 4931 (↓45.9%) | 86.6 (↓0.7%) | 46.0 (↓45.9%) | 4080 (↓48.4%) | 86.5 (↓0.6%) |
| Q + S + R | √ | √ | √ | 41.3 (↓58.7%) | 3900 (↓57.2%) | 87.0 (↓0.2%) | 37.5 (↓55.9%) | 3050 (↓61.4%) | 86.8 (↓0.2%) |
| Configuration | Quantization (Q) | Sparse Attention (S) | Routing (R) | LLaMA-7B | GPT-NeoX-20B | ||||
|---|---|---|---|---|---|---|---|---|---|
| Latency (ms) | Memory (MB) | Accuracy (%) | Latency (ms) | Memory (MB) | Accuracy (%) | ||||
| Baseline | × | × | × | 100.0 | 9119 | 87.2 | 280.0 | 19130 | 86.8 |
| Q | √ | × | × | 72.0 (↓28.0%) | 6218 (↓31.8%) | 86.8 (↓0.5%) | 202.1 (↓27.8%) | 13293 (↓30.5%) | 85.3 (↓1.7%) |
| S | × | √ | × | 78.5 (↓21.5%) | 7125 (↓21.9%) | 86.9 (↓0.3%) | 225.5 (↓19.5%) | 14583 (↓23.8%) | 85.5 (↓1.5%) |
| R | × | × | √ | 80.0 (↓20.0%) | 7073 (↓22.4%) | 87.1 (↓0.1%) | 232.1 (↓17.1%) | 14381 (↓24.8%) | 85.6 (↓1.4%) |
| Q + S | √ | √ | × | 56.2 (↓43.8%) | 5210 (↓42.9%) | 86.5 (↓0.8%) | 172.4 (↓38.4%) | 10943 (↓42.8%) | 85.1 (↓2.0%) |
| Q + R | √ | × | √ | 54.1 (↓45.9%) | 5012 (↓45.0%) | 86.7 (↓0.6%) | 169.3 (↓39.5%) | 10753 (↓43.8%) | 85.3 (↓1.7%) |
| S + R | × | √ | √ | 53.8 (↓46.2%) | 4931 (↓45.9%) | 86.6 (↓0.7%) | 175.3 (↓37.4%) | 10890 (↓43.1%) | 85.2 (↓1.8%) |
| Q + S + R | √ | √ | √ | 41.3 (↓58.7%) | 3900 (↓57.2%) | 87.0 (↓0.2%) | 96.3 (↓65.6%) | 7489 (↓60.9%) | 86.2 (↓0.7%) |
| Method | A100 | |||||
|---|---|---|---|---|---|---|
| Latency (ms) | Memory (MB) | CLIP Score | FID | Throughput (Images/s) | ||
| 1 | Baseline [21] | 114.0 | 5402 | 0.819 | 12.0 | 8.8 |
| 2 | GPTQ [59] | 82.5 | 4120 | 0.801 | 13.5 | 12.1 |
| 3 | SparseGPT [43] | 71.1 | 3951 | 0.794 | 16.2 | 13.6 |
| 4 | FlashAttention2 [60] | 85.3 | 4213 | 0.808 | 13.1 | 11.3 |
| 5 | DiffMoE [50] | 66.4 | 3871 | 0.813 | 12.5 | 14.2 |
| 6 | Qurs (Q + S + R) | 52.8 | 3180 | 0.815 | 11.7 | 18.9 |
| NVIDIA Jetson Orin NX | ||||||
| Latency (ms) | Memory (MB) | CLIP Score | FID | Throughput (images/s) | ||
| 7 | Baseline | 2200.1 | 7901 | 0.812 | 12.4 | 0.47 |
| 8 | GPTQ | 1450.2 | 5311 | 0.796 | 13.9 | 0.76 |
| 9 | SparseGPT | 1250.1 | 5031 | 0.761 | 16.8 | 0.82 |
| 10 | FlashAttention2 | 1500.2 | 5470 | 0.772 | 13.8 | 0.71 |
| 11 | DiffMoE | 1150.1 | 4721 | 0.798 | 12.9 | 0.93 |
| 12 | Qurs (Q + S + R) | 865.3 | 3182 | 0.811 | 12.1 | 1.16 |
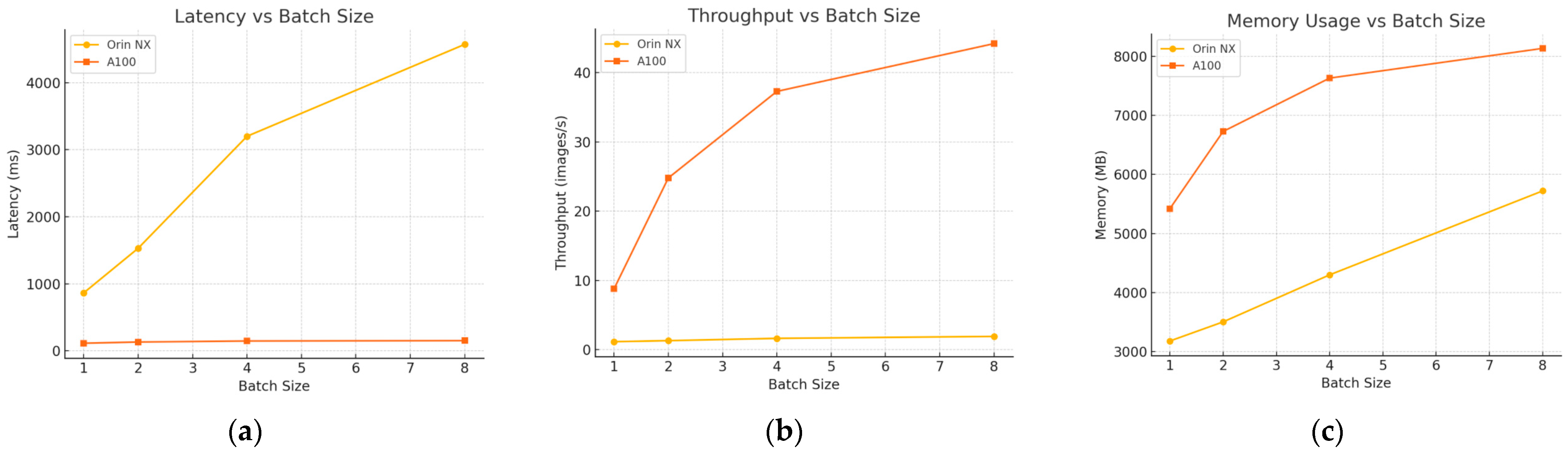
| Platform | Model | Batch Size | Latency (ms) | Throughput (Images/s or Tokens/s) | Memory (MB) | |
|---|---|---|---|---|---|---|
| 1 | Jetson Orin NX | Stable Diffusion v1.5 | 1 | 865 | 1.16 | 3180 |
| 2 | Jetson Orin NX | Stable Diffusion v1.5 | 2 | 1530 | 1.31 | 3504 |
| 3 | Jetson Orin NX | Stable Diffusion v1.5 | 4 | 3200 | 1.64 | 4300 |
| 4 | Jetson Orin NX | Stable Diffusion v1.5 | 8 | 4571 | 1.92 | 5721 |
| 5 | A100 GPU | Stable Diffusion v1.5 | 1 | 114 | 8.8 | 5421 |
| 6 | A100 GPU | Stable Diffusion v1.5 | 2 | 132 | 24.8 | 6728 |
| 7 | A100 GPU | Stable Diffusion v1.5 | 4 | 147 | 37.3 | 7631 |
| 8 | A100 GPU | Stable Diffusion v1.5 | 8 | 152 | 44.2 | 8134 |
| Input Complexity | Model | Platform | Avg Active Experts | Avg Latency (ms) | FID/Acc | |
|---|---|---|---|---|---|---|
| 1 | Text Length 64 | LLAMA-7B | A100 | 1.4 | 4.2 | 87.3% |
| 2 | Text Length 256 | A100 | 2.3 | 8.5 | 86.4% | |
| 3 | Text Length 1024 | A100 | 3.4 | 14.3 | 85.8% | |
| 4 | Text Length 64 | Jetson Orin NX | 1.2 | 11.5 | 86.1% | |
| 5 | Text Length 256 | Jetson Orin NX | 2.1 | 25.7 | 85.3% | |
| 6 | Text Length 1024 | Jetson Orin NX | 3.1 | 41.2 | 86.2% | |
| 7 | Resolution 224 × 224 | Stable Diffusion v1.5 | A100 | 1.1 | 96.5 | 11.9 |
| 8 | Resolution 256 × 256 | A100 | 1.7 | 112.4 | 11.6 | |
| 9 | Resolution 521 × 512 | A100 | 2.6 | 129.4 | 11.3 | |
| 10 | Resolution 224 × 224 | Jetson Orin NX | 1.2 | 865.7 | 12.5 | |
| 11 | Resolution 256 × 256 | Jetson Orin NX | 2.2 | 1231.4 | 12.1 | |
| 12 | Resolution 521 × 512 | Jetson Orin NX | 3.1 | 1610.3 | 11.8 |
| Method | Baseline Throughput (Tokens/s) | Constrained Throughput (Tokens/s) | Throughput Retention | Latency Variance (%) | |
|---|---|---|---|---|---|
| 1 | GPTQ | 34.3 | 20.5 | 59.8 | 28.4 |
| 2 | FlashAttention2 | 33.5 | 19.7 | 58.8 | 32.1 |
| 3 | DiffMoE | 39.2 | 29.8 | 76.0 | 18.7 |
| 4 | Ours (Q + S + R) | 52.8 | 45.0 | 85.2 | 9.3 |
| Method | Perturbation Type | Task Type | Accuracy (%) | FID (↓) | Avg. Expert Activation | Recovery Strategy | Observed Failure Mode | |
|---|---|---|---|---|---|---|---|---|
| 1 | GPTQ | Irrelevant Clause | Arithmetic | 80.5 | N/A | 1.3 | None | Wrong numeric reference |
| 2 | GPTQ | Token Reorder | Arithmetic | 83.6 | N/A | 1.5 | N/A | Early stop |
| 3 | GPTQ | Low-res blur | Image | N/A | 16.1 | 1.4 | N/A | Blurred edges, broken shapes |
| 4 | FlashAttention2 | Numeric distractor insertion | Arithmetic | 84.0 | N/A | 1.2 | N/A | Random hallucination |
| 5 | FlashAttention2 | Occlusion mask | Image | N/A | 17.0 | 1.3 | N/A | Misses occluded object parts |
| 6 | DiffMoE | Token reorder | Arithmetic | 87.1 | N/A | 2.4 | Re-balances MoE routing | Minor errors |
| 7 | DiffMoE | Blur + occlusion | Image | N/A | 14.3 | 2.5 | Partial recovery via fallback experts | Shape distortion |
| 8 | Ours (Q + S + R) | Distractor clause + reorder | Arithmetic | 96.3 | N/A | 2.9 | Selective routing + sparse expansion | Rare misalignment on punctuation |
| 9 | Ours (Q + S + R) | Blur + occlusion + mismatch | Image | N/A | 11.7 | 3.1 | Enhanced expert activation on details | Structure preserved |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, J. A Unified and Resource-Aware Framework for Adaptive Inference Acceleration on Edge and Embedded Platforms. Electronics 2025, 14, 2188. https://doi.org/10.3390/electronics14112188
Wang Y, Zhao J. A Unified and Resource-Aware Framework for Adaptive Inference Acceleration on Edge and Embedded Platforms. Electronics. 2025; 14(11):2188. https://doi.org/10.3390/electronics14112188
Chicago/Turabian StyleWang, Yiyang, and Jing Zhao. 2025. "A Unified and Resource-Aware Framework for Adaptive Inference Acceleration on Edge and Embedded Platforms" Electronics 14, no. 11: 2188. https://doi.org/10.3390/electronics14112188
APA StyleWang, Y., & Zhao, J. (2025). A Unified and Resource-Aware Framework for Adaptive Inference Acceleration on Edge and Embedded Platforms. Electronics, 14(11), 2188. https://doi.org/10.3390/electronics14112188






