A Structured Method to Generate Self-Test Libraries for Tensor Cores

Abstract

Modern computing systems increasingly rely on specialized hardware accelerators, such as Graphics Processing Units (GPUs), to meet growing computational demands. GPUs are essential for accelerating a wide range of applications, from machine learning and scientific computing to safety-critical domains like autonomous systems and aerospace. To enhance performance, modern GPUs integrate dedicated in-chip units, such as Tensor Cores(TCs), which are designed for efficient mixed-precision matrix operations. However, as semiconductor technologies scale down, reliability challenges emerge. Permanent hardware faults caused by aging, process variations, or environmental stress can lead to Silent Data Corruptions, which silently compromise computation results. In order to detect such faults, self-test libraries (STLs) are widely used, corresponding to suitably crafted pieces of code, able to activate faults and propagate their effects to visible points (e.g., the memory) and possibly signal their occurrence. This work introduces a structured method for generating STLs to detect permanent hardware faults that may arise in TCs. By leveraging the parallelism and regular structure of TCs, the method facilitates the creation of effective STLs for in-field fault detection without hardware modifications and with minimal requirements in terms of test time and memory. The proposed approach was validated on an NVIDIA GeForce RTX 3060 Ti GPU, installed in a Hewlett-Packard Z2 G5 workstation with an Intel Core i9-10800 CPU and 32 GB RAM, available at the Department of Control and Computer Engineering (DAUIN), Politecnico di Torino, Turin, Italy.This setup was used to address stuck-at faults in the arithmetic units of TCs. The results demonstrate that the methodology offers a practical, scalable, and non-intrusive solution for enhancing GPU reliability, applicable in both high-performance and safety-critical environments.

1. Introduction

Tensor cores (TCs), embedded within Graphics Processing Units (GPUs), are crucial for the efficient execution of general matrix multiplication (GEMM)—a fundamental operation in applications such as artificial intelligence (AI), scientific computing, robotics, and automotive systems [1,2]. As these fields increasingly depend on advanced autonomy and real-time decision making, computational workloads are escalating not only in complexity but also in scale due to the incorporation of data-intensive tasks and extensive sensor arrays [3,4]. To address these challenges, modern computing platforms utilize highly parallel architectures, particularly TCs, to enhance GEMM performance through mixed-precision execution and structured dataflow [1].

Although GPUs with TCs offer significant performance and energy efficiency, their reliability can be compromised by permanent hardware defects that arise during in-field operation [5]. In safety-critical environments, such as automotive or aerospace, even a single undetected hardware defect might lead to silent data corruptions (SDCs) with potentially catastrophic consequences, as it was recently demonstrated for data centers [6,7,8]. Hardware defects may arise from manufacturing imperfections, aging, or harsh environmental conditions and can remain latent until being activated during runtime [9,10]. Thus, to guarantee the reliable execution of GEMM workloads in such systems, robust in-field fault detection mechanisms that can operate during normal execution, i.e., in-field testing, are required. In particular, permanent hardware fault models—such as stuck-at faults (SAFs)—are commonly used to represent physical defects. Moreover, these are also used to evaluate and validate testing and mitigation mechanisms as suggested by safety standards like ISO 26262 [11].

Several fault detection strategies have been explored in the literature, including hardware-based mechanisms such as Logic Built-In Self-Test (LBIST) and NVIDIA’s In-System Test (IST) [12,13]. These approaches are typically limited to power-on or power-off tests and struggle to detect datapath-level faults during runtime. Similarly, Reliability, Availability, and Serviceability (RAS) features—while effective for memory and control logic—do not extend to computational engines like TCs [14]. Moreover, these hardware-based solutions often require complex design-time integration and deep architectural knowledge, making them inaccessible to system integrators or third-party developers.

As a more flexible alternative, software-based self-testing (SBST) methodologies offer a practical approach for in-field testing without requiring hardware modifications [15]. This strategy has been widely adopted by many companies for testing digital components in the field (e.g., CPUs, MCUs, and memory interfaces) used in safety-critical applications such as in automotive contexts [16]. SBST techniques are used to develop Software Test Libraries (STLs), which activate, propagate, and observe fault effects using carefully designed routines. STLs are also effective in validating key GPU modules [17,18,19]. However, their application to highly parallel and specialized accelerators, such as TCs, remains limited. The development of STLs for these units typically requires low-level programming expertise and careful workload mapping to prevent excessive overhead.

In order to validate the generated STLs (i.e., to compute the fault coverage they can achieve), suitable fault injection solutions are required. Several frameworks, such as SASSIFI [20], GPU-Qin [21], NVBit [22], and SIFI [23], have explored software-based fault injection and architectural vulnerability analysis. While useful for diagnostics and fault characterization, these tools often rely on privileged execution, architecture-specific instrumentation, or internal error injection hooks—factors that limit their practical deployment in production systems. Moreover, they mainly support transient fault models, while STLs target permanent faults. Consequently, they have not been considered for this work (apart from NVBit, which was used for a specific validation task).

To the best of our knowledge, only one prior work [24] has investigated permanent fault detection in TCs within GPUs. That approach employed a Universal Test Pattern (UTP) methodology, achieving 92% stuck-at fault coverage with low detection latency. However, it required detailed internal hardware descriptions and fine-grain architectural access, which are typically unavailable to system integrators. Hence, this approach is impractical for deployment outside of chip design environments.

This work proposes a user-oriented methodology for constructing STLs capable of detecting permanent faults in the field possibly arising in tensor cores. The generated STLs can be easily stored in some non-volatile memory on board the target system (together with the application code) and activated with a specified frequency (e.g., by the operating system). The most common usage of STLs is based on activating them during the idle times of the application or at power-on. By leveraging the inherent parallelism and structured execution model of TCs, they enable fault detection during normal runtime execution without requiring hardware modifications. Unlike prior works, our approach does not require a deep knowledge of the internal structure of the TC or the hosting GPU. It can thus be easily adopted by system integrators, offering a practical, scalable, and low-overhead alternative to hardware-dependent techniques. We validate the proposed method through a custom CUDA-based STL deployed on an NVIDIA GeForce RTX 3060 Ti GPU, hosted in an HP Z2 G5 workstation featuring an Intel Core i9-10800 CPU (20 cores) and 32 GB of RAM. The system is located at the Department of Control and Computer Engineering (DAUIN), Politecnico di Torino, Turin, Italy.While the study targets NVIDIA devices, the underlying methodology can be extended to other GPU architectures featuring similar tensor-processing capabilities.

Our experimental evaluation confirms that the proposed method can effectively and systematically transform the test vectors designed to detect faults in a given TC’s arithmetic unit into STLs that perform matrix multiplication. These STLs activate and propagate faults in TC datapaths with minimal overhead regarding execution time and memory footprint. Rather than solely focusing on maximizing theoretical fault coverage, this work emphasizes a structured, reproducible methodology for constructing GPU-compatible STLs that balance detection effectiveness, performance overhead, and implementation accessibility.

The major contributions of this work are summarized as follows:

• We propose a software-based fault detection mechanism for Tensor Cores in GPUs, leveraging software test libraries (STLs) for in-field fault testing without requiring hardware modifications.
• We introduce a systematic methodology for constructing STLs that execute HMMA instructions on TCs and are orchestrated through CUDA-based kernels. This design enables the precise activation and propagation of permanent fault effects while maintaining compatibility with standard GPU programming workflows.
• We demonstrate that our approach enables accessible, low-overhead, and high-performance in-field fault testing, making it suitable for adoption by system integrators across diverse application domains.

The manuscript is organized as follows. Section 2 provides background information about GPUs as well as the organization and operation of TCs. Section 3 presents the current work relative to the state of the art and discusses it. Section 4 introduces the proposed method for applying software-based testing libraries to TC cores. Section 5 outlines the case study. Section 6 analyzes the experimental results of the case study and discusses the findings. Finally, Section 7 presents the conclusions and addresses future work.

2. Background

This section introduces the architectural structure of Graphics Processing Units (GPUs) and the execution of matrix multiplication ($M\times M$) on their in-chip accelerators, known as Tensor Cores (TCs).

2.1. Organization of Graphics Processing Units (GPUs)

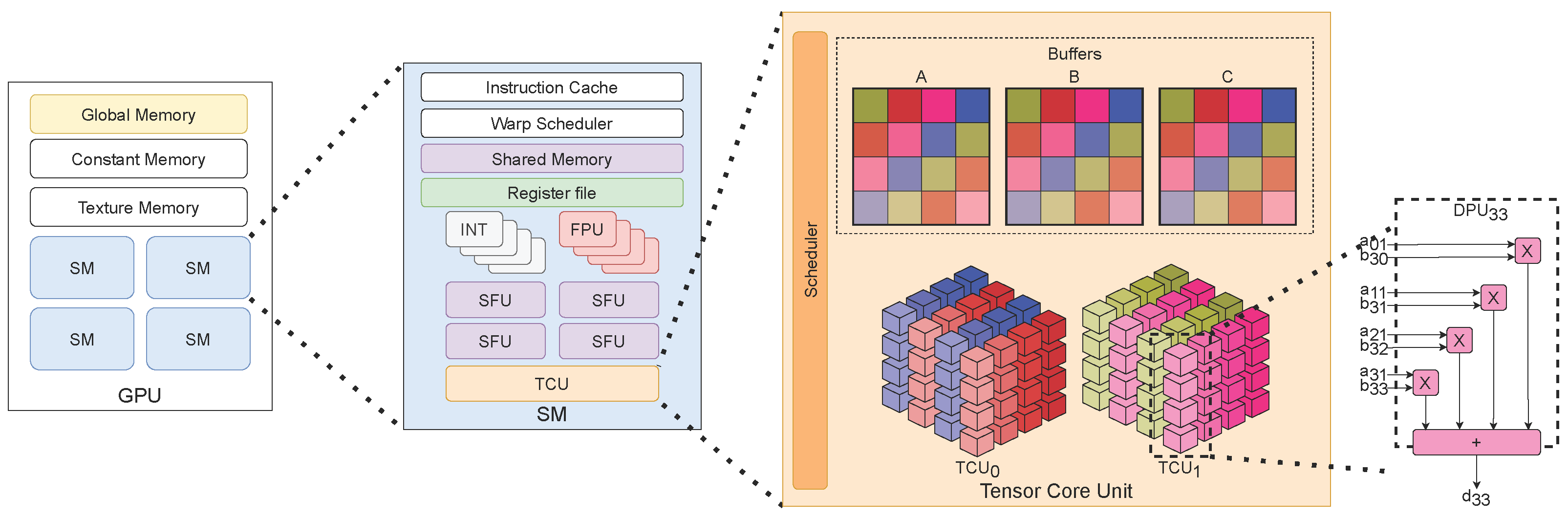
Modern GPUs are high-performance accelerators designed to maximize computational throughput through arrays of homogeneous clusters of parallel cores, known as Streaming Multiprocessors (SMs). SMs serve as the fundamental execution units, integrating multiple sub-cores to enhance parallel thread execution. These sub-cores facilitate the concurrent execution of multiple threads organized into warps (e.g., 32 threads), by leveraging a combination of integer units (INTs), floating-point units (FPUs), special function units (SFUs), and Tensor Cores (TCs). The heterogeneous architecture, combined with dedicated register file banks, memory structures, and advanced scheduling mechanisms, ensures the efficient execution of large-scale workloads while minimizing latency.

Each SM typically consists of 32 to 64 INTs and FPUs, 4 SFUs, and 2 TCs, collectively accelerating general-purpose computations, neural network inference, and scientific computing. Figure 1 provides an overview of GPU architecture, illustrating the integration of TCs within the memory hierarchy and scheduler components. TCs are tightly coupled with the SM’s execution pipelines, optimizing data movement and computation while reducing external memory dependencies.

The vectorized execution model of TCs necessitates highly optimized thread scheduling and memory management within an SM. These optimizations extend to the GPU’s Instruction Set Architecture (ISA), ensuring efficient TC utilization. The next subsection details the operational characteristics of TCs as specialized in-chip accelerators within GPUs.

2.2. Architecture and Operation of TCs

TCs are dedicated hardware units optimized for matrix-multiply-and-accumulate (MMAC) operations, extensively used in deep learning, scientific computing, and signal processing [1,27,28,29]. These units process matrix tiles (e.g., $4\times 4$) in half-precision, mixed-precision, and integer arithmetic (e.g., INT8/INT4), achieving exceptionally high throughput, often exceeding hundreds of teraFLOPS [1].

Recent NVIDIA GPU architectures—such as Volta—feature multiple TCs per SM, typically two per sub-core, resulting in up to eight TCs per SM. Each TC consists of 16 parallel four-element dot-product units (DPUs) and dedicated memory structures (buffers, immediate registers, or near-registers) [30]. These units generate a $4\times 4$ output per clock cycle, efficiently executing dense matrix operations. To maximize throughput, a single warp utilizes two TCs in parallel, ensuring that a $16\times 16$ tile computation is decomposed into smaller and more manageable $4\times 4$ operations.

Warp execution is structured hierarchically to optimize memory locality and register reuse. A warp is divided into eight thread groups, with tiles A and B (e.g., $16\times 16$) being loaded multiple times across different thread groups. These thread groups are further organized into octets, which collectively compute $8\times 8$ sub-results. The warp coordinates these octets, executing multiple sets of partial outer products, leading to a final $16\times 16$ output tile [25].

To efficiently handle large matrix computations, NVIDIA GPUs implement warp-wide matrix instructions (WMMA), which break down large matrix operations (e.g., $16\times 16$) into smaller, sequential tensor core operations. These WMMA instructions are compiled into hardware-level HMMA SASS instructions, which execute the actual matrix computations within TCs [25].

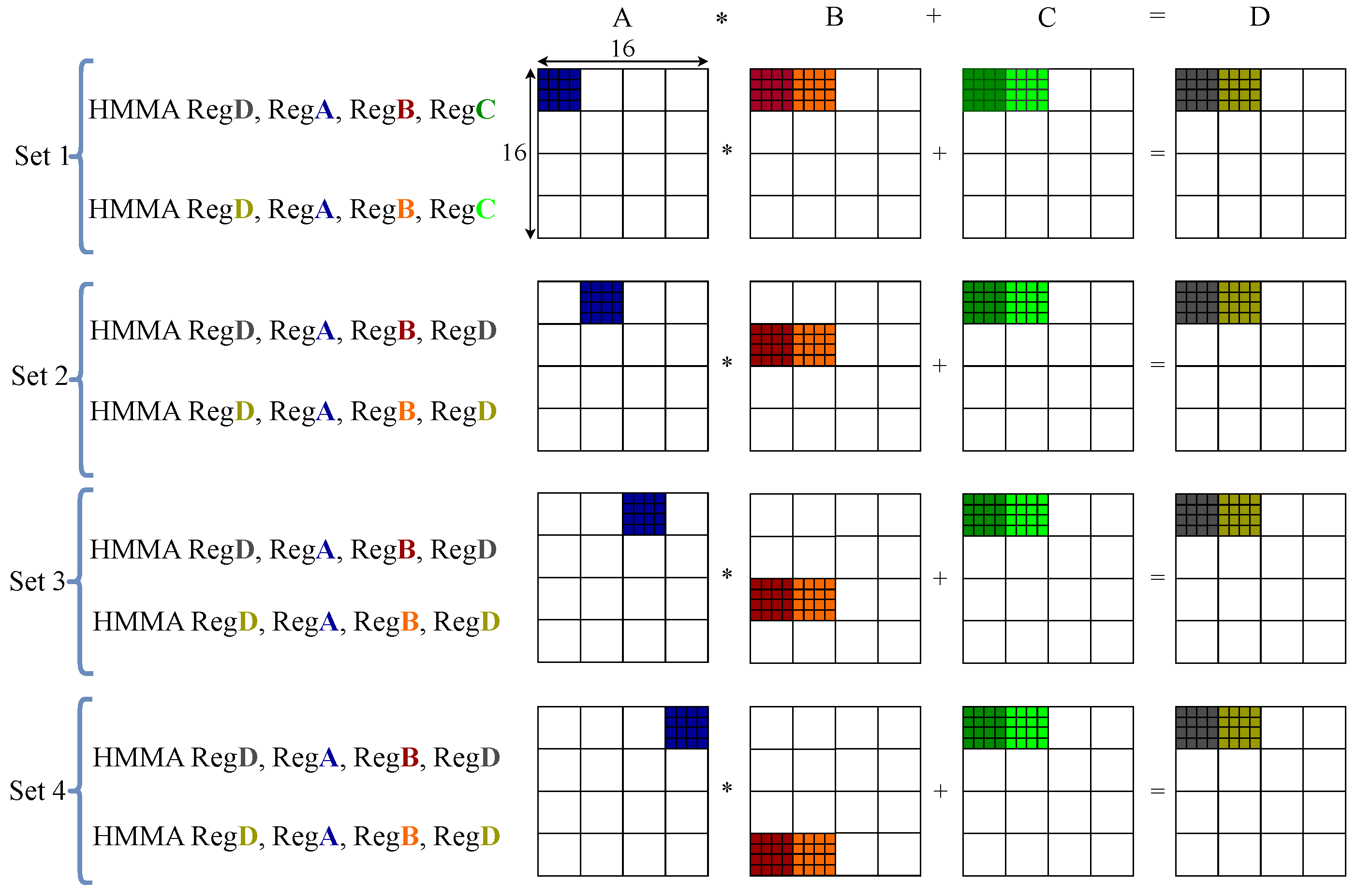
Each WMMA instruction is decomposed into multiple sets, each consisting of several HMMA instructions that operate on register pairs holding matrix fragments. These matrix fragments are $4\times 4$ submatrices extracted from larger operand tiles (such as $8\times 8$ or $16\times 16$) and serve as the fundamental computational units handled by individual DPUs within a TC. Each fragment contains operand values loaded into registers and processed independently by the DPUs during matrix multiply-accumulate operations. For instance, in $16\times 16$ mode, a single WMMA expands into eight HMMA instructions, divided into four sets, with each set further subdivided into two steps. During each step, $4\times 4$ matrix sub-blocks are processed within the TC, grouped into four sets, with each set further subdivided into two steps. During each step, the TC processes $4\times 4$ matrix sub-blocks in parallel. Figure 2 illustrates this execution for thread group 0, showing how input segments are processed through a sequence of HMMA instructions to produce the final output.

This execution model optimizes scheduling and register reuse while ensuring that each computation step can be executed independently. By structuring tensor core execution hierarchically, GPUs achieve efficient memory access patterns, reduced register pressure, and improved data locality, as intermediate results remain within high-speed shared memory rather than being offloaded to global memory.

By following this structured execution approach, GPUs maximize computational throughput, memory efficiency, and flexible hardware scheduling, significantly enhancing the performance for massively parallel matrix operations, such as deep learning inference and scientific simulations.

In detail, to support efficient large matrix multiplications, GPUs commonly apply a hierarchical tiling strategy [31]. Global matrices are partitioned into tiles (e.g., $128\times 128$) assigned to thread blocks, which further divide them into $16\times 16$ subtiles mapped to warps. Each warp splits its tile into $8\times 8$ or $4\times 4$ fragments aligned with HMMA instruction granularity and DPU datapaths. Threads cooperatively load these fragments into registers or shared memory, enabling efficient data reuse and coalesced access. This multilevel decomposition maximizes parallelism, registers utilization, and memory locality while maintaining compatibility with the TC execution model.

3. Related Works

In recent years, the growing complexity of modern accelerators has underscored the need for effective and efficient in-field testing methods. Early research on software-based self-testing for GPUs and their internal components—such as functional units, memory structures, and schedulers—demonstrated the feasibility of self-test libraries (STLs) executed at functional speed. These approaches reduce reliance on external testers while enabling the high-speed fault coverage of critical GPU components [18,19,32,33].

However, the inherently parallel nature of GPUs introduces significant challenges for self-testing. Traditional assembly-coded STLs offer fine-grain control over hardware execution, but they are architecture-specific, labor-intensive to develop, and often impractical for system-level deployment. More recently, the adoption of high-level programming models (e.g., CUDA) has enabled more productive and portable STL development [34]. Compiler-aware strategies have shown that a substantial portion of a GPU’s functional logic can be effectively exercised. However, achieving comprehensive fault coverage for internal structures like registers and schedulers still often requires low-level access.

An important factor affecting STL effectiveness is the role of compiler optimizations. Compilers such as NVIDIA’s NVCC apply aggressive transformations—including instruction reordering, register allocation, and loop unrolling—to enhance performance [35]. While these optimizations improve execution throughput, they can also influence fault propagation and detection, as redundant instructions that might mask errors are eliminated. Studies have demonstrated that optimized code (e.g., compiled with -O3) tends to exhibit a higher error sensitivity compared to unoptimized versions (-O0), though it may complete more correct computations before failing. Additionally, compiler flags such as -ftz=true and -use_fast_math further impact fault behavior by altering floating-point operations and unit utilization. Therefore, compiler configuration plays a critical role in shaping the reliability of GPU-based STL methods.

Recent studies have also explored the reliability at the register file level, which represents a significant source of soft-error vulnerability in GPUs. One proposed hardware-level solution employs resistive memory, such as STT-RAM, to enhance soft-error robustness while reducing leakage power. This approach achieves 86% vulnerability reduction and 61% energy savings with negligible performance overhead [36]. In contrast, a compiler-guided method replaces traditional error correction codes (ECCs) with lightweight error detection and idempotent recovery. This software-based technique delivers ECC-level resilience with only 3% runtime overhead while reducing hardware complexity [37]. Together, these works demonstrate complementary hardware and software strategies for improving soft-error tolerance in GPU register files.

Beyond the impact of compiler optimizations on fault propagation, other testing methodologies have been developed to assess reliability in GPU memory structures and functional units. Functional testing strategies for specialized memory structures in SMs have achieved up to 100% stuck-at-fault coverage by leveraging parallelism and signature-per-thread techniques [32]. Additionally, memory fault primitives (e.g., single and coupling faults) have been mapped into high-level CUDA routines to detect permanent errors in warp scheduler memory [19]. By exploiting the advanced thread divergence and memory access patterns, these techniques have achieved up to 100% coverage for both single- and multi-cell static faults.

In addition to memory testing, researchers have examined self-testing techniques for functional units responsible for transcendental and mathematical operations [18]. A proposed self-testing approach targeting GPU Special Function Units integrates test vectors generated by an Automatic Test Pattern generator (ATPG) and then hand-tuned, achieving up to 90% stuck-at-fault coverage while maintaining minimal testing duration and memory overhead. Additionally, variants of STLs (e.g., Image Test Libraries) have been introduced to identify hardware faults within GPU devices and their floating-point multipliers [33]. The reported findings indicate fault coverage of up to 95% when detecting permanent faults in the specific modules of a GPU (e.g., arithmetic ones).

Despite these advancements, testing methodologies for dedicated on-chip GPU accelerators such as Tensor Cores (TCs) remain scarce. To the best of our knowledge, only one prior study [24] has explicitly focused on detecting permanent faults in TCs. That work introduced a Universal Test Pattern (UTP) strategy, using structured test sequences to stress dense multiply–accumulate (MAC) datapaths across FP16, BF16, and INT8 precision modes. The method achieved over 92% stuck-at fault coverage with low detection latency and outperformed pseudo-random testing. However, it was designed for internal test environments and assumed complete access to the TC’s microarchitectural description, including fine-grained datapaths and control logic. As such, it is not suitable for system integrators or developers without hardware-level access. Additionally, the limited methodological transparency hinders reproducibility and adaptation to evolving GPU architectures.

To address these limitations, this work introduces a user-oriented methodology for developing Software Test Libraries (STLs) targeting permanent fault detection in TCs. By leveraging the structured execution model and inherent parallelism of TCs, the proposed approach enables efficient, non-invasive, and scalable in-the-field testing without requiring hardware modifications or privileged access. Unlike prior methods, our technique is designed for portability and accessibility. It operates using HMMA instructions carried out by TCs, while being managed through CUDA-based kernels, introducing minimal runtime and memory overhead. These features make it well suited for high-performance and safety-critical environments, where reliability and in-field testing are essential.

4. Software-Based Testing Library for Tensor Cores

This section presents our methodology for the in-field testing of Tensor Cores (TCs), specifically targeting permanent hardware faults in the Dot Product Units (DPUs)—the core arithmetic blocks within TCs. The approach uses HMMA SASS instructions to execute test routines at the thread-block level. These routines embed controlled patterns into input matrices and analyze the output for anomalies, enabling fault activation and propagation within the TC hardware.

Given the parallel nature of GPU architectures, developing effective STLs presents several challenges, including the synchronized execution and practical observation of fault effects. To address these challenges, the proposed method emphasizes structured test execution and the efficient control of data movement. Although test pattern generation (e.g., via ATPG or pseudo-random techniques) is outside the scope of this work, our method is compatible with both. The primary focus is on systematically translating these patterns into GPU-executable routines that apply stimuli to DPU inputs and propagate their effects to observable outputs (e.g., memory).

The STL development process begins with test vectors derived from the low-level models of arithmetic modules (e.g., DPUs), either via ATPG or pseudo-random generation when structural models are unavailable. Regardless of origin, the methodology ensures these patterns are applied in a structured and observable way, conforming to the GPU programming model.

The methodology accommodates both single and multiple TCs per SM. As TCs operate concurrently, test execution is adapted to reflect the hardware’s layout and scheduling model, ensuring that each unit is evaluated systematically.

As TCs perform $M\times M$ matrix operations, the proposed method directly embeds standard test patterns into the input matrices. The testing process consists of a two-fold approach. First, it maps structured test patterns onto the matrix operands to ensure the systematic activation of individual DPUs. Then, it analyzes the resulting output matrix to identify deviations from the expected results. These steps are detailed in the following subsections.

4.1. Mapping Test Patterns to Input Matrices

Test patterns are systematically encoded into matrix operands used by HMMA instructions. Unlike WMMA, which abstracts operations at the warp level, HMMA provides thread-block-level control, exposing matrix fragments that align with internal TC datapaths. This enables the deterministic injection of test patterns with fine-grained control over execution and thread scheduling.

Each test operation follows the GEMM form $D=A\times B+C$, where test patterns are encoded into A, B, and C to target specific DPUs. A pattern includes four values from A, four from B, and one accumulation value from C, producing a scalar output in D. These values are encoded in IEEE 754 32-bit format to ensure precise datapath stimulation. These encoded values are inserted into predetermined positions in the global matrix layout to target specific DPUs. Algorithm 1 describes this translation process in detail.

Algorithm 1 Translating Test Patterns into Matrix Operands

Input: Test patterns $P=\{p_0,p_1,...,p_{n-1}\}$ Output: Matrix operands A, B, and C   1: Initialize matrices A, B, and C with zeros   2: for each test pattern $p\in P$ do   3:       Extract sub-patterns: $\{a_0,a_1,a_2,a_3\},\{b_0,b_1,b_2,b_3\},c\leftarrow extractSubpatterns\left(p\right)$   4:       Encode each value to IEEE 754 format: $a_i,b_i,c\leftarrow encodeToFP32(·)$   5:       for $i=0$ to 3 do   6:             Assign $A\left[\mathrm{targetColumn}\right]\left[i\right]\leftarrow a_i$   7:             Assign $B\left[i\right]\left[\mathrm{targetRow}\right]\leftarrow b_i$   8:       end for   9:       Assign $C\left[\mathrm{targetColumn}\right]\left[\mathrm{targetRow}\right]\leftarrow c$ 10: end for

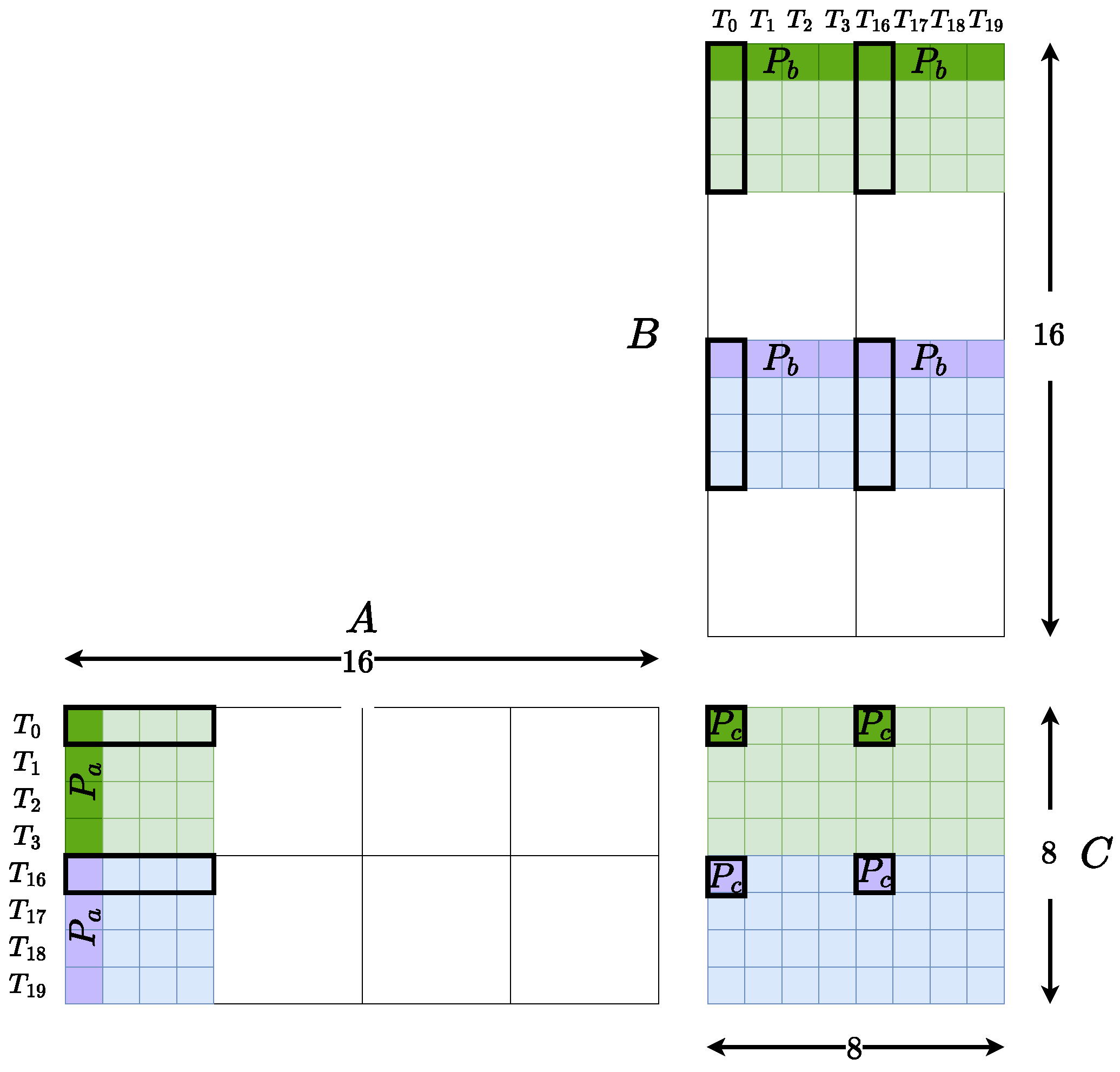
Operand matrices (A, B, and C) are organized into fragments to align test patterns with specific DPUs. In a standard $16\times 16$ GEMM operation, one HMMA instruction computes an $8\times 8$ tile, further decomposed into $4\times 4$ fragments, each mapped to a DPU. These fragments correspond to distinct lane and register combinations across threads in a warp.

Figure 3 illustrates this mapping strategy for an $8\times 8\times 16$ matrix multiplication. Colored regions (green and purple) represent two test patterns $P_x$, with lighter shades showing distributed input encoding and darker blocks highlighting the directly activated DPU fragment. Thread-level tile assignments (e.g., T0–T3, T16–T19) are outlined with black borders, representing how the test data propagate through the compute path.

To achieve full coverage across all TCs, the kernel is launched with as many thread blocks as there are SMs. Each block loads identical test matrices into shared memory and executes the same test routine using HMMA instructions. CUDA’s dynamic scheduler ensures that all SMs are engaged uniformly. To target all DPUs, the kernel is executed multiple times with spatially shifted versions of the test matrices. These controlled shifts allow complete datapath coverage without requiring knowledge of internal DPU mappings.

The use of HMMA enables the explicit management of shared memory and register allocations, ensuring isolation between concurrent test executions. This structure ensures the deterministic activation of faults by aligning input values to precise operand locations and controlling execution flow. The methodology guarantees observability by tightly binding data placement to compute fragments, avoiding cross-interference and enabling parallel, scalable, and low-overhead test campaigns.

4.2. Processing and Analyzing the Output Matrix

After the matrix multiplication, the output matrix D is retrieved from device memory. Each element in D represents a dot-product result from a specific DPU. Faults are detected by comparing D against a reference matrix $D_{\mathrm{expected}}$, which is precomputed using the original test vectors. We create this reference matrix ($D_{expected}$) directly from the original test vector, which can be either ATPG-generated or pseudo-random. For each test configuration, we simulate the GEMM-style operation offline to obtain accurate reference values. This approach eliminates the runtime numerical variations and ensures a precise bit-level comparison.

After execution, the matrix D is compared element-wise with $D_{\mathrm{expected}}$. Any mismatch is flagged as a fault. Given that each matrix element corresponds to a unique activation path within a DPU, discrepancies can be directly mapped to specific datapath regions, aiding fault localization.

The verification step is parallelized across GPU threads, ensuring fast and scalable output analysis. Matrix fragments are assigned to threads in a manner consistent with their original test pattern placement, reducing overhead in correlating inputs and outputs. Because memory access patterns are regular and aligned, the overall latency introduced by verification is minimal.

In summary, this methodology enables scalable, fine-grained fault detection in Tensor Cores using only software-level constructs. By combining deterministic test injection, structured scheduling, and parallel result analysis, it supports in-field testing with a minimal performance impact, without requiring privileged access or hardware instrumentation.

5. Study Case

The proposed method can systematically transform existing test patterns into corresponding STLs that apply the patterns to TCs and propagate the faults’ effects. To validate it, we focused on permanent faults within the TC cores of the NVIDIA GeForce RTX 3060 Ti. This GPU, based on the NVIDIA Ampere architecture, supports a Compute Capability of 8.6, manages up to 255 registers per thread, and allows a maximum of 64 active warps per SM. The Ampere architecture supports matrix computations across diverse operand shapes and tiling configurations (e.g., $16\times 8\times 16$, $16\times 8\times 4$, and $8\times 8\times 16$), allowing flexible adaptation to different matrix sizes and precision modes. These configurations determine how input operands are partitioned and executed by the TC datapath.

To evaluate the effectiveness of the proposed method, we adopted the standard TC configuration operating in full-precision mode, where both the input and output matrices used 32-bit elements. In this context, the SASS HMMA.8816 instruction—designed for $8\times 8\times 16$ matrix operations—was employed to validate the methodology. This instruction was selected because it represents a commonly used configuration in practical workloads, ensuring that the evaluation aligned with real-world execution scenarios.

As discussed in Section 2, TC cores consist of DPUs that perform MAC operations of the form $d=a\times b+c$. In this context, a and b are four-element vectors, and c is a scalar. Each DPU computes a scalar result of the form

$$d=a\left[0\right]\times b\left[0\right]+a\left[1\right]\times b\left[1\right]+a\left[2\right]\times b\left[2\right]+a\left[3\right]\times b\left[3\right]+c$$

While each DPU operates on scalar values, the overall matrix operation is applied across tile fragments extracted from the full input matrices, A, B, and C, enabling parallel computation across the TC core. However, due to the proprietary nature of NVIDIA’s DPU microarchitecture, direct fault behavior analysis was not feasible.

To tackle this challenge, we used an open source DPU implementation from the FloPoCo soft-core generator [38]. The core was not meant to replicate NVIDIA’s design exactly. Instead, it served as a structurally realistic and publicly available datapath to support ATPG-based test pattern generation and derive patterns targeting common datapath faults (e.g., stuck-at faults in FP32 multipliers and adders).

Test pattern generation was conducted using the gate-level netlist of this core after logic synthesis with a 15 nm technology library [39], using the Design Compiler (Synopsys) without optimizations. The synthesized netlist allowed for accurate fault modeling at the hardware level, ensuring that test patterns effectively targeted structural defects in DPUs.

To construct a comprehensive set of test patterns, we used an ATPG tool—TetraMAX by Synopsys—configured to target stuck-at faults (both SA0 and SA1) across all internal nets and the I/O pins of the synthesized DPU datapath. The tool was allowed to generate exhaustive patterns for all detectable faults without enforcing a fixed fault coverage threshold. In total, 559 distinct test patterns were produced for detecting stuck-at faults.

Using the proposed method, each pattern was encoded into matrix operands and structured into test matrices for execution in STLs performing GEMM operations. Each matrix contains two strategically positioned patterns designed to activate specific fault conditions while ensuring compatibility with the GPU’s parallel execution model. In total, we generated 840 test matrices (280 matrices for each of the input matrices A, B, and C).

Furthermore, to demonstrate the applicability of the proposed method in scenarios without access to detailed hardware models, we also generated and applied pseudo-random test patterns. These patterns populated the input matrices A, B, and C with randomly generated 32-bit floating-point values. The generated patterns were divided into three categories, each reflecting a different type of workload:

• Narrow: Uniform values in the range $[-1.0,1.0]$, representing normalized inputs typical in machine learning workloads, where inputs are normalized (e.g., ReLU, sigmoid inputs).
• Wide: Uniform values in $[-2.0,2.0]$, representing broader data distributions.
• Full-Range: Random values spanning the whole 32-bit floating-point domain (including values up to $2^{31}-1$), intended to stress-test extreme datapath conditions.

For each category, 1500 test matrices were produced—500 per input matrix (A, B, and C). These matrices were generated independently for each run. To capture statistical variation and enhance the representativeness of the fault detection results, each run was repeated five times. The same GEMM-based test routine used for ATPG patterns was used for these pseudo-random matrices, allowing a direct and fair comparison between deterministic and randomized approaches to fault detection.

Once the STLs have been generated, the execution flow follows a synchronous model as depicted in Algorithm 2. First, the GPU is initialized, and the test matrices generated by the method are uploaded to the system memory. The STL multiplying each test matrix is then run, resorting to the HMMA.8816 instruction to apply the target test patterns to the TC cores. After executing a matrix multiplication, the output matrix D is compared against a precomputed reference $D_{\mathrm{expected}}$. Bit-exact comparison ensures strict fault detection, avoiding false negatives—an essential requirement under ISO 26262 [11] for safety-critical systems.

Algorithm 2 Synchronous test application flow.

1: Initialize GPU resources   2: Load $Test\_Matrices$ to memory   3: for each $test\_matrix$ in $Test\_Matrices$ do   4:       Configure HMMA instruction for execution   5:       Apply STL by performing $test\_matrix$ multiplication   6:       $Output\_Matrix\leftarrow$ Retrieve GPU results   7:       Compare($Output\_Matrix$, $Expected\_Matrix$)   8:       if discrepancy detected then   9:             Flag faulty DPU 10:       end if 11: end for 12: End testing and generation of the fault report

Although this study used a synchronous flow for deterministic validation, performance can be improved using CUDA streams and asynchronous memory operations (Algorithm 3). Overlapping memory transfers with computation might reduce idle time and improve SM utilization. Persistent kernels and CUDA graphs offer further opportunities for runtime efficiency in production deployments. While these techniques were not activated in the current study to maintain tight control over fault injection, they offer strong potential for future STL engines in performance-sensitive environments.

Algorithm 3 Asynchronous test application flow.

1: Initialize GPU resources and create multiple CUDA streams   2: Load all Test_Matrices into host memory   3: for each test_matrix in Test_Matrices do   4:       Assign stream $S_i$ for test_matrix   5:       cudaMemcpyAsync(test_matrix_to_device, stream = $S_i$)   6:       Launch HMMA-based kernel in stream $S_i$   7:       Add a callback or flag to check for completion   8: end for   9: cudaMemcpyAsync(output_matrix_to_host, stream = $S_i$) 10: Synchronize all streams 11: for each output_matrix do 12:       Compare(Output_Matrix, Expected_Matrix) 13:       if discrepancy detected then 14:            Flag faulty DPU 15:       end if 16: end for 17: End testing and generate a fault report

To verify that STLs triggered the correct execution paths, we used NVBit [22], a dynamic instrumentation tool for NVIDIA GPUs. NVBit enabled the instruction-level tracing of executed SASS instructions, allowing us to confirm that the HMMA.8816 instructions matched the test matrices and kernel structure. Although NVBit does not perform fault injection or validation, it served as a reliable tool for verifying execution alignment and operand dispatch. Additionally, performance profiling was conducted with NVIDIA Nsight Compute [40], allowing a detailed analysis of kernel execution characteristics, including clock cycles, instruction counts, and warp divergence statistics.

6. Experimental Results

This section presents the experimental results we gathered, providing a comprehensive evaluation of the proposed methodology. The primary objective was to assess the ability to transform existing test vectors, capable of detecting permanent faults in TCs, into structured matrices suitable for execution via GEMM kernels. We begin by analyzing the resulting fault coverage, execution time, and memory footprint associated with the STLs. We then validated instruction-level correctness using NVIDIA’s NVBit tool to ensure accurate test execution across the hardware datapaths. Finally, we present a comparative discussion that positions our approach with respect to existing fault detection strategies in terms of performance, deployability, and hardware requirements. To validate the strategy, we employed both ATPG-generated and pseudo-random test patterns.

The experiments were conducted using an open source DPU implementation from a modern soft-core generator [38]. A total of 88,880 stuck-at-faults (SAFs) were considered using the core’s gate-level model to generate test patterns. Additionally, a functional safety analysis was performed using JasperGold (Cadence), which identified 6628 functionally untestable faults (i.e., faults that can never produce a failure during the operational phase). Among these, 1616 were structurally safe (i.e., activated but not propagated), and 5012 were activation safe, meaning they could not be triggered from any combination of primary input conditions and are therefore not detectable under standard excitation scenarios [41]. These functionally untestable faults were excluded from the fault coverage (FC) calculation [42]. To evaluate runtime behavior and memory usage, the generated test matrices were executed on an NVIDIA GeForce RTX 3060 Ti GPU, integrated into an HP Z2 G5 workstation with an Intel Core i9-10800 CPU (20 cores) and 32 GB of RAM. The system is located at the Department of Control and Computer Engineering (DAUIN), Politecnico di Torino, Turin, Italy.

6.1. Fault Coverage and Performance Overhead

To assess the method’s fault detection capabilities, we first generated 559 ATPG-based test vectors targeting the DPU’s arithmetic datapath. These were transformed into 840 structured test matrices—280 for each of the input matrices A, B, and C—which represent the input for GEMM-based STLs. Secondly, we generated 1000 pseudo-random test vectors for each of the three input categories (Narrow, Wide, and Full-Range). Each category resulted in 1500 test matrices (500 per input matrix). To ensure statistical significance, we generated five independent sets of pseudo-random test vectors per category and averaged the results over these five executions using the same GEMM-based infrastructure.

Table 1. Fault coverage and overhead results.

Test Type	Test Patterns	Test Matrices	FC (%)	Executed SASS Inst	Memory Usage (KB)	CC Total (Avg./Matrix)
ATPG-based	559	840	$97.35$	$14.5\times {10}^6$	420	$37,569\times {10}^6$ $(134.17\times {10}^3)$
Pseudo-random Narrow	1000	1500	$80.03\pm 0.16$	$25.9\times {10}^6$	720	$67,087\times {10}^6$ $(134.17\times {10}^3)$
Pseudo-random Wide	1000	1500	$81.26\pm 0.32$	$25.9\times {10}^6$	720	$67,087\times {10}^6$ $(134.17\times {10}^3)$
Pseudo-random Full-Range	1000	1500	$82.23\pm 0.61$	$25.9\times {10}^6$	720	$67,087\times {10}^6$ $(134.17\times {10}^3)$

reports the fault coverage, total number of executed SASS instructions, memory usage, and the total amount of clock cycles (CCs) required for each test configuration. For the pseudo-random-based STLs, we present both the average and standard deviation across five runs. The reported fault coverage (FC) refers specifically to the subset of testable stuck-at faults in the synthesized DPU datapath. In addition, the reported clock cycle count includes both the total number of cycles required for the complete STL execution and the average number of cycles required to compute a single $8\times 8\times 16$ matrix multiplication.

The results confirmed that the transformation of vectors into STL-compatible inputs preserved the fault activation and propagation characteristics of the original test patterns. The ATPG-based STLs achieved the highest coverage (97.35%), demonstrating that the GEMM-based testing structure effectively maintained fault detectability throughout GPU execution.

Furthermore, the feasibility of deploying such STLs without in-depth hardware knowledge was validated using pseudo-randomly generated test vectors. Obviously, pseudo-random tests exhibited lower—but still substantial—fault coverage. Notably, the results showed a positive correlation between the diversity of input values and the ability to detect faults. In detail, the Narrow configuration achieved 80.03%, the Wide configuration improved to 81.26%, and the Full-Range test reached 82.23%.

These findings are attributed to the broader numerical ranges exercised by full-range patterns—including small, large, positive, and negative floating-point values—which generate a greater variety of bit-level combinations. These combinations stimulate more of the datapath’s internal logic, including sign handling, exponent normalization, and overflow/underflow detection circuits [43]. Such diversity increases the likelihood of toggling internal logic lines that may remain inactive under narrower or repetitive input distributions. These results highlight the importance of input value selection in pseudo-random testing, particularly when applied to hardware self-test campaigns.

While ATPG-based testing provides superior diagnostic accuracy, pseudo-random STLs are significantly easier to generate and deploy. They require no extensive architectural knowledge, synthesis tools, or hardware-level access, making them highly practical for system integrators in real-world environments. Our method applies equally well to both scenarios.

To assess runtime costs, we compared the number of executed SASS instructions between our STL-based method and a standard GEMM kernel executing $8\times 8\times 16$ matrix multiplications. As shown in Table 1, the total number of SASS instructions reflects the cumulative execution across the entire GPU. Standard GEMM kernels required approximately $14.3\times {10}^3$ instructions per matrix. In contrast, our STL-based implementation averaged around $17.3\times {10}^3$ instructions per matrix—a 21% increase—primarily due to additional steps for comparing the results. Importantly, more than 90% of the executed instructions belonged to the arithmetic pipeline, confirming that the test logic was efficiently fused into the matrix computation path.

We also measured warp divergence statistics to evaluate control flow efficiency. Across all test campaigns, warp divergence remained below 1.7% on average, with most divergence occurring in the result checking logic, where conditional branches compare the computed and expected outputs. The core GEMM execution itself exhibited minimal to no divergence, as expected from tile-structured matrix operations. These low divergence rates confirm that the STL kernels maintain high SIMD (Single Instruction, Multiple Data) utilization and are well suited for efficient GPU execution, even in the presence of conditional checking mechanisms.

In terms of execution time, each GEMM kernel processing an $8\times 8\times 16$ matrix completes in approximately $134.175\times {10}^3$ clock cycles, corresponding to roughly 96 ms on the NVIDIA GeForce RTX 3060 Ti. For the whole STL campaign, the total clock cycles amounted to $37.5\times {10}^6$ for the ATPG-based (deterministic) test suite and $67\times {10}^6$ for the pseudo-random (heuristic) variant. These figures reflect the cumulative execution across all test matrices and confirm that the runtime overhead remains within acceptable bounds for in-field testing. Notably, the predictable and bounded nature of this overhead makes the method suitable for periodic or background reliability checks in safety-critical and high-performance environments.

We also outline the fact that the generated input matrices for STLs can be used in a flexible manner. particularly if the required time for running the overall resulting STLs is too large, they can be easily split, each GEMM operation runs independently, and the computed results are checked.

The experimental findings confirmed the effectiveness of the proposed approach for generating STLs for TCs. The proposed methodology requires an acceptable runtime cost, limited additional memory, and efficient scaling with GPU parallelism—key attributes for in-field reliability assurance.

6.2. Instruction-Level Execution Validation

To ensure the correctness of test pattern translation into matrices, extensive profiling was conducted using NVBit [22]. This validation process was essential in confirming that each test pattern was executed independently within its designated DPU, preventing unintended interactions that could compromise fault detection accuracy.

The profiling confirmed that the method reliably mapped test patterns into matrices, achieving deterministic execution and consistent fault detection. Maintaining execution isolation was crucial to prevent fault masking effects. Additionally, the validation results demonstrated that the methodology scaled effectively across multiple execution units, underscoring its compatibility with different GPU architectures.

6.3. Discussion

The experimental results demonstrate that the proposed methodology effectively transforms both deterministic (ATPG-based) and stochastic (pseudo-random) test vectors into matrix-based STLs, achieving the high observability of permanent faults in TCs. These STLs are compatible with GEMM-style execution and introduce only modest overhead in terms of runtime and memory usage, which makes them suitable for embedded and high-performance environments.

A key advantage of the approach is its complete independence from low-level hardware access. Unlike prior methods that rely on microarchitectural knowledge or privileged execution modes [24], our technique operates entirely in user space, using standard CUDA intrinsics. This design enables seamless deployment in production systems, particularly in safety-critical domains such as automotive, aerospace, and high-performance computing, where hardware introspection is impractical or prohibited. It also contributes to silent data corruption (SDC) mitigation by enabling the runtime fault detection without interrupting normal GPU operations.

Moreover, our method addresses a fundamental limitation of previous work. Techniques like SASSIFI [20] and GPU-Qin [21] focus on fault injection for vulnerability characterization. While valuable for architectural studies, they require instrumentation layers or privileged access and are not applicable to runtime fault detection in field-deployed systems. Similarly, UTP [24], though closer in goal, requires microarchitectural access unavailable to most users, limiting its real-world applicability.

By contrast, our method provides lightweight, direct fault detection that is fully deployable without architectural transparency. Even in black-box scenarios, pseudo-random test campaigns—particularly those with full-range input values—achieved over 82% fault coverage, approaching ATPG-level effectiveness. This robustness confirms that the method is not only technically sound but also broadly adaptable.

It is also important to emphasize the hardware-agnostic nature of the proposed technique. Although our implementation targets NVIDIA GPUs using HMMA instructions, the underlying principles—translating test patterns into matrix operands and verifying results against a golden reference—are architecture-neutral. As long as the structured matrix execution and output visibility are supported, the approach is portable. This allows the method to be applied to other accelerators, such as Intel NPUs (e.g., via the matmul() API [44]) and AMD GPUs with matrix core support through ROCm MFMA instructions [45]. The effectiveness of fault detection depends on the specific architecture of the datapath and the test patterns utilized. However, the method can be implemented on different platforms with minimal modifications at the kernel or API level, as long as comparable low-level matrix operations are available.

Table 2. Quantitative comparison with representative GPU fault detection methods.

Method	Hardware Access	In-Field Deployable	Runtime Overhead	Memory Usage
UTP [24]	Requires microarchitectural access Fault detection	✗	Medium	Medium
Proposed method	No/Optional special access Fault detection	✓	Low (21%)	Low (420–720 KB)

Note: ✓ indicates “Yes”; ✗ indicates “No”.

summarizes key distinctions between our approach and existing GPU fault-handling frameworks. While approaches like UTP [24] offer internal diagnostic capabilities, they are restricted to vendor-controlled or privileged execution contexts. In contrast, our method enables runtime fault detection at the application level using standard APIs, requiring no special system privileges or vendor instrumentation. This makes it well suited for scalable deployment in real-world environments.

In summary, the proposed methodology offers a scalable, non-intrusive, and fully software-driven solution for permanent fault detection in tensor cores. It advances the state of the art by eliminating the need for hardware modifications, supporting dynamic and stochastic testing strategies, maintaining high fault coverage, and enabling straightforward integration into safety-critical and high-performance deployments. These characteristics position our method as a practical and portable alternative to conventional GPU test strategies.

7. Conclusions and Future Work

This paper introduced a software-based methodology for testing Tensor Cores (TCs) in modern GPU architectures, targeting the detection of permanent faults in their Dot-Product Units (DPUs). The approach leverages HMMA-based matrix operations to embed deterministic and pseudo-random test patterns directly into GEMM-style operands. The methodology supports coarse-grained yet precise fault activation and observation, fully implemented in software without requiring hardware modifications or privileged architectural access.

Designed for portability and runtime applicability, the method enables developers to deploy lightweight fault detection capabilities within user-space GPU applications. This makes it particularly relevant for safety-critical and high-performance domains, where architectural transparency is limited and intrusive techniques are impractical.

Experimental validation demonstrated that the ATPG-based STL variant achieved over 97% fault coverage with only a 21% instruction overhead. Though pseudo-random campaigns are more straightforward to generate, they still deliver substantial fault activation potential, particularly when using full-range input values, highlighting the method’s robustness even in black-box testing scenarios.

Overall, the proposed methodology offers a scalable and architecture-agnostic solution for in-field reliability assurance across GPU platforms. Its ability to transform test patterns into executable matrix operands with minimal system disruption positions it as a practical tool for enhancing dependability in both embedded and large-scale computing environments.

Future work will aim to extend the methodology to support additional fault models (e.g., delay faults), deployment in multi-GPU and heterogeneous systems, and evaluation on non-NVIDIA platforms such as AMD and Intel matrix accelerators. These efforts aim to broaden the methodology’s applicability and further enhance its resilience under diverse operating conditions.