1. Introduction
The rapid development of autonomous driving technology relies on high-performance semantic segmentation models, which can accurately identify key targets such as lane lines, pedestrians, and vehicles in road scenes pixel by pixel to provide information for decision-making systems. A high-precision semantic segmentation model requires massive and diverse driving data to ensure generalization, and it is difficult for a single vehicle or car company to collect sufficiently comprehensive data independently. The data collected by the vehicle camera contains sensitive information, and the traditional direct upload to the central server for centralized training has the risk of privacy disclosure. At the same time, this training method has a high communication cost, and it is unrealistic to upload all the massive data to the server for training. Due to the irreconcilable contradiction between data utility and privacy protection, the rigid demand for federal learning [
1] in the field of autonomous driving has been spawned.
Federated learning allows multiple edge devices to compute and share parameter updates to train models collaboratively without directly exchanging raw data, ensuring data privacy while enabling collaborative learning. When training the semantic segmentation model, the vehicle only uploads the model update gradient, while multiple clients work together to optimize the global model, and the transmission of parameters is significantly reduced compared to the original data.
FedAvg [
2] is the earliest federated learning method, which uses its individual data to optimize the local model and simply does a weighted average to aggregate the weights in the server. A series of methods [
3,
4,
5,
6,
7,
8] have been proposed and applied to image classification, but the implementation of a federated learning framework in semantic segmentation is a serious challenge. The current semantic segmentation data have non-IID characteristics due to the significant difference in the distribution of data collected by different clients, and the occurrence frequency of different classes in the dataset is systematically biased. In addition, the high model complexity of semantic segmentation tasks brings significant computational and communication burdens to clients in federated learning systems. The number of parameters in a typical segmentation network can reach millions of levels, which seriously restricts the updating frequency and system response speed of federated learning. For example, FedSeg [
9] uses federated learning to improve the accuracy of semantic segmentation training, but ignores the computational and communication efficiency of training.
Therefore, the research in this paper faces inherent challenges in semantic segmentation federated learning, especially the problem of client data heterogeneity and efficient communication [
10]. A Federal Street view segmentation method, FedSS, is proposed, and an algorithm combining local continuous update and parallel communication is designed for automatic driving scenarios. It is called Continuous Parallel Federal Street View Segmentation (CP-FedSS) and a communication-efficient federal learning method, Communication Efficient Federal Street View Segmentation (CE-FedSS).
In response to the heterogeneity of client data, CP-FedSS improves the cross-entropy loss function and introduces the probability of non-local labels in the loss calculation process to alleviate the adverse impact of data distribution heterogeneity on the federated learning model. In addition, in order to alleviate the impact of data obsoleting caused by communication delay on learning efficiency and convergence speed, and improve the efficiency of local computing resources, we change the federal communication process from synchronous waiting for global updates to local continuous updates. For the problem of obsoleting transmission gradient caused by adding parallel local training, a gradient compensation strategy based on Taylor series is proposed to improve the utilization efficiency of local computing resources.
CE-FedSS uses the Top-k sparse strategy to compress the uploaded data in the upload path from the client to the central server. By identifying and selecting key gradient information for transmission, CE-FedSS reduces the high communication cost caused by frequent full model parameter exchange in federated learning and ensure efficient model training even in environments with limited bandwidth and high communication costs.
In summary, the contributions of this paper are as follows:
- (1)
We propose an improved cross-entropy loss function and design a local continuous update and gradient compensation strategy to significantly improve the performance of the semantic segmentation model;
- (2)
We adopt a sparse strategy to compress the number of gradient transmission parameters, and achieve higher communication efficiency under the condition that the model performance is slightly reduced and acceptable, demonstrating the potential of efficient federated learning systems;
- (3)
We evaluate our algorithm on two semantic segmentation datasets, including Cityscapes and CamVID, and demonstrate the effectiveness of our work.
2. Related Work
2.1. Semantic Segmentation
In addition to recognizing objects in the image, semantic segmentation can also accurately locate the exact boundaries of these objects. Its network model classifies each pixel in an image and is able to identify and understand the different objects and regions within it, ensuring that each pixel is accurately labeled. Therefore, semantic segmentation is also regarded as a pixel-level fine-grained classification task.
FCN [
11] is a representative work of a deep learning application in image segmentation. It replaces all the connected layers in the network with convolutional layers, so that the network becomes composed of convolutions. Based on Mask region mask RCNN [
12], based on Faster RCNN [
13], full convolutional networks are used to perform pixel-to-pixel mask prediction on mask branches for identified object categories. U-Net [
14] improved the full convolutional network and designed an expansion path to retrieve the extracted abstract features by upsampling and decoding to the input image size. The work LSTM [
15] uses recurrent neural networks to overcome the problem of underutilization of global context information. Salvador et al. [
16] proposed a cyclic model based on the encoder-decoder architecture that sequentially generates a binary mask and its associated class probability for each object in the image. Visin et al. [
17] proposed a structured prediction architecture named ReSeg based on recurrent neural networks, which combined the local common features extracted by convolutional neural networks and the ability of recurrent neural networks to retrieve remote dependencies. Shuai et al. [
18] proposed a directed acyclic graph recurrent neural network DAG-RNNS for directed acyclic graph DAG structure images to improve the discriminant ability of local representations by simulating long-distance semantic dependency between image units.
The work Segmenter [
19], a Transformer model for semantic segmentation, classifies the output embeddings of image blocks through a point-like linear decoder or a masked Transformer decoder. Xu et al. [
20] proposed a novel three-branch network architecture PIDNet, which connects convolutional neural networks with proportional–integral–differential controllers, and the three branches are used to analyze details, context information, and boundary information, respectively. Cao et al. [
21] proposed a dual attention network (DANet) based on a self-attention mechanism. The global context network (GCNet) [
22] found in the study that the non-local network (NLNet) [
23] modeled the global context of different query locations almost the same, and adopted a formula independent of the query location to simplify the network structure and capture long-term dependencies efficiently. At the same time, NLNet is similar to SENet [
24] in structure, and a lightweight global context module is designed. Huang et al. [
25] proposed a cross-sectional network (CCNet) to calculate the context information between each target feature pixel and all pixels on the vertical and horizontal path in the feature map.
2.2. Federated Learning
The core of federated learning is that data are kept locally in the client, and machine learning models are built by transferring model data. Current research on federated learning focuses on solving heterogeneity [
26] and improving communication efficiency. In order to deal with the system heterogeneity and statistical heterogeneity among clients, Li et al. [
3] proposed the FedProx method, which introduced a regularization term into the local optimization to balance the differences between the local update and the global model. Kim et al. [
4] proposed to graft local and global subnetworks on different levels of each client model, construct multiple auxiliary branches, and learn the consistent representation of the main path and auxiliary mixed path in the client model through online knowledge distillation. Arivazhaga et al. [
5] proposed the FedPer method to improve the robustness of the algorithm against data heterogeneity by adding a personalized layer on the basis of a deep feedforward neural network. Wang et al. [
6] proposed a standardized averaging method, FedNova, to effectively solve the global model bias problem by improving the aggregation mechanism. Li et al. [
7] used local batch normalization to reduce the feature deviation before the average model and improve the convergence speed. The MOON framework [
27] uses the similarity between model representations to correct the local training of each client. Zhang et al. proposed an adaptive local aggregation method, FedALA [
8], to improve the personalization performance of client models by capturing the necessary information in the global model.
In order to reduce communication burden and increase distributed gradient descent, Condat et al. proposed the TAMUNA algorithm [
28], which combines two commonly used strategies of reducing communication frequency and transmitting compressed information, and allows some clients to participate. Ma et al. developed an innovative horizontal federation XGBoost framework [
29]. This framework improves privacy and communication efficiency by making the learning rate of aggregation tree collections learnable. Furthermore, Hu et al. [
30] proposed a novel secure FL-compatible hybrid gradient compression framework (HGC). Through the proposed optimization method based on compression ratio correction and dynamic momentum correction, the trade-off between communication cost and model performance was improved. Gao et al. [
31] believe that distributed training usually relies on compression to reduce communication overhead. They introduced the EControl error compensation mechanism to achieve rapid convergence under standard strong convex, general convex, and non-convex Settings. In terms of privacy protection, Huang et al. [
32] proposed self-driven Fisher Calibration (SDFC), which utilizes Fisher information to calculate the parameter importance of locally unknowable and globally verified distributions, preventing attacks on sensitive features and protecting local data privacy.
3. Methods
3.1. Overview
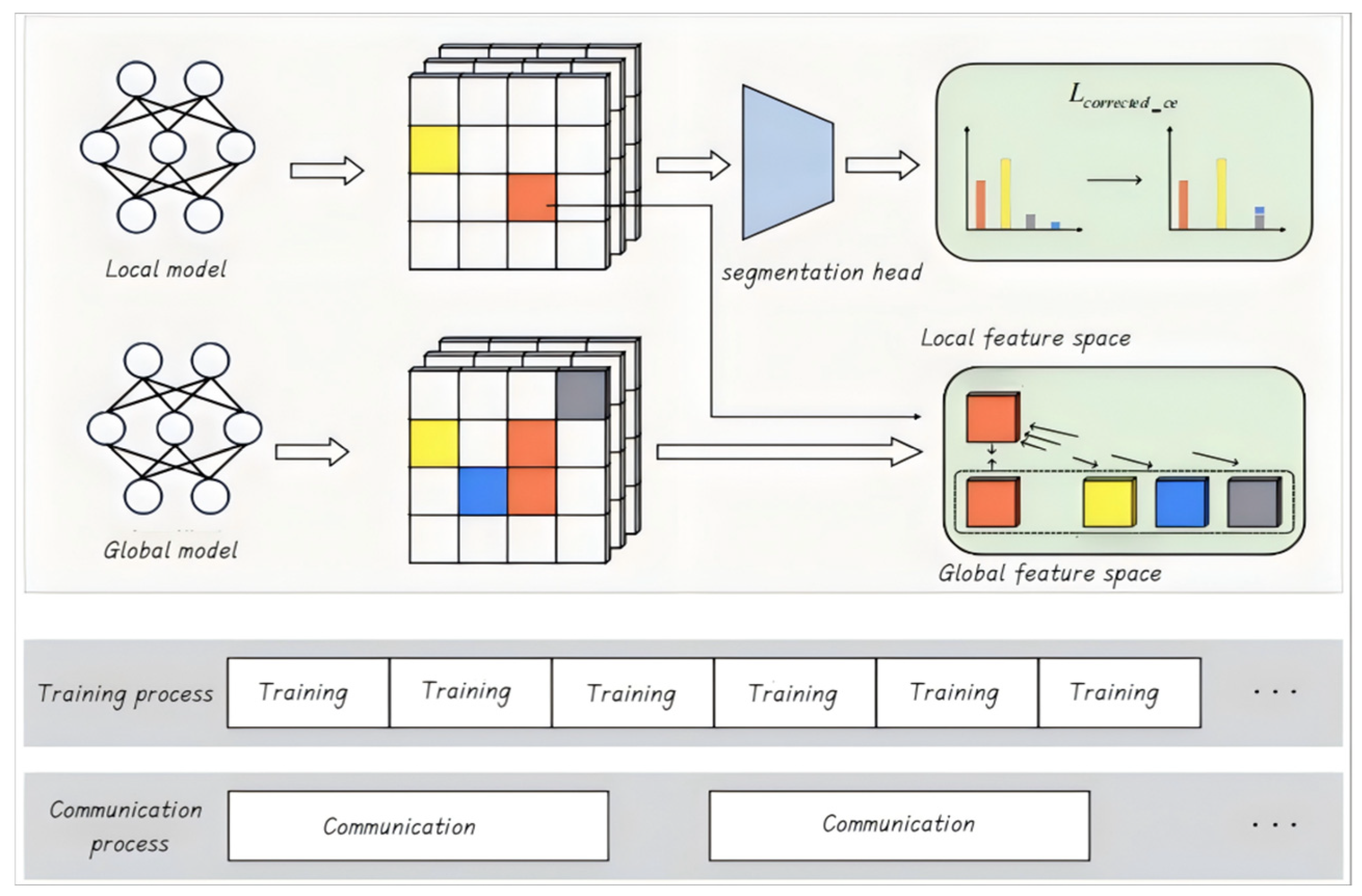
In this section, we formally propose our CP-FedSS algorithm, as depicted in
Figure 1. The CP-FedSS workflow consists of five steps:
Step 1: Initialize the global model on the central server and push it to all clients;
Step 2: Each client uses its own local data for E iterations of the local model training;
Step 3: When the local update is complete, the client continues the local training and pushes the local update to the central server using the communication process;
Step 4: When the central server receives the updated data from the client, it uses Teller series expansion and Fisher information matrix [
33] to compensate the model weight, and then updates the global model with the compensated weight;
Step 5: The central server pushes the latest global model to the client. In the CP-FedSS algorithm, the local update of the client uses an improved cross-entropy loss function and pixel-level contrast learning loss to solve the impact of data heterogeneity on convergence.
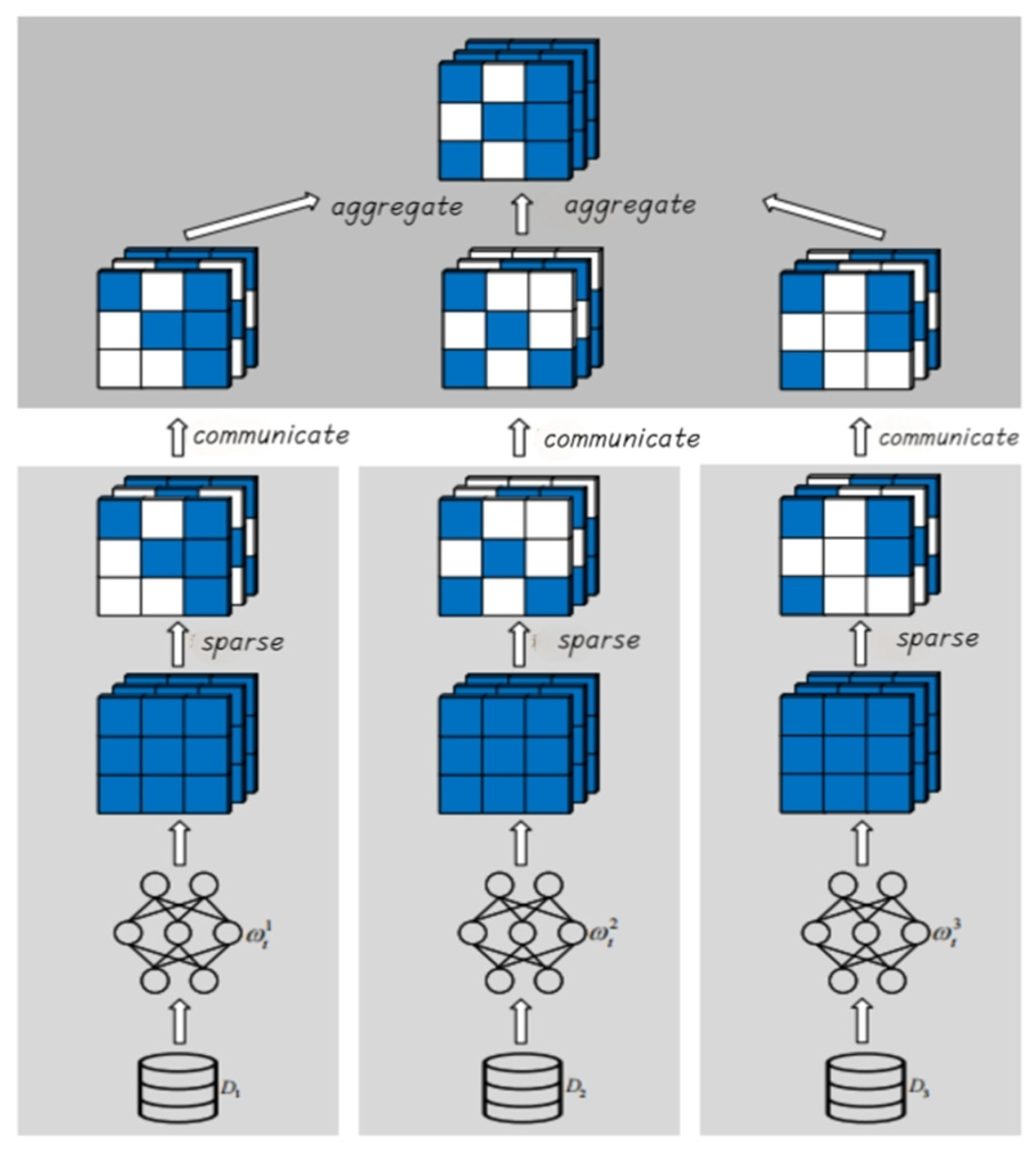
The CE-FedSS algorithm is inspired by network compression technology, as depicted in
Figure 2. It turns the compressed object into federated learning communication data, and the client trains the model on its own local data to obtain updated data. After sparse operation, the updated data are compressed and then transmitted to the central server, and the central server generates a new global model based on the sparse updated data.
3.2. Cross-Client Semantic Correction
Now, assume that there are N clients, each with a local semantically segmented dataset . Since the client daa distribution of federated learning generally has non-IID characteristics, where c stands for category, that is , the distribution probabilities of the same classes in the local datasets of different clients are not similar; the semantic classes that appear frequently in the local data of clients have more annotation labels, while the semantic classes that do not appear frequently have less annotation data. Semantic class objects that occur frequently are considered the foreground of the client, and semantic classes that occur less frequently are considered the background of the client. This indicates that data on clients is heterogeneous.
The federated learning task is to indirectly use all numbers to complete the model training by transmitting model parameters or gradient updates of the client without the constraint of transmitting the local original data of the client. In the centralized learning paradigm, the cross-entropy loss function is commonly used in semantic segmentation tasks:
where
and
represent data and labels, respectively, and
are the true value labels of pixel
;
represents the set of annotated pixels, and
is the prediction probability of pixel
; background pixels without annotated information will be ignored. In the federated learning framework, there are large differences in the optimization direction between clients with only some semantic classes after local optimization, resulting in poor convergence of the global model. Therefore, taking into account information about other semantic classes that are not present in this client, the cross-entropy loss is modified by aggregating the probabilities of these classes, providing gradient directions to other classes to correct the optimization direction of local updates. The modified objective function can correct client optimization in federated learning, making it similar to traditional centralized training. The objective function used by the client after modification is:
Here,
is changed from the pixel set of the foreground class only to the set of all pixels.
is defined as follows, after introducing the semantic class probability of the aggregate non-current client:
where
is the set of overall semantic classes,
is the set of semantic classes in client
, and
is the total number of classes. Due to the introduction of different categories of information existing in the data of other clients, the local model of each client learns the relative positions of the features of the local category data and the features of other categories of data in the feature space. In this way, the global model can effectively distinguish different semantic features through the relative positions in the global update and aggregation, and avoid the overlap of different features in the feature space.
3.3. Parallel Gradient Compensation
Using the idea of asynchronous federated learning, the chain constraint that the client can only enter the next round of local training by obtaining globally updated model parameters in synchronous federated learning mode is released, and the parallel between the local training stage and client–server communication stage is realized. The time t of model parameters is defined according to the global perspective of the central server. The central server begins to send model parameters, and the central server receives the model parameters uploaded by each client and updates them to obtain new global model parameters. FedAvg’s client update rules are described as follows:
Take the round
communication as an example, the initial global model parameters of the central server are
the global update obtained at the end of the round is
weighted by the aggregation of the local update results
of all clients. The model parameters
updated locally by the client are obtained by e times of local iterative training. Because the local continuous update and communication are parallel, the global update cannot achieve the
time parameters and gradient information, and can only obtain and use the client-sent t time information. Therefore, local continuous updates need
to be considered for global updates, and to be
as close as possible to the use of the update effect. The update rules are denoted as follows:
Inspired by the delay compensation strategy in asynchronous distributed deep learning training methods, Taylor series expansion and Fisher information matrix are used to alleviate the gradient obsoletion problem, and the task of estimating
by
is realized, namely:
where
is the Hessian matrix. The Hessian matrix is a matrix composed of the second-order partial derivatives of the loss function with respect to the model parameters, in order to improve the problem that the Hessian matrix slows down the calculation speed of the model, an approximate calculation of Hessian matrix is introduced by using Fisher information matrix to realize gradient compensation.
We adopt the method based on Monte Carlo sampling to approximate the Fisher information matrix. The main operation is to calculate the first-order partial derivative of the log-likelihood function with respect to the parameters for the sampled samples, and then perform simple summation and averaging operations. Compared with calculating the Hessian matrix composed of second-order partial derivatives, the amount of calculation is significantly reduced.
For the parameter vector
, the element
of the Fisher information matrix is theoretically defined as:
Among them, is the input data, is the corresponding label, is the distribution of the data, and is the predicted distribution under the given parameter .
However, in the actual calculation, since it is difficult to obtain the true expectations, we approximate the calculation by sampling
samples
from the training dataset. The specific formula is as follows:
This method of sampling approximation is more feasible for calculation. From a theoretical perspective, based on the law of large numbers, when the sample size is large enough, this approximation can approach the true Fisher information matrix relatively well.
3.4. Sparse Analysis
Since the FedAvg method was proposed, most federated learning methods have been using model parameter aggregation to update global model parameters, and the updating of model parameters through the client is mathematically consistent with the gradient updating through the local training of the client. Therefore, using sparse operations to process the transmitted gradient data can achieve a higher compression rate of the data. Ensure that the model can still make critical updates using high-precision gradient data.
In this paper, the Top-k method is introduced and applied to gradient sparse. Its advantage is that k is a controllable threshold, which controls the compression degree of data, and combines environmental factors to achieve sparse rate adaptive data compression.
Top-k sparsity means that only the most important k values are kept in the data, while all other values are set to zero. “Importance” is determined by the absolute value of the data, that is, keeping the k elements with the largest absolute value. This process can be described by formulas (5). Here, is the threshold determined based on the value k after gradient is sorted, is the indicator function, taking the value 1 when the condition is satisfied, and 0 otherwise, and represents the gradient data after sparse. The Top-k sparsity method is used on the transmitted gradient data; only the most important k gradient values are retained, and the other gradient values are set to zero. This is based on the assumption that the absolute value of the gradient can be used as a proxy for its importance and that larger gradient values contribute more to the updating of the model. After using Top-k sparsity, because the gradients that need to be uploaded in each training round become k, the amount of communication data is significantly reduced, and the communication time of each round is shortened, thus speeding up the overall training process. Despite the sparse compression of the data, the Top-k method can still ensure the effectiveness of the model update, because the Top-k method retains the maximum gradient values for transmission, which are considered to be the most important for model improvement.
After Top-k sparsity is added, the training process of federated learning is as follows: First, the model parameters before the client model training start are recorded, and then the local training starts according to the set rules. After the end of the local training phase, the client calculates the gradient data of the model. The data-sparse operation is performed locally on the client. The first k largest gradient values are selected according to the absolute value of the gradient data, and other gradients are set to zero. Only effective gradient information is transmitted during communication to achieve efficient communication.
4. Experiments
4.1. Experimental Settings
4.1.1. Datasets
We perform experiments on two semantically segmented datasets.
Cityscapes [
34] is a large-scale dataset dedicated to the study of urban scene understanding, with a particular focus on semantic understanding tasks related to autonomous driving, with the aim of promoting research progress in the field of autonomous driving and scene understanding. It contains street view images from 50 different cities, covering 30 categories such as roads, vehicles, pedestrians, etc. Because there is less relevant data for some categories, 19 commonly used semantic segmentation classes are generally used for training and evaluation of semantic segmentation networks.
Cambridge Driving tag video database (CamVID) [
35] is an urban street view video sequence dataset publicly released by the University of Cambridge. It is mainly used in the research of road scene analysis and automatic driving. It contains 11 semantic classes and provides detailed pixel-level annotations for images extracted from video sequences.
To simulate the non-IID environment, since the Cityscapes and CamVID datasets are street view semantic segmentation datasets with 19 and 11 semantic classes, respectively, we divide them into 19 and 11 subsets, and each subset contains only one or two semantic classes. For the basic Settings of the federated learning experiment, based on the differences between the two datasets, the model convergence degrees of the global communication rounds on the Cityscapes and CamVID datasets were set to 1500 and 800, respectively. In each round of training, we adopted the strategy of randomly selecting a fixed number of clients in each round. The Cityscapes dataset has a total of 152 clients, and the CamVID dataset has a total of 22 clients. Five clients were randomly selected for each round of both to participate in the communication. This setting is applicable to the three experiments in
Section 4.2,
Section 4.3 and
Section 4.4.
4.1.2. Setup
In this paper, two common metrics are used to evaluate the effectiveness of the semantic segmentation task: MIoU represents the intersection between predicted pixels and ground reality pixels, and averages are taken across all categories. Pixel accuracy (Acc) represents the proportion of correctly classified pixels. All experiments in this chapter are run on Python 3.9.18, Pytorch 2.1.1, and an NVIDIA GeForce RTX 4090 GPU. The batch size is 8, the learning rate is 0.05, and the random client selection strategy is adopted. The gradient descent method is SGD. The activation function is ReLu, and the basic semantic segmentation model is BiseNetV2.
4.2. Experiments on Cross-Client Semantic Correction
We chose FedSeg as the baseline of the experiment. As a representative work of the combination of federated learning and semantic segmentation, this algorithm is systematically compared with classic federated learning methods such as FedAvg and FedProx, and has significant advantages in core indicators such as segmentation accuracy.
FedSS algorithm uses the improved cross-entropy loss function Lcorrected_ce. As shown in
Table 1, compared with Fedag, the MIoU of FedSS on the cityscapes dataset and the camvid dataset improved by 29.65%/29.35%, and the accuracy rate increased by 25.32%/22.10%, respectively. The performance of the model is also slightly improved compared to FedSeg. This shows that the optimized correction behavior of the improved cross-entropy loss function in calculating the loss and aggregation background is helpful to better train the semantic segmentation model in the NO-IID case. By adding the probability of a non-local client semantic class to the loss calculation, we can better handle cases where there are other global classes of client data that are not labeled accordingly.
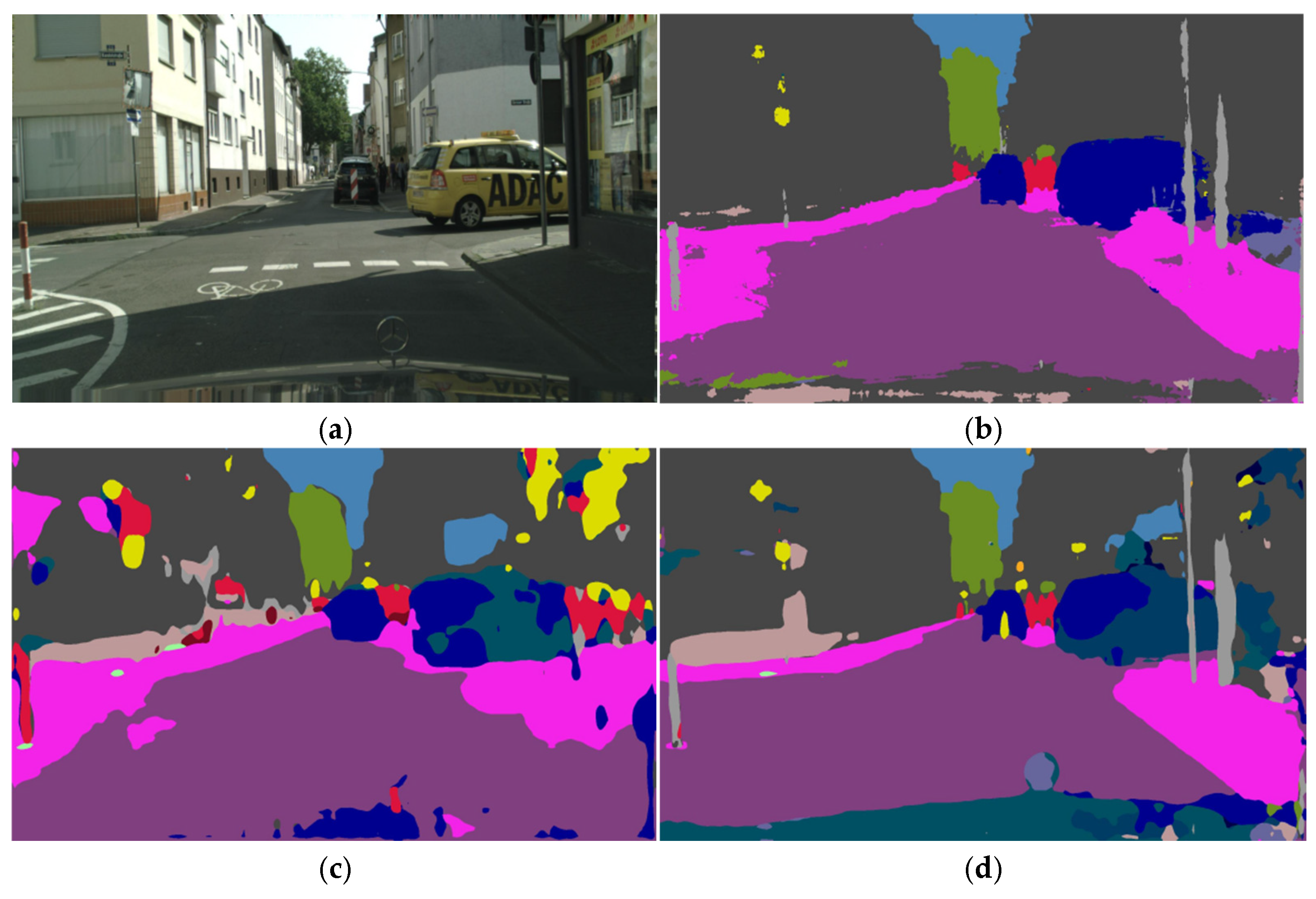
Figure 3 shows the segmentation effect. The model is more accurate and smooth in the division of lanes and sidewalks, and can finely divide traffic signs that block vehicles ahead.
4.3. Experiments on Parallel Gradient Compensation
As can be seen from
Table 2, compared with the FedSeg method, the mIoU and Acc of CP-FedSS increased by 4.11%/2.78% and 1.79%/0.58% in the cityscapes and cammvid datasets. The CP-FedSS method adopts a local continuous update and communication parallel strategy, which shows that the method can improve the performance of the training model to a certain extent. As shown in
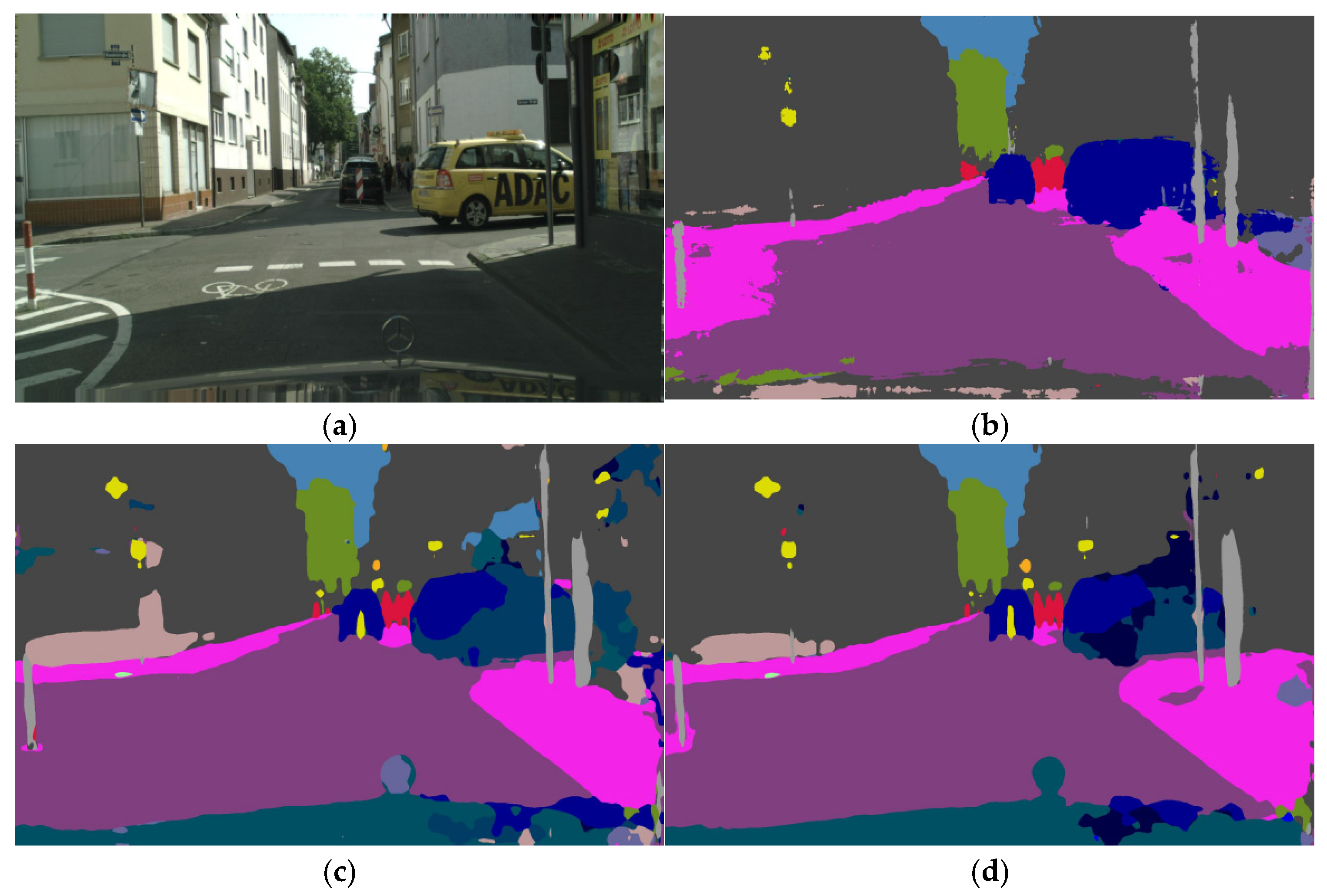
Figure 4, CP-FedSS significantly reduced the incorrect division of building walls, but slightly increased the incorrect division of sidewalks. After careful examination, the method more accurately divided the traffic sign in front of the car, its edge closely matched the shape of the sign, and correctly identified part of the telephone pole below the sign.
4.4. Experiments on the Client Quantity
To study the influence of the number of clients on CP-FedSS, we set up three groups of experiments with different numbers of clients (22, 44, and 55 clients), while keeping other parameters consistent. These parameters include the learning rate, the number of clients selected in each round, and the number of training rounds, based on the CamVID dataset. The experimental results are shown in
Table 3 as follows. For comparison, we also included the performance of FedAvg and FedSeg under the same number of clients.
The experimental results show that when the number of clients increases, different methods perform differently. Although the performance of CP-FedSS shows a downward trend, it is still superior to FedAvg and FedSeg in most cases, demonstrating certain generalization and adaptability. The performance fluctuation of FedAvg is relatively small, and it is not significantly affected by the change in the number of clients, but its improvement ability is limited. The performance of FedSeg continuously decreases with the increase in the number of clients, and its adaptability to changes in data distribution is poor.
The gradient compensation and weighted aggregation mechanism in CP-FedSS have played a positive role in ensuring the convergence stability of the model. However, with the increase in the number of clients, the complex data distribution caused by non-independent co-distribution may be the key factor affecting the performance of CP-FedSS.
4.5. Experiments on Sparsity
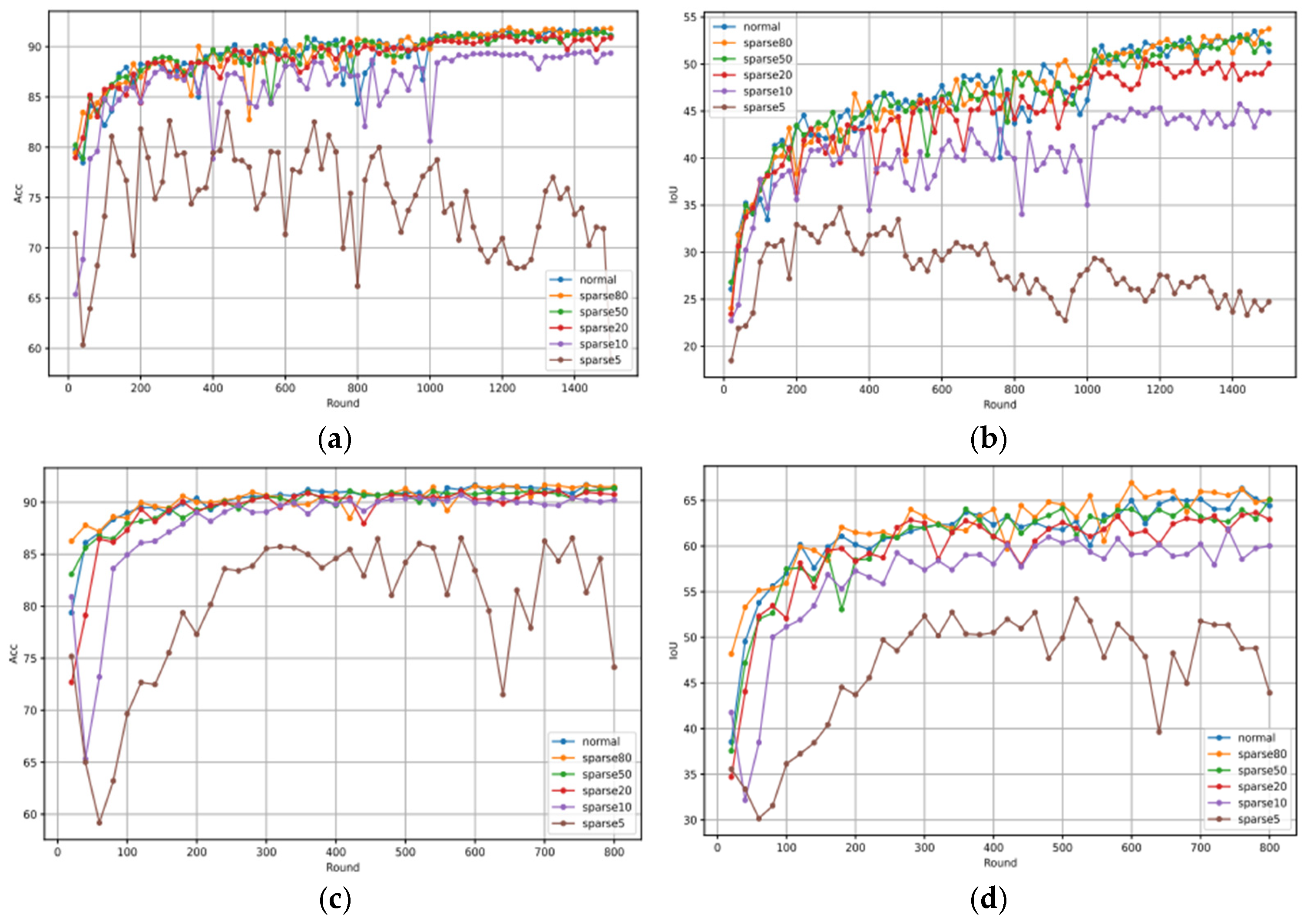
The sparse rate represents the sparse retention rate and the percentage of the transmitted communication data in the original updated data after the updated data to be transmitted is sparse based on the Top-k policy. If the sparsity rate is 80, it means that the amount of communication data transmitted accounts for 80% of the original updated data, and the corresponding experiment is named sparse80a. The sparsity rates were set to 80, 50, 20, 10, and 5.
All experimental results are shown in
Table 4, where normal indicates that the sparsity operation is not used. When the sparsity rate is set to 80, the performance of mIoU and Acc on cityscapes dataset is improved by 2.40% and 0.70% compared with normal datasets, which is slightly improved compared with models without sparsity operation training, because the introduction of appropriate sparsity operation can filter out some redundant information and improve model accuracy. However, in the experiment with a sparsity rate of 20, the performance of the model decreased only slightly compared to the model without the sparsity operation. At the same time, the sparsity rate decreases, and the compression degree of communication data increases. At this point, the performance of the model decreases significantly, indicating that a sparse rate of 10 or less will cause great damage to the model’s performance. This is because a high sparsity rate will cause many important updates to be filtered out, depriving the model of the opportunity to learn some key features.
The performance of the model trained on the CamVID dataset is not significantly different from that of the model trained when the sparsity rate is set to 80, 50, 20, and no sparsity condition, respectively. Similarly, the performance of the training model is best when the sparsity rate is set to 80. This shows that in the low complexity environment, the semantic segmentation model trained by federation learning can accept a higher sparsity rate.
In
Figure 5, the performance trends of sparse80, sparse50, and sparse20 are basically the same as those of normal models without sparse operations, and the sparse10 and 5-trained models show performance bottlenecks before and after early communication rounds. A high sparsity rate will result in the loss of a large amount of key information, which seriously damages the convergence ability of the model.
5. Conclusions
This paper studies the implementation of semantic segmentation task of automatic driving street view under the federal learning and training paradigm, and is committed to solving the impact of problems such as participant data distribution heterogeneity in practical application scenarios on the data heterogeneity and communication performance of the federal learning and training model, so that the data information collected during the operation of intelligent networked vehicles can be fully utilized. Together, we build perceptual models that train high generalization ability. However, there are limitations in this study, and further exploration can be carried out from the following aspects in the future:
In order to solve the waste of local computing resources of participants in the federated learning communication stage, this paper enables participants to carry out parallel local computing in the communication stage. The gradient update after the introduction of parallel is estimated by gradient compensation on the central server, which inevitably introduces errors in the estimation process. The future research direction can be based on the gradient compensation strategy to explore and find an estimation method with less introduction error;
In the process of improving the communication efficiency of federated learning, this paper uses a sparse strategy to compress the upstream communication data of participants to the central server. It is worth noting that in the process of federated learning communication, there is also the downlink communication between the central server and each participant. The downlink communication usually uses the model parameters instead of the update gradient as the transmission data, so the sparse strategy cannot be simply moved to the downlink communication.
Effective strategies to solve this problem can be explored from multiple aspects in the future. For example, model quantization reduces the amount of data transmitted by model parameters by decreasing the representation accuracy of model parameters, while ensuring that the performance loss of the model is acceptable. Weight pruning is to remove the unimportant connection weights in the model, reduce the model size, and thereby lower the communication overhead. The update strategy based on distillation utilizes the knowledge transfer between the teacher model and the student model to optimize the model information received by the client and improve the communication efficiency. These strategies provide potential directions for solving the problem of downlink communication overhead, but the specific implementation details and effects still need further research and verification.
- 3.
At present, the proposed FedSS framework has a strong coupling problem with BiSeNetV2, which limits its application in other segmentation models such as DeepLabV3+ and SegFormer. In the future, we will attempt to reconstruct the loss function to make it independent of the output of a specific model and introduce a universal feature processing module to unify the output feature formats of different models and enhance the compatibility of the framework.
Author Contributions
Conceptualization, Q.C. and L.S.; methodology, Q.C.; software, L.S.; validation, L.S. and Y.Z.; formal analysis, L.S.; investigation, Q.C.; resources, L.S.; data curation, L.S.; writing—original draft preparation, Y.Z.; writing—review and editing, K.P. and P.D.; visualization, L.S.; supervision, W.X.; visualization, D.W.; formal analysis, K.S.; project administration, K.P.; funding acquisition, Q.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Open Topics from the Lion Rock Labs of Cyberspace Security under Project LRL24005, the Natural Science Basic Research Program of Shaanxi (Program No. 2025JC-YBQN-798), the Fundamental Research Funds for the Central Universities, China (Grant no. ZYTS25069) and the Guangdong S&T Program: Guangdong Provincial Key Laboratory of Automotive Electrical and Electronic Architecture (2023) (No. 2023B1212020010).
Data Availability Statement
The original data presented in the study are openly available in Cambridge Driving Tag Video Database (CamVID) at [
35].
Conflicts of Interest
Author Wei Xu and Daihan Wang were employed by the company Guangzhou Automobile Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Non-IID | Non-Independent and Identically Distributed |
| FedSS | Federal Street View Segmentation |
| CP-FedSS | Continuous Parallel Federal Street View Segmentation |
| CE-FedSS | Communication Efficient Federal Street View Segmentation |
| CamVID | Cambridge Driving tag video database |
| MIoU | Mean Intersection over Union |
| Acc | Pixel accuracy |
| SGD | stochastic gradient descent |
| ReLu | Rectified Linear Unit |
References
- Nguyen, A.; Do, T.; Tran, M.; Nguyen, B.X.; Duong, C.; Phan, T.; Tjiputra, E.; Tran, Q.D. Deep Federated Learning for Autonomous Driving. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 1824–1830. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. y Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Kim, J.; Kim, G.; Han, B. Multi-Level Branched Regularization for Federated Learning. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 11058–11073. [Google Scholar]
- Arivazhagan, M.G.; Aggarwal, V.; Singh, A.K.; Choudhary, S. Federated Learning with Personalization Layers. arXiv 2019, arXiv:1912.00818. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 7611–7623. [Google Scholar]
- Li, X.; Jiang, M.; Zhang, X.; Kamp, M.; Dou, Q. Fedbn: Federated Learning on Non-Iid Features via Local Batch Normalization. arXiv 2021, arXiv:2102.07623. [Google Scholar]
- Zhang, J.; Hua, Y.; Wang, H.; Song, T.; Xue, Z.; Ma, R.; Guan, H. Fedala: Adaptive Local Aggregation for Personalized Federated Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11237–11244. [Google Scholar]
- Miao, J.; Yang, Z.; Fan, L.; Yang, Y. Fedseg: Class-Heterogeneous Federated Learning for Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 8042–8052. [Google Scholar]
- Asad, M.; Moustafa, A.; Ito, T.; Aslam, M. Evaluating the Communication Efficiency in Federated Learning Algorithms. In Proceedings of the 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 552–557. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-Cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-Cnn: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Salvador, A.; Bellver, M.; Campos, V.; Baradad, M.; Marques, F.; Torres, J.; Giro-i-Nieto, X. Recurrent Neural Networks for Semantic Instance Segmentation. arXiv 2017, arXiv:1712.00617. [Google Scholar]
- Visin, F.; Ciccone, M.; Romero, A.; Kastner, K.; Cho, K.; Bengio, Y.; Matteucci, M.; Courville, A. Reseg: A Recurrent Neural Network-Based Model for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 41–48. [Google Scholar]
- Shuai, B.; Zuo, Z.; Wang, B.; Wang, G. Dag-Recurrent Neural Networks for Scene Labeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3620–3629. [Google Scholar]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 7262–7272. [Google Scholar]
- Xu, J.; Xiong, Z.; Bhattacharyya, S.P. PIDNet: A Real-Time Semantic Segmentation Network Inspired by PID Controllers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 19529–19539. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Cao, Y.; Xu, J.; Lin, S.; Wei, F.; Hu, H. Gcnet: Non-Local Networks Meet Squeeze-Excitation Networks and Beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019; pp. 1971–1980. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-Local Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. Ccnet: Criss-Cross Attention for Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 603–612. [Google Scholar]
- Qu, L.; Zhou, Y.; Liang, P.P.; Xia, Y.; Wang, F.; Adeli, E.; Fei-Fei, L.; Rubin, D. Rethinking Architecture Design for Tackling Data Heterogeneity in Federated Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10061–10071. [Google Scholar]
- Li, Q.; He, B.; Song, D. Model-Contrastive Federated Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10713–10722. [Google Scholar]
- Condat, L.; Agarskỳ, I.; Malinovsky, G.; Richtárik, P. Tamuna: Doubly Accelerated Federated Learning with Local Training, Compression, and Partial Participation. In Proceedings of the International Workshop on Federated Learning in the Age of Foundation Models in Conjunction with NeurIPS 2023, New Orleans, LA, USA, 16 December 2023. [Google Scholar]
- Ma, C.; Qiu, X.; Beutel, D.; Lane, N. Gradient-Less Federated Gradient Boosting Tree with Learnable Learning Rates. In Proceedings of the 3rd Workshop on Machine Learning and Systems, Rome, Italy, 8 May 2023; pp. 56–63. [Google Scholar]
- Hu, S.; Jiang, L.; He, B. Practical Hybrid Gradient Compression for Federated Learning Systems. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, Jeju, Republic of Korea, 3–9 August 2024; pp. 4147–4155. [Google Scholar]
- Gao, Y.; Islamov, R.; Stich, S.U. EControl: Fast Distributed Optimization with Compression and Error Control. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Huang, W.; Ye, M.; Shi, Z.; Du, B.; Tao, D. Fisher Calibration for Backdoor-Robust Heterogeneous Federated Learning. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 247–265. [Google Scholar]
- Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Brostow, G.J.; Shotton, J.; Fauqueur, J.; Cipolla, R. Segmentation and Recognition Using Structure from Motion Point Clouds. In Proceedings of the Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Proceedings, Part I 10; Springer: Berlin/Heidelberg, Germany, 2008; pp. 44–57. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).