Adaptive Measurement of Space Target Separation Velocity Based on Monocular Vision
Abstract
1. Introduction
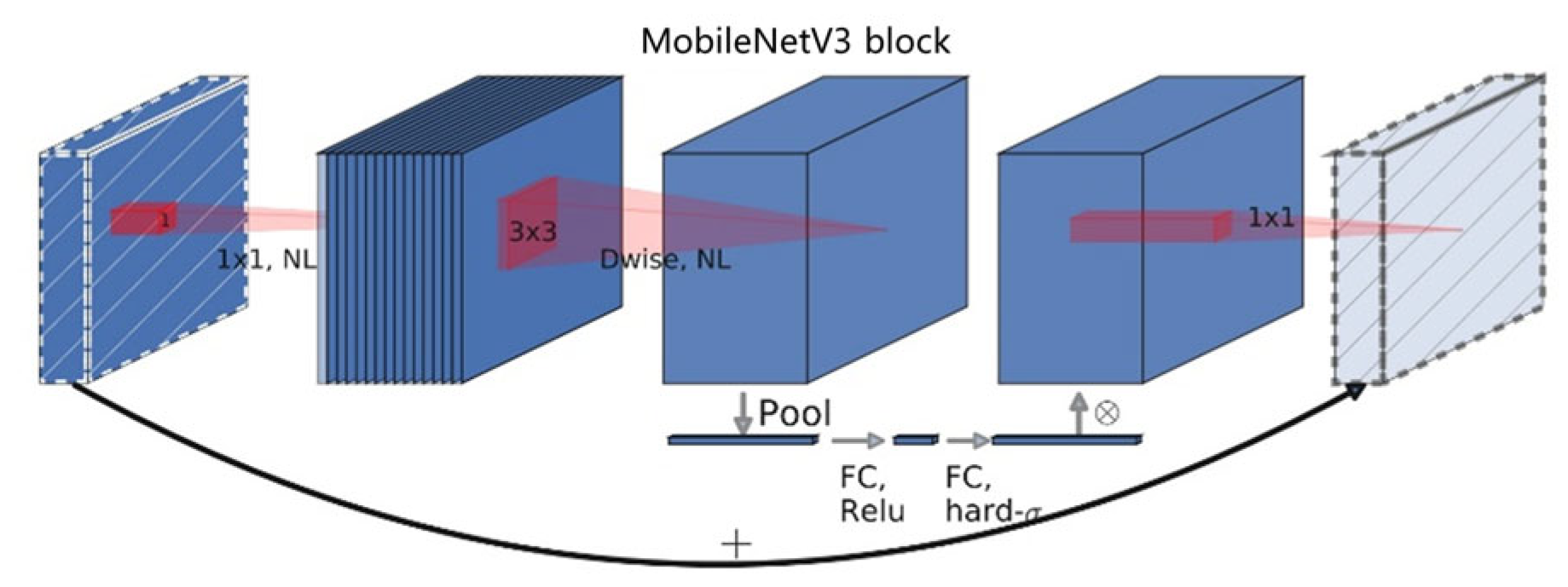
- The MobileNetV3 network of MobileNet series is used to replace the backbone network of YOLOv8_n, which significantly reduces the number of model parameters and the amount of computation.
- The circle fitting algorithm based on RANSAC is improved, and the anti-interference performance and adaptability to various light environments of target circle feature detection are improved.
- The separation velocity is calculated based on monocular vision.
- An experimental platform is built, and additional ground experiments are carried out to verify the correctness of the proposed algorithm.
2. Methods
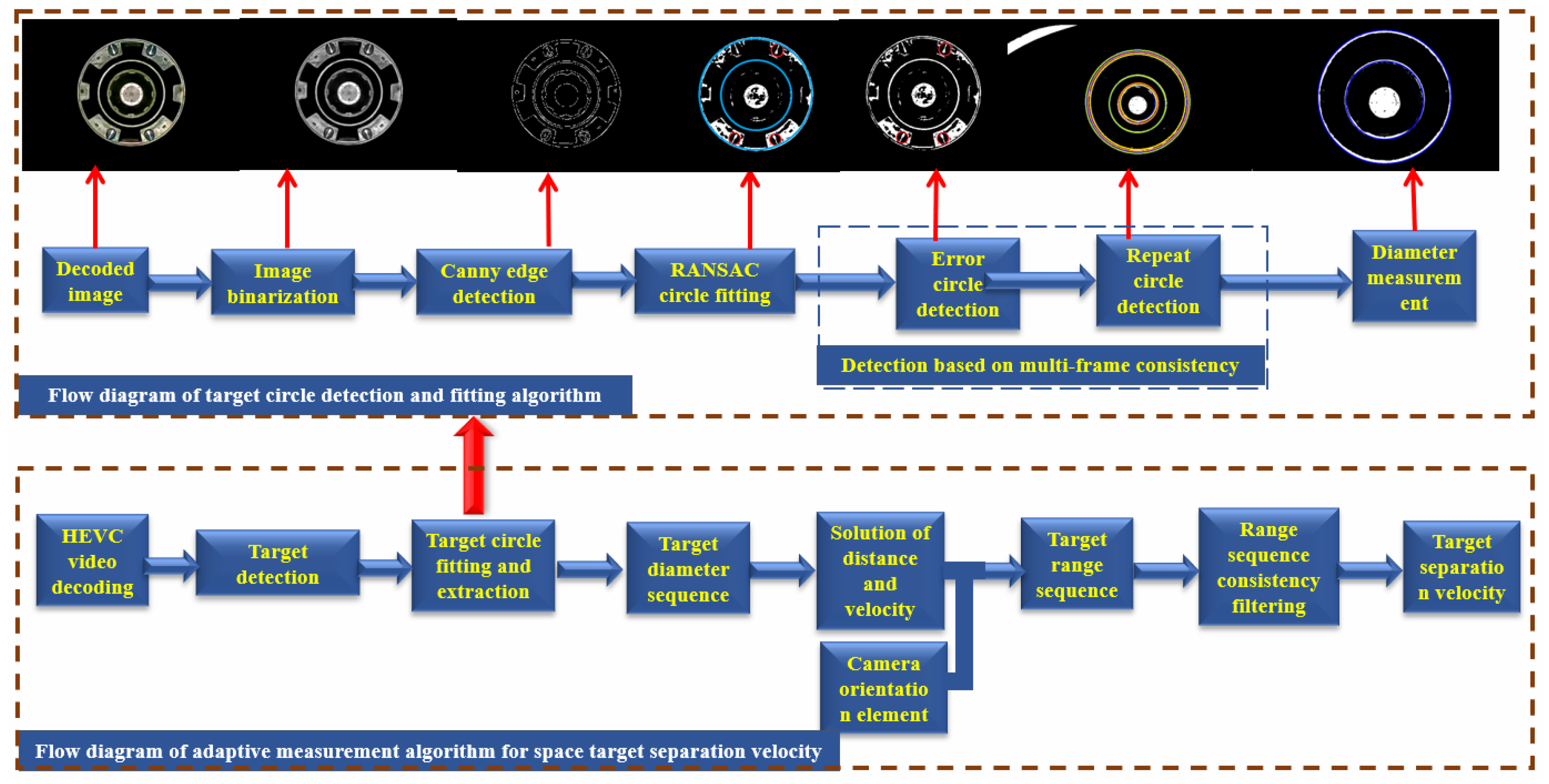
2.1. Algorithm Flow of Space Object Separation Velocity Measurement Based on Monocular Vision
2.2. Target Detection
2.3. Improvement of the Circle Fitting Algorithm Based on Random Sampling Consistency
2.3.1. Video Processing
2.3.2. RANSAC Circle Fitting Based on Multi-Frame Consistency Detection
- Preprocess the detected images and extract edges and establish a point set composed of the coordinates of all edge points. Let the current cycle number be Initialize the inlier point set and the history radius storage queue . Set the initial value of the range of radius and the best model score ;
- Randomly extract 3 points from the boundary point set , calculate the parameters of the circle determined by these 3 points [] (center of the circle (), radius ). If the radius of the circle r is within the pre-set range, then continue to step 3; otherwise, move to step 7;
- Calculate the distance d from each boundary point to the center of the circle obtained in step 2. If abs ( is the acceptable inlier point deviation margin), the point is considered an inlier point, and its coordinates are stored in the inlier point set ; otherwise, it is regarded as an external point;
- Calculate the number for the inlier point set on the circle. If is greater than the threshold , it is considered that the estimated circle model is reasonable enough, and these inlier points can also be regarded as valid points. In this case, continue to step 5.; otherwise move to step 7;
- The parameter model of the circle is recalculated by the least-square method for all points in the point set ;
- If is greater than the best score of the model, update the best fitting model; the best score of the model is updated to ;
- ; if , return the best fit model parameters and finish; otherwise return to step 2.
- The circle radius parameters calculated by the current frame are stored in the radius storage queue of the history frame, and the threshold values of the radius range and are dynamically updated according to the mean plus or minus two times the standard deviation. At the same time, in order to ensure the rationality of the radius range (such as negative values), reasonable boundary values and need to be set.
| Algorithm 1: Circle Fitting By Multi-Frame RANSAC |
| Initial & Input: Edge Points Set: Iterations: Inlinear Set: = 0 Maximum iterations = Threshold of number of effective inlier points = Allowable initial circle radius range = Acceptable distance error threshold Output: ← Queue( )
|
2.3.3. Extraction of the Target Circle

2.4. Separation Velocity Solution Based on Monocular Vision
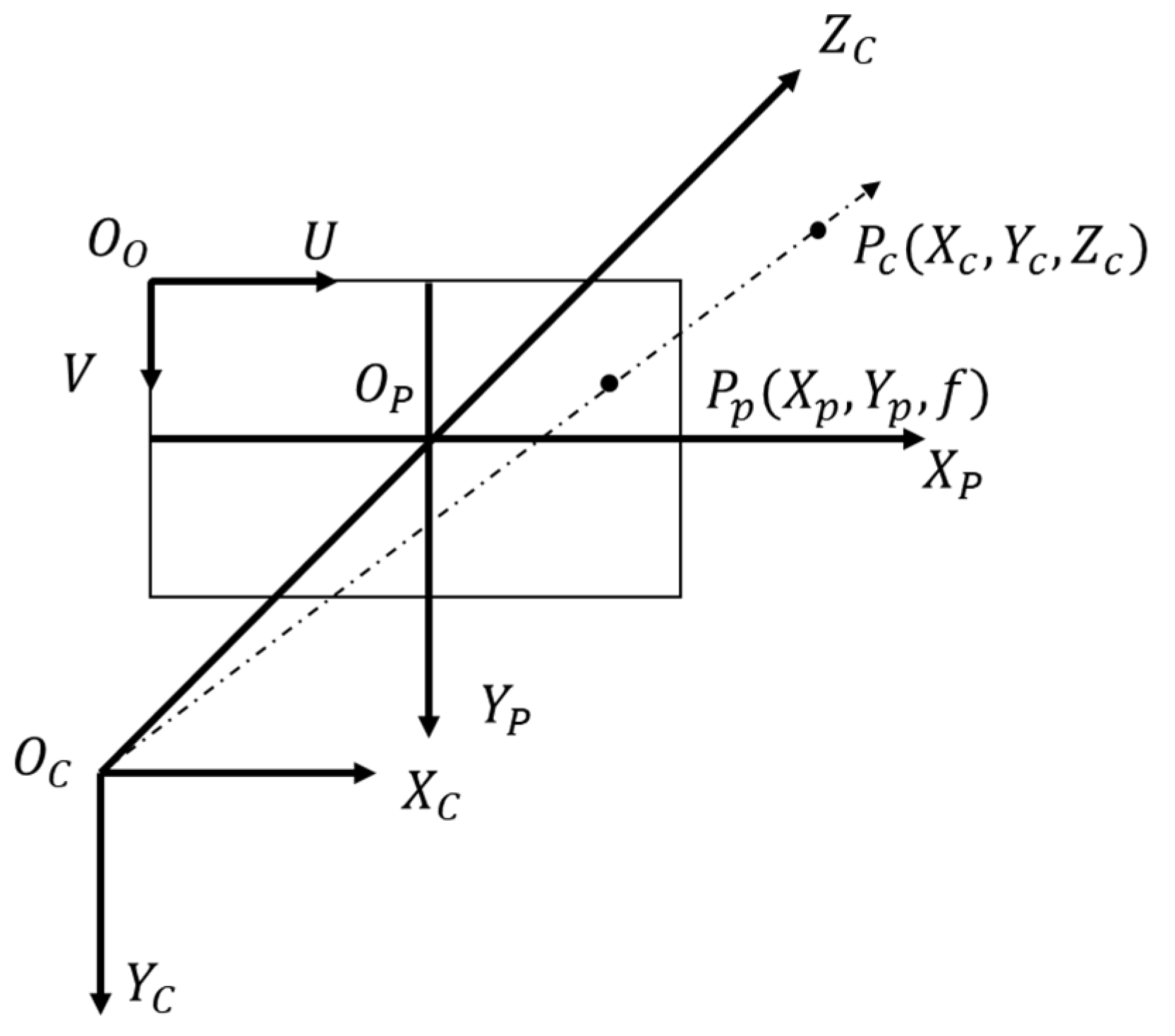
2.4.1. Extraction of the Target Diameter
2.4.2. Solution of the Separation Velocity
3. Analysis of the Experimental Results
3.1. Experimental Results Based on Space-Based Video Verification of the YOLOV8_n Algorithm
3.2. Experimental Results Based on the Space-Based Video
3.2.1. Verification of Circle Detection
3.2.2. Verification of Circle Detection When Using the YOLOV8_n Algorithm
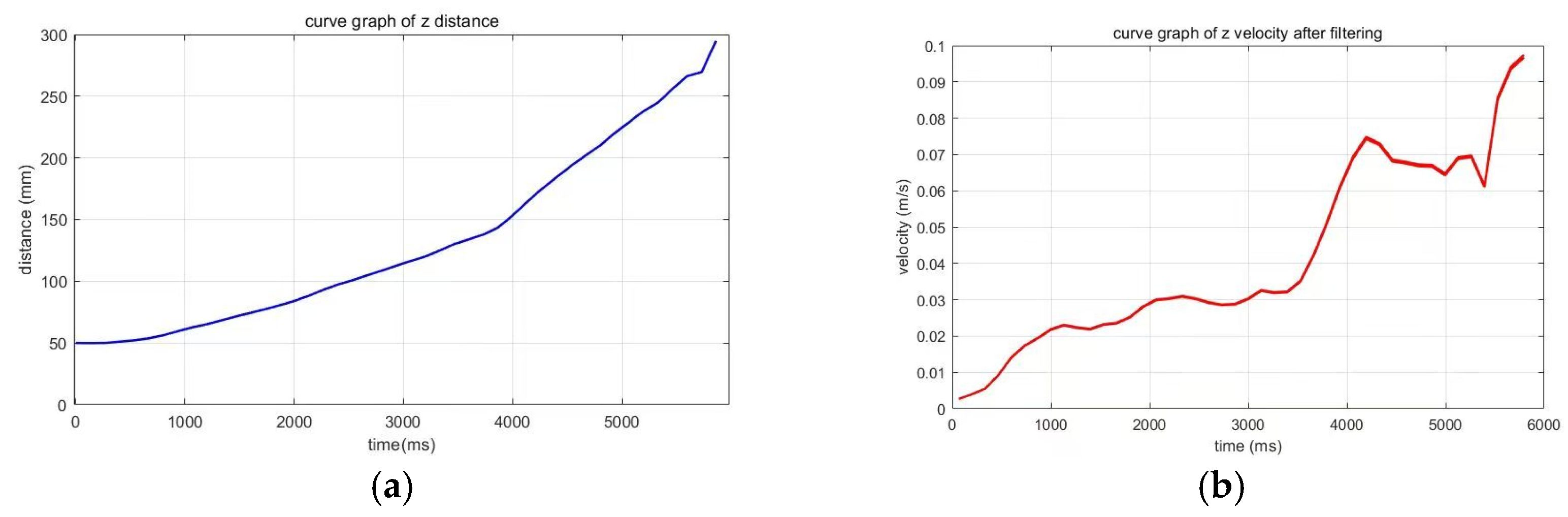
3.2.3. Results of the Velocity Measurement of the Space Target
3.3. Experimental Results Based on Ground Verification
3.3.1. Experimental Environment
3.3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, F.; Xue, Y.; Miu, C.; Hao, H.; Qiao, Z.; Ding, N. Investigation on the Impact of Initial Velocity on Cold Separation Between the Missile and the Booster. Mod. Def. Technol. 2025, 53, 55–65. [Google Scholar]
- Shiquan, Z.; Zhengui, H.; Yongjie, G.; Qizhong, T.; Zhihua, C. Numerical Investigations on Wedge Control of Separation of a Spacecraft from an Aircraft. Def. Sci. J. 2018, 68, 583–588. [Google Scholar]
- Shuling, T.; Rongjie, L.; Ke, X. Investigation of Aeroelasticity Effect on Missile Separation from the Internal Bay. Int. J. Aerosp. Eng. 2023, 2023, 9875622. [Google Scholar] [CrossRef]
- Zhang, S.; Rao, P.; Zhang, H.; Chen, X. Velocity Estimation for Space Infrared Dim Targets Based on Multi-Satellite Observation and Robust Locally Weighted Regression. Remote Sens. 2023, 15, 2767. [Google Scholar] [CrossRef]
- Chen, M.Y.; Su, C.; Chang, Y.H.; Chu, Y. Identification and removal of aircraft clutter to improve wind velocity measurement made with Chung-Li VHF Radar. J. Atmos. Ocean. Technol. 2022, 39, 1217–1228. [Google Scholar] [CrossRef]
- Pellegrini, C.C.; Moreira, E.D.O.; Rodrigues, M.S. New analytical results on the study of aircraft performance with velocity dependent forces. Rev. Bras. Ensino Física 2022, 44, e20210410. [Google Scholar] [CrossRef]
- Wilhelm, P.; Eggert, M.; Oertel, S.; Hornig, J. Mobile system for wind velocity measurement. Tm-Tech. Mess. 2023, 90, 595–603. [Google Scholar] [CrossRef]
- Shi, A.; Li, H.; Shi, W. Infrared characteristics of Hypersonic cruise vehicles in Near Space. J. Ornol. 2022, 043, 796–803. [Google Scholar]
- Poltavskiy, A.V.; Tyugashev, A.A. Optimization of the Information and Measurement System of An Unmanned Aircraft. Reliab. Qual. Complex Syst. 2022, 4, 44–55. [Google Scholar] [CrossRef]
- Li, X.; Sun, D.; Cao, Z. Mitigation method of acoustic doppler velocity measurement bias. Ocean Eng. 2024, 306, 118082. [Google Scholar] [CrossRef]
- Yu, Z.; Shen, G.; Zhao, Z.; Wu, Z.; Liu, Y. An improved method of concentric circle positioning in visual measurement. Opt. Commun. 2023, 544, 129620. [Google Scholar] [CrossRef]
- Jia, G.; Yin, P.; Shao, S. Near-field frequency domain imaging algorithm for diagnosing electromagnetic scattering characteristics of aircraft. J. Natl. Univ. Def. Technol. 2024, 045, 10–19. [Google Scholar]
- Yu, C.; Zhang, L. Research on distance and speed measurement method of vehicle ahead based on deep learning. Comput. Inf. Technol. 2023, 31, 5–8+42. [Google Scholar] [CrossRef]
- Zheng, L.; Liu, L.; Lu, J.; Tian, J.; Cheng, Y.; Yin, W. Research on distance measurement of vehicles in front of campus patrol vehicles based on monocular vision. Pattern Anal. Appl. 2024, 27, 146. [Google Scholar] [CrossRef]
- Xu, Z.; Lin, Z.; Xu, M.; Huang, F. Single image distance information analysis model. J. Shenyang Univ. (Nat. Sci. Ed.) 2021, 33, 88–95. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, X.; Huo, J. Attitude measurement of ultraclose-rangespacecraft based on improved YOLOv5s andadaptive Hough circle extraction. Appl. Opt. 2024, 63, 1364–1376. [Google Scholar] [CrossRef]
- He, L. Research on Depth Measurement of Monocular Visual Image. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2018. [Google Scholar]
- Guo, Y.; Guo, G.; Jia, R.; Wang, Z.; Li, L. Separated Image Analysis Method based on Monocular Vision. Missiles Space Veh. 2022, 4, 130–133. [Google Scholar]
- Liu, Z.; Li, Y.; Wang, C.; Liu, L.; Guan, B.; Shang, Y.; Yu, Q. AstroPose: Astronaut pose estimation using a monocular camera during extravehicular activities. Sci. China-Technol. Sci. 2024, 67, 1933–1945. [Google Scholar] [CrossRef]
- Lu, R.; Zhang, G.; Cao, J.; Chen, W.; Guo, H.; Zhang, H.; Zhang, Z.; Mei, C.; Guan, L. Research on measurement technology of rocket recovery height based on monocular vision. Opt. Precis. Eng. 2024, 32, 2166–2188. [Google Scholar] [CrossRef]
- Zhou, S.; Li, L.; Zhang, W.; Ju, Y.; Zhang, Z.; Wang, T.; Su, Z.; Zhang, D. Position determination of strain gauges and applications based on videometrics. J. Exp. Mech. 2023, 38, 176–184. [Google Scholar]
- Wang, X.; Cui, W.; Li, J.; He, Y.; Li, H. A method to correct catalog orbit determination velocity. Mech. Eng. 2020, 42, 163–169. [Google Scholar]
- Jiang, L. A fast and accurate circle detection algorithm based on random sampling—ScienceDirect. Future Gener. Comput. Syst. 2021, 123, 245–256. [Google Scholar] [CrossRef]
- Ou, Y.; Deng, H.; Liu, Y.; Zhang, Z.; Ruan, X.; Xu, Q.; Peng, C. A Fast Circle Detection Algorithm Based on Information Compression. Sensors 2022, 22, 7267. [Google Scholar] [CrossRef] [PubMed]
- Jocher, G.; Qiu, J. YOLO by Ultralytics. DB/OL. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 25 December 2024).
- Han, Y.; Liu, X.; Wang, X.; Wang, S.; Qi, P.; Dou, D.; Wang, Q.; Zhang, Q. Cloth Flaw Detection Method for Improving YOLOv5, Involves Obtaining Rgb Image of Cloth from the Data Set, Training Se-YOLOv5 Model, Importing Rgb Image Into Trained SEYOLOv5 Model for Defect Detection, and Outputting Detection Result. CN115700741-A, 7 February 2023. [Google Scholar]
- Ye, X.; Han, Z.; Zhou, Y.; Zuo, J.; Cheng, J.; Mu, C.; Chen, Q. Method for Diagnosing Fault of Photovoltaic Component Based on MobileNetV3, Involves Inputting Data To-Be-Detected to Target MobileNetV3 Network Model, and Outputting Different Diagnosis Result and Corresponding Frequency. CN117274680-A, 22 December 2023. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. arXiv 2019, arXiv:1905.02244. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Li, X.; Kong, Y. Human Face Living Body Detection Method Combining Attention Mechanism and Residual Network Involves Using Trained Se-Resnet50 Network Model to Detect Face. CN114648815-A, 21 June 2022. [Google Scholar]
- Luo, Y.; Huang, W.; Wu, J.; Li, W. Ransac Algorithm Based Robust Machine Learning Meta-Algorithm Classifier Construction Method, Involves Determining Classifier Model with Samples as Final Selected Classifier Model, and Calculating Corresponding Classification Accuracy. CN108090512-A, 29 May 2018. [Google Scholar]
- Wang, Z. Method for Correcting Monocular Vision Scale in a Vehicle, Involves Determining Actual Value of Distance Between First Locating Point and Second Locating Point, and Correcting Scale of Monocular Vision Map Based on Proportional Relation. CN112102406-A, 18 December 2020. [Google Scholar]
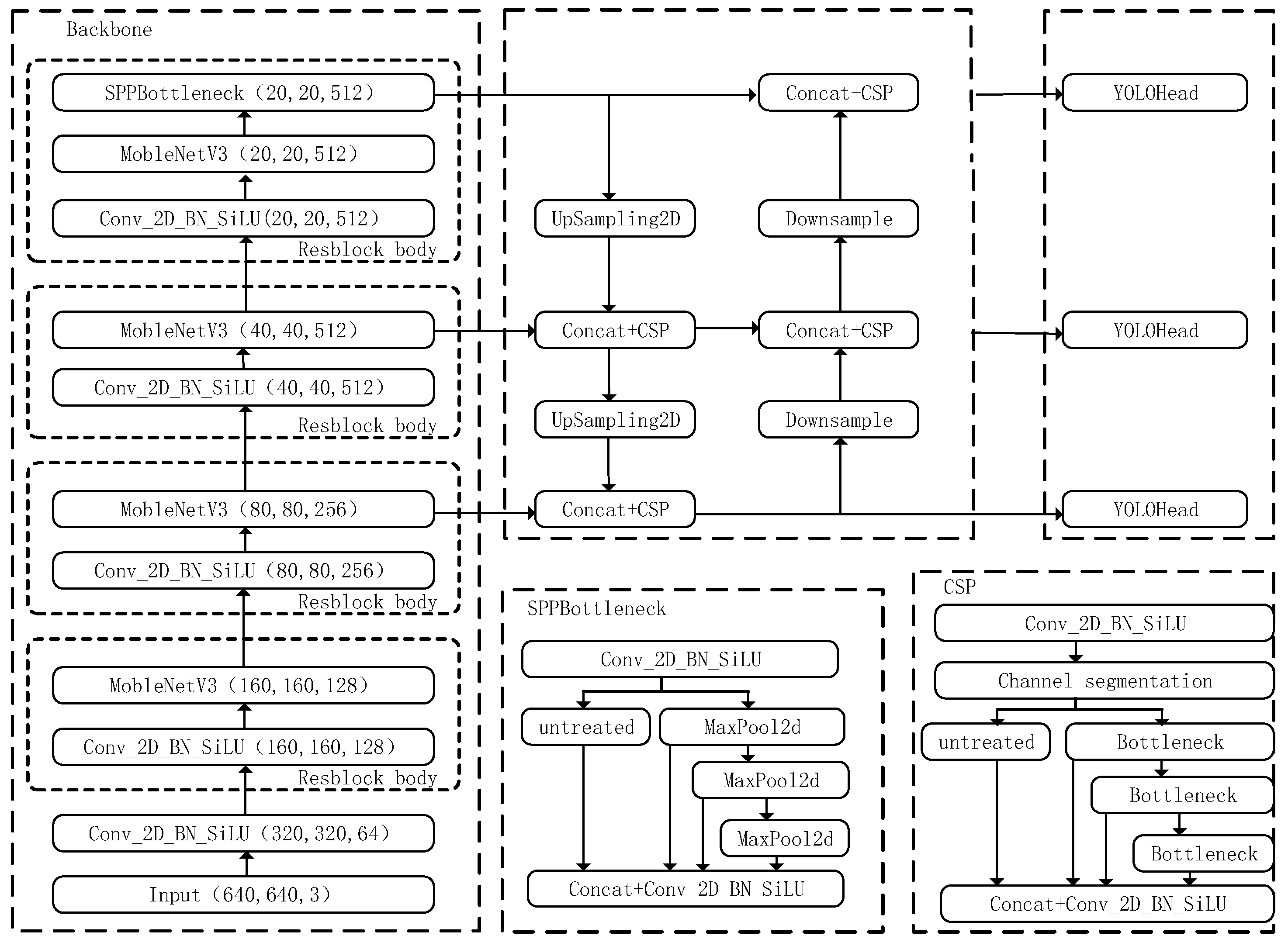








| Stage | Input | Operator | Exp_Size | Output |
|---|---|---|---|---|
| MobileNetV3 (160,160,128) | 160 × 160 × 128 | Conv1 + DWConv + SE + Conv2 | 256 | 160 × 160 × 128 |
| MobileNetV3 (80,80,256) | 80 × 80 × 256 | Conv1 + DWConv + SE + Conv2 | 512 | 80 × 80 × 256 |
| MobileNetV3 (40,40,512) | 40 × 40 × 512 | Conv1 + DWConv + SE + Conv2 | 1024 | 40 × 40 × 512 |
| MobileNetV3 (20,20,512) | 20 × 20 × 512 | Conv1 + DWConv + SE + Conv2 | 1024 | 20 × 20 × 512 |
| Model | mAP/% | GFLOPs | Params/M |
|---|---|---|---|
| YOLOv8_n | 99.13 | 8.1 | 3.1 |
| YOLOv8_n+ MobileNetV3 | 98.86 | 4.8 | 1.7 |
| Model | mAP/% | GFLOPs | Params/M |
|---|---|---|---|
| YOLOv5_n | 94.73 | 4.5 | 1.9 |
| SSD-ResNet50 | 92.65 | 35 | 23.6 |
| YOLOv7-tiny | 95.63 | 13.2 | 6.2 |
| YOLOX_nano | 97.48 | 1.7 | 1.9 |
| YOLOv8_n | 99.13 | 8.1 | 3.1 |
| YOLOv8_n+ MobileNetV3 | 98.86 | 4.8 | 1.7 |
| Number | RANSAC | Time/FPS (ms) |
|---|---|---|
| 1 | Improved RANSAC | 1043 |
| 2 | Improved YOLOv8_n + Improved RANSAC | 42 + 648 |
| Number | Time (ms) | Actual Distance (mm) | Measured Distance (mm) | Error (mm) | Error (Error/Actual Distance) % |
|---|---|---|---|---|---|
| 1 | 0 | 50 | 50 | 0 | 0 |
| 2 | 500 | 55 | 54 | +1 | 1.8 |
| 3 | 1000 | 60 | 60 | 0 | 0 |
| 4 | 2000 | 80 | 82 | −2 | 2.5% |
| 5 | 3000 | 120 | 118 | +2 | 1.67% |
| 6 | 4000 | 150 | 153 | −3 | 2% |
| 7 | 5000 | 225 | 226 | −1 | 0.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ai, H.; He, Z.; Liu, D.; Cao, J.; Mei, C. Adaptive Measurement of Space Target Separation Velocity Based on Monocular Vision. Electronics 2025, 14, 2137. https://doi.org/10.3390/electronics14112137
Zhang H, Ai H, He Z, Liu D, Cao J, Mei C. Adaptive Measurement of Space Target Separation Velocity Based on Monocular Vision. Electronics. 2025; 14(11):2137. https://doi.org/10.3390/electronics14112137
Chicago/Turabian StyleZhang, Haifeng, Han Ai, Zeyu He, Delian Liu, Jianzhong Cao, and Chao Mei. 2025. "Adaptive Measurement of Space Target Separation Velocity Based on Monocular Vision" Electronics 14, no. 11: 2137. https://doi.org/10.3390/electronics14112137
APA StyleZhang, H., Ai, H., He, Z., Liu, D., Cao, J., & Mei, C. (2025). Adaptive Measurement of Space Target Separation Velocity Based on Monocular Vision. Electronics, 14(11), 2137. https://doi.org/10.3390/electronics14112137






