Synthetic-Aperture Passive Localization Utilizing Distributed Phased Moving-Antenna Arrays
Abstract
:1. Introduction
2. SADPA Framework and Signal Model
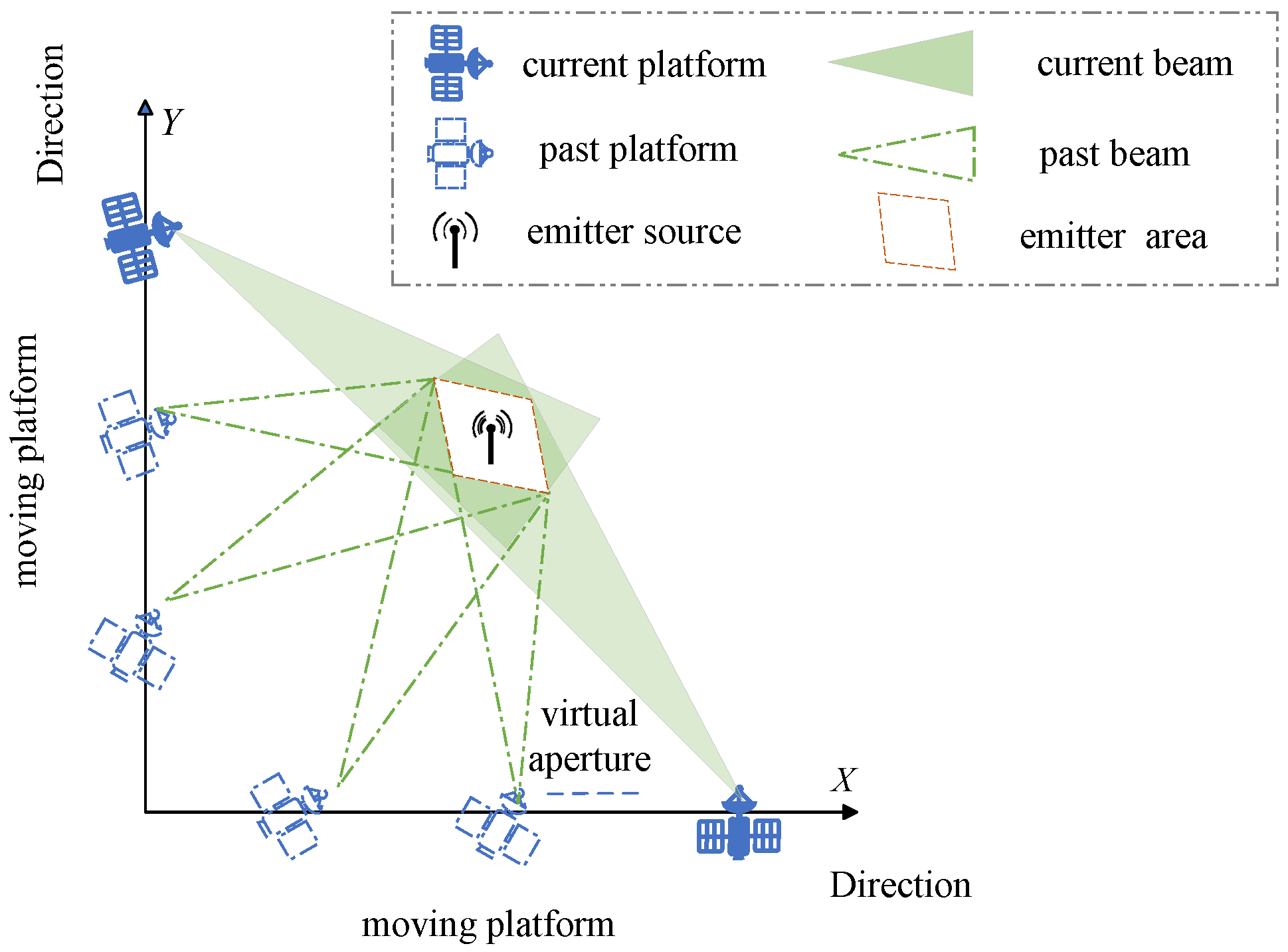
2.1. Localization Scenario
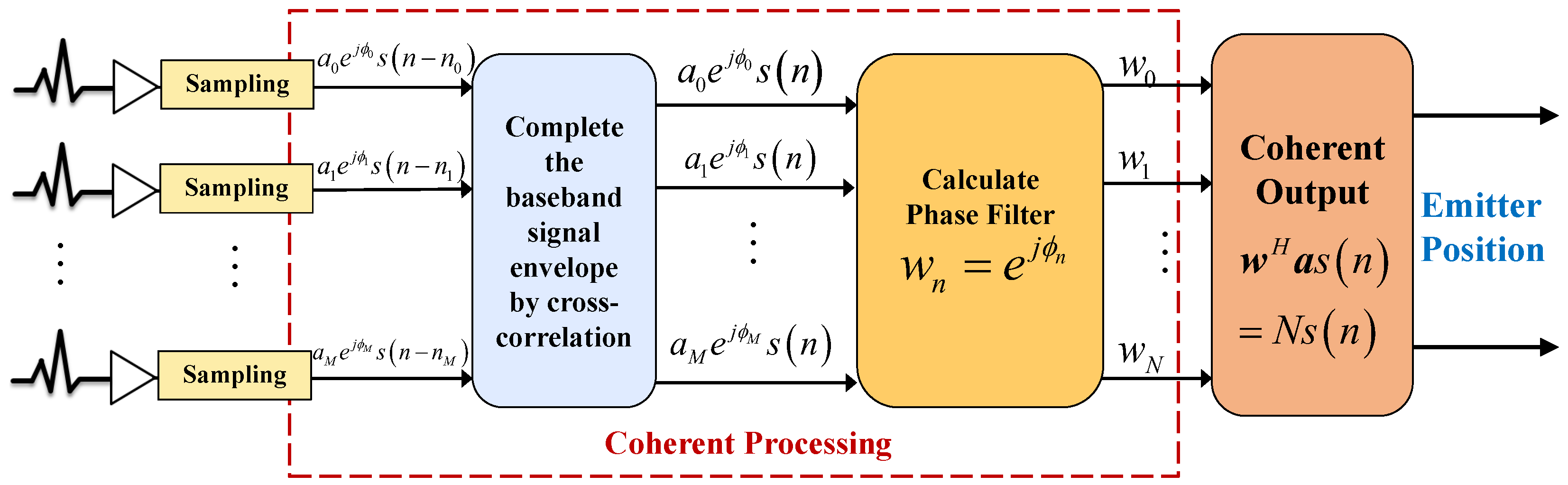
2.2. Signal Processing and Framework of DPAA System
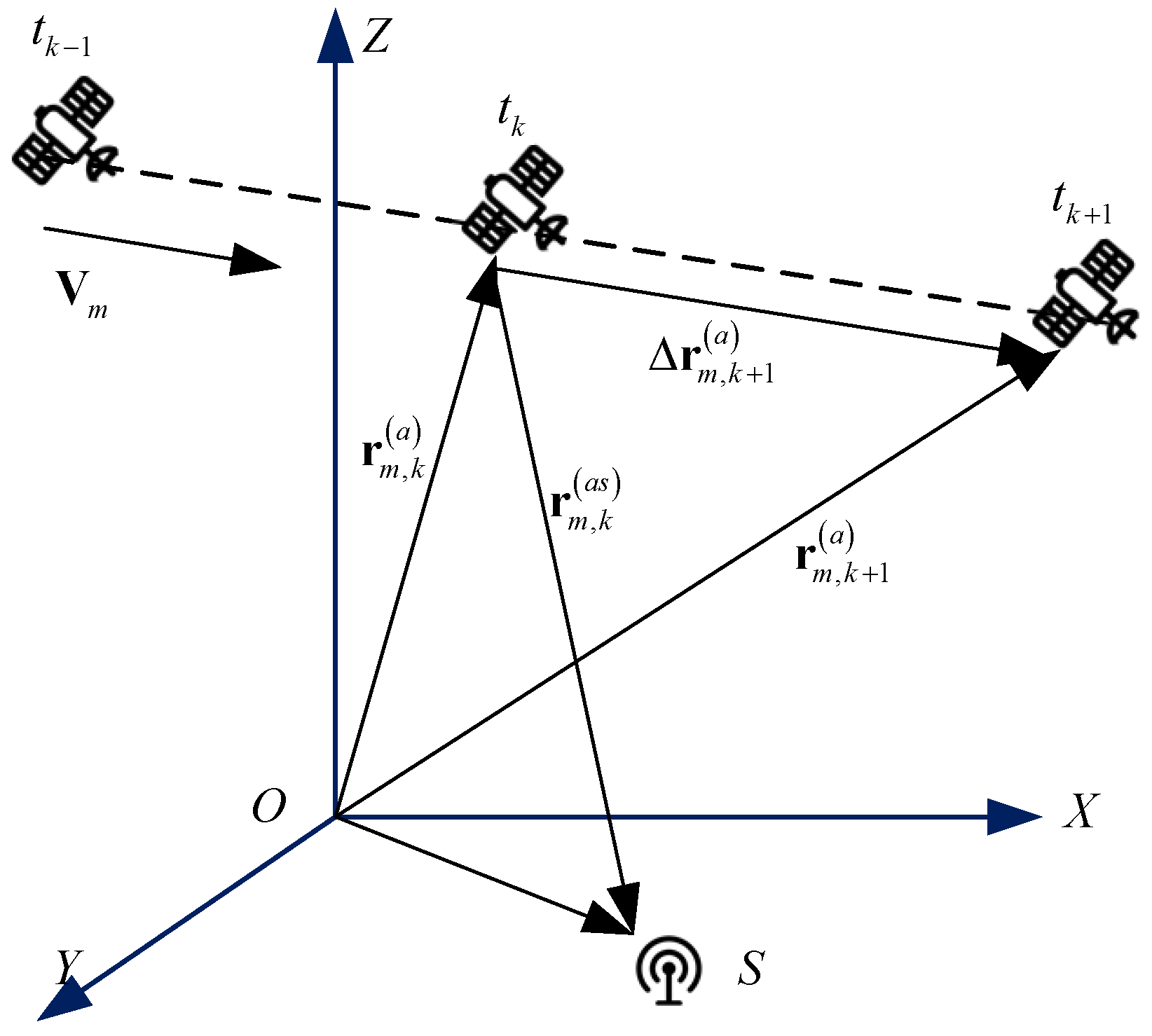
2.3. Signal Model of SADPA System
3. Localization Algorithm Utilizing SADPA
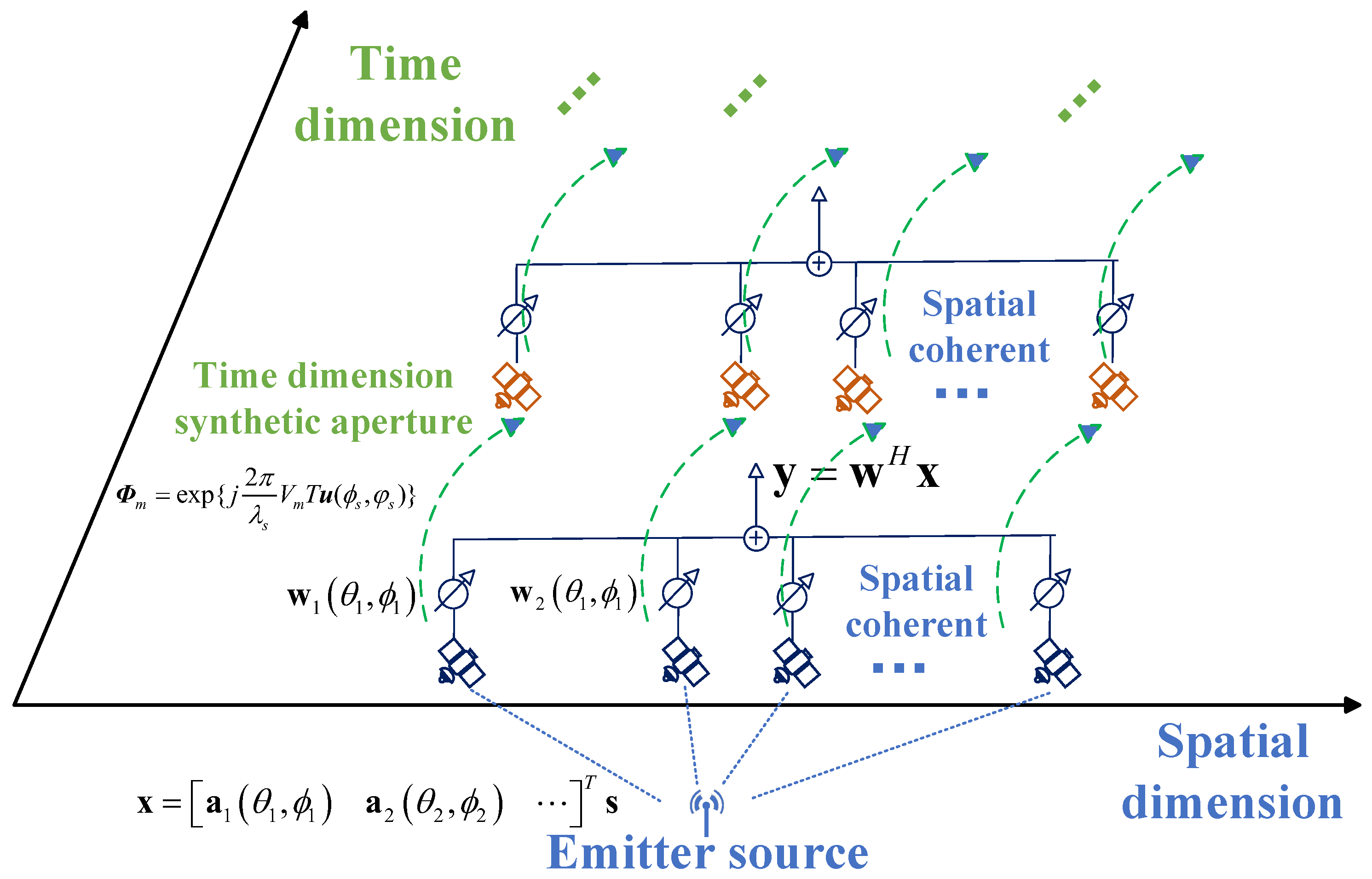
3.1. Long-Synthetic-Aperture Localization Algorithm for Distributed Moving Platforms
3.2. Long Synthetic Aperture Based on Motion Compensation
3.3. Improved MUSIC-DPD Algorithm
| Algorithm 1 The steps of the improved MUSIC-DPD algorithm for the SADPA system. |
1: Sample and share received signals, and define emitter region of interest. 2: while All the grids are calculated do 3: Fix a searching grid region, construct the factor . 4: Construct the compensated sample . 5: Obtain the spectrum power by (19). 6: Search and calculate next gird region. 7: end while 8: return emitter source position. |
3.4. CRB of the Proposed Method
4. Performance Analysis
4.1. Simulation Environment Parameters
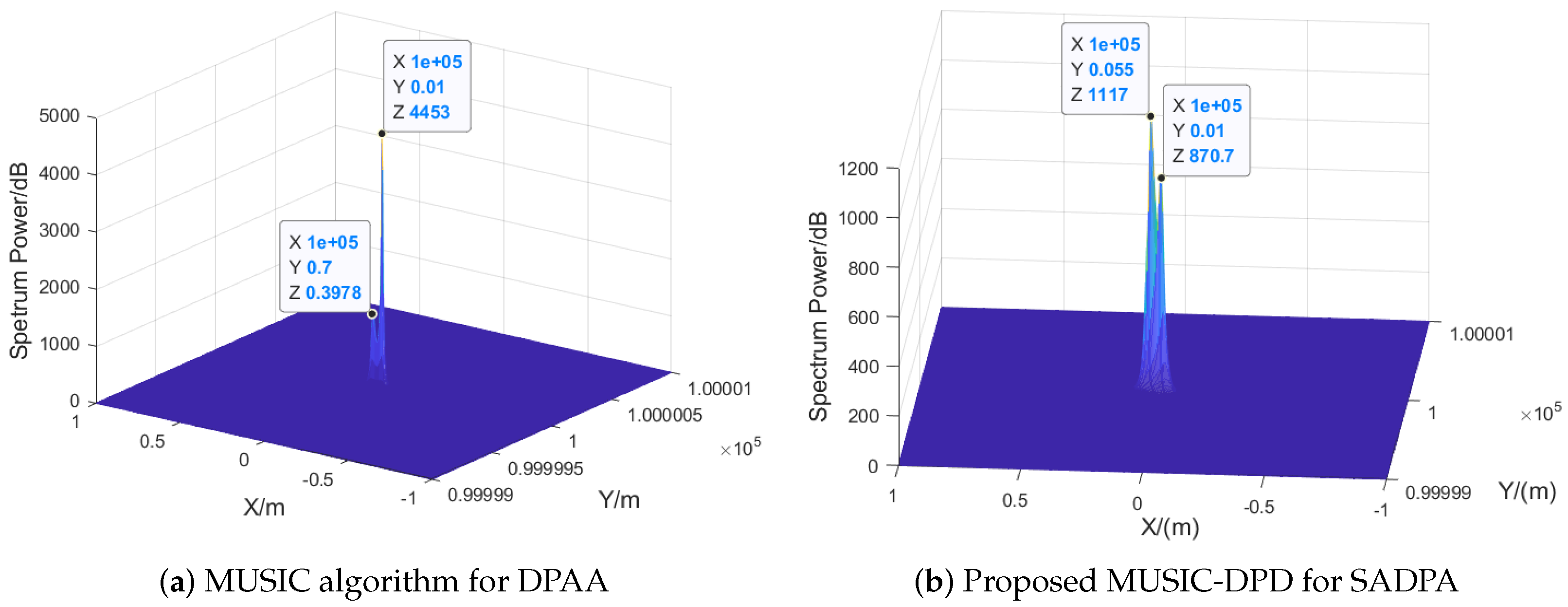
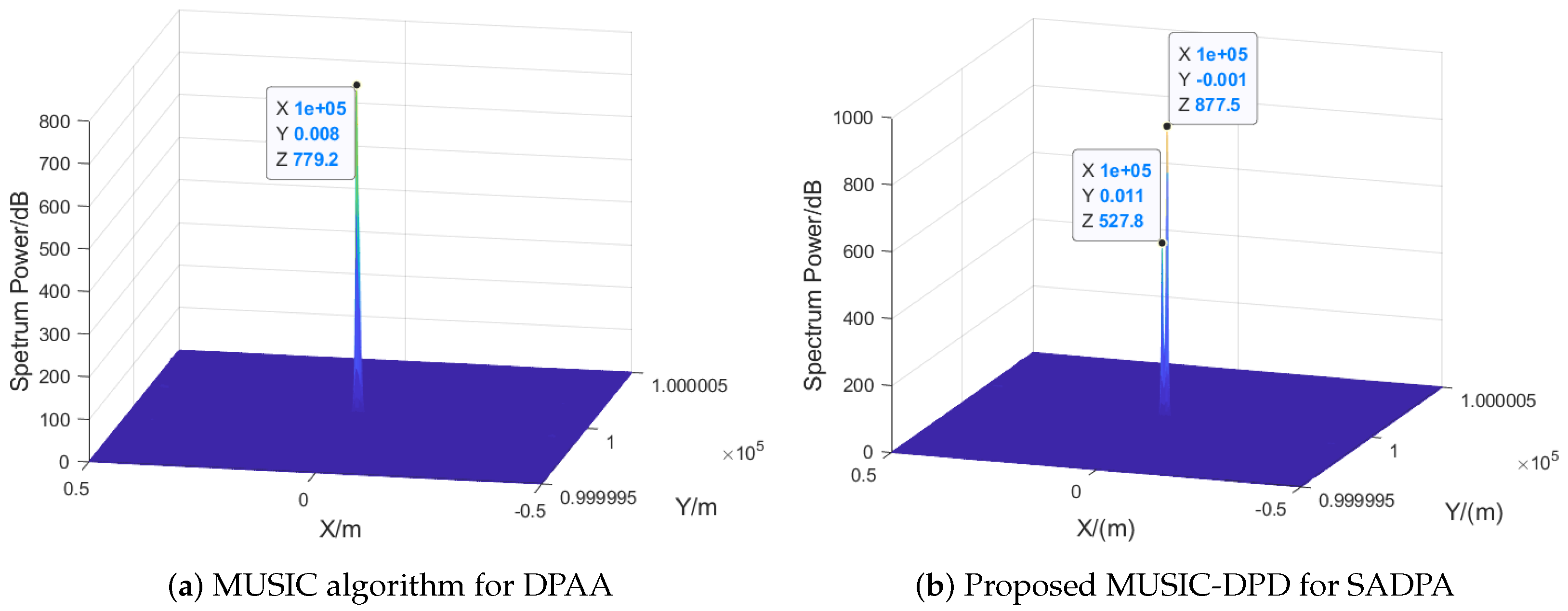
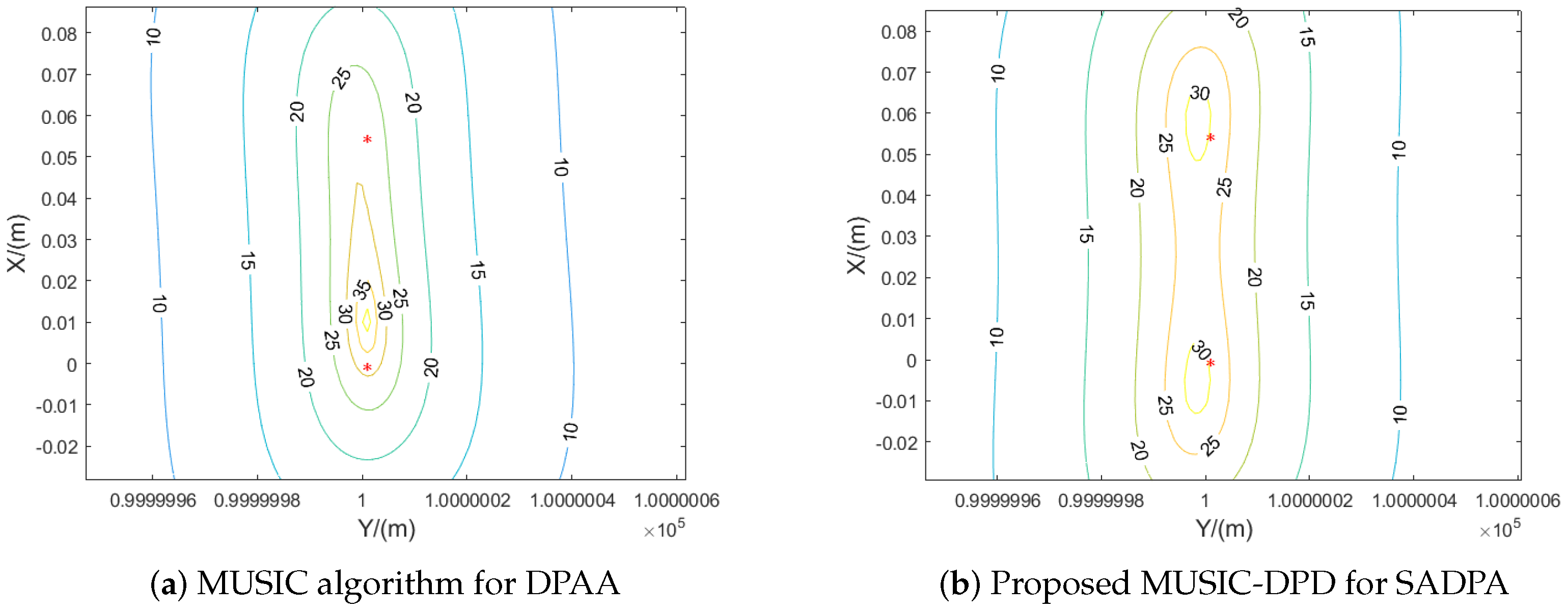
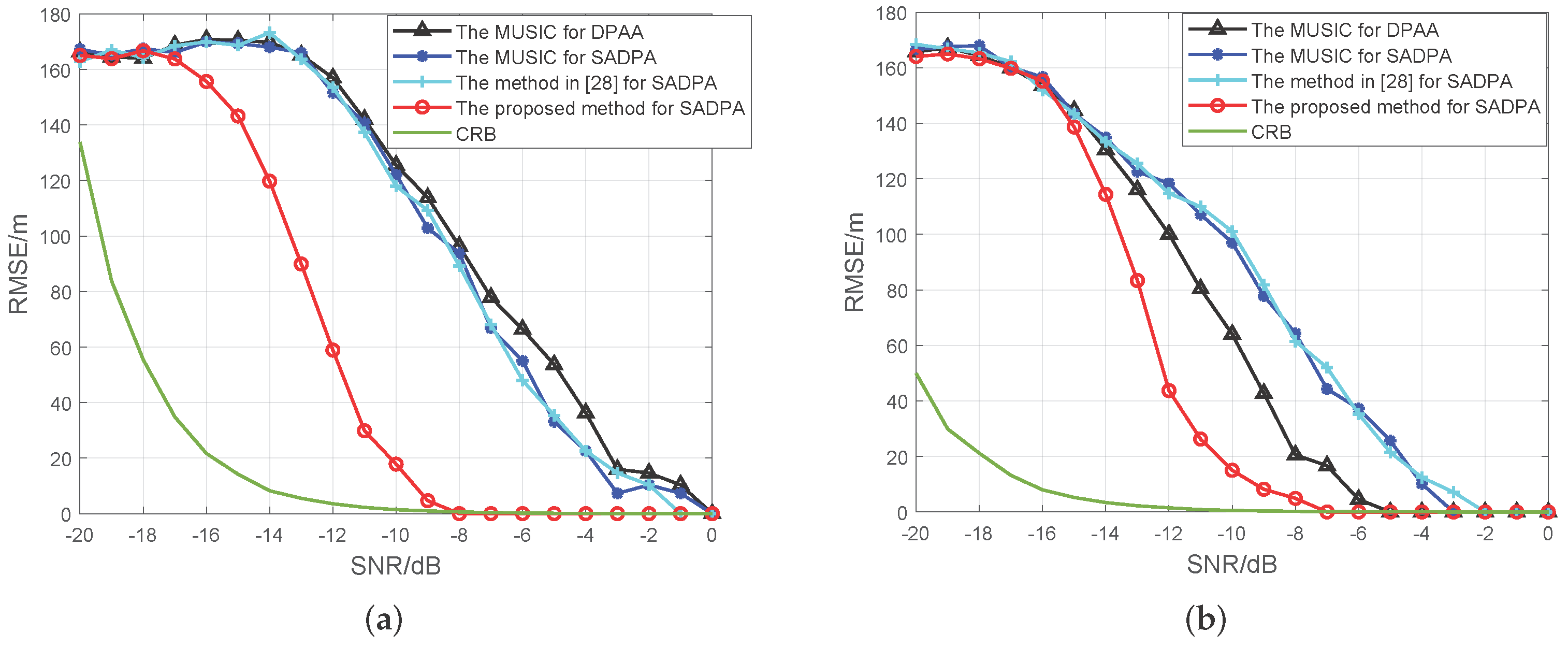
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jung, D.H.; Kim, D.H.; Azim, M.T.; Park, J.; Park, S.O. A novel signal processing technique for Ku-band automobile FMCW fully polarimetric SAR system using triangular LFM. IEEE Trans. Instrum. Meas. 2020, 70, 1–10. [Google Scholar] [CrossRef]
- Renga, A.; Graziano, M.D.; Moccia, A. Formation flying SAR: Analysis of imaging performance by array theory. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 1480–1497. [Google Scholar] [CrossRef]
- Huang, L.; Liu, G. Convolutional feature aggregation network with self-supervised learning and decision fusion for SAR target recognition. IEEE Trans. Instrum. Meas. 2024, 73, 2526714. [Google Scholar] [CrossRef]
- Renga, A.; Gigantino, A.; Graziano, M.D. Multi-Platform Image Synthesis for Distributed Synthetic Aperture Radar in Long Baseline Bistatic Configurations. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9267–9284. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5034–5055. [Google Scholar] [CrossRef]
- Lombardo, P.; Pastina, D.; Turin, F. Ground moving target detection based on MIMO SAR systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5081–5095. [Google Scholar] [CrossRef]
- Yeredor, A.; Angel, E. Joint TDOA and FDOA estimation: A conditional bound and its use for optimally weighted localization. IEEE Trans. Signal Process. 2010, 59, 1612–1623. [Google Scholar] [CrossRef]
- Cao, S.; Chen, X.; Zhang, X.; Chen, X. Combined weighted method for TDOA-based localization. IEEE Trans. Instrum. Meas. 2019, 69, 1962–1971. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, J.; Liu, H.; Ho, K.; Yang, Z.; Gao, S. Optimal Sensor Placement and Velocity Configuration for TDOA-FDOA Localization and Tracking of a Moving Source. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8255–8272. [Google Scholar] [CrossRef]
- Hassan, E.S.; Alharbi, A.A.; Oshaba, A.S.; El-Emary, A. Enhancing smart irrigation efficiency: A new WSN-based localization method for water conservation. Water 2024, 16, 672. [Google Scholar] [CrossRef]
- Weiss, A.J. Direct position determination of narrowband radio frequency transmitters. IEEE Signal Process. Lett. 2004, 11, 513–516. [Google Scholar] [CrossRef]
- Lin, C.; Huang, C.; Su, Y. A coherent signal processing method for distributed radar system. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; pp. 2226–2230. [Google Scholar]
- Weiss, A.J.; Amar, A. Direct position determination of multiple radio signals. EURASIP J. Adv. Signal Process. 2005, 2005, 653549. [Google Scholar] [CrossRef]
- Cuomo, K.; Coutts, S.; McHarg, J.; Pulsone, N.; Robey, F. Wideband aperture coherence processing for next generation radar (NexGen). MIT Linc. Lab. 2004, 2, 810-005. [Google Scholar]
- Fletcher, A.S.; Robey, F.C. Performance bounds for adaptive coherence of sparse array radar. In Proceedings of the 12th Annual Workshop on Adaptive Sensor Array Processing, Lexington, MA, USA, 16–18 March 2004. [Google Scholar]
- Zeng, T.; Yin, P.; Liu, Q. Wideband distributed coherent aperture radar based on stepped frequency signal: Theory and experimental results. IET Radar Sonar Navig. 2016, 10, 672–688. [Google Scholar] [CrossRef]
- Zhang, Z.; Meng, W.; Song, M.; Zhao, Z.; Li, F.; Feng, X.; Zhao, Y. Multi-domain extended ELM-DOA subarray localization method based on distributed coherent aperture radar. IEEE Trans. Veh. Technol. 2023, 73, 3469–3484. [Google Scholar] [CrossRef]
- Oispuu, M.; Nickel, U. 3D passive source localization by a multi-array network: Noncoherent vs. coherent processing. In Proceedings of the 2010 International ITG Workshop on Smart Antennas (WSA), Bremen, Germany, 23–24 February 2010; pp. 300–305. [Google Scholar]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localization accuracy gain in MIMO radar-based systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef]
- Hadaschik, N.; Sackenreuter, B.; Schäfer, M.; Faßbinder, M. Direct positioning with multiple antenna arrays. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–10. [Google Scholar]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. UHF RFID localization based on phase evaluation of passive tag arrays. IEEE Trans. Instrum. Meas. 2014, 64, 913–922. [Google Scholar] [CrossRef]
- Vukmirović, N.; Erić, M.; Janjić, M.; Djurić, P.M. Direct wideband coherent localization by distributed antenna arrays. Sensors 2019, 19, 4582. [Google Scholar] [CrossRef]
- Vukmirović, N.; Janjić, M.; Djurić, P.M.; Erić, M. Position estimation with a millimeter-wave massive MIMO system based on distributed steerable phased antenna arrays. EURASIP J. Adv. Signal Process. 2018, 2018, 1–17. [Google Scholar] [CrossRef]
- Garcia, N.; Wymeersch, H.; Larsson, E.G.; Haimovich, A.M.; Coulon, M. Direct localization for massive MIMO. IEEE Trans. Signal Process. 2017, 65, 2475–2487. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Friedlander, B. Localization of signals in the near-field of an antenna array. IEEE Trans. Signal Process. 2019, 67, 3885–3893. [Google Scholar] [CrossRef]
- Zhang, G.; He, X.; Wang, L.; Yang, D.; Chang, K.; Duffy, A. Step frequency TR-MUSIC for soft fault detection and location in coaxial cable. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Demissie, B.; Oispuu, M.; Ruthotto, E. Localization of multiple sources with a moving array using subspace data fusion. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–7. [Google Scholar]
- Oispuu, M.; Nickel, U. Direct detection and position determination of multiple sources with intermittent emission. Signal Process. 2010, 90, 3056–3064. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, G. A direct localization method for moving narrowband source based on Doppler frequency shifts. Acta Electron. Sin. 2017, 45, 591–598. [Google Scholar]
- Wu, G.; Zhang, M.; Guo, F.; Xiao, X. Direct position determination of coherent pulse trains based on Doppler and Doppler rate. Electronics 2018, 7, 262. [Google Scholar] [CrossRef]
- Autrey, S.W. Passive synthetic arrays. J. Acoust. Soc. Am. 1988, 84, 592–598. [Google Scholar] [CrossRef]
- Zhang, L.; Huan, H.; Tao, R.; Wang, Y. Emitter localization algorithm based on passive synthetic aperture. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2687–2701. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, G.c.; Xing, M.; Xiang, J.; Zhang, Z.; Guo, L. Long Synthetic Aperture Passive Localization Using Azimuth Chirp-Rate Contour Map. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 928–931. [Google Scholar]
- Chen, B.; Wang, Y.; Sun, G.C.; Xing, M.; Zhang, Z.; Yang, X. A Long Synthetic Aperture Passive Localization Method Using Two Planes. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 767–769. [Google Scholar]
- Wang, Y.; Sun, G.C.; Zhang, X.; Yang, J.; Wang, A.; Xing, M.; Yang, X. An Ultra High Resolution Positioning Algorithm for Satellite Ultra Long Duration Data Based on Synthetic Aperture Technique. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5209512. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Shang, X.; Liu, J. CRB analysis for mixed-ADC based DOA estimation. IEEE Trans. Signal Process. 2024, 72, 3043–3058. [Google Scholar] [CrossRef]
- Hung, H.s.; Kaveh, M. On the statistical sufficiency of the coherently averaged covariance matrix for the estimation of the parameters of wideband sources. In Proceedings of the ICASSP’87. IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 6–9 April 1987; Volume 12, pp. 33–36. [Google Scholar]



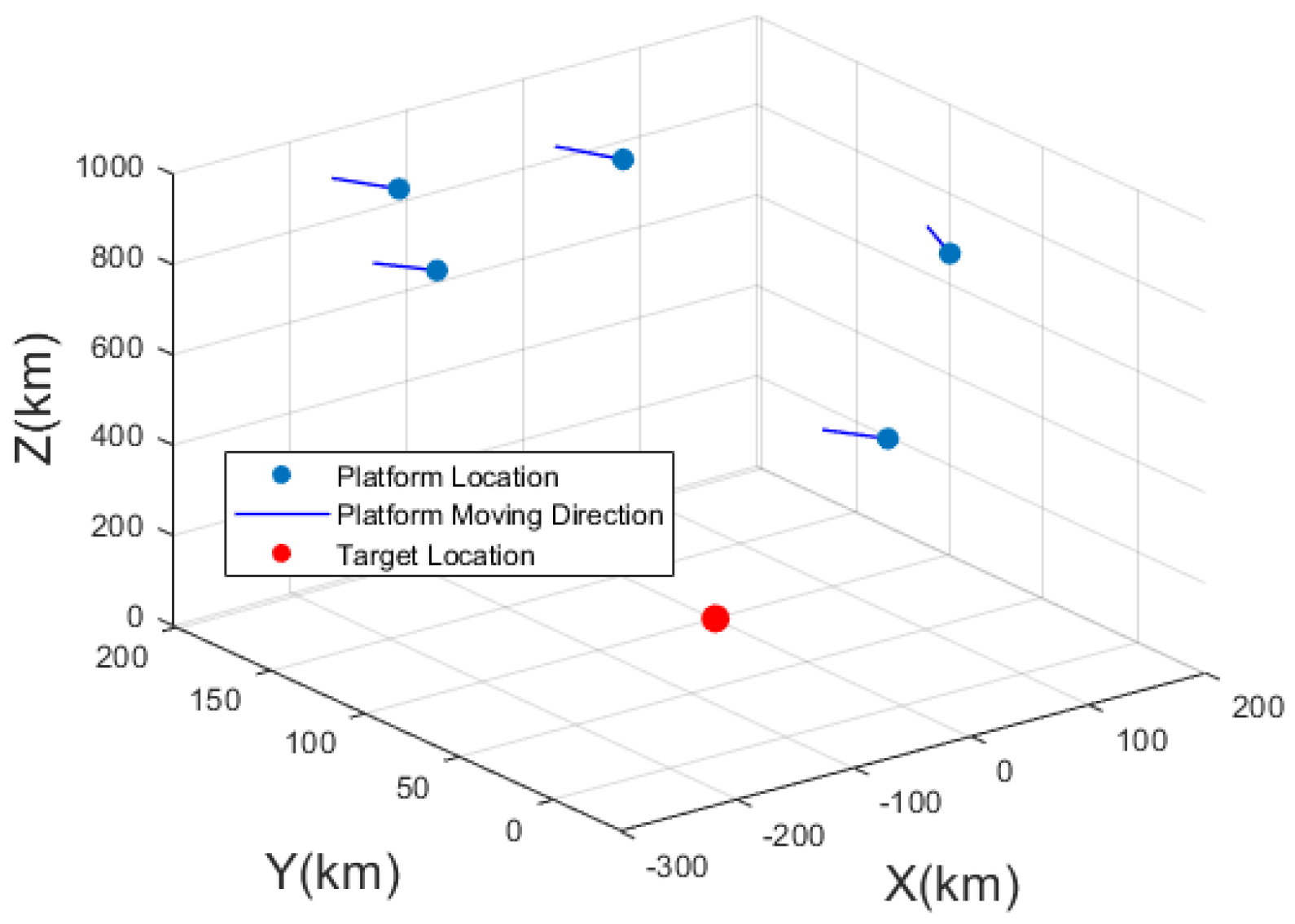
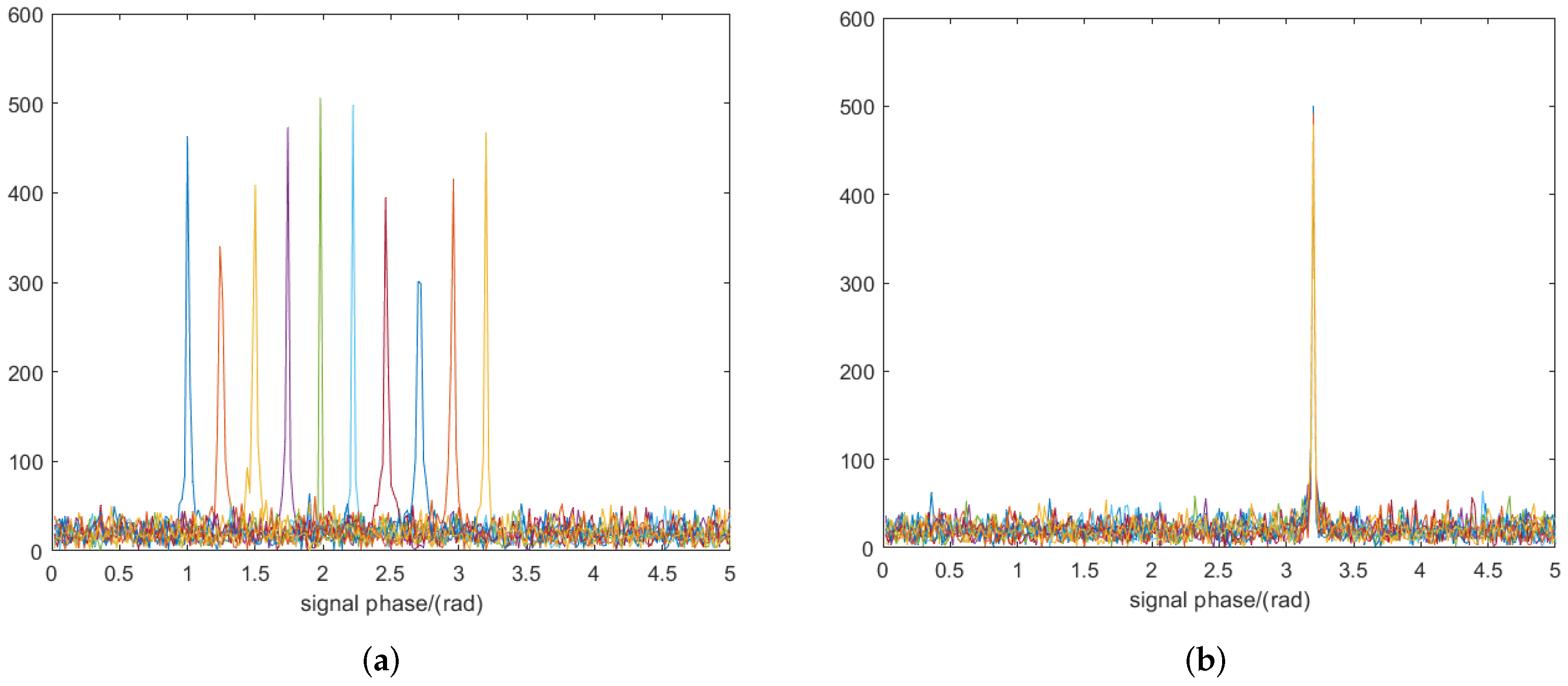

| X Coordinate (km) | Y Coordinate (km) | Z Coordinate (km) |
|---|---|---|
| −217.96 | 112.46 | 896.18 |
| 8.06 | 154.18 | 903.48 |
| −139.76 | 181.53 | 889.68 |
| 177.87 | 86.01 | 706.18 |
| −71.69 | −36.59 | 706.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Sun, G.; Li, D.; Liu, Z.; Ji, Y. Synthetic-Aperture Passive Localization Utilizing Distributed Phased Moving-Antenna Arrays. Electronics 2025, 14, 2114. https://doi.org/10.3390/electronics14112114
Zhang X, Sun G, Li D, Liu Z, Ji Y. Synthetic-Aperture Passive Localization Utilizing Distributed Phased Moving-Antenna Arrays. Electronics. 2025; 14(11):2114. https://doi.org/10.3390/electronics14112114
Chicago/Turabian StyleZhang, Xu, Guohao Sun, Dingkang Li, Zhengyang Liu, and Yuandong Ji. 2025. "Synthetic-Aperture Passive Localization Utilizing Distributed Phased Moving-Antenna Arrays" Electronics 14, no. 11: 2114. https://doi.org/10.3390/electronics14112114
APA StyleZhang, X., Sun, G., Li, D., Liu, Z., & Ji, Y. (2025). Synthetic-Aperture Passive Localization Utilizing Distributed Phased Moving-Antenna Arrays. Electronics, 14(11), 2114. https://doi.org/10.3390/electronics14112114






