Time Series Forecasting via an Elastic Optimal Adaptive GM(1,1) Model
Abstract
1. Introduction
- Adaptive sequence generation mechanism: We improve the architecture of the gray system model by employing an adaptive sequence generation method that integrates the accumulation of historical data with the timing of recent observations. This enhanced framework effectively captures and characterizes the inherent complex temporal patterns in the system’s evolution by strengthening the dynamic representation of temporal features.
- Elastic modeling window: We integrate stationarity testing into the gray system to dynamically adjust the sequence length used for prediction within the gray system. This reduces the adverse impact of changes in data distribution on prediction accuracy.
- Candidate sequence evaluation system: We propose an optimal sequence selection method to evaluate whether replacing actual values with predicted values can improve the accuracy of subsequent predictions. The optimal sequence is then chosen to dynamically correct the prediction errors.
- Applications and validation: The proposed model is applied to forecast dynamic systems, including China’s GDP and indigenous thermal energy consumption. Comparative analysis against other models reveals that our approach delivers superior predictive accuracy for dynamic systems.
2. Related Work
- Accumulated generating operation (AGO): The original dataset undergoes an accumulated transformation to yield a new sequence, emphasizing the system’s development trend and rendering the data’s evolution more discernible.
- A first-order linear differential equation is constructed based on the accumulated sequence, describing the data’s progression. Parameters are estimated using statistical methods, such as the least squares method.
- Optimization focuses on estimating the development coefficient and other parameters critical for the model’s accuracy.
3. Materials and Methods
3.1. Traditional GM(1,1) Model
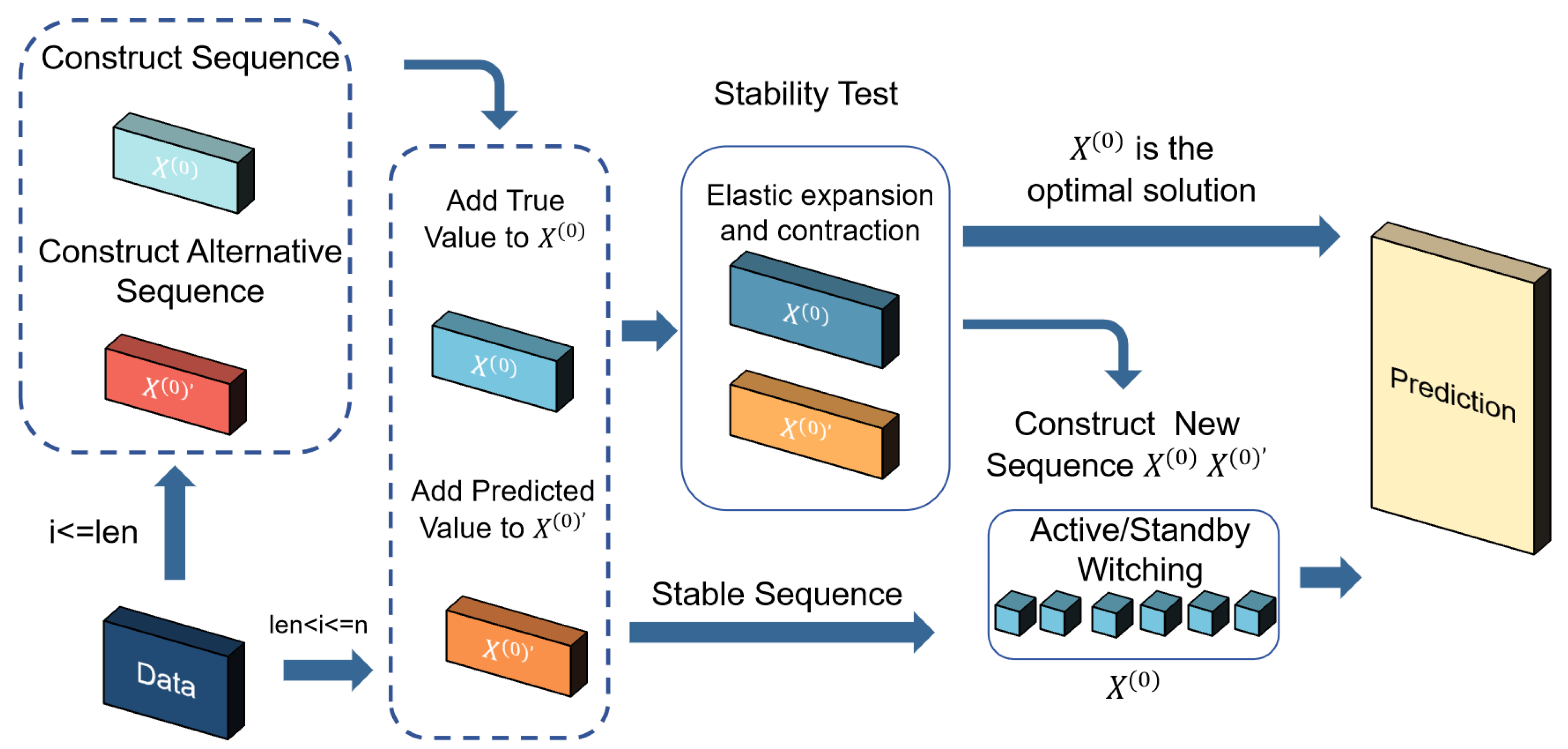
3.2. The Elastic Optimal Adaptive GM(1,1) Model
- Sequences construction: This step involves generating two types of sequences, the original sequence and the candidate sequence, to ensure robust prediction capability.
- Stationarity detection: The EOAGM model improves on the AGM by using the ADF test to evaluate the stability of sequences. Stationarity ensures the model’s parameters accurately represent the system’s behavior, leading to better prediction accuracy.
- Optimal sequence selection: This step identifies the sequence that provides the best prediction accuracy by evaluating the performance of both original and candidate sequences.
3.2.1. Sequences Construction
- Defining sequence length: The optimal length is set for both the original and candidate sequences.
- Data insertion: When the sequence length is not more than , new data points are directly added to both sequences. When the sequence length exceeds , the observed value is appended to the original sequence, while the predicted value is added to the candidate sequence.
- Maintaining sequence length: To keep the sequence length fixed, the oldest value is discarded from both sequences.
- Temporary storage of discarded values: Discarded values are stored temporarily, allowing the model to revert to previous states during the stationarity detection phase if instability is detected. This structured approach ensures the sequences are robust, adaptable, and ready for subsequent stationarity detection and optimization steps.
3.2.2. Stationarity Detection
| Algorithm 1: Elastic adjustment process. |
 |
3.2.3. Optimal Sequence Selection
| Algorithm 2: Optimal sequence selection. |
 |
4. Experimental Results and Discussion
- Cumulative GM(1,1) Model (CGM) [54]: The CGM recalculates and iteratively by incorporating new data. While this method improves adaptability by considering growing datasets, the increasing sequence length may introduce noise and irrelevant information, reducing prediction precision over time.
- Adaptive GM(1,1) Model (AGM) [22]: The AGM dynamically adjusts the data sequence by discarding older data and incorporating new observations. This approach enhances forecasting accuracy for dynamic systems by reflecting real-time changes. However, removing older data may destabilize predictions, and incorporating new data (including anomalies) may reduce prediction reliability.
- Simultaneous Gray Model (SimGM) [42]: This model can improve the algorithm for calculating and [55]. Traditional GM(1,1) employs ordinary least squares (OLS) to estimate and . However, since real-world systems are governed by interconnected and evolving factors, a single differential equation may inadequately capture these relationships. To address this limitation, the SimGM has been proposed, which significantly improves prediction accuracy compared to conventional single-equation models.
- Nonlinear Gray Model (NonlGM) [56]: The NonlGM proposes an enhanced GM(1,N) model incorporating nonlinear optimization techniques to improve forecasting accuracy and robustness. The background value in the TGM(1,1) model is defined as . In the process of background value optimization, the fixed weight coefficient (0.5) can be optimized. In the NonlGM, , where a is optimized.
- Improved Gray Model (ImGM) [37]: This model is an improved optimized background value determination method for the GM(1,1) model. In this method, background value optimization can also be achieved through the exponential background value and dynamic adaptive background value using data characteristics methods.
- Lagged [57]: This model employs a non-gray modeling approach for data forecasting, specifically utilizing a quantile regression framework with lagged and asymmetric effects.
4.1. Performance Comparison with Base Lines
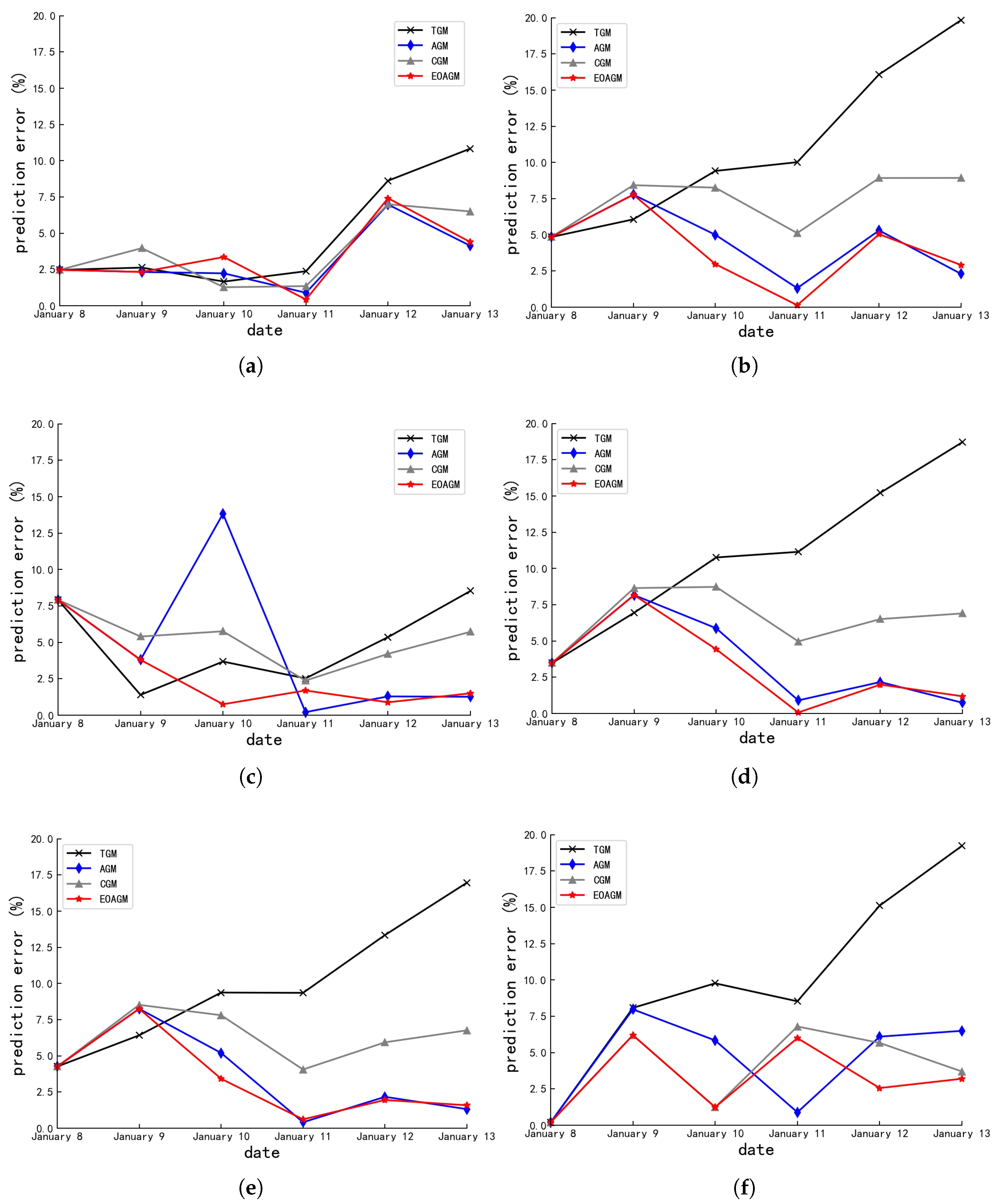
4.1.1. National GDP Prediction
4.1.2. Indigenous Thermal Energy Prediction
4.1.3. JYA-CMTD Prediction
4.1.4. On Model Comparison
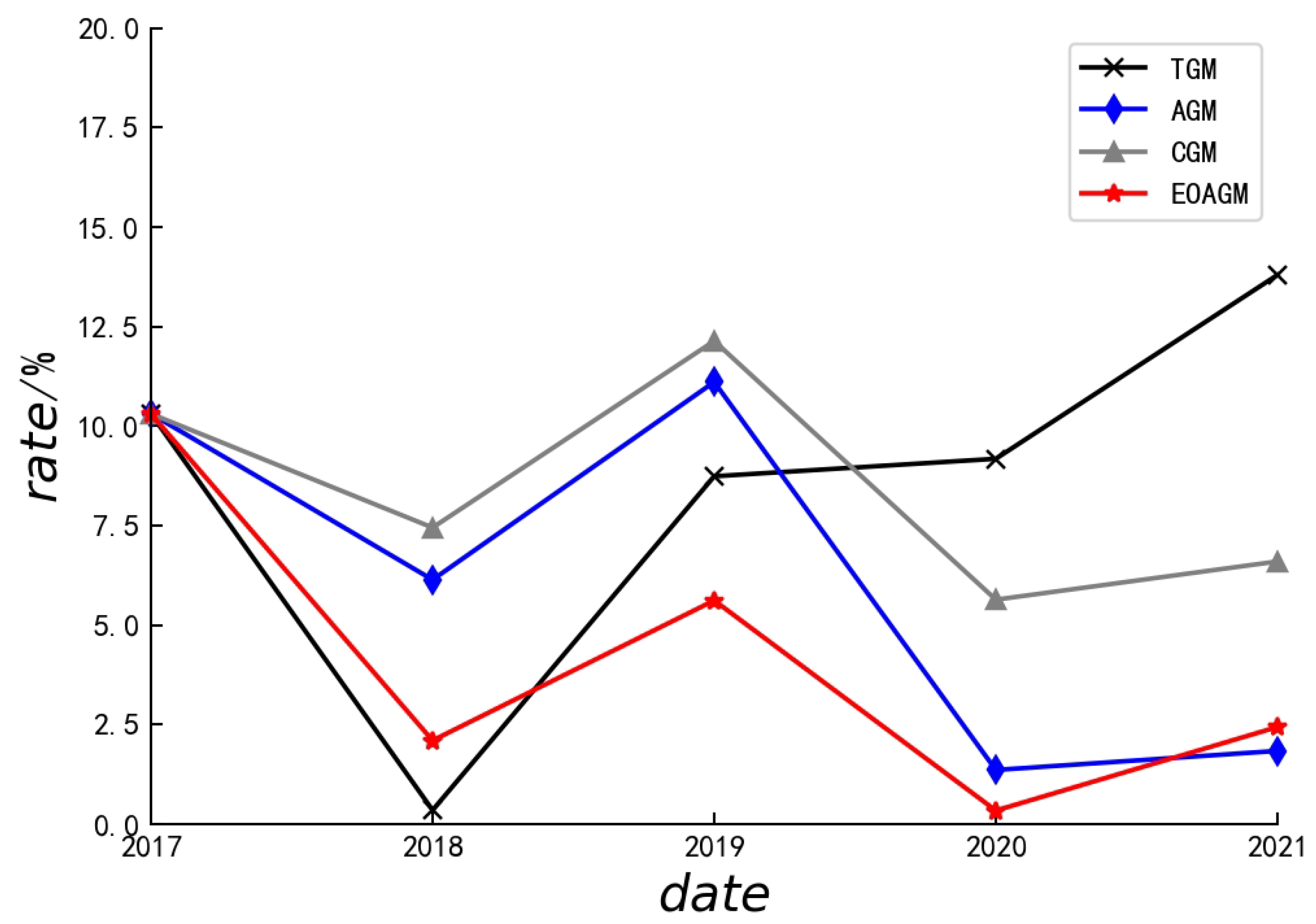
4.2. Ablation Experiment
- EOAGM-A: We replace the dynamic adaptive adjustment of sequences with a cumulative aggregation mode for data prediction.
- EOAGM-O: We remove optimal sequence selection for data prediction.
- EOAGM-E: We omit stationarity detection for data prediction.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alqahtani, A.; Ali, M.; Xie, X.; Jones, M.W. Deep time-series clustering: A review. Electronics 2021, 10, 3001. [Google Scholar] [CrossRef]
- Hu, Y.; Zhan, P.; Xu, Y.; Zhao, J.; Li, Y.; Li, X. Temporal representation learning for time series classification. Neural Comput. Appl. 2021, 33, 3169–3182. [Google Scholar] [CrossRef]
- Liu, F.; Chen, L.; Zheng, Y.; Feng, Y. A prediction method with data leakage suppression for time series. Electronics 2022, 11, 3701. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.; Du, M.; Hu, Y.; Ji, C. Adaptive shapelet selection for time series classification. In Proceedings of the International Conference on Computer Supported Cooperative Work in Design, Rio de Janeiro, Brazil, 24–26 May 2023; pp. 1607–1612. [Google Scholar]
- Hu, Y.; Ji, C.; Jing, M.; Ding, Y.; Kuai, S.; Li, X. A continuous segmentation algorithm for streaming time series. In Proceedings of the Collaborate Computing: Networking, Applications and Worksharing: 12th International Conference, CollaborateCom 2016, Beijing, China, 10–11 November 2016; Proceedings 12. Springer: Berlin/Heidelberg, Germany, 2017; pp. 140–151. [Google Scholar]
- Ji, C.; Hu, Y.; Liu, S.; Pan, L.; Li, B.; Zheng, X. Fully convolutional networks with shapelet features for time series classification. Inf. Sci. 2022, 612, 835–847. [Google Scholar] [CrossRef]
- Hu, Y.; Ren, P.; Luo, W.; Zhan, P.; Li, X. Multi-resolution representation with recurrent neural networks application for streaming time series in IoT. Comput. Netw. 2019, 152, 114–132. [Google Scholar] [CrossRef]
- Hu, Y.; Jiang, Z.; Zhan, P.; Zhang, Q.; Ding, Y.; Li, X. A novel multi-resolution representation for streaming time series. Procedia Comput. Sci. 2018, 129, 178–184. [Google Scholar] [CrossRef]
- Liu, F.; Yin, B.; Cheng, M.; Feng, Y. n-Dimensional chaotic time series prediction method. Electronics 2022, 12, 160. [Google Scholar] [CrossRef]
- Wan, R.; Tian, C.; Zhang, W.; Deng, W.; Yang, F. A multivariate temporal convolutional attention network for time-series forecasting. Electronics 2022, 11, 1516. [Google Scholar] [CrossRef]
- Kim, M.; Lee, S.; Jeong, T. Time series prediction methodology and ensemble model using real-world data. Electronics 2023, 12, 2811. [Google Scholar] [CrossRef]
- Yuan, H.; Liao, S. A time series-based approach to elastic kubernetes scaling. Electronics 2024, 13, 285. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Wan, H.; Li, M. Anomaly-PTG: A time series data-anomaly-detection transformer framework in multiple scenarios. Electronics 2022, 11, 3955. [Google Scholar] [CrossRef]
- Zhong, Y.; He, T.; Mao, Z. Enhanced Solar Power Prediction Using Attention-Based DiPLS-BiLSTM Model. Electronics 2024, 13, 4815. [Google Scholar] [CrossRef]
- Ma, X.; Chang, S.; Zhan, J.; Zhang, L. Advanced Predictive Modeling of Tight Gas Production Leveraging Transfer Learning Techniques. Electronics 2024, 13, 4750. [Google Scholar] [CrossRef]
- Dai, L.; Liu, J.; Ju, Z. Attention Mechanism and Bidirectional Long Short-Term Memory-Based Real-Time Gaze Tracking. Electronics 2024, 13, 4599. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, M.; Su, X.; Gao, Z.; Nie, L. Video moment localization via deep cross-modal hashing. IEEE Trans. Image Process. 2021, 30, 4667–4677. [Google Scholar] [CrossRef]
- Zeng, B.; Luo, C.; Liu, S.; Bai, Y.; Li, C. Development of an optimization method for the GM(1,N) model. Eng. Appl. Artif. Intell. 2016, 55, 353–362. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine learning advances for time series forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Molnár, A.; Csiszárik-Kocsir, Á. Forecasting economic growth with v4 countries’ composite stock market indexes—A granger causality test. Acta Polytech. Hung. 2023, 20, 135–154. [Google Scholar] [CrossRef]
- Wang, Z.X.; Li, Q.; Pei, L.L. A seasonal GM(1,1) model for forecasting the electricity consumption of the primary economic sectors. Energy 2018, 154, 522–534. [Google Scholar] [CrossRef]
- Fan, G.; Li, B.; Mu, W.; Ji, C. The Application of the Optimal GM(1,1) Model for Heating Load Forecasting. In Proceedings of the 2015 4th International Conference on Mechatronics, Materials, Chemistry and Computer Engineering, Xi’an, China, 12–13 December 2015; Atlantis Press: Paris, France, 2015. [Google Scholar]
- Ren, Y.; Xia, L.; Wang, Y. An improved GM(1,1) forecasting model based on Aquila Optimizer for wind power generation in Sichuan Province. Soft Comput. 2024, 28, 8785–8805. [Google Scholar] [CrossRef]
- Prakash, S.; Agrawal, A.; Singh, R.; Singh, R.K.; Zindani, D. A decade of grey systems: Theory and application–bibliometric overview and future research directions. Grey Syst. Theory Appl. 2023, 13, 14–33. [Google Scholar] [CrossRef]
- Cai, L.; Wu, F.; Lei, D. Pavement condition index prediction using fractional order GM(1,1) model. IEEE Trans. Electr. Electron. Eng. 2021, 16, 1099–1103. [Google Scholar] [CrossRef]
- Ding, S. A novel self-adapting intelligent grey model for forecasting China’s natural-gas demand. Energy 2018, 162, 393–407. [Google Scholar] [CrossRef]
- Han, H.; Jing, Z. Anomaly Detection in Wireless Sensor Networks Based on Improved GM Model. Teh. Vjesn. 2023, 30, 1265–1273. [Google Scholar]
- Javanmardi, E.; Liu, S.; Xie, N. Exploring the challenges to sustainable development from the perspective of grey systems theory. Systems 2023, 11, 70. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, B. Dynamic change analysis and forecast of forestry-based industrial structure in China based on grey systems theory. J. Sustain. For. 2020, 39, 309–330. [Google Scholar] [CrossRef]
- Cheng, M.; Liu, B. Application of a novel grey model GM (1,1, exp× sin, exp× cos) in China’s GDP per capita prediction. Soft Comput. 2024, 28, 2309–2323. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wang, Z.W.; Li, Q. Forecasting the industrial solar energy consumption using a novel seasonal GM(1,1) model with dynamic seasonal adjustment factors. Energy 2020, 200, 117460. [Google Scholar] [CrossRef]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Li, J.; Feng, S.; Zhang, T.; Ma, L.; Shi, X.; Zhou, X. Study of Long-Term Energy Storage System Capacity Configuration Based on Improved Grey Forecasting Model. IEEE Access 2023, 11, 34977–34989. [Google Scholar] [CrossRef]
- Delcea, C.; Javed, S.A.; Florescu, M.S.; Ioanas, C.; Cotfas, L.A. 35 years of grey system theory in economics and education. Kybernetes 2025, 54, 649–683. [Google Scholar] [CrossRef]
- Chia-Nan, W.; Nhu-Ty, N.; Thanh-Tuyen, T. Integrated DEA Models and Grey System Theory to Evaluate Past-to-Future Performance: A Case of Indian Electricity Industry. Sci. World J. 2015, 2015, 638710. [Google Scholar]
- Zhan, T.; Xu, H. Nonlinear optimization of GM(1,1) model based on multi-parameter background value. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Beijing, China, 29–31 October 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 15–19. [Google Scholar]
- Ma, Y.; Wang, S. Construction and application of improved GM(1,1) power model. J. Quant. Econ. 2019, 36, 84–88. [Google Scholar]
- Chen, F.; Zhu, Y. A New GM(1,1) Based on Piecewise Rational Linear/linear Monotonicity-preserving Interpolation Spline. Eng. Lett. 2021, 29, 3. [Google Scholar]
- Wang, X.; Qi, L.; Chen, C.; Tang, J.; Jiang, M. Grey System Theory based prediction for topic trend on Internet. Eng. Appl. Artif. Intell. 2014, 29, 191–200. [Google Scholar] [CrossRef]
- Liu, S.; Tao, L.; Xie, N.; Yang, Y. On the new model system and framework of grey system theory. In Proceedings of the 2015 IEEE International Conference on Grey Systems and Intelligent Services (GSIS), Leicester, UK, 18–20 August 2015; pp. 1–11. [Google Scholar]
- Tang, L.; Lu, Y. An Improved Non-equal Interval GM(1,1) Model Based on Grey Derivative and Accumulation. J. Grey Syst. 2020, 32, 77. [Google Scholar]
- Cheng, M.; Cheng, Z. A novel simultaneous grey model parameter optimization method and its application to predicting private car ownership and transportation economy. J. Ind. Manag. Optim. 2023, 19, 3160–3171. [Google Scholar] [CrossRef]
- Zeng, X.; Xu, M.; Hu, Y.; Tang, H.; Hu, Y.; Nie, L. Adaptive edge-aware semantic interaction network for salient object detection in optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Yuhong, W.; Jie, L. Improvement and application of GM(1,1) model based on multivariable dynamic optimization. J. Syst. Eng. Electron. 2020, 31, 593–601. [Google Scholar] [CrossRef]
- Gianfreda, A.; Maranzano, P.; Parisio, L.; Pelagatti, M. Testing for integration and cointegration when time series are observed with noise. Econ. Model. 2023, 125, 106352. [Google Scholar] [CrossRef]
- Chang, Y.; Park, J.Y. On the asymptotics of ADF tests for unit roots. Econom. Rev. 2002, 21, 431–447. [Google Scholar] [CrossRef]
- Alam, M.B.; Hossain, M.S. Investigating the connections between China’s economic growth, use of renewable energy, and research and development concerning CO2 emissions: An ARDL Bound Test Approach. Technol. Forecast. Soc. Change 2024, 201, 123220. [Google Scholar] [CrossRef]
- Hassan, M.K.; Kazak, H.; Adıgüzel, U.; Gunduz, M.A.; Akcan, A.T. Convergence in Islamic financial development: Evidence from Islamic countries using the Fourier panel KPSS stationarity test. Borsa Istanb. Rev. 2023, 23, 1289–1302. [Google Scholar] [CrossRef]
- Lin, J.X.; Chen, G.; Pan, H.S.; Wang, Y.C.; Guo, Y.C.; Jiang, Z.X. Analysis of stress-strain behavior in engineered geopolymer composites reinforced with hybrid PE-PP fibers: A focus on cracking characteristics. Compos. Struct. 2023, 323, 117437. [Google Scholar] [CrossRef]
- Asgari, H.; Moridian, A.; Havasbeigi, F. The Impact of Economic Complexity on Income Inequality with Emphasis on the Role of Human Development Index in Iran’s Economy with ARDL Bootstrap Approach. J. Dev. Cap. 2024, 9, 35–56. [Google Scholar]
- Yung, Y.F.; Bentler, P.M. Bootstrap-corrected ADF test statistics in covariance structure analysis. Br. J. Math. Stat. Psychol. 1994, 47, 63–84. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, J. The existence of periodic and subharmonic solutions of subquadratic second order difference equations. J. Lond. Math. Soc. 2003, 68, 419–430. [Google Scholar] [CrossRef]
- Liu, S.F.; Forrest, J. Advances in grey systems theory and its applications. In Proceedings of the 2007 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 18–20 November 2007; pp. 1–6. [Google Scholar]
- Romano, J.L.; Kromrey, J.D.; Owens, C.M.; Scott, H.M. Confidence interval methods for coefficient alpha on the basis of discrete, ordinal response items: Which one, if any, is the best? J. Exp. Educ. 2011, 79, 382–403. [Google Scholar] [CrossRef]
- Fu, Z.; Yang, Y.; Wang, T. Prediction of urban water demand in Haiyan county based on improved nonlinear optimization GM (1, N) model. Water Resour. Power 2019, 37, 44–47. [Google Scholar]
- Dawar, I.; Dutta, A.; Bouri, E.; Saeed, T. Crude oil prices and clean energy stock indices: Lagged and asymmetric effects with quantile regression. Renew. Energy 2021, 163, 288–299. [Google Scholar] [CrossRef]
- Han, Y.; Hu, Y.; Song, X.; Tang, H.; Xu, M.; Nie, L. Exploiting the social-like prior in transformer for visual reasoning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 2058–2066. [Google Scholar]
- Tang, H.; Hu, Y.; Wang, Y.; Zhang, S.; Xu, M.; Zhu, J.; Zheng, Q. Listen as you wish: Fusion of audio and text for cross-modal event detection in smart cities. Inf. Fusion 2024, 110, 102460. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, K.; Liu, M.; Tang, H.; Nie, L. Semantic collaborative learning for cross-modal moment localization. ACM Trans. Inf. Syst. 2023, 42, 1–26. [Google Scholar] [CrossRef]
| Date | No. 11 | No. 12 | No. 13 | No. 14 | No. 15 | No. 16 |
|---|---|---|---|---|---|---|
| 01-01 | 13,900.29 | 3326.23 | 2536.82 | 2295.93 | 4926.74 | 17,017.67 |
| 01-02 | 13,556.13 | 3396.63 | 2530.54 | 2304.05 | 4882.54 | 16,663.45 |
| 01-03 | 13,209.10 | 3333.60 | 1914.24 | 2267.04 | 4844.14 | 16,070.78 |
| 01-04 | 12,385.61 | 3059.22 | 2964.36 | 2118.25 | 4544.05 | 14,970.55 |
| 01-05 | 12,313.99 | 3054.51 | 2338.64 | 2106.83 | 4535.83 | 14,551.11 |
| 01-06 | 13,223.57 | 3160.68 | 2366.73 | 2150.19 | 4633.16 | 15,105.55 |
| 01-07 | 13,267.33 | 3090.40 | 2349.92 | 2117.3 | 4585.94 | 15,458.17 |
| 01-08 | 12,532.19 | 2840.63 | 2218.29 | 1980.02 | 4277.26 | 14,559.78 |
| 01-09 | 13,145.06 | 3111.99 | 2423.01 | 2164.07 | 4703.21 | 15,530.5 |
| 01-10 | 12,972.85 | 3166.90 | 2475.54 | 2218.12 | 4793.15 | 15,543.7 |
| 01-11 | 13,024.71 | 3128.9 | 2441.32 | 2189.76 | 4729.36 | 14,660.22 |
| 01-12 | 13,868.68 | 3292.88 | 2509.36 | 2255.72 | 4882.86 | 15,947.28 |
| 01-13 | 14,165.04 | 3382.87 | 2591.21 | 2312.53 | 5029.03 | 16,464.54 |
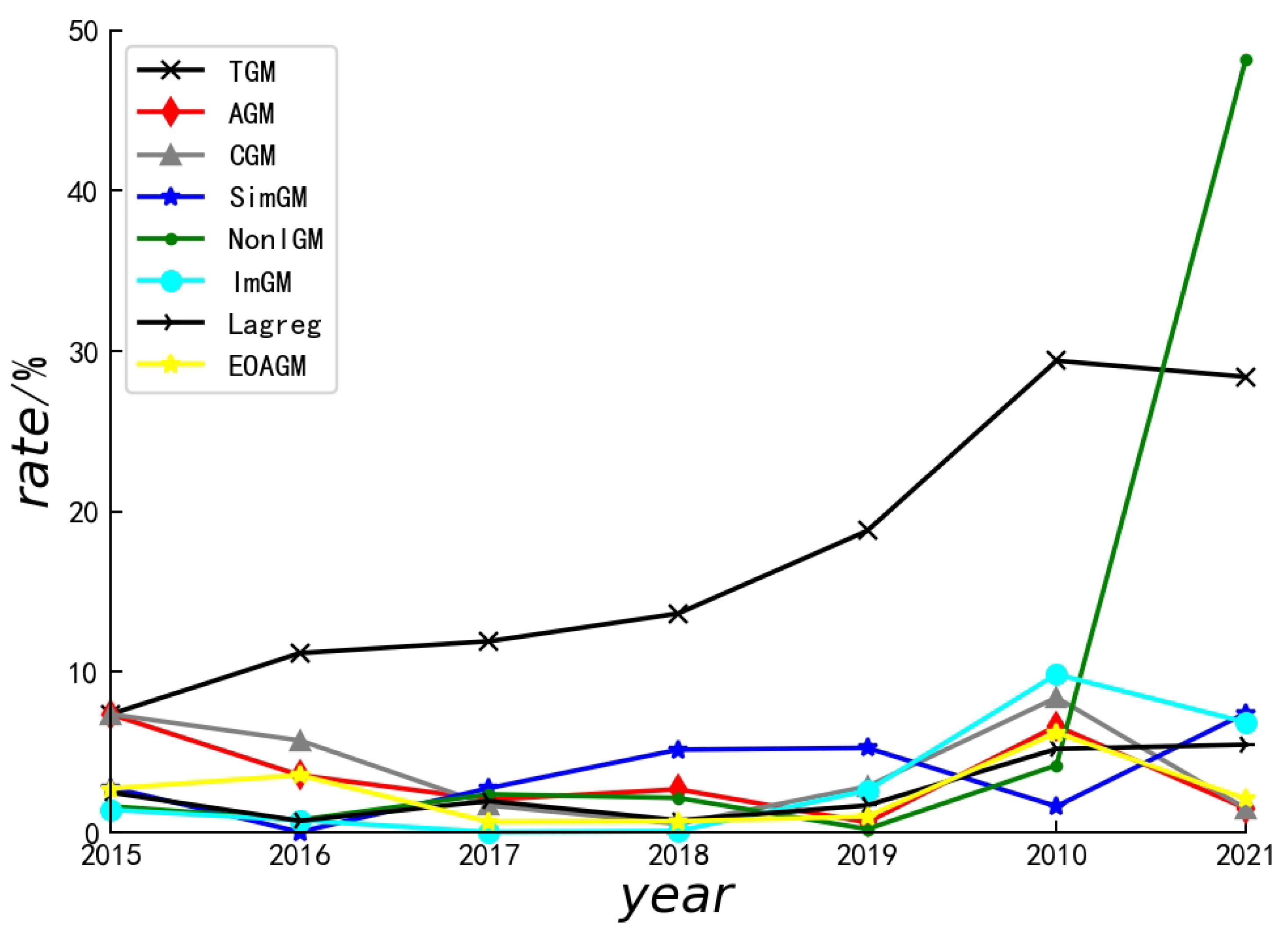
| Errors (%) | Algorithms | |||||||
|---|---|---|---|---|---|---|---|---|
| TGM | AGM | CGM | SimGM | NonlGM | ImGM | Lagreg | EOAGM | |
| 7.36 | 7.36 | 7.36 | 2.8 | 1.63 | 1.40 | 2.48 | 2.72 | |
| 11.17 | 3.56 | 5.73 | 0.02 | 0.77 | 0.749 | 0.712 | 3.56 | |
| 11.91 | 2.03 | 1.68 | 2.75 | 2.37 | 3.27 × 10−5 | 1.95 | 0.65 | |
| 13.64 | 2.68 | 0.52 | 5.15 | 2.14 | 0.078 | 0.746 | 0.69 | |
| 18.8 | 0.62 | 2.86 | 5.26 | 0.20 | 2.60 | 1.68 | 0.98 | |
| 29.4 | 6.63 | 8.40 | 1.62 | 4.18 | 9.85 | 5.2 | 6.21 | |
| 28.4 | 1.49 | 1.48 | 7.43 | 48.2 | 6.86 | 5.46 | 2.09 | |
| 17.241 | 3.48 | 4.53 | 3.57 | 8.50 | 3.07 | 2.60 | 2.41 | |
| Algorithms | Average Errors (%) | |||||
|---|---|---|---|---|---|---|
| No. 11 | No. 12 | No. 13 | No. 14 | No. 15 | No. 16 | |
| TGM | 4.76 ± 3.92 | 11.04 ± 5.82 | 4.902.89 | 11.04 ± 5.49 | 9.95 ± 4.61 | 10.16 ± 6.53 |
| AGM | 3.17 ± 2.13 | 2.31 ± 3.92 | 4.71 ± 5.26 | 3.55 ± 2.9 | 3.60 ± 2.90 | 3.97 ± 3.22 |
| CGM | 3.76 ± 2.51 | 7.42 ± 3.92 | 1.90 ± 1.84 | 6.54 ± 2.06 | 6.23 ± 1.83 | 4.58 ± 2.74 |
| EOAGM | 3.39 ± 2.37 | 3.95 ± 2.57 | 3.06 ± 2.75 | 3.22 ± 2.88 | 3.34 ± 2.74 | 3.22 ± 2.45 |
| Errors (%) | Algorithms | |||
|---|---|---|---|---|
| TGM | AGM | CGM | EOAGM | |
| 10.31 | 10.31 | 10.31 | 10.31 | |
| 0.35 | 6.14 | 7.45 | 2.10 | |
| 8.74 | 11.11 | 12.14 | 5.62 | |
| 9.18 | 1.36 | 5.64 | 0.34 | |
| 13.80 | 1.84 | 6.60 | 2.44 | |
| 8.47 | 6.84 | 8.42 | 4.16 | |
| Dateset | Average Errors (%) | |||
|---|---|---|---|---|
| EOAGM-A | EOAGM-O | EOAGM-E | EOAGM | |
| 4.01 | 2.43 | 3.08 | 2.41 | |
| 3.48 | 3.17 | 3.39 | 3.39 | |
| 6.85 | 4.28 | 4.16 | 3.95 | |
| 4.87 | 4.53 | 3.21 | 3.06 | |
| 6.35 | 3.55 | 3.22 | 3.22 | |
| 5.91 | 3.60 | 3.34 | 3.34 | |
| 4.27 | 3.68 | 3.54 | 3.22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Nie, J.; Qiu, G.; Li, Z.; Ji, C.; Li, X. Time Series Forecasting via an Elastic Optimal Adaptive GM(1,1) Model. Electronics 2025, 14, 2071. https://doi.org/10.3390/electronics14102071
Li T, Nie J, Qiu G, Li Z, Ji C, Li X. Time Series Forecasting via an Elastic Optimal Adaptive GM(1,1) Model. Electronics. 2025; 14(10):2071. https://doi.org/10.3390/electronics14102071
Chicago/Turabian StyleLi, Teng, Jiajia Nie, Guozhi Qiu, Zhen Li, Cun Ji, and Xueqing Li. 2025. "Time Series Forecasting via an Elastic Optimal Adaptive GM(1,1) Model" Electronics 14, no. 10: 2071. https://doi.org/10.3390/electronics14102071
APA StyleLi, T., Nie, J., Qiu, G., Li, Z., Ji, C., & Li, X. (2025). Time Series Forecasting via an Elastic Optimal Adaptive GM(1,1) Model. Electronics, 14(10), 2071. https://doi.org/10.3390/electronics14102071









