Abstract
The direct porting of the Range Migration Algorithm to GPUs for three-dimensional (3D) cylindrical synthetic aperture radar (CSAR) imaging faces difficulties in achieving real-time performance while the architecture and programming models of GPUs significantly differ from CPUs. This paper proposes a GPU-optimized implementation for accelerating CSAR imaging. The proposed method first exploits the concentric-square-grid (CSG) interpolation to reduce the computational complexity for reconstructing a uniform 2D wave-number domain. Although the CSG method transforms the 2D traversal interpolation into two independent 1D interpolations, the interval search to determine the position intervals for interpolation results in a substantial computational burden. Therefore, binary search is applied to avoid traditional point-to-point matching for efficiency improvement. Additionally, leveraging the partition independence of the grid distribution of CSG, the 360° data are divided into four streams along the diagonal for parallel processing. Furthermore, high-speed shared memory is utilized instead of high-latency global memory in the Hadamard product for the phase compensation stage. The experimental results demonstrate that the proposed method achieves CSAR imaging on a dataset in 0.794 s, with an acceleration ratio of 35.09 compared to the CPU implementation and 5.97 compared to the conventional GPU implementation.
1. Introduction
Cylindrical synthetic aperture radar (CSAR), a variant of SAR technology that allows for 360° omnidirectional detection to eliminate blind zones, is widely used in security and non-destructive inspection fields [1,2,3,4]. CSAR can obtain high-resolution three-dimensional (3D) images of the target for detection. However, the execution of the CSAR imaging system on Central Processing Unit (CPU) platforms faces difficult challenges in real-time imaging [5,6].
As shown in Figure 1, Graphics Processing Units (GPUs) with powerful parallel computing capabilities have emerged as powerful accelerators for computationally intensive tasks in SAR imaging [7,8]. Plenty of studies have explored GPU-accelerated strategies to address real-time imaging problems [9,10,11,12,13,14,15,16]. Wu [10] proposed a scheme to accelerate the Back-Projection Algorithm (BPA) by leveraging the combination of CPU and GPU platforms. At an image scale of 4 km × 4 km, this approach achieved a speedup of 163.96 times compared to the CPU-only implementation. Yang [11] proposed a parallel computing method for Range-Doppler and Map Drift algorithms through unifying memory management, shared memory, and cuFFT configuration. For data, the proposed method realized imaging in 135 milliseconds based on an embedded GPU platform, achieving a speedup of 39.78 times over the CPU-based approach. Li [12] proposed an efficient BPA based on time-shifted upsampling-improved cubic spline interpolation, which was accelerated on GPUs using shared memory and 2D thread. The proposed method demonstrated a performance improvement of 1.79 times compared to the approach utilizing 1D threads and global memory. Tan [13] proposed a combined GPU and OpenMp-based approach to greatly accelerate ground-based SAR real-time imaging through host stream, blocking stream, and non-blocking stream multi-stream processing. The proposed method achieved imaging in 0.637 s for data, which was 22.8 times faster than conventional imaging. Ren Z. [15] proposed a GPU-based extended two-step approach for full-aperture SAR data processing, consisting of data division and the stream technique. The proposed method processed SAR data in 45.78 s and achieved more than 18.75 times faster than CPU processing. Ding L. [16] proposed a hybrid GPU and CPU parallel computing method to accelerate the Range Migration Algorithm (RMA), which processed data 15 times faster than the CPU-only method and 2 times faster than the GPU-only method. Previous works have shown that the powerful parallel computing capability of GPUs significantly improves the processing efficiency of SAR imaging. However, most studies focus on other SAR imaging modalities rather than CSAR. With the increase in dimensionality and changes in application scenarios, it is still an important challenge to fully optimize the CSAR imaging algorithms on the GPU platform.
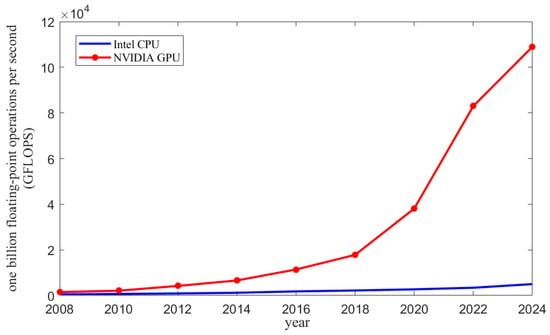
Figure 1.
Comparison of single-precision floating-point computing power between NVIDIA GPUs and Intel CPUs.
RMA is commonly used for 3D CSAR imaging due to its ability to effectively eliminate distance migration with low computational complexity and minimal approximation errors [17,18,19,20]. The main stages of this algorithm include 2D Fourier transform (FT), phase compensation, 1D inverse FT, 2D interpolation, and 3D inverse FT. The direct porting of RMA makes it hard to effectively improve the real-time performance due to the significant differences in architecture and programming models of CPU and GPU. Therefore, this paper optimizes the GPU implementation based on the detailed analysis of each stage of the 3D cylindrical RMA.
Operations involving the FTs and inverse FTs can be efficiently implemented using the cuFFT library provided by Computational Unified Device Architecture (CUDA). In the phase-compensation stage, high-speed shared memory is employed to accelerate the Hadamard product instead of global memory with the highest latency. Two-dimensional interpolation constitutes the most computationally intensive stage of RMA due to its high computational complexity and logic-intensive operations required for reconstructing a uniform 2D wave-number domain. To address this, this paper adopts the concentric-square-grid (CSG) interpolation with low computational complexity [21], which transforms the conventional 2D traversal interpolation into two independent 1D interpolations. A key challenge in the GPU implementation of the CSG method is how to efficiently determine the position intervals of the points to be interpolated. A binary search is introduced to enhance search efficiency by halving the search range at each iteration. Furthermore, the proposed method leverages the partition independence of the grid distribution of CSG, allowing the 360° data to be divided into four CUDA streams for parallel processing to improve interpolation efficiency. In this way, the proposed method optimizes the 3D cylindrical RMA by improving memory access, interpolation interval search, and parallel processing. Tested on a hardware setup comprising a 13th Gen Intel® Core™ i9-13900K CPU and NVIDIA GeForce RTX 4090 GPU, the proposed method achieves 3D CSAR imaging of (azimuth × distance × height) points in 0.794 s for the echo data of (angle × frequency × height) points, which indicates an acceleration ratio of 35.09 compared to the CPU implementation and 5.97 compared to the conventional GPU implementation.
2. Three-Dimensional Cylindrical RMA
The 3D cylindrical imaging scene is shown in Figure 2. The height of the antenna array is , scanning circularly with radius R. denotes the azimuth of antenna rotation at a given moment. Let the position coordinates of any sample of the antenna array be , where R and are the radius and angle of the sampled antenna in the polar coordinate system. A scattering point on the target is denoted as , where r and are the radius and angle of the target point E in the polar coordinate system.
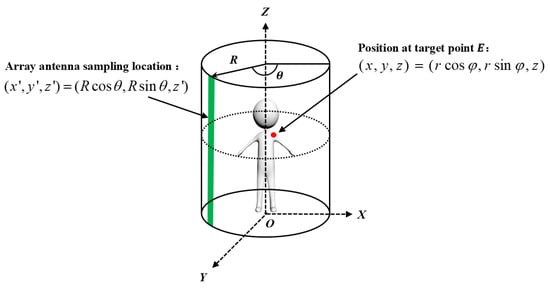
Figure 2.
The model of the 3D cylindrical imaging system.
The received reflected echo signal can be expressed as [22,23,24]:
where corresponds to the backscattering coefficient, is the speed of light, and is the wave number.
In order to realize the digital processing, discrete sampling is required for the angle, frequency, and height dimensions of the continuous echo signal.
where , , denote the sampling intervals for the three dimensions and , , denote the numbers of sampling points for the three dimensions. The echo corresponds to the m-th angle, n-th frequency, and the p-th height can be rewritten as:
where , , denote the numbers of points in the azimuth, as well as the distance and height dimensions of the scene of interest, and denotes the wave number at the n-th frequency. Based on Equation (3), the details of 3D cylindrical RMA are shown in Algorithm 1.
| Algorithm 1: Three-dimensional cylindrical RMA |
|
3. The Implementation on GPU
Based on Algorithm 1, it can be observed that the 3D cylindrical RMA primarily consists of the operations of FTs, inverse FTs, the Hadamard product, and 2D interpolation. The flow of the proposed method is shown in Figure 3. The red arrows represent the GPU implementations of the indicated algorithmic stages.
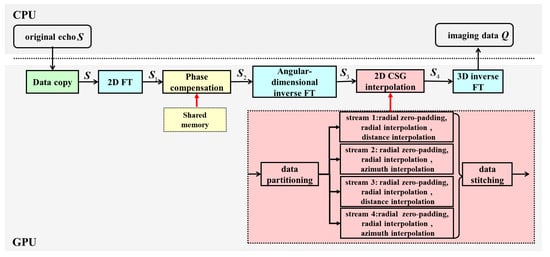
Figure 3.
A flowchart of the proposed GPU implementation of the 3D cylindrical RMA algorithm.
3.1. Fourier Transform
As shown in Figure 3, FTs and inverse FTs are required in several stages. Among the available libraries for FT, the cuFFT library is specifically optimized for GPU architectures, exploiting their massive parallelism to significantly achieve lower execution times compared to CPU-based libraries such as FFTW. Furthermore, the cuFFT library offers seamless integration with the CUDA programming environment, ensuring efficient memory management and minimal overhead. These advantages make the cuFFT library the optimal choice for implementing the Fourier transform stage.
3.2. Phase Compensation
The phase-compensation stage in CUDA is implemented as the Hadamard product, which is highly parallelizable and well suited for GPU-based execution. Conventionally, the Hadamard product is operated in global memory. However, global memory is the memory with the highest latency and lowest access speed, potentially leading to significant performance bottlenecks. Shared memory offers a latency reduction of approximately 20 to 30 times [26,27], making it much more efficient for memory-intensive operations. By utilizing shared memory within the kernel function, the phase-compensation stage can be optimized to improve memory access speed and reduce latency. The detailed operations are shown in Algorithm 2.
| Algorithm 2: Phase compensation |
|
3.3. Two-Dimensional CSG Interpolation
The 2D interpolation stage exploits the CSG method [21], which transforms traditional 2D interpolation into two independent 1D interpolations. This method reduces computational complexity without compromising imaging accuracy and makes it easy to implement parallelization on GPU platforms.The principle of CSG interpolation is shown in Figure 4. The original wave-number domain is divided into four intervals along the square diagonal, as shown in Figure 4a. Radial interpolation and distance interpolation are applied to the data in intervals 1 and 3, while radial interpolation and azimuth interpolation are performed on the data in intervals 2 and 4.
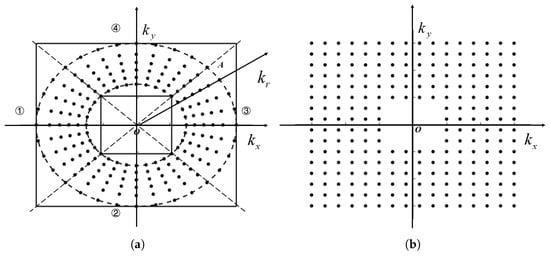
Figure 4.
Wave-number distribution for a given height dimension in the CSG method. (a) Initial wave number; (b) interpolated wave number.
In the GPU-based implementation of CSG interpolation, a key challenge is the large number of interval-search operations required for interpolation tasks. The interval search determines the position interval of points to be interpolated, which are sequentially arranged in a fixed and static order. This distribution satisfies the prerequisite condition for binary search, an efficient approach for locating data points. Taking radial interpolation as an example, let the initial radial position array be listed as , and the uniform radial position array as , where and denote the lengths of the arrays. The linear search and binary search are shown in Figure 5, where finding the corresponding position in for is taken as an example, where and are even numbers and .
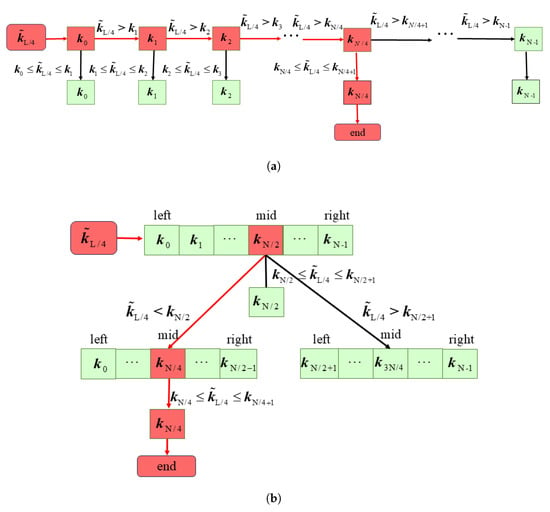
Figure 5.
Interval-search methods. (a) Linear search; (b) binary search.
As shown in Figure 5a, linear search involves each element in the array being sequentially compared with each two adjacent elements in the array to determine the interval where a specific element from . Therefore, the time complexity is . Leveraging the parallelism capability of GPU, the comparisons for each element in array can be executed concurrently across multiple threads, reducing the time complexity to . Although the steps of binary search are more tedious than the conventional method, it halves the search range with each iteration until the target interval is located, which reduces the time complexity to [28,29]. The pseudo-code is shown in Algorithm 3. From Figure 6, it can be seen that the larger the size of the interpolated data, the better the performance of binary search.
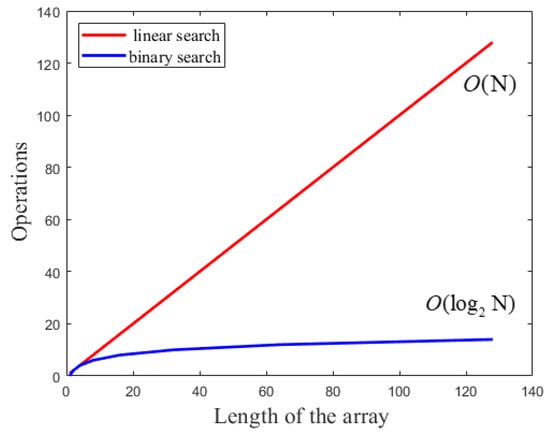
Figure 6.
Time-complexity curves of linear search and binary search.
| Algorithm 3: Binary search |
|
Since the processing of the four groups of data divided based on the partition independence of the grid distribution of CSG is independent of each other, it is well suited for parallel execution. To maximize GPU computational efficiency, the CUDA streaming technique is utilized to assign each group of data to a separate stream, as shown in Figure 7. The upper dashed line shows the conventional interpolation method without the specified streams, while the lower dashed line shows the parallel execution of four streams. Four groups of data divided along the diagonal of the CGS grid are bound to independent CUDA streams to realize coarse-grained pipeline parallelism. Within each stream, CUDA events are used to ensure the sequential execution of kernel functions, including radial zero-padding, radial interpolation, and 1D interpolation (the distance or azimuth interpolation). Meanwhile, the inter-stream asynchronous feature is utilized to realize the parallel processing of the four groups of data. A global synchronization point, established via cudaStreamSynchronize, ensures that all streams complete their tasks before the four groups of data are stitched together for 3D inverse FT to obtain the final imaging.
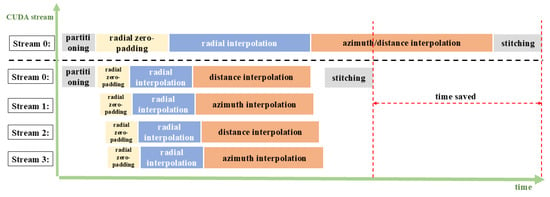
Figure 7.
Schematic of CUDA stream interpolation parallel processing.
4. Experimental Results and Analysis
In this section, experiments are conducted to validate the performance of the proposed GPU implementation and to check the imaging differences with the CPU and the conventional GPU implementation. The experimental hardware platforms are 13th Gen Intel® Core™i9-13900K CPU and NVIDIA GeForce RTX 4090 GPU. The experimental software platforms are MATLAB R2024b, Windows Visual Studio 2022 and CUDA 12.4. The parameters of the simulation experiment are enumerated in Table 1 and the detailed implementation of the three methods is shown in Table 2. The single-point simulation experimental imaging results of the CPU implementation and the proposed GPU implementation are shown in Figure 8 and Figure 9.

Table 1.
The parameters of the simulation experiment.

Table 2.
Detailed implementation of three methods.
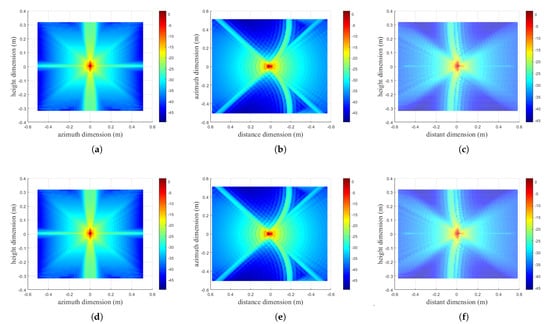
Figure 8.
Imaging results comparison. (a–c) are the front, top, and side views obtained by the CPU implementation; (d–f) are the front, top, and side views obtained by the proposed GPU implementation.
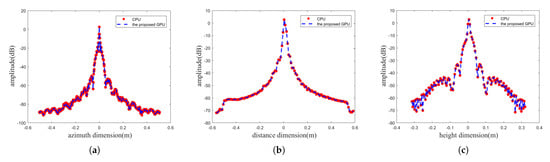
Figure 9.
Imaging profiles for each scenario. (a) azimuth-dimension profile; (b) distance-dimension profile; (c) height-dimension profile.
Figure 8 shows the front, top, and side views of two imaging results obtained from the CPU implementation and the proposed GPU implementation, which are clearly shown and have no obvious differences when observed with the human eye. In order to further confirm the correctness of the proposed GPU-implemented imaging data, the above imaging results are profiled in azimuth, distance, and height dimensions in Figure 9. As shown in Table 3, the imaging quality metrics of the proposed GPU implementation, including peak-side lobe ratio (PSLR), integrated-side lobe ratio (ISLR), and impulse response width (IRW), remain essentially the same as with those of the CPU implementation.

Table 3.
Quality metrics comparison of the simulation experiment.
The actual imaging experiments of the CPU and the proposed GPU implementation are performed, where the parameters are the same as those of the simulation experiment. The experimental results are shown in Figure 10. The imaging quality metrics, including structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR), are shown in Table 4. It can be determined that the proposed GPU implementation is capable of correct imaging.
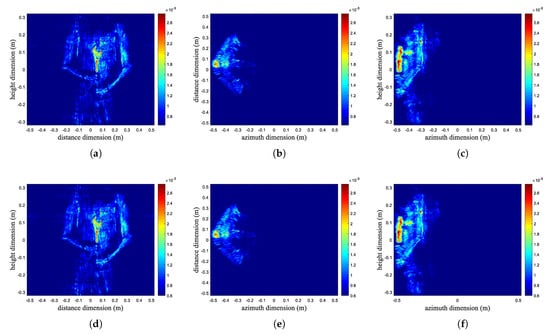
Figure 10.
Imaging results of the actual experiment. (a–c) are the front, top, and side views obtained by the CPU implementation; (d–f) are the front, top, and side views obtained by the proposed GPU implementation.

Table 4.
Imaging quality metrics of the actual experiment.
The comparison of the execution time of each for three methods is shown in Figure 11. The total time is specified from the beginning of parameter setting, reading echo data, to the successful construction of the imaging matrix. The computation time of the GPU-CUDA platform is much smaller than that of the CPU-MATLAB platform, both for the whole process and for each stage. The proposed GPU implementation achieves an acceleration ratio of 35.09 compared to the CPU implementation and 5.97 compared to the conventional GPU implementation. It can be seen that the proposed method can significantly improve imaging efficiency.
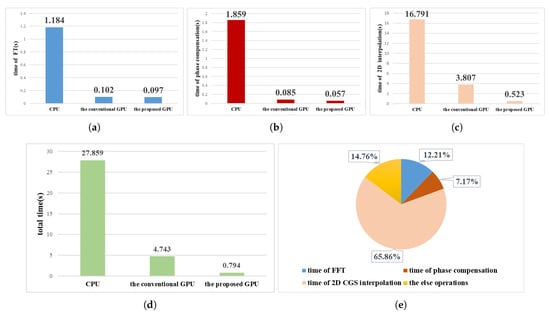
Figure 11.
Comparison of time consumption of each stage for three methods. (a) The FT stage; (b) the phase-compensation stage; (c) the 2D interpolation stage; (d) the total time; (e) the percentage of each stage of the proposed GPU.
To further evaluate the acceleration performance of the proposed GPU implementation, the acceleration ratio is tested for processing the echo data with different frequency-dimension points. As shown in Figure 11e, the maximum time-consuming stage of RMA is 2D interpolation. , the number of the frequency-dimension points which can affect the calculation of 2D interpolation and thus change the size of the imaging matrix, is changed to 25, 50, 75, 100 and 110. The results obtained by processing the echo data with different numbers of frequency-dimension points are shown in Figure 12. When is less than 50, the acceleration ratio of the proposed GPU implementation over the CPU implementation decreases with the increase in the number of points. When is greater than 50, the acceleration ratio of the proposed GPU implementation against the CPU implementation stabilizes at around 35. The speedup ratio of the proposed GPU implementation over the conventional GPU implementation increases with the increase in the number of points, but the increase is not significant. Therefore, when the data size increases, the speedup of the proposed method over CPU and conventional GPU stabilizes.
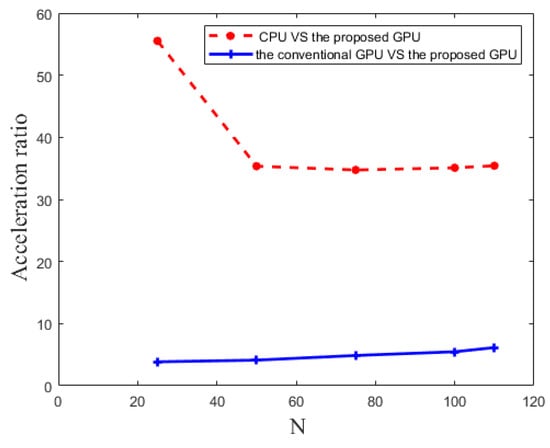
Figure 12.
Acceleration ratios by different frequency-dimension points.
To quantify the contribution of an optimization technique to the overall performance of the proposed GPU implementation, an ablation study is conducted. Binary search and CUDA stream are optimization techniques based on CSG interpolation, so the ablation experiments for these two techniques need to be conducted based on CSG interpolation. As shown in Table 5, the CGS interpolation contributes the most to the performance improvement of the algorithm, where stream parallelism in the CSG optimization technique leads to better performance improvement.

Table 5.
Time consumption of individual optimizations.
5. Conclusions
This paper presents a comprehensive analysis of the 3D cylindrical RMA and its hardware acceleration with GPU on the CUDA platform. The proposed method exploits four CUDA streams for the parallel execution of the CSG method and employs binary search to improve interval search, significantly reducing computational complexity. Additionally, shared memory is utilized to accelerate the Hadamard product, cutting time consumption during the phase-compensation stage. Tested on a hardware setup comprising a 13th Gen Intel® Core® i9-13900K CPU and NVIDIA GeForce RTX 4090 GPU, the proposed method achieves CSAR imaging in 0.794 s in data of . It is 35.09 times faster compared to CPU implementation and 5.97 times faster than the conventional GPU implementation. This conclusively demonstrates that the proposed method achieves substantial performance improvements over both CPU and conventional GPU implementations at this configuration, validating its effectiveness for real-time 3D CSAR imaging. When the data size increases to a certain threshold, the acceleration achieved by the proposed method tends to stabilize when compared to the CPU and conventional GPU implementations.
Author Contributions
Conceptualization, M.C. and P.L.; methodology, M.C. and P.L.; software, M.C. and P.L.; validation, M.C., P.L. and Z.B.; formal analysis, M.C.; investigation, P.L.; resources, M.C., P.L. and M.X.; data curation, Z.B. and M.X.; writing—original draft preparation, M.C. and L.D.; writing—review and editing, M.C. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data can be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lorente, D.; Limbach, M.; Gabler, B.; Esteban, H.; Boria, V.E. Sequential 90 Rotation of Dual-polarized Antenna Elements in Linear Phased Arrays with Improved Cross-polarization Level for Airborne Synthetic Aperture Radar Applications. Remote Sens. 2021, 13, 1430. [Google Scholar] [CrossRef]
- Liu, C.A.; Chen, Z.X.; Shao, Y.; Chen, J.S.; Hasi, T.; Pan, H.Z. Research Advances of SAR Remote Sensing for Agriculture Applications: A Review. J. Integr. Agric. 2019, 18, 506–525. [Google Scholar] [CrossRef]
- Gao, J.; Deng, B.; Qin, Y.; Wang, H.; Li, X. An Efficient Algorithm for MIMO Cylindrical Millimeter-wave Holographic 3-D Imaging. IEEE Trans. Microw. Theory Tech. 2018, 66, 5065–5074. [Google Scholar] [CrossRef]
- Sheen, D.M.; Jones, A.M.; Hall, T.E. Simulation of Active Cylindrical and Planar Millimeter-wave Imaging Systems. In Proceedings of the Passive and Active Millimeter-Wave Imaging XXI, Orlando, FL, USA, 15–19 April 2018; SPIE: Bellingham, WA USA, 2018; pp. 47–57. [Google Scholar]
- Alibakhshikenari, M.; Virdee, B.S.; Limiti, E. Wideband Planar Array Antenna Based on SCRLH-TL for Airborne Synthetic Aperture Radar Application. J. Electromagn. Waves Appl. 2018, 32, 1586–1599. [Google Scholar] [CrossRef]
- Appleby, R.; Wallace, H.B. Standoff Detection of Weapons and Contraband in the 100 GHz to 1 THz Region. IEEE Trans. Antennas Propag. 2007, 55, 2944–2956. [Google Scholar] [CrossRef]
- Kim, B.; Yoon, K.S.; Kim, H.J. Gpu-accelerated Laplace Equation Model Development Based on CUDA Fortran. Water 2021, 13, 3435. [Google Scholar] [CrossRef]
- Gao, Y.; Han, J.; Tian, H.; Zhang, R.; Zheng, S.; Wang, H. GPU Acceleration Method Based on Range-Doppler Highly Squint Algorithm. In Proceedings of the 2023 4th China International SAR Symposium (CISS), Xi’an, China, 4–6 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–4. [Google Scholar]
- Cui, Z.; Quan, H.; Cao, Z.; Xu, S.; Ding, C.; Wu, J. SAR Target CFAR Detection via GPU Parallel operation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4884–4894. [Google Scholar] [CrossRef]
- Wu, S.; Xu, Z.; Wang, F.; Yang, D.; Guo, G. An Improved Back-projection Algorithm for GNSS-R BSAR Imaging Based on CPU and GPU Platform. Remote Sens. 2021, 13, 2107. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, X.; Xu, Q.; Zhang, S.; Wang, T. An Embedded-GPU-Based Scheme for Real-Time Imaging Processing of Unmanned Aerial Vehicle Borne Video Synthetic Aperture Radar. Remote Sens. 2024, 16, 191. [Google Scholar] [CrossRef]
- Li, Z.; Qiu, X.; Yang, J.; Meng, D.; Huang, L.; Song, S. An Efficient BP Algorithm Based on TSU-ICSI Combined with GPU Parallel Computing. Remote Sens. 2023, 15, 5529. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, H.; Lai, T. Real-Time Imaging Scheme of Short-Track GB-SAR Based on GPU+ OpenMP. IEEE Sens. J. 2024, 25, 4990–5002. [Google Scholar] [CrossRef]
- Gou, L.; Li, Y.; Zhu, D.; Wei, Y. A Real-time Algorithm for Circular Video SAR Imaging Based on GPU. Radar Sci. Technol. 2019, 17, 550–556. [Google Scholar]
- Ren, Z.; Zhu, D. A GPU-Based Two-Step Approach for High Resolution SAR Imaging. In Proceedings of the 2021 IEEE 6th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 22–24 October 2021; IEEE: New York, NY, USA, 2021; pp. 376–380. [Google Scholar]
- Ding, L.; Dong, Z.; He, H.; Zheng, Q. A Hybrid GPU and CPU Parallel Computing Method to Accelerate Millimeter-Wave Imaging. Electronics 2023, 12, 840. [Google Scholar] [CrossRef]
- Li, J.; Song, L.; Liu, C. The Cubic Trigonometric Automatic Interpolation Spline. IEEE/CAA J. Autom. Sin. 2017, 5, 1136–1141. [Google Scholar] [CrossRef]
- Liu, J.; Qiu, X.; Huang, L.; Ding, C. Curved-path SAR Geolocation Error Analysis Based on BP Algorithm. IEEE Access 2019, 7, 20337–20345. [Google Scholar] [CrossRef]
- Wang, G.; Qi, F.; Liu, Z.; Liu, C.; Xing, C.; Ning, W. Comparison between Back Projection Algorithm and Range Migration Algorithm in Terahertz Imaging. IEEE Access 2020, 8, 18772–18777. [Google Scholar] [CrossRef]
- Miao, X.; Shan, Y. SAR Target Recognition via Sparse Representation of Multi-view SAR Images with Correlation Analysis. J. Electromagn. Waves Appl. 2019, 33, 897–910. [Google Scholar] [CrossRef]
- Ding, L.; He, H.; Wang, T.; Chu, D. Cylindrical SAR Imaging Based on a Concentric-square-grid Interpolation Method. J. Electron. Inf. Technol. 2024, 46, 249–257. [Google Scholar]
- Soumekh, M. Reconnaissance with Slant Plane Circular SAR Imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef]
- Xueming, P.; Wen, H.; Yanping, W.; Kuoye, H.; Yirong, W. Downward Looking Linear Array 3D SAR Sparse Imaging with Wave-front Curvature Compensation. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC 2013), Kunming, China, 5–8 August 2013; IEEE: New York, NY, USA, 2013; pp. 1–4. [Google Scholar]
- Berland, F.; Fromenteze, T.; Decroze, C.; Kpre, E.L.; Boudesocque, D.; Pateloup, V.; Di Bin, P.; Aupetit-Berthelemot, C. Cylindrical MIMO-SAR Imaging and Associated 3-D Fourier Processing. IEEE Open J. Antennas Propag. 2021, 3, 196–205. [Google Scholar] [CrossRef]
- Xin, W.; Lu, Z.; Weihua, G.; Pcng, F. Active Millimeter-wave Near-field Cylindrical Scanning Three-dimensional Imaging System. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 7–11 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar]
- Yang, T.; Xu, Q.; Meng, F.; Zhang, S. Distributed Real-time Image Processing of Formation Flying SAR Based on Embedded GPUs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6495–6505. [Google Scholar] [CrossRef]
- Tian, H.; Hua, W.; Gao, Y.; Sun, Z.; Cai, M.; Guo, Y. Research on Real-time Imaging Method of Airborne SAR Based on Embedded GPU. In Proceedings of the 2022 3rd China International SAR Symposium (CISS), Shanghai, China, 2–4 November 2022; IEEE: New York, NY, USA, 2022; pp. 1–4. [Google Scholar]
- Lin, A. Binary search algorithm. WikiJournal Sci. 2019, 2, 1–13. [Google Scholar] [CrossRef]
- Bajwa, M.S.; Agarwal, A.P.; Manchanda, S. Ternary search algorithm: Improvement of Binary Search. In Proceedings of the 2015 2nd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 11–13 March 2015; IEEE: New York, NY, USA, 2015; pp. 1723–1725. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).