Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features
Abstract
1. Introduction
- Employing Fast Fourier Transform (FFT) to extract frequency-domain features from the data, capturing periodicity and frequency characteristics, thus providing a richer and more accurate feature representation that enhances the model’s understanding of complex signal patterns.
- Performing CEEMDAN signal decomposition to separate the electricity sequence into different frequency components, each of which is handled separately. This module addresses the complexity of the components in the electricity sequence and provides more precise inputs for subsequent predictions, thereby improving the model’s prediction performance.
- Integrating iTransformer and LSTM in the feature extraction and prediction process. The iTransformer model focuses on handling high-frequency, rapidly changing IMFs, while the LSTM model addresses low-frequency, long-term IMF changes. By combining these two models, we improve the overall prediction performance, enabling more accurate forecasting of electricity sequences.
2. Related Work
3. The Overall Framework of the Proposed Model for Power Prediction
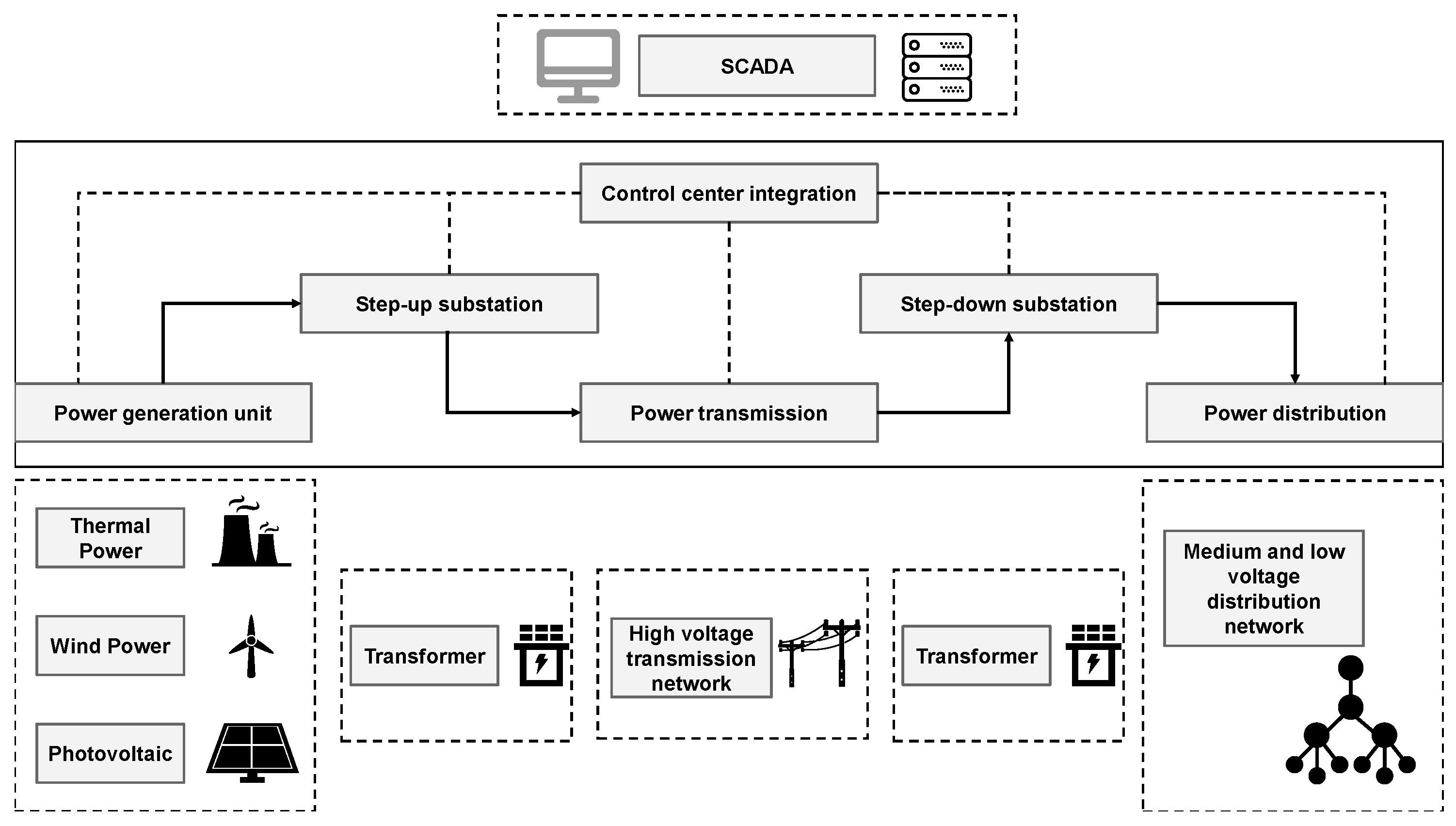
3.1. Power System Components and Sensor Deployment
3.2. Problem Description
3.3. Overview of Our Structure
- First, the original power sequence data are input and decomposed using the CEEMDAN algorithm, resulting in several intrinsic mode function (IMF) components and a residual. Typically, IMF1 represents the high-frequency components of the signal, while IMF2, IMF3, ⋯, and IMFn represent the mid- and low-frequency components, which correspond to the medium- and long-term trends in the power sequence.
- Second, a fast Fourier transform (FFT) is applied to the first IMF to extract frequency domain features. These frequency features are transformed into real numbers and combined with time domain features to form a richer feature space. This step facilitates the capture of the periodic and frequency characteristics of the signal.
- The frequency and time domain features of IMF1 are then fed into the iTransformer model for forecasting. First, the frequency and time domain features of IMF1 are mapped to a high-dimensional space via an embedding layer, treating each feature as an individual token. Subsequently, a self-attention mechanism processes these tokens to identify and emphasize key features and patterns within the time series. In addition, a feed-forward neural network further refines and processes these features to enhance the model’s understanding of the time series dynamics. Finally, the iTransformer model outputs the forecasted results for IMF1.
- For the remaining IMF components and the residual, an LSTM is employed for forecasting. Each IMF component is independently input into the LSTM model, which leverages its recurrent structure to memorize past information and predict future values.
- Finally, the forecasted results of each IMF component and the residual are aggregated through summation to yield the complete forecast for the entire power sequence.
3.4. CEEMDAN
- The noise-added sequence is decomposed using EMD to extract the first-order mode component . By averaging the mode components obtained from N experiments, the IMF of the CEEMDAN decomposition is obtained as Equation (2):The residual after removing is then calculated as Equation (3):
- Gaussian white noise is added to the residual , and the EMD process is repeated to extract the next intrinsic mode function and update the residual .
- This process is continuously repeated until the residual signal exhibits a monotonic trend, at which point the decomposition is terminated. Consequently, the original sequence is decomposed into K sub-sequences along with a residual sequence as Equation (4):where K denotes the total number of intrinsic mode functions obtained, and is the final residual signal.
3.5. Fast Fourier Transformer
3.6. iTransformer
3.6.1. Embedding Layer
3.6.2. Multi-Head Self-Attention Mechanism
- Query, Key, and Value Mappings: The input data are first mapped into three distinct representations, namely, query, key, and value, using different weight matrices. Assume that there are h attention heads, each with independent linear transformations for queries, keys, and values. For the i-th attention head as Equation (6):where are the weight matrices for the i-th attention head, is the dimension of the query and key, and denotes the model’s dimension.
- Dot-Product Attention: Each head independently computes the dot product between the queries and keys, scales the result, and then applies the softmax function for normalization to obtain the attention weights as Equation (7):where represents the attention weights.
- Weighted Sum: The obtained attention weights are used to compute a weighted sum of the values, yielding the self-attention score for each head as Equation (8):
- Merging the Heads: The outputs from all heads are concatenated to obtain the final output, typically achieved through concatenation followed by a linear transformation as Equation (9):where is the concatenated matrix, and is the output linear transformation matrix.
3.6.3. Feed-Forward Network
3.6.4. Normalization and Residual Connections
- Normalization and Residual Connection After the Self-Attention Mechanism as Equation (11):where X is the input, is the output of the self-attention layer, and is the output after the normalization and residual connection.
- Normalization and Residual Connection After the Feed-Forward Network as Equation (12):where is the output of the feed-forward network, and is the final output.
3.7. LSTM
4. Experiments and Performance Evaluation
4.1. Experiment Environment
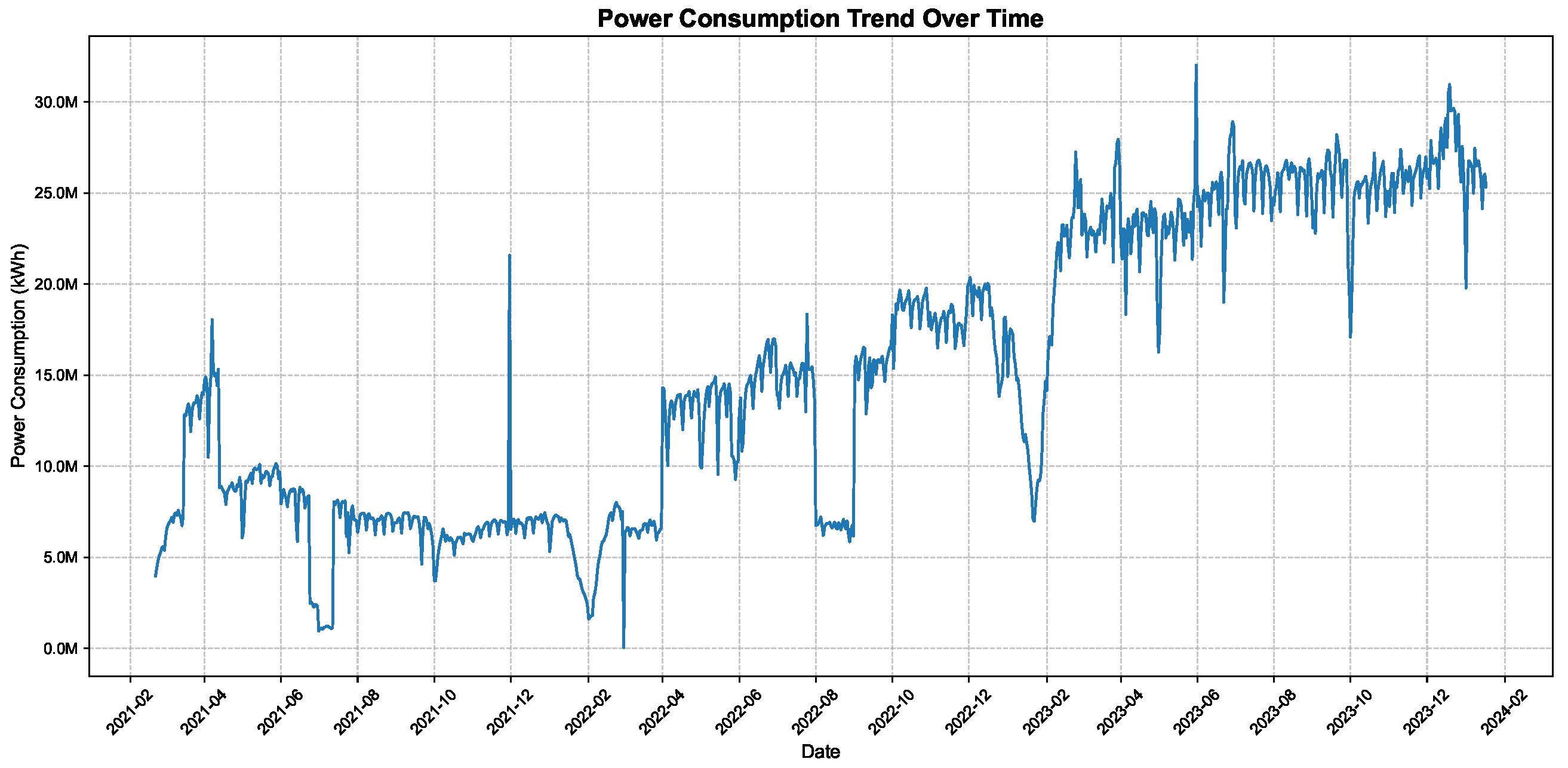
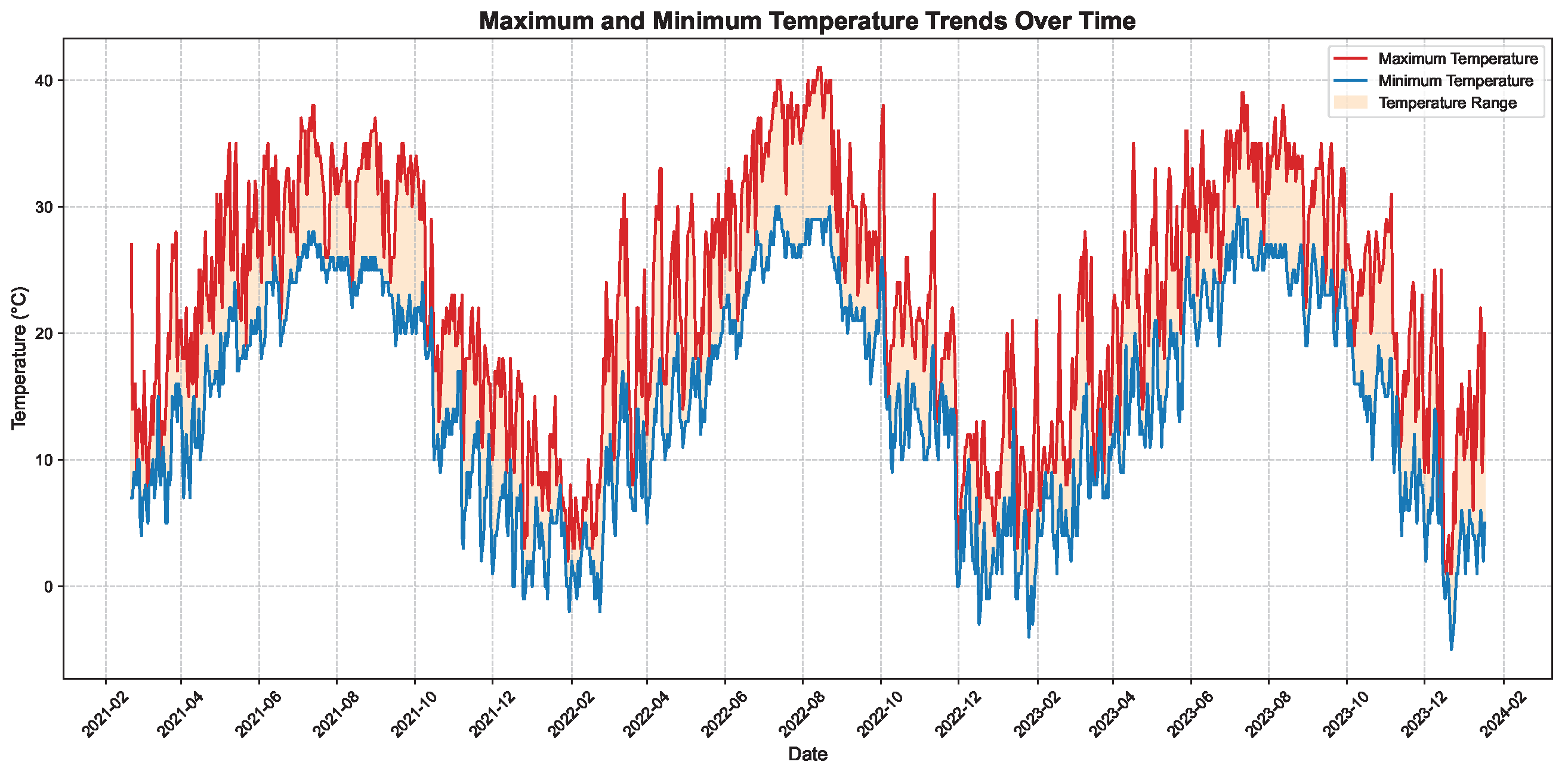
4.2. Dataset
4.3. Evaluation Metrics
4.4. Hyperparameter Selection
4.4.1. Lookback_len
4.4.2. Epochs
4.4.3. Learning Rate
4.4.4. All Hyperparameters
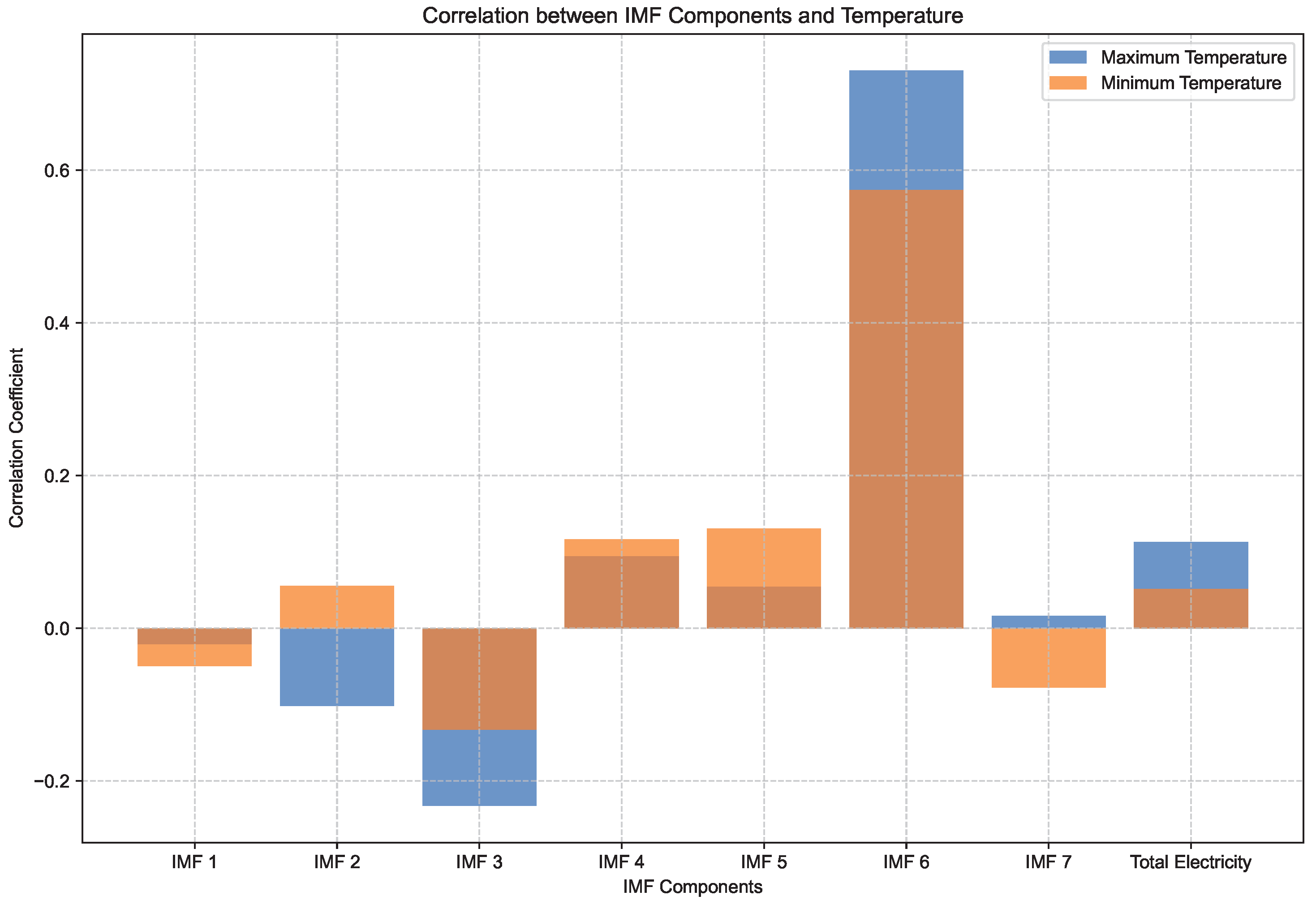
4.5. Analysis of IMFs
4.6. Experiments on the Electricity Dataset
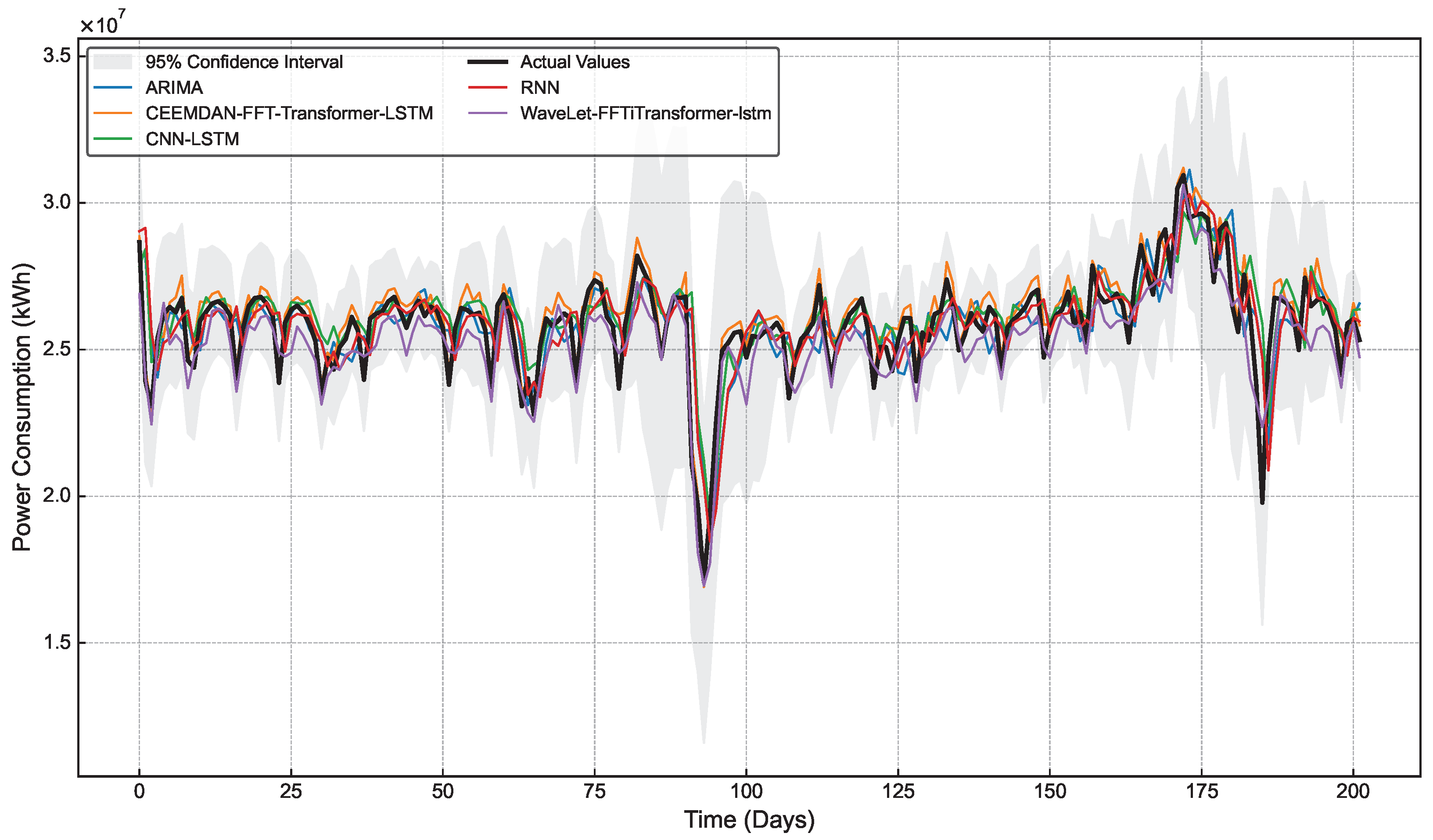
4.6.1. Comparison of Different Models
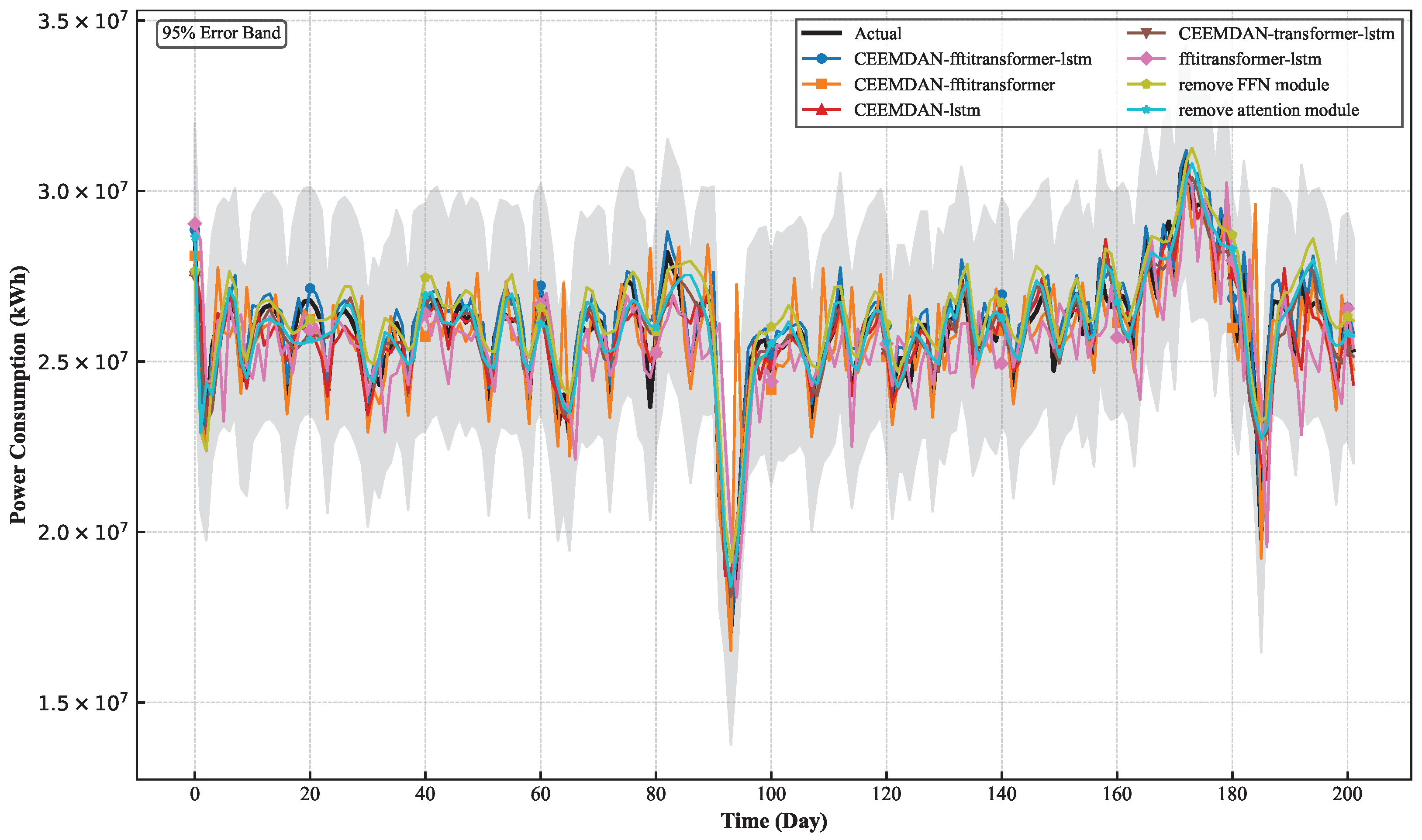
4.6.2. The Influence of Different Modules
5. Conclusions
- Firstly, the model accurately captures both the short-term fluctuations and long-term trends of power loads, substantially improving forecasting accuracy. This not only aids power companies in optimizing the scheduling of generation and energy storage systems, thereby reducing unnecessary energy waste and operating costs, but also decreases the demand for large-scale storage systems.
- Secondly, the stability of the power grid relies on balancing power supply and demand. The high-precision load forecasting provided by our model can significantly reduce power fluctuations, thereby mitigating safety issues associated with such fluctuations. A more stable power supply enhances grid safety and delivers more reliable power services to consumers.
- Lastly, our model offers high-precision data support and optimized scheduling capabilities for smart grids, fostering the intelligent development of the power system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, D. International energy agency (IEA). In The Palgrave Encyclopedia of Global Security Studies; Springer: Berlin/Heidelberg, Germany, 2023; pp. 830–836. [Google Scholar]
- Maheswaran, D.; Rangaraj, V.; Kailas, K.J.; Kumar, W.A. Energy efficiency in electrical systems. In Proceedings of the 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; IEEE: New York, NY, USA, 2012; pp. 1–6. [Google Scholar]
- Van Heddeghem, W.; Lambert, S.; Lannoo, B.; Colle, D.; Pickavet, M.; Demeester, P. Trends in worldwide ICT electricity consumption from 2007 to 2012. Comput. Commun. 2014, 50, 64–76. [Google Scholar] [CrossRef]
- McRuer, D.T.; Graham, D.; Ashkenas, I. Aircraft Dynamics and Automatic Control; Princeton University Press: Princeton, NJ, USA, 2014; Volume 2731. [Google Scholar]
- Mourshed, M.; Robert, S.; Ranalli, A.; Messervey, T.; Reforgiato, D.; Contreau, R.; Becue, A.; Quinn, K.; Rezgui, Y.; Lennard, Z. Smart grid futures: Perspectives on the integration of energy and ICT services. Energy Procedia 2015, 75, 1132–1137. [Google Scholar] [CrossRef]
- Khalil, M.I.; Jhanjhi, N.; Humayun, M.; Sivanesan, S.; Masud, M.; Hossain, M.S. Hybrid smart grid with sustainable energy efficient resources for smart cities. Sustain. Energy Technol. Assessments 2021, 46, 101211. [Google Scholar] [CrossRef]
- Pao, H.T. Comparing linear and nonlinear forecasts for Taiwan’s electricity consumption. Energy 2006, 31, 2129–2141. [Google Scholar] [CrossRef]
- Zhang, B.; Yin, J.; Jiang, H.; Chen, S.; Ding, Y.; Xia, R.; Wei, D.; Luo, X. Multi-source data assessment and multi-factor analysis of urban carbon emissions: A case study of the Pearl River Basin, China. Urban Clim. 2023, 51, 101653. [Google Scholar] [CrossRef]
- Efekemo, E.; Saturday, E.; Ofodu, J. Electricity demand forecasting: A review. Educ. Res. IJMCER 2022, 4, 279–301. [Google Scholar]
- Lai, X.; He, M.; Hu, W.; Zhang, Y.; Du, P.; Liu, R.; Song, X.; Zheng, T. Multi-factor Electric Load Forecasting Based on Improved Variational Mode Decomposition and Deep Learning. Comput. Eng. 2025, 51, 375–386. [Google Scholar] [CrossRef]
- Li, S. FFT-CNN-LSTM-Based Short-Term Electric Load Forecasting. Master’s Thesis, Nanchang University, Nanchang, China, 2021. [Google Scholar]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Muzaffar, S.; Afshari, A. Short-term load forecasts using LSTM networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Morid, M.A.; Sheng, O.R.L.; Dunbar, J. Time series prediction using deep learning methods in healthcare. ACM Trans. Manag. Inf. Syst. 2023, 14, 1–29. [Google Scholar] [CrossRef]
- Zhu, S.; Ma, H.; Chen, L.; Wang, B.; Wang, H.; Li, X.; Gao, W. Short-term load forecasting of an integrated energy system based on STL-CPLE with multitask learning. Prot. Control Mod. Power Syst. 2024, 9, 71–92. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; He, Y.; Wang, Y. Short-term load-forecasting method based on wavelet decomposition with second-order gray neural network model combined with ADF test. IEEE Access 2017, 5, 16324–16331. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Jiang, Y.; Sun, L.; Zhao, R.; Yan, K.; Wang, W. Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model. J. Clean. Prod. 2022, 354, 131724. [Google Scholar] [CrossRef]
- Cao, J.; Li, Z.; Li, J. Financial time series forecasting model based on CEEMDAN and LSTM. Phys. A Stat. Mech. Its Appl. 2019, 519, 127–139. [Google Scholar] [CrossRef]
- Schwarz, K.; Sideris, M.; Forsberg, R. The use of FFT techniques in physical geodesy. Geophys. J. Int. 1990, 100, 485–514. [Google Scholar] [CrossRef]
- Jha, A.; Dorkar, O.; Biswas, A.; Emadi, A. iTransformer Network Based Approach for Accurate Remaining Useful Life Prediction in Lithium-Ion Batteries. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Rosemont, IL, USA, 19–21 June 2024; IEEE: New York, NY, USA, 2024; pp. 1–8. [Google Scholar]
- Voita, E.; Talbot, D.; Moiseev, F.; Sennrich, R.; Titov, I. Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned. arXiv 2019, arXiv:1905.09418. [Google Scholar]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Cavus, M.; Dissanayake, D.; Bell, M. Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies 2025, 18, 995. [Google Scholar] [CrossRef]
- Cavus, M.; Ugurluoglu, Y.F.; Ayan, H.; Allahham, A.; Adhikari, K.; Giaouris, D. Switched auto-regressive neural control (S-ANC) for Energy Management of Hybrid Microgrids. Appl. Sci. 2023, 13, 11744. [Google Scholar] [CrossRef]
- He, Y.L.; Chen, L.; Gao, Y.; Ma, J.H.; Xu, Y.; Zhu, Q.X. Novel double-layer bidirectional LSTM network with improved attention mechanism for predicting energy consumption. ISA Trans. 2022, 127, 350–360. [Google Scholar] [CrossRef] [PubMed]
- Kalpakis, K.; Gada, D.; Puttagunta, V. Distance measures for effective clustering of ARIMA time-series. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; IEEE: New York, NY, USA, 2001; pp. 273–280. [Google Scholar]
- Tokgöz, A.; Ünal, G. A RNN based time series approach for forecasting turkish electricity load. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Zhang, K.; Gençay, R.; Yazgan, M.E. Application of wavelet decomposition in time-series forecasting. Econ. Lett. 2017, 158, 41–46. [Google Scholar] [CrossRef]
- Francia, G.A., III; El-Sheikh, E. NERC CIP standards: Review, compliance, and training. In Global Perspectives on Information Security Regulations: Compliance, Controls, and Assurance; IGI Global Scientific Publishing: Hershey, PA, USA, 2022; pp. 48–71. [Google Scholar]



| Component | Hyperparameter | Value |
|---|---|---|
| iTransformer | Number of Attention Heads | 4 |
| Model Dimension () | 128 | |
| Feed-Forward Dimension () | 512 | |
| Lookback_len | 13 | |
| LSTM | Hidden Units | 128 |
| Number of Layers | 2 | |
| Lookback_len | 13 | |
| Training Protocol | Batch Size | 64 |
| Optimizer | Adam | |
| Learning Rate | 0.0005 | |
| Dropout Rate | 0.1 | |
| Epochs | 30 |
| Model | MAE | RMSE | MAPE | Runing Time | |
|---|---|---|---|---|---|
| ARIMA | 0.4082 | 978,364 | 1,373,665 | 3.9482 | 437.79 s |
| RNN | 0.4216 | 947,789 | 1,318,733 | 3.7781 | 350.45 s |
| CNN-LSTM | 0.4561 | 839,569 | 1,222,934 | 3.4421 | 508.21 s |
| Wavelet-FFTiTransformer-lstm | 0.6481 | 752,242 | 1,055,756 | 2.8513 | 730.46 s |
| CEEMDAN-FFTiTransformer-lstm | 0.9055 | 413,919 | 557,146 | 1.6794 | 691.21 s |
| Model | MAE | RMSE | MAPE | |
|---|---|---|---|---|
| FFTiTansformer-lstm | 0.4105 | 933,443 | 1,352,483 | 3.7655 |
| CEEMDAN-FFTiTansformer | 0.5735 | 808,920 | 1,106,976 | 3.0205 |
| Remove attention module | 0.6141 | 784,584 | 942,812 | 2.934 |
| Remove FFN module | 0.6237 | 764,367 | 931,723 | 2.914 |
| CEEMDAN-lstm | 0.6756 | 735,593 | 919,846 | 2.8432 |
| CEEMDAN-iTransformer-lstm | 0.7878 | 654,113 | 831,325 | 2.2797 |
| CEEMDAN-FFTiTransformer-lstm | 0.9055 | 413,919 | 557,146 | 1.6794 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Shen, W.; Wu, C.Q. Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features. Electronics 2025, 14, 2036. https://doi.org/10.3390/electronics14102036
Jin Y, Shen W, Wu CQ. Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features. Electronics. 2025; 14(10):2036. https://doi.org/10.3390/electronics14102036
Chicago/Turabian StyleJin, Yucheng, Wei Shen, and Chase Q. Wu. 2025. "Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features" Electronics 14, no. 10: 2036. https://doi.org/10.3390/electronics14102036
APA StyleJin, Y., Shen, W., & Wu, C. Q. (2025). Power Prediction Based on Signal Decomposition and Differentiated Processing with Multi-Level Features. Electronics, 14(10), 2036. https://doi.org/10.3390/electronics14102036







