FICConvNet: A Privacy-Preserving Framework for Malware Detection Using CKKS Homomorphic Encryption
Abstract
1. Introduction
- Lightweight Ciphertext Inference Architecture and Acceleration Strategy
- −
- Integrating Depthwise Separable Convolution (DS Conv) with Sparse Projection techniques reduces the number of homomorphic multiplications and ciphertext rotations, thereby decreasing computational overhead. Based on this, we designed a ciphertext-friendly convolution module FICConv to achieve efficient Ciphertext Inference.
- −
- We proposed a Dynamic Multi-byte Mapping Algorithm to generate malicious code images through weighted arithmetic and mean value, compressing data volume while retaining key features.
- Adaptive Learning Activation Function and Accuracy Compensation Mechanisms
- −
- We designed a dynamic parametric polynomial activation function (ALPolyAct), combined with L2 regularization and Residual Connection, to adapt to the feature distribution across different network layers, enhancing the model’s expressiveness and inference accuracy.
- End-to-End Non-Interactive Framework for Privacy Protection
- −
- Zero-decryption inference is achieved through the use of single ciphertext inference technology. Users upload only encrypted data and receive encrypted results, reducing communication overhead and eliminating the risk of data leakage due to the absence of decryption operations on the server side.
2. Related Works
2.1. DL for Malware Detection
2.2. Neural Network Model Based on HE
3. Method
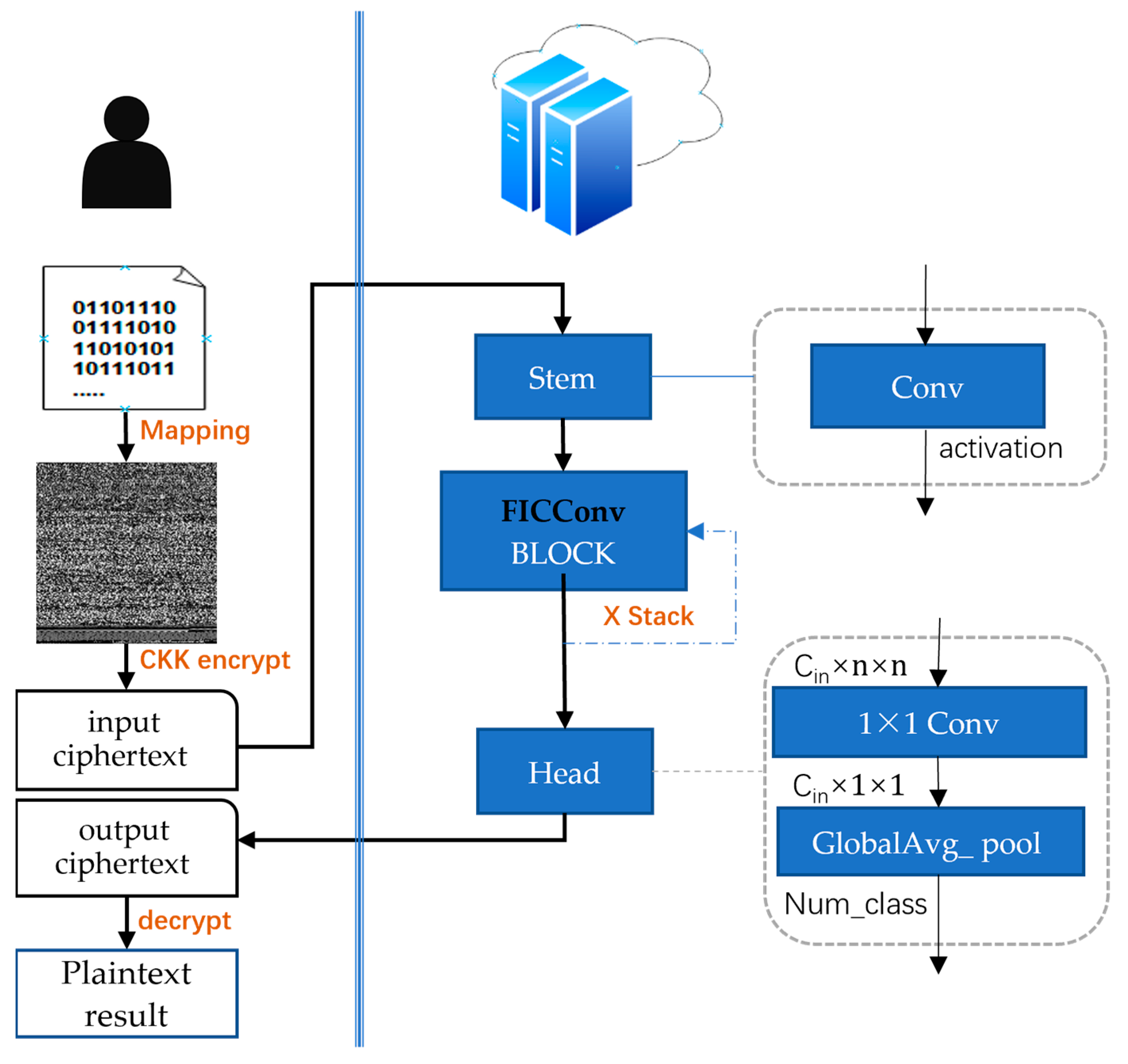
3.1. Overall Architecture Design
3.1.1. Client Side
- Visualization:
- Encrypted Input:
- Decrypted output:
3.1.2. Server Side
- Stem
- Backbone
- Head
3.2. Data Preprocessing
3.3. Ciphertext Inference Model Optimization
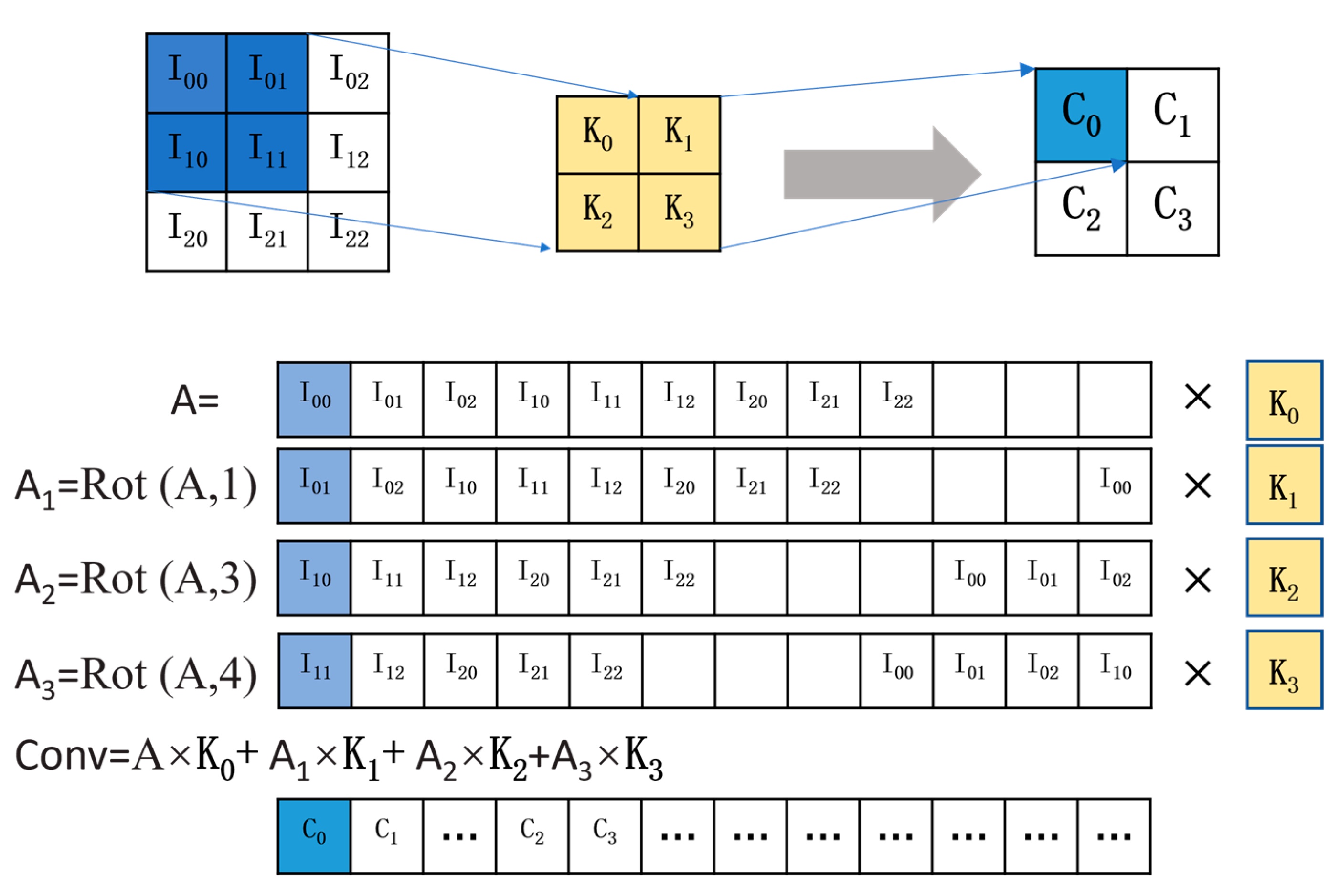
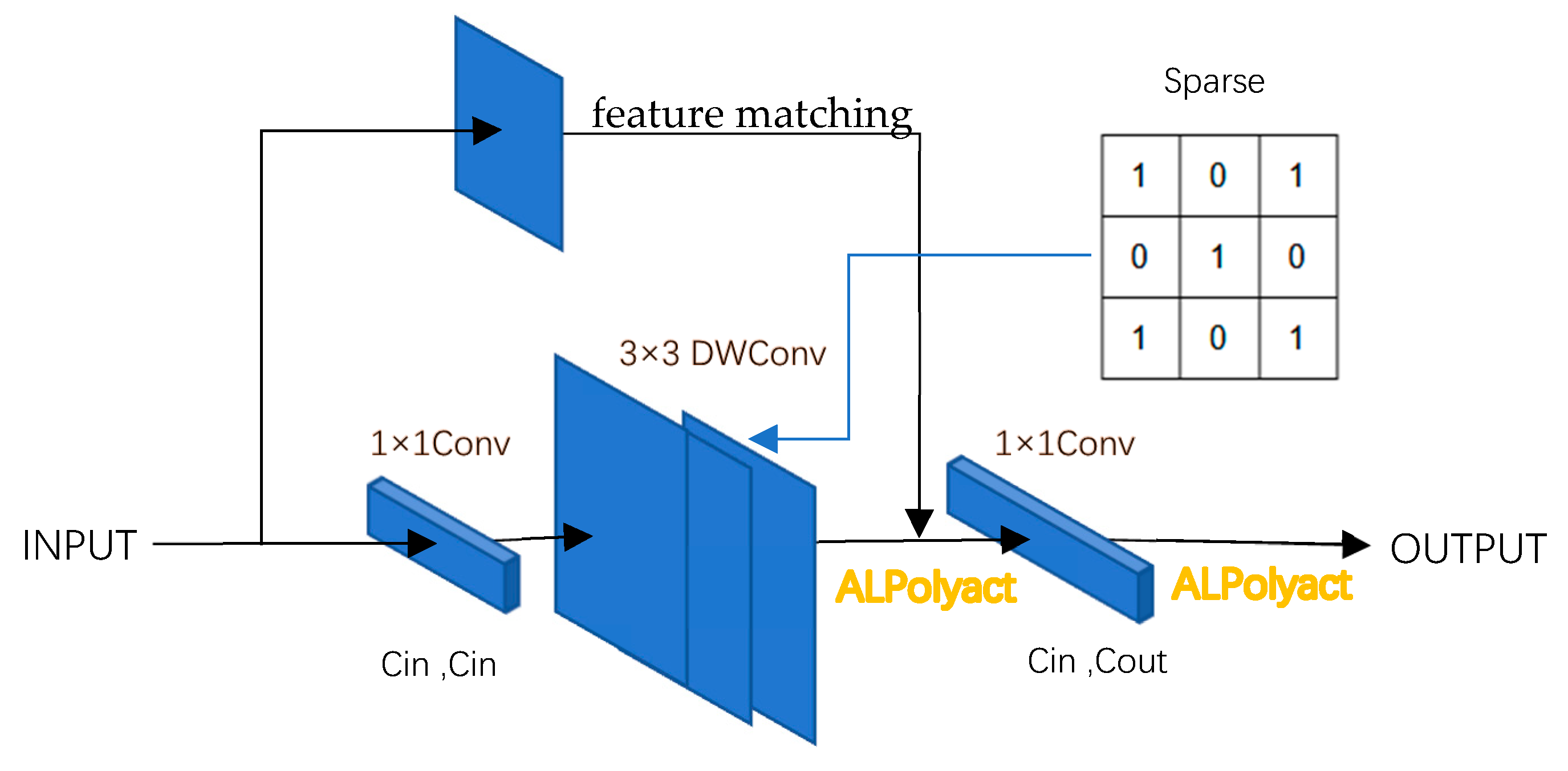
3.3.1. Convolution Layer Optimization
- Rotated Ciphertext Convolution Algorithm
- DS Conv
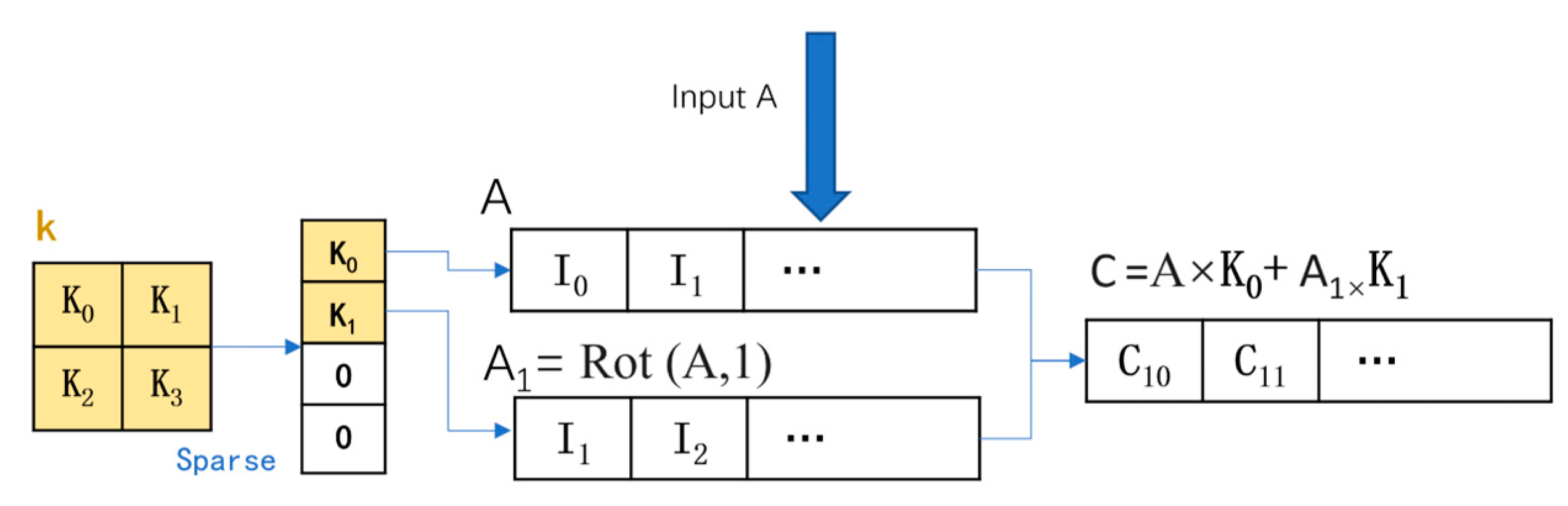
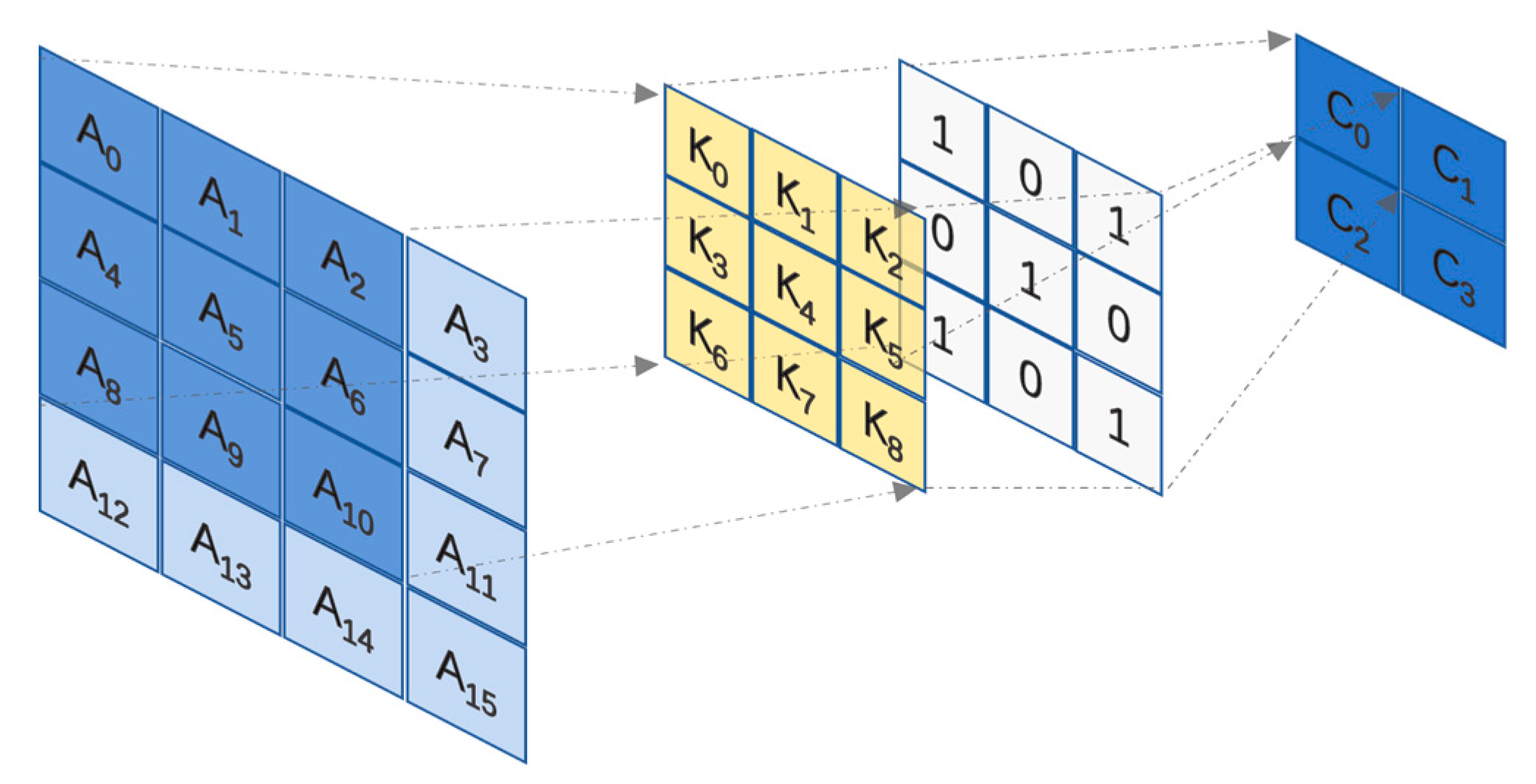
- Sparse projection
3.3.2. A Learning Polynomial Activation Function (ALPolyAct)
| Algorithm 1 ALPolyAct Parameter Training |
| Input: Training dataset D, regularization strength λ = 0.01, learning rate η, epoch N. Output: For each ALPolyAct layer l 1: Start 2: Initialize ALPolyAct for each layer l: α1(l) = 0.4, α2(l) = 0.3, α3(l) = 0.2. 3: for epoch = 1 to N do 4: Forward propagation 5: for each layer l = 1 to L do 6: 7: // Per-layer ALPolyAct 8: Compute Loss 9: 10: 11: 12: Backward propagation and parameter update 13: Compute gradients for all layers 14: for each ALPolyAct layer l do 15: //Update parameters 16: 17: 18: End |
3.3.3. Pooling Layer
3.4. Fast-Inference Ciphertext Convolution (FICConv)
4. Experimental Results
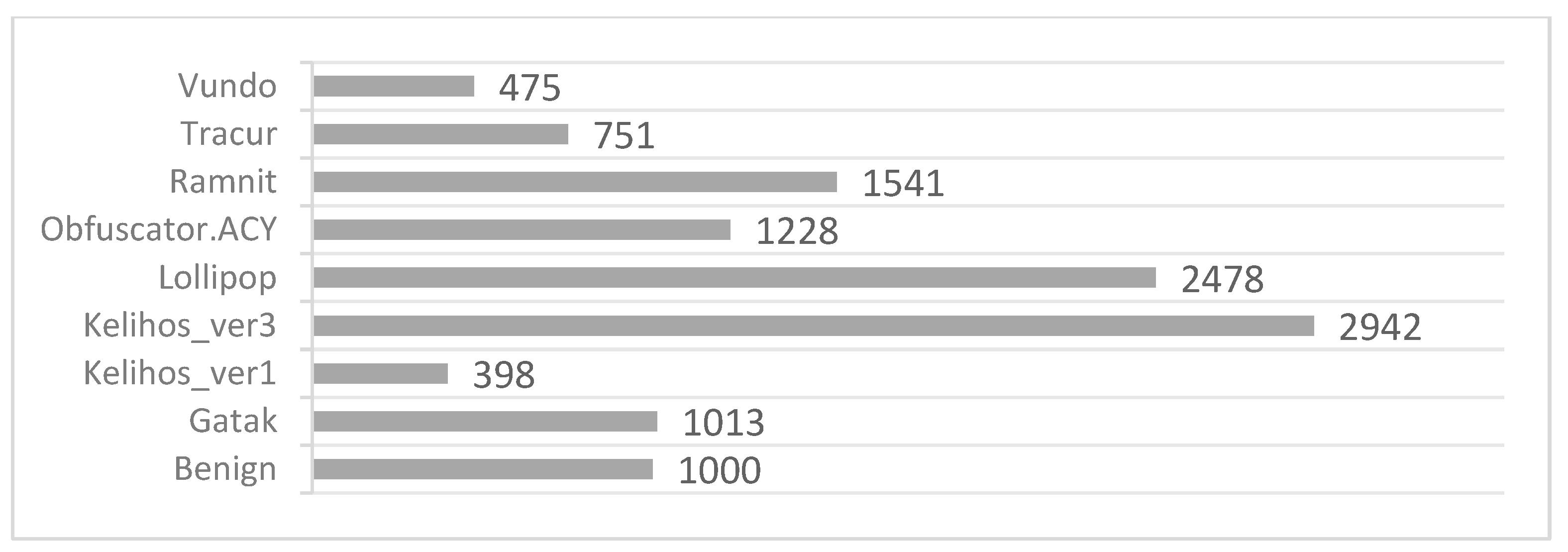
4.1. Experimental Setup, Dataset, and Validation
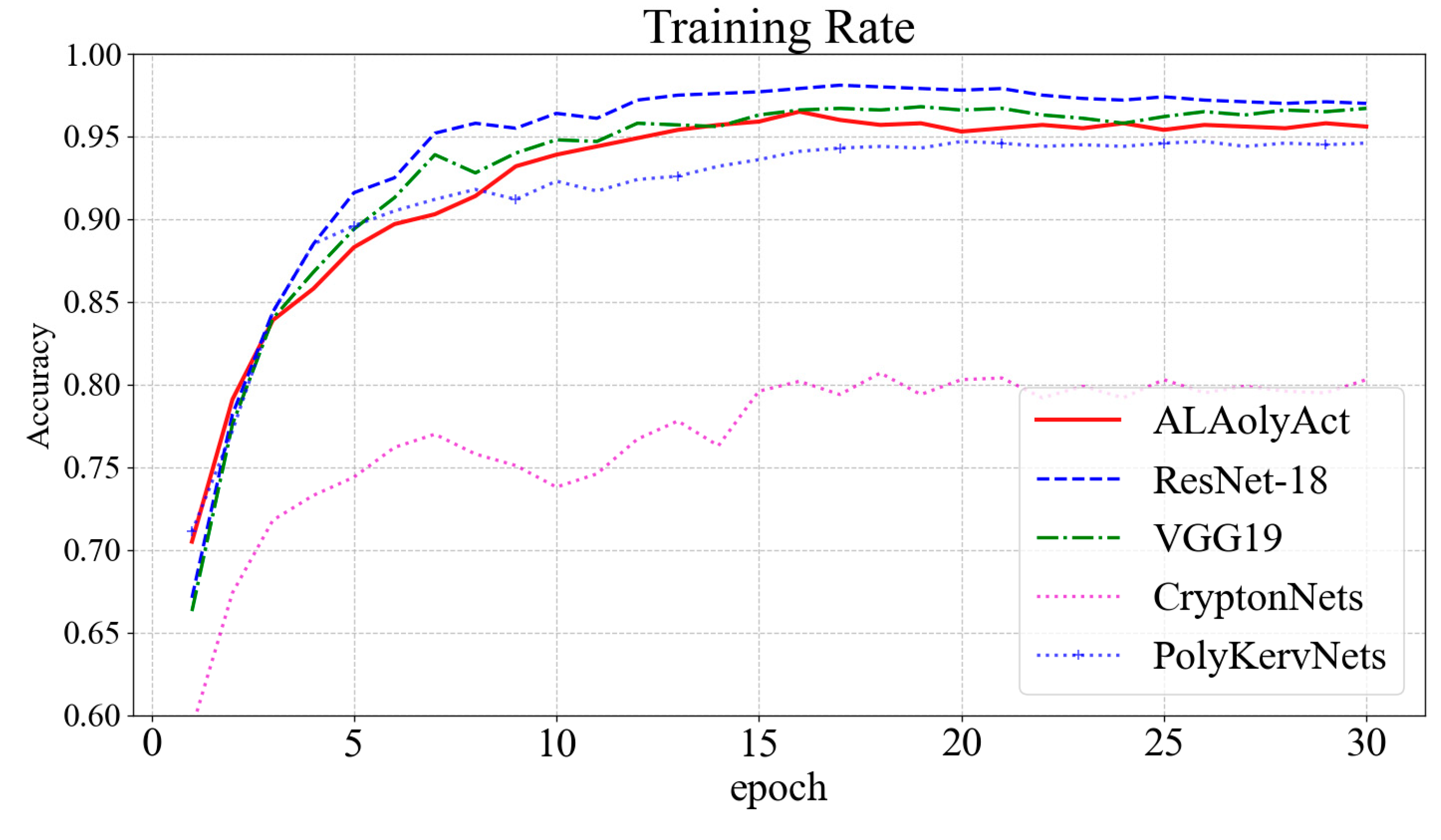
4.2. Comparative Experiments
4.3. Ablation Experiment
5. Discussion
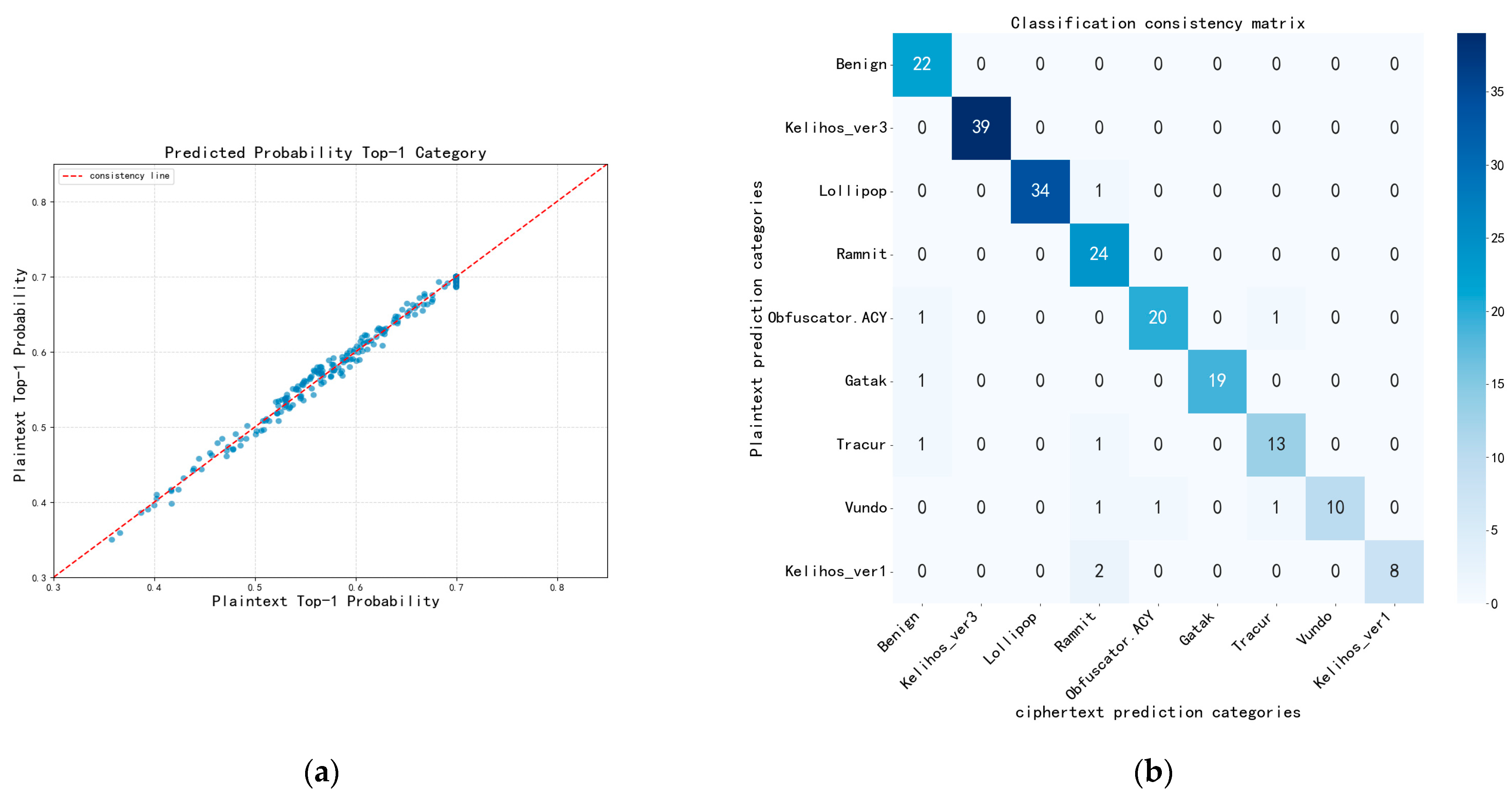
5.1. Security Discussion
5.2. Communications Cost Analysis
5.3. Scalability Discussion
5.4. Limitations Discussion
- Latency Issues
- Detection Accuracy
- Multi-user Environment
- Impact of Homomorphic Encryption
- Dataset Limitations
6. Conclusions and Future Work
- Ciphertext reasoning acceleration: In this paper, we only optimize the reasoning computation at the model level, but this is far from meeting the requirements of practical applications, and in the future, we will study how to further compress the computation latency by combining hardware acceleration techniques (GPU/FPGA).
- Model Capacity Enhancement: Due to the limitations of ciphertext computing, our current models are not yet able to introduce overly complex network building blocks. Therefore, we will explore how the efficient network modules implemented on ciphertext can enhance the model learning capability; introduce knowledge distillation or federated learning framework to cope with the capacity constraints of the ciphertext model capacity by using the knowledge migration of the instructor model.
- We will also focus on deployment issues in real-world scenarios to identify and address the challenges and limitations that may arise in practical environments. This includes evaluating the model’s encryption levels under varying security requirements, optimizing system communication in multi-user contexts, and ensuring the scalability and efficiency of the model when integrated into existing infrastructures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ANY.RUN. Malware Trends Report: Q4. 2024. Available online: https://any.run/cybersecurity-blog/malware-trends-q4-2024 (accessed on 1 January 2024).
- ENISA. ENISA Threat Landscape 2024. 2024. Available online: https://www.enisa.europa.eu/publications/enisa-threat-landscape-2024 (accessed on 25 January 2025).
- Vellela, S.S.; Balamanigandan, R.; Praveen, S.P. Strategic Survey on Security and Privacy Methods of Cloud Computing Environment. J. Next Gener. Technol. 2022, 2, 70–78. [Google Scholar]
- Choi, S.; Jang, S.; Kim, Y.; Kim, J. Malware Detection using Malware Image and Deep Learning. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 18–20 October 2017; pp. 1193–1195. [Google Scholar]
- Nataraj, L.; Karthikeyan, S.; Jacob, G.; Manjunath, B.S. Malware images: Visualization and automatic classification. In Proceedings of the 8th International Symposium on Visualization for Cyber Security, Pittsburgh, PA, USA, 20 July 2011; pp. 1–7. [Google Scholar]
- Cui, Z.; Xue, F.; Cai, X.; Cao, Y.; Wang, G.G.; Chen, J. Detection of malicious code variants based on deep learning. IEEE Trans. Ind. Inform. 2018, 14, 3187–3196. [Google Scholar] [CrossRef]
- Kalash, M.; Rochan, M.; Mohammed, N.; Bruce, N.D.; Wang, Y.; Iqbal, F. Malware classification with deep convolutional neural networks. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 26–28 February 2018; pp. 1–5. [Google Scholar]
- Jang, S.; Li, S.; Sung, Y. Generative adversarial network for global image-based local image to improve malware classification using convolutional neural network. Appl. Sci. 2020, 10, 7585. [Google Scholar] [CrossRef]
- Ma, X.; Guo, S.Z.; Li, H.Y.; Pan, Z.S.; Qiu, J.Y.; Ding, Y.; Chen, F.Q. How to Make Attention Mechanisms More Practical in Malware Classification. IEEE Access 2019, 7, 155270–155280. [Google Scholar] [CrossRef]
- Wu, X.; Song, Y.F. An Efficient Malware Classification Method Based on the AIFS-IDL and Multi-Feature Fusion. Information 2022, 13, 571. [Google Scholar] [CrossRef]
- Singh, J.; Thakur, D.; Gera, T.; Shah, B.B.; Abuhmed, T.; Ali, F. Classification and Analysis of Android Malware Images Using Feature Fusion Technique. IEEE Access 2021, 9, 90102–90117. [Google Scholar] [CrossRef]
- Nobakht, M.; Javidan, R.; Pourebrahimi, A. DEMD-IoT: A deep ensemble model for IoT malware detection using CNNs and network traffic. Evol. Syst. 2023, 14, 461–477. [Google Scholar] [CrossRef]
- Agrawal, R.; Stokes, J.W.; Selvaraj, K.; Marinescu, M. Attention in recurrent neural networks for ransomware detection. In Proceedings of the 44th IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3222–3226. [Google Scholar]
- Aldehim, G.; Arasi, M.A.; Khalid, M.; Aljameel, S.S.; Marzouk, R.; Mohsen, H.; Yaseen, I.; Ibrahim, S.S. Gauss-Mapping Black Widow Optimization With Deep Extreme Learning Machine for Android Malware Classification Model. IEEE Access 2023, 11, 87062–87070. [Google Scholar] [CrossRef]
- Miao, C.Y.; Kou, L.; Zhang, J.L.; Dong, G.Z. A Lightweight Malware Detection Model Based on Knowledge Distillation. Mathematics 2024, 12, 4009. [Google Scholar] [CrossRef]
- Aldhafferi, N. Android Malware Detection Using Support Vector Regression for Dynamic Feature Analysis. Information 2024, 15, 23. [Google Scholar] [CrossRef]
- Dowlin, N.; Gilad-Bachrach, R.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Chabanne, H.; De Wargny, A.; Milgram, J.; Morel, C.; Prouff, E. Privacy-preserving classification on deep neural network. Cryptol. Eprint Arch. 2017, in press. [Google Scholar]
- Hesamifard, E.; Takabi, H.; Ghasemi, M. Cryptodl: Deep neural networks over encrypted data. arXiv 2017, arXiv:1711.05189. [Google Scholar]
- Lee, J.-W.; Kang, H.; Lee, Y.; Choi, W.; Eom, J.; Deryabin, M.; Lee, E.; Lee, J.; Yoo, D.; Kim, Y.-S. Privacy-preserving machine learning with fully homomorphic encryption for deep neural network. IEEE Access 2022, 10, 30039–30054. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Panaousis, E.; Liang, K. Deep binarized convolutional neural network inferences over encrypted data. In Proceedings of the 2020 7th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2020 6th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), New York, NY, USA, 1–3 August 2020; pp. 160–167. [Google Scholar]
- Nandakumar, K.; Ratha, N.; Pankanti, S.; Halevi, S. Towards deep neural network training on encrypted data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Al Badawi, A.; Jin, C.; Lin, J.; Mun, C.F.; Jie, S.J.; Tan, B.H.M.; Nan, X.; Aung, K.M.M.; Chandrasekhar, V.R. Towards the alexnet moment for homomorphic encryption: Hcnn, the first homomorphic cnn on encrypted data with gpus. IEEE Trans. Emerg. Top. Comput. 2020, 9, 1330–1343. [Google Scholar] [CrossRef]
- Chen, T.; Bao, H.; Huang, S.; Dong, L.; Jiao, B.; Jiang, D.; Zhou, H.; Li, J.; Wei, F. The-x: Privacy-preserving transformer inference with homomorphic encryption. arXiv 2022, arXiv:2206.00216. [Google Scholar]
- Zhu, Y.; Wang, X.; Ju, L.; Guo, S. FxHENN: FPGA-based acceleration framework for homomorphic encrypted CNN inference. In Proceedings of the 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Montreal, QC, Canada, 25 February–1 March 2023; pp. 896–907. [Google Scholar]
- Kim, D.; Park, J.; Kim, J.; Kim, S.; Ahn, J.H. Hyphen: A hybrid packing method and its optimizations for homomorphic encryption-based neural networks. IEEE Access 2023, 12, 3024–3038. [Google Scholar] [CrossRef]
- Aremu, T.; Nandakumar, K. Polykervnets: Activation-free neural networks for efficient private inference. In Proceedings of the 2023 IEEE Conference on Secure and Trustworthy Machine Learning (SaTML), Raleigh, NC, USA, 8–10 February 2023; pp. 593–604. [Google Scholar]
- Microsoft SEAL (Release 3.2); Microsoft Research: Redmond, WA, USA, 2019; Available online: https://github.com/Microsoft/SEAL (accessed on 29 July 2024).
- Juvekar, C.; Vaikuntanathan, V.; Chandrakasan, A. GAZELLE: A low latency framework for secure neural network inference. In Proceedings of the 27th USENIX Security Symposium (USENIX Security 18), Baltimore, MD, USA, 15–17 August 2018; pp. 1651–1669. [Google Scholar]
- Panconesi, A.; Marian, W.; Cukierski, W.; BIG Cup Committee. Microsoft Malware Classification Challenge (BIG 2015). Kaggle. 2015. Available online: https://kaggle.com/competitions/malware-classification (accessed on 16 November 2024).


| File Size Range | k |
|---|---|
| Tiny (<10 KB) | 1 |
| Small (10–50 KB) | 4 |
| Medium (50–200 KB) | 8 |
| Large (200–800 KB) | 16 |
| Oversize (>800 KB) | 32 |
| k × k Conv | ROT | HE-Mult |
|---|---|---|
| Conv2d | Cin × k2 − 1 | k2 × Cout × Cin |
| DS Conv | Cin × k2 − 1 | k2 × Cin + Cout × Cin |
| sparse projection | S × Cin × k2 − 1 | S × k2 × Cout × Cin |
| DS Conv + sparse projection | S × Cin × k2 − 1 | S × k2 × Cin + Cout × Cin |
| FICConvNet-4 | Input Size | Output Size | Detial |
|---|---|---|---|
| Stem | 1 × 64 × 64 | 4 × 62 × 62 | 3 × 3 conv, stride = 1 |
| Avg_pool | 4 × 62 × 62 | 4 × 31 × 31 | - |
| FICConv1 | 4 × 31 × 31 | 8 × 15 × 15 | 3 × 3 dw_conv, stride = 2 |
| FICConv2 | 8 × 15 × 15 | 16 × 7 × 7 | 3 × 3 dw_conv, stride = 2 |
| FICConv3 | 16 × 7 × 7 | 32 × 5 × 5 | 3 × 3 dw_conv, stride = 1 |
| FICConv4 | 32 × 5 × 5 | 64 × 3 × 3 | 3 × 3 dw_conv, stride = 1 |
| Head | 64 × 3 × 3 | 9 × 1 × 1 | - |
| Hyperparameter | Setting Value |
|---|---|
| Poly Modulus Degree (N) | 8192 |
| Rescale Parameter of Q | 240 |
| Δ | 230 |
| optimizer | SGD |
| Learning Rate (η) | 0.005 |
| Momentum (μ) | 0.9 |
| Weight Decay (λ) | 5 × 104 |
| Model | Accuracy | Precision | Recall | F1 Score | Privacy |
|---|---|---|---|---|---|
| FICConvNet-4 | 95.86% (±0.15) | 94.84% (±0.11) | 94.20% (±0.10) | 94.47% (±0.12) | √ |
| ResNet18 | 97.56% (±0.10) | 96.40% (±0.08) | 95.85% (±0.09) | 96.12% (±0.10) | × |
| VGG19 | 96.51% (±0.11) | 95.57% (±0.09) | 94.89% (±0.09) | 95.21% (±0.10) | × |
| CryptoNets | 80.31% (±0.20) | 80.71% (±0.18) | 78.89% (±0.20) | 79.76% (±0.19) | √ |
| PolyKervNets | 94.52% (±0.10) | 93.53% (±0.09) | 92.90% (±0.08) | 93.15% (±0.09) | √ |
| MAE (Average) | Classification Consistency Rate | |
|---|---|---|
| FICConvNet-4 | 0.007 | 96.5% |
| Method | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Multi-byte mapping | 95.86% (±0.15) | 94.84% (±0.11) | 94.20% (±0.10) | 94.47% (±0.12) |
| Single-byte mapping | 96.14% (±0.11) | 95.01% (±0.09) | 94.67% (±0.08) | 94.84% (±0.10) |
| Model | Accuracy | F1 Score | Time (s) | Description of Changes |
|---|---|---|---|---|
| FICConv | 95.86% (±0.15) | 94.47% (±0.12) | 166.71 | - |
| A | 96.21% (+0.35%; ±0.14) | 95.22% (+0.75%; ±0.12) | 830.97 | Replace DS Conv in FICConv for + sparse projection with standard 3 × 3 convolution. |
| B | 96.10% (+0.24%; ±0.12) | 94.79% (+0.32%; ±0.10) | 767.95 | Replacement with regular convolution + sparse projection. |
| C | 95.91% (+0.05%; ±0.11) | 94.61% (+0.14%; ±0.09) | 183.59 | Removal of sparse projection. |
| D | 92.32% (−3.54%; ±0.16) | 91.12% (−3.35%; ±0.15) | 159.47 | Remove residual branches and keep only FICConv main path Conv and activation. |
| E | 91.49% (−4.37%; ±0.17) | 90.19% (−4.39%; ±0.16) | 170.37 | Fix the ALAolyAct of FICConv to be f(x) = 0.4x + 0.3x2 + 0.2. |
| Stage | FICConv | A | B | C | D |
|---|---|---|---|---|---|
| Stem | 1.27 s | 1.27 s | 1.27 s | 1.27 s | 1.27 s |
| Avg_pool | 0.22 s | 0.22 s | 0.22 s | 0.22 s | 0.22 s |
| FICConv1 | 2.48 s | 9.96 s | 8.03 s | 3.10 s | 2.35 s |
| FICConv2 | 8.91 s | 39.44 s | 34.53 s | 9.23 s | 8.12 s |
| FICConv3 | 29.65 s | 153.67 s | 143.21 s | 36.06 s | 27.71 s |
| FICConv4 | 105.61 s | 607.84 s | 562.12 s | 122.44 s | 101.23 s |
| Head | 18.57 s | 18.57 s | 18.57 s | 18.57 s | 18.57 s |
| Sum | 166.71 s | 830.97 s | 767.95 s | 190.89 s | 159.47 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, S.; Wen, J.; Liang, S.; Huang, B. FICConvNet: A Privacy-Preserving Framework for Malware Detection Using CKKS Homomorphic Encryption. Electronics 2025, 14, 1982. https://doi.org/10.3390/electronics14101982
Pang S, Wen J, Liang S, Huang B. FICConvNet: A Privacy-Preserving Framework for Malware Detection Using CKKS Homomorphic Encryption. Electronics. 2025; 14(10):1982. https://doi.org/10.3390/electronics14101982
Chicago/Turabian StylePang, Si, Jing Wen, Shaoling Liang, and Baohua Huang. 2025. "FICConvNet: A Privacy-Preserving Framework for Malware Detection Using CKKS Homomorphic Encryption" Electronics 14, no. 10: 1982. https://doi.org/10.3390/electronics14101982
APA StylePang, S., Wen, J., Liang, S., & Huang, B. (2025). FICConvNet: A Privacy-Preserving Framework for Malware Detection Using CKKS Homomorphic Encryption. Electronics, 14(10), 1982. https://doi.org/10.3390/electronics14101982





