Abstract
We have employed a time-domain behavioral simulator to analyze how different design options for bang-bang Clock and Data Recovery (CDR) impact the Jitter Tolerance (JTOL) performance of High-Speed Serial Interfaces (HSSIs) with PAM-4 signaling. The simulator includes the effect of Inter-Symbol Interference (ISI) due to the transmission channel, various equalization schemes and a detailed description of the CDR architecture. Many design options have been investigated, with particular focus on transition filtering and on the algorithm to identify the Early/Late (E/L) information from data and edge samples after deserialization. It has been found that if majority voting is employed to derive a single set of E/L information from an array of phase detectors working on deserialized data and edges, the different filtering strategies provide the same JTOL, meaning that one can avoid transition filtering and furthermore use a single edge sampler with a zero threshold, significantly simplifying the CDR architecture. Instead, if summation of the E/L information from deserialized data and edges is performed, the decision to use one or three thresholds for the edge sampling and the choice of whether to implement transition filtering both impact JTOL; however, better performance is achieved under these conditions than when employing majority voting on the deserialized E/L signals.
1. Introduction
High-Speed Serial Interfaces (HSSIs) are key elements in many modern electronic systems due to the high computational power of digital ICs together with the limited number of available I/O pins dedicated to data transfer [1,2,3,4,5,6,7,8].
Data rates as high as 224 Gb/s per lane have been demonstrated in full transceivers [9] and in single transmitter and receiver implementations [10,11,12]. Working at such high rates requires complex transmitter (TX) and receiver (RX) circuits implementing equalization schemes [13] to compensate the Inter-Symbol Interference (ISI) associated with the frequency dependence of the channel attenuation as well as Clock and Data Recovery (CDR) algorithms to extract the clock from the received data [14].
The design choices for implementing CDR hardware and algorithms expand significantly with PAM-4 signaling at high data rates. In particular, one has to decide how many threshold levels to use for edge sampling and how to filter out transitions that may lead to erroneous Early/Late (E/L) information [15]. Furthermore, the CDR is usually applied to deserialized edge and data samples, and different schemes can be used to combine the information from each phase detector.
A systematic analysis of the different options in terms of threshold and transition filtering is carried out in [15], where a pseudo-linear model for the phase detector for all cases above (e.g., the number of threshold levels to use for edge sampling, deserializing or not deserializing the sampled edges and implementing transition filtering) is derived and the effect of the phase detection algorithm on the CDR bandwidth and on quantization noise is analyzed. A receiver working at the baud rate is considered, and the channel is modeled as a low-pass filter that introduces ISI. Here, we complement some cases of the investigation in [15] by considering a more complete description of the transmission channel and associated equalization schemes as well as different architectural options for the CDR; in particular, we consider different ways to combine the E/L information obtained from the deserialized data and edge samples. We will see that, if majority voting on the deserialized outputs of either one-threshold or three-threshold phase detectors is used for this task, the different options for filtering lead to the same result. We will also analyze the impact on the Jitter Tolerance (JTOL) [14] of many parameters of the CDR loop.
The analysis is carried out with a time-domain simulator recently developed for PAM-2 HSSIs [16] that has been extended to PAM-4 signaling. The numerical model makes it possible to take into account a realistic description of the channel and to include the effect of the main equalization strategies. We have also derived a simple analytical model that closely matches the results of the numerical simulator in most cases and can be used to help with the selection of the CDR parameters. As a relevant example, we consider a receiver operating according to the PCIe 6.0 standard at 64 Gb/s with PAM-4 signaling [17], although we simplify the architecture and the analysis by neglecting the presence of spread-spectrum clocking.
The paper proceeds as follows. The problems associated with CDR in PAM-4 systems are reviewed in Section 2. The time-domain simulator is briefly described in Section 3.1. Details of the channel and CDR architecture used in the case study are provided in Section 3.2 and Section 3.3, respectively. The analytical model of JTOL is derived in Section 3.4. The results are reported in Section 4. Conclusions are drawn in Section 5.
2. Challenges Associated with Phase Detection in PAM-4 Signaling
The use of PAM-4 signaling doubles the symbol time () with respect to PAM-2/NRZ coding, and the consequent reduction by a factor of two of the Nyquist frequency corresponds to lower channel attenuation and thus reduced ISI for the same data rate. One of the drawbacks, however, is that the use of four voltage levels complicates the architecture employed for phase detection and CDR. In fact, as can be seen in Figure 1, there are 16 possible transitions between these four levels, but, as discussed below, care should be taken in how some of these transitions are handled when employing an Alexander bang-bang phase detector (PD) [18].
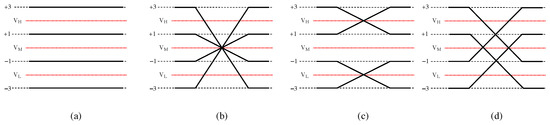
Figure 1.
All possible data transitions in PAM-4 signaling. Plot (a) indicates the 4 transitions where the symbol does not change. Plot (b) refers to 4 transitions that are symmetric with respect to the middle threshold (indicated with and usually set to zero). Plot (c) instead sketches the 4 transitions symmetric with respect to the high () and low () thresholds. The other 4 transitions (sketched in plot (d)) cross two voltage thresholds.
Of course, the four transition types where the signal remains at the same level (Figure 1a) do not provide any timing information. The symmetric transitions crossing the zero threshold (Figure 1b) are the easiest to process and provide correct timing, also allowing the use of comparators with a zero threshold for edge detection. In fact, transition filtering algorithms keep only these transitions and filter out all the others [19]. Figure 1c shows transitions that are symmetric with respect to the high and low thresholds. These can be exploited if comparators with all three thresholds are available, adding complexity to the analog hardware operating at high speed. The transitions in Figure 1d can lead to wrong Early/Late (E/L) information if not handled with care, since they are not symmetric. A possible countermeasure is to use a single comparator with a zero threshold and implement partial filtering [20]; this means that in the presence of jitter, 50% of these transitions (the very early and very late) are indeed useful. In the case of multi-threshold architectures, all the transitions in Figure 1d can be used by applying either majority voting or summation to the outputs of the three comparators [21].
It is clear that the different options described above (multi-threshold, transition filtering, partial filtering and no filtering), by basing the detection of the E/L information on different sets of transitions, correspond to different bandwidths of the CDR loop. In this respect, Figure 2 presents a linear model of a second-order CDR (left plot) and a sketch of the performance in terms of JTOL (right): using fewer transitions corresponds to lowering the open-loop gain of the system, thus leading to worse JTOL (see the expressions in Section 3.4).
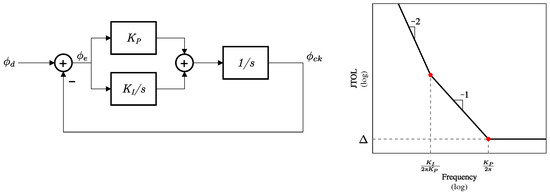
Figure 2.
(Left) Linear model of a second-order CDR loop. (Right) Sketch of the JTOL performance assuming that (as it can be simply derived from Equations (2) and (3) in Section 3.4 later in this paper).
3. Methods
3.1. Numerical Model
The numerical model employed in the forthcoming sections has been presented in [16] (see the summary in Figure 1 therein) for PAM-2 transceivers, and it is based on a time-domain approach. In the present work, this model has been extended to handle transceivers with PAM-4 coding. The model considers the chain of the TX driver, channel and RX Continuous-Time Linear Equalizer (CTLE) as a linear time-invariant (LTI) system, so that their combined step response can be determined by using the analysis methods for LTI systems. With respect to [16], the channel is now modeled with a transfer function computed from the frequency-dependent contributions of dielectric loss [1] and the skin effect [22] rather than a geometrical model:
where is the loss angle and is a parameter representing the influence of the skin effect. We have verified that the expression for dielectric loss gives results (in terms of pulse response) very close to the experiments in [23]. The resulting step response is then used to compute the waveform at the output of the CTLE corresponding to a random sequence of transmitted bits to which PAM-4 coding and Feed-Forward Equalization (FFE) are applied. The timing of the step is given by the symbol period plus the jitter contributions, consisting of both a sinusoidal component (needed to calculate JTOL) and a random component describing the absolute jitter of the PLL in the TX. The resulting waveform after the CTLE is processed to include the effect of Decision-Feedback Equalization (DFE), and it is then fed to a procedure that emulates the behavior of the CDR circuit. By examining the bathtub opening for a given BER and increasing the amplitude and frequency of the sinusoidal jitter at the TX, one can determine the JTOL curve of the receiver.
The time-domain approach simulates a few million symbol periods, such that the BER can be estimated only down to roughly . This corresponds to the requirement of our application, since the target BER (before Forward-Error Correction, FEC) for PCIe 6.0 working at 64 Gb/s is [17]. For additional details on the numerical model, the reader is referred to [16].
3.2. Channel Parameters
The model parameters for the channel transfer function in Equation (1) ( = 4.763 ps/rad, = 2 ns, = 62.832 Grad/s and ) have been selected to reproduce the attenuation mask of the 64 Gb/s option of the PCIe 6.0 standard [17], as shown in Figure 3 (compare blue solid line and black dashed lines). We see that the attenuation at the Nyquist frequency of 16 GHz is 28 dB. A sixth-order CTLE is applied to flatten the frequency response of the channel + CTLE at low frequency. This corresponds to the behavioral CTLE required by the standard for proper qualification of the transmitter. Among the various CTLE settings proposed in the standard [17], we have chosen the one with DC gain of dB, hence resulting in 12.7 dB of peaking.
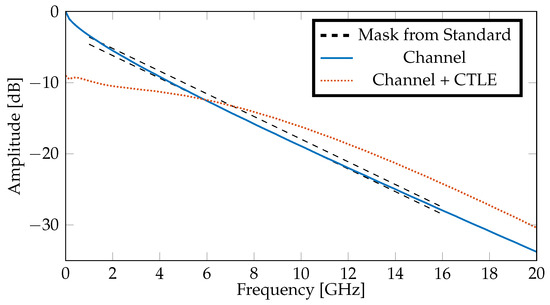
Figure 3.
Channel attenuation vs. frequency. The blue solid line is the result of Equation (1) (with parameters = 4.763 ps/rad, = 2 ns, = 62.832 Grad/s and ) compared to the PCIe 6.0 mask [17] (dashed lines). The dotted orange line adds the CTLE transfer function to the channel.
The channel response to a pulse of 31 ps duration (i.e., 1/32 GHz) and 1 V amplitude is reported in Figure 4. We see that, without any equalization, the pulse response shows a significant amount of ISI and extends over many unit intervals (UIs). This is only partially improved by including the aforementioned CTLE, which results in the dotted orange lines in Figure 3 and in Figure 4. Inclusion of FFE significantly reduces the first precursor. We have selected the pre-set Q6 of the standard [17], since it is the one giving the lowest precursor/main-cursor ratio for the channel under study. Eventually, including a one-tap DFE reduces the first postcursor and leads to an acceptable amount of ISI. We will see in the next section that this results in open bathtubs at BER = 10−6.
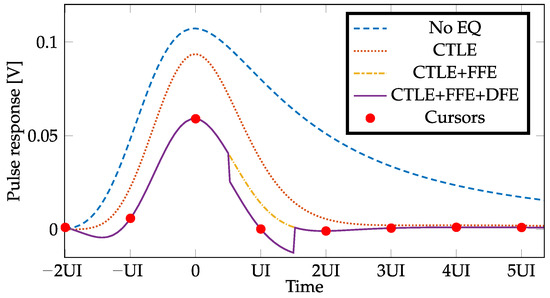
Figure 4.
Pulse response of the channel reported in Section 3.2 with the sequential addition of different equalization schemes. The red dots are the cursors sampled after equalization.
3.3. CDR Architecture and Parameters
The receiver architecture including the CDR considered in this analysis is sketched in Figure 5. We assume for simplicity a full-rate receiver so that data and edge comparators are clocked by two phases offset by . Data samples are represented by four levels, i.e., two-bit signals, whereas edges are one- or two-bit signals depending on the number of threshold levels employed for edge sampling. These data and edge samples are deserialized, leading to data and edge signals to be input to the phase detector (PD). For example, for = 32 at 64 Gb/s and considering edge comparators with zero threshold, after deserialization, we have a 64-bit data word and a 32-bit edge word updated at 1 GHz. This provides an array of size out of the PDs containing the E/L from each transition (in principle, one can obtain E/L signals if the last edge sample is stored to be employed in the next received word; here, we simplify the hardware and consider E/L signals).
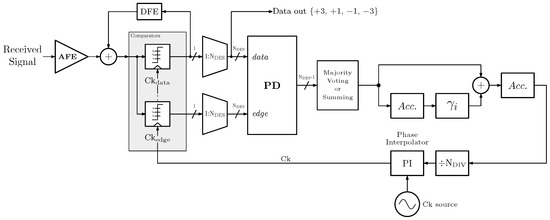
Figure 5.
Block diagram of the receiver considered in this work. Quantities output by the comparators (highlighted in gray) can be either thermometer or binary encoded since a single comparator is made up of 3 slicers with thresholds of VH, VM and VL. In addition to the blocks related to the CDR, the figure also reports the Analog Front End (AFE) and the Decision-Feedback Equalizer (DFE).
The different options available for the single elements in the array of PDs to derive the E/L information are listed below:
- No filtering (NoF) uses a single comparator with zero threshold for edge sampling and considers all transitions in plots (b) and (d) of Figure 1;
- Transition filtering (TrF) uses a single comparator with zero threshold for edge sampling and considers only the transitions in Figure 1b;
- Partial filtering (PF) [15] uses a single comparator with zero threshold for edge sampling, while considering all transitions in Figure 1b and only those in plot (d) which can unambiguously provide correct timing information (e.g., the transition from +3 to −1 will look Early even if the CDR is correctly locked, and therefore only the Late information is retained, whereas the Early information is always discarded);
- Multi-threshold (Mth) performs majority voting on the results of three comparators with low, high and zero thresholds, thus taking into account all transitions in plots (b), (c) and (d) of Figure 1.
The resulting array of E/L can undergo either majority voting (thus obtaining a single E/L signal with value ) or summation (yielding a multi-bit signed digital word). In either case, the resulting signal is forwarded into a proportional path with gain equal to one and an integral path consisting of an accumulator (Acc.) followed by gain . Proportional and integral paths are then combined and accumulated to obtain a second-order CDR loop. The output is then divided by , discarding all decimal digits. This is equivalent to removing LSBs from the output word of the accumulator. This quantity is eventually fed to a Phase Interpolator (PI), with phases, that aligns the local clock source with the incoming data.
In the following, we will analyze the effect of the parameters , , and as well as voting and filtering options on the CDR performance. Nominal parameters are reported in Table 1. We also assume that the digital implementation of the CDR requires digital clock cycles [clock cycles at the deserialized data frequency, i.e., ] from any phase detection event to the corresponding adjustment of the sampling point.

Table 1.
Default parameters of the CDR considered in this work (see block diagram in Figure 5).
Notice that the sinusoidal jitter from the TX is not the only source of jitter in the system: additional jitter is introduced by the finite number of PI phases [24], and we have also included the phase noise of the PLLs that provide the local clock to the TX and RX, respectively (it is assumed that the PSD of the PLL is a low-pass one that is determined by the total absolute jitter and by the PLL bandwidth; the square root of the PSD with a random phase is anti-transformed to obtain a random sequence of jitter instants). According to the standard, it has a bandwidth = 0.75 MHz and absolute jitter with standard deviation = 0.215 ps.
3.4. Analytical Model for JTOL
The results obtained with the numerical model have been interpreted with a simple linear model reported on the left side of Figure 2. Its open-loop transfer function in the Laplace domain is as follows:
As discussed in [14], JTOL is then given by
and it has the frequency dependence shown in Figure 2 (right). is the timing margin when no sinusoidal jitter is applied at the transmitter, or, in other words, the value of JTOL when the sinusoidal jitter at the TX is at a frequency large enough not to be filtered by the high-pass characteristic of the CDR loop. In our model is just an input parameter obtained using the time-domain model. In this respect, the model is not fully predictive, but it is a useful tool to understand the various trends of the JTOL with respect to the different CDR parameters and architectures. In our model, both JTOL and are normalized with respect to .
The s-domain model of the CDR block diagram of Figure 5 is reported in Figure 6. Transitioning from the z-domain to the s-domain was performed by approximating the transfer function of the accumulators as , since the clock period of the digital CDR algorithm working on the deserialized data and edges is .

Figure 6.
Linear model in the s-domain of the CDR architecture reported in Figure 5.
The parameter in Figure 6 accounts for transition filtering. It has been set to in the case of majority voting for the deserialized E/L signal (because we safely assume that at least one useful Early or Late is obtained over received symbols), while in the case of summation of deserialized E/L signals, we have
These values have been obtained by estimating the fraction of the E/L samples containing useful information (i.e., Early or Late) in the various cases, as discussed with reference to Figure 1 in Section 2. For example, if no transition filtering is applied and a single threshold edge comparator is used, on average, only eight out of sixteen possible transitions provide useful timing information. If, instead, the edge is sampled using three comparators with low, high and zero thresholds, four additional transitions are taken into account (which results in an average of 12 pieces of useful information out of 16 possible transitions).
From Figure 6, it readily follows that the gain of the proportional path is
while that of the integral path is
The gain of the PD is computed as
which is the gain of a non-linear block with output limited to values of with a sinusoidal input of amplitude [25]. This approximation holds as far as the sinusoidal jitter from the TX is the dominant jitter contribution. In such a case, the border between the pass and fail regions of the JTOL plot corresponds to the receiver PD driven by sinusoidal jitter with an amplitude we will denote as . Instead, when other jitter contributions are dominant, more complex expressions should be used [26], but this goes beyond the scope of the present work.
4. Results
In this section, we report simulation results for a 64 Gb/s PAM-4 HSSI with channel model and CDR architecture as described in Section 3.2 and Section 3.3. The aim is to show how the CDR parameters impact the JTOL performance. The prediction of the numerical model described in Section 3.1 will be compared with the simple linear model described in Section 3.4.
In this section, we assume that the frequency of the RX clock is exactly the same as that of the TX clock. Results with a frequency offset between the two are presented in Appendix A.
The simulated eye diagram corresponding to the channel described in Section 3.2 and the CDR whose parameters are listed in Section 3.3 is reported in Figure 7. Consistent with the cursors indicated in Figure 4, we see that equalization has been effective in compensating ISI and the three eyes are open. We also see that the time aperture of the eyes is satisfactory (12 ps), meaning that the system jitter does not induce significant closing of the eyes.
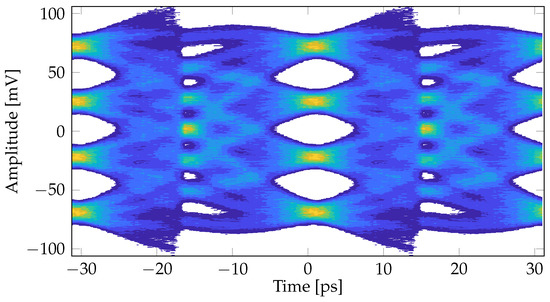
Figure 7.
Eye diagram (constructed from the received signal using as a “trigger” the timing information from the CDR, whose parameters are listed in Section 3.3) corresponding to the channel in Section 3.2 after applying FFE, CTLE and DFE.
Before performing the JTOL analysis, we first simulate the receiver behavior without adding the sinusoidal jitter at the TX. The numerical model provides the bathtub plot, that is reported in Figure 8 for a few cases. We see that the procedure makes it possible to determine BER values below 10−6, and it is thus adequate for the PCIe 6.0 at 64 Gb/s. In Figure 8a,b, we also see that, with the default CDR parameters of Table 1, the results are hardly affected by the CDR algorithm, meaning that different transition filtering techniques, as well as the choice between using majority voting or summation on the E/L signals coming from either one-threshold or three-threshold phase detectors, have a very limited influence on the bathtub.
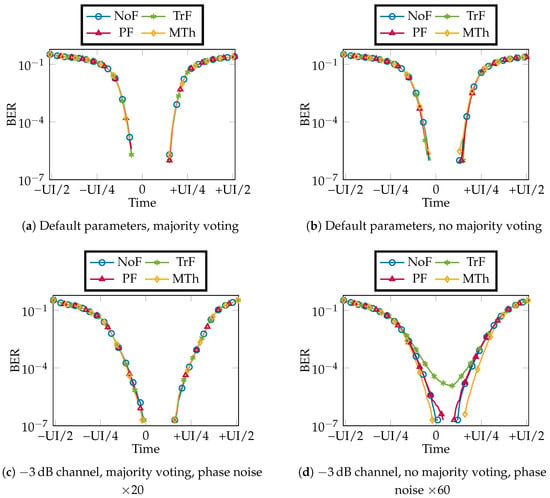
Figure 8.
Simulated bathtub plots considering different options: default CDR parameters (Table 1) and channel as described in Section 3.2 with (a) and without (b) majority voting of the deserialized E/L signals; RX PLL jitter multiplied by 20 ((c), in the case of majority voting of the deserialized E/L) or by 60 ((d), in the case of summation of the E/L signals) considering a dB channel at the Nyquist frequency.
These options essentially affect the CDR bandwidth, but this has limited influence on the jitter contributions related to channel ISI (the so-called data-dependent jitter) and to the one due to the finite number of phases in the PI [16] that dominates in our system. These jitter contributions are white and thus only marginally reduced by the high-pass characteristic of the CDR. Thus, to magnify the impact of the CDR bandwidth on the results we have increased the phase noise of the RX PLL and considered a channel with a much lower attenuation (3 dB), as can be seen in Figure 8c,d. In particular, in the numerical experiment, the phase noise of the PLL is increased by a factor of 20 in the case of Majority Voting between the E/L signals and by a factor of 60 when a sum over the E/L signals is performed. The data-dependent jitter due to the limited bandwidth of the channel has a negligible impact so that, in the bathtub plots, the major contribution is due to the oscillator’s phase noise that passes through the CDR’s high-pass transfer function. When performing Majority Voting over the deserialized E/L signals [Figure 8c], the CDR bandwidth is not affected by the filtering algorithm, as will be extensively discussed in the following, such that the bathtub is essentially the same in all cases. Instead, if summation of the deserialized E/L signals is performed [Figure 8d], the filtering algorithm clearly affects the CDR bandwidth and thus the bathtub.
Having shown that the choice of the transition filtering options and the choice between voting and summation of deserialized E/L signals have a minor impact on the jitter generated by the receiver (considering a channel with relevant ISI and thus large data-dependent jitter), we now analyze the JTOL performance. As seen in Figure 2, JTOL also depends on the CDR bandwidth, which is directly linked to the capability of the loop to rapidly respond to misalignments between data and the clock and thus to making a decision based on as many transitions as possible. Therefore, we expect transition filtering to play a key role here.
We begin the investigation by considering a channel with negligible attenuation at Nyquist frequency (3 dB) instead of the one in Figure 3 in order to separate the effect of CDR bandwidth from the reduced tolerance due to data-dependent jitter, which depends on ISI. This channel does not require any equalization. Figure 9 shows the dependence of JTOL on some relevant CDR parameters considering summation between deserialized E/L signals. In plot (a), we vary considering a multi-threshold phase detector: small values of this parameter result in large CDR bandwidths [24] and thus better JTOL. We have verified that this holds also when varying . Figure 9b instead, analyzes the effect of and . The parameter is the ratio between the gain of the integral and proportional paths (see Equation (6) in Section 3.4) and thus, according to Figure 2, it controls the frequency at which the slope of JTOL changes from −2 to −1 (in logarithmic scales, i.e., decades of normalized UI versus decades of frequency). We see that for , the region with slope −2 disappears and the parameter does not have any impact on the results. On the other hand, for non-null , smaller values of result in better JTOL. The trends of Figure 9a,b also hold for the other transition filtering options. Figure 9c, instead, shows the influence on JTOL of the different CDR options discussed at the end of Section 3.3: the ones exploiting more transitions result in better JTOL, as expected since more E/L signals are combined together. For all plots in Figure 9, we see a good match between the numerical model of Section 3.1 and the analytical model of Section 3.4, meaning that the latter can be used to explain the main trends and to obtain back-of-the-envelope estimations of JTOL.
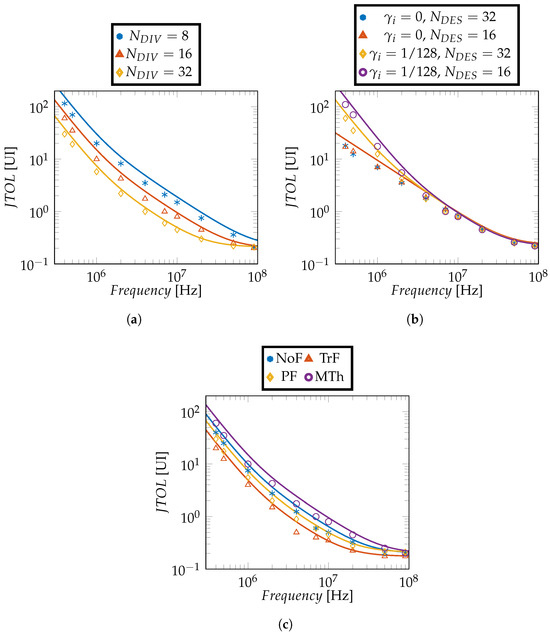
Figure 9.
JTOL for a channel with 3 dB attenuation at the Nyquist frequency considering different CDR options, all employing summation of the deserialized E/L signals that are output by the array of PDs. We report only the parameters that are modified with respect to their default values of Table 1 except for , which, in this case, is set to a value of 16. Symbols refer to the time-domain numerical model described in Section 3.1, whereas lines are the results from the analytical model of Section 3.4. In plots (a,b), we consider a Multi-Threshold Phase Detector while (c) compares different Phase Detectors and transition filtering techniques.
Figure 10 complements the analysis by considering a CDR implementing majority voting between the E/L signals out of the PDs. The effect of on JTOL is the same as in Figure 9 and it is not reported again. On the other hand, Figure 10a shows that has a big effect, much larger than in the previous case: this is expected since we extract a single piece of E/L information out of outputs of the PDs, resulting in a loss of bandwidth with respect to the case where the E/L signals out of the PDs are summed together. The case with has been simulated considering the different filtering options, that however have no effect on JTOL. This is not surprising since, regardless of the filtering option, at least one piece of useful E/L information will come out from an array of 31 transitions. In fact, when we work with at least , considering random data sequences, the case where no E/L is observed over a sequence of 16 deserialized symbols has a very low probability of occurring, and thus, its impact on JTOL would be very limited.
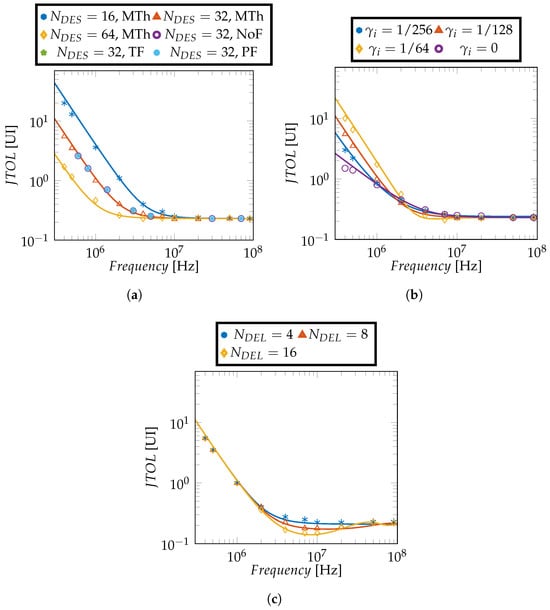
Figure 10.
JTOL results for a channel with an attenuation of 3 dB at the Nyquist frequency considering different CDR options but with majority voting between the E/L signals output by the PD. Plot (a) shows the impact of using different filtering options, whereas (b,c) consider a Multi-Threshold Phase Detector and analyze the impact of and , respectively.
In Figure 10b, we can observe the impact of the factor, that, as in the previous analysis, sets the point where the slope of the JTOL curve changes from −2 to −1 (on a logarithmic scale). The impact of the parameter on JTOL is limited, as shown in Figure 10c, although cannot be too large to prevent the JTOL at medium frequencies from deteriorating.
Figure 11 considers two sets of CDR parameters yielding the same bandwidth and plots the simulated JTOL considering a channel with 3 dB attenuation. The results further validate the model in Equation (3), which closely matches the outcome of the time-domain numerical model. Two cases are considered: the blue markers represent a CDR with without any filtering on the E/L signal outputs from the PD [which implies ], while the orange markers denote a configuration where transition filtering is performed on the E/L signals [that is ], hence compensating its loss in bandwidth by setting , i.e., half the previous case. Not surprisingly, both configurations have the same JTOL characteristic, having the same bandwidth. The black solid line represents the model in Equation (3), which obviously kept the same values for both the considered CDR configurations. The figure thus points out that the loss of bandwidth induced by the transition filtering can be compensated by reducing the division factor. The same applies if the bandwidth loss is compensated varying . This analysis has been further extended considering two CDR configurations with either majority voting or summing of the E/L signals out from the PDs, see Figure 12. Similarly to Figure 11, the loss in bandwidth due to majority voting (a loss of ) is compensated through a smaller factor, resulting in the same JTOL characteristic. We have verified that the JGEN characteristic (i.e., the tails of the bathtub plot) does not change as well.
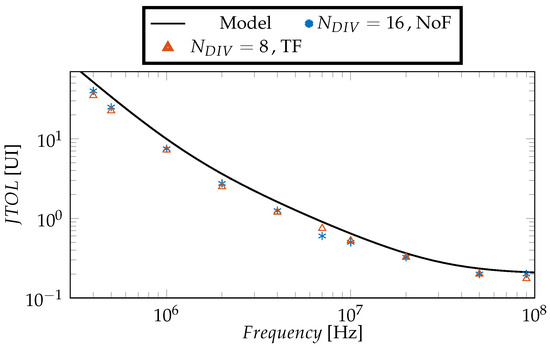
Figure 11.
JTOL results for a channel with an attenuation of 3 dB at the Nyquist frequency considering different CDR options yielding the same bandwidth, all employing summation of E/L signals that are output by the PDs. In this example, the loss in bandwidth caused by transition filtering is compensated by using a smaller factor.
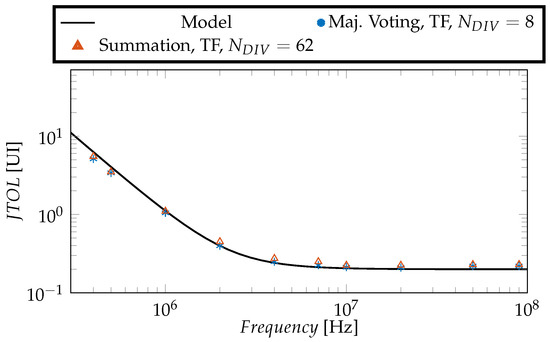
Figure 12.
JTOL results for a channel with an attenuation of 3 dB at the Nyquist frequency considering different CDR options yielding the same bandwidth. In blue symbols, majority voting on the E/L signals from the PDs is performed, which sets , whereas in orange, a summation of the E/L signals from the PDs is performed considering transition filtering with as remarked in Equation (4). To compensate the gain in bandwidth caused by summation with respect to the first case, we set .
The trends observed using the channel with 3 dB attenuation at the Nyquist frequency have been confirmed by repeating the analysis using the channel of Figure 3. Sample results are reported in Figure 13 and Figure 14, comparing the numerical time-domain model and the simple linear model of Section 3.4 with the mask of the PCIe 6.0 standard [17]. Figure 13a shows that, in this case as well, the transition filtering algorithm affects JTOL if summation between the E/L signals output by the PD is applied. Plot (b) instead shows that the influence of is the same as in Figure 9a. The same analysis is shown in Figure 14 for the case of majority voting. The same results have been obtained regardless of the transition filtering algorithm. Comparison between Figure 13b and Figure 14 clearly shows that the use of majority voting of the deserialized E/L signals degrades JTOL performance at low frequency, whereas it slightly improves the JTOL value at high frequency ( value in Figure 2, which is essentially the eye opening without sinusoidal jitter at the TX, as shown in Section 3.4). In fact, as discussed in [24], the summation of the deserialized E/L signals increases the CDR bandwidth but also amplifies the RX jitter associated with the finite number of PI phases. We also see that in Figure 13 and Figure 14 is lower than in the cases with the 3 dB attenuation channel due to the presence of relevant data-dependent jitter associated with ISI. As a final remark, we see that the analytical model of Section 3.4 nicely reproduces the simulation results, although in the case of Figure 13 we had to artificially adjust the value of the PD gain by using instead of the value used in the other figures of the paper. This modification of the PD gain is reasonable since many mechanisms contribute to RX jitter in addition to the sinusoidal jitter applied at the TX. A proper model for the PD gain in such a situation can be found in [26], but its inclusion in this analysis is beyond the scope of our work.
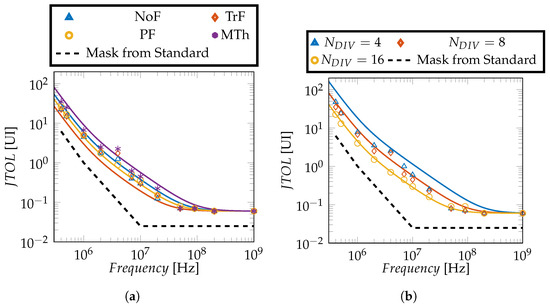
Figure 13.
Simulated JTOL for the receiver with CDR parameters reported in Table 1 and channel of Figure 3 considering summation of the deserialized E/L signals output by the array of PDs. The numerical time-domain model of Section 3.1 (symbols) is compared with the analytical model of Section 3.4 (lines) and with the mask of the PCIe 6.0 standard [17]. In (a) different Phase Detectors and transition filtering techniques are compared, while in (b), a Multi-Threshold Phase Detector is used. The value of considered in the analytical model for JTOL has been adjusted to a value of instead of the expression discussed in Section 3.4.
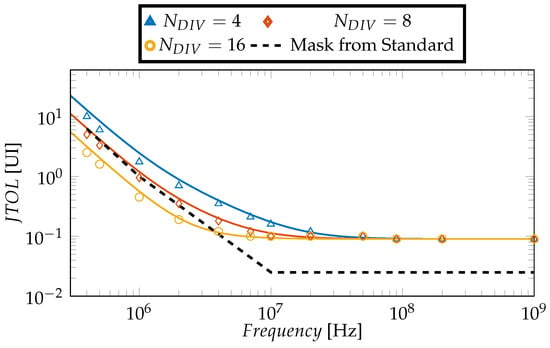
Figure 14.
Simulated JTOL for the receiver with CDR parameters reported in Table 1 and channel of Figure 3 considering majority voting of the deserialized E/L signals output by the array of PDs. The numerical time-domain model of Section 3.1 (symbols) is compared with the analytical model of Section 3.4 (lines) and with the mask of the PCIe 6.0 standard [17]. A Multi-Threshold Phase Detector is employed here but the same result can be obtained considering different transition filtering algorithms.
5. Discussion and Conclusions
We have analyzed the impact on JTOL of various CDR parameters and architectural choices in PAM-4 HSSIs. A time-domain numerical model has been employed and compared against the prediction of a simple linear model. The analysis has been mainly focused on the different transition filtering options used to derive the Early/Late information and on how to aggregate the array of deserialized E/L signals output by the phase detectors (majority voting vs. summation). It has been found that if majority voting is used, so that at least one useful transition is present in the array, then the features of the transition filtering algorithm are irrelevant and one can resort to a single comparator, without filtering the transitions.
On the other hand, summation significantly increases the bandwidth of the CDR loop, improving JTOL at low frequency, although the JTOL at high frequency (as well as the jitter contribution added by the CDR itself due to the finite number of PI phases) is degraded. When employing summation, applying transition filtering reduces the CDR bandwidth with respect to algorithms exploiting more transitions. In any case, the bandwidth is larger than when performing majority voting of the deserialized E/L signals. Furthermore the reduction of the CDR bandwidth due to transition filtering can be compensated by lowering the value of the divider placed in the loop.
These results may appear in contrast with those in [15], but one should consider that the CDR architecture considered in that work differs from the ones analyzed here. First, CDR is applied to baud rate data and edge samples. Secondly, a VCO is used instead of a PI (as in our analysis) to generate the aligned clock. This makes the jitter in [15] more affected by the quantization noise of the PD, while, in our system, the quantization noise of the PI dominates. When the PD quantization noise dominates, the reduction of the CDR gain induced by transition filtering can be indeed compensated by increasing the gain of the following blocks (divider, etc). This compensates JTOL but results in an amplification of the PD quantization noise. In our architecture, this does not occur, and any bandwidth reduction due to transition filtering can be compensated.
The simulation framework that has been developed is quite general and makes it possible to investigate the impact of any CDR parameter on JTOL and JGEN. Although, in this paper, many blocks have been assumed to be ideal, it is almost straightforward to include in the model effects such as offset and delay of the comparators, non-linearity of the PI and duty-cycle errors in the clock.
Author Contributions
Conceptualization, A.C., D.M., A.B., F.D. and P.P.; methodology, A.C., D.M. and P.P.; software, A.C. and D.M.; validation, A.C. and P.P.; formal analysis, A.C., D.M. and P.P.; investigation, A.C., D.M., A.B., F.D. and P.P.; data curation, A.C.; writing—original draft preparation, A.C., D.M., A.B., F.D. and P.P.; writing—review and editing, A.C., D.M., A.B., F.D. and P.P.; visualization, A.C.; supervision, A.B., F.D. and P.P.; project administration, P.P. and F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data supporting the findings of this study are included within the article.
Acknowledgments
The authors would like to thank Anthony Sanders, Roberto Nonis and Werner Grollitsch of Infineon Technologies for their support and many helpful discussions.
Conflicts of Interest
Authors Davide Menin and Andrea Bandiziol are employed by the company Infineon Technologies Austria AG. The authors declare that the research was conducted in the absence of any conflict of interest.
Appendix A. Inclusion of Frequency Offsets Between TX and RX
In the main text, we have assumed that the TX and RX clocks have exactly the same frequency. However, in real systems for similar use cases to PCIe 6.0, the clock is not forwarded to the RX, and different crystal oscillators are used in the TX and RX, leading to a frequency offset. This is equivalent to a phase ramp at the input of the CDR that is compensated by the integral path. On the other hand, if no integral path is present, the frequency offset between TX and RX clocks may cause the CDR algorithm to fail. From simple timing considerations, it is easy to show that the maximum tolerable time difference between the RX and TX clock periods is given by the following:
This simplified model does not include the delay of the digital core, i.e., it assumes an instantaneous update of the PI code.
The validity of Equation (A1) has been verified against time-domain simulations (compare lines and symbols in Figure A1).
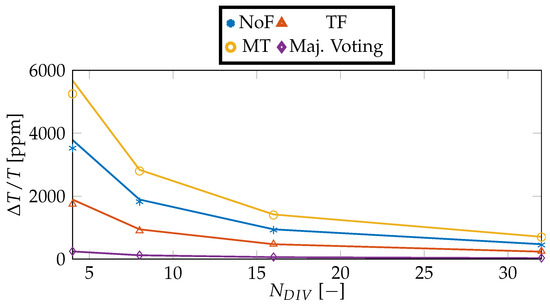
Figure A1.
Maximum frequency offset allowed considering a channel with an attenuation of 3 dB at the Nyquist frequency, , different CDR architectures and factors in the numerical model (markers) and that given by Equation (A1) (solid lines). The other CDR parameters are kept as in Table 1 except for , which is kept at 0. Summation is performed over the E/L signals from the PD except for the case where majority voting is performed (therefore setting , making independent of the CDR architecture as remarked in Equation (A1)).
The figure and the equation clearly show that the reduction in the parameter associated with transition filtering lowers the maximum period offset that can be tolerated. Of course, as for JTOL, this can be compensated by lowering either or .
References
- Carusone, T.C. Introduction to Digital I/O: Constraining I/O Power Consumption in High-Performance Systems. IEEE Solid-State Circuits Mag. 2015, 7, 14–22. [Google Scholar] [CrossRef]
- Tamura, H. Looking to the Future: Projected Requirements for Wireline Communications Technology. IEEE Solid-State Circuits Mag. 2015, 7, 53–62. [Google Scholar] [CrossRef]
- Palermo, S.; Hoyos, S.; Cai, S.; Kiran, S.; Zhu, Y. Analog-to-Digital Converter-Based Serial Links: An Overview. IEEE Solid-State Circuits Mag. 2018, 10, 35–47. [Google Scholar] [CrossRef]
- den Besten, G.W. 30.1 Single-Pair Automotive PHY Solutions from 10 Mb/s to 10 Gb/s and Beyond. In Proceedings of the 2019 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 474–476. [Google Scholar] [CrossRef]
- Tajalli, A.; Hormati, A.; Shokrollahi, A. Chord Signaling for High-Speed Data Movement: Employing Advanced Communication and Circuit Techniques to Augment Data-Transfer Bandwidth. IEEE Solid-State Circuits Mag. 2019, 11, 78–85. [Google Scholar] [CrossRef]
- Wilson, J.M.; Turner, W.J.; Poulton, J.W. Ground-Referenced Single-Ended Signaling: Applications for High-Density, Short-Haul Communication Systems. IEEE Solid-State Circuits Mag. 2019, 11, 54–68. [Google Scholar] [CrossRef]
- Razavi, B. Low-Power Techniques for Wireline Systems. In Proceedings of the ESSCIRC 2021—IEEE 47th European Solid State Circuits Conference (ESSCIRC), Grenoble, France, 13–22 September 2021; pp. 515–522. [Google Scholar] [CrossRef]
- Mirabbasi, S.; Fujino, L.C.; Smith, K.C. Through the Looking Glass—The 2022 Edition: Trends in Solid-State Circuits from ISSCC. IEEE Solid-State Circuits Mag. 2022, 14, 54–72. [Google Scholar] [CrossRef]
- Pfaff, D.; Nummer, M.; Hai, N.; Xia, P.; Yang, K.G.; Mohsenpour, M.M.; LaCroix, M.A.; Zamanlooy, B.; Eeckelaert, T.; Petrov, D.; et al. 7.3 A 224Gb/s 3pJ/b 40dB Insertion Loss Transceiver in 3nm FinFET CMOS. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; Volume 67, pp. 128–130. [Google Scholar] [CrossRef]
- Kim, J.; Kundu, S.; Balankutty, A.; Beach, M.; Kim, B.C.; Kim, S.; Liu, Y.; Murthy, S.K.; Wali, P.; Yu, K.; et al. A 224Gb/s DAC-Based PAM-4 Transmitter with 8-Tap FFE in 10nm CMOS. In Proceedings of the 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 126–128. [Google Scholar] [CrossRef]
- Seual, Y.; Laufer, A.; Khairj, A.; Krupnik, Y.; Cusmai, M.; Levin, I.; Gordon, A.; Saban, Y.; Rahinskj, V.; Ori, G.; et al. A 1.41pJ/b 224Gb/s PAM-4 SerDes Receiver with 31dB Loss Compensation. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; pp. 114–116. [Google Scholar] [CrossRef]
- Cusmai, M.; Familia, N.; Kuperberg, E.; Nashash, M.; Gottesman, D.; Marcus, Z.; Horwitz, Y.; Zalcman, S.; Kim, J.; Kundu, S.; et al. A 0.92-pJ/b PAM-4 and 0.61-pJ/b PAM-6 224-Gb/s DAC-Based Transmitter in 3-nm FinFET. IEEE J. Solid-State Circuits 2025, 60, 23–34. [Google Scholar] [CrossRef]
- Bulzacchelli, J.F. Equalization for Electrical Links: Current Design Techniques and Future Directions. IEEE Solid-State Circuits Mag. 2015, 7, 23–31. [Google Scholar] [CrossRef]
- Amirkhany, A. Basics of Clock and Data Recovery Circuits: Exploring High-Speed Serial Links. IEEE Solid-State Circuits Mag. 2020, 12, 25–38. [Google Scholar] [CrossRef]
- Verbeke, M.; Torfs, G.; Rombouts, P. The Truth About 2-Level Transition Elimination in Bang-Bang PAM-4 CDRs. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 469–482. [Google Scholar] [CrossRef]
- Cortiula, A.; Menin, D.; Bandiziol, A.; Grollitsch, W.; Nonis, R.; Palestri, P. A Time-Domain Simulation Framework for the Modeling of Jitter in High-Speed Serial Interfaces. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 940–951. [Google Scholar] [CrossRef]
- PCI-SIG. PCI Express® Base Specification Revision 6.0; Version 1.0; PCI-SIG: Beaverton, OR, USA, 2021. [Google Scholar]
- Alexander, J.D.H. Clock Recovery from Random Binary Signals. Electron. Lett. 1975, 11, 541–542. [Google Scholar] [CrossRef]
- Farjad-Rad, R.; Yang, C.K.; Horowitz, M. A 0.3-/spl mu/m CMOS 8-Gb/s 4-PAM serial link transceiver. IEEE J.-Solid-State Circuits 2000, 35, 757–764. [Google Scholar] [CrossRef]
- Dehlaghi, B.; Shahramian, S.; Liang, J.; Bespalko, R.; Dunwell, D.; Bailey, J.; Wang, B.; Sharif-Bakhtiar, A.; O’Farrell, M.; Tang, K.; et al. A 1.41-pJ/b 56-Gb/s PAM-4 Receiver Using Enhanced Transition Utilization CDR and Genetic Adaptation Algorithms in 7-nm CMOS. IEEE Solid-State Circuits Lett. 2019, 2, 248–251. [Google Scholar] [CrossRef]
- Zerbe, J.; Werner, C.; Stojanovic, V.; Chen, F.; Wei, J.; Tsang, G.; Kim, D.; Stonecypher, W.; Ho, A.; Thrush, T.; et al. Equalization and clock recovery for a 2.5-10-Gb/s 2-PAM/4-PAM backplane transceiver cell. IEEE J. Solid-State Circuits 2003, 38, 2121–2130. [Google Scholar] [CrossRef]
- Wigington, R.L.; Nahman, N.S. Transient Analysis of Coaxial Cables Considering Skin Effect. Proc. IRE 1957, 45, 166–174. [Google Scholar] [CrossRef]
- Djordjevic, A.; Biljie, R.; Likar-Smiljanic, V.; Sarkar, T. Wideband frequency-domain characterization of FR-4 and time-domain causality. IEEE Trans. Electromagn. Compat. 2001, 43, 662–667. [Google Scholar] [CrossRef]
- Palestri, P.; Elnaqib, A.; Menin, D.; Shyti, K.; Brandonisio, F.; Bandiziol, A.; Rossi, D.; Nonis, R. Analytical Modeling of Jitter in Bang-Bang CDR Circuits Featuring Phase Interpolation. IEEE Trans. Very Large Scale Integr. (Vlsi) Syst. 2021, 29, 1392–1401. [Google Scholar] [CrossRef]
- Lee, T.H. The Design of CMOS Radio-Frequency Integrated Circuits, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Park, M.J.; Kim, J. Pseudo-Linear Analysis of Bang-Bang Controlled Timing Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1381–1394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).