Abstract
Unmanned aerial vehicle networks (UAVNs) are widely used to collect various location-related data, with applications ranging from military reconnaissance to the low-altitude economy. Data security and privacy are critical concerns when outsourcing location-related data to a public cloud. To alleviate these concerns, location-related data are encrypted before outsourcing to the public cloud. However, encryption decreases the operability of the outsourced encrypted data; thus, unmanned aerial vehicles cannot operate on the encrypted data directly. Among operations on encrypted location-related data, the forward-secure range query is one of the most fundamental operations. In this paper, we present a forward-secure range query based on spatial division to achieve a highly efficient range query on encrypted location-related data while preserving both data security and privacy. Specifically, various space-filling curves were experimentally investigated for both the range query and the k-nearest-neighbor query. Then, a forward-secure range query (namely, OSFC-FSQ) was constructed on an encrypted dual dictionary. The proposed scheme was evaluated on real-world datasets, and the results show that it outperforms state-of-the-art schemes in terms of accuracy and query time in the cloud.
1. Introduction
Unmanned aerial vehicle networks (UAVNs) [1] are widely used to collect various location-related data, with applications ranging from military reconnaissance to the low-altitude economy. UAVNs are composed of numerous unmanned aerial vehicles (UAVs) that are capable of completing crowdsourcing tasks, such as data collection, fire risk inspection, and so on. The above tasks inevitably use query operations on location-related data, which are usually outsourced to a public cloud to reduce the costs of infrastructure investments and maintenance. Among these query operations, the range query is a typical operation that retrieves all data points within a given range to monitor the statuses of UAVs, plan flight paths, and mine hotspot tasks, among other tasks.
However, malicious attacks on public clouds can occur at any time, posing significant challenges to privacy and security [2,3]. Recently, by integrating non-orthogonal multiple access and autonomous aerial vehicles, He et al. [4] proposed an innovative approach to enhance both communication efficiency and data security in vehicle platooning scenarios within the IoV. The focus on maximizing secure rates and incorporating robust optimization techniques underscores their commitment to addressing critical data security challenges in modern vehicular networks. Karmakar et al. [5] introduced IntSHU, which is a significant advancement in the management of handovers in UAV-enabled 5G networks, with a strong emphasis on data security. Through the integration of dynamic parameter adjustment, PUF-based encryption, and blockchain technology, IntSHU not only improves the reliability of handovers but also fortifies the network against potential security threats. However, the above solutions are not sufficient to resolve data security problems in UAVNs. In particular, this outsourcing model for location-based data query services poses the risk of leaking users’ private data. By integrating users’ query records with datasets containing location information, the cloud can infer sensitive private information, such as users’ preferences, occupations, addresses, and even health conditions. In the spring of 2024, several Snowflake customers experienced data breaches as cybercriminals claimed to have obtained datasets from prominent clients, including TicketMaster, LendingTree, Neiman Marcus, and Santander (https://www.breaches.cloud/incidents/snowflake/, accessed on 7 May 2025).
In UAVNs, location-related data consist of sensitive information for both UAVs and consumers, and they are also subject to the same privacy leakage risks as discussed above. Due to their sensitive nature, these data cannot be directly outsourced to a public cloud. Before outsourcing, it is advisable to encrypt these data using a pre-defined security policy to protect the security and privacy of the data [6]. However, encryption breaks the semantics of location-related data, and thus, UAVs cannot operate on the encrypted data directly. To address this issue, researchers have proposed a series of searchable encryption schemes to support secure query operations in the cloud [7]. Searchable encryption schemes pre-construct a secure index for the original dataset and upload it to the cloud together with the encrypted dataset. The cloud can quickly locate the query results based on the secure index, thereby reducing the computational complexity to an acceptable level.
Among searchable encryption schemes, there exist several models [8,9] that focus on resolving range queries on encrypted location-related data. Most of them employ various space-filling curves to build secure indices for fast and secure data pruning. The main objectives of these schemes are to design a secure index structure. However, there are various kinds of space-filling curves [10] (row-wise curve, z-order curve, Gray curve, Hilbert curve, etc.), and their performance on range queries has not been well investigated. The selection of space-filling curves directly affects the query performance of a searchable encryption scheme. Additionally, most existing secure range query schemes cannot resist file-injection attacks and, thus, are not forward-secure. Forward security is a critical security property for secure range query schemes. It ensures that the security of the current key cannot be compromised even if previous keys are leaked. However, it is still challenging to design a forward-secure range query scheme for UAVNs.
In this paper, we propose a forward-secure query scheme—namely, OSFC-FSQ—for spatial data (i.e., location-related data, as mentioned above) that balances security, query efficiency, and result accuracy. We first constructed an index for spatial data in plaintext form using space-filling curves. Through extensive experimental analysis, we identified the optimal curve for range queries and k-nearest-neighbor (kNN) queries, as illustrated in Figure 1, two commonly used query types. By partitioning the original points using the optimal curve, we built a secure index that enables forward-secure queries over spatial data.
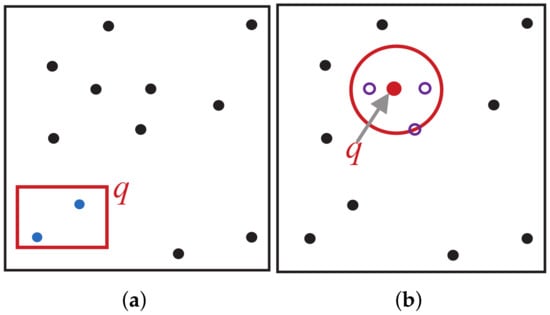
Figure 1.
An illustration of both a range query and a k-nearest-neighbor (kNN) query. (a) Range query. (b) kNN query with . The query is marked in red, the results for the range query are marked in solid blue, and the results for the kNN query are marked in hollow blue.
The main contributions of this study are as follows:
- The performance of four classic space-filling curves, namely, row-wise, Z-order, Gray, and Hilbert curves, is investigated. We constructed spatial indices on plaintext datasets using encoding algorithms specifically designed for each curve. Subsequently, we conducted query experiments on real-world geographic information datasets, focusing on two classic query types, range queries and kNN queries. Finally, by leveraging the unique properties of each space-filling curve, we performed both theoretical and experimental analyses to identify the optimal curves for different query scenarios.
- A forward-secure range query scheme is presented. We first partition the original dataset into subsets using the corresponding optimal curves. We then apply a greedy merging algorithm and a dummy-point insertion algorithm to balance the number of data points within each subset, resulting in greedy subsets. Each greedy subset is encrypted with a distinct key, and a key mapping table is generated accordingly. We construct a secure index based on these encrypted subsets and upload it to the cloud server along with the ciphertext dataset. Finally, a concrete forward-secure range query scheme is proposed.
- We implemented the proposed scheme and conducted extensive experiments on both real-world and synthetic datasets containing 100 million to 1 billion objects. The experimental results demonstrate that our scheme significantly outperforms existing schemes in terms of query time and accuracy. In particular, the accuracy of our scheme is improved by 20% to 30%, and the query time is reduced by 8% to 15% compared to the state-of-the-art schemes.
The rest of this paper is organized as follows. In Section 2, we review related works. In Section 3, we present the system overview, security model, and preliminaries. Then, the performance of various space-filling curves is investigated in Section 4. In Section 5, we describe the proposed OSFC-FSQ scheme in detail, followed by a theoretical analysis in Section 6. In Section 7, we evaluate the performance of OSFC-FSQ based on the results of extensive experiments. Finally, we conclude this paper in Section 8.
2. Related Works
In the domain of secure queries on spatial data, there are three primary approaches to achieving secure queries: query methods based on complex cryptographic techniques, query methods based on anonymity, and query methods based on secure indices.
Semantically secure solutions. Among these, most methods based on complex cryptographic techniques adopt traditional security models, such as IND-CPA, and customized semantic security. For instance, in 2007, Boneh et al. [11] proposed a complex cryptographic query scheme based on bilinear pairings, which is applicable to both relational and spatial databases. In 2015, Gay et al. [12] introduced a secure query scheme based on homomorphic encryption. In 2018, Yang et al. [13] proposed a secure query scheme that incorporates predicate encryption, while these methods ensure the confidentiality of spatial data, they do not address long-term storage and retrieval security in the context of frequent data updates in the big data era.
Anonymous solutions. The anonymity-based query approach leverages k-anonymity techniques [14], adding k − 1 random noises to the queries to confuse potential attackers, thereby limiting the probability that an attacker can identify the query point to no more than 1/k. Subsequent improvements to anonymity-based secure query methods have been proposed. However, to date, none have guaranteed forward security, and the addition of random noise increases bandwidth consumption.
Solutions for secure range queries. In 2007, Khoshgozaran et al. [8] proposed a query scheme that constructs a secure index structure based on linear ordering, addressing both nearest-neighbor and range queries over encrypted spatial data. Subsequently, researchers improved upon traditional R-tree structures to develop novel tree-based secure index structures. For instance, in 2009, Yiu et al. [15] introduced a secure index leveraging symmetric encryption. Then, in 2016, Demertzis et al. [16] proposed a secure index utilizing the Paillier homomorphic encryption method. Following that, in 2019, Cui et al. [17] presented a secure index structure based on bilinear pairings. These tree-based secure index structures ensure the security of indices, data, and queries during the secure query process. However, similar to the aforementioned methods based on complex cryptographic and anonymity techniques, they adopt traditional security models, resulting in multiple rounds of interaction between the client and the server, which leads to high communication overhead and low computational efficiency. In 2022, Peng et al. [9] proposed the forward-secure range query scheme LS-RQ, which uses locality-sensitive hashing (LSH) to map two-dimensional spatial data to one dimension before constructing a secure index. This scheme achieves single-round interaction between the user and the cloud server in a cloud-based service model, reducing communication overhead. Moreover, it is one of the few spatial query schemes that provide forward security.
To summarize, existing solutions predominantly concentrate on enhancing efficiency, bolstering security, or attaining forward security. Regrettably, they overlook the pivotal role that the selection of space-filling curves plays in shaping the performance of query schemes. The choice of space-filling curves is of paramount significance to the efficiency of query schemes, as it has a direct bearing on the construction of secure indices and the query process itself. Unfortunately, current schemes fail to offer a comprehensive analysis of various space-filling curves, which may result in suboptimal performance in terms of query efficiency and accuracy. Against this backdrop, designing a query scheme that concurrently satisfies requirements for efficiency, accuracy, and forward security by leveraging an optimized space-filling curve emerges as not only a highly promising research direction but also an urgent issue that demands immediate attention in the domain of secure queries.
3. System Overview and Preliminaries
In this section, we describe the system overview, security model, and preliminaries in detail.
3.1. System Overview
There are three entities in OSFC-FSQ, as illustrated in Figure 2.
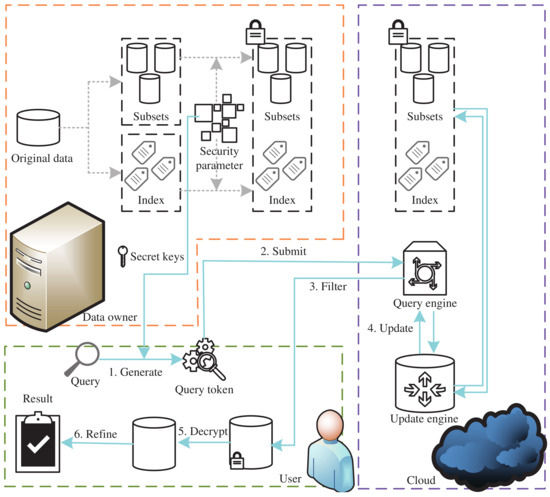
Figure 2.
An overview of the forward-secure range query.
- The data owner is assumed to be fully honest and trustworthy and will not perform any malicious operations on users’ spatial data, such as privately replacing data, altering outputs, or selling data. The data owner is responsible for managing the security parameters and the related keys generated based on these parameters. The data owner also handles all tasks required to preprocess the original dataset, including partitioning data subsets, encrypting original data points, and constructing secure indices. After completing preprocessing, the encrypted dataset and the secure index are uploaded to the cloud server.
- The cloud is assumed to be semi-honest. This means that it follows the protocol and does not perform malicious attacks on the data, such as modifying the data or altering the results of inputs and outputs. However, it remains highly curious about the data it stores, for example, by recording intermediate results and inferring additional information based on them. After the data owner completes data preprocessing, the cloud server receives and stores the uploaded encrypted dataset and secure index. During the query process, the cloud server retrieves the ciphertext labels of the candidate structure set by matching the received query token with the secure index. Finally, it completes the query based on the ciphertext and returns the candidate result set to the user.
- The user initiates a query request by specifying the query range and generating a query token locally using the security parameters. The query token is then sent to the cloud. Upon receiving the encrypted candidate result set from the cloud, the user decrypts it and performs a secondary fine-grained query to obtain the final query result set.
The secure range query, as shown in Figure 1a, can be achieved by instantiating an OSFC-FSQ scheme. First, the user generates a query token based on the specified query range and sends to the cloud. The cloud server then matches the query token with the secure index to retrieve the encrypted candidates that fall within with a high probability. These encrypted candidates are returned to the user. Finally, the user decrypts the encrypted candidate set and performs a linear scan on it to obtain the final query result.
3.2. Security Model
To conduct a security evaluation of a security model, it is first necessary to define a leakage function, and the standard security definition follows the ideal or real simulation paradigm [18,19]. The core of this standard security definition is that an attacker cannot obtain any information beyond what is provided by the leakage function itself and what can be inferred from it. Moreover, through this security definition, the information that an attacker might obtain can be distilled into a describable algorithm.
Corresponding to the framework introduced in Section 3.1, the leakage function in this paper is defined in Equation (1). Specifically, correspond to the leakage functions for initialization, query, addition, deletion, and update, respectively. The compound leakage function is defined as follows:
Definition 1
(-forward-adaptive security for OSFC-FSQ). An OSFC-FSQ scheme is -forward-adaptive secure if, for any probabilistic polynomial-time adversary , there exists an efficient simulator and a leakage function such that the following equations hold:
Here, denotes the real game, denotes the ideal game, and denotes a negligible function. denotes the inserted dataset, and denotes the corresponding IDs of the inserted data.
3.3. Preliminaries
In this section, we introduce the basic concepts and definitions used in OSFC-FSQ.
3.3.1. Inverted and Forward Indices
Both inverted and forward indices are data structures designed for file data retrieval. The construction of the secure index in this study draws on the principles of their indexing methods.
Specifically, the data structure of an inverted index is based on keywords, where each keyword corresponds to a set of file labels that represent the files containing the keyword. The collection of such “keyword–file label” pairs constitutes an inverted index, also commonly referred to as a reverse index (as shown in Figure 3a). In contrast, a forward index is based on files, with each file corresponding to all the keywords it contains. The collection of “file label–keyword” pairs forms a forward index, also known as a direct index (as shown in Figure 3b).
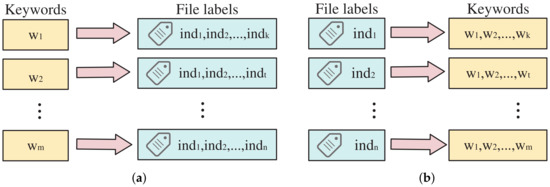
Figure 3.
Illustrated examples of both the inverted index and forward index. (a) Inverted index. (b) Forward index.
For large-scale file collections, when users need to retrieve files containing a specific keyword, an inverted index can be employed to efficiently map the keyword to its corresponding file labels, thereby directly locating the relevant files. This approach significantly reduces the computational overhead associated with linearly scanning all files in the collection, as would be required in a brute-force search. However, when the retrieval requirement shifts to finding keywords within files, especially in scenarios involving the addition or deletion of files, the inverted index becomes less efficient. In such cases, locating all keywords associated with a file in the inverted index and updating the corresponding file labels can involve high computational complexity, rendering the inverted index unsuitable. In contrast, a forward index allows the direct retrieval of all keywords contained in a file based on its file label. Adding or deleting a file simply involves creating or removing an index block, respectively.
3.3.2. Pseudo-Random Function
A pseudo-random function (PRF) [20] is a deterministic function that behaves like a random function. Specifically, a PRF is a function that satisfies the following two properties:
- Efficiency: For any input , the function can be computed in polynomial time.
- Pseudo-randomness: For any probabilistic polynomial-time adversary , the probability that can distinguish between F and a truly random function is negligible.
3.3.3. Proxy Re-Encryption
Proxy re-encryption (PRE) [21] is a cryptographic primitive that allows a semi-trusted proxy to transform ciphertext encrypted with one key into ciphertext encrypted with another key. Specifically, a PRE scheme consists of three pivotal algorithms: , , and . The algorithm generates a public key and a secret key for the data owner. The algorithm generates a re-encryption key for the proxy. The inputs of the algorithm are a ciphertext encrypted with the data owner’s public key and the re-encryption key generated by the proxy, and the output is a new ciphertext encrypted with the proxy’s public key.
A PRE scheme must have the following security properties:
- Correctness: For any ciphertext c encrypted with the data owner’s public key , if the proxy generates a re-encryption key , then the ciphertext obtained by re-encrypting c using must be decryptable using the data owner’s secret key .
- Security: For any probabilistic polynomial-time adversary , the probability that can distinguish between a ciphertext c encrypted with the data owner’s public key and a ciphertext obtained by re-encrypting c using generated by the proxy is negligible.
4. Analyses of Space-Filling Curves for Spatial Data
In this section, a spatial data query framework is first introduced based on indexing using space-filling curves, and the characteristics of these curves are analyzed. Subsequently, encoding algorithms are designed for each type of curve to generate uniformly structured codes for spatial data points according to the specific encoding rules of different curves. Spatial indices are then constructed for plaintext data points based on the obtained codes. Extensive experiments were conducted in range query and k-nearest-neighbor query scenarios. The analysis combines the characteristics of the curves with experimental results to derive conclusions on the optimal curves suitable for different scenarios.
4.1. Spatial Query Framework
The spatial query framework based on space-partitioning indexing is illustrated in Figure 4. The whole process can be divided into the following steps:
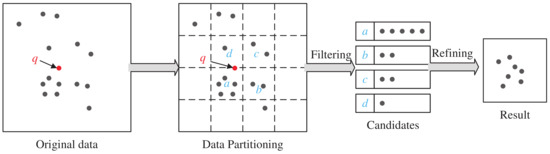
Figure 4.
A query framework for evaluating space-filling curves.
- Data partitioning: The space containing the original spatial data is divided into grids, thereby partitioning the original data into subsets corresponding to each grid. When constructing indices using space-filling curves, each grid is traversed non-repetitively according to the rules of the specific curve, and a unique, incrementally assigned identifier is allocated to each traversed grid. This process reduces unordered two-dimensional or higher-dimensional spatial data from a multidimensional space to a one-dimensional space, resulting in a linear sequence.
- Filtering: The input query conditions (query point or query range) are processed to obtain a query identifier using the same rules as those for the original data points. The corresponding number of candidate sets is returned based on the specific query conditions.
- Refining: An exact query is conducted within the candidate set obtained in step (2), significantly reducing the number of query points and thereby shortening the query time.
The space-filling curves investigated in this paper include the row-wise curve, Z-order curve, Gray curve, and Hilbert curve, as illustrated in Figure 5, which are typical curves adopted in various studies. Tao et al. [22] proposed the LSB-Forest index structure, which incorporates space-filling curves into the LSH index. Their focus was on using the Z-order curve to adaptively expand the search radius during nearest-neighbor queries. Liu et al. [23] introduced SK-LSH, aiming to improve I/O efficiency by reordering data points reduced by LSH using row-wise curve and Hilbert curve techniques, respectively, thereby reducing disk access during queries. Gustavo Niemeyer’s GeoHash algorithm encodes geographic data by independently encoding latitude and longitude coordinates and merging them in the traversal order of the Z-order curve [24]. The Google S2 [25] library maps spherical coordinates to a plane, divides the plane into grids according to specific rules, and uses Hilbert curve techniques to assign one-dimensional encodings to each grid, simplifying subsequent spatial indexing. However, to date, no studies or experiments have explicitly compared the performance of different space-filling curves in terms of query efficiency and accuracy when constructing indices for two-dimensional spatial data.
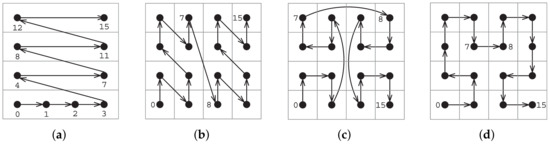
Figure 5.
Typical space-filling curves. (a) Row-wise curve. (b) Z-order curve. (c) Gray curve. (d) Hilbert curve.
4.2. Encoding Algorithms for Space-Filling Curves
Different space-filling curves traverse the divided grids according to their own rules and incrementally assign a unique number to each grid. This number serves as the dimensionality reduction result for the two-dimensional data points within the grid. Consequently, it is necessary to design encoding algorithms for spatial data tailored to each type of curve, enabling each spatial data point to obtain uniformly formatted encodings from different curves.
Here, we employ binary encoding for spatial data and introduce a parameter, length, to represent the encoding length, that is, the number of bits in the binary code. Correspondingly, the number of grids is . For example, when an original data space is divided into 2 × 2 grids, the encoding length is set to length = 2, and the encodings for the four grids are sequentially 00, 01, 10, and 11. For different space-filling curves, the total number of bits and the format of the encoding for each data point remain the same. However, the encoding order for data points at the same position varies according to the traversal rules of different curves. The following sections sequentially describe the process of obtaining curve-specific encodings for spatial data with row-wise, Z-order, Gray, and Hilbert curves.
Encoding algorithm for the row-wise curve: Assume that the coordinates of a grid are , and the total number of grids along the Y-axis is I. The grid index can be calculated using . However, the coordinate values of data points along both the X- and Y-axes have been normalized to the interval during deployment. Therefore, the coordinate values of the data points must be separately processed to obtain the desired encoding. The specific procedure is detailed in Algorithm 1.
| Algorithm 1 Encoding algorithm for row-wise curve |
|
Encoding algorithm for the Z-order curve: The process of encoding using the Z-order curve is recursive in nature. Essentially, it involves encoding each dimension separately and then concatenating the encodings of the two dimensions in the order of the x-coordinate followed by the y-coordinate to obtain the final encoding. The specific procedure is detailed in Algorithm 2.
| Algorithm 2 Encoding algorithm for Z-order curve |
|
| Algorithm 3 Encoding algorithm |
|
Encoding algorithm for Gray curve: The filling process of the Gray space-filling curve can be regarded as the generation process of Gray codes. An n-bit Gray code can be constructed by appending a single “0” or “1” to an (n-1)-bit Gray code ; the detailed principle behind this construction is not provided in this section. A Gray code of length can be obtained using the following equation:
Encoding algorithm for Hilbert curve: The Hilbert curve is a continuous yet nowhere differentiable curve that can fill an entire space regardless of how finely the space is divided into grids. Moreover, as the encoding length increases, that is, as the number of grids in the space grows, the positions of data points along the curve become increasingly stable. The encoding algorithm for the Hilbert curve is detailed in Algorithm 4.
| Algorithm 4 Encoding algorithm for Hilbert curve |
|
4.3. Experimental Analysis of Space-Filling Curves
Space-filling curves exhibit distinct characteristics based on their unique filling rules. When applied to the two classic querying methods (i.e., range queries and kNN queries), each curve’s performance varies due to these inherent differences. This section first provides a theoretical analysis of the curves’ performance for each querying method. Subsequently, comparative experiments on curve performance are presented, and the results are analyzed to identify the optimal curves for both query types. The performance evaluation metrics for different curves in spatial data querying primarily include query efficiency, search accuracy, etc.
To evaluate the trends in query accuracy and efficiency for range and kNN queries, increases in the length value from 2 to 16 in increments of 2 are illustrated in Figure 6. This corresponds to the number of grids increasing from 4 to 216 in multiples of 4. The data shown are experimental results from the HK dataset, with fixed inputs of 100 range query intervals and 100 query points and a fixed k value of 10.
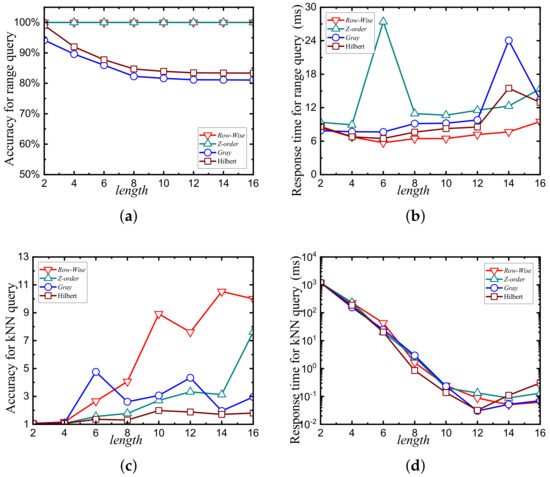
Figure 6.
Effect of adjustment on length of encoding. (a) Accuracy of range query. (b) Average response time of range query. (c) Accuracy of kNN query. (d) Average response time of kNN query.
As shown in Figure 6a,c, the query accuracy gradually decreases with increasing length values until it stabilizes around a length value of 10. For range queries, the row-wise and Z-order curves maintain a query accuracy of 1 throughout, while the Gray and Hilbert curves exhibit a decreasing–stabilizing pattern. For kNN queries, the ratio value increases and gradually stabilizes as it moves away from 1, also following a decreasing–stabilizing trend in query accuracy. Figure 6b indicates that the query efficiency for range queries follows an increasing–stabilizing–decreasing trend as the length value increases. Figure 6d shows that the query efficiency for kNN queries increases and stabilizes with increasing length values, with significant changes observed as the length increases from 2 to 6. The subsequent segment is less visible in the figure due to the large timescale differences. However, in actual data, when the length value exceeds 12, the ART value also exhibits a slight upward trend.
In sum, for range queries, it is essential to ensure that data points within the same locality in a two-dimensional space have identical or similar encodings in a one-dimensional space. The row-wise curve performs optimally in this regard. For kNN queries, the encoding order in one dimension must preserve the spatial proximity of data points when mapped back to two dimensions. The Hilbert curve achieves the best performance in this context.
5. Construction of OSFC-FSQ
In this section, we describe the construction of OSFC-FSQ by detailing the secure index construction and query mechanism.
5.1. Secure Index Construction
In OSFC-FSQ, after the index construction, each data item is represented as a triplet . Here, and represent the encrypted label and coordinate value of the data point, respectively. The coordinate value has practical significance, namely, the true geographical location information. represents the encrypted label of the subset derived from the partitioning of the original dataset. The security parameter provided by the user is applied to the hash function , and the label encryption of the data point subset is completed according to the hash function .
As mentioned above, both queries and data updates are followed by immediate updates to the ciphertext dataset and the security index to ensure the forward security of the scheme. Since the encryption methods for index values and data point values differ, the security index of this scheme can withstand the aforementioned passive attacks. Moreover, the cloud server in this scheme is assumed to be semi-honest and will not launch active attacks on the stored data. Thus, the aforementioned active attack scenarios can be disregarded.
In the preprocessing phase of this scheme, each spatial coordinate point in the original dataset is encoded using an optimal space-filling curve. Data points with the same encoding are grouped into the same data subset, and this encoding serves as the label for the subset. However, spatial data inherently have non-uniform distributions, which can lead to uneven numbers of data points in the resulting subsets. This uneven distribution may partially reveal the underlying data distribution, allowing attackers to infer the overall dataset from the ciphertext and potentially obtain the plaintext. To address this issue, before constructing the secure index, we introduce the greedy merging algorithm and the dummy-point insertion algorithm to balance the number of data points in each curve-encoded subset.
Then, the security index is represented as , which is stored in the form of a dictionary, where denotes the triplet entry corresponding to each original data item. Kim et al. [26] designed a dual-dictionary data structure that incorporates both inverted and forward indices. The inverted index is used for fast data retrieval, while the forward index is employed for quickly locating data to be updated, primarily targeting document data.
After spatial data are partitioned into corresponding subsets using a space-filling curve, the subsets can be analogized to document data. The idea of inverted and forward indices can then be applied to construct the entire dictionary. The label corresponding to each data subset acts as the identifier keyword in document data, while the data points within the subset correspond to the specific content within the document. Each triplet data item e has the following mappings: from to , indicating a one-to-one correspondence between a data point and its greedy subset, and from to the set of data points , representing the correspondence between a greedy subset label and all data points within that subset. All of these mappings constitute .
In summary, the secure index enables data queries by mapping from to the set of data points , returning the candidate subset as the preliminary query result. Data updates, including replacement, addition, and deletion, are performed by mapping from to . Specifically, the location of the greedy subset corresponding to the data point is first identified, and the update operation is then completed by the cloud server.
5.2. Query Mechanism
The query mechanism of OSFC-FSQ is divided into three stages: trapdoor generation, the query on the cloud, and the query on the user side.
Trapdoor generation: To complete a query (taking the range query as an example), the user must provide the query range and security parameters, while the data owner must supply two mapping tables. These elements are used to generate a secure query token and the key mapping table for the encrypted candidate set within the query range. The key mapping table is defined as and is utilized for subsequent decryption. Here, is used to encrypt existing data, is used to encrypt inserted data, and is used to re-encrypt both of the aforementioned data types for forward security. The secure query token is then transmitted to the cloud to formally initiate the query request. Given a range query , the trapdoor generation process is detailed in Algorithm 5.
| Algorithm 5 Trapdoor generation algorithm |
|
Query on the cloud: The cloud server receives the secure query token and performs a search on based on the greedy subset information contained within . It identifies the ciphertext labels of each greedy subset and retrieves all data points within these subsets as the initial query candidate set. The mapping between the greedy subset labels and the candidate subsets is recorded in the mapping table . During this process, the cloud server also considers the inserted dataset, where represents the original dataset and represents the inserted dataset. To ensure the forward security of the query process, the cloud server uses the re-encryption keys contained in the query token to re-encrypt the data points within each subset without decryption. The labels of the greedy subsets are updated from to . The re-encrypted ciphertext dataset and the updated greedy subset labels are then merged into the corresponding encrypted dataset and secure index . Finally, the candidate set and its corresponding greedy subset labels are returned to the client. The query process in the cloud is detailed in Algorithm 6.
| Algorithm 6 Query algorithm in the cloud |
|
Query on the user side: The user first initializes the candidate result set and the final result set to be empty. Upon receiving the candidate set from the cloud, the client retrieves the corresponding ciphertext subsets and decryption keys from and using the ciphertext greedy subset labels obtained from Algorithm 7. It then decrypts the returned encrypted candidate set and traverses the decrypted results to filter out false positives, thereby obtaining the candidate result set . Finally, the client performs an exact query within the remaining plaintext candidate set based on the query range to obtain the final result Res. The query process on the user side is detailed in Algorithm 7.
| Algorithm 7 Query algorithm on the user side |
|
6. Theoretical Analysis
In this section, OSFC-FSQ is theoretically analyzed from the perspectives of security and complexity.
6.1. Security Analysis
Forward-secure range queries represent a promising direction in dynamic searchable symmetric encryption. Like most dynamic symmetric searchable encryption schemes, the cloud server in the proposed OSFC-FSQ scheme is assumed to be semi-honest. With the secure query, the cloud server can return the corresponding results according to the established protocol without gaining any additional plaintext information. The following sections provide a security analysis of OSFC-FSQ from two aspects: access pattern leakage and -adaptive forward security.
Resistance to access pattern attack: In the field of searchable encryption, researchers have identified security vulnerabilities that allow attackers to reconstruct one-dimensional datasets by exploiting access patterns leaked during the query process. For instance, in the query scenarios discussed in this paper, the number of data points in the range query results [27,28] and the access patterns themselves [29,30] can be utilized. The implementation of the aforementioned attacks hinges on two conditions. The first is that elements within the dataset must exhibit a clear partial order, and the second is that the leakage of access patterns must be specific and accurate.
Firstly, datasets with explicit partial orders typically consist of elements with inherent keywords or one-dimensional numerical values (e.g., salary or age). This is because the mapping relationships constructed based on such data inherently contain keywords, and the partial order of one-dimensional numerical values is naturally defined. However, for the dataset containing spatial data (i.e., two-dimensional data) targeted in this study’s experiments, a clear partial order cannot be established between any pair of data points unless their coordinates are identical. Moreover, it is challenging to precisely define the relationship between two-dimensional geographic coordinates. Therefore, OSFC-FSQ does not satisfy the first condition.
Moreover, in many existing secure query mechanisms, the returned encrypted candidate sets are specific and accurate, containing no false positives or false negatives. That is, the leakage of their access patterns is entirely correlated with the true results, thus satisfying the second condition. In contrast, in the proposed OSFC-FSQ scheme, the preprocessing phase encodes all data points in the dataset using a space-filling curve and groups points with identical encodings into the same subset. During ciphertext-based retrieval in the cloud, the scheme returns all data points within the queried subset. As shown in Section 3.3.2, the results of plaintext retrieval using space-filling curves indicate a non-negligible proportion of false positives. Therefore, the access patterns available to the cloud server are neither specific nor accurate, and OSFC-FSQ does not meet the second condition.
In summary, OSFC-FSQ fails to meet either of the two critical conditions required for attacks based on access pattern leakage. Consequently, it can be demonstrated that OSFC-FSQ is resilient to access pattern attacks.
-adaptive forward security: The OSFC-FSQ scheme satisfies L-adaptive forward security, with the leakage function defined as follows:
In the above expression, denotes the sequence of all issued queries, where each tuple in the sequence is of the form . Here, is a temporal identifier, and q represents the query itself. The search pattern is represented as a two-dimensional matrix , where if and only if . denotes the list of historical access points, containing queries. From the aforementioned definitions, it is evident that , , and do not leak any information, while leaks and , and only leaks the ID set of the added dataset.
Moreover, during the query period of OSFC-FSQ, all transmitted data are encrypted using proxy re-encryption algorithms, ensuring the confidentiality of both data and queries. In OSFC-FSQ, the leakage during the addition phase is merely the ID set of the newly added points, and the ciphertext dataset is promptly updated after data addition, followed by re-encryption using the re-encryption keys. This ensures the forward security of the scheme. Therefore, OSFC-FSQ satisfies the two necessary conditions for -adaptive forward security.
In summary, OSFC-FSQ is L-adaptive forward-secure and resilient to attacks based on access pattern leakage.
6.2. Complexity Analysis
To facilitate the quantitative analysis of time and space overheads in the subsequent sections, we define the following key parameters and their corresponding variables for OSFC-FSQ. We define the following parameters for OSFC-FSQ: n as the size of the original dataset, as the size of the added dataset, as the encoding length of the space-filling curve determining grid granularity and data subset size, as the size of data subsets after preprocessing, c as the number of greedy subsets within the query range , as the security parameter determining bit lengths for the hash function H and label encryption, as the time for a single hash function H, as the time for a single update operation on the secure index, as the time for a single deduplication operation, as the time for a single encryption operation, as the time for a single decryption operation, as the time for a single re-encryption operation, as the time to generate a key pair, as the time to generate a re-encryption key, and as the time for a single pseudo-random permutation.
Time complexity for the data owner: During the process, the primary time-consuming operations involve regenerating the greedy subset labels for the user-submitted query range and generating re-encryption keys, with a time overhead of . In the data addition process, the data owner is responsible for preprocessing the added data, incurring a time overhead of . The time overhead for the data update and deletion operations is .
Storage complexity for the data owner: The data owner manages two mapping tables: for mapping curve-based subset labels to greedy subset labels, and for mapping greedy subset labels to their key pairs. These tables are stored in the form of and , respectively. The storage space overhead for the data owner is bits.
Time complexity for the cloud: During a single query process in the cloud, the most time-consuming operation is the update of the secure index, with a time overhead of . For data addition, update, and deletion operations, the time overhead in the cloud is .
Storage complexity for the cloud: The cloud server is responsible for storing the secure index and the encrypted dataset. These are stored in the forms and , respectively. Ignoring the number of dummy points, the storage space overhead in the cloud server is bits.
Time complexity for the user: During the fine-grained query process, the primary time overhead for the user involves decrypting and filtering the returned candidate set, with a time cost of .
7. Experimental Evaluation
In this section, OSFC-FSQ is validated and analyzed based on the results of simulation experiments. We first introduce and explain the experimental settings, including the experimental environment, datasets used, and performance evaluation metrics. Subsequently, multiple experiments are designed to analyze the impact of key parameters on the query performance, the accuracy of query results, and the efficiency of the query process based on the experimental outcomes.
7.1. Compared Schemes
To evaluate the performance of OSFC-FSQ, we compare it with two existing schemes: CRT [31], SKD, and LS-RQ [9]. In the CRT scheme, the dataset is organized using an R-tree, in which all nodes are encrypted using a symmetric encryption algorithm, while recursively searching the R-tree, the cloud server sends the encrypted nodes to the client for decryption and determining the child nodes to be accessed. In this way, the client can obtain the query results without revealing the data to the cloud server. SKD is a novel range query scheme that encrypts nodes in a KD-tree using comparable encryption (CE) [32]. This encryption scheme is highly efficient and allows for direct comparisons between ciphertexts. Both CRT and SKD are used as reference schemes to demonstrate the superiority of over popular index structures such as R-tree and KD-tree. The LS-RQ scheme is a recent approach that utilizes a Z-order curve to construct a secure index for range queries. The comparison of OSFC-FSQ with CRT, SKD, and LS-RQ allows us to highlight its advantages in terms of both query efficiency and security.
7.2. Experimental Settings
All experiments in this section were conducted on a platform equipped with an CPU at 2.20 GHz and 256 GB of memory and running Ubuntu 16.04. In the experimental studies, the PRE described in [33] was adopted. SHA1 was adopted as the hash function with the security parameter . To comprehensively evaluate the performance of the proposed scheme, four datasets were employed: two real-world geographic datasets and two synthetic datasets.
- The NE dataset contains 123,593 data points, each representing real location information in the northeastern United States.
- The HK dataset contains 1,384,420 data points, each representing real location information in the Hong Kong region.
- The UN dataset is a synthetic dataset with 1,000,000 data points uniformly distributed in a two-dimensional space.
- The GA dataset is also a synthetic dataset with 1,000,000 data points following a Gaussian distribution in a two-dimensional space.
The experimental results and corresponding analyses are presented in terms of result accuracy, query efficiency, and storage overhead. The accuracy of the query results is evaluated based on the ratio of the number of true positive data points to the total number of data points in the query result. The query efficiency is measured by the average response time (ART) of the query process, which is the time taken to complete a single query. The storage overhead is calculated based on the number of bits required to store the secure index and the encrypted dataset.
7.3. Effect of
The parameter , representing the number of bits in the space-filling curve encoding for each data point, directly affects the granularity of grid partitioning and is a crucial factor influencing both the query accuracy and efficiency of OSFC-FSQ. As shown in the experimental results in Section 4.3, the impact of on query accuracy is minimal for range queries. However, due to the incorporation of the greedy merging algorithm and dummy-point insertion algorithm during secure index construction, the query process relies on returning candidate subsets based on greedy subsets. Therefore, this subsection re-evaluates the optimal value by considering its combined effects on query accuracy and efficiency.
Figure 6 illustrates the trends in query accuracy and efficiency for range queries as the value increases from 2 to 16 in increments of 2 (i.e., the number of grids increases from 4 to in multiples of 4). The figure includes results from the NE dataset with a fixed input of 100 range query intervals. All other datasets exhibit similar trends, with the results omitted for brevity.
In OSFC-FSQ, even though ciphertext queries in the cloud are based on greedy subsets, the row-wise curve maintains its superiority in query result accuracy during the ciphertext query process. This is because the index values for the query range, generated during query token creation, follow the curve encoding values corresponding to greedy subset encodings obtained from the mapping table . As a result, the row-wise curve ensures an accuracy rate of 1 with all four datasets. Smaller values, which make the query process closer to a brute-force search, lead to a significant increase in the ART.
When the value reaches 10, the average response time of the client stabilizes. This is because, as the grid granularity becomes finer, the size of the candidate set returned by the query process also stabilizes. However, when the value exceeds 14, the ART begins to rise again. This is due to the increased number of greedy subsets in the returned candidate set as the grid granularity continues to decrease, which slows down the filtering and decryption processes, thereby reducing query efficiency.
In summary, for the subsequent experiments, length was fixed at , as illustrated in Table 1.

Table 1.
Details of parameters.
7.4. Preprocessing Performance
In OSFC-FSQ, the preprocessing step lays the foundation for the entire query process. During this step, the client generates the secure index and the ciphertext dataset, which are then uploaded to the cloud server. This enables the cloud server to perform ciphertext-based queries using the secure index and the secure query tokens submitted by the client. Specifically, the client’s preprocessing tasks include partitioning the curve encoding subsets, partitioning the greedy subsets, constructing the mapping table from curve encoding subsets to greedy subsets, constructing the mapping table from greedy subsets to key pairs, and executing a series of encryption operations. The encryption targets include the ID values of data points in the original dataset, the encoding values of greedy subsets, and the coordinate information of data points. This subsection provides details on preprocessing experiments, which were conducted on all four datasets. The experimental results show that, compared to the encryption process, the time required for other operations is negligible. Additionally, since the number of data points in the dataset is much larger than the number of greedy subsets, the encryption time for greedy subset encodings is also negligible. Therefore, the preprocessing time overhead is defined as the sum of the encryption times for data point IDs and data point coordinates. The experimental results are shown in Figure 7.
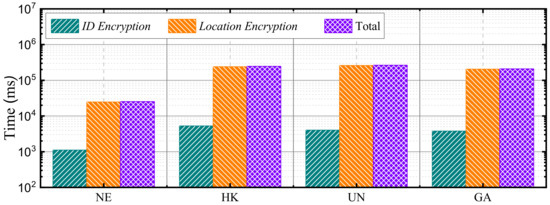
Figure 7.
The performance of preprocessing.
To ensure the forward security of the query scheme, the encryption method used in the preprocessing phase employs proxy re-encryption algorithms, thereby facilitating subsequent key update operations. Except for the NE dataset, which has a smaller data scale, the encryption time for data point IDs is on the order of seconds, while the encryption time for data point coordinates is on the order of minutes for the other three datasets. Although the preprocessing time overhead is significant due to the use of proxy re-encryption, it remains acceptable.
7.5. Storage Performance
The storage performance is summarized in Table 2 for all datasets. The data indicate that the size of the ciphertext storage is positively correlated with the size of the original plaintext dataset. Specifically, the UN dataset, which is uniformly distributed in a two-dimensional space, has a more even distribution of data points within its space-filling curve encoding subsets compared to the other datasets. As a result, fewer subsets need to be merged by the greedy merging algorithm, leading to a higher number of greedy subsets requiring dummy points. This also reflects the spatial distance-preserving property of space-filling curves. The storage overhead in the fourth column of the table represents the sum of the storage costs for each ciphertext data point. The storage format of the ciphertext dataset is , where the ciphertext label occupies 48 bytes, and the ciphertext coordinate information occupies 4684 bytes. These values can be used to calculate the storage overhead for the ciphertext dataset.

Table 2.
Storage performance for all datasets.
7.6. Query Performance and Comparison
This subsection compares the proposed scheme with the existing LS-RQ scheme [9] in terms of query result accuracy and query efficiency. To ensure a consistent hardware environment, the comparison scheme was locally re-implemented in this study. Specific experimental results and analyses are provided based on this implementation.
To ensure the stability of the test results, the following experiments employed a fixed set of 100 randomly generated query ranges without any specific constraints. For each of the five query range spans (1%, 2%, 3%, 4%, and 5%), 100 queries were conducted sequentially, and the final results were averaged.
Comparison of accuracy. Figure 8 presents a comprehensive comparison of query result accuracy between the OSFC-FSQ scheme and the other compared schemes. Our findings indicate that OSFC-FSQ consistently outperforms LS-RQ in terms of query precision, regardless of whether a fixed query range span is specified. This superior performance of OSFC-FSQ can be primarily attributed to the unique dimension-prioritized traversal property of the row-wise curve. This property ensures that the curve encoding values on the one-dimensional line order can fully cover all data points within the query range in rectangular queries. As a result, it introduces only a few false-positive objects and significantly enhances query accuracy. However, this approach is inherently limited by the characteristics of the space-filling curves used. Nevertheless, the precision of OSFC-FSQ is improved by 20% to 30% compared to other schemes. Our extensive experiments further validated the accuracy advantage of the row-wise curve over other space-filling curves, especially in range queries. The row-wise curve’s ability to cover all relevant data points without significant false positives leads to more precise query results. Additionally, the other two compared schemes (i.e., CRT and SKD) exhibit lower or nearly equal accuracy rates compared to OSFC-FSQ. This is primarily because both schemes utilize a tree-based index structure, which inherently limits their ability to accurately capture the spatial relationships between data objects. In summary, the OSFC-FSQ scheme, leveraging the row-wise curve, demonstrates a clear and substantial improvement in query result accuracy. This makes OSFC-FSQ a more effective solution for range queries compared to the LS- RQ scheme.
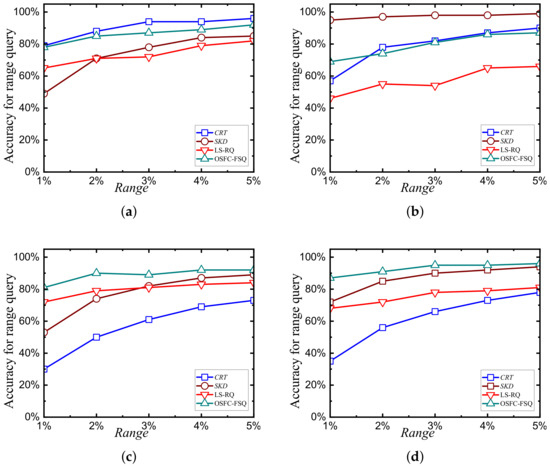
Figure 8.
Comparison of accuracy on various datasets: (a) NE. (b) HK. (c) UN. (d) GA.
Comparison of query efficiency. We evaluated multiple schemes for query processing, including SKD, CRT, OSFC-FSQ, and LS-RQ. Among these, the SKD scheme achieves the highest query efficiency by utilizing symmetric cryptographic techniques. However, this approach comes at a significant cost: it fails to provide forward security, a critical requirement for ensuring the long-term confidentiality and integrity of data. The CRT scheme, on the other hand, involves multiple rounds of interaction between the client and the server. This multi-round interaction significantly increases the communication overhead and latency compared to single-round interaction schemes such as OSFC-FSQ and LS-RQ. As a result, CRT’s performance is notably inferior in terms of query efficiency and overall system responsiveness. Given these limitations, our detailed comparison is focused on the OSFC-FSQ and LS-RQ schemes in the following sections.
The average client response times for the four datasets are illustrated in Figure 9. As the query range span increases, the time overhead also rises. This is because a larger query range span results in a larger candidate set, thereby increasing the decryption overhead on the client side. For the smaller NE dataset, the response time is measured in seconds, while for larger datasets with broader query ranges, it is measured in minutes. Comparative experiments across the four datasets reveal that OSFC-FSQ incurs significantly lower client time overhead than LS-RQ, which is forward-secure. This is attributed to the use of the row-wise curve for data mapping during subset partitioning in our scheme, which, while ensuring high query result accuracy, also leads to a lower number of false positives in the candidate set. Additionally, both the CRT and SKD schemes exhibit lower client response times compared to OSFC-FSQ, primarily because both schemes are less secure than OSFC-FSQ and LS-RQ. The compromise of security in these schemes allows for faster query processing, but at the cost of data confidentiality. In contrast, OSFC-FSQ and LS-RQ prioritize security while maintaining reasonable query efficiency.
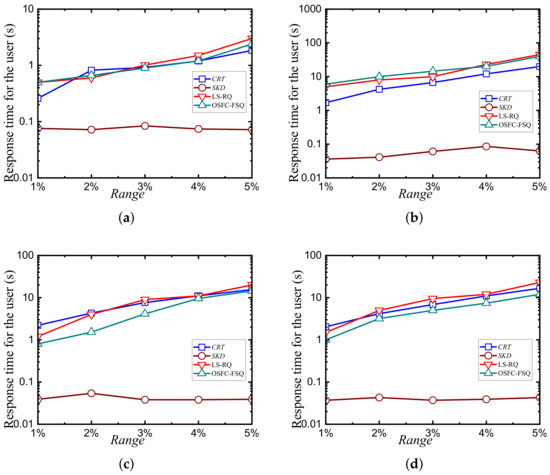
Figure 9.
Comparison of response times for the user on various datasets: (a) NE. (b) HK. (c) UN. (d) GA.
Furthermore, the time overhead for the cloud server using the four datasets is illustrated in Figure 10. Similar to the client-side time overhead, the query time for the cloud server increases with the query range span and is on the order of minutes in the hardware environment used in this study. The query times with the OSFC-FSQ and LS-RQ schemes for the cloud server are quite close, with the former showing a slight advantage. This is because the use of multiple LSH functions to reduce false positives in the LS-RQ scheme increases the ciphertext storage overhead and the ciphertext update overhead at the cloud server.
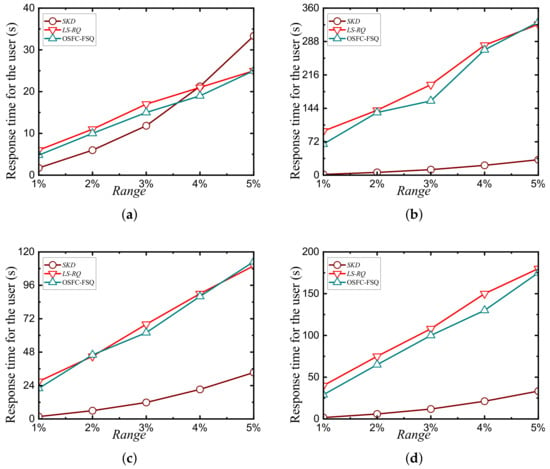
Figure 10.
Comparison of response times for the cloud on various datasets. (a) NE. (b) HK. (c) UN. (d) GA.
In summary, the scheme proposed in this paper demonstrates lower overheads for both the client and the cloud server. However, the client query overhead is significantly smaller than that for the cloud server. Specifically, our scheme achieves a 20% to 30% improvement in accuracy and an 8% to 15% reduction in query time compared to state-of-the-art schemes. By ensuring forward security, the majority of the computational burden shifts to the cloud server, thereby reducing the client query overhead. The experimental results confirm that our scheme significantly outperforms existing schemes in terms of query time and accuracy.
8. Conclusions
This study focused on secure data retrieval in UAVNs when data are outsourced to third-party cloud computing platforms. Through experimental analysis, we identified the optimal space-filling curves for range queries and k-nearest-neighbor queries, which are commonly used in location-based data. Using these optimal curves, we partitioned the original points (i.e., spatial data) into subsets and then applied the greedy merging algorithm and dummy-point insertion algorithm to achieve uniformly sized greedy subsets. Drawing on the concepts of inverted and forward indices, we constructed OSFC-FSQ to resolve forward-secure range queries. Finally, leveraging proxy re-encryption algorithms, we implemented forward-secure queries on spatial data. The experimental results demonstrate that our scheme significantly outperforms existing schemes in terms of query time and accuracy. In particular, the accuracy of our scheme is improved by 20% to 30% and the query time is reduced by 8% to 15% when compared to the state-of-the-art schemes.
The OSFC-FSQ scheme proposed in this paper currently supports only a single type of query based on a single secure index. However, in practical applications, it is highly desirable to use a single indexing framework to support multiple types of queries to reduce deployment costs. This capability is expected to be a key focus and an emerging trend in future research within this field.
Author Contributions
Conceptualization, Z.L. and Y.P.; data curation, X.L.; formal analysis, Z.L.; funding acquisition, J.H.; methodology, Z.L. and X.L.; project administration, J.H.; resources, X.L.; software, X.L. and J.H.; supervision, Y.P.; validation, X.L.; visualization, Z.L., Y.P. and J.H.; writing—original draft, Z.L. and Y.P.; writing—review and editing, Z.L. and Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Shenzhen Science and Technology Program (No. KCXFZ20211020174801002) and Natural Science Foundation of Shaanxi Province (No.2024JC-YBQN-0637).
Data Availability Statement
All real-world datasets used in this study are available on the Internet. The NE dataset can be downloaded from http://www.rtreeportal.org accessed on 7 May 2025. The HK dataset can be downloaded from http://archive.org/download/metro.teczno.com accessed on 7 May 2025. The synthetic datasets (i.e., GA and UN) generated and analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
We acknowledge the contributions from Qing Hu (School of Environmental Science and Engineering, Southern University of Science and Technology), the editors, and the reviewers.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ART | Average response time |
| kNN | k-nearest neighbor |
| IND-CPA | Indistinguishability under chosen-plaintext attack |
| LSH | Locality-sensitive hashing |
| PRF | Pseudo-random function |
| PRE | Proxy re-encryption |
| UAV | Unmanned aerial vehicle |
| UAVN | Unmanned aerial vehicle network |
References
- Hu, Z.; Zhou, D.; Shen, C.; Wang, T.; Liu, L. Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission. Electronics 2025, 14, 446. [Google Scholar] [CrossRef]
- Singh, S.; Jeong, Y.S.; Park, J.H. A survey on cloud computing security: Issues, threats, and solutions. J. Netw. Comput. Appl. 2016, 75, 200–222. [Google Scholar] [CrossRef]
- Zolfaghari, B.; Abbasmollaei, M.; Hajizadeh, F.; Yanai, N.; Bibak, K. Secure UAV (Drone) and the Great Promise of AI. ACM Comput. Surv. 2024, 56, 1–37. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Chen, B.; Li, T.; Zhang, R. Performance Analysis and Optimization Design of AAV-Assisted Vehicle Platooning in NOMA-Enhanced Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 1–10. [Google Scholar] [CrossRef]
- Karmakar, R.; Kaddoum, G.; Akhrif, O. IntSHU: A Security-Enabled Intelligent Soft Handover Approach for UAV-Aided 5G and Beyond. IEEE Trans. Cogn. Commun. Netw. 2025, 1. [Google Scholar] [CrossRef]
- Wu, W.; Shi, H. Pairing-Free Searchable Encryption for Enhancing Security Against Frequency Analysis Attacks. Electronics 2025, 14, 552. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, S&P 2000, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar] [CrossRef]
- Khoshgozaran, A.; Shahabi, C. Blind Evaluation of Nearest Neighbor Queries Using Space Transformation to Preserve Location Privacy. In Proceedings of the Advances in Spatial and Temporal Databases; Papadias, D., Zhang, D., Kollios, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 239–257. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, L.; Cui, J.; Liu, X.; Li, H.; Ma, J. LS-RQ: A lightweight and forward-secure range query on geographically encrypted data. IEEE Trans. Dependable Secur. Comput. 2022, 9, 388–401. [Google Scholar] [CrossRef]
- Gaede, V.; Günther, O. Multidimensional access methods. ACM Comput. Surv. 1998, 30, 170–231. [Google Scholar] [CrossRef]
- Boneh, D.; Waters, B. Conjunctive, Subset, and Range Queries on Encrypted Data. In Proceedings of the Theory of Cryptography; Vadhan, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 535–554. [Google Scholar] [CrossRef]
- Gay, R.; Méaux, P.; Wee, H. Predicate Encryption for Multi-dimensional Range Queries from Lattices. In Proceedings of the Public-Key Cryptography–PKC 2015; Katz, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 752–776. [Google Scholar] [CrossRef]
- Yang, W.; Xu, Y.; Nie, Y.; Shen, Y.; Huang, L. TRQED: Secure and Fast Tree-Based Private Range Queries over Encrypted Cloud. In Proceedings of the Database Systems for Advanced Applications; Pei, J., Manolopoulos, Y., Sadiq, S., Li, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 130–146. [Google Scholar] [CrossRef]
- Bösch, C.; Hartel, P.; Jonker, W.; Peter, A. A Survey of Provably Secure Searchable Encryption. ACM Comput. Surv. 2014, 47, 18:1–18:51. [Google Scholar] [CrossRef]
- Yiu, M.L.; Ghinita, G.; Jensen, C.S.; Kalnis, P. Outsourcing Search Services on Private Spatial Data. In Proceedings of the 2009 IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 1140–1143. [Google Scholar] [CrossRef]
- Demertzis, I.; Papadopoulos, S.; Papapetrou, O.; Deligiannakis, A.; Garofalakis, M. Practical Private Range Search Revisited. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD ’16, New York, NY, USA, 20–22 June 2016; pp. 185–198. [Google Scholar] [CrossRef]
- Cui, N.; Yang, X.; Wang, B.; Geng, J.; Li, J. Secure range query over encrypted data in outsourced environments. World Wide Web 2020, 23, 491–517. [Google Scholar] [CrossRef]
- Bost, R.; Minaud, B.; Ohrimenko, O. Forward and Backward Private Searchable Encryption from Constrained Cryptographic Primitives. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS ’17, New York, NY, USA, 30 October–3 November 2017; pp. 1465–1482. [Google Scholar] [CrossRef]
- Sun, S.F.; Yuan, X.; Liu, J.K.; Steinfeld, R.; Sakzad, A.; Vo, V.; Nepal, S. Practical Backward-Secure Searchable Encryption from Symmetric Puncturable Encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 763–780. [Google Scholar] [CrossRef]
- Goldreich, O.; Goldwasser, S.; Micali, S. How to construct random functions. J. ACM 1986, 33, 792–807. [Google Scholar] [CrossRef]
- Qin, Z.; Xiong, H.; Wu, S.; Batamuliza, J. A Survey of Proxy Re-Encryption for Secure Data Sharing in Cloud Computing. IEEE Trans. Serv. Comput. 2016, 1. [Google Scholar] [CrossRef]
- Tao, Y.; Yi, K.; Sheng, C.; Kalnis, P. Quality and efficiency in high dimensional nearest neighbor search. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, SIGMOD ’09, New York, NY, USA, 29 June–2 July 2009; pp. 563–576. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.; Huang, Z.; Li, H.; Shen, H.T. SK-LSH: An efficient index structure for approximate nearest neighbor search. Proc. VLDB Endow. 2014, 7, 745–756. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, F.; Sang, X.; Hu, B.; Tao, J. Precise Epidemic Control based on GeoHash. In Proceedings of the 2022 9th International Conference on Dependable Systems and Their Applications (DSA), Wulumuqi, China, 4–5 August 2022; pp. 1040–1048. [Google Scholar] [CrossRef]
- Jiang, B.; Zhou, W.; Han, H. Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Appl. Sci. 2024, 14, 1115. [Google Scholar] [CrossRef]
- Kim, K.S.; Kim, M.; Lee, D.; Park, J.H.; Kim, W.H. Forward Secure Dynamic Searchable Symmetric Encryption with Efficient Updates. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS ’17, New York, NY, USA, 30 October–3 November 2017; pp. 1449–1463. [Google Scholar] [CrossRef]
- Ghareh Chamani, J.; Papadopoulos, D.; Papamanthou, C.; Jalili, R. New Constructions for Forward and Backward Private Symmetric Searchable Encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 1038–1055. [Google Scholar] [CrossRef]
- Amjad, G.; Kamara, S.; Moataz, T. Forward and Backward Private Searchable Encryption with SGX. In Proceedings of the 12th European Workshop on Systems Security, EuroSec ’19, New York, NY, USA, 25–28 March 2019. [Google Scholar] [CrossRef]
- Grubbs, P.; Lacharite, M.S.; Minaud, B.; Paterson, K.G. Pump up the Volume: Practical Database Reconstruction from Volume Leakage on Range Queries. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 315–331. [Google Scholar] [CrossRef]
- Grubbs, P.; Lacharité, M.S.; Minaud, B.; Paterson, K.G. Learning to Reconstruct: Statistical Learning Theory and Encrypted Database Attacks. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–22 May 2019; pp. 1067–1083. [Google Scholar] [CrossRef]
- Yiu, M.L.; Ghinita, G.; Jensen, C.S.; Kalnis, P. Enabling search services on outsourced private spatial data. VLDB J. 2010, 19, 363–384. [Google Scholar] [CrossRef]
- Furukawa, J. Request-Based Comparable Encryption. In European Symposium on Research in Computer Security (ESORICS); Springer: Berlin/Heidelberg, Germany, 2013; pp. 129–146. [Google Scholar] [CrossRef]
- Nuñez, D.; Agudo, I.; Lopez, J. NTRUReEncrypt: An Efficient Proxy Re-Encryption Scheme Based on NTRU. In Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, ASIA CCS ’15, New York, NY, USA, 14–17 April 2015; pp. 179–189. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).