AI-Based Impact Location in Structural Health Monitoring for Aerospace Application Evaluation Using Explainable Artificial Intelligence Techniques
Abstract
1. Introduction
2. Materials and Methods
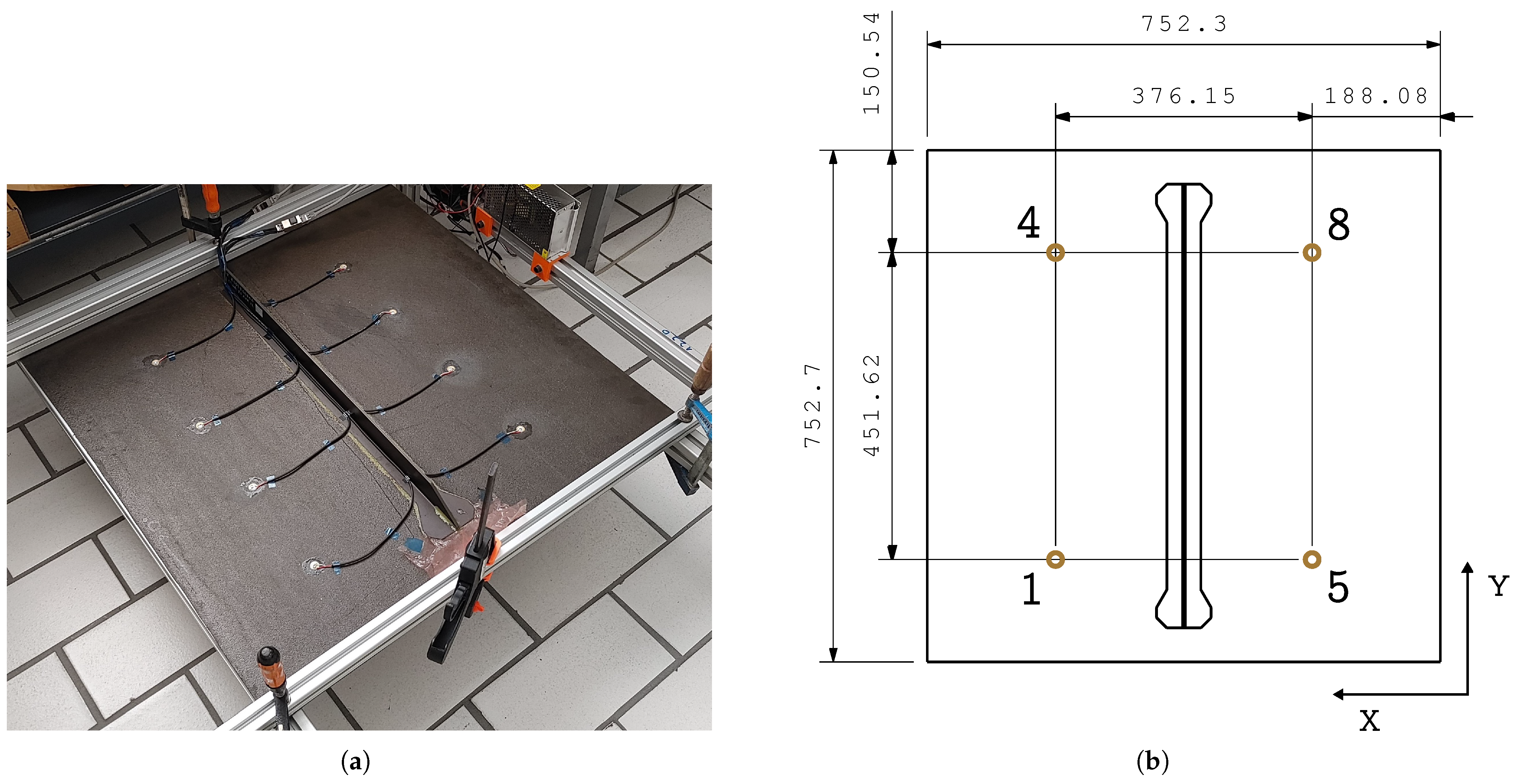
2.1. Specimen, Impactor, and Dataset
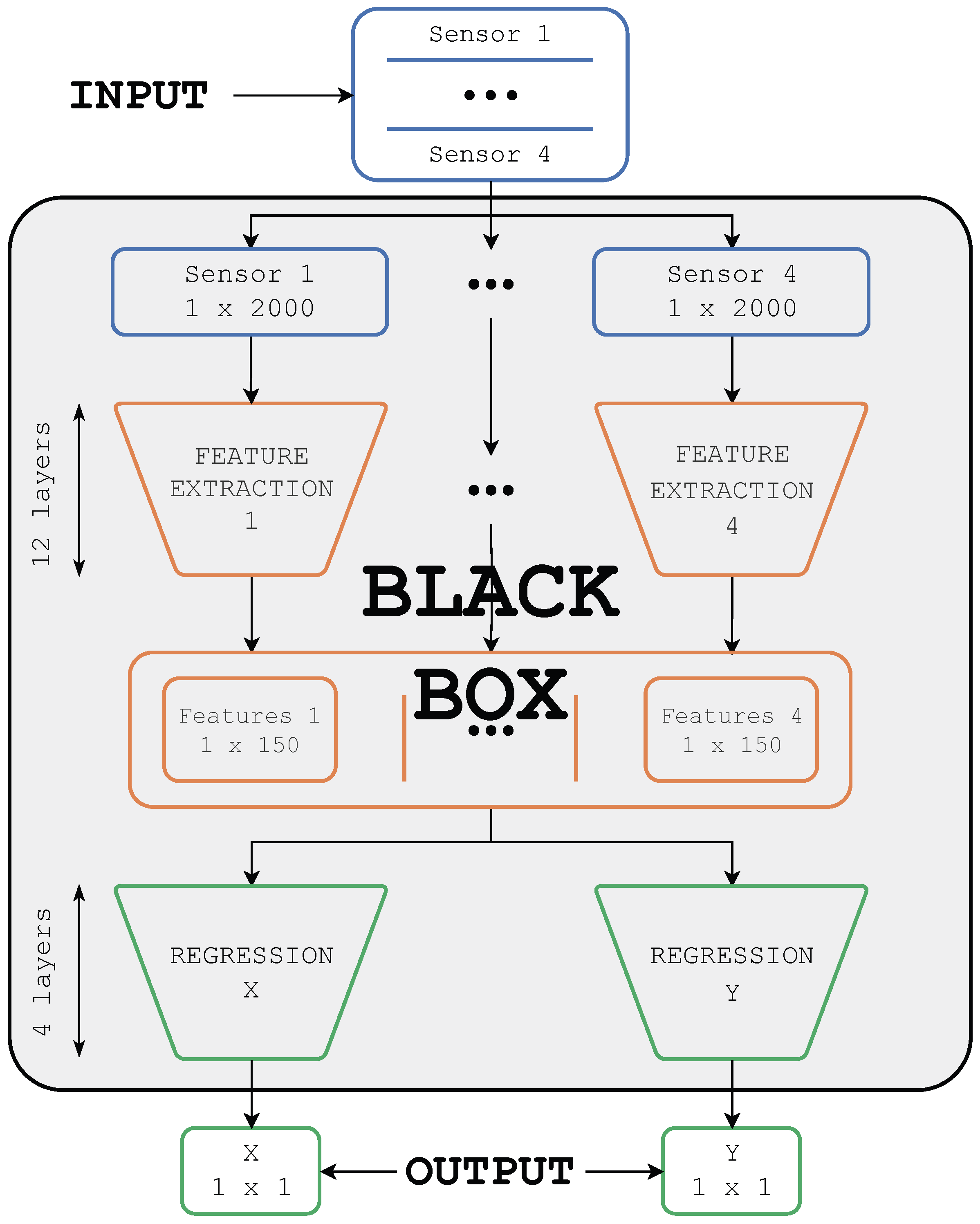
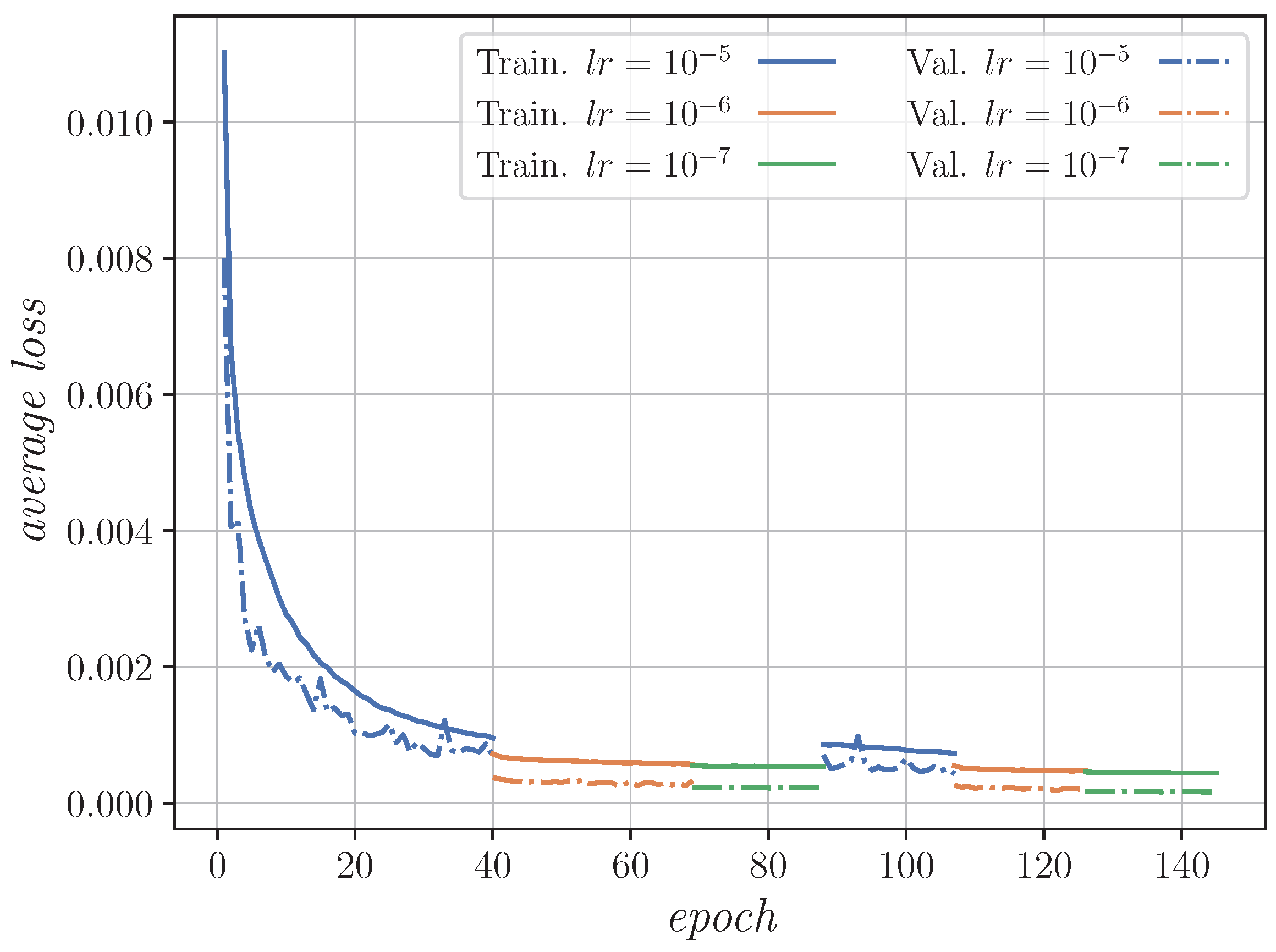
2.2. Impact-Locator-AI Model Evaluated
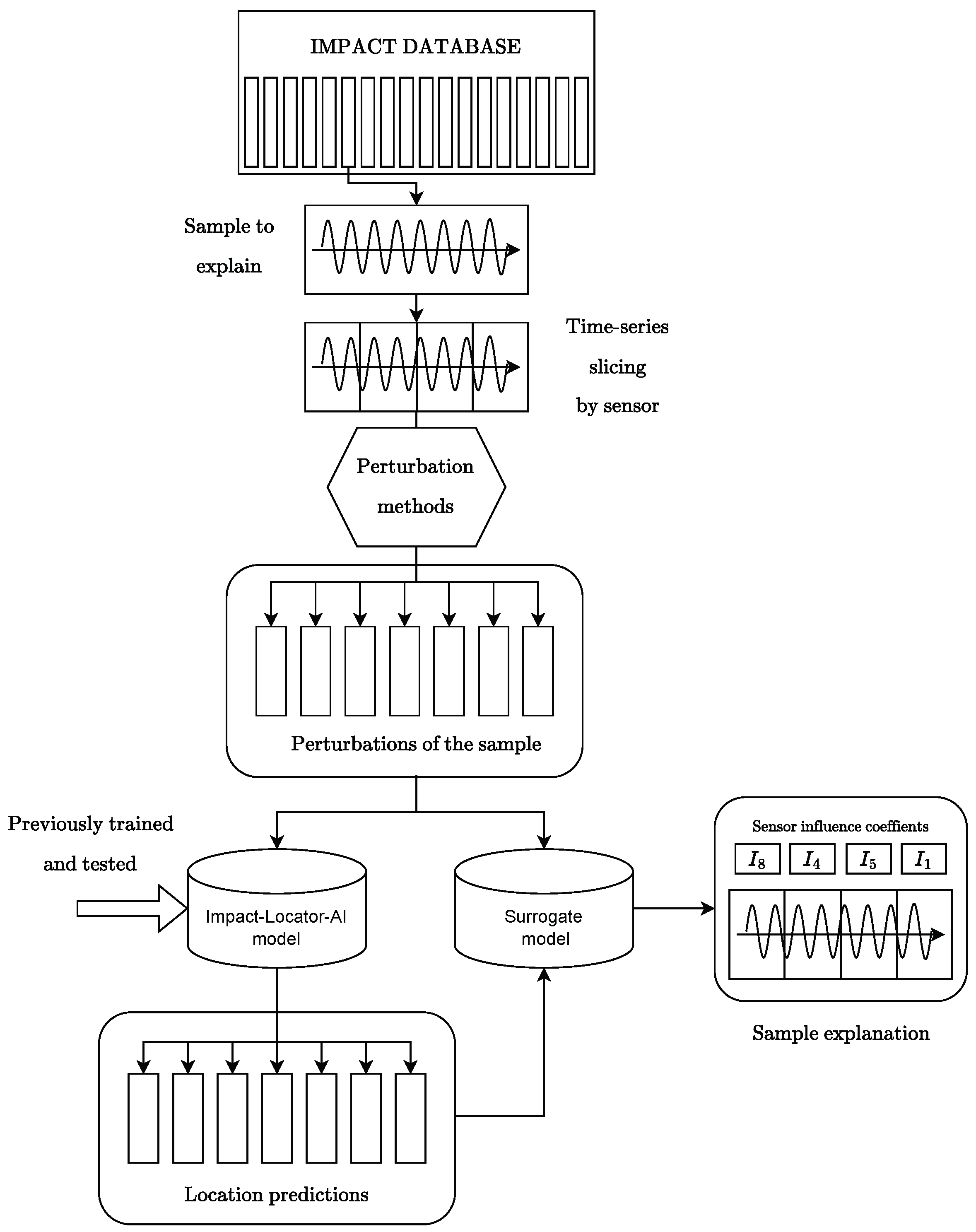
2.3. Explainable Artificial Intelligence
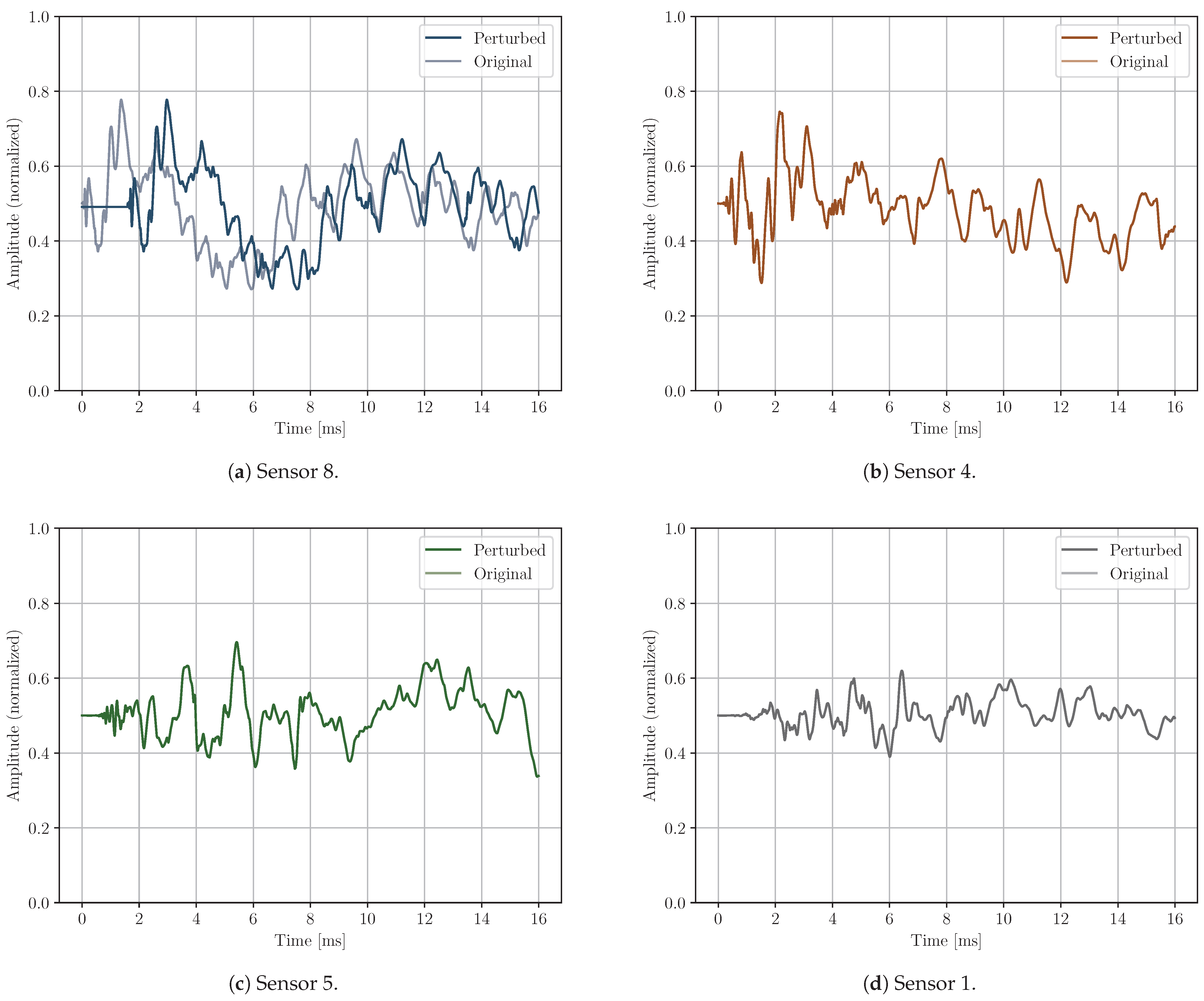
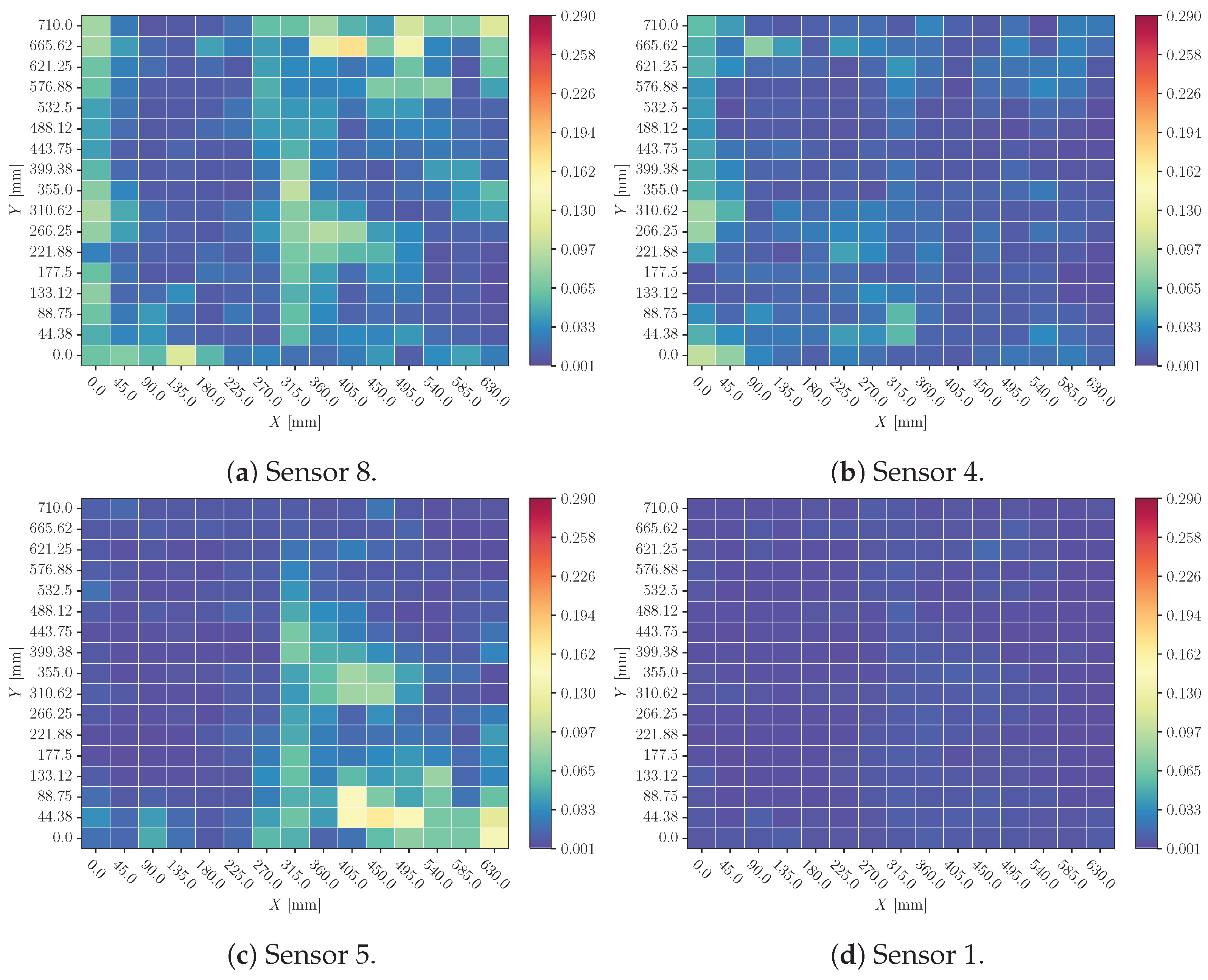
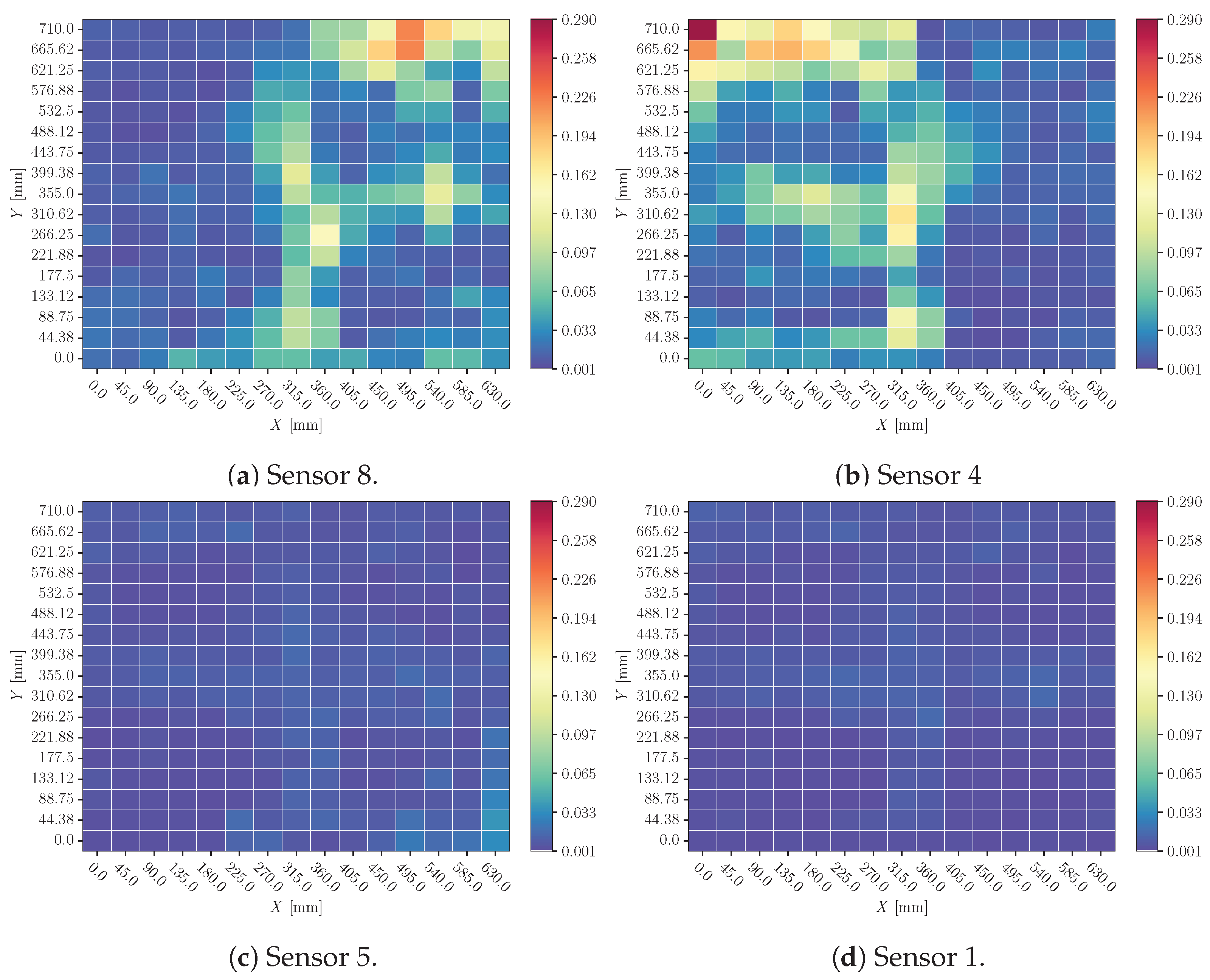
- Time delay: the signal is shifted and zeroes are appended to the beginning or the end of the signal (see Figure 7). This perturbation modifies the ToA of the signal of one sensor. From a practical standpoint, it simulates a displacement of the sensor relative to the position it occupied during the model’s training phase.
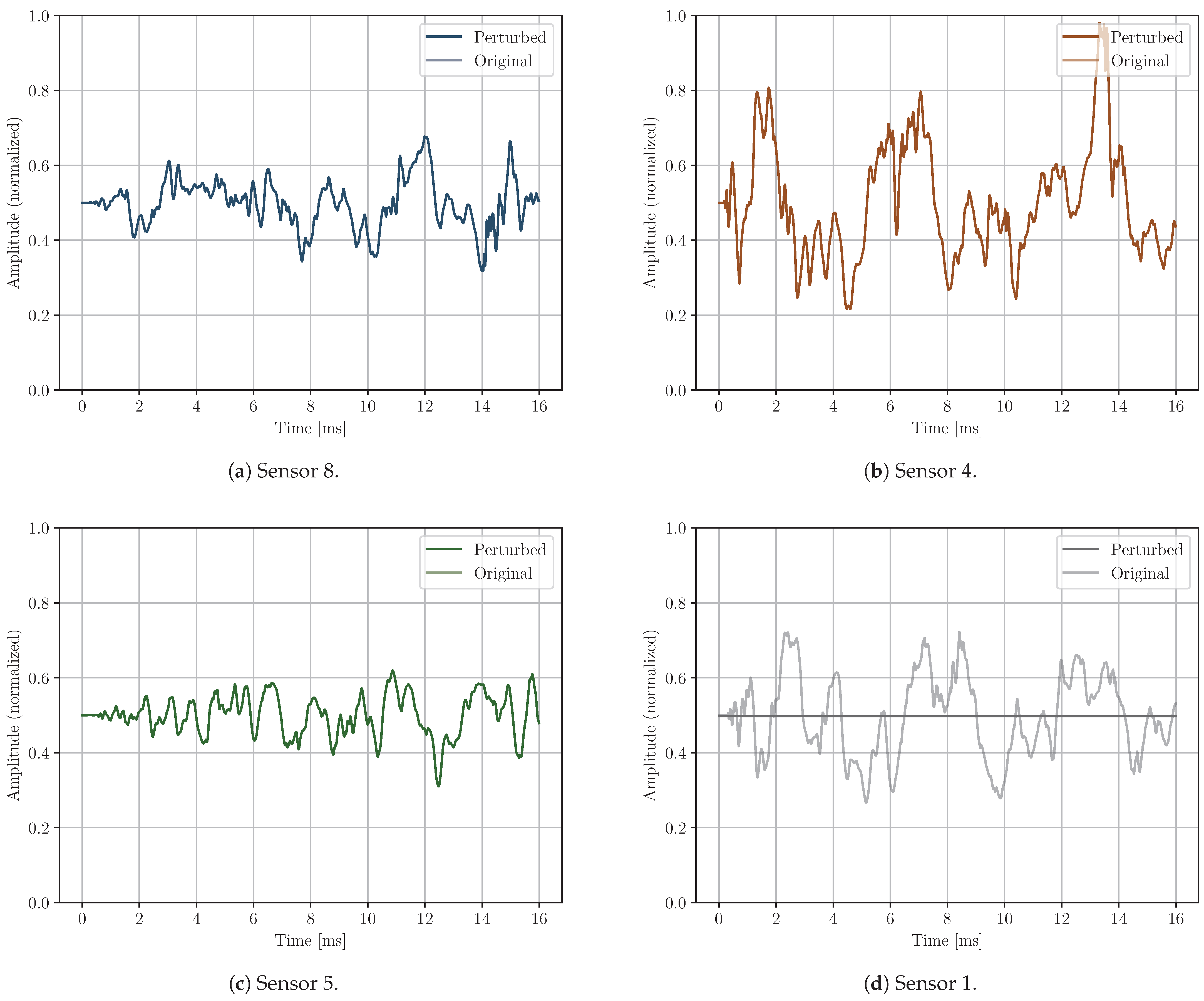
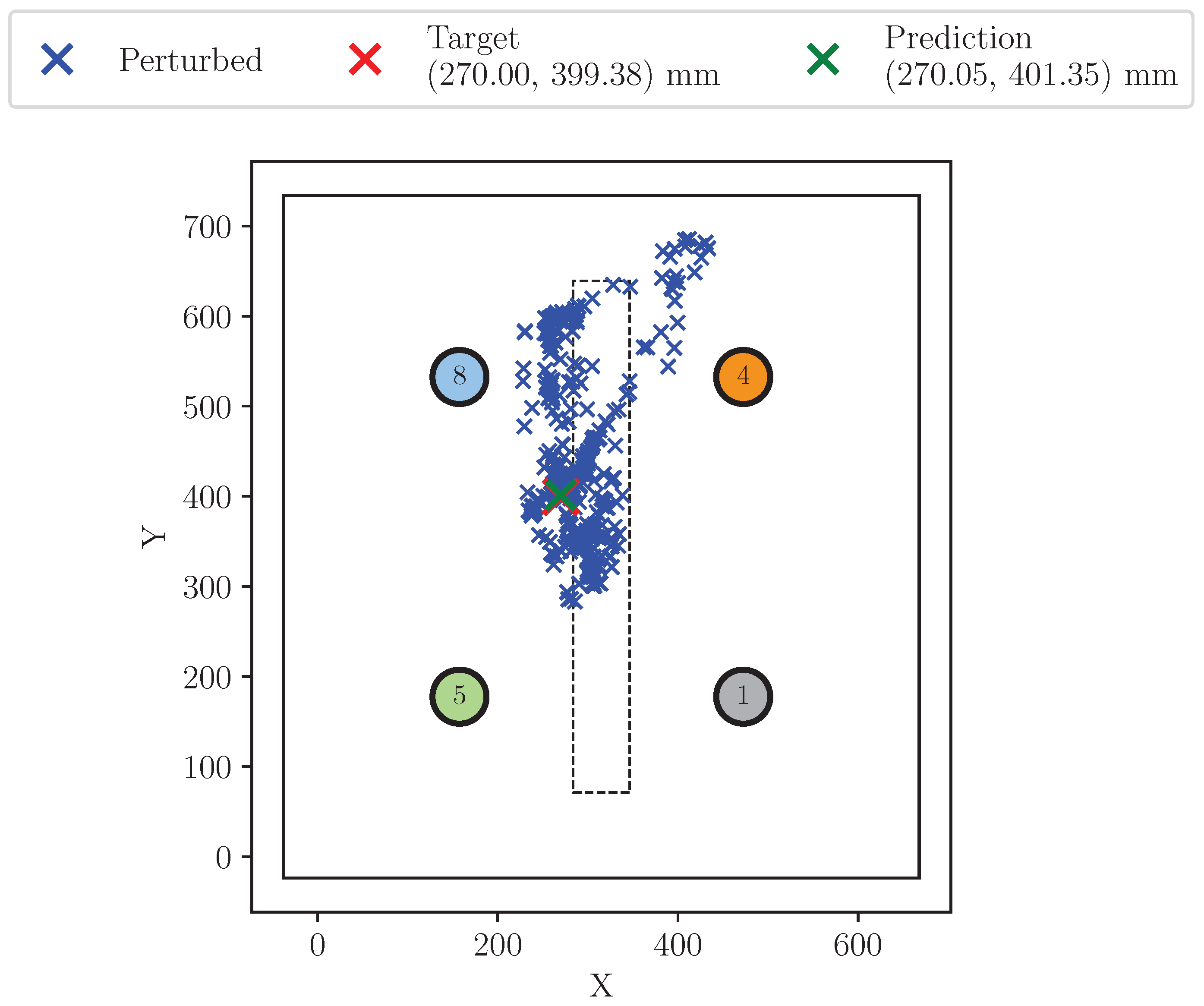
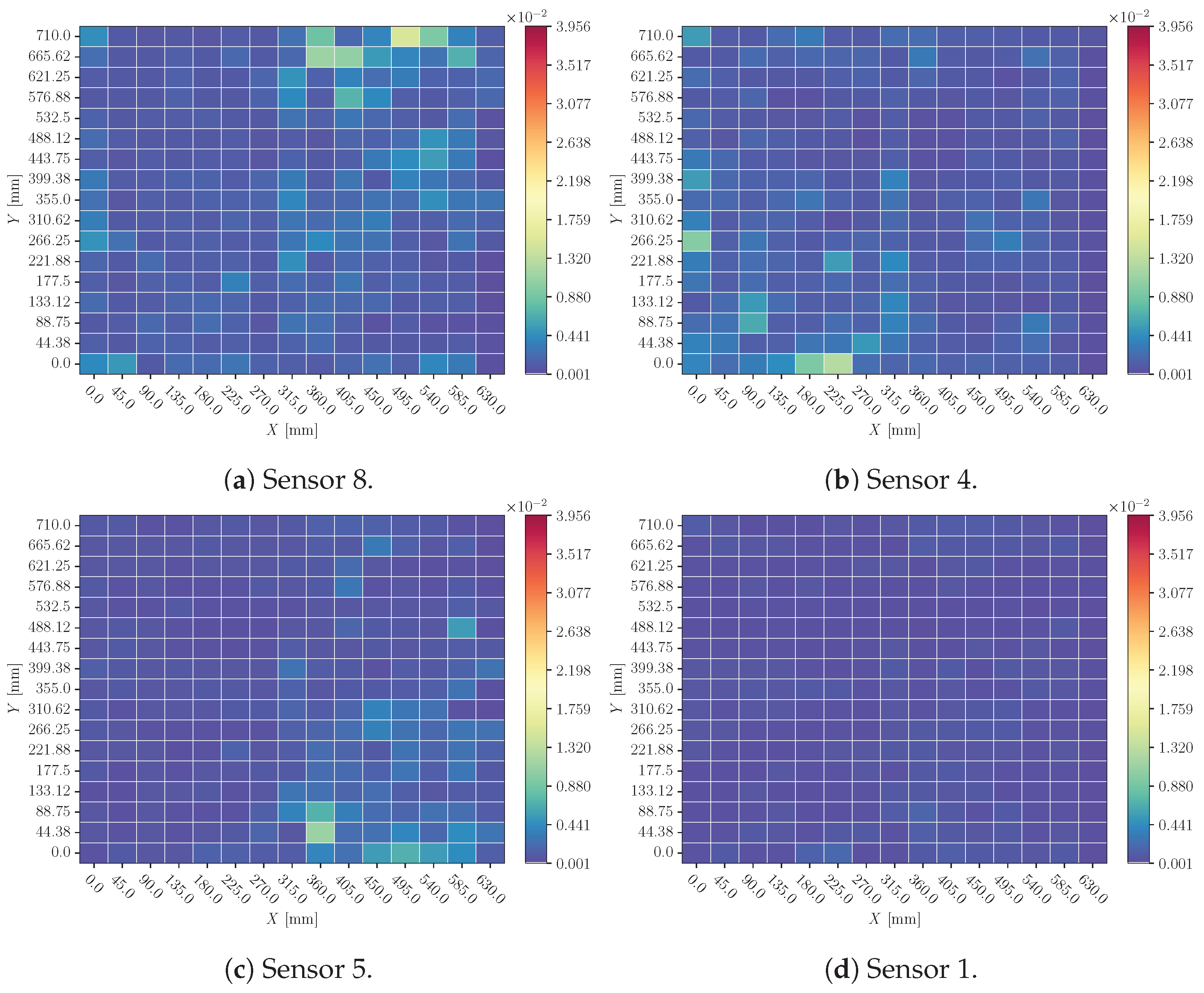
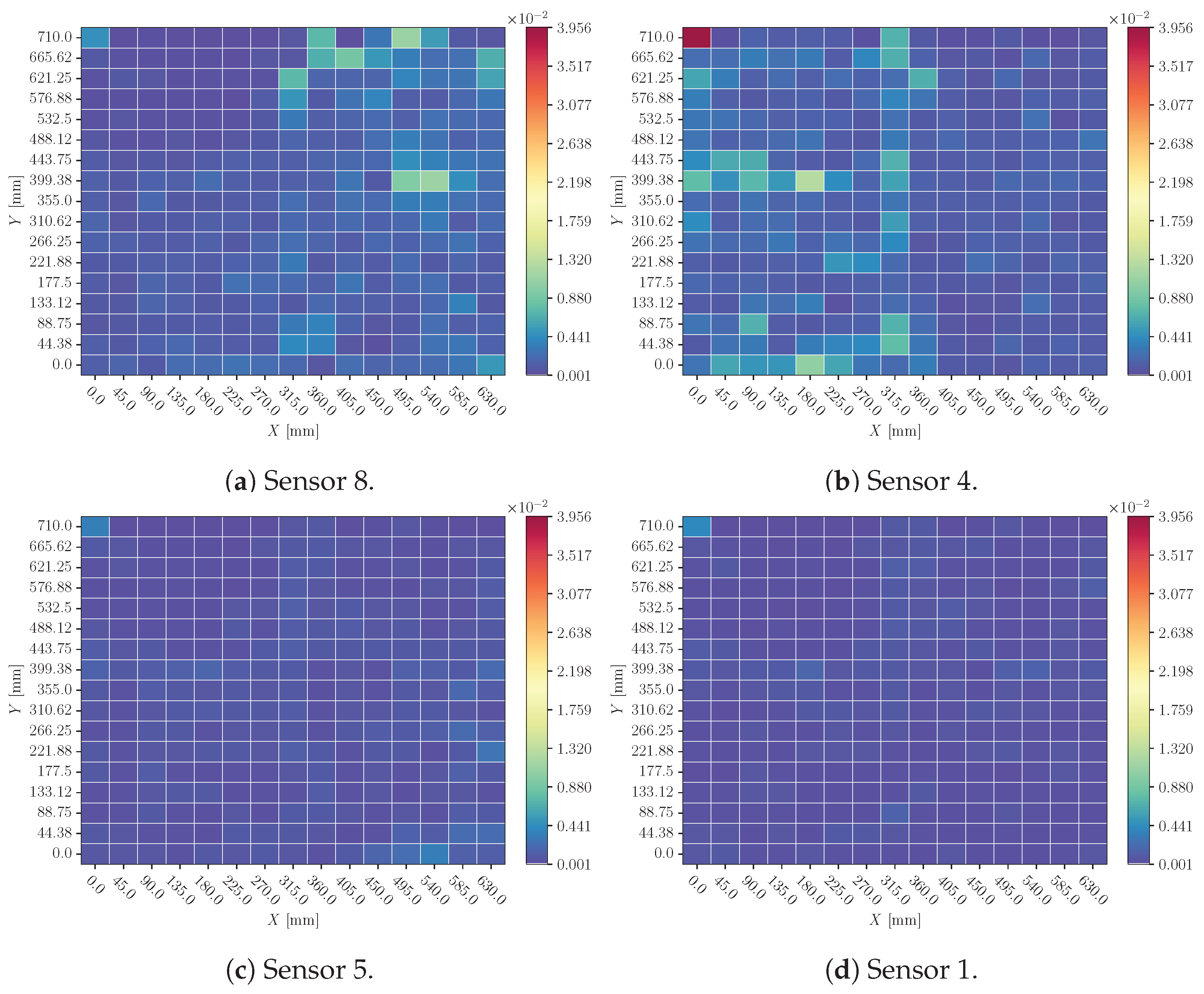
- Sensor cancelation: a sensor’s signal is substituted by its mean value as if it has no signal recorded (see Figure 8). This perturbation allows for the assessment of model performance in the absence of information from a specific sensor. From a practical standpoint, it simulates one sensor breakage during the operational life of the monitored aerostructure.
3. Results
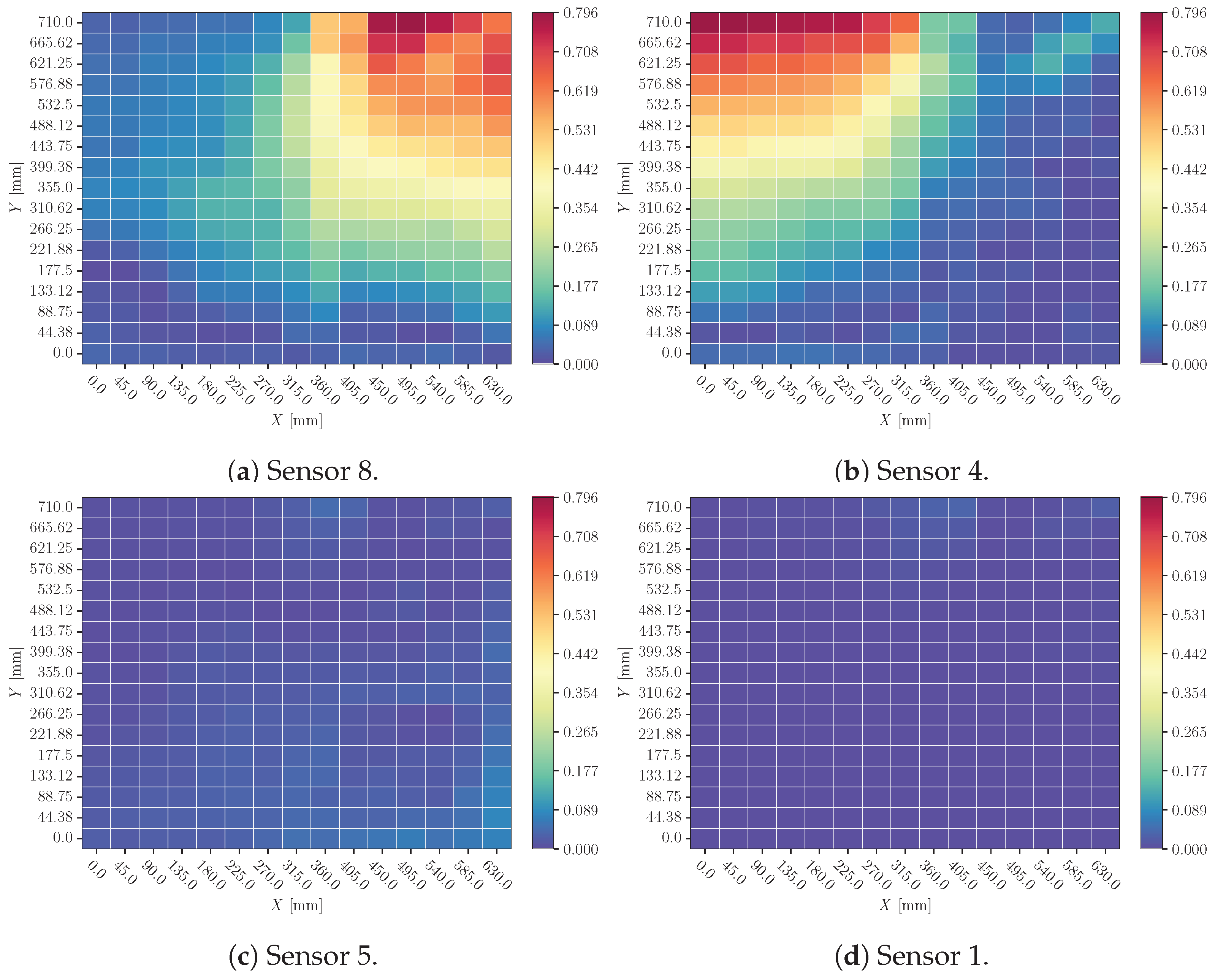
3.1. Time Delay
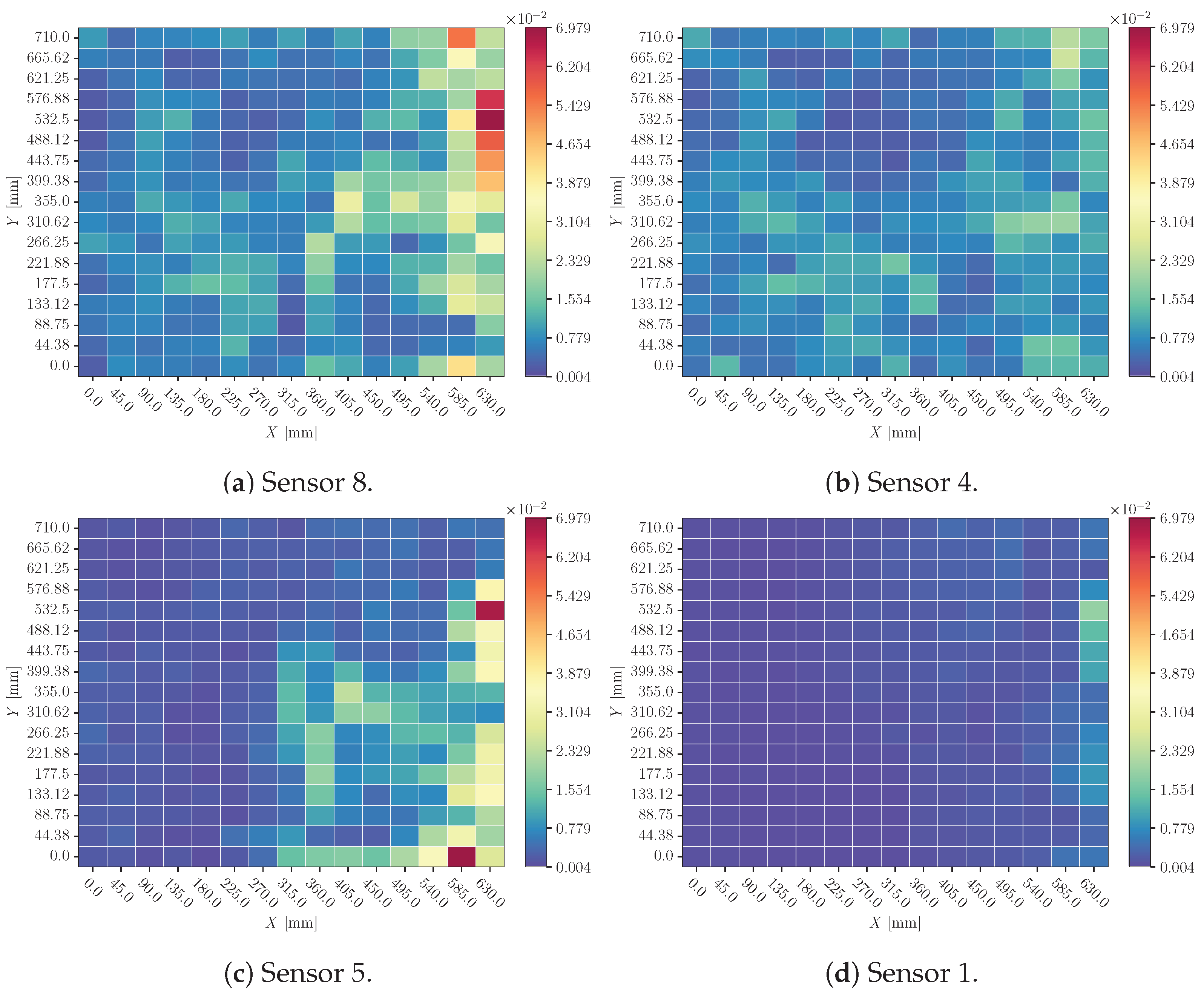
3.2. Sensor Cancelation
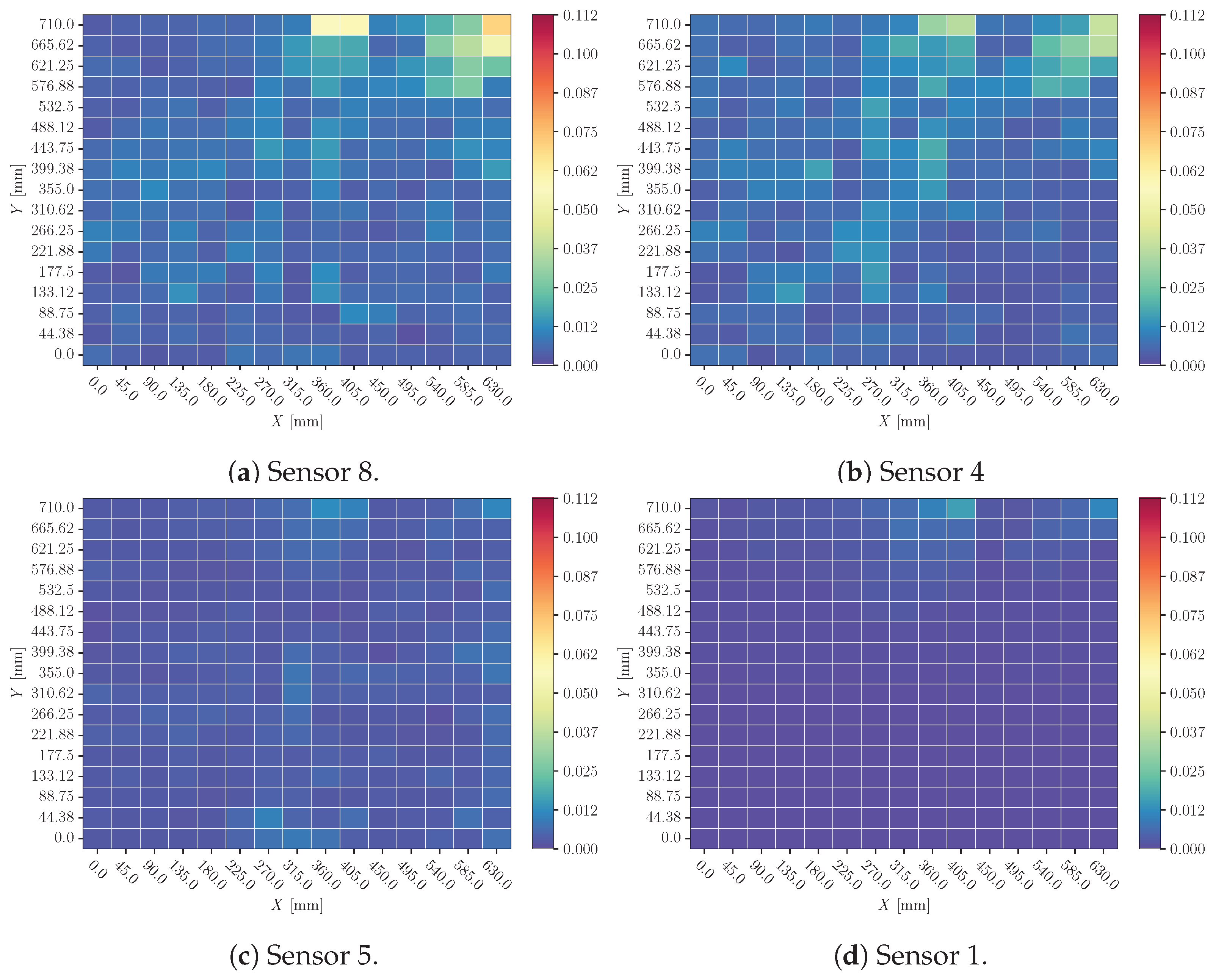
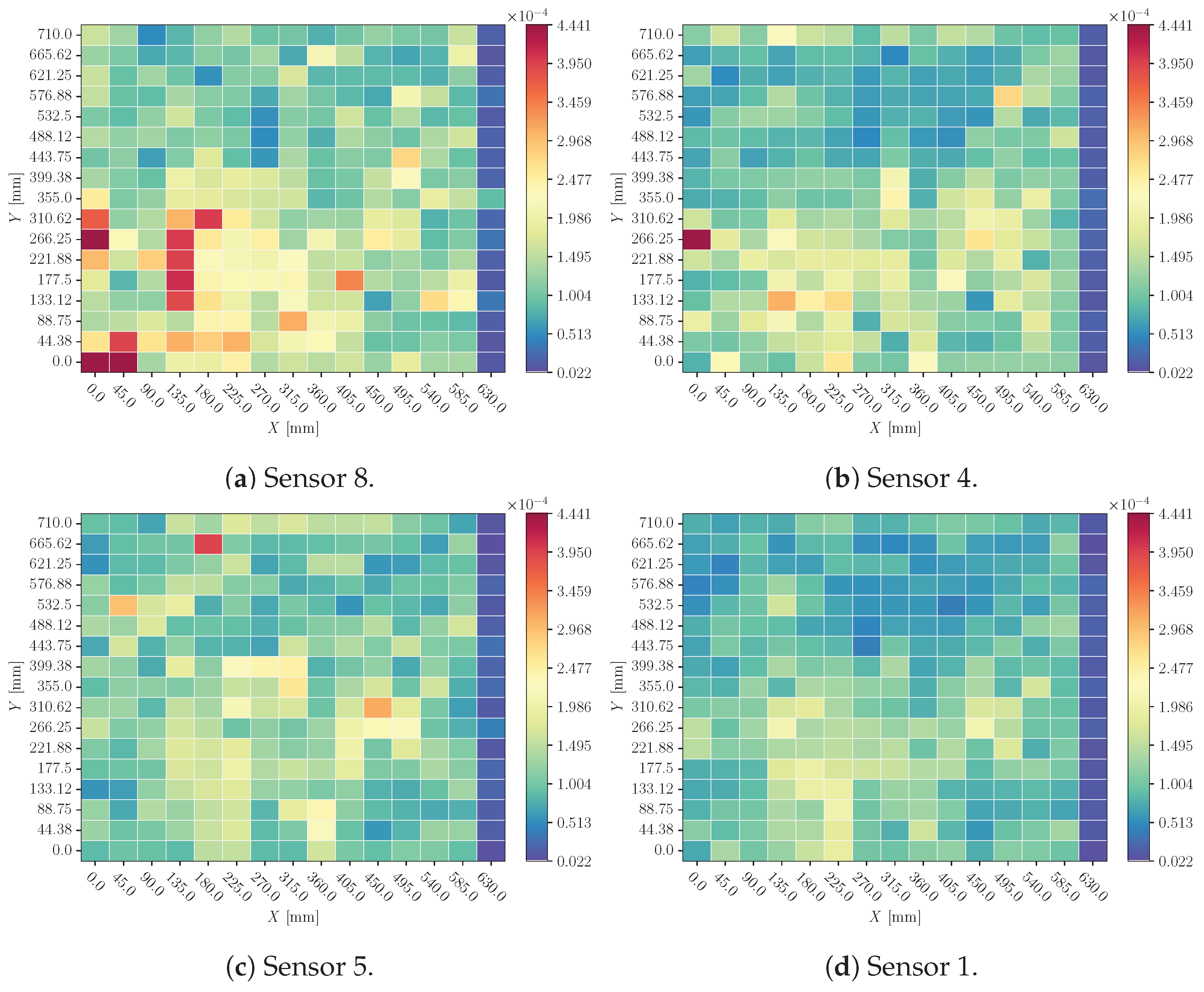
3.3. Noise
4. Discussion
4.1. Time Delay
4.2. Sensor Cancelation
4.3. Noise
5. Conclusions
- Even though time delay must be the most relevant perturbation at the time of making a prediction, the model is not highly affected by this effect. This leads to the conclusion that the model compares different sensor signals to make a more robust prediction relating the Times of Arrival between sensors. When different time delay ranges of perturbation are studied, the model seems to have a consistent response, which is a desirable characteristic.
- When a sensor’s signal is canceled, the influence is significant. This behavior is consistent with the time-delay results. Due to the lack of a signal, the relationship between sensors cannot be properly obtained, and the model prediction is highly influenced.
- Noise perturbation has no remarkable influence over the sensors, and no sensor is especially more affected. This means that the model is filtering the signal prior to making the prediction, which is a valuable characteristic if the SHM system is embedded in an aeronautical structure.
- Mass and velocity have no influence on the locator model when the perturbations are performed, which means that the model is able to understand the signal correctly.
- Sensor 0 perturbations do not have a major influence on the final decision. This means that the model is discarding it, which is absolutely logical considering that only three sensors are needed to triangulate a position.
- The two values predicted by the model (X and Y impact coordinates) have a slightly different behavior. This can be related to the stiffener presence and the different boundary conditions in the structure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SHM | Structural Health Monitoring |
| AI | Artificial Intelligence |
| XAI | Explainable Artificial Intelligence |
| ToA | Time of Arrival |
| PZT | Piezoelectric |
| FBG | Fiber Bragg Gratings |
| LIME | Local Interpretable Model-Agnostic Explanations |
| SHAP | Shapley Additive Explanations |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| SNR | Signal-to-Noise Ratio |
References
- Mittelman, A. Low-energy repetitive impact in carbon-epoxy composite. J. Mater. Sci. 1992, 27, 2458–2462. [Google Scholar] [CrossRef]
- Davies, G.A.O.; Olsson, R. Impact on composite structures. Aeronaut. J. 2004, 108, 541–563. [Google Scholar] [CrossRef]
- Aryal, B.; Morozov, E.V.; Wang, H.; Shankar, K.; Hazell, P.J.; Escobedo-Diaz, J.P. Effects of impact energy, velocity, and impactor mass on the damage induced in composite laminates and sandwich panels. Compos. Struct. 2019, 226, 111284. [Google Scholar] [CrossRef]
- Pavier, M.J.; Clarke, M.P. Experimental techniques for the investigation of the effects of impact damage on carbon-fibre composites. Compos. Sci. Technol. 1995, 55, 157–169. [Google Scholar] [CrossRef]
- Corum, J.M.; Battiste, R.L.; Ruggles-Wrenn, M.B. Low-energy impact effects on candidate automotive structural composites. Compos. Sci. Technol. 2003, 63, 755–769. [Google Scholar] [CrossRef]
- Zabala, H.; Aretxabaleta, L.; Castillo, G.; Urien, J.; Aurrekoetxea, J. Impact velocity effect on the delamination of woven carbon-epoxy plates subjected to low-velocity equienergetic impact loads. Compos. Sci. Technol. 2014, 94, 48–53. [Google Scholar] [CrossRef]
- Tai, N.H.; Yip, M.C.; Lin, J.L. Effects of low-energy impact on the fatigue behavior of carbon/epoxy composites. Compos. Sci. Technol. 1998, 58, 1–8. [Google Scholar] [CrossRef]
- Batra, R.C.; Gopinath, G.; Zheng, J.Q. Damage and failure in low energy impact of fiber-reinforced polymeric composite laminates. Compos. Struct. 2012, 94, 540–547. [Google Scholar] [CrossRef]
- De Medeiros, R.; Vandepitte, D.; Tita, V. Structural health monitoring for impact damaged composite: A new methodology based on a combination of techniques. Struct. Health Monit. 2017, 17, 185–200. [Google Scholar] [CrossRef]
- Scott, I.; Scala, C. A review of non-destructive testing of composite materials. NDT Int. 1982, 15, 75–86. [Google Scholar] [CrossRef]
- Boopathy, G.; Surendar, G.; Anand, T.P.P.; Nema, A. Review on Non-Destructive Testing of Composite Materials in Aircraft Applications. Int. J. Mech. Eng. Technol. 2017, 8, 1334–1342. [Google Scholar]
- Iglesias, F.S.; Serrano, A.G.; Rodriguez, A.P.; López, A.F. Validation of a ray-tracing-based guided Lamb wave propagation methodology in aerostructures. Struct. Health Monit. 2025, 24, 1043–1059. [Google Scholar] [CrossRef]
- Šplíchal, J.; Hlinka, J. Modelling of health monitoring signals and detection areas for aerospace structures. In Proceedings of the 13th Research and Education in Aircraft Design Conference 2018, Brno, Czech Republic, 7–9 November 2018; pp. 170–188. [Google Scholar] [CrossRef]
- Tavares, A.; Lorenzo, E.D.; Peeters, B.; Coppotelli, G.; Silvestre, N. Damage Detection in Lightweight Structures Using Artificial Intelligence Techniques. Exp. Tech. 2021, 45, 389–410. [Google Scholar] [CrossRef]
- Ross, R. Structural Health Monitoring and Impact Detection Using Neural Networks for Damage Characterization. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Newport, RI, USA, 1–4 May 2006. [Google Scholar] [CrossRef]
- Capineri, L.; Bulletti, A.; Calzolai, M.; Francesconi, D. A real-time electronic system for automated impact detection on aircraft structures using piezoelectric transducers. Procedia Eng. 2014, 87, 1243–1246. [Google Scholar] [CrossRef]
- Dragašius, E.; Eidukynas, D.; Jurenas, V.; Mažeika, D.; Galdikas, M.; Mystkowski, A.; Mystkowska, J. Piezoelectric Transducer-Based Diagnostic System for Composite Structure Health Monitoring. Sensors 2021, 21, 253. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Y. Virtual Time-reversal Tomography for Impact Damage Detection in Self-sensing Piezoelectric Composite Plates. In Proceedings of the 4th International Conference on Structural Health Monitoring and Integrity Management, Hangzhou, China, 21–23 October 2019. [Google Scholar]
- Torres-Arredondo, M.; Fritzen, C. Impact Monitoring in Smart Structures Based on Gaussian Processes. In Proceedings of the 4th International Symposium on NDT in Aerospace, Augsburg, Germany, 13–15 November 2012. [Google Scholar]
- Perelli, A.; Caione, C.; De Marchi, L.; Brunelli, D.; Marzani, A.; Benini, L. Design of a low-power structural monitoring system to locate impacts based on dispersion compensation. Health Monit. Struct. Biol. Syst. 2013, 8695, 338–347. [Google Scholar] [CrossRef]
- Delebarre, C.; Grondel, S.; Rivart, F. Autonomous piezoelectric structural health monitoring system for on-production line use. Adv. Appl. Ceram. 2015, 114, 205–210. [Google Scholar] [CrossRef]
- Coelho, C.K.; Hiche, C.; Chattopadhyay, A. An application of support vector regression for impact load estimation using fiber bragg grating sensor. Struct. Durab. Health Monit. 2011, 7, 65–81. [Google Scholar]
- Hiche, C.; Coelho, C.K.; Chattopadhyay, A. A Strain Amplitude-Based Algorithm for Impact Localization on Composite Laminates. J. Intell. Mater. Syst. Struct. 2011, 22, 2061–2067. [Google Scholar] [CrossRef]
- Luckey, D.; Fritz, H.; Legatiuk, D.; Peralta Abadía, J.; Walther, C.; Smarsly, K. Explainable Artificial Intelligence to Advance Structural Health Monitoring. In Structural Health Monitoring Based on Data Science Techniques; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Peralta, J.J.; Fritz, H.; Dadoulis, G.I.; Dragos, K. An explainable artificial intelligence approach for damage detection in structural health monitoring. In Proceedings of the 32nd Forum Bauinformatik, Online, 9–10 September 2021. [Google Scholar]
- Wan, S.; Li, S.; Chen, Z.; Tang, Y. An ultrasonic-AI hybrid approach for predicting void defects in concrete-filled steel tubes via enhanced XGBoost with Bayesian optimization. Case Stud. Constr. Mater. 2025, 22, e04359. [Google Scholar] [CrossRef]
- Guestrin, C.; Ribeiro, M.T.; Singh, S. Why Should I Trust You?: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- SHAP. SHAP Latest Documentation. Available online: https://shap.readthedocs.io/en/latest/ (accessed on 8 May 2025).
- Del Río-Velilla, D.; Pedraza, A.; Fernández-López, A. Impact localization in composite structures with Deep Neural Networks. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Guestrin, C.; Ribeiro, M.T.; Singh, S. Emanuel-Metzenthin/Lime-for-Time: Application of the LIME Algorithm by Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin to the Domain of Time Series Classification. Available online: https://github.com/emanuel-metzenthin/Lime-For-Time (accessed on 15 February 2023).
- Metzenthin, E. Lime-for-Time: Explainability for Time Series Models. 2023. Available online: https://github.com/emanuel-metzenthin/Lime-For-Time/tree/master (accessed on 24 March 2025).




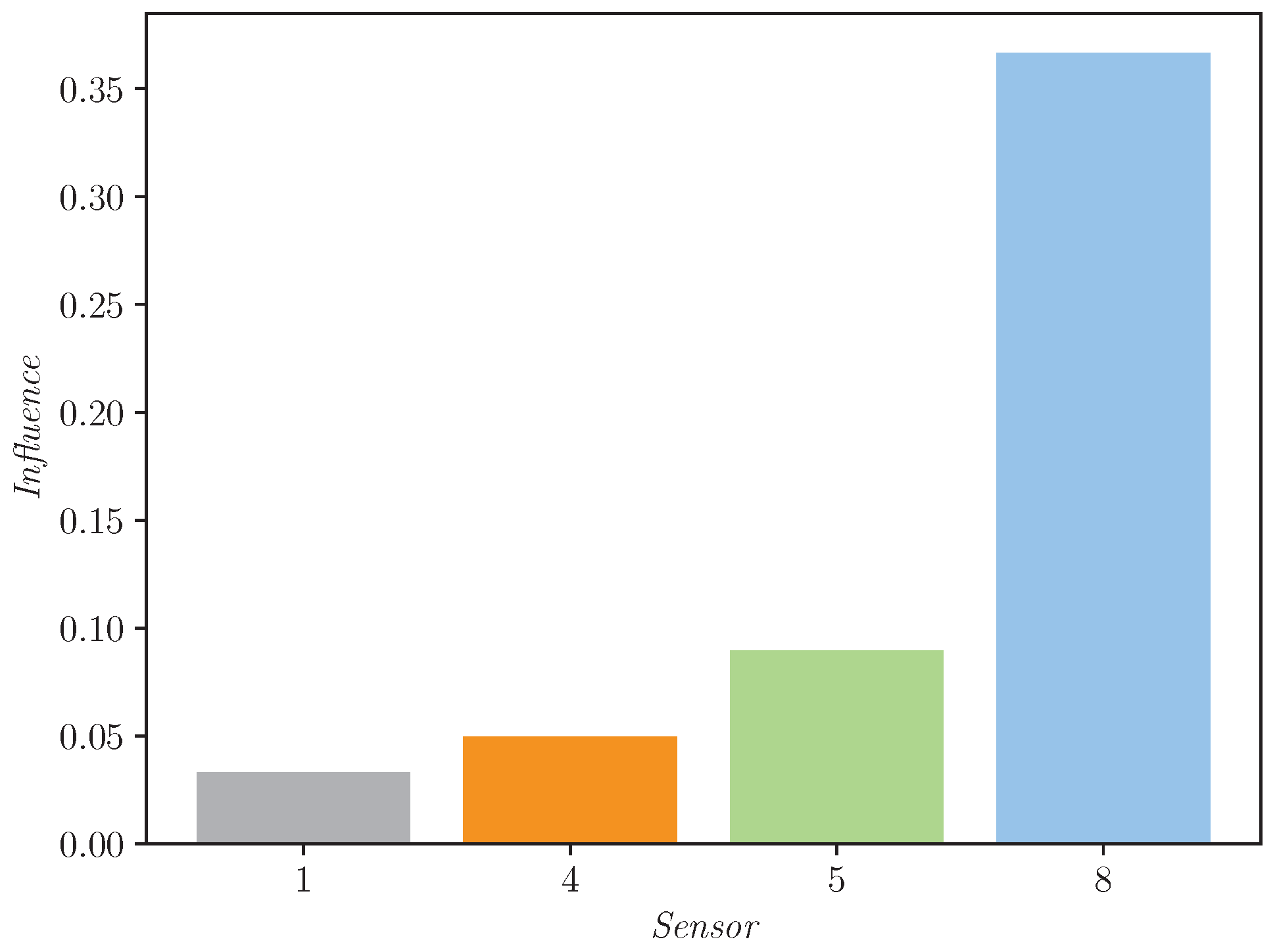



| Model [k] | [mm] | [mm] |
|---|---|---|
| 1 | 3.54 | 2.29 |
| 2 | 3.37 | 2.29 |
| 3 | 3.50 | 2.25 |
| 4 | 3.47 | 2.38 |
| Average | 3.47 | 2.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedraza, A.; del-Río-Velilla, D.; Fernández-López, A. AI-Based Impact Location in Structural Health Monitoring for Aerospace Application Evaluation Using Explainable Artificial Intelligence Techniques. Electronics 2025, 14, 1975. https://doi.org/10.3390/electronics14101975
Pedraza A, del-Río-Velilla D, Fernández-López A. AI-Based Impact Location in Structural Health Monitoring for Aerospace Application Evaluation Using Explainable Artificial Intelligence Techniques. Electronics. 2025; 14(10):1975. https://doi.org/10.3390/electronics14101975
Chicago/Turabian StylePedraza, Andrés, Daniel del-Río-Velilla, and Antonio Fernández-López. 2025. "AI-Based Impact Location in Structural Health Monitoring for Aerospace Application Evaluation Using Explainable Artificial Intelligence Techniques" Electronics 14, no. 10: 1975. https://doi.org/10.3390/electronics14101975
APA StylePedraza, A., del-Río-Velilla, D., & Fernández-López, A. (2025). AI-Based Impact Location in Structural Health Monitoring for Aerospace Application Evaluation Using Explainable Artificial Intelligence Techniques. Electronics, 14(10), 1975. https://doi.org/10.3390/electronics14101975







