A Self-Supervised Point Cloud Completion Method for Digital Twin Smart Factory Scenario Construction

Abstract

In the development of digital twin (DT) workshops, constructing accurate DT models has become a key step toward enabling intelligent manufacturing. To address challenges such as incomplete data acquisition, noise sensitivity, and the heavy reliance on manual annotations in traditional modeling methods, this paper proposes a self-supervised deep learning approach for point cloud completion. The proposed model integrates self-supervised learning strategies for inferring missing regions, a Feature Pyramid Network (FPN), and cross-attention mechanisms to extract critical geometric and structural features from incomplete point clouds, thereby reducing dependence on labeled data and improving robustness to noise and incompleteness. Building on this foundation, a point cloud-based DT workshop modeling framework is introduced, incorporating transfer learning techniques to enable domain adaptation from synthetic to real-world industrial datasets, which significantly reduces the reliance on high-quality industrial point cloud data. Experimental results demonstrate that the proposed method achieves superior completion and reconstruction performance on both public benchmarks and real-world workshop scenarios, achieving an average CD-${\ell }_2$ score of 15.96 on the 3D-EPN dataset. Furthermore, the method produces high-fidelity models in practical applications, providing a solid foundation for the precise construction and deployment of virtual scenes in DT workshops.

1. Introduction

With the rapid advancement of intelligent manufacturing technologies, digital twin (DT) smart factories have become a key paradigm for future industrial production [1]. By creating high-fidelity digital replicas of physical workshops, these systems facilitate seamless integration between physical and virtual environments, thereby enhancing production efficiency, optimizing resource allocation, and enabling real-time monitoring and intelligent decision-making.

The construction of DTs heavily relies on the acquisition of reliable 3D point cloud data from industrial workshops—a task significantly more complex than in conventional environments. In manufacturing settings, dense machinery layouts and intricate structures frequently lead to severe occlusions and substantial unscanned regions, resulting in sparse and incomplete point clouds. Additionally, reflective and transparent surfaces introduce noise through reflections and refractions, further compromising data quality. The use of heterogeneous sensors with varying resolutions and scanning capabilities also produces uneven point densities, complicating the integration of multi-source data.

These challenges significantly undermine DT construction: incomplete geometries impair accurate modeling and path planning, noise disrupts object recognition and semantic understanding, and irregular data distributions increase computational burden. Therefore, an effective point cloud completion strategy is urgently needed to reconstruct missing regions, suppress noise, and ensure consistent density, thereby enabling the creation of high-fidelity DTs.

To tackle these challenges, effective point cloud completion techniques are essential for enhancing both the geometric and semantic integrity of the data. Such techniques aim to infer and reconstruct missing regions, thereby enriching the original dataset with critical geometric details and semantic consistency to produce a more complete representation.

In recent years, the rapid advancement of deep learning and computer vision technologies has brought significant attention to deep learning-based point cloud completion methods. These approaches leverage geometric features inherent in existing point cloud data to learn and predict missing components, markedly improving both the accuracy and efficiency of the reconstruction process.

However, when applied to complex industrial environments, existing methods encounter notable limitations. The diversity of equipment shapes, the complexity of workshop layouts, and factors such as large-scale spatial configurations and heterogeneous sensors frequently lead to uneven point cloud density. Moreover, the scarcity of annotated data in industrial settings remains a significant obstacle to the scalability of supervised learning-based approaches, resulting in reduced performance in fine-grained modeling and cross-domain generalization.

To overcome these issues, this study proposes a deep learning framework for DT workshop modeling using incomplete and noisy point cloud data. This research specifically targets two core objectives: enhancing the precision of point cloud completion and minimizing dependence on large-scale annotated datasets.

The first objective is to enhance the geometric precision and semantic consistency of the reconstructed point clouds under complex industrial conditions. This is achieved by designing a completion network that leverages multi-scale feature extraction through Feature Pyramid Networks (FPNs) and reinforces local and global contextual reasoning via cross-attention mechanisms.

The second objective is to minimize the dependency on extensive labeled datasets, which are often scarce and costly to obtain in industrial environments. To this end, the framework incorporates self-supervised learning strategies that exploit inherent geometric structures within the point clouds, as well as transfer learning techniques that adapt knowledge from related domains to improve model generalization.

The proposed method offers a robust and scalable solution for high-fidelity point cloud reconstruction in DT smart factories. Compared with the state-of-the-art ACL-SPC [2] under the same single-partial setting, it achieves superior accuracy, highlighting its effectiveness and practical applicability in complex industrial scenarios.

2. Related Works

DT technology has evolved from theoretical exploration to practical application, with the construction of twin models becoming a fundamental component of DT scenarios and a prerequisite for the successful deployment of DT systems. In recent years, substantial research has focused on leveraging deep learning to enhance the construction of twin models. These advancements have effectively bridged the gap between time-consuming, high-precision modeling methods and fully manual CAD-based approaches [3].

However, the acquisition of sufficient data to train deep learning models remains a significant challenge due to the limited availability of industrial datasets and stringent confidentiality constraints. To mitigate this issue, transfer learning has emerged as a promising approach, enabling cross-domain knowledge transfer and reducing the reliance on large-scale annotated datasets [4]. This section presents a systematic review of existing studies on DT model construction techniques, deep learning-based point cloud completion algorithms, and transfer learning strategies.

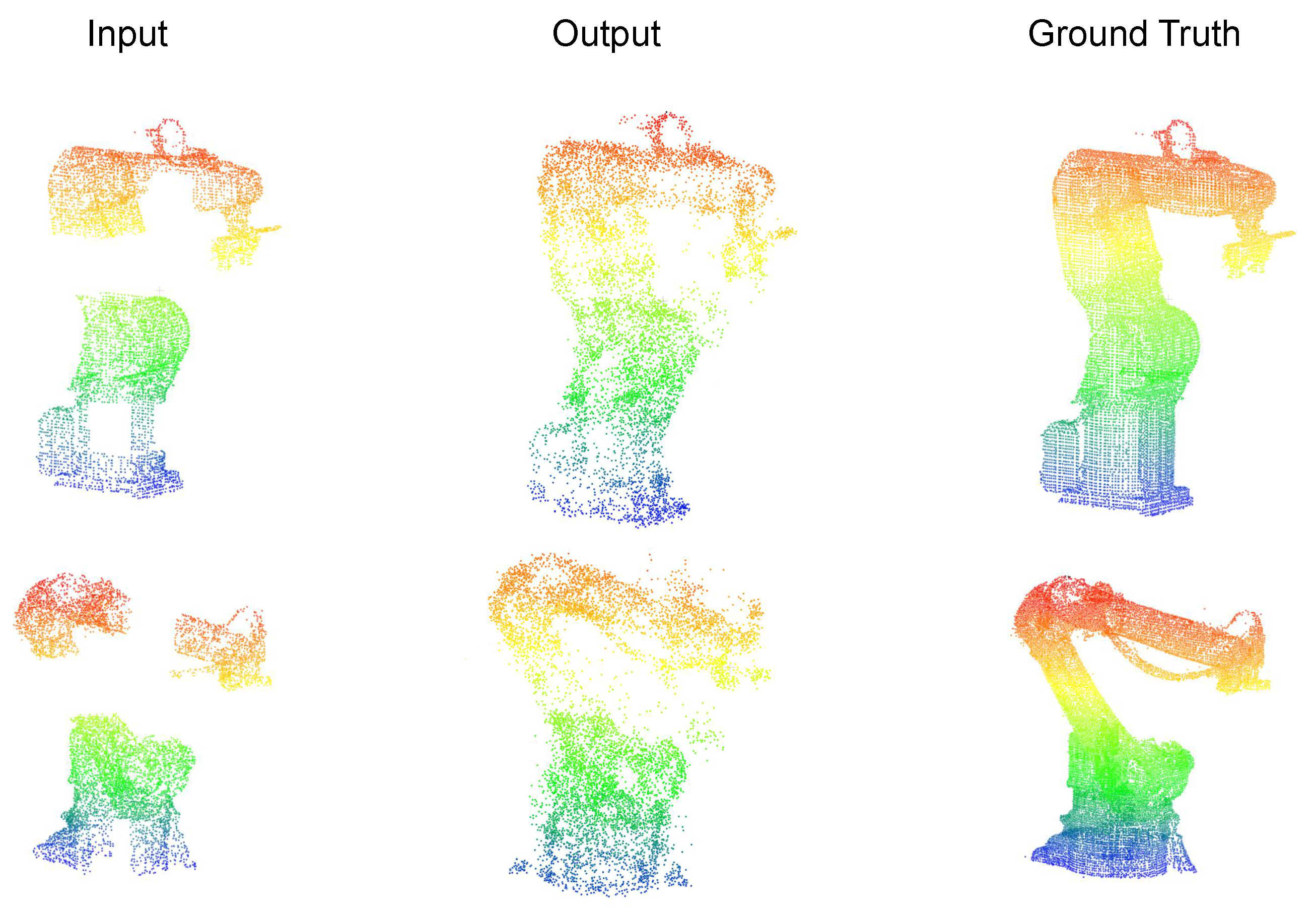
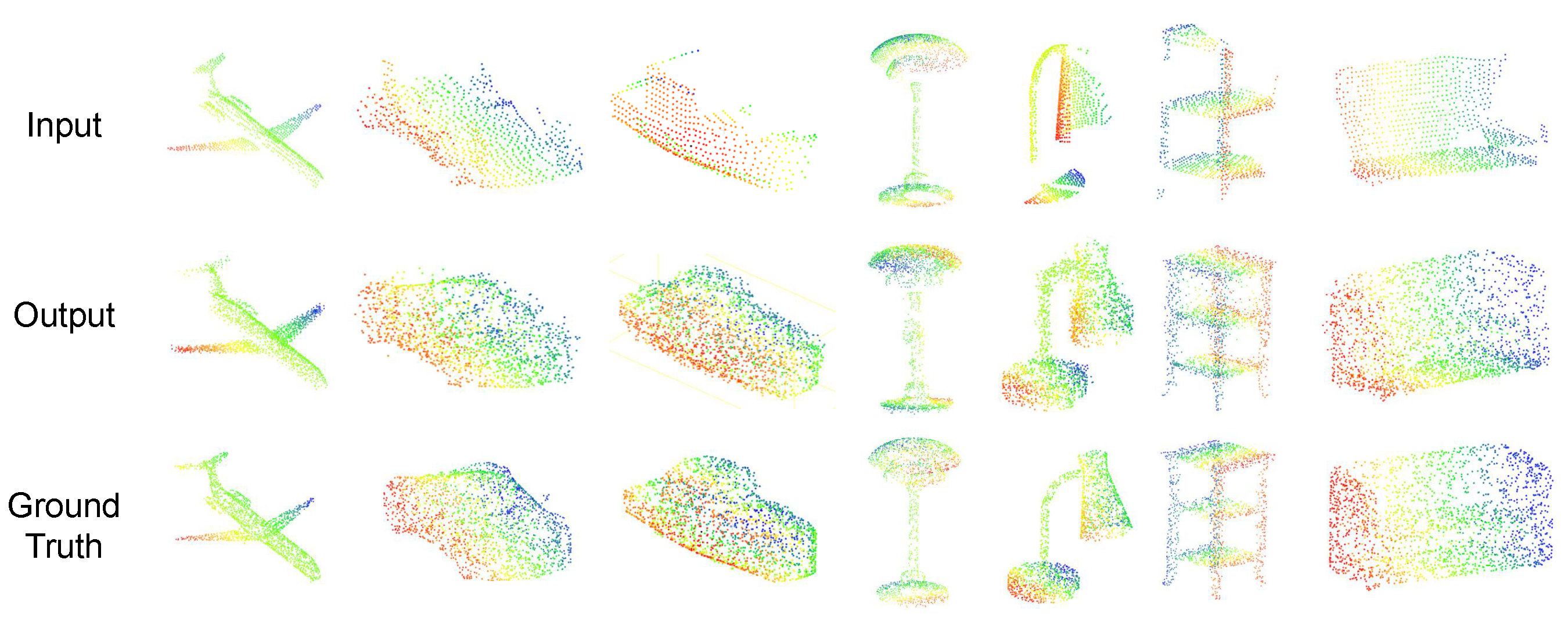2.1. Research Status of 3D Modeling Methods

DT modeling lies at the heart of accurately virtualizing physical entities. Driven by data, DT technology enables monitoring, simulation, prediction, and optimization, supporting a wide range of industrial applications [5]. Within these applications, the accuracy and reliability of DT models are critical, as they directly influence the overall performance and decision-making capabilities of DT systems in real-world scenarios.

High-precision and high-reliability models not only ensure accuracy in monitoring and forecasting but also provide trustworthy results during optimization and simulation processes. This, in turn, significantly enhances production efficiency, reduces operational costs, and ensures the safety and stability of manufacturing operations [6].

Geometric modeling, as a traditional 3D modeling approach, typically employs computer-aided design (CAD) tools to construct precise geometric models. These models represent object shapes and features using geometric elements such as points, lines, and surfaces, and are usually stored in the form of polygonal meshes or parameterized surfaces [7]. The main advantage of geometric modeling lies in its precision and accuracy, making it suitable for modeling industrial components and mechanical equipment that require detailed descriptions [8]. However, this method often relies heavily on manual operations, making the modeling process time-consuming and costly, and limiting its applicability in dynamic or complex environments [8]. Moreover, manual modeling lacks flexibility when applied to large-scale or intricate scenarios.

In recent years, diffusion models have achieved remarkable progress in image generation and novel view synthesis. Wu et al. [9] proposed ReconFusion, which leverages a diffusion model to regularize the optimization process of Neural Radiance Fields (NeRF), enabling robust 3D reconstruction under sparse-view conditions. Although ReconFusion demonstrates strong capability in novel view synthesis under limited viewpoints, it primarily relies on regularization in the image space. This strong dependence on image modality introduces high computational costs during reconstruction. Moreover, in industrial workshops populated with a large number of machines and equipment, modeling each unit from 2D images becomes impractical, whereas point cloud data offer a more suitable and efficient alternative.

Point cloud modeling has emerged in recent years as an alternative approach, driven by advances in 3D scanning technologies such as LiDAR and RGB-D cameras [10]. A point cloud is a data structure composed of numerous points in 3D space, capable of representing the shape and surface features of objects with high fidelity [11]. Point cloud-based modeling methods typically involve steps such as registration, denoising, segmentation, and reconstruction to generate 3D object models [12]. The key advantage of this approach is its ability to rapidly acquire 3D environmental or object data, making it well suited for complex and dynamic settings like construction sites and factory workshops [13]. Nevertheless, point cloud data often suffer from sparsity, incompleteness, and noise, necessitating advanced processing and completion techniques to ensure modeling quality and precision.

In practical applications, the selection of an appropriate modeling method often involves trade-offs among accuracy requirements, modeling speed, and computational resources. In complex industrial and dynamic environments, point cloud modeling is particularly favored due to its capability to rapidly capture 3D geometric information. Compared with traditional geometric modeling, point cloud approaches offer higher automation and better adaptability to intricate environments.

However, the inherent sparsity, incompleteness, and noise of point cloud data remain major obstacles to achieving high modeling accuracy. As a result, recent research has increasingly focused on deep learning-based point cloud registration, segmentation, completion, and reconstruction techniques. The integration of convolutional neural networks (CNNs), generative adversarial networks (GANs), and Transformer-based models has significantly improved the processing capabilities and effectiveness of point cloud analysis. Moving forward, the development of point cloud modeling is likely to focus on improving data processing efficiency and algorithmic robustness, while further optimizing deep learning techniques to meet the high-precision modeling demands of industrial and architectural applications.

2.2. Research Status of Point Cloud Completion Algorithms

With the advancement of 3D scanning technologies—such as RGB-D scanners, laser scanners, and LiDAR—point cloud acquisition has become increasingly efficient and accurate [14]. These technologies have enabled the widespread collection of 3D spatial data in fields such as industry, architecture, and autonomous driving. However, occlusions, limited sensor resolution, and environmental interference often result in sparse, incomplete point clouds with notable geometric loss [15].

The inherent incompleteness of point clouds poses major challenges for applications such as analysis, modeling, and object recognition, all of which depend on complete and accurate 3D data for optimal performance. Consequently, completing missing regions in partial point clouds and generating high-quality 3D reconstructions has become a key research focus.

Point cloud completion seeks to algorithmically infer and recover missing geometric structures, reconstructing complete models from partial data. As a core task, it directly influences the performance of downstream applications like classification, reconstruction, and semantic segmentation [16]. Enhancing its accuracy and robustness is therefore crucial for advancing 3D data processing. Furthermore, accurate point cloud modeling is vital for simulating scheduling optimization in DT systems [17]. It improves the simulation’s credibility and predictive accuracy, thereby ensuring the reliability of physical system optimization.

To address these challenges, researchers have developed a range of point cloud completion methods. These approaches can be broadly classified into four categories:

The first category includes parametric model-based methods, which complete point clouds by fitting and optimizing geometric parameters. Groueix et al. [18] introduced a method that generates 3D surfaces by mapping 2D planes onto a set of learnable parametric surface elements. Their approach effectively reconstructs fine surface details on datasets like ShapeNet, addressing common issues in voxel- and point-based methods, such as limited resolution and poor connectivity. However, the reliance on local parameterization can lead to patch seams and discontinuities, impairing global mesh consistency. Moreover, limited local representations hinder the model’s ability to reconstruct complex topologies and detailed geometries.

The second category involves generative adversarial networks (GANs), originally successful in image synthesis and later adapted for point cloud completion to enhance output realism. GANs estimate the distribution of generated point sets via adversarial learning [19]: a generator produces plausible point clouds by sampling from a prior distribution, while a discriminator distinguishes real from generated data. Zhang et al. [20] proposed an unsupervised GAN-based framework incorporating inverse mapping to predict missing regions by learning latent encodings from complete shapes. Sarmad et al. [21] further extended the framework with a reinforcement learning (RL) agent built atop a pre-trained autoencoder and latent-space GAN. While effective in coarse reconstruction, this method struggles with recovering fine local details and suffers from classification bias in complex scenes due to limited semantic discrimination capabilities.

Third, folding-based methods utilize an encoder with graph structures to extract local geometric features and a decoder that continuously “folds” a fixed 2D grid into 3D space to reconstruct object surfaces. This approach significantly reduces decoder parameters and theoretically supports the generation of arbitrary 3D shapes by projecting multi-dimensional point sets onto the original surface [22]. TopNet [23] extends this idea with a hierarchical root–tree decoder that organizes points as nested child-node groupings. To enhance structural feature learning, Wen et al. [24] proposed the skip-attention network, combining skip-attention mechanisms for capturing partial input details with a hierarchical folding decoder to retain geometric information. Building upon this, Zong et al. [25] developed ASHF-Net, integrating a denoising autoencoder with adaptive sampling and a gated skip-attention-based hierarchical decoder to recover fine-grained structures at multiple resolutions.

Despite their strengths, folding-based methods struggle with complex topologies due to their fixed 2D grid initialization, which limits geometric flexibility.

Finally, Transformer-based point cloud completion methods demonstrate superior capability in modeling long-range dependencies due to self-attention mechanisms. Initially developed for sentence encoding in natural language processing [26], Transformers were later adopted in 2D computer vision [27,28], and subsequently in 3D point cloud processing, with models such as PCT [29], Pointformer [30], and PointTransformer [31] being among the earliest examples.

Yu et al. [15] formulated point cloud completion as a set-to-set translation task, designing a Transformer-based encoder–decoder that represents unordered point sets with positional embeddings and translates them into complete point clouds via point proxies. SnowflakeNet [16] progressively densifies point clouds via snowflake point deconvolution (SPD), preserving local structures through a coarse-to-fine refinement approach.

Lin et al. [32] introduced PCTMA-Net, leveraging attention mechanisms to capture local context and structure for predicting missing shapes. PMP-Net++ [33], an enhanced version of PMP-Net [34], incorporates Transformer-based representation learning to improve completion quality. Zhang et al. [35] proposed a coarse-to-fine Transformer framework featuring a Skeleton-Detail Transformer, which models hierarchical relationships between global skeletons and local geometries via cross-attention. Although effective, this method assumes input completeness and structural coherence, limiting its performance in industrial scenarios with severe occlusions and fragmented distributions.

Tang et al. [36] proposed CONTRINET, a triple-flow network that robustly fuses multi-scale features by dynamically aggregating modality-specific and complementary cues through a shared encoder and specialized decoders. This structured fusion strategy offers valuable insights for point cloud completion under noisy and incomplete conditions.

Transformer-based point cloud completion methods typically rely on large volumes of annotated data for supervised training. However, such annotations are often scarce and expensive in real-world scenarios. To alleviate this limitation, Cui et al. [37] proposed P2C, a self-supervised framework that operates on a single incomplete sample. By incorporating local region partitioning, region-aware Chamfer distance, and normal consistency constraints, the model learns structural priors without requiring complete annotations. Building on this, Xu et al. [38] introduced CP-Net, which decouples point cloud geometry into structural contours and semantic content. This design enhances the model’s focus on semantically relevant regions during reconstruction, improving both representational capacity and transferability. In a related direction, Song and Yang [39] proposed OGC, an unsupervised segmentation framework that leverages geometry consistency from sequential point clouds to identify object structures without any human annotations, providing further insights into self-supervised point cloud understanding.

These self-supervised strategies not only increase the sensitivity of Transformer-based networks to local geometric features but also offer promising solutions for point cloud completion under limited data conditions. Enhancing local feature perception and exploiting latent geometric cues from unannotated data remain essential directions for future research in this domain.

2.3. Research Status of Transfer Learning

In recent years, transfer learning (TL) has emerged as an effective machine learning technique and has been widely applied in domains where data are scarce or annotations are difficult to obtain. Its core idea is to transfer knowledge from a source domain to a target domain to improve model performance on the target task [40]. Particularly in 3D point cloud processing, transfer learning effectively alleviates the issues of insufficient data and expensive annotations by reducing the distribution discrepancies between the source and target domains [41]. As point clouds represent an unstructured form of data—characterized by sparsity, incompleteness, and noise—traditional deep learning methods struggle to handle them, whereas transfer learning offers a novel approach to 3D point cloud processing [42].

The fundamental idea behind transfer learning is to leverage the knowledge embedded in pre-trained models to address problems of data scarcity or distribution mismatch, especially through techniques such as Domain Adaptation (DA), which reduce the differences in feature distributions between the source and target domains [40]. In the context of point cloud completion tasks, transfer learning is primarily implemented through several approaches: (1) Feature Transfer: extracting geometric features from source domain data and applying them to the target domain’s point cloud completion tasks to enhance the model’s capability to comprehend and restore incomplete point clouds [43]; (2) Model Transfer: fine-tuning a pre-trained completion model for the target domain, which can still achieve satisfactory completion performance even with a small dataset [44]; and (3) Unsupervised Transfer Learning: employing unsupervised adaptive learning to align data from different domains, thereby addressing discrepancies caused by variations in sensors or scenarios in point clouds [45].

The existing literature demonstrates significant advantages of transfer learning in point cloud completion tasks. For instance, Li et al. proposed a transfer learning-based point cloud completion method that transfers models from large-scale synthetic datasets (e.g., ShapeNet) to small-scale real-world point cloud datasets, achieving efficient recovery of missing point clouds in complex scenarios [46]. Moreover, research by Chen et al. shows that transfer learning can alleviate overfitting in point cloud completion, particularly when handling high noise and incomplete data, with domain adaptation techniques markedly enhancing model robustness and accuracy [47].

Despite these advances, several challenges remain. Firstly, the differences in data distributions between the source and target domains—especially regarding 3D structures and geometric shapes—can lead to instability in transfer learning performance [48]. In manufacturing DT workshops, the high cost of data acquisition and the difficulty of obtaining annotations result in significant discrepancies between the source and target data [48]. While existing transfer learning methods perform well when abundant annotated data are available, models often exhibit insufficient generalization in industrial scenarios with scarce or unannotated data. Additionally, industrial workshop point clouds are frequently accompanied by noise, occlusions, and data loss—especially in complex equipment structures or during operational processes—which further challenges the effectiveness of domain adaptation techniques [44]. Thus, how to leverage transfer learning to enhance the accuracy and robustness of point cloud completion under limited industrial data conditions remains an open problem.

Overall, transfer learning opens up new possibilities for point cloud completion by enabling deep learning models to exploit the knowledge acquired during pre-training, even in the face of limited training data. Consequently, further exploration of more robust domain adaptation methods that can improve model adaptability in scenarios with substantial differences in geometric structures between the source and target domains is an important research direction for future transfer learning applications in industrial point cloud completion tasks.

2.4. Research Gaps

In the construction of DT workshops, the generation of accurate models is a critical factor for the successful application of DT scenarios. Despite recent advances in DT, point cloud completion, and transfer learning, key research gaps remain when these approaches are applied to real-world industrial settings.

Firstly, existing large-scale DT modeling approaches for industrial workshops lack an effective and unified framework, resulting in low modeling efficiency and limited accuracy. Secondly, current point cloud completion algorithms underperform when confronted with complex industrial equipment geometries, particularly in recovering fine-grained local structures, thereby affecting the overall quality of the generated models. Lastly, the scarcity and difficulty in acquiring high-quality industrial datasets limit the generalization capability of existing deep learning models, constraining their applicability in practical industrial scenarios.

To address these challenges, the main contributions of this paper are as follows:

1.

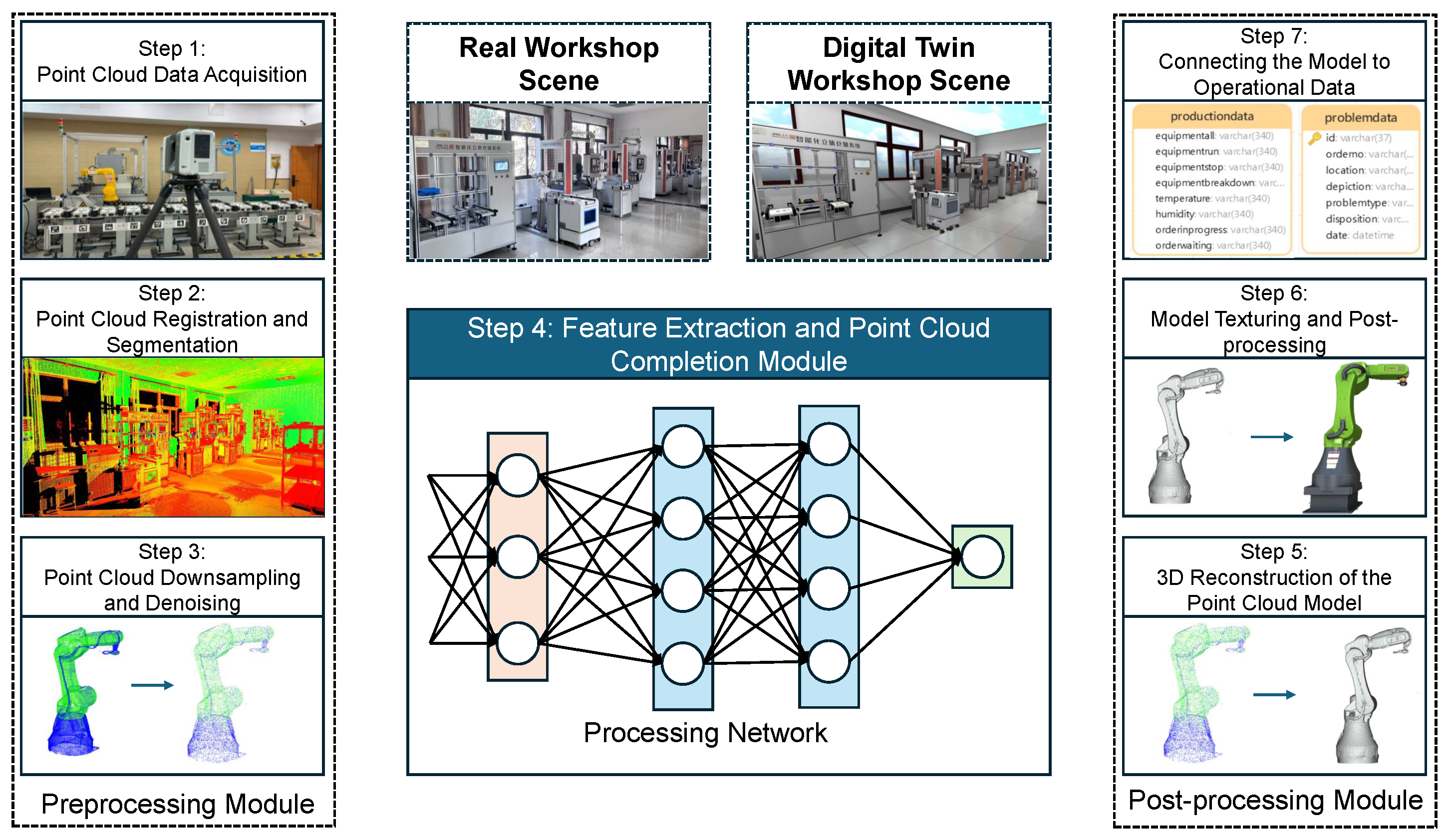
Point Cloud-Based DT Workshop Modeling Framework:

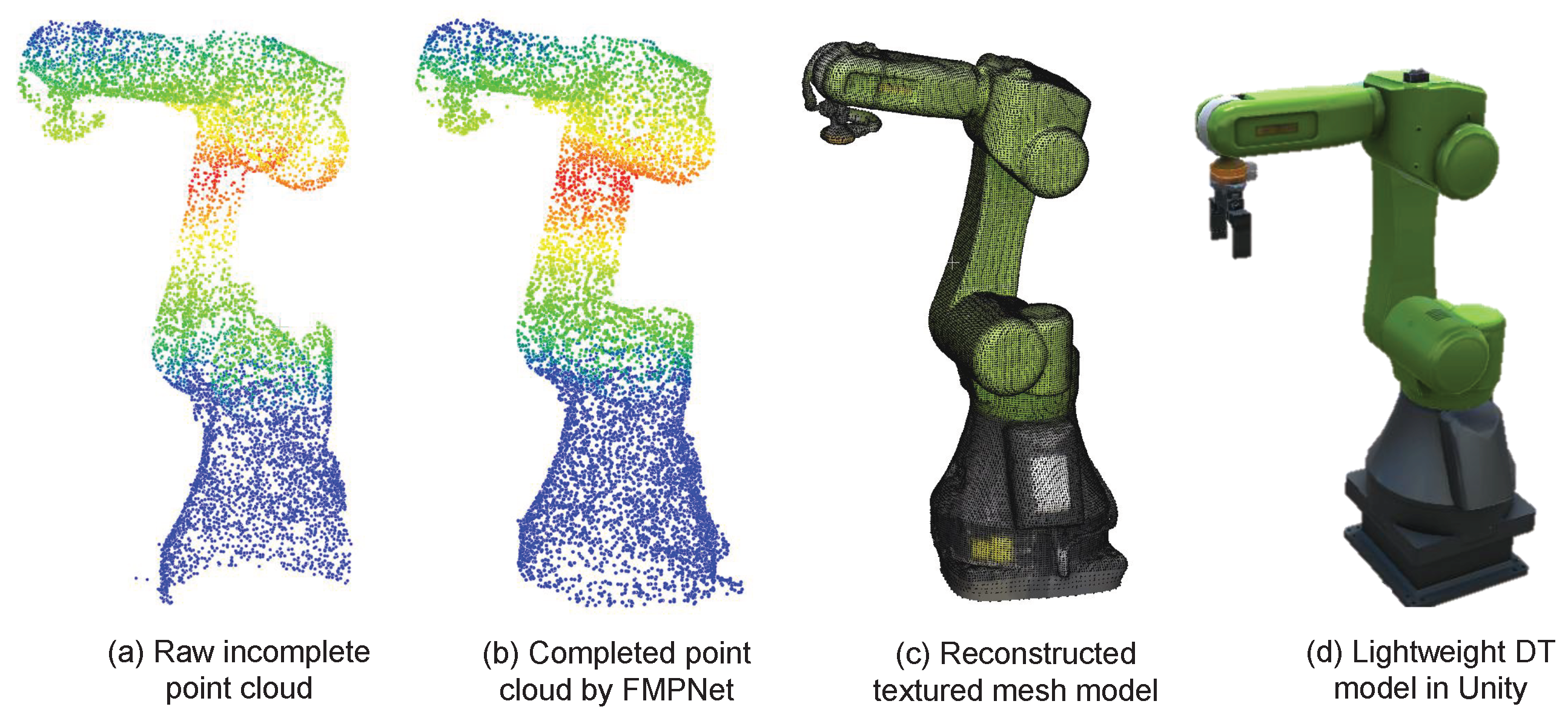
A novel DT workshop modeling framework is introduced, based on point cloud data. By leveraging deep learning techniques, this framework enables automated processing and 3D reconstruction of workshop point clouds. Compared to traditional geometry modeling methods that require substantial manual intervention, our approach significantly reduces labor costs while improving both modeling speed and accuracy. This provides a practical pathway for the efficient construction of DTs in complex industrial environments.

2.

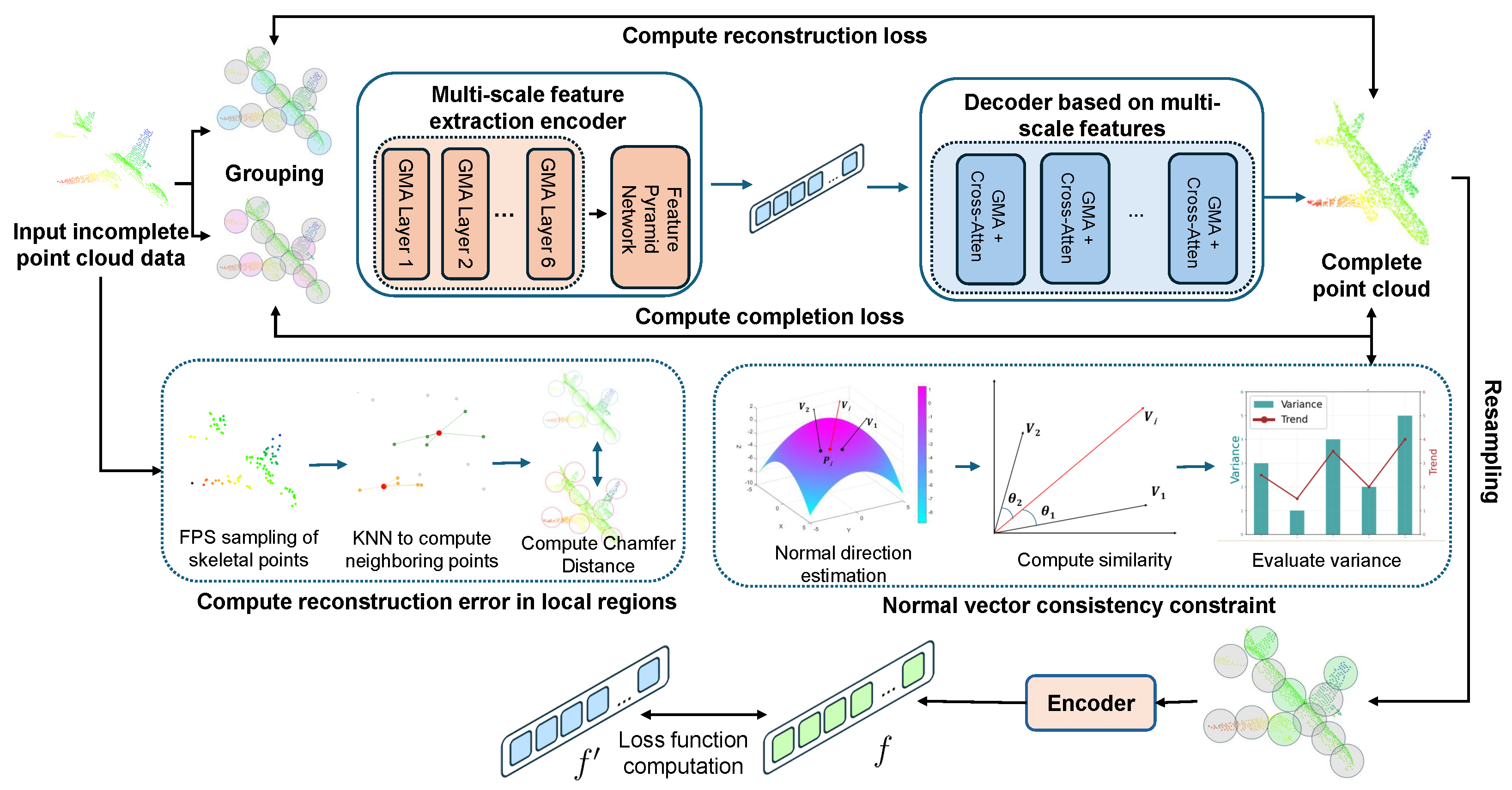
Point Cloud Completion Algorithm:

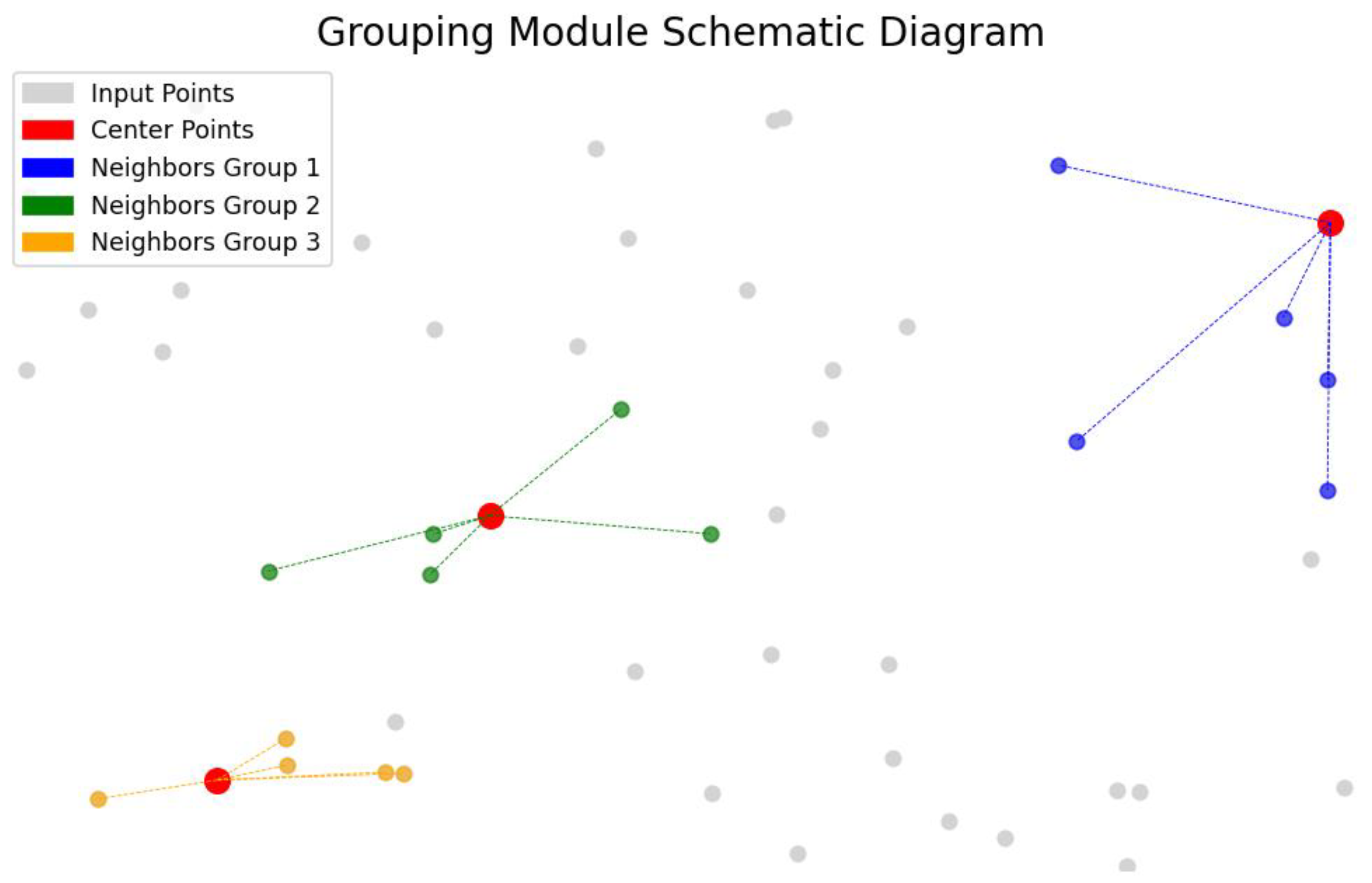
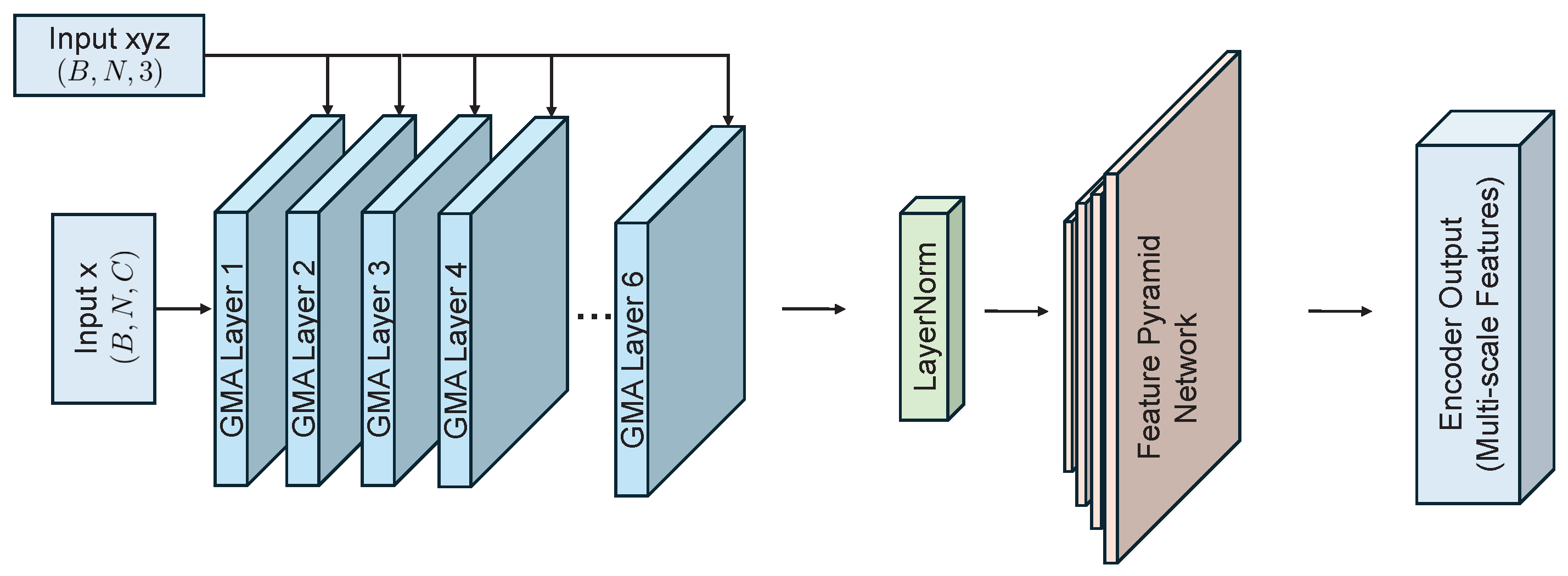
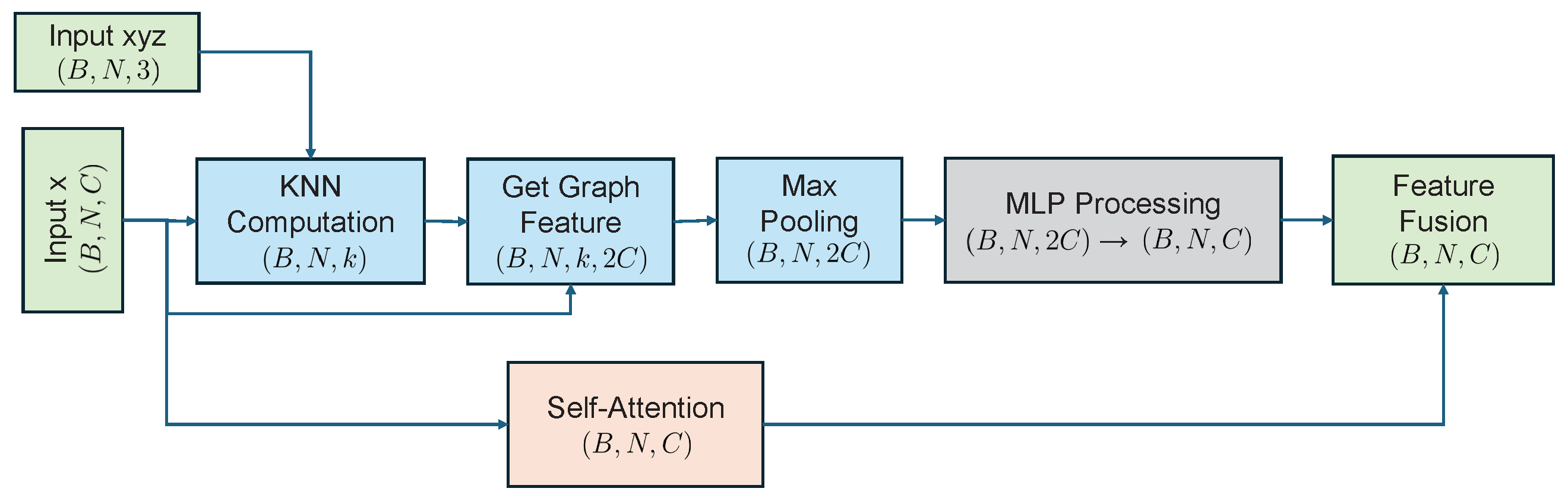
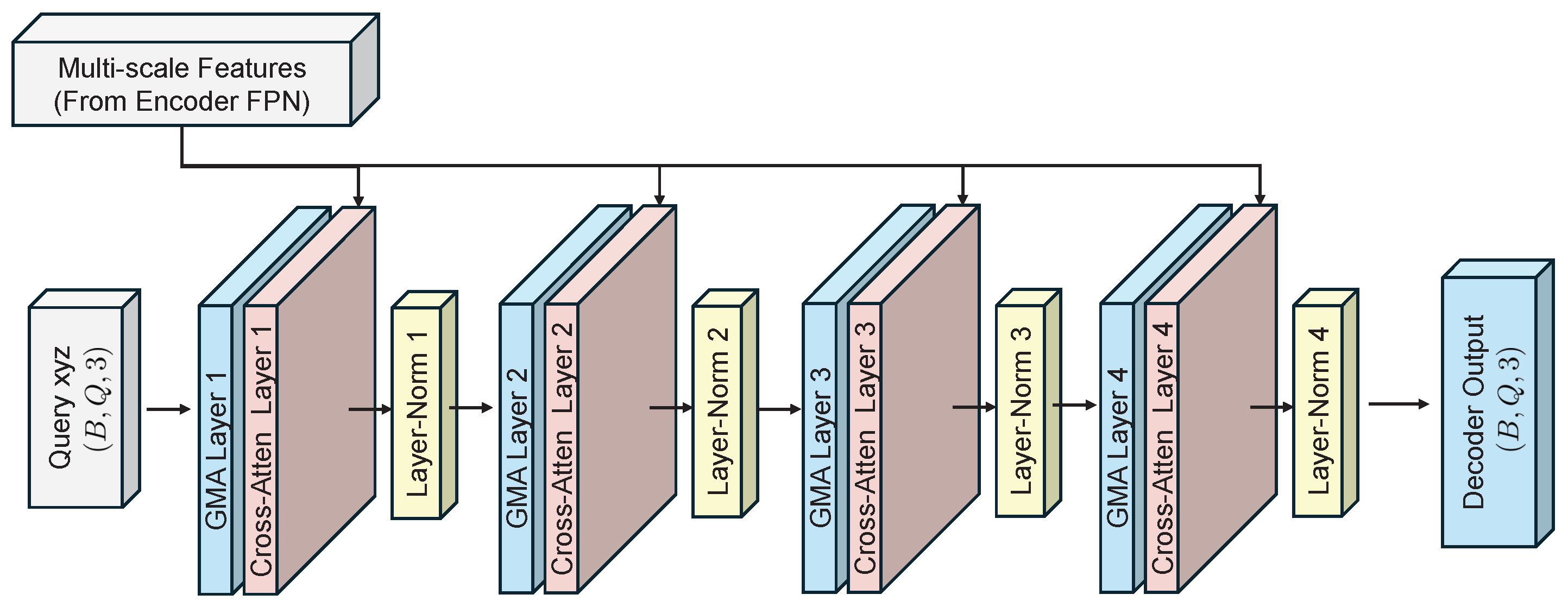
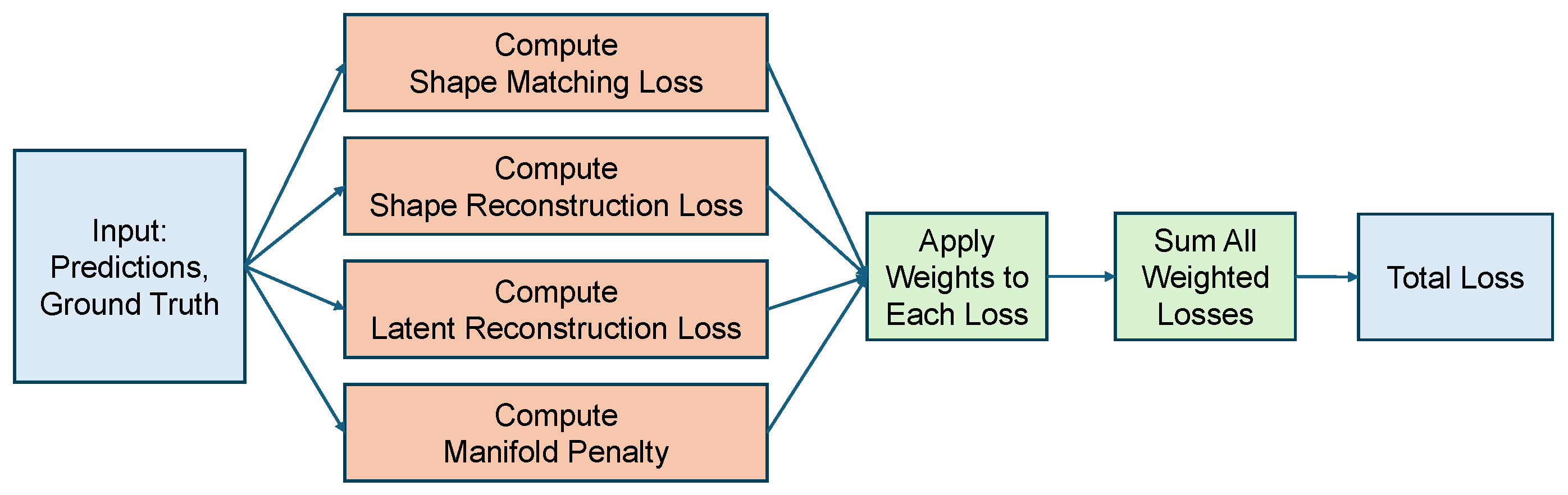
A self-supervised point cloud completion algorithm is introduced, which effectively extracts latent geometric information from incomplete data without requiring large-scale manual annotations. The algorithm integrates multi-scale feature extraction with a cross-attention mechanism, substantially enhancing the ability to capture local geometric features. This ensures high-precision recovery of structural details while maintaining global consistency in the completed point clouds. A multi-objective loss function is further designed to optimize both completeness and local accuracy of the reconstructed data.

3.

Application of Transfer Learning in Industrial Scenarios:

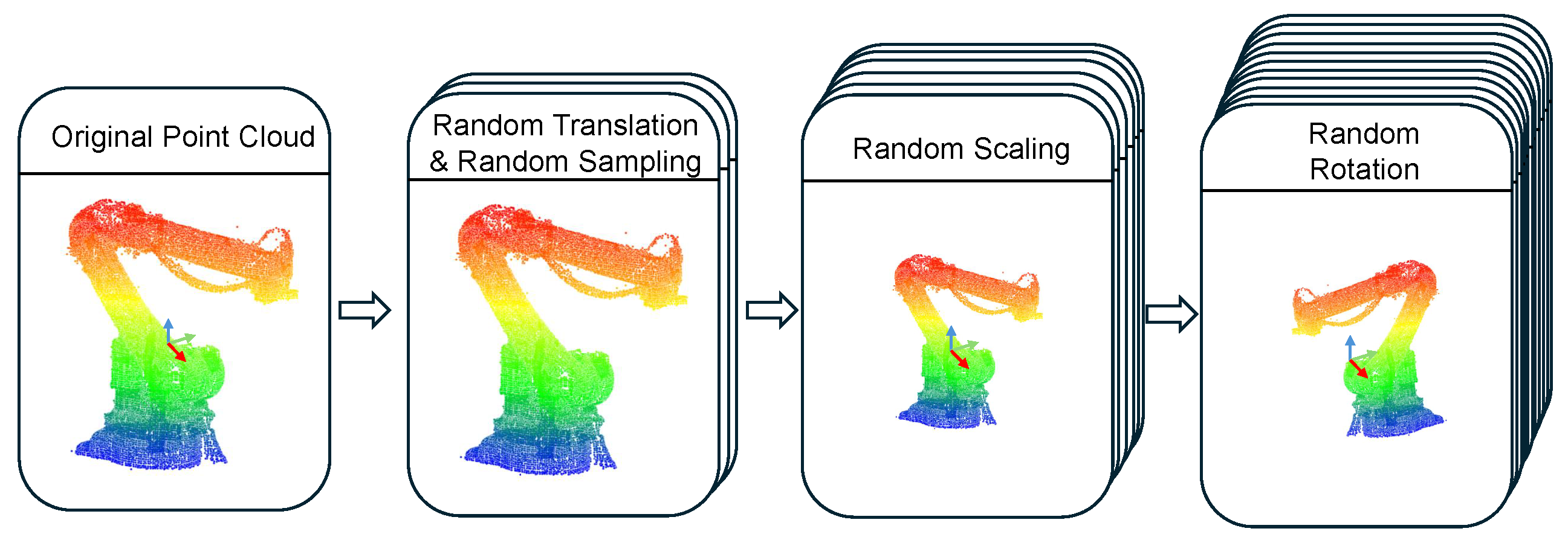
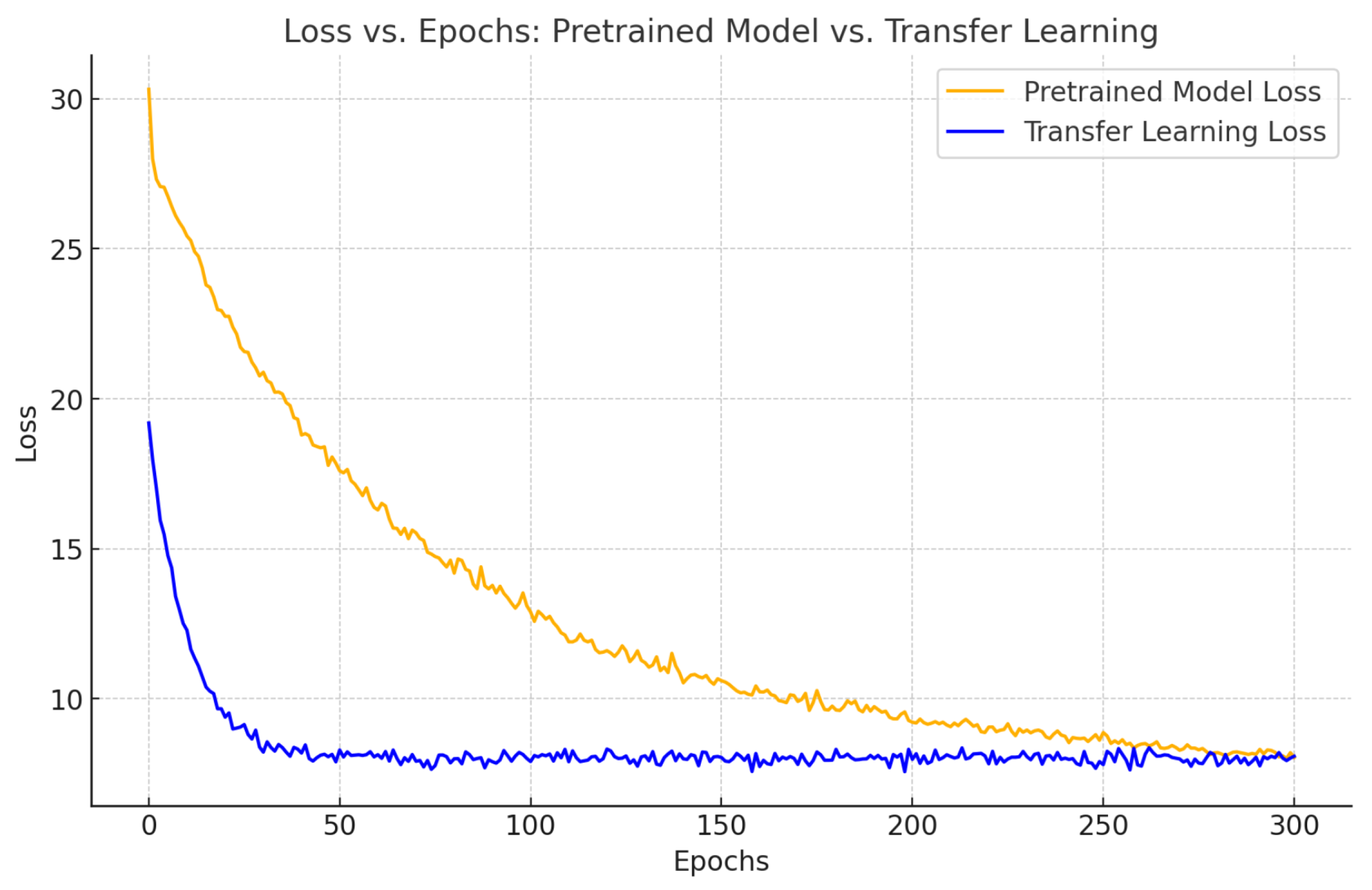
To mitigate the issue of limited industrial datasets, transfer learning techniques are employed to adapt the model from large-scale synthetic datasets to small-scale real-world industrial data. Combined with self-supervised pre-training, transfer learning significantly improves the model’s robustness under noisy and data-scarce conditions and enhances its generalizability across different scenarios. This effectively reduces the reliance on high-quality annotated industrial point clouds.

In summary, this paper addresses key challenges in modeling efficiency, fine-grained structural reconstruction, and data scarcity by proposing a novel DT workshop modeling framework, a self-supervised point cloud completion algorithm, and an integrated transfer learning strategy. Collectively, these contributions provide a comprehensive solution and methodological foundation for advancing the adoption of DT technologies in intelligent manufacturing.

3. Point Cloud-Based Modeling Framework for DT Shopfloors

3.1. System Architecture Overview

The overall deep learning-based DT modeling framework proposed in this study is illustrated in Figure 1. It consists of three core modules: data acquisition and pre-processing, point cloud completion, 3D reconstruction, and post-processing. These modules function collaboratively to produce high-precision DT models, enabling real-time synchronization and interaction between the physical workshop and its virtual counterpart.

3.2. Data Acquisition and Pre-Processing Module

Accurate and comprehensive 3D data acquisition is fundamental to ensuring the precision and reliability of DT modeling. To obtain high-quality point cloud data that meet the modeling requirements, this study employs LiDAR (Light Detection and Ranging) technology to perform multiple scans of the workshop environment. These scans capture high-resolution geometric information over a wide coverage area, including equipment shapes, spatial layouts, and structural dimensions. Once acquired, the raw point cloud data are transmitted to the pre-processing module, where they undergo three critical stages: registration, downsampling, and denoising—each of which plays a vital role in ensuring high-quality input for the subsequent completion and modeling processes.

1.

Point Cloud Registration:

Since a single LiDAR scan typically cannot cover the entire workshop environment, multiple scans from different viewpoints are necessary. To eliminate pose discrepancies between these scans, precise point cloud registration is performed in the pre-processing phase. The Iterative Closest Point (ICP) algorithm is employed to align point clouds spatially by iteratively minimizing the distance between corresponding point pairs. When the initial pose estimates are sufficiently close, ICP achieves efficient and accurate alignment. As a result, the point clouds from various views are unified into a consistent coordinate system, producing a coherent and complete 3D representation of the scene.

2.

Downsampling:

Industrial workshop environments usually generate massive point cloud datasets, often comprising millions or even tens of millions of points. Retaining all points for downstream processing imposes a significant burden on storage and computation. Therefore, after registration, downsampling is applied to reduce data size while preserving the primary geometric structures. Random sampling is adopted as a fast and practical downsampling strategy. By randomly selecting a subset of points, it achieves a favorable balance between computational efficiency and geometric fidelity in most industrial scenarios.

3.

Denoising:

To enhance the clarity and accuracy of the point cloud data, it is essential to remove outlier points caused by laser reflection artifacts, environmental interference, or sensor noise. This study employs Radius Outlier Removal for denoising, which identifies and eliminates points with an insufficient number of neighbors within a defined search radius. This method is particularly effective in complex industrial settings, helping to produce a cleaner point cloud with accurate topological relationships—thereby laying a solid foundation for subsequent point cloud completion and DT modeling.

Through the coordinated execution of these three steps, the pre-processing module effectively reduces noise and compresses data volume while preserving key geometric features. This significantly enhances the applicability and accuracy of downstream point cloud completion and 3D reconstruction tasks.

3.3. Feature Extraction and Point Cloud Completion Module

Complete point cloud data are essential for accurate and practical DT modeling outcomes. However, due to factors such as equipment occlusion, sensor viewpoint limitations, and dynamic industrial environments, point cloud data acquired in real-world scenarios often suffer from incompleteness and missing regions.

To address these challenges, this study proposes a deep learning-based point cloud completion module that automatically infers and reconstructs missing regions, thereby enhancing both the structural integrity and granularity of the 3D models.

The core algorithm adopted in this research is the Feature Multi-scale Point Network (FMPNet), which comprises an encoder and a decoder. By leveraging multi-scale feature extraction and attention mechanisms, FMPNet is capable of efficiently completing incomplete point clouds within industrial environments. The architecture is detailed as follows:

Encoder: The encoder is responsible for extracting hierarchical geometric and structural features from the input incomplete point clouds. It consists of multiple feature extraction units, each comprising convolution and pooling operations, which progressively distill both local and global information. The integration of a Multi-Scale Feature Fusion (MSFF) strategy allows the network to capture spatial features at various scales via parallel convolutional pathways, thereby enhancing its ability to recognize complex geometries and intricate local details.

Decoder: The decoder maps the multi-scale features extracted by the encoder back into the 3D coordinate space to generate a complete and detailed point cloud. It employs an attention-based feature fusion strategy, utilizing cross-attention mechanisms to selectively extract geometrically relevant information from the encoder’s output at each decoding stage. This design enhances the decoder’s global semantic understanding while emphasizing critical local regions, ultimately enabling the reconstruction of point clouds that balance structural coherence with high-fidelity detail.

Multi-Objective Loss and Transfer Learning Strategy: To achieve robust and accurate point cloud completion in industrial scenarios, FMPNet introduces a multi-objective loss function that integrates shape reconstruction loss, shape matching loss, latent space alignment loss, and manifold regularization. These objectives collectively ensure both global consistency and local accuracy, while also promoting smoothness in the reconstructed surfaces. Furthermore, the model is pre-trained on a large-scale synthetic dataset and subsequently fine-tuned on a smaller-scale industrial dataset. This transfer learning approach significantly enhances adaptability to diverse industrial environments and reduces the reliance on extensive, high-quality annotated data.

By incorporating this point cloud completion module, the proposed framework substantially enhances the geometric and topological completeness of DT models, providing a robust data foundation for subsequent 3D reconstruction and post-processing. The algorithmic details and implementation of the point cloud completion approach are elaborated in Section 4.

3.4. Three-Dimensional Reconstruction and Post-Processing Module

Following pre-processing, the 3D reconstruction module integrates multi-source point cloud data and performs meshing and visualization of the completed point cloud, generating a comprehensive 3D model of the workshop. Initially, the Poisson surface reconstruction algorithm is employed to convert the completed point cloud into a triangulated mesh with topological structure, facilitating subsequent rendering and analysis. According to specific requirements, external image textures can be mapped onto the mesh to enhance the visual realism of the model. To balance rendering efficiency and model accuracy, the generated 3D model is further simplified and optimized by removing redundant vertices and mesh elements.

In the post-processing phase, to ensure consistency and interactivity between the virtual model and its physical counterpart, the initially reconstructed 3D model undergoes geometric adjustment to align with the actual dimensions and layout of industrial equipment. Subsequently, the kinematic relationships of the equipment are embedded into the model, enabling accurate simulation of physical motion and functional operations within the virtual environment. Based on the structural characteristics and workflows of workshop equipment, logical mappings and physical associations between objects are established, enabling real-time synchronization and effective interaction between the DT model and the physical workshop.

4. Deep Learning-Based Point Cloud Completion Method

Fine-grained DT modeling in industrial scenarios requires precise 3D point cloud reconstruction based on LiDAR or image-matching data. However, due to the complexity of real-world factory environments and the limited perspectives of sensing devices, the acquired point clouds often suffer from incompleteness or missing regions. Consequently, point cloud completion techniques play an indispensable role in such applications, significantly enhancing the completeness and usability of 3D models.

To address the dual challenges of insufficient point cloud data and the high cost of annotation in industrial settings, this study proposes a point cloud completion method named FMPNet. The core idea is to leverage a well-trained model on public datasets as a set of pre-trained weights and adapt it to industrial data through a transfer learning strategy. This approach yields a deep learning model that retains the ability to represent general geometric features while being tailored to the specific characteristics of industrial scenarios. During each training iteration, the model is optimized based on a multi-objective loss function and corresponding evaluation metrics, aiming to improve the quality of point cloud completion.

As illustrated in Figure 2, the overall architecture of FMPNet comprises key components such as local feature extraction, a Feature Pyramid Network (FPN), and multi-scale feature enhancement modules. By hierarchically capturing both local geometric details and global structural information of the point cloud, the network demonstrates superior robustness against noise and missing data in complex industrial environments. Notably, the integration of multi-scale feature fusion and attention mechanisms enables the model to focus on critical geometric structures and effectively reconstruct missing regions, thereby achieving high completion accuracy while maintaining computational efficiency.

4.1. Grouping Module

In point cloud completion tasks, effectively capturing local geometric features is essential for accurately reconstructing missing regions. However, directly processing large-scale point cloud data at the original resolution imposes a significant computational burden on the model, making it difficult to balance efficiency and accuracy. To address this challenge, an efficient grouping module—illustrated in Figure 3—is introduced to partition the large-scale point cloud into multiple spatially coherent subsets, thereby reducing computational cost while preserving critical local features.

The grouping module primarily integrates Farthest Point Sampling (FPS) and the K-Nearest Neighbors (KNN) algorithm to extract local geometric features efficiently. The detailed procedure is as follows:

Center Point Selection (FPS): Given an input point cloud $P\in {\mathbb{R}}^{N\times 3}$, FPS is employed to select G representative center points. This algorithm iteratively selects the point farthest from the already chosen set, ensuring that the center points are evenly distributed across the spatial domain.

Neighborhood Search (KNN): For each center point, the KNN algorithm is used to retrieve its M nearest neighbors from the original point cloud, forming a local region or a point cloud subset around each center.

Coordinate Normalization: To eliminate spatial bias across different local regions, the coordinates of neighborhood points are normalized by subtracting the corresponding center point:

$$p_{i,j}^{\prime }=p_{i,j}-c_i,$$

(1)

where $p_{i,j}^{\prime }$ denotes the j-th neighbor of the i-th center point, and $c_i$ is the coordinate of the i-th center point.

Partitioning the point cloud into localized subsets enables the model to effectively capture region-specific geometric features—such as curvature and surface normals—crucial for reconstructing intricate structures. This strategy also reduces computational complexity and mitigates the impact of local noise or missing data. By facilitating localized feature extraction while preserving global context, it allows the encoder to generate a hierarchical representation that empowers the decoder to produce accurate and high-fidelity 3D reconstructions.

4.2. Feature Pyramid Network (FPN) Encoder

When processing point cloud data from workshop environments, it is essential to preserve both local geometric details and the global structural layout to accurately model complex object shapes and scene configurations. However, incomplete point clouds often exhibit inconsistencies in resolution, texture, and viewpoint.

Relying solely on a single scale or a basic convolutional network is insufficient to simultaneously capture fine-grained and global features. To address this, an encoder architecture is introduced, integrating a Feature Pyramid Network (FPN) with Geometric Attention Layers (as illustrated in Figure 4). The design enhances encoder adaptability by leveraging hierarchical geometric features, improving robustness to complex industrial point clouds.

4.2.1. Geometric Attention Layer

The Geometric Attention Layer aims to exploit local geometry and neighborhood structures, addressing key industrial challenges such as fine-scale features, missing regions, and noise. Specifically, this layer enhances feature expressiveness by fusing the feature differences between each center point and its neighboring points, enabling the model to capture the interactions between local deformations and global context.

Given an input point cloud $\mathbb{X}\in {\mathbb{R}}^{B\times N\times 3}$, where B is the batch size, N is the number of points, and the last dimension represents the 3D coordinates $(x,y,z)$, the encoder first applies Farthest Point Sampling (FPS) to select a set of center points $\mathbb{C}\in {\mathbb{R}}^{B\times G\times 3}$, with G denoting the number of sampled points. For each center point, the k-Nearest Neighbors (KNN) algorithm is used to identify its corresponding local neighborhood.

The structure of the geometric attention mechanism is illustrated in Figure 5.

For each center point ${\mathbf{c}}_i$ and its corresponding neighborhood ${\left\{{\mathbf{p}}_j\right\}}_{j=1}^k$, the local feature differences are computed as follows:

$$\Delta F_{ij}=F\left({\mathbf{p}}_j\right)-F\left({\mathbf{c}}_i\right).$$

(2)

$F(·)$ denotes the feature representation of a point. Subsequently, the feature of each center point is concatenated with the difference between the center point and its neighboring features to form a new composite feature representation:

$$H_{ij}=[F\left({\mathbf{c}}_i\right),\Delta F_{ij}].$$

(3)

These features are processed through a Multi-Layer Perceptron (MLP) to perform nonlinear transformations, resulting in updated feature representations:

$$F^{\prime }\left({\mathbf{c}}_i\right)=\underset{j=1,\dots ,k}{max}\sigma \left(\mathbf{W}{H}_{ij}+\mathbf{b}\right).$$

(4)

Here, $\sigma (·)$ denotes the activation function, while $\mathbf{W}$ and $\mathbf{b}$ represent learnable weights and biases. The max operation performs max pooling over all neighboring points to aggregate local features.

The introduction of the geometric attention layer is critical for thoroughly extracting local deformations and geometric details from multi-view point clouds. By explicitly encoding this neighborhood geometry-based attention mechanism within the neural network, the model is able to retain key structural information during subsequent multi-scale fusion, thereby significantly enhancing the accuracy of point cloud completion and reconstruction.

4.2.2. Feature Pyramid Network

In industrial environments, point clouds often exhibit both highly detailed local microstructures and large-scale, complex scenes spanning across multiple devices. Relying solely on single-layer or single-scale features is typically insufficient to fully capture the global layout and detailed distribution. Therefore, integrating a Feature Pyramid Network (FPN) into the encoder facilitates the comprehensive extraction of multi-level feature information. The structural diagram of the FPN is illustrated in Figure 6, and its core process can be summarized as follows:

$${\mathbf{P}}_l={\mathbf{F}}_l+\mathrm{Upsample}\left({\mathbf{P}}_{l+1}\right).$$

(5)

Here, ${\mathbf{P}}_l$ represents the fused features at the l-th layer, while ${\mathbf{F}}_l$ denotes the output features from the geometric attention layer at the same level. The $\mathrm{Upsample}(·)$ operation maps high-level semantic features to the resolution of the current layer.

Finally, a convolution operation is applied to further enhance the fused features:

$${\mathbf{F}}_l=\mathrm{Conv}3\times 3\left({\mathbf{P}}_l\right).$$

(6)

Through this process, based on the detailed representations provided by the geometric attention layer, the FPN further integrates features from various levels. This enhances the network’s robustness and adaptability in handling challenges such as occlusion, missing data, and noise. Consequently, the encoder outputs a multi-scale fused feature representation $\{{\mathbf{F}}_1,{\mathbf{F}}_2,\dots ,{\mathbf{F}}_L\}$, which supplies the decoder with rich contextual information.

Table 1. Configuration details of the Feature Pyramid Network (FPN) layers.

Layer Type	Size (Input → Output)	Conv (Kernel/Channels)
FPN Lateral Conv (1–6)	$(B,768,L_x)\to (B,256,L_x)$	1D Conv (kernel = 1), 768 → 256
FPN Output Conv (1–6)	$(B,256,L_x)\to (B,256,L_x)$	1D Conv (kernel = 3), 256 → 256

Notes: B denotes the batch size; $L_x$ (L1–L6) represents the sequence length at different feature pyramid levels. Nearest-neighbor interpolation is used during upsampling. No activation function is applied after convolutions.

lists the architecture and parameter settings of the Feature Pyramid Network (FPN), including the input and output sizes and the convolutional configurations at each level. Each lateral convolution uses a kernel size of 1 to reduce the dimensionality of the feature maps, while the output convolutions apply a kernel size of 3 to enhance local feature aggregation. All output channels are set to 256 to maintain consistent feature dimensions across pyramid levels. Nearest-neighbor interpolation is adopted for upsampling operations.

4.3. Decoder with Multi-Scale Feature Integration

The primary objective of the decoder is to generate complete point cloud data by leveraging the multi-scale features extracted by the encoder. This is achieved through a decoder architecture that integrates multi-scale feature fusion and a cross-attention mechanism, as shown in Figure 7. The cross-attention mechanism is particularly well suited for this application because it selectively highlights critical information from each encoder scale, ensuring that both global geometry and fine-grained details are effectively transferred to the decoder. By aligning incomplete input features with comprehensive encoder outputs, cross-attention aids in reconstructing missing regions more precisely under varying levels of occlusion and noise.

The decoder consists of three main components: query feature initialization, self-attention layers, and cross-attention layers. Through the collaborative functioning of these modules, the decoder is able to perform high-precision point cloud completion by effectively integrating and refining both local and global structural features.

4.3.1. Query Feature Initialization

The decoder first generates a set of initial query points $\mathbf{Q}\in {\mathbb{R}}^{B\times N_q\times 3}$, where $N_q$ is the number of query points. These query points can be obtained either through random initialization or by sampling from the input point cloud. Correspondingly, the initial query features ${\mathbf{F}}_q\in {\mathbb{R}}^{B\times N_q\times d}$ are established, where d denotes the feature dimension, typically consistent with the encoder’s output dimension.

4.3.2. Self-Attention Mechanism

To capture the correlations among the query points, the decoder applies a self-attention mechanism to the query features.

$$\mathbf{Q}={\mathbf{H}}_q^{l-1}{\mathbf{W}}_Q,\mathbf{K}={\mathbf{H}}_q^{l-1}{\mathbf{W}}_K,\mathbf{V}={\mathbf{H}}_q^{l-1}{\mathbf{W}}_V.$$

(7)

Here, ${\mathbf{W}}_Q,{\mathbf{W}}_K,{\mathbf{W}}_V\in {\mathbb{R}}^{d\times d}$ are learnable weight matrices. Subsequently, the attention weights are computed as follows:

$${\mathbf{A}}_{\mathrm{self}}=\mathrm{Softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}^{\top }}{\sqrt{d}}}\right),$$

(8)

where ${\mathbf{A}}_{\mathrm{self}}\in {\mathbb{R}}^{B\times N_q\times N_q}$ denotes the self-attention weights. Next, the features are updated according to the following:

$${\mathbf{F}}_q^{\prime }={\mathbf{A}}_{\mathrm{self}}\mathbf{V}.$$

(9)

Through the self-attention mechanism, the updated query features ${\mathbf{F}}_q^{\prime }$ are able to fully integrate information among the query points, thereby enhancing the internal consistency of the feature representations.

4.3.3. Cross-Attention Mechanism

To fully leverage the multi-scale features extracted by the encoder, the decoder establishes an interaction between the self-attention processed query features ${\mathbf{F}}_q^{\prime }$ and the encoder features ${\mathbf{F}}_e$. The implementation is as follows:

• Linear Transformation of Encoder Features:

$${\mathbf{K}}_e={\mathbf{F}}_e{\mathbf{W}}_K^{\prime },{\mathbf{V}}_e={\mathbf{F}}_e{\mathbf{W}}_V^{\prime },$$

(10)

where ${\mathbf{F}}_e\in {\mathbb{R}}^{B\times L\times d}$ denotes the multi-scale features output by the encoder, L is the number of scale layers, and ${\mathbf{W}}_K^{\prime },{\mathbf{W}}_V^{\prime }\in {\mathbb{R}}^{d\times d}$ are learnable weight matrices.

• Cross-Attention Weight Computation:

$${\mathbf{A}}_{\mathrm{cross}}=\mathrm{Softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}_e^{\top }}{\sqrt{d}}}\right).$$

(11)

• Weight Fusion:

$${\mathbf{F}}_q^{″}={\mathbf{A}}_{\mathrm{cross}}{\mathbf{V}}_e.$$

(12)

Here, ${\mathbf{A}}_{\mathrm{cross}}\in {\mathbb{R}}^{B\times N_q\times N_q}$ represents the cross-attention weights. Through this mechanism, the query features ${\mathbf{F}}_q^{″}$ can selectively fuse the encoder’s multi-scale features, enabling the decoder to focus on important scales and key geometric regions, thereby dynamically enhancing the feature representation.

4.3.4. Point Cloud Generation

After multiple layers of self-attention and cross-attention processing, the decoder obtains updated query features ${\mathbf{F}}_q^{″}\in {\mathbb{R}}^{B\times N_q\times d}$. Finally, a fully connected layer maps these query features to three-dimensional coordinates, generating the complete point cloud:

$$\widehat{\mathbf{X}}={\mathbf{F}}_q^{″}{\mathbf{W}}_{\mathrm{out}}+{\mathbf{b}}_{\mathrm{out}},$$

(13)

where ${\mathbf{W}}_{\mathrm{out}}\in {\mathbb{R}}^{d\times 3}$ and ${\mathbf{b}}_{\mathrm{out}}\in {\mathbb{R}}^{d\times 3}$ are learnable weight and bias matrices, and $\widehat{\mathbf{X}}\in {\mathbb{R}}^{B\times N_q\times 3}$ represents the generated complete point cloud.

4.4. Loss Functions and Constraints

The design of loss functions during training plays a crucial role in determining the model’s ability to accurately reconstruct missing regions and maintain robustness in noisy environments. To balance global shape consistency with the preservation of local geometric details, a set of complementary loss functions is introduced during the training phase, including shape reconstruction loss, shape matching loss, latent space alignment loss, and manifoldness constraint.

As shown in Figure 8, these loss functions guide the network’s parameter updates from multiple perspectives, enabling the model to achieve a desirable trade-off between geometric completeness and surface smoothness.

4.4.1. Shape Reconstruction Loss

The shape reconstruction loss is used to measure the discrepancy between the locally generated point cloud and the ground-truth point cloud. The Chamfer Distance (CD) based on the $L_1$ norm is adopted as the primary evaluation metric, defined as follows:

$${\mathcal{L}}_{\mathrm{recon}}={\displaystyle \frac{1}{|\widehat{X}|}}\sum _{p\in \widehat{X}}\underset{q\in X_{\mathrm{gt}}}{min}{\parallel p-q\parallel }_1+{\displaystyle \frac{1}{|X_{\mathrm{gt}}|}}\sum _{q\in X_{\mathrm{gt}}}\underset{p\in \widehat{X}}{min}{\parallel q-p\parallel }_1.$$

(14)

Here, $\widehat{X}$ denotes the set of point clouds generated by the model, $X_{\mathrm{gt}}$ denotes the set of ground-truth point clouds, and ${\parallel ·\parallel }_1$ represents the $L_1$ norm.

By computing the nearest-neighbor distance between the predicted and ground-truth point clouds, this loss function encourages the generated point cloud to maintain local structural consistency with the real data, thereby enhancing the accuracy of the completion.

4.4.2. Shape Matching Loss

The shape matching loss is designed to ensure that the overall global shape generated by the model aligns with the ground-truth shape. Similar to the shape reconstruction loss, the Chamfer Distance is employed as the metric, defined as follows:

$${\mathcal{L}}_{\mathrm{match}}={\displaystyle \frac{1}{|\widehat{C}|}}\sum _{p\in \widehat{C}}\underset{q\in C_{\mathrm{gt}}}{min}{\parallel p-q\parallel }_1+{\displaystyle \frac{1}{|C_{\mathrm{gt}}|}}\sum _{q\in C_{\mathrm{gt}}}\underset{p\in \widehat{C}}{min}{\parallel q-p\parallel }_1.$$

(15)

Here, $\widehat{C}$ denotes the set of center points generated by the model, and $C_{\mathrm{gt}}$ represents the set of ground-truth center points.

By employing this loss function, the model not only focuses on the precise reconstruction of local point clouds but also ensures the overall consistency of the global shape, thereby enhancing the overall quality of the completed point cloud.

4.4.3. Latent Space Alignment Loss

To promote the alignment between the model’s latent feature space and the real data, a latent space alignment loss is introduced. This loss utilizes the Smooth $L_1$ loss function to measure the discrepancy between the predicted features and the ground-truth features, defined as follows:

$${\mathcal{L}}_{\mathrm{latent}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathrm{SmoothL}1(F_i,F_i^{\mathrm{gt}}),$$

(16)

where N is the feature dimensionality, and $F_i$, $F_i^{\mathrm{gt}}$ denote the i-th component of the predicted and ground-truth features, respectively.

The Smooth $L_1$ loss function is defined as follows:

$$\mathrm{SmoothL}1(x,y)=\left\{\begin{array}{cc}0.5{(x-y)}^2,\hfill & \mathrm{if}|x-y|<1\hfill \\ |x-y|-0.5,\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(17)

By reducing the discrepancies in the latent feature space, this loss function enhances the model’s generalization ability across different inputs and stabilizes the feature representation.

4.4.4. Manifoldness Constraint

To ensure that the generated point cloud lies on a smooth manifold, a manifoldness constraint is introduced. This constraint penalizes inconsistencies in the normals of neighboring points, thereby promoting smoothness of the point cloud surface. The specific steps are as follows:

For each point, compute its normal vector ${\mathbf{n}}_i$ using the points within its neighborhood.

Then, compute the cosine similarity between the normal vectors of neighboring points:

$$\mathrm{Cos}\mathrm{Sim}({\mathbf{n}}_i,{\mathbf{n}}_j)={\displaystyle \frac{{\mathbf{n}}_i·{\mathbf{n}}_j}{\parallel {\mathbf{n}}_i\parallel \parallel {\mathbf{n}}_j\parallel }},$$

(18)

where ${\mathbf{n}}_i$ and ${\mathbf{n}}_j$ represent the normal vectors of the i-th and j-th points, respectively.

The manifold constraint loss is then defined as follows:

$${\mathcal{L}}_{\mathrm{manifold}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(1-{\displaystyle \frac{1}{K}}\sum _{j\in \mathcal{N}\left(i\right)}\mathrm{Cos}\mathrm{Sim}({\mathbf{n}}_i,{\mathbf{n}}_j)\right),$$

(19)

where N is the total number of points, K is the number of neighboring points, and $\mathcal{N}\left(i\right)$ denotes the neighborhood of the i-th point.

This loss function encourages the model to generate neighboring points with consistent normal directions, thereby ensuring the smoothness and continuity of the point cloud surface and reducing noise and discontinuities.

4.4.5. Total Loss

Combining the aforementioned losses, the total loss function of the model is defined as follows:

$${\mathcal{L}}_{\mathrm{total}}=\alpha {\mathcal{L}}_{\mathrm{recon}}+\beta {\mathcal{L}}_{\mathrm{match}}+\gamma {\mathcal{L}}_{\mathrm{latent}}+\delta {\mathcal{L}}_{\mathrm{manifold}},$$

(20)

where $\alpha$, $\beta$, $\gamma$, and $\delta$ are the weight hyperparameters corresponding to the shape reconstruction loss, shape matching loss, latent space alignment loss, and manifoldness constraint, respectively. These weights are used to balance the influence of different loss components during training and can be adjusted according to the specific task requirements to optimize overall model performance.

4.4.6. Evaluation Metrics

To evaluate the performance in point cloud completion, two distance-based metrics, CD-${\ell }_2$ and UCD-${\ell }_2$, are employed. These metrics are widely used to measure point-level discrepancies between predicted outputs and ground-truth data.

$$\mathrm{CD}\text{-}{\ell }_2(S_{\mathrm{pred}},S_{\mathrm{gt}})={\displaystyle \frac{1}{|S_{\mathrm{pred}}|}}\sum _{p\in S_{\mathrm{pred}}}\underset{q\in S_{\mathrm{gt}}}{min}{\parallel p-q\parallel }_2^2+{\displaystyle \frac{1}{|S_{\mathrm{gt}}|}}\sum _{q\in S_{\mathrm{gt}}}\underset{p\in S_{\mathrm{pred}}}{min}{\parallel q-p\parallel }_2^2,$$

(21)

$$\mathrm{UCD}\text{-}{\ell }_2(S_{\mathrm{pred}},S_{\mathrm{gt}})={\displaystyle \frac{1}{|S_{\mathrm{pred}}|}}\sum _{p\in S_{\mathrm{pred}}}\underset{q\in S_{\mathrm{gt}}}{min}{\parallel p-q\parallel }_2^2.$$

(22)

Here, $S_{\mathrm{pred}}$ and $S_{\mathrm{gt}}$ denote the predicted and ground-truth point sets, respectively, and ${\parallel ·\parallel }_2$ represents the squared Euclidean distance.

CD-${\ell }_2$ evaluates the bidirectional nearest-neighbor discrepancy: it penalizes both missing regions (if points in $S_{\mathrm{gt}}$ find no close match in $S_{\mathrm{pred}}$) and superfluous parts (if points in $S_{\mathrm{pred}}$ deviate from $S_{\mathrm{gt}}$). Therefore, CD-${\ell }_2$ provides a holistic view of the reconstruction quality and is particularly helpful in assessing fine-grained geometry restoration.

By contrast, UCD-${\ell }_2$ focuses on the one-way distance from predicted points to the ground-truth point set. This metric is beneficial when completeness or coverage of the ground-truth geometry is the main priority, as it highlights whether the reconstructed shape appropriately covers the observed regions without excessively penalizing slight overshoot or additional artifacts.

These two metrics jointly offer a comprehensive measure of reconstruction fidelity and coverage, enabling robust comparisons among different point cloud completion approaches.

4.5. Transfer Learning

In industrial scenarios, obtaining high-quality, annotated point cloud data is challenging and expensive due to equipment limitations, environmental complexity, and factors such as data privacy. This has become a major bottleneck limiting the practical performance of deep learning models. To address this challenge, this paper introduces transfer learning technology to transfer knowledge pre-trained on a large-scale synthetic dataset to actual industrial datasets, thereby enhancing the model’s generalization capability and data utilization efficiency.

Transfer learning leverages the knowledge learned in the source domain to help the model converge faster and achieve better performance in the target domain. Specifically, the advantages of transfer learning in this study include the following:

• Improved Generalization Ability: By pre-training on a diverse synthetic dataset, the model learns feature representations with stronger generalizability, enabling it to adapt to various industrial scenarios.
• Reduced Data Requirements: Transfer learning decreases the reliance on large amounts of point cloud training data in the target domain, lowering the costs associated with data acquisition and dataset construction.
• Accelerated Training Process: The pre-trained model provides a robust initialization for the weights, thereby reducing the training time required for the model to converge in the target domain.

This paper adopts a transfer learning strategy based on pre-training and fine-tuning, with the following specific process:

The model is first pre-trained on the large-scale synthetic dataset 3D-EPN [49] to learn general geometric features and point cloud structures. This step applies the same total loss function $L_{\mathrm{total}}$ as defined earlier, ensuring consistency across stages:

$$L_{\mathrm{total}}^{\mathrm{source}}=\alpha L_{\mathrm{recon}}^{\mathrm{source}}+\beta L_{\mathrm{match}}^{\mathrm{source}}+\gamma L_{\mathrm{latent}}^{\mathrm{source}}+\delta L_{\mathrm{manifold}}^{\mathrm{source}},$$

(23)

where the source domain point cloud sets are $S_{\mathrm{source}}$ and $C_{\mathrm{source}}$. The weights from the pre-trained model are then used as the initialization, and the model is subsequently fine-tuned on the target industrial dataset (i.e., the actual workshop point cloud dataset). During fine-tuning, the loss function is adjusted to correspond to the target domain point cloud sets $S_{\mathrm{target}}$ and $C_{\mathrm{target}}$:

$$L_{\mathrm{total}}^{\mathrm{target}}=\alpha L_{\mathrm{recon}}^{\mathrm{target}}+\beta L_{\mathrm{match}}^{\mathrm{target}}+\gamma L_{\mathrm{latent}}^{\mathrm{target}}+\delta L_{\mathrm{manifold}}^{\mathrm{target}}.$$

(24)

The core of transfer learning is to optimize the loss function for the new target domain while retaining the knowledge learned from the source domain. Let ${\theta }_{\mathrm{source}}$ represent the model parameters obtained from pre-training on the source domain; the goal during fine-tuning is to find new parameters ${\theta }_{\mathrm{target}}$ that minimize the total loss in the target domain.

To facilitate effective transfer learning, a selective fine-tuning strategy is employed, wherein lower encoder layers are frozen to retain generalizable geometric priors, while higher layers and the decoder are adapted to the target domain. A hierarchical learning rate schedule further refines this process, promoting domain-specific adaptation in deeper layers while preserving foundational representations. This approach ensures stable optimization, mitigates catastrophic forgetting, and enhances the model’s capacity to generalize across domains.

Specifically, the optimization process can be expressed as follows:

$${\theta }_{\mathrm{target}}={\theta }_{\mathrm{source}}-\eta {\nabla }_{\theta }{L}_{\mathrm{total}}^{\mathrm{target}}\left({\theta }_{\mathrm{source}}\right),$$

(25)

where $\eta$ denotes the learning rate, and ${\nabla }_{\theta }$ represents the gradient of the loss function with respect to the parameters.

5. Experiments

To validate the effectiveness of the proposed FMPNet in multi-scale feature extraction and fine-grained detail reconstruction, experiments were conducted on the publicly available 3D-EPN [49] dataset as well as a custom-built industrial workshop point cloud dataset. The 3D-EPN [49] dataset contains a diverse range of 3D object categories, providing a rich source of data for pre-training. The industrial dataset was acquired from real manufacturing environments and comprises representative modules of smart factory operations, including AGV systems, robotic workcells, machine tools, inspection units, and handling stations. These components span key functional domains—logistics, machining, assembly, and quality control—and exhibit diverse spatial configurations, materials, and occlusion patterns. The resulting point clouds capture realistic sensing challenges such as clutter, partial observability, and surface artifacts, reflecting the geometric and semantic complexity typical of modern industrial settings. This dataset thus provides a robust basis for evaluating model performance under practical deployment conditions. Combined with the synthetic 3D-EPN benchmark, it enables comprehensive assessment across both controlled and real-world domains.

5.1. Data Sources and Pre-Processing

Eight known categories from the 3D-EPN [49] dataset were selected, which comprises a total of 283,622 virtually scanned 3D models and is commonly adopted as a benchmark for unpaired shape completion methods. The original 3D models are sourced from the ShapeNet [50] repository. To generate training data, a virtual scanning pipeline is employed to simulate realistic depth sensor acquisition. Specifically, each CAD model is rendered from six randomized camera trajectories to produce partial observations that emulate varying levels of occlusion and incompleteness. These partial scans are converted into volumetric representations using the truncated signed distance field (TSDF), encoding both distance values and known/unknown space. The corresponding ground-truth shapes are represented as unsigned distance fields (DFs). All training samples are voxelized at a resolution of ${32}^3$, forming paired TSDF-DF volumes suitable for supervised learning.

The industrial dataset was collected from several typical machining workshops in Nanjing, China. The experiments were conducted using the following hardware and software environment: Processor (CPU): Intel I9 13980HX (Intel Corporation, Santa Clara, CA, USA); RAM: 48 GB; Graphics Processor (GPU): NVIDIA RTX 4070 8 GB (NVIDIA Corporation, Santa Clara, CA, USA); Programming Language: Python 3.7; and Deep Learning Framework: PyTorch 1.11.0. All training and testing were performed on a single GPU to ensure the reproducibility and consistency of the experimental results.

It is noteworthy that industrial point cloud datasets are difficult to obtain. To fully leverage the industrial dataset, the raw point clouds underwent a series of pre-processing and data augmentation steps. In order to ensure that the model maintains robust generalization capabilities in the presence of various noise, occlusions, and other complex environmental conditions, several data augmentation strategies were employed. As illustrated in Figure 9, during each training iteration, these random processing techniques are applied to the input point clouds, significantly enhancing the model’s adaptability to diverse data and reducing the risk of overfitting.

1.

Random Mirroring: With a certain probability, the point cloud is mirrored along the x-axis or z-axis to enhance data diversity and prevent overfitting.

2.

Random Rotation: The point cloud is randomly rotated within a specified range to improve the model’s adaptability to different orientations.

3.

Random Point Sampling: For each point cloud sample, random sampling is performed during each training iteration by selecting different subsets of points. This enables the model to learn from diverse point distributions while preserving intrinsic geometric properties.

4.

Noise Injection: A small amount of Gaussian noise is added to the point cloud coordinates to simulate real-world sensor interference. This increases the model’s robustness to noisy inputs.

5.2. Model Validation and Training

All models were implemented using the PyTorch framework and trained with the AdamW optimizer. The specific training settings are shown in

Table 2. Training and loss hyperparameter settings.

Learning Rate	Weight Decay	Epochs	Batch Size	Points	Mask Ratio
$1\times {10}^{-4}$	$1\times {10}^{-4}$	300	8	2048	[20%, 40%, 4%]
Loss Weight	$\alpha$  (Reconstruction)		$\beta$  (Matching)	$\gamma$  (Latent)	$\delta$  (Manifold)
Value	1		1000	0.1	0.01
Optimizer	Scheduler			BN Momentum Scheduler
AdamW	LambdaLR (decay 0.9 every 20 epochs)			Lambda (decay 0.5 every 21 epochs)

.

Inv network [20] (complete), Pcl2Pcl [47] (unpaired), Gu et al. [51] and PPNet [52] (multi-view), ACL-SPC [2] (single-partial), and the proposed FMPNet (single-partial) are compared across multiple categories on the 3D-EPN dataset, with the quantitative results summarized in

Table 3. Quantitative comparison on the 3D-EPN [49] dataset using CD-${\ell }_2$ ($\times {10}^4$).

Category	Inv [20]	Pcl2Pcl [47]	Gu et al. [51]	PPNet [52]	ACL-SPC [2]	Ours
Plane	4.3	4.0	5.9	5.6	3.38	5.6
Cabinet	20.7	19.0	20.8	46.6	21.72	22.2
Car	11.9	10.0	9.5	22.4	5.87	13.4
Chair	20.6	20.0	20.4	24.3	17.38	14.0
Lamp	25.9	23.0	34.9	46.1	34.73	16.6
Sofa	54.8	26.0	27.1	28.4	23.03	23.7
Table	38.0	26.0	36.7	36.4	20.24	17.9
Watercraft	12.8	11.0	14.8	15.0	14.73	12.3
Average	23.63	17.38	21.26	28.10	17.63	15.96

.

To comprehensively evaluate our approach, we compare it with representative methods under different supervision paradigms. Specifically, methods in the complete setting adopt a fully supervised strategy, where each partial input is paired with a corresponding complete ground truth to compute direct reconstruction losses. The unpaired setting relaxes this requirement by assuming two disjoint sets of partial and complete shapes without one-to-one correspondence, often relying on generative or distributional alignment techniques. In the multi-view setting, multiple partial observations of the same object are available from different viewpoints, enabling weak supervision through cross-view consistency.

In contrast, our method is evaluated under the most challenging single-partial setting, where each object instance is represented by only a single incomplete observation, without access to complete shapes, paired samples, or multi-view redundancy. This comparison setup allows us to fairly assess the effectiveness of our self-supervised learning scheme against existing approaches that rely on varying levels of external supervision.

As shown in Table 3, under the more challenging single-partial setting—where only a single incomplete observation is provided per object—our method achieves a notably low average CD-${\ell }_2$ of 15.96. Despite the absence of explicit supervision, it outperforms Pcl2Pcl [47] (unpaired) by 8.12% and exceeds the performance of Gu et al. [51] and PPNet [52] (multi-view) by 25.00% and 43.20%, respectively. Compared to Inv [20] (complete), which leverages fully supervised training and reports a CD-${\ell }_2$ of 23.63, our approach yields a substantial 32.46% improvement. Furthermore, against ACL-SPC [2] (single-partial), a recent single-view completion framework that achieves an average error of 17.63, our method still achieves a relative gain of 9.49%. These results collectively underscore the robustness and effectiveness of our approach under highly constrained supervision conditions.

As shown in Figure 10, the proposed point cloud completion model can effectively reconstruct missing regions from incomplete input point clouds while maintaining overall shape consistency.

The enhanced multi-scale feature extraction in FMPNet improves its ability to capture both local and global structures in point clouds. Consequently, in categories such as airplanes, cars, chairs, lamps, tables, and watercraft—where reconstructing complex details is crucial—the model is better able to recover subtle object structures, exhibiting higher accuracy and reliability in point cloud completion tasks.

5.3. Transfer Learning Validation and Case Analysis

In this section, the effectiveness of FMPNet is evaluated in real industrial scenarios by fine-tuning the model from a synthetic dataset to a self-collected industrial workshop point cloud dataset. The primary objective is to assess FMPNet’s performance in handling complex and realistic industrial environments under data scarcity and high-noise conditions. Specifically, this subsection details the transfer learning procedure, experimental configurations, and an in-depth analysis of the outcomes, highlighting the practical implications for industrial applications.

5.3.1. Experimental Setup

The training was conducted on a custom dataset encompassing diverse industrial facilities, such as workstations, robotic manipulators, and control cabinets. Due to intrinsic industrial complexities—ranging from significant background noise to missing areas and limited data volume—a fine-tuning strategy is employed to adapt the pre-trained model to these challenging conditions. The fine-tuning hyperparameter settings, including hierarchical learning rates and selective layer freezing, are detailed in

Table 4. Fine-tuning hyperparameter settings (differences from pre-training).

Component	Setting
Frozen Layers	Encoder Layers 1–3
Learning Rate (Encoder Layers 4–5)	$1\times {10}^{-5}$
Learning Rate (Encoder Layer 6 and FPN)	$1\times {10}^{-4}$
Optimizer	AdamW (same as pre-training)
Scheduler	LambdaLR (same as pre-training)
BatchNorm Momentum Scheduler	Lambda (same as pre-training)

. To gauge the completion accuracy, the same Chamfer Distance (CD-${\ell }_2$) metric used in the preceding experiments is employed, comparing predicted point clouds against ground-truth industrial scans. Additionally, Uniform Chamfer Distance (UCD-${\ell }_2$) is introduced to comprehensively assess coverage quality in the reconstructed point clouds.

5.3.2. Quantitative Results

Table 5. Transfer learning results on self-collected dataset using CD-${\ell }_2$ and UCD-${\ell }_2$ ($\times {10}^4$).

Category	CD-${\mathit{\ell }}_2$	UCD-${\mathit{\ell }}_2$
Workstation	3.7	2.54
Robotic Manipulator	14.2	1.25
Control Cabinet	11.4	2.25
Average	12.0	2.01

presents the quantitative results on the self-collected dataset, highlighting that FMPNet demonstrates marked improvements after transfer learning. The model converges more efficiently while maintaining high completion fidelity. Notably, the overall averages of CD-${\ell }_2$ and UCD-${\ell }_2$ reach 12.0 and 2.01, respectively, showcasing robust performance across varied equipment types.

5.3.3. Convergence Analysis

Figure 11 compares the pre-training loss curve and the transfer learning loss curve. After initializing with pre-trained weights, FMPNet not only converges faster but also achieves a lower final loss plateau, underlining the utility of its pre-trained representations in complex real-world tasks.

5.3.4. Qualitative Visualization

As illustrated in Figure 12, FMPNet successfully completes intricate structures within noisy, partially missing industrial datasets, demonstrating strong robustness and adaptability. Recovered point clouds maintain geometric fidelity even in sparse regions, demonstrating the model’s fine-grained reconstruction capability.

5.3.5. Case Study

To demonstrate the practical applicability of the proposed point cloud completion and modeling framework, a high-precision FANUC robotic arm was selected as a representative use case. This equipment features multiple articulated joints and recessed structures, which frequently result in missing regions during LiDAR scanning. Its requirement for geometric and behavioral fidelity in digital simulation makes it an ideal candidate for DT modeling and validation.

The robotic arm was scanned using a Leica RTC360 terrestrial laser scanner (Leica Geosystems AG, Heerbrugg, Switzerland) under operational conditions. The segmented object-level point cloud contained 94,806 points, with visible occlusions near the wrist and base joints. The raw data were downsampled and denoised to 2048 points before being processed by the proposed FMPNet. After outlier filtering, a complete and topologically consistent point cloud was reconstructed, as shown in Figure 13a,b. Normal vectors were then computed to support surface reconstruction.

The completed point cloud was imported into 3ds Max for surface reconstruction. The reconstructed mesh was optimized in Pixyz Studio to reduce computational load while retaining key geometric details, especially near joint areas. Operations such as hidden removel and polygon decimation were applied to simplify the geometry while maintaining topological consistency and feature boundaries. To enhance realism, high-quality textures were created and applied using Substance Painter. The finalized model was then exported in .fbx format and prepared for deployment in a Unity-based DT platform, as illustrated in Figure 13c,d.

To enable kinematic behavior and motion control, the 3D model was imported into Unity3D and organized into a hierarchical joint structure aligned with the robot’s physical configuration. Each of the seven rotational joints was defined as a separate node, facilitating direct binding with motion data and ensuring accurate articulation, as shown in the center of Figure 14. Parenting relationships and local coordinate alignment were configured to support joint-level transformations and rule-based simulation logic.

A MySQL-based relational database was built to facilitate communication between physical devices and their DTs. Real-time joint angle and velocity data were streamed from the robot controller and mapped to the Unity model through structured database tables. This enabled bidirectional synchronization, allowing physical device states to be visualized in the digital environment and virtual simulation outcomes to guide physical behavior under test scenarios, as depicted on the right of Figure 14.

By combining data-driven modeling, point cloud completion, geometric reconstruction, and hierarchical structuring, the proposed workflow enables a high-fidelity DT that mirrors both the structure and behavior of the physical robotic system. The results confirm the feasibility and effectiveness of the approach for DT applications in intelligent manufacturing.

5.3.6. Discussion of Advantages and Limitations

The experimental results presented above underscore the advantages of the proposed FMPNet-based DT modeling framework from both qualitative and quantitative perspectives. A deeper analysis is provided below to contextualize these outcomes relative to recent representative methods, namely Pcl2Pcl [47] and ACL-SPC [2].

• Enhanced Structural Completeness: Compared with Pcl2Pcl, which relies on adversarial training under an unpaired supervision regime, FMPNet achieves more accurate and topologically coherent reconstructions by leveraging cross-attention-guided multi-scale decoding. Unlike the coarse-to-fine structure of ACL-SPC, which generates completions from single partial inputs using semantic-aware anchors, FMPNet explicitly models both global skeleton and local region geometry through hierarchical feature grouping and a feature pyramid backbone. This design enables better detail preservation and structural regularity, as evidenced by the lower CD-${\ell }_2$ scores reported in Table 5 and the finer local reconstructions in Figure 12.
• Resilience to Noise and Incompleteness: Real-world industrial data often suffer from heavy occlusion and sensor-induced noise. The integration of geometric attention and manifold-aware loss functions in FMPNet substantially enhances its robustness. Unlike ACL-SPC, which struggles with fragmented input, and Pcl2Pcl, which lacks region-level guidance, FMPNet adaptively attends to critical geometry using its hierarchical decoder and produces stable reconstructions across varying levels of degradation, as shown in Figure 12.
• Improved Efficiency via Transfer Learning: As evidenced by the faster convergence in Figure 11, initializing FMPNet with pre-trained knowledge accelerates adaptation to new industrial categories. This strategy reduces the reliance on extensive annotated datasets in resource-constrained environments.

Despite these advantages, certain limitations remain. The proposed FMPNet demonstrates strong capability in reconstructing incomplete point clouds with fine-grained structural fidelity. However, as shown in

Table 6. Comparison of computational overhead between FMPNet and baseline models.

Model	FLOPs (GMac)	Params (M)	Inference Time (ms/Sample)
FMPNet (ours)	3.22	64.92	13.30
Baseline-avg	1.71	23.90	6.32

, it incurs higher computational overhead compared to baseline models: requiring 3.22 GMac FLOPs and 64.92 M parameters, nearly double the complexity and inference time of average alternatives.

This overhead is acceptable within the context of offline, one-time completion tasks, which is the primary application scenario in DT modeling pipelines. Yet, when deployed across large-scale industrial workshops with high-resolution scanning and extensive sensor arrays, such complexity may impact practical usability.

Therefore, although real-time inference is not essential in our offline point cloud completion pipeline, scalability remains a critical consideration for large-scale industrial deployments. Addressing this challenge requires improving architectural efficiency and data handling strategies. Promising directions include scene partitioning for region-wise processing, model pruning to reduce redundancy, and quantization to lower computation and memory demands. These strategies offer practical means to enhance the scalability and deployability of the proposed framework in complex DT environments.

In addition to scalability, another challenge lies in the model’s behavior under extreme sensing conditions. While FMPNet performs reliably in standard industrial scenarios, it exhibits degraded reconstruction quality when confronted with severely sparse or heavily occluded point clouds. For instance, when the input contains less than 10% of the original surface geometry, or is heavily corrupted by sensor noise, the network may fail to recover fine structural details, resulting in oversmoothed or topologically distorted outputs. These failure cases reveal the limitations of relying solely on geometric priors in data-deficient settings.

To overcome this issue, future extensions could incorporate multi-modal data fusion, utilizing additional modalities such as RGB images, depth maps, or thermal signals to enrich the input context. Complementary information helps disambiguate corrupted regions and improves reconstruction fidelity. Incorporating uncertainty-aware decoding and cross-modal attention may further suppress artifacts and enhance plausibility in challenging scenarios.

Overall, the transfer learning validation underscores the practicality of our framework in handling complex industrial environments, affirming that the proposed approach effectively addresses data scarcity, noise interference, and diverse equipment structures. This robust performance lays a strong foundation for subsequent industrial applications of DT technology, including real-time monitoring, simulation, and predictive maintenance.

5.4. Ablation Experiment

To thoroughly analyze the impact of each component within the FMPNet model on the performance of point cloud completion, a systematic ablation study was conducted. By progressively removing or substituting key modules of the model, the contribution of each component to the overall performance was evaluated, aiming to validate the effectiveness of the design of each part.

In this study, the complete FMPNet model was used as the baseline, and the following components were individually modified or removed:

1.

Geometric Attention Module (GAM): enhances local feature representation and improves the model’s sensitivity to fine-grained structural details.

2.

Feature Pyramid Network (FPN): fuses multi-scale features to boost the model’s ability to capture fine-grained details at various scales.

3.

Cross-Attention Module (CAM): facilitates effective interaction between the encoder and decoder features in the decoder, thereby optimizing the reconstruction outcome.

4.

Normal Consistency Constraint (NCC): encourages local surface continuity by penalizing normal-vector inconsistencies in neighboring points, thus refining the smoothness and accuracy of the reconstructed point cloud.

Experimental Setup: To assess the individual contributions of the core components, four model variants were designed in which each key module was either replaced, simplified, or removed, depending on its structural necessity.

Table 7. Ablation study results on 3D-EPN dataset using CD-${\ell }_2$ ($\times {10}^4$).

Model	GAM	FPN	CAM	NCC	CD-${\mathit{\ell }}_2$
Baseline	✓	✓	✓	✓	11.5
Model A	✗	✓	✓	✓	12.4
Model B	✓	✗	✓	✓	12.1
Model C	✓	✓	✗	✓	12.9
Model D	✓	✓	✓	✗	11.7

summarizes the performance of each model variant on the robotic manipulator dataset, providing a quantitative comparison to evaluate the contribution of each key component to the overall point cloud completion performance.

The results indicate that modifying or removing any key component leads to a performance drop. Specifically, disabling multi-scale feature extraction (Model A) increases the CD-${\ell }_2$ metric from 11.5 to 12.4, highlighting its critical role in capturing both local details and global structures. Omitting the Geometric Attention Module (GAM, Model B) causes a 0.6 increase in CD-${\ell }_2$, suggesting that removing adaptive local geometry weighting compromises the reconstruction of fine details. Excluding the Cross-Attention Module (CAM, Model C) yields a CD-${\ell }_2$ of 12.9, reflecting less effective integration of encoder–decoder features and leading to suboptimal overall structural consistency. Finally, removing the Normal Consistency Constraint (NCC, Model D) weakens local surface smoothness enforcement, resulting in noticeable discontinuities and noise on the completed point cloud.

Overall, these ablation studies confirm that each component—multi-scale feature extraction, GAM, CAM, and NCC—plays a vital role in achieving robust and high-quality point cloud completion, thereby validating the effectiveness of our proposed design.

6. Conclusions and Outlook

This study addresses critical challenges in DT workshop modeling, particularly the issues of incomplete point cloud data and the scarcity of annotated samples in industrial environments. A self-supervised deep learning framework is proposed, encompassing the full workflow from data acquisition and pre-processing to point cloud completion, 3D reconstruction, and post-processing. This framework facilitates accurate mapping and real-time synchronization between physical workshops and their virtual counterparts.

At the core of the framework is a self-supervised point cloud completion network that integrates a Feature Pyramid Network (FPN) and Cross-Attention Mechanism (CAM). Augmented by transfer learning, the network achieves high-precision inference of missing regions while significantly reducing the reliance on large-scale annotated datasets, thereby enhancing both reconstruction accuracy and efficiency.

The proposed method is applied to a complete industrial case involving industrial robotic manipulators, effectively bridging the gap between point cloud inference and DT deployment in smart factory scenarios. Experiments show the proposed method achieves superior CD-${\ell }_2$ scores and visual quality compared to state-of-the-art approaches on the 3D-EPN dataset. These findings offer strong theoretical support for DT modeling in complex industrial contexts and establish a technological foundation for downstream applications such as real-time monitoring and path planning.

Future work will aim to extend the scalability and adaptability of this framework in large-scale digital workshops. Key research directions include the following:

• Model Efficiency Optimization: future studies should investigate methods such as pruning, quantization, and scene partitioning to reduce the computational complexity introduced by multi-scale feature extraction and attention mechanisms.
• Multi-Modal Data Fusion: integrating visual images, depth maps, and other sensor modalities to enhance accuracy and robustness in challenging environments.
• Cross-Domain Generalization: evaluating model performance on diverse datasets such as PCN and SemanticKITTI to validate robustness beyond industrial scenarios.