Fractional Kelvin–Voigt Model for Beam Vibrations: Numerical Simulations and Approximation Using a Classical Model
Abstract
1. Introduction
2. Formulation, Solution, and Computational Methods
2.1. Governing Equation and Solution Using the Rayleigh–Ritz Method
2.2. Solution of the Temporal Equation and Numerical Methods
2.3. Identification of Equivalent Harmonic Oscillator Parameters: Geometric and Optimization Approaches
2.3.1. Geometric Approach to Parameter Identification
2.3.2. Genetic Algorithm Approach to Parameter Identification
3. Results
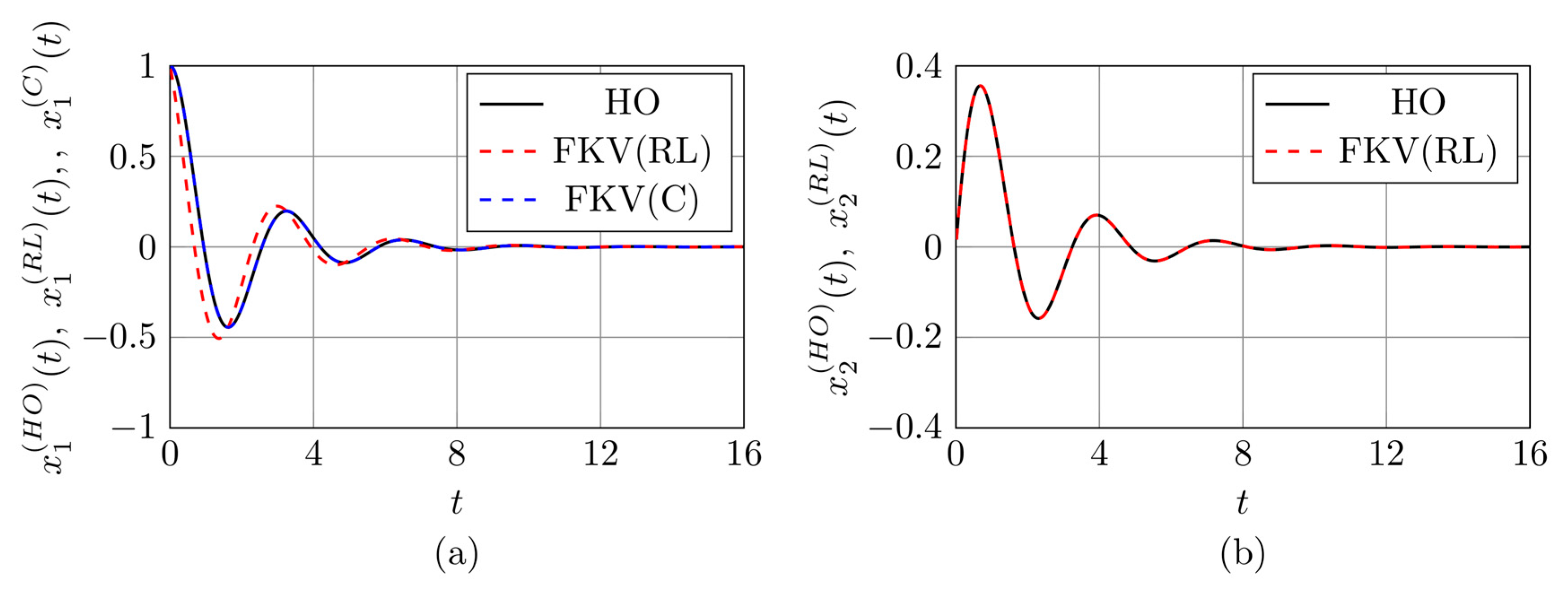
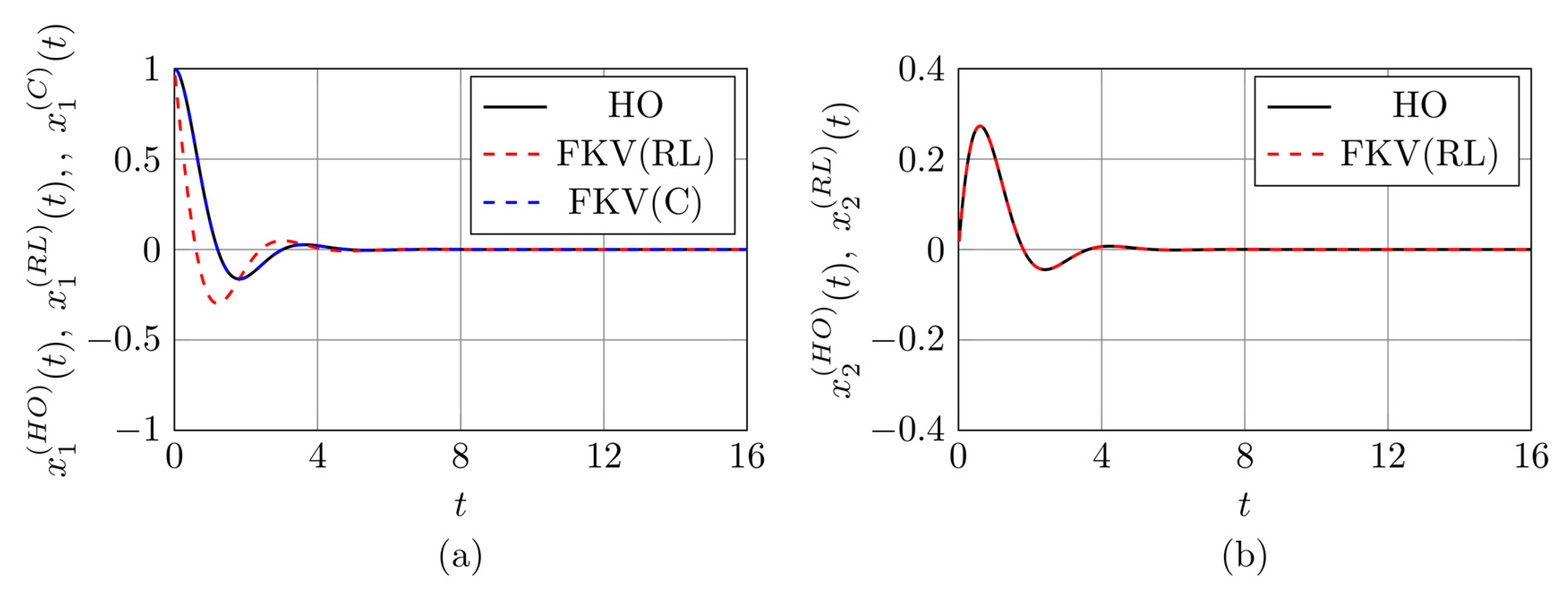
3.1. Verification of the Wynn Epsilon Method for Solving the FKV Oscillator Equation
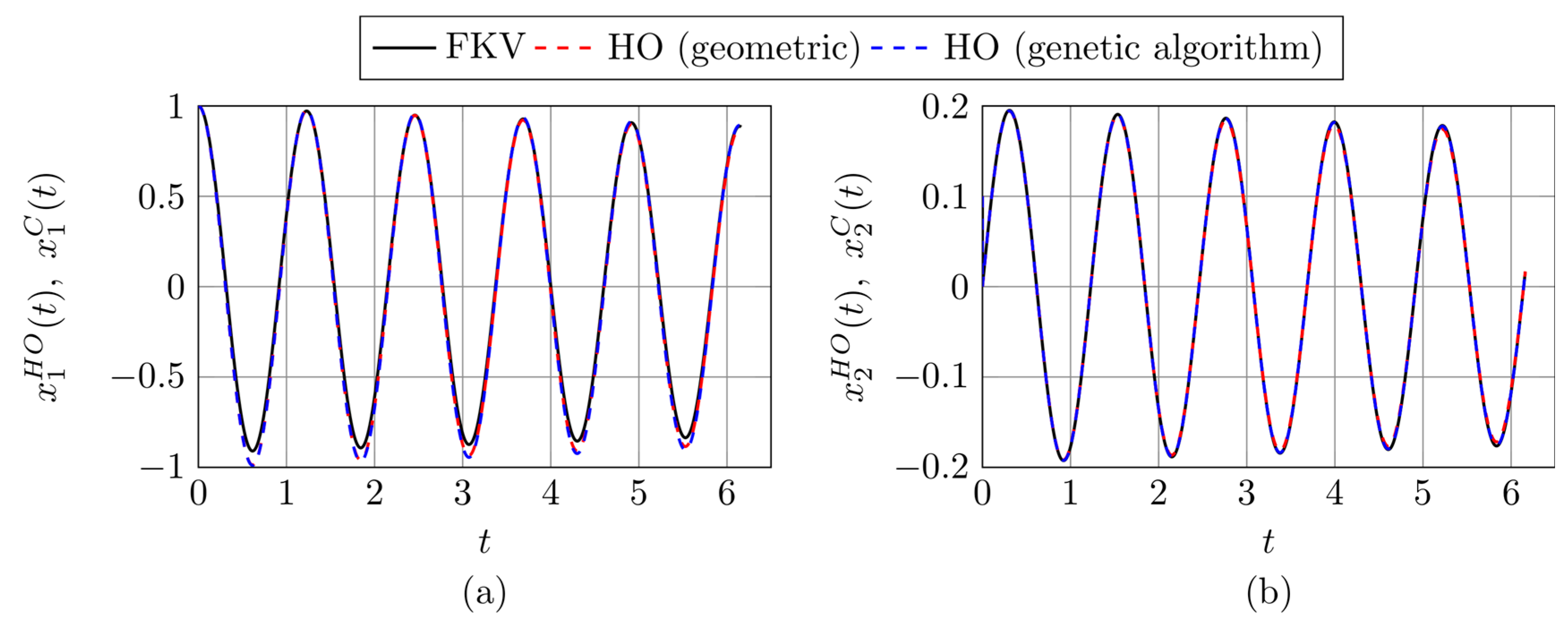
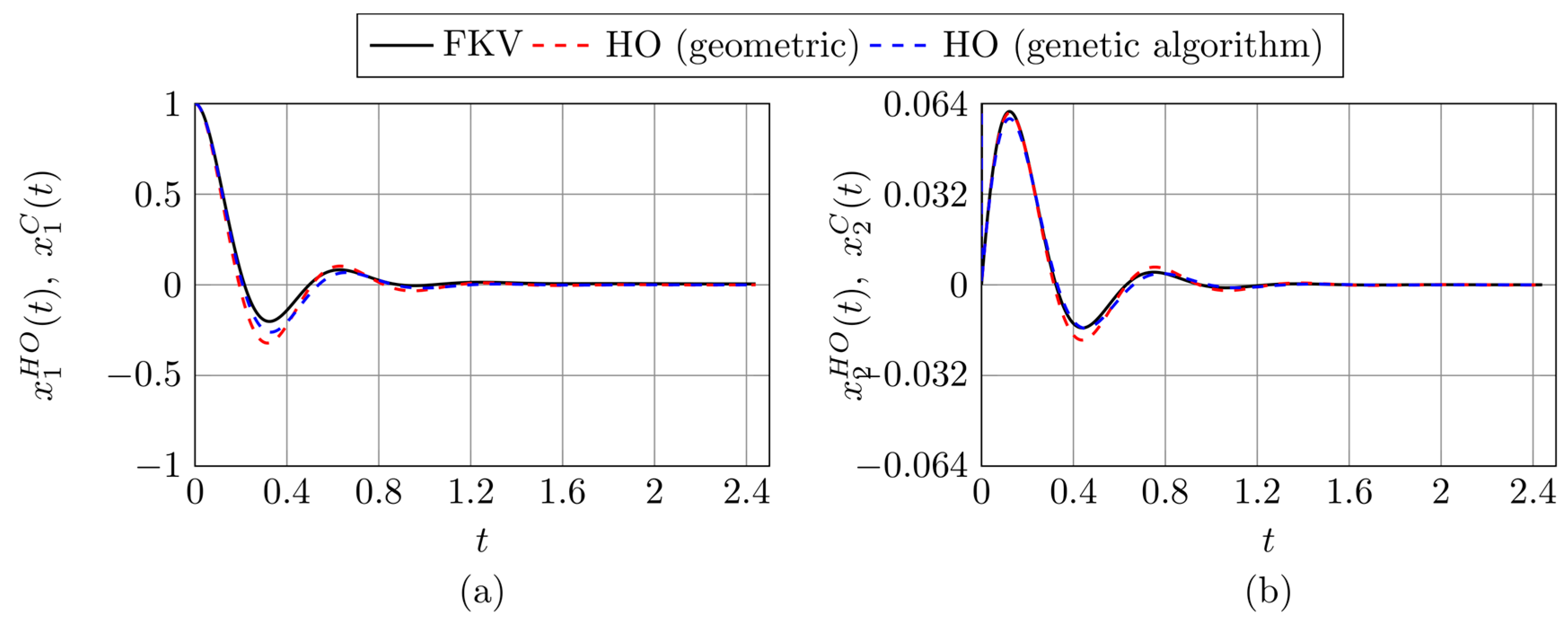
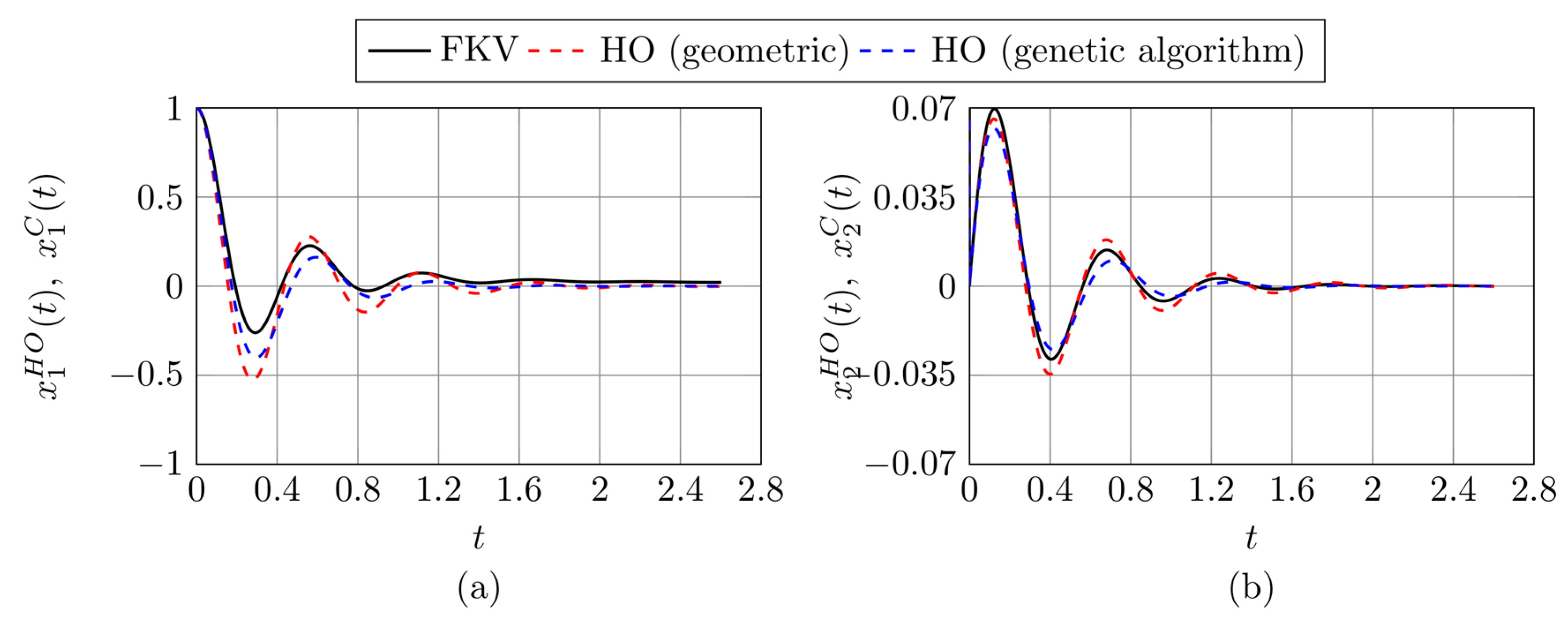
3.2. Results Based on the Proposed Identification Methods
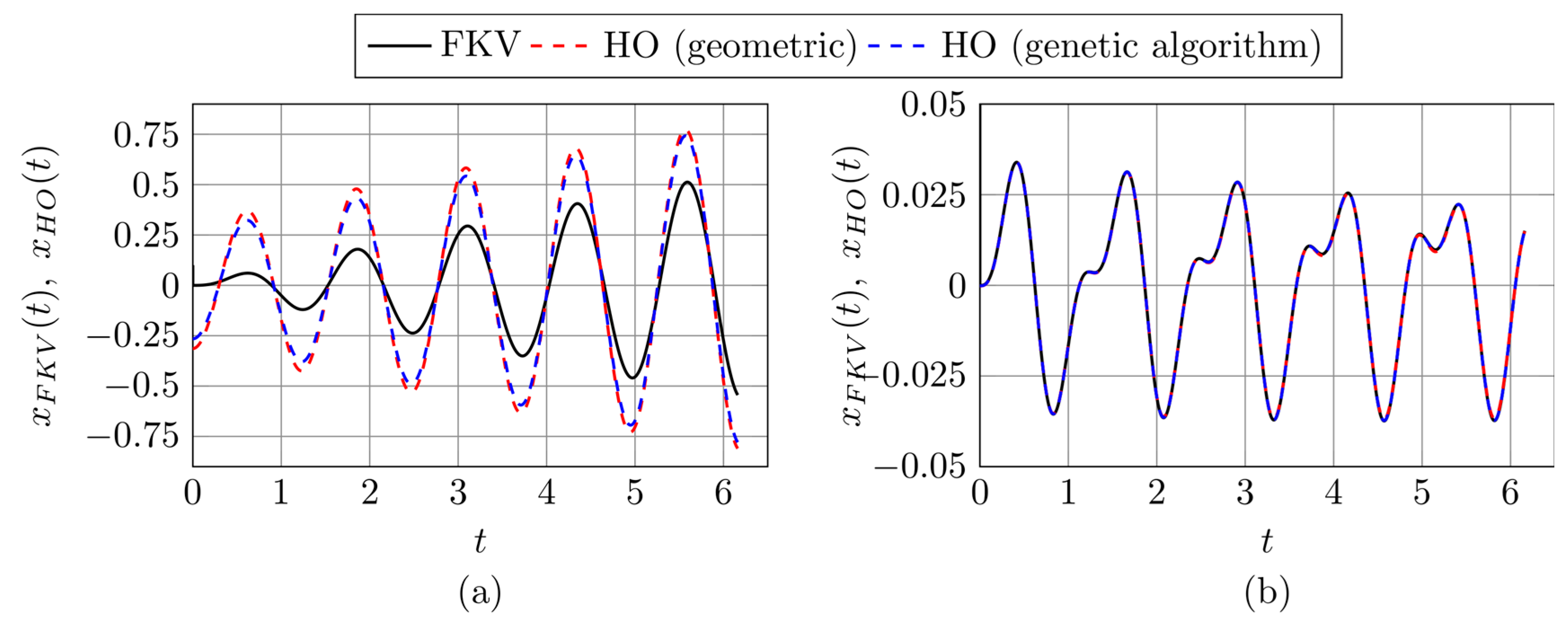
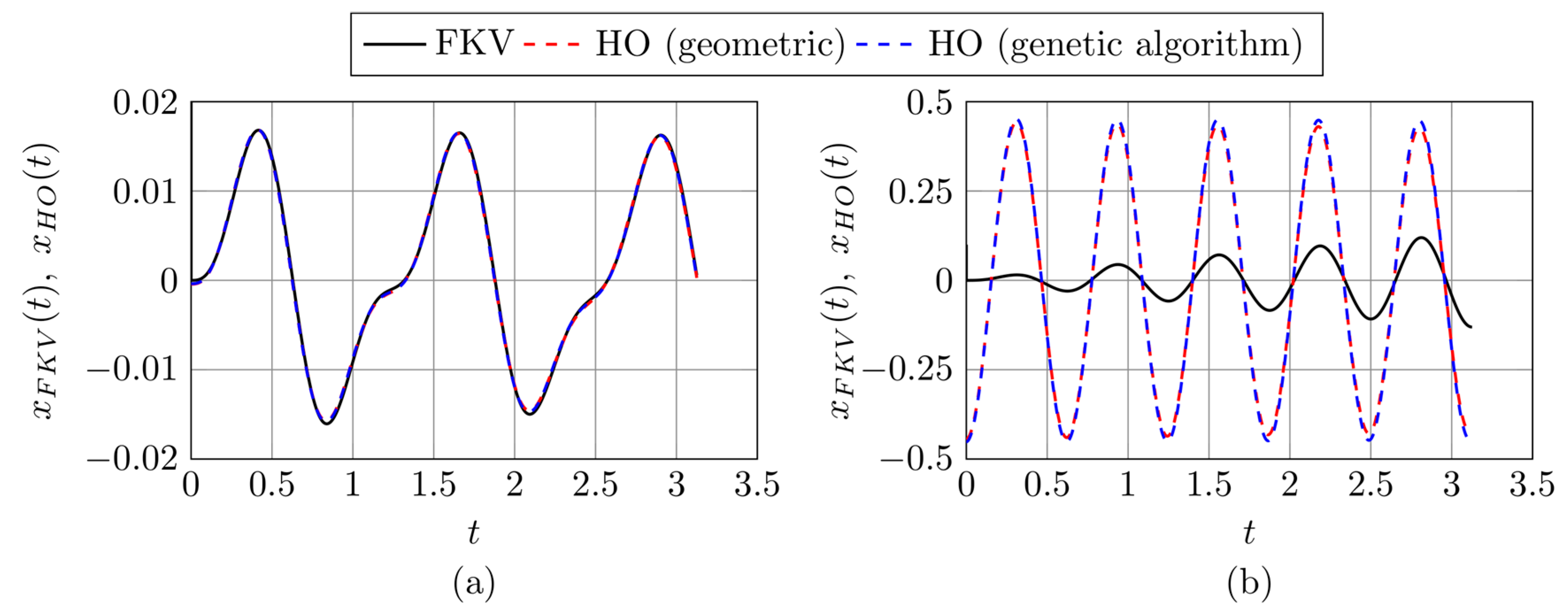
3.3. Testing Harmonic Models in the Nonhomogeneous Case
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FKV | Fractional Kelvin–Voigt |
| HO | Harmonic oscillator |
| RL | Riemann–Liouville (fractional derivative) |
| C | Caputo (fractional derivative) |
References
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9780470682548. [Google Scholar]
- Basson, M.; De Villiers, M.; Van Rensburg, N.F.J. Solvability of a Model for the Vibration of a Beam with a Damping Tip Body. J. Appl. Math. 2014, 2014, 298092. [Google Scholar] [CrossRef]
- Paunović, S.; Cajić, M.; Karličić, D.; Mijalković, M. A Novel Approach for Vibration Analysis of Fractional Viscoelastic Beams with Attached Masses and Base Excitation. J. Sound Vib. 2019, 463, 114955. [Google Scholar] [CrossRef]
- Freundlich, J. Transient Vibrations of a Fractional Kelvin-Voigt Viscoelastic Cantilever Beam with a Tip Mass and Subjected to a Base Excitation. J. Sound Vib. 2019, 438, 99–115. [Google Scholar] [CrossRef]
- Freundlich, J. Transient Vibrations of a Fractional Zener Viscoelastic Cantilever Beam with a Tip Mass. Meccanica 2021, 56, 1971–1988. [Google Scholar] [CrossRef]
- Xu, J.; Chen, N. A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory. Appl. Sci. 2025, 15, 2768. [Google Scholar] [CrossRef]
- Makkad, G.; Khalsa, L.; Yadav, A.K.; Varghese, V. Non-Local Fractional Thermoviscoelastic Bending Analysis of Non-Simple Nanobeam Under Ramp-Type Heating. J. Elast. 2025, 157, 28. [Google Scholar] [CrossRef]
- Cao, J.; Syta, A.; Litak, G.; Zhou, S.; Inman, D.J.; Chen, Y. Regular and Chaotic Vibration in a Piezoelectric Energy Harvester with Fractional Damping. Eur. Phys. J. Plus 2015, 130, 103. [Google Scholar] [CrossRef]
- Sengha, G.G.; Kenfack, W.F.; Bekoa, D.J.O.; Siewe, M.S.; Tabi, C.B.; Kofane, T.C. Fractional Properties’ Effects on a Hybrid Energy Harvesting System Dynamics. Meccanica 2021, 56, 2451–2469. [Google Scholar] [CrossRef]
- Kwuimy, C.A.K.; Litak, G.; Borowiec, M.; Nataraj, C. Fractional Dynamics of a Piezoelectric Energy Harvester with Nonlinear Magnetic Coupling. Appl. Phys. Lett. 2015, 106, 24103. [Google Scholar] [CrossRef]
- Zhou, Y.; Ionescu, C.; Tenreiro Machado, J.A. Fractional Dynamics and Its Applications. Nonlinear Dyn. 2015, 80, 1661–1664. [Google Scholar] [CrossRef]
- Agarwal, P.; Martínez, L.V.; Lenzi, E.K. Recent Trends in Fractional Calculus and Its Applications; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Hilfer, R.; Kleiner, T. Fractional Calculus for Distributions; Springer International Publishing: Berlin/Heidelberg, Germany, 2024; Volume 27, ISBN 1354002400306. [Google Scholar]
- Zhao, K.; Liu, J.; Lv, X. A Unified Approach to Solvability and Stability of Multipoint BVPs for Langevin and Sturm–Liouville Equations with CH–Fractional Derivatives and Impulses via Coincidence Theory. Fractal Fract. 2024, 8, 111. [Google Scholar] [CrossRef]
- Fasana, A.; Marchesiello, S. Rayleigh-Ritz Analysis of Sandwich Beams. J. Sound Vib. 2001, 241, 643–652. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010; ISBN 9781848163300. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. Application of Fractional Calculus for Dynamic Problems of Solid Mechanics: Novel Trends and Recent Results. Appl. Mech. Rev. 2010, 63, 010803. [Google Scholar] [CrossRef]
- Zhang, W.; Shimizu, N. Damping Properties of the Viscoelastic Material Described by Fractional Kelvin-Voigt Model. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1999, 42, 1–9. [Google Scholar] [CrossRef][Green Version]
- Rossikhin, Y.A.; Shitikova, M.V. Application of Fractional Derivatives to the Analysis of Damped Vibrations of Viscoelastic Single Mass Systems. Acta Mech. 1997, 120, 109–125. [Google Scholar] [CrossRef]
- Vaz, J.; de Oliveira, E.C. On the Fractional Kelvin-Voigt Oscillator. Math. Eng. 2022, 4, 1–23. [Google Scholar] [CrossRef]
- Cao, Q.; Hu, S.L.J.; Li, H. Frequency/Laplace Domain Methods for Computing Transient Responses of Fractional Oscillators. Nonlinear Dyn. 2022, 108, 1509–1523. [Google Scholar] [CrossRef]
- Kim, V.A.; Parovik, R.I. Application of the Explicit Euler Method for Numerical Analysis of a Nonlinear Fractional Oscillation Equation. Fractal Fract. 2022, 6, 274. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 129, ISBN 978-0-444-51832-3. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Volume 198: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198, ISBN 978-0125588409. [Google Scholar]
- Li, M. Three Classes of Fractional Oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, Y.; Liu, J.; Shi, B.; Gai, M.; Yang, S. Mechanical Energy and Equivalent Differential Equations of Motion for Single-Degree-of-Freedom Fractional Oscillators. J. Sound Vib. 2017, 397, 192–203. [Google Scholar] [CrossRef]
- Ding, W.; Hollkamp, J.P.; Patnaik, S.; Semperlotti, F. On the Fractional Homogenization of One-Dimensional Elastic Metamaterials with Viscoelastic Foundation. Arch. Appl. Mech. 2022, 93, 261–286. [Google Scholar] [CrossRef]
- Łabędzki, P.; Pawlikowski, R. On the Equivalence between Fractional and Classical Oscillators. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106871. [Google Scholar] [CrossRef]
- Wynn, P. On a Device for Computing the em(Sn) Transformation. Math. Tables Other Aids Comput. 1956, 10, 91–96. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781482253818. [Google Scholar]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Little, J.A.; Mann, B.P. Optimizing Logarithmic Decrement Damping Estimation through Uncertainty Propagation. J. Sound Vib. 2019, 457, 368–376. [Google Scholar] [CrossRef]
- Weaver, W., Jr.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 1976; ISBN 9780070542358. [Google Scholar]





| FKV Oscillator Parameters (µ, α, ω) | Geometric Approach | Genetic Algorithm |
|---|---|---|
| (1, 0.1, 5) | (5.115, 0.0043), 0.077 | (5.115, 0.0036), 0.079 |
| (1, 0.5, 5) | (5.158, 0.0032), 0.068 | (5.153, 0.0032), 0.067 |
| (1, 0.9, 5) | (5.052, 0.086), 0.019 | (5.056, 0.085), 0.015 |
| (1, 0.1, 10) | (10.062, 0.0018), 0.023 | (10.062, 0.0011), 0.021 |
| (1, 0.5, 10) | (10.111, 0.0126), 0.037 | (10.11, 0.0112), 0.026 |
| (1, 0.9, 10) | (10.055, 0.0041), 0.019 | (10.057, 0.0394), 0.009 |
| (5, 0.1, 10) | (10.307, 0.0055), 0.102 | (10.057, 0.0048), 0.104 |
| (5, 0.9, 10) | (10.267, 0.1895), 0.048 | (10.235, 0.1989), 0.032 |
| (10, 0.9, 10) | (10.581, 0.34), 0.124 | (10.35, 0.393), 0.065 |
| (12, 0.7, 10) | (11.512, 0.2), 0.279 | (11.08, 0.2785), 0.147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łabędzki, P. Fractional Kelvin–Voigt Model for Beam Vibrations: Numerical Simulations and Approximation Using a Classical Model. Electronics 2025, 14, 1918. https://doi.org/10.3390/electronics14101918
Łabędzki P. Fractional Kelvin–Voigt Model for Beam Vibrations: Numerical Simulations and Approximation Using a Classical Model. Electronics. 2025; 14(10):1918. https://doi.org/10.3390/electronics14101918
Chicago/Turabian StyleŁabędzki, Paweł. 2025. "Fractional Kelvin–Voigt Model for Beam Vibrations: Numerical Simulations and Approximation Using a Classical Model" Electronics 14, no. 10: 1918. https://doi.org/10.3390/electronics14101918
APA StyleŁabędzki, P. (2025). Fractional Kelvin–Voigt Model for Beam Vibrations: Numerical Simulations and Approximation Using a Classical Model. Electronics, 14(10), 1918. https://doi.org/10.3390/electronics14101918






