Whole-Body Control with Uneven Terrain Adaptability Strategy for Wheeled-Bipedal Robots
Abstract
1. Introduction
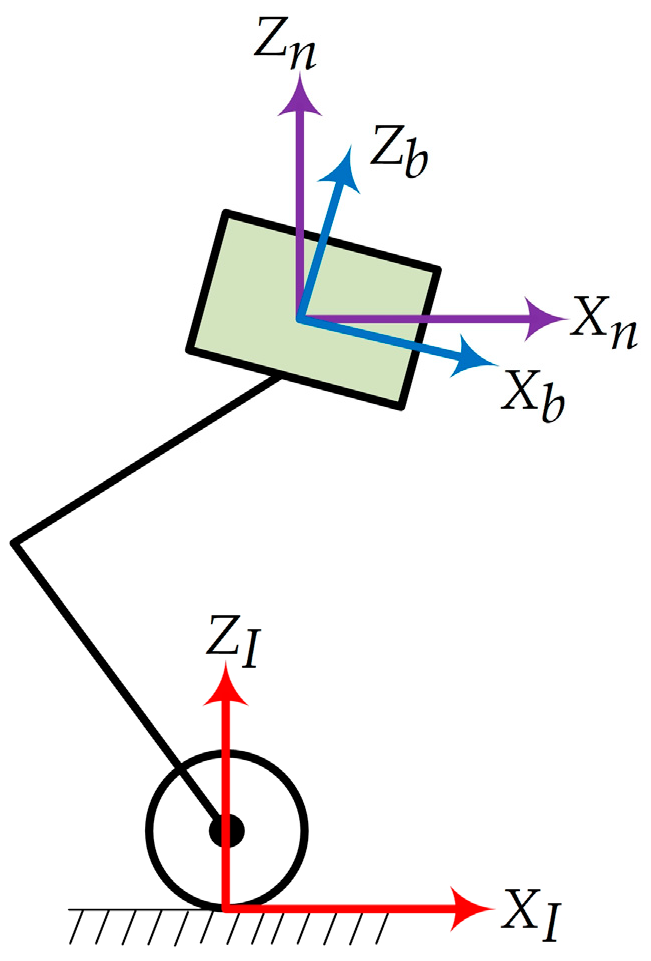
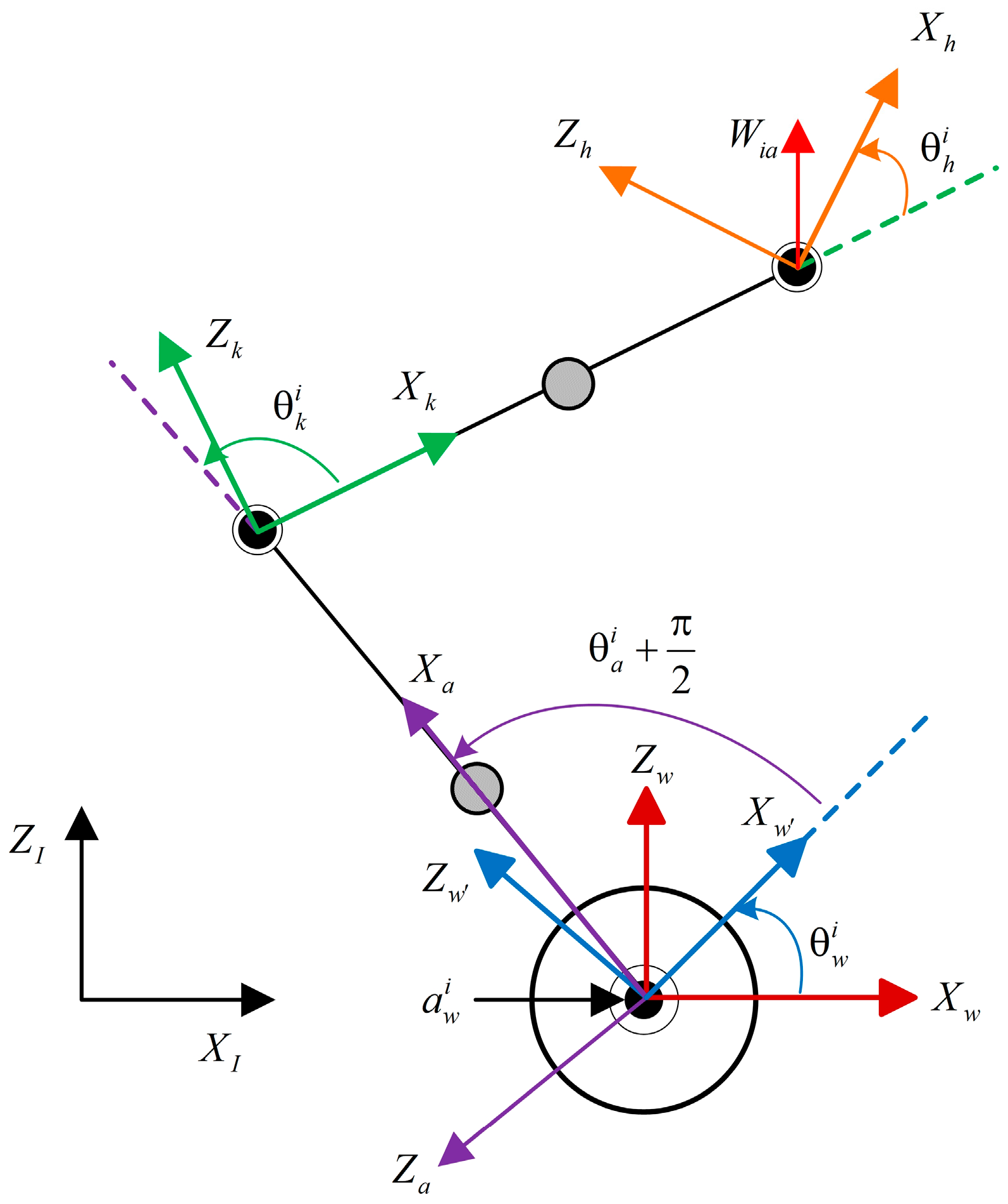
2. Robot Basic Information
3. Dynamical Modeling
3.1. Single Rigid-Body Model of Torso
3.2. Wheeled Leg Integration Model
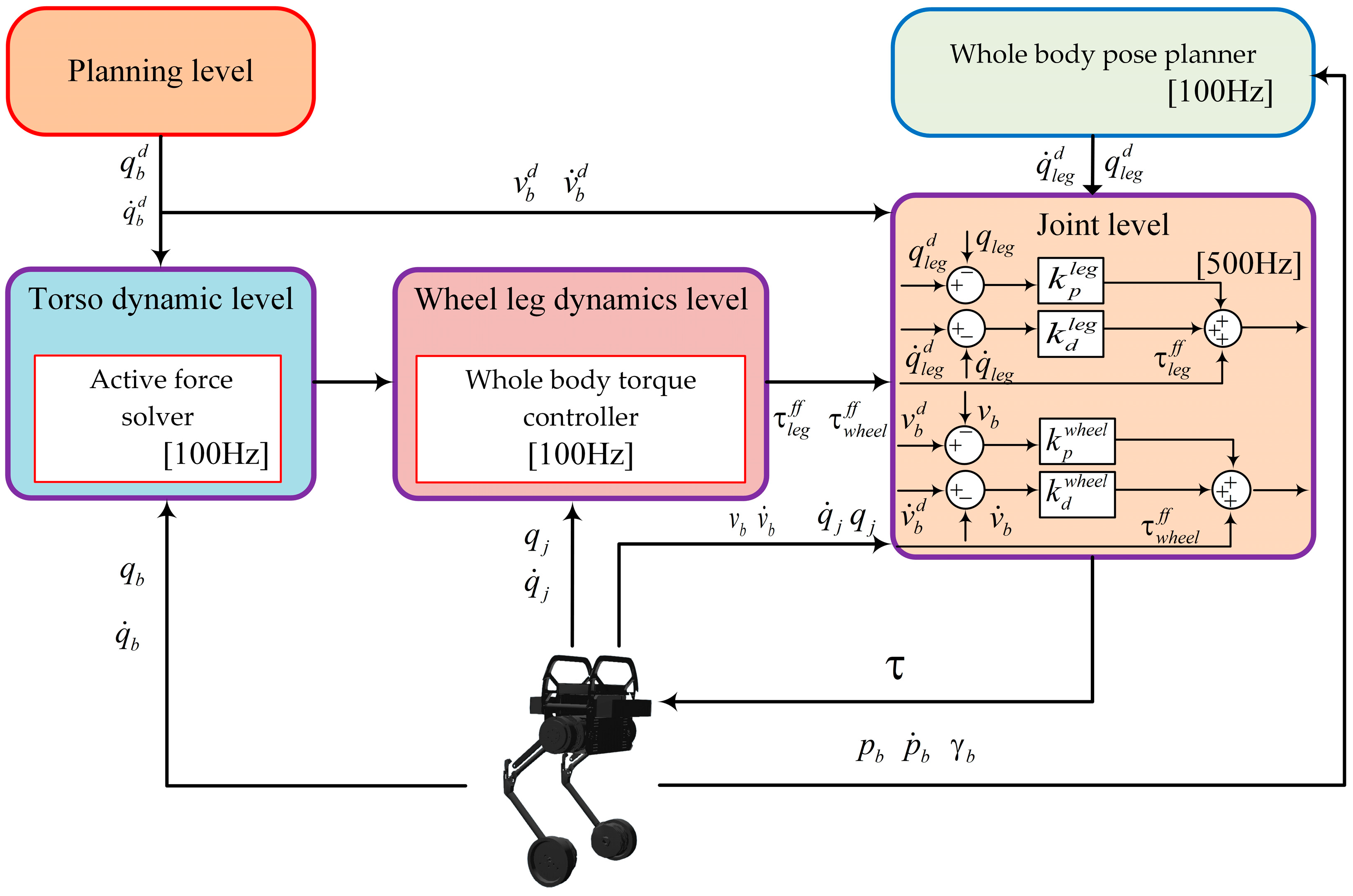
4. Control Framework Construction
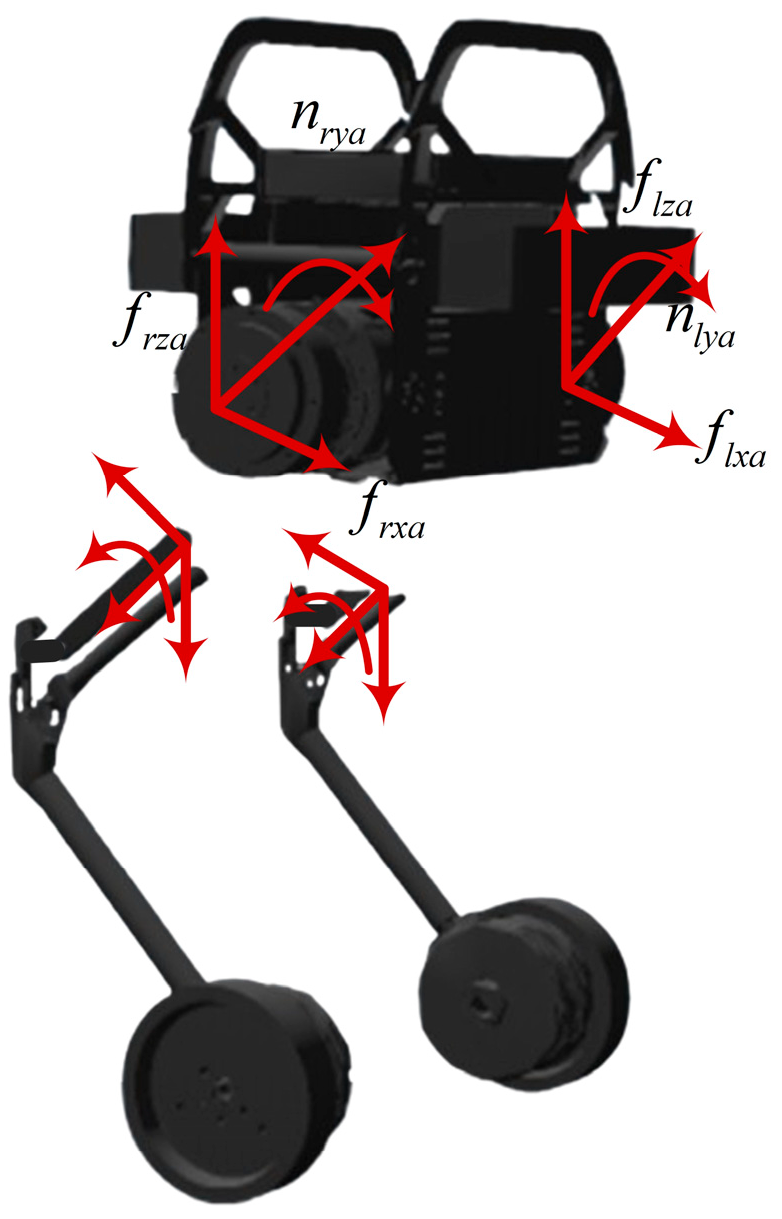
4.1. Active Force Solver Based on Model Predictive Control
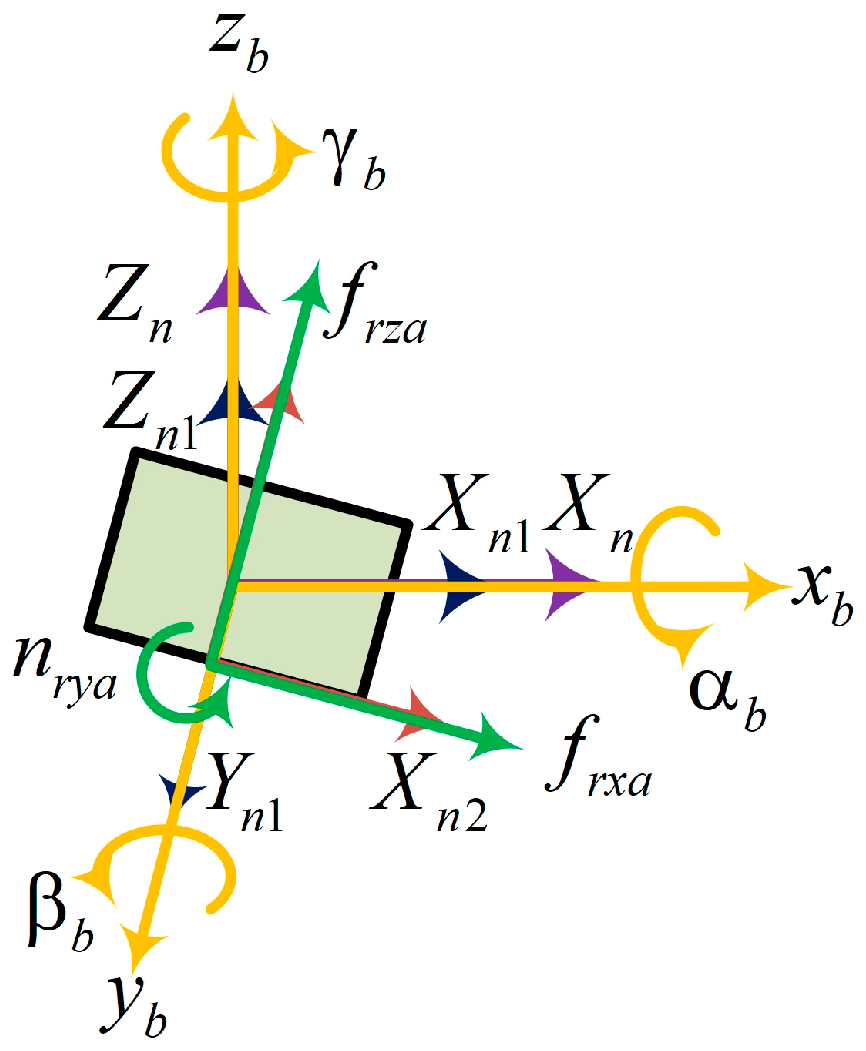
4.2. Whole-Body Pose Planner with Terrain Adaptability Strategy
4.3. Whole-Body Torque Controller
5. Simulation Experiment
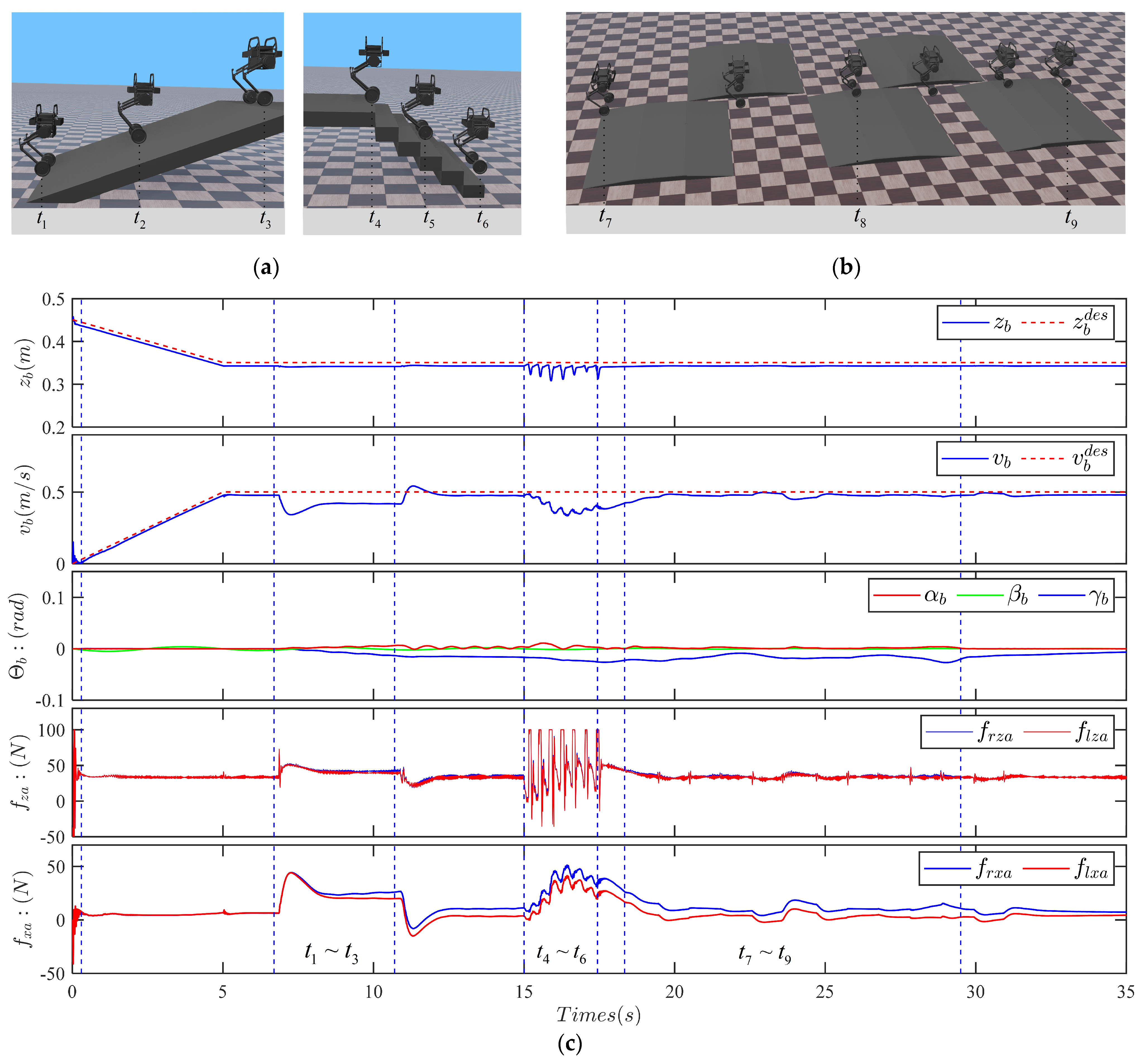
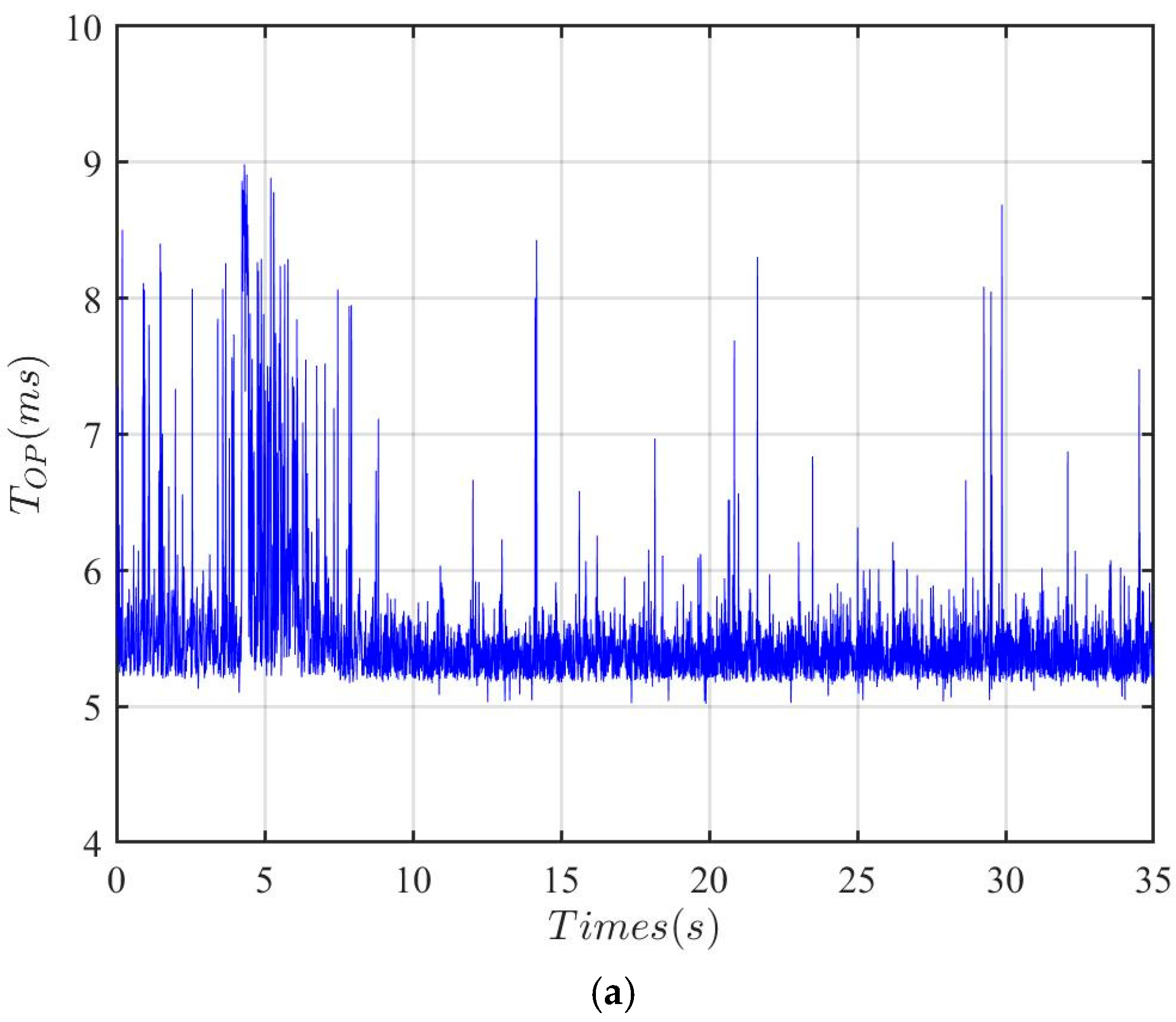
5.1. Going Uphill, Going Down Stairs and Crossing One-Sided Bridges
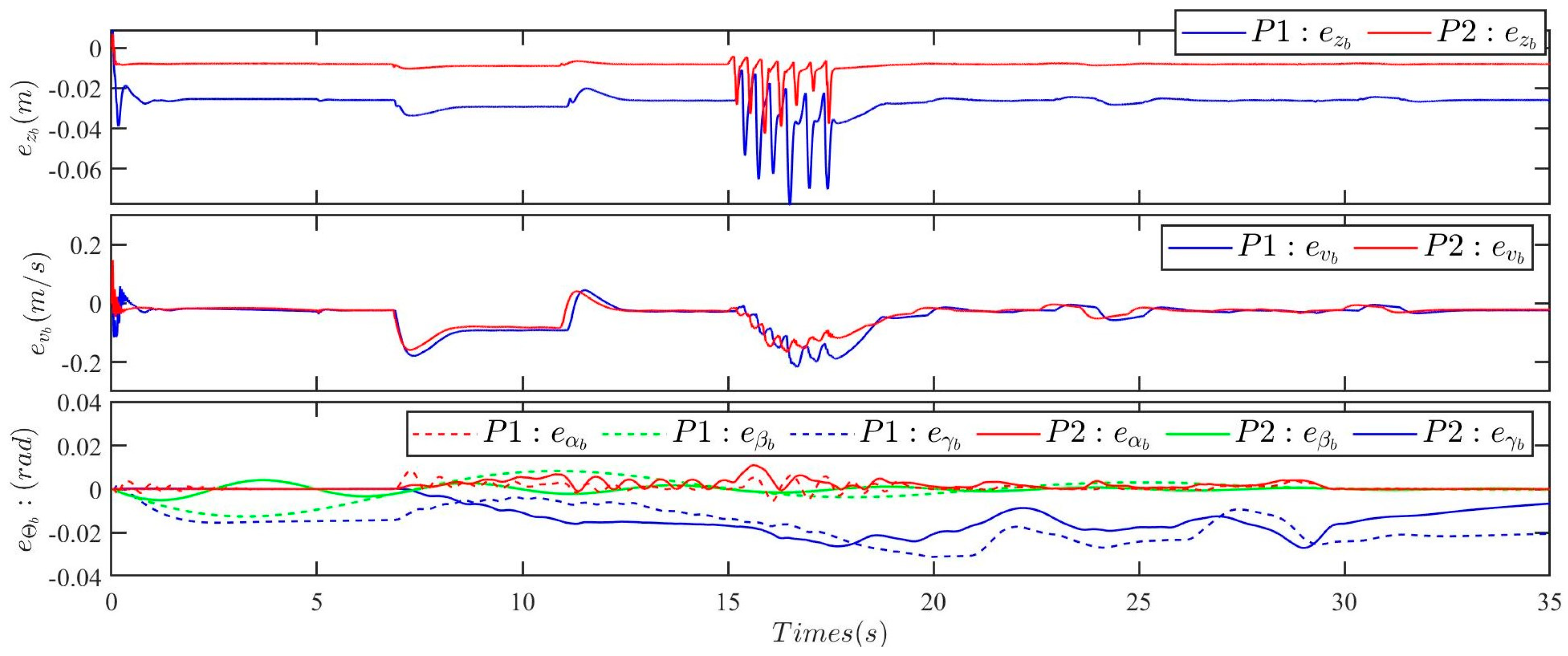
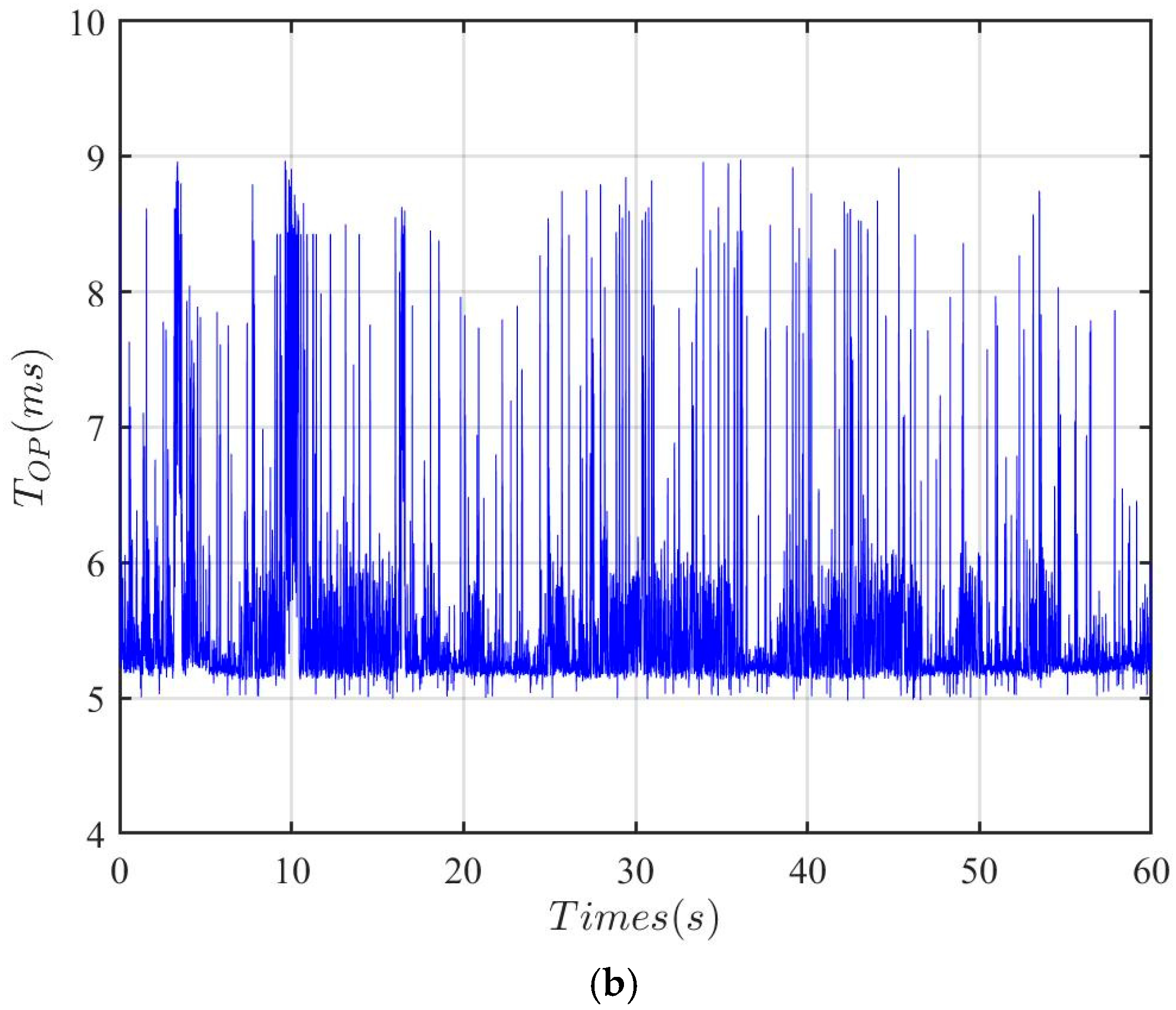
5.2. Simulation Experiments on Uneven Terrain
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hougen, D.F.; Benjaafar, S.; Bonney, J.C.; Budenske, J.R.; Dvorak, M.; Gini, M.; French, H.; Krantz, D.G.; Li, P.Y.; Malver, F.; et al. A miniature robotic system for reconnaissance and surveillance. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 501–507. [Google Scholar] [CrossRef]
- Pedro, G.D.G.; Bermudez, G.; Medeiros, V.S.; Cruz Neto, H.J.d.; Barros, L.G.D.d.; Pessin, G.; Becker, M.; Freitas, G.M.; Boaventura, T. Quadruped Robot Control: An Approach Using Body Planar Motion Control, Legs Impedance Control and Bézier Curves. Sensors 2024, 24, 3825. [Google Scholar] [CrossRef] [PubMed]
- Bruzzone, L.; Quaglia, G. Locomotion systems for ground mobile robots in unstructured environments. Mech. Sci. 2012, 3, 49–62. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, C.; Song, S.; Meng, M.Q.H. Dynamic height balance control for bipedal wheeled robot based on ROS-Gazebo. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; IEEE: New York, NY, USA, 2019; pp. 1875–1880. [Google Scholar] [CrossRef]
- Bellicoso, C.D.; Jenelten, F.; Fankhauser, P.; Gehring, C.; Hwangbo, J.; Hutter, M. Dynamic locomotion and whole-body control for quadrupedal robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: New York, NY, USA, 2017; pp. 3359–3365. [Google Scholar] [CrossRef]
- Liu, X.; Yang, L.; Chen, Z.; Zhong, J.; Gao, F. Motion Planning for a Legged Robot with Dynamic Characteristics. Sensors 2024, 24, 6070. [Google Scholar] [CrossRef] [PubMed]
- Fahmi, S.; Mastalli, C.; Focchi, M.; Semini, C. Passive whole-body control for quadruped robots: Experimental validation over challenging terrain. IEEE Robot. Autom. Lett. 2019, 4, 2553–2560. [Google Scholar] [CrossRef]
- Chen, T.; Sun, X.; Xu, Z.; Li, Y.; Rong, X.; Zhou, L. A trot and flying trot control method for quadruped robot based on optimal foot force distribution. J. Bionic Eng. 2019, 16, 621–632. [Google Scholar] [CrossRef]
- Faigl, J.; Čížek, P. Adaptive locomotion control of hexapod walking robot for traversing rough terrains with position feedback only. Robot. Auton. Syst. 2019, 116, 136–147. [Google Scholar] [CrossRef]
- Khadiv, M.; Herzog, A.; Moosavian, S.A.A.; Righetti, L. Walking control based on step timing adaptation. IEEE Trans. Robot. 2020, 36, 629–643. [Google Scholar] [CrossRef]
- Hutter, M.; Sommer, H.; Gehring, C.; Hoepflinger, M.; Bloesch, M.; Siegwart, R. Quadrupedal locomotion using hierarchical operational space control. Int. J. Robot. Res. 2014, 33, 1047–1062. [Google Scholar] [CrossRef]
- Stilman, M.; Wang, J.; Teeyapan, K.; Marceau, R. Optimized control strategies for wheeled humanoids and mobile manipulators. In Proceedings of the 2009 9th IEEE-RAS International Conference on Humanoid Robots, Paris, France, 7–10 December 2009; IEEE: New York, NY, USA, 2009; pp. 568–573. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, Z.; Han, L.; Chen, X.; Qiu, X.; Huang, Q. Compliant Motion Control of Wheel-Legged Humanoid Robot on Rough Terrains. IEEE/ASME Trans. Mechatron. 2023, 29, 1949–1959. [Google Scholar] [CrossRef]
- Li, X.; Fu, Y. Design and Experimental Evaluation of WLR-III. In Proceedings of the 2023 IEEE International Conference on Robotics and Biomimetics (ROBIO), Koh Samui, Thailand, 4–9 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Zhou, H.; Feng, H.; Fu, Y. Locomotion adaption for hydraulic humanoid wheel-legged robots over rough terrains. Int. J. Humanoid Robot. 2021, 18, 2150001. [Google Scholar] [CrossRef]
- Zhou, H.; Li, X.; Feng, H.; Li, J.; Zhang, S.; Fu, Y. Model decoupling and control of the wheeled humanoid robot moving in sagittal plane. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Li, X.; Zhou, H.; Zhang, S.; Feng, H.; Fu, Y. WLR-II, a hose-less hydraulic wheel-legged robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: New York, NY, USA, 2019; pp. 4339–4346. [Google Scholar] [CrossRef]
- Li, X.; Zhou, H.; Feng, H.; Zhang, S.; Fu, Y. Design and experiments of a novel hydraulic wheel-legged robot (WLR). In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: New York, NY, USA, 2018; pp. 3292–3297. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Salzmann, C.; Tschopp, F.; Bodie, K.; Gulich, L.; Küng, N.; Mannhart, D.; Pfister, C.; Vierneisel, M.; et al. Ascento: A two-wheeled jumping robot. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: New York, NY, USA, 2019; pp. 7515–7521. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Gulich, L.; Mannhart, D.; Rohr, D.; Kamel, M.; de Viragh, Y.; Siegwart, R. LQR-assisted whole-body control of a wheeled bipedal robot with kinematic loops. IEEE Robot. Autom. Lett. 2020, 5, 3745–3752. [Google Scholar] [CrossRef]
- Xin, S.; Vijayakumar, S. Online dynamic motion planning and control for wheeled biped robots. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; IEEE: New York, NY, USA, 2020; pp. 3892–3899. [Google Scholar] [CrossRef]
- Cao, H.; Lu, B.; Liu, H.; Liu, R.; Guo, X. Modeling and MPC-based balance control for a wheeled bipedal robot. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: New York, NY, USA, 2022; pp. 420–425. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Wang, H.; Lai, J.; Bing, Z.; Jiang, Y.; Zheng, Y.; Zhang, Z. An adaptive approach to whole-body balance control of wheel-bipedal robot Ollie. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: New York, NY, USA, 2022; pp. 12835–12842. [Google Scholar] [CrossRef]
- Chen, Z.; Zhan, G.; Jiang, Z.; Zhang, W.; Rao, Z.; Wang, H.; Li, J. Adaptive impedance control for docking robot via Stewart parallel mechanism. ISA Trans. 2024, 155, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Chen, Z.; Deng, C.; Wang, S.; Wang, J. LCDL: Towards Dynamic Localization for Autonomous Landing of Unmanned Aerial Vehicle Based on LiDAR-Camera Fusion. IEEE Sens. J. 2024, 24, 26407–26415. [Google Scholar] [CrossRef]
- Abbasimoshaei, A.; Stein, T.; Rothe, T.; Kern, T.A. Design and impedance control of a hydraulic robot for paralyzed people. In Proceedings of the 8th RSI International Conference on Robotics and Mechatronics, ICRoM 2020, Virtual, Online, 19 November 2020. [Google Scholar]
- Wei, Z.; Deng, W.; Feng, Z.; Wang, T.; Huang, X. An MPC-DCM Control Method for a Forward-Bending Biped Robot Based on Force and Moment Control. Electronics 2024, 13, 4374. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, M.; Zhang, T.; Ji, A. A Rigid–Flexible Supernumerary Robotic Arm/Leg: Design, Modeling, and Control. Electronics 2024, 13, 4106. [Google Scholar] [CrossRef]
- Xin, Y.; Chai, H.; Li, Y.; Rong, X.; Li, B.; Li, Y. Speed and acceleration control for a two wheel-leg robot based on distributed dynamic model and whole-body control. IEEE Access 2019, 7, 180630–180639. [Google Scholar] [CrossRef]
- Xin, Y.; Rong, X.; Li, Y.; Li, B.; Chai, H. Movements and balance control of a wheel-leg robot based on uncertainty and disturbance estimation method. IEEE Access 2019, 7, 133265–133273. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, T.; Rong, X.; Zhang, G.; Li, Y.; Xin, Y. Design and Control of SKATER: A Wheeled-Bipedal Robot With High-Speed Turning Robustness and Terrain Adaptability. IEEE/ASME Trans. Mechatron. 2024, 1–12. [Google Scholar] [CrossRef]




| Component Name | Parameter Name | Parameter Values | Parameter Name | Parameter Values |
|---|---|---|---|---|
| Thigh | 0.21 m | 1 kg | ||
| Calf | 0.24 m | 0.73 kg | ||
| Wheel | 0.04 m | 0.59 kg |
| Component Name | Maximum Torque | Joint Range of Motion |
|---|---|---|
| Hip motors | [−0.2 rad, 1 rad] | |
| Knee motors | [−2.1 rad, −1 rad] | |
| Wheel joint motors | —— |
| Sensor Position | Sensor Type |
|---|---|
| Skater-I center of mass position Hip position | IMU sensors Position sensor |
| Knee position | Position sensor |
| Ankle position | Position sensor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Xin, Y.; Chen, C.; Song, Z.; Sun, B.; Guo, T. Whole-Body Control with Uneven Terrain Adaptability Strategy for Wheeled-Bipedal Robots. Electronics 2025, 14, 198. https://doi.org/10.3390/electronics14010198
Wang B, Xin Y, Chen C, Song Z, Sun B, Guo T. Whole-Body Control with Uneven Terrain Adaptability Strategy for Wheeled-Bipedal Robots. Electronics. 2025; 14(1):198. https://doi.org/10.3390/electronics14010198
Chicago/Turabian StyleWang, Biao, Yaxian Xin, Chao Chen, Zihao Song, Baoshuai Sun, and Tianshuai Guo. 2025. "Whole-Body Control with Uneven Terrain Adaptability Strategy for Wheeled-Bipedal Robots" Electronics 14, no. 1: 198. https://doi.org/10.3390/electronics14010198
APA StyleWang, B., Xin, Y., Chen, C., Song, Z., Sun, B., & Guo, T. (2025). Whole-Body Control with Uneven Terrain Adaptability Strategy for Wheeled-Bipedal Robots. Electronics, 14(1), 198. https://doi.org/10.3390/electronics14010198






