Heterogeneous Multi-Agent Risk-Aware Graph Encoder with Continuous Parameterized Decoder for Autonomous Driving Trajectory Prediction
Abstract
1. Introduction
- Heterogeneous Multi-agent Risk-aware Graph Attention Encoder: By computing agent risk assessment attributes and map these features to a graph structure, the graph built by graph optimization and clustering method. These edge and node features are then processed through a node attention mechanism to model complex agent interactions, enhancing trajectory prediction accuracy and robustness.
- Low-Rank Temporal Transformer: We introduced a low-rank temporal transformer layer to reduce computational complexity and maintain accuracy, improving robustness in dynamic environments.
- Continuous Parameterized Trajectory Prediction Decoder: We proposed a continuous parameterized trajectory decoder, generating control points influenced by an adaptive knot vector, enabling precise trajectory predictions and handling sudden motion changes effectively.
2. Related Works
2.1. Homogeneous Graph Interaction in Trajectory Prediction
2.2. Risk Assessment in Trajectory Forecasting
2.3. Trajectory Representation for Trajectory Forecasting
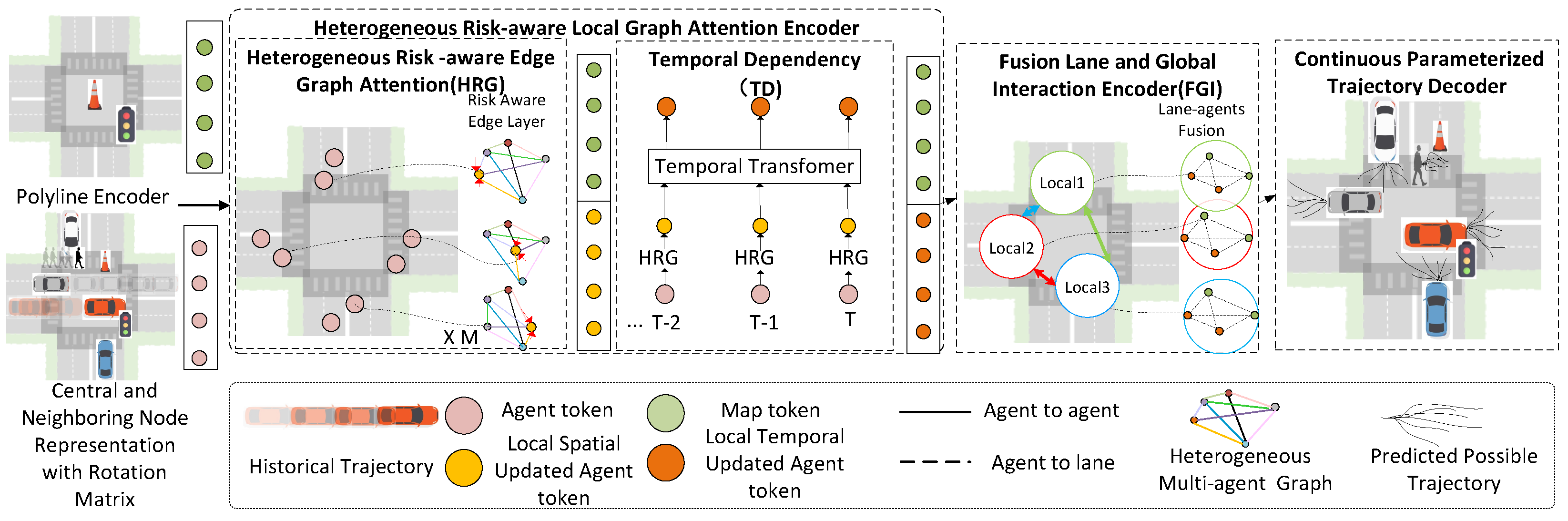
3. Methods
3.1. Problem Formulation and Approach Overview
- Section 3.2: Central and neighboring node representation.
- Section 3.3: Heterogeneous risk-aware local graph attention encoder with low-rank temporal transformer.
- Section 3.4: Fusion lane and global interaction encoder.
- Section 3.5: Continuous parameterized trajectory prediction decoder.
3.2. Central and Neighboring Node Representation
3.3. Heterogeneous Risk-Aware Local Graph Attention Encoder
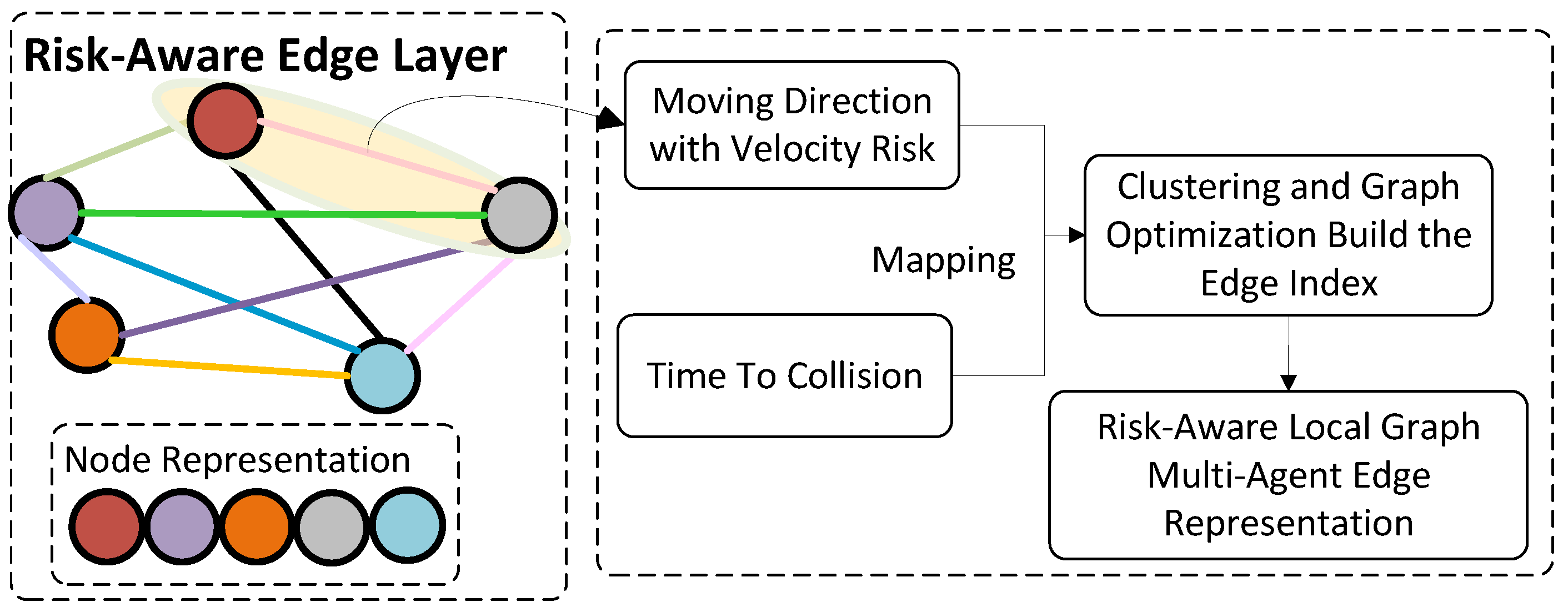
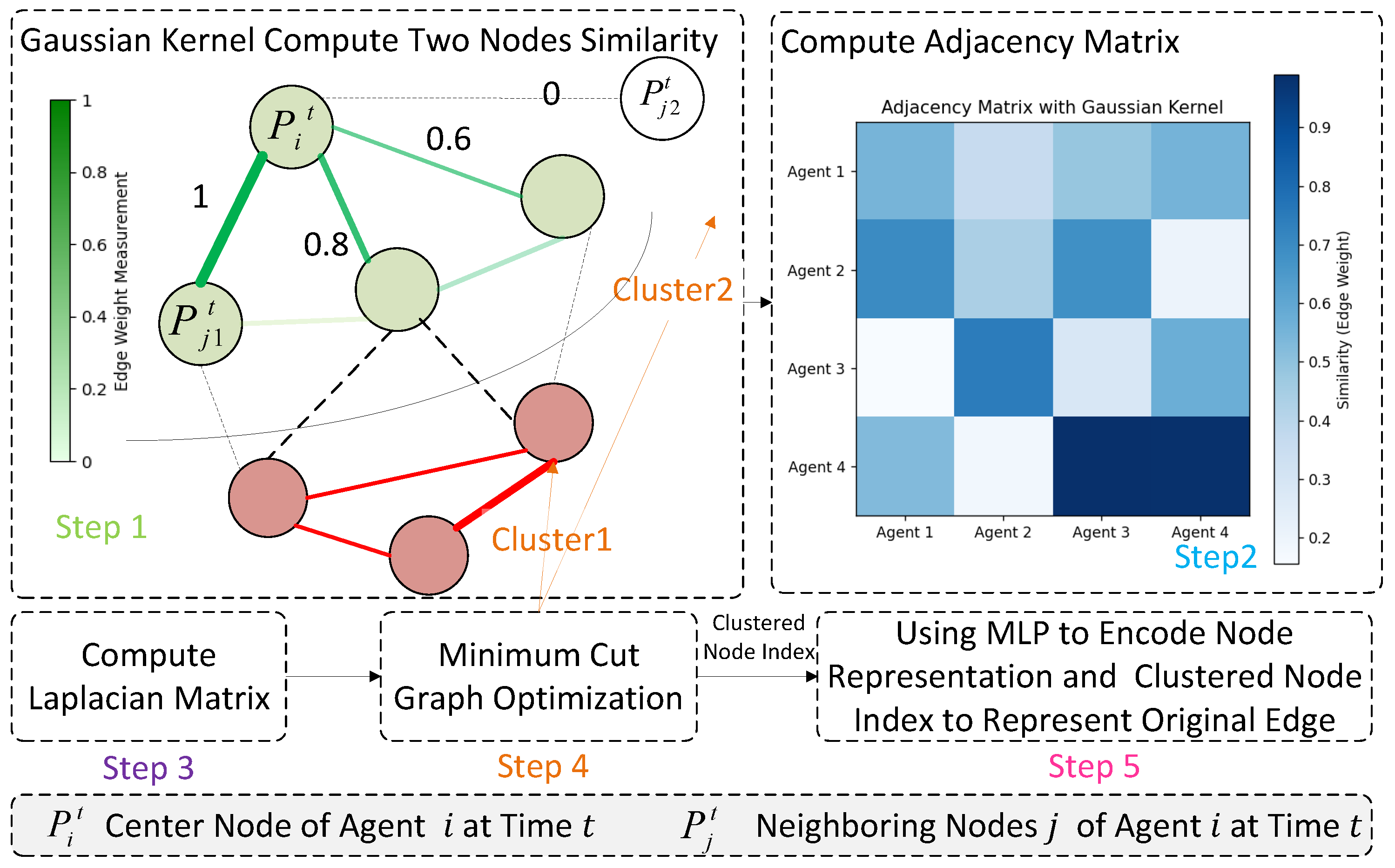
3.3.1. Risk-Aware Edge Layer
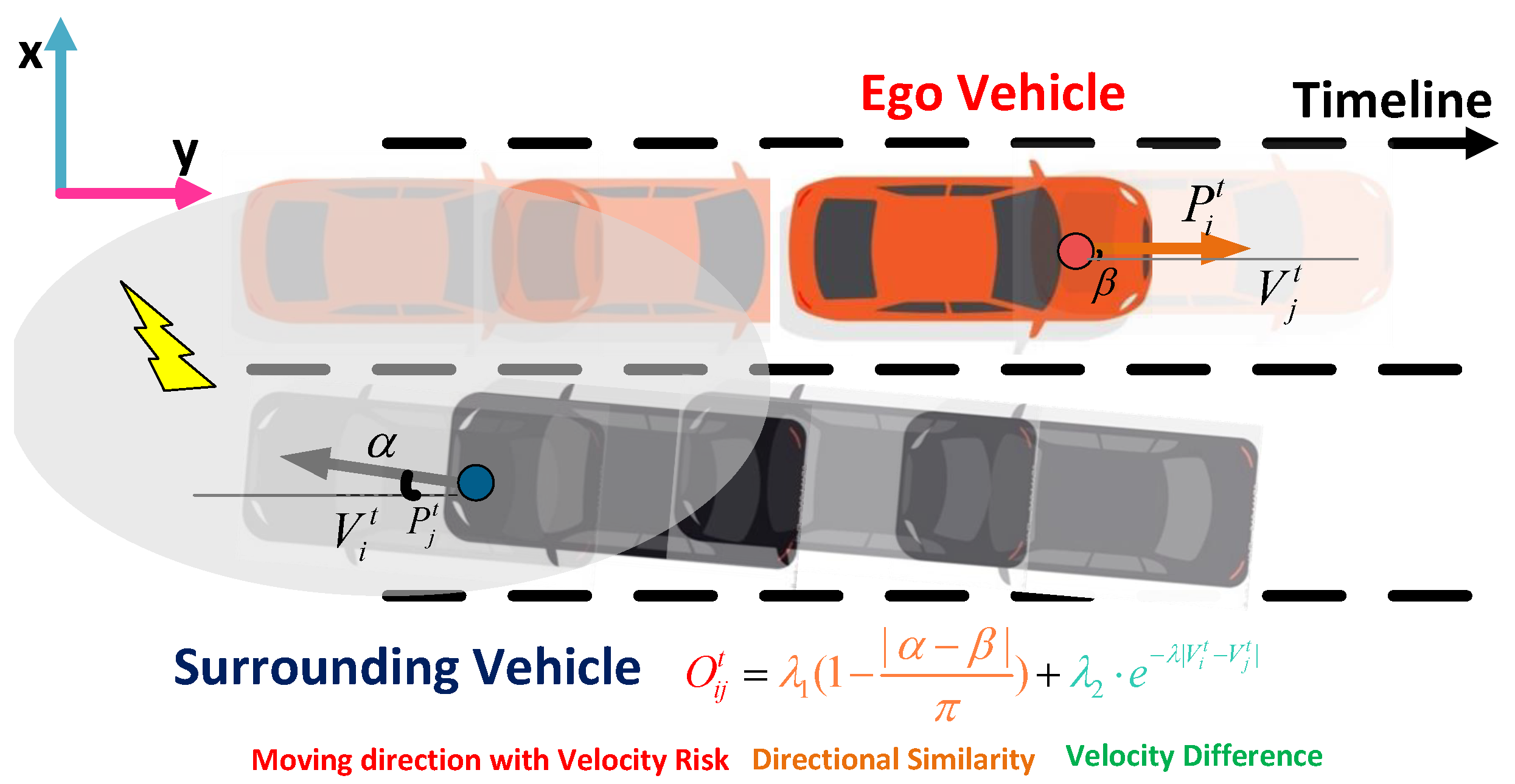
Moving Direction with Velocity Risk
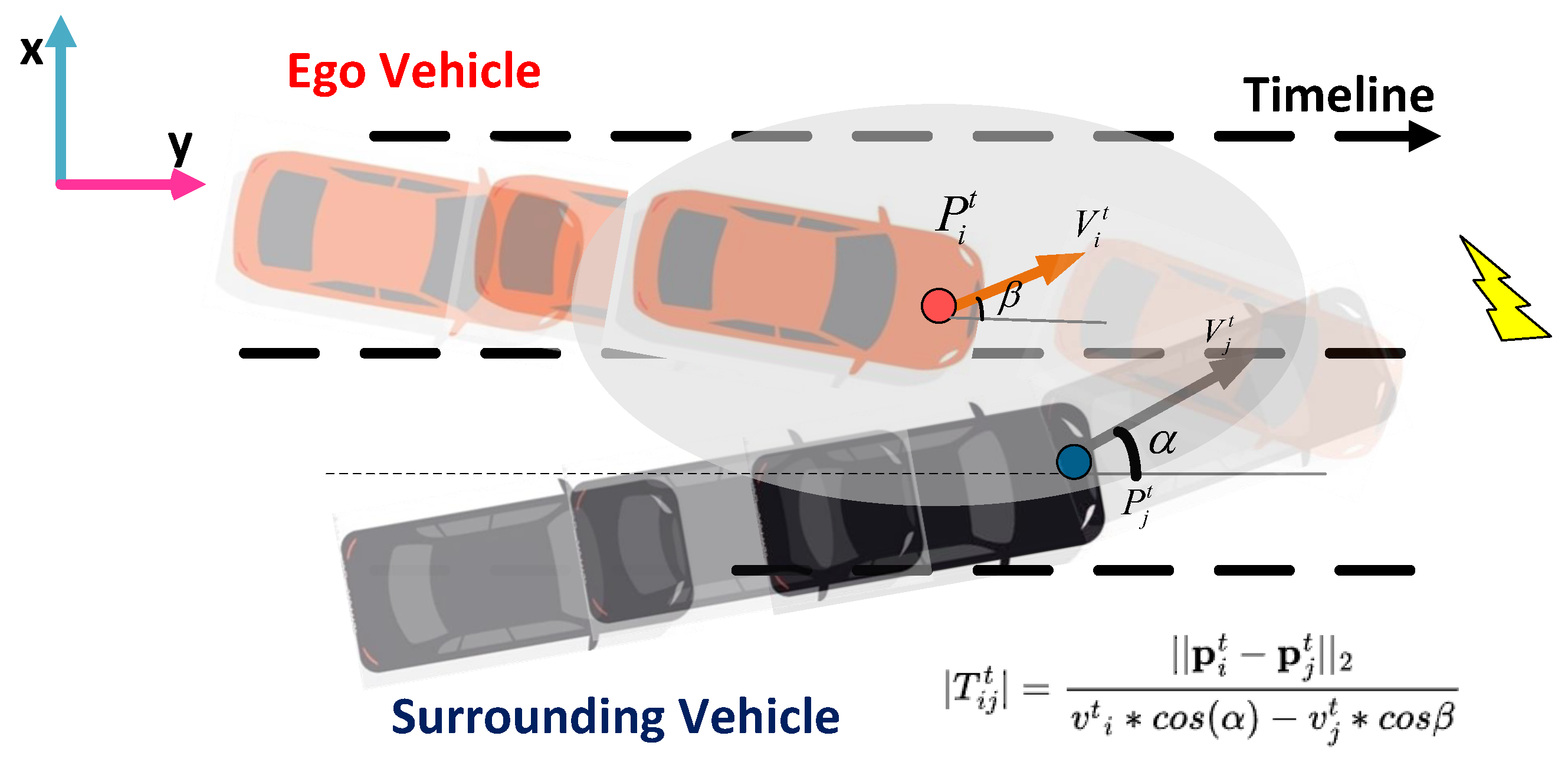
Time to Collision
Edge Index via Graph Optimization and Clustering
3.3.2. Risk-Aware Edge Graph Attention
3.3.3. Low-Rank Temporal Transformer
Singular Value Decomposition
Low-Rank Approximation for K and V
Attention Computation with Low-Rank Q, K, V
3.4. Fusion Lane and Global Interaction Encoder
3.5. Continuous Parameterized Trajectory Decoder
3.5.1. B-Spline Curve
B-Spline Representation
B-Spline Basis Function
3.5.2. Knot Vector Adaptation
Knot Vector Adaption
- is the new knot vector value at the j-th position;
- is a scaling factor that controls the adjustment magnitude;
- is the velocity of the trajectory at point v;
- is the curvature of the trajectory at point v;
- is a weight parameter that controls the influence of curvature on the adjustment.
3.5.3. Predicted Trajectory Matrix
4. Expertiments
4.1. Experiments Setup
4.1.1. Datasets
4.1.2. Evaluation Metrics
Minimum Average Displacement Error (minADE)
Minimum Final Displacement Error (minFDE)
Miss Rate (MR)
4.1.3. Implementation Details
4.2. Ablation Studies
4.2.1. Ablation Studies on Each Encoder Component
4.2.2. Ablation Study of Decoder Variants with Continuous Trajectory Decoder
4.3. Results
4.3.1. Comparison with State-of-the-Art
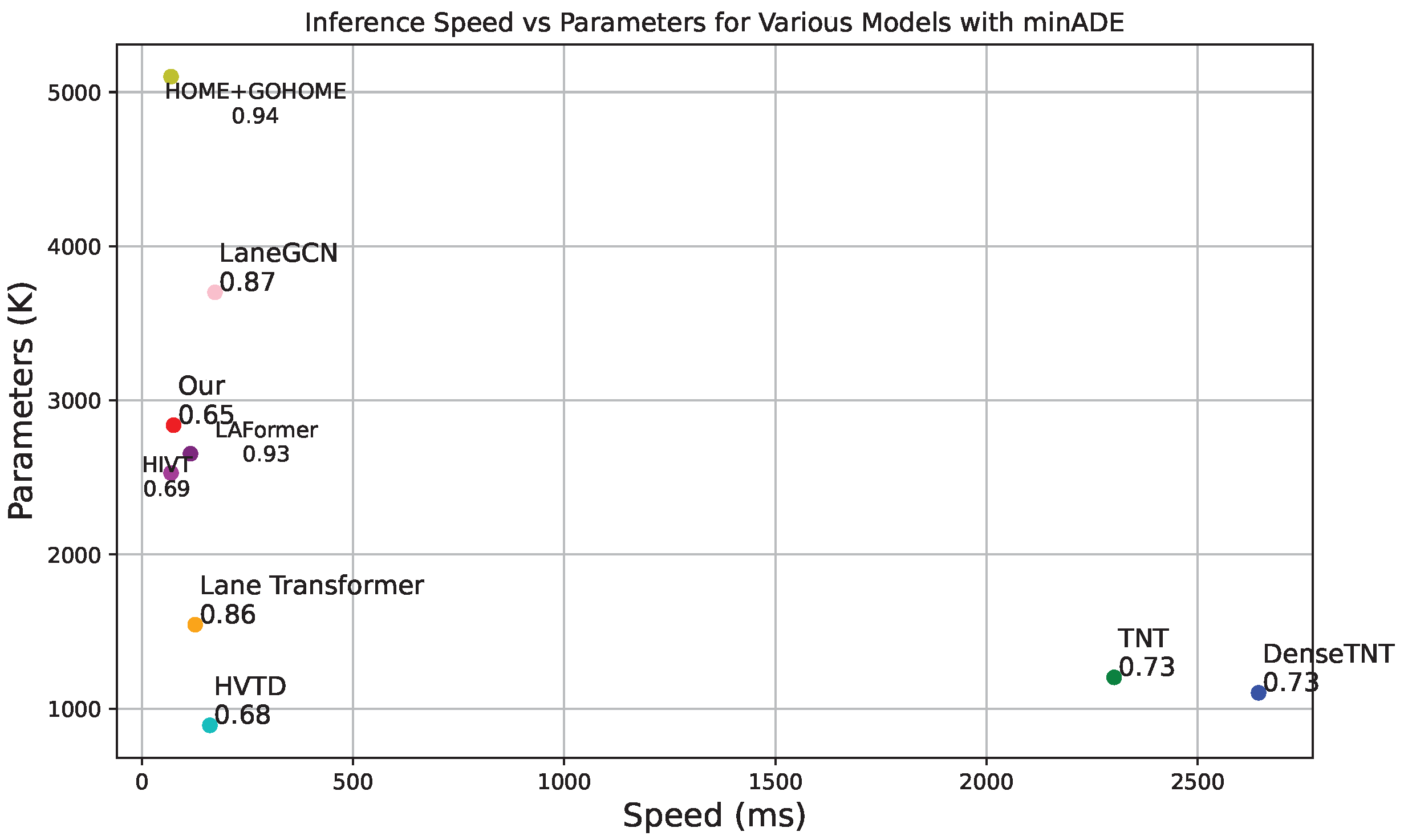
4.3.2. Inference Speed
4.3.3. Visualization
Intersection Successful Case
Continuous Parameterized Trajectory Prediction Performance Analysis
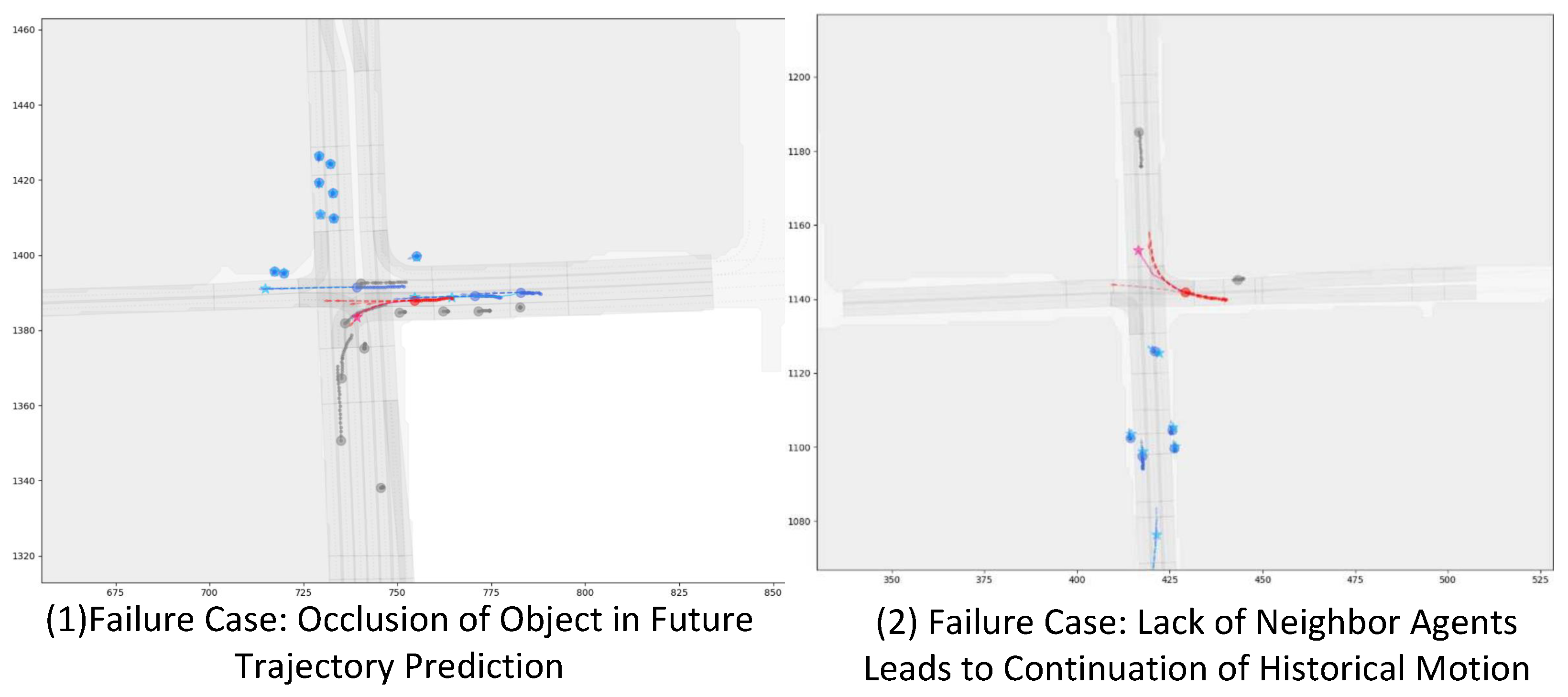
Failure Case
5. Conclusions
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, S.; Shi, C.; Wang, C.; Zhou, Q.; Sun, R.; Xiao, B.; Ding, Y.; Xi, G. Intra-Frame Graph Structure and Inter-Frame Bipartite Graph Matching with ReID-Based Occlusion Resilience for Point Cloud Multi-Object Tracking. Electronics 2024, 13, 2968. [Google Scholar] [CrossRef]
- Sun, S.; Shi, C.; Wang, C.; Liu, X. A Novel Adaptive Graph Transformer For Point Cloud Object Detection. In Proceedings of the 2023 7th International Conference on Communication and Information Systems (ICCIS), Chongqing, China, 20–22 October 2023; pp. 151–155. [Google Scholar]
- Sun, S.; Wang, C.; Liu, X.; Shi, C.; Ding, Y.; Xi, G. Spatio-Temporal Bi-directional Cross-frame Memory for Distractor Filtering Point Cloud Single Object Tracking. arXiv 2024, arXiv:2403.15831. [Google Scholar]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16. Springer: Cham, Switzerland, 2020; pp. 683–700. [Google Scholar]
- Mo, X.; Huang, Z.; Xing, Y.; Lv, C. Multi-agent trajectory prediction with heterogeneous edge-enhanced graph attention network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9554–9567. [Google Scholar] [CrossRef]
- Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. Vectornet: Encoding hd maps and agent dynamics from vectorized representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11525–11533. [Google Scholar]
- Zhao, H.; Gao, J.; Lan, T.; Sun, C.; Sapp, B.; Varadarajan, B.; Shen, Y.; Shen, Y.; Chai, Y.; Schmid, C.; et al. Tnt: Target-driven trajectory prediction. In Proceedings of the Conference on Robot Learning, Cambridge, MA, USA, 8–11 November 2021; pp. 895–904. [Google Scholar]
- Gu, J.; Sun, C.; Zhao, H. Densetnt: End-to-end trajectory prediction from dense goal sets. In Proceedings of the the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 15303–15312. [Google Scholar]
- Liang, M.; Yang, B.; Hu, R.; Chen, Y.; Liao, R.; Feng, S.; Urtasun, R. Learning lane graph representations for motion forecasting. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. Springer: Cham, Switzerland, 2020; pp. 541–556. [Google Scholar]
- Zeng, W.; Liang, M.; Liao, R.; Urtasun, R. Lanercnn: Distributed representations for graph-centric motion forecasting. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 532–539. [Google Scholar]
- Gilles, T.; Sabatini, S.; Tsishkou, D.; Stanciulescu, B.; Moutarde, F. Home: Heatmap output for future motion estimation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 500–507. [Google Scholar]
- Gilles, T.; Sabatini, S.; Tsishkou, D.; Stanciulescu, B.; Moutarde, F. Gohome: Graph-oriented heatmap output for future motion estimation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 9107–9114. [Google Scholar]
- Jia, X.; Wu, P.; Chen, L.; Liu, Y.; Li, H.; Yan, J. Hdgt: Heterogeneous driving graph transformer for multi-agent trajectory prediction via scene encoding. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13860–13875. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Ye, L.; Wang, J.; Wu, K.; Lu, K. Hivt: Hierarchical vector transformer for multi-agent motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8823–8833. [Google Scholar]
- Fang, J.; Zhu, C.; Zhang, P.; Yu, H.; Xue, J. Heterogeneous trajectory forecasting via risk and scene graph learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12078–12091. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Jiang, K.; Zhou, Z.; Nam, K.; Yin, C. Interactive trajectory prediction using a driving risk map-integrated deep learning method for surrounding vehicles on highways. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19076–19087. [Google Scholar] [CrossRef]
- Varadarajan, B.; Hefny, A.; Srivastava, A.; Refaat, K.S.; Nayakanti, N.; Cornman, A.; Chen, K.; Douillard, B.; Lam, C.P.; Anguelov, D.; et al. Multipath++: Efficient information fusion and trajectory aggregation for behavior prediction. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 7814–7821. [Google Scholar]
- Shi, S.; Jiang, L.; Dai, D.; Schiele, B. Motion transformer with global intention localization and local movement refinement. Adv. Neural Inf. Process. Syst. 2022, 35, 6531–6543. [Google Scholar]
- Zhang, L.; Li, P.; Liu, S.; Shen, S. SIMPL: A Simple and Efficient Multi-agent Motion Prediction Baseline for Autonomous Driving. IEEE Robot. Autom. Lett. 2024, 9, 3767–3774. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous graph attention network. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2022–2032. [Google Scholar]
- Hong, H.; Guo, H.; Lin, Y.; Yang, X.; Li, Z.; Ye, J. An attention-based graph neural network for heterogeneous structural learning. AAAI Conf. Artif. Intell. 2020, 34, 4132–4139. [Google Scholar] [CrossRef]
- Ye, M.; Cao, T.; Chen, Q. Tpcn: Temporal point cloud networks for motion forecasting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11318–11327. [Google Scholar]
- Zhang, Y.; Qian, D.; Li, D.; Pan, Y.; Chen, Y.; Liang, Z.; Zhang, Z.; Zhang, S.; Li, H.; Fu, M.; et al. Graphad: Interaction scene graph for end-to-end autonomous driving. arXiv 2024, arXiv:2403.19098. [Google Scholar]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Li, Y.; Li, K.; Zheng, Y.; Morys, B.; Pan, S.; Wang, J. Threat assessment techniques in intelligent vehicles: A comparative survey. IEEE Intell. Transp. Syst. Mag. 2020, 13, 71–91. [Google Scholar] [CrossRef]
- Lee, D.N. A theory of visual control of braking based on information about time-to-collision. Perception 1976, 5, 437–459. [Google Scholar] [CrossRef] [PubMed]
- Minderhoud, M.M.; Bovy, P.H. Extended time-to-collision measures for road traffic safety assessment. Accid. Anal. Prev. 2001, 33, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Alonso-Mora, J.; Wang, M. Probabilistic risk metric for highway driving leveraging multi-modal trajectory predictions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19399–19412. [Google Scholar] [CrossRef]
- Tang, B.; Zhong, Y.; Neumann, U.; Wang, G.; Chen, S.; Zhang, Y. Collaborative uncertainty in multi-agent trajectory forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 6328–6340. [Google Scholar]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar] [CrossRef]
- Chang, M.F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3d tracking and forecasting with rich maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8748–8757. [Google Scholar]
- Loshchilov, I. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Choi, S.; Kim, J.; Yun, J.; Choi, J.W. R-pred: Two-stage motion prediction via tube-query attention-based trajectory refinement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 8525–8535. [Google Scholar]
- Tang, Y.; He, H.; Wang, Y. Hierarchical vector transformer vehicle trajectories prediction with diffusion convolutional neural networks. Neurocomputing 2024, 580, 127526. [Google Scholar] [CrossRef]
- Lee, N.; Choi, W.; Vernaza, P.; Choy, C.B.; Torr, P.H.; Chandraker, M. Desire: Distant future prediction in dynamic scenes with interacting agents. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 336–345. [Google Scholar]
- Park, S.H.; Lee, G.; Seo, J.; Bhat, M.; Kang, M.; Francis, J.; Jadhav, A.; Liang, P.P.; Morency, L.P. Diverse and admissible trajectory forecasting through multimodal context understanding. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XI 16. Springer: Cham, Switzerland, 2020; pp. 282–298. [Google Scholar]
- Chai, Y.; Sapp, B.; Bansal, M.; Anguelov, D. Multipath: Multiple probabilistic anchor trajectory hypotheses for behavior prediction. arXiv 2019, arXiv:1910.05449. [Google Scholar]


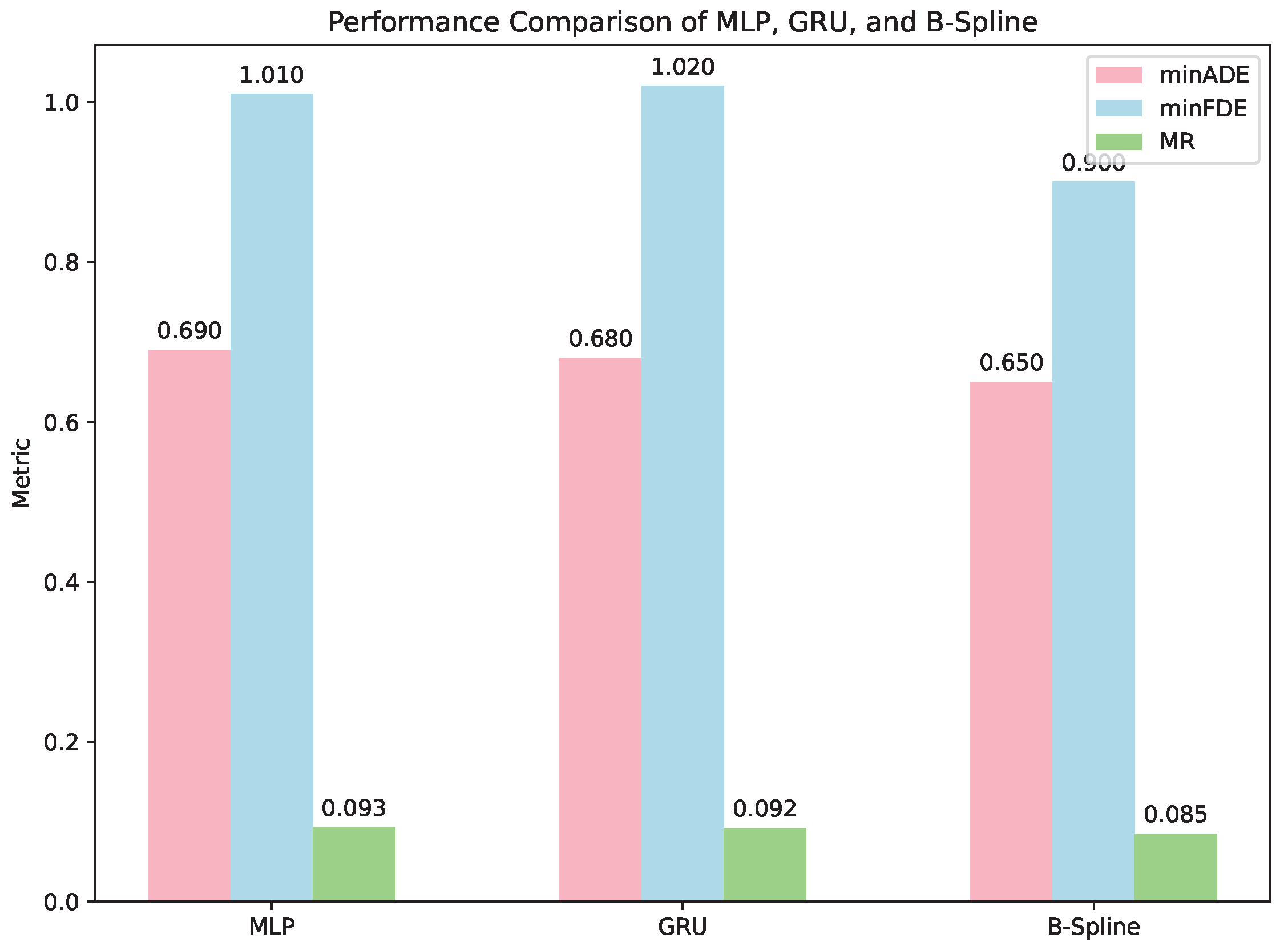

| Hyperparameter | Source | Value |
|---|---|---|
| Equation (4) | ||
| Equation (4) | ||
| Equation (4) | ||
| Equation (19) | 96 | |
| degree (d) | Section 3.5 | 5 |
| Equation (24) | ||
| Equation (24) |
| HRG | TD | minADE | minFDE | MR | ||
|---|---|---|---|---|---|---|
| ✓ | ✓ | ✓ | 0.71 | 1.07 | 0.11 | |
| ✓ | ✓ | ✓ | 1.10 | 1.48 | 0.22 | |
| ✓ | ✓ | ✓ | 0.69 | 1.01 | 0.13 | |
| ✓ | ✓ | ✓ | 0.68 | 1.00 | 0.10 | |
| ✓ | ✓ | ✓ | ✓ | 0.650 | 0.900 | 0.085 |
| Model | minADE | minFDE | MR |
|---|---|---|---|
| DESIRE [37] | 0.92 | 1.77 | 0.18 |
| DATF [38] | 0.92 | 1.52 | |
| MultiPath [39] | 0.80 | 1.68 | 0.14 |
| LaneRCNN [10] | 0.77 | 1.19 | 0.082 |
| DenseTNT [8] | 0.75 | 1.05 | 0.10 |
| TNT [7] | 0.73 | 1.29 | 0.093 |
| TPCN [24] | 0.73 | 1.15 | 0.11 |
| LaneGCN [9] | 0.71 | 1.08 | 0.10 |
| R-Pred [35] | 0.657 | 0.945 | 0.0869 |
| HVTD [36] | 0.68 | 1.02 | 0.10 |
| HiVT-128 [14] | 0.66 | 0.96 | 0.09 |
| Ours | 0.65 | 0.90 | 0.085 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Wang, C.; Xiao, B.; Liu, X.; Shi, C.; Sun, R.; Han, R. Heterogeneous Multi-Agent Risk-Aware Graph Encoder with Continuous Parameterized Decoder for Autonomous Driving Trajectory Prediction. Electronics 2025, 14, 105. https://doi.org/10.3390/electronics14010105
Sun S, Wang C, Xiao B, Liu X, Shi C, Sun R, Han R. Heterogeneous Multi-Agent Risk-Aware Graph Encoder with Continuous Parameterized Decoder for Autonomous Driving Trajectory Prediction. Electronics. 2025; 14(1):105. https://doi.org/10.3390/electronics14010105
Chicago/Turabian StyleSun, Shaoyu, Chunyang Wang, Bo Xiao, Xuelian Liu, Chunhao Shi, Rongliang Sun, and Ruijie Han. 2025. "Heterogeneous Multi-Agent Risk-Aware Graph Encoder with Continuous Parameterized Decoder for Autonomous Driving Trajectory Prediction" Electronics 14, no. 1: 105. https://doi.org/10.3390/electronics14010105
APA StyleSun, S., Wang, C., Xiao, B., Liu, X., Shi, C., Sun, R., & Han, R. (2025). Heterogeneous Multi-Agent Risk-Aware Graph Encoder with Continuous Parameterized Decoder for Autonomous Driving Trajectory Prediction. Electronics, 14(1), 105. https://doi.org/10.3390/electronics14010105






