A 12 μW 10 kHz BW 58.9 dB SNDR AC-Coupled Incremental ADC for Neural Recording
Abstract
1. Introduction
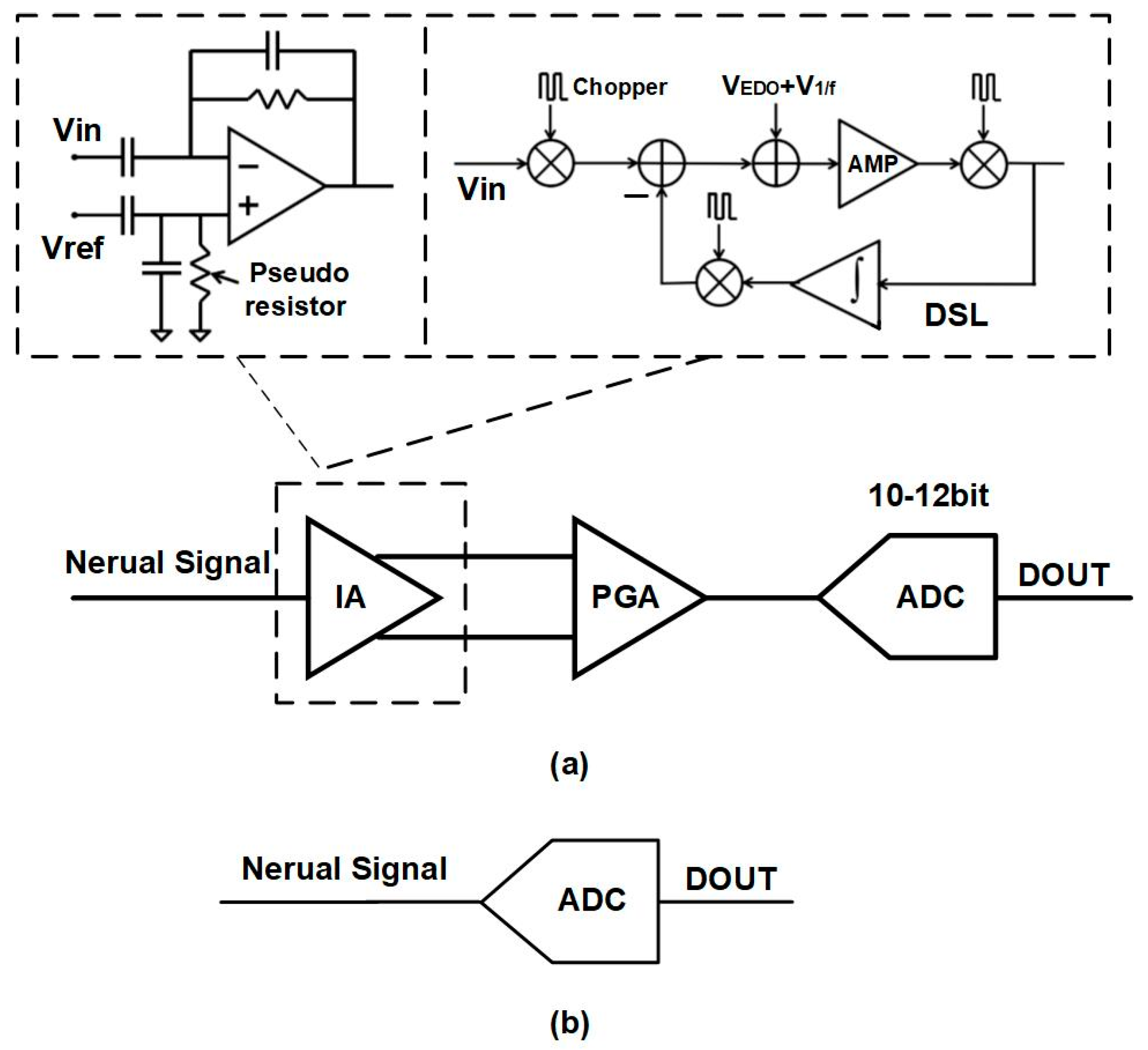
2. System Architecture of the ADC
3. Circuit Implementation
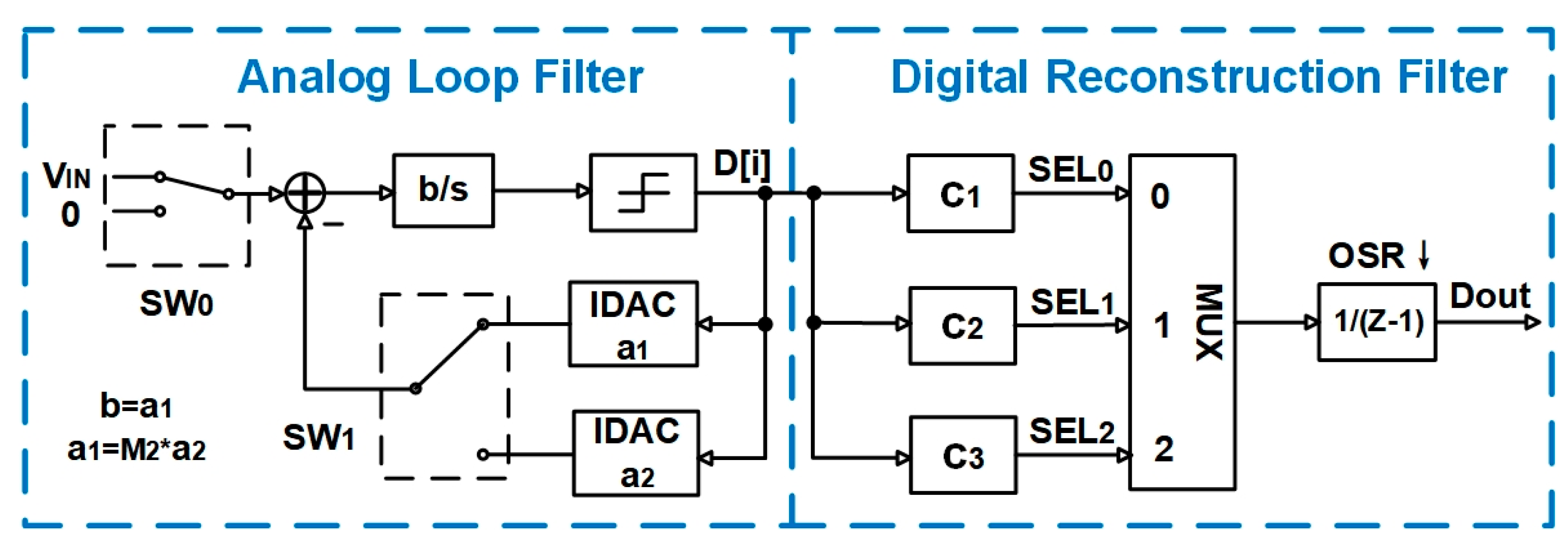
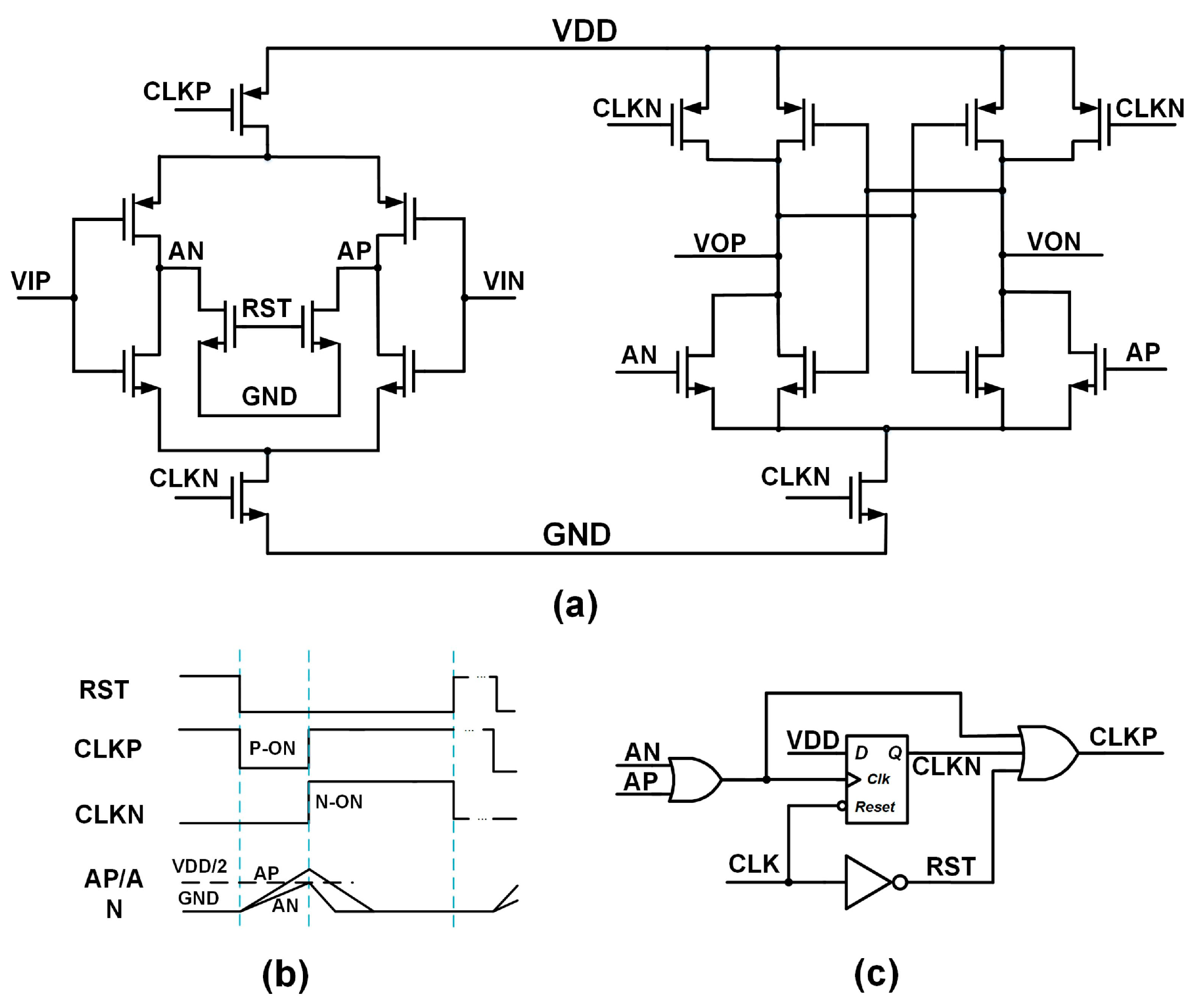
3.1. Circuit Implementation of the ADC
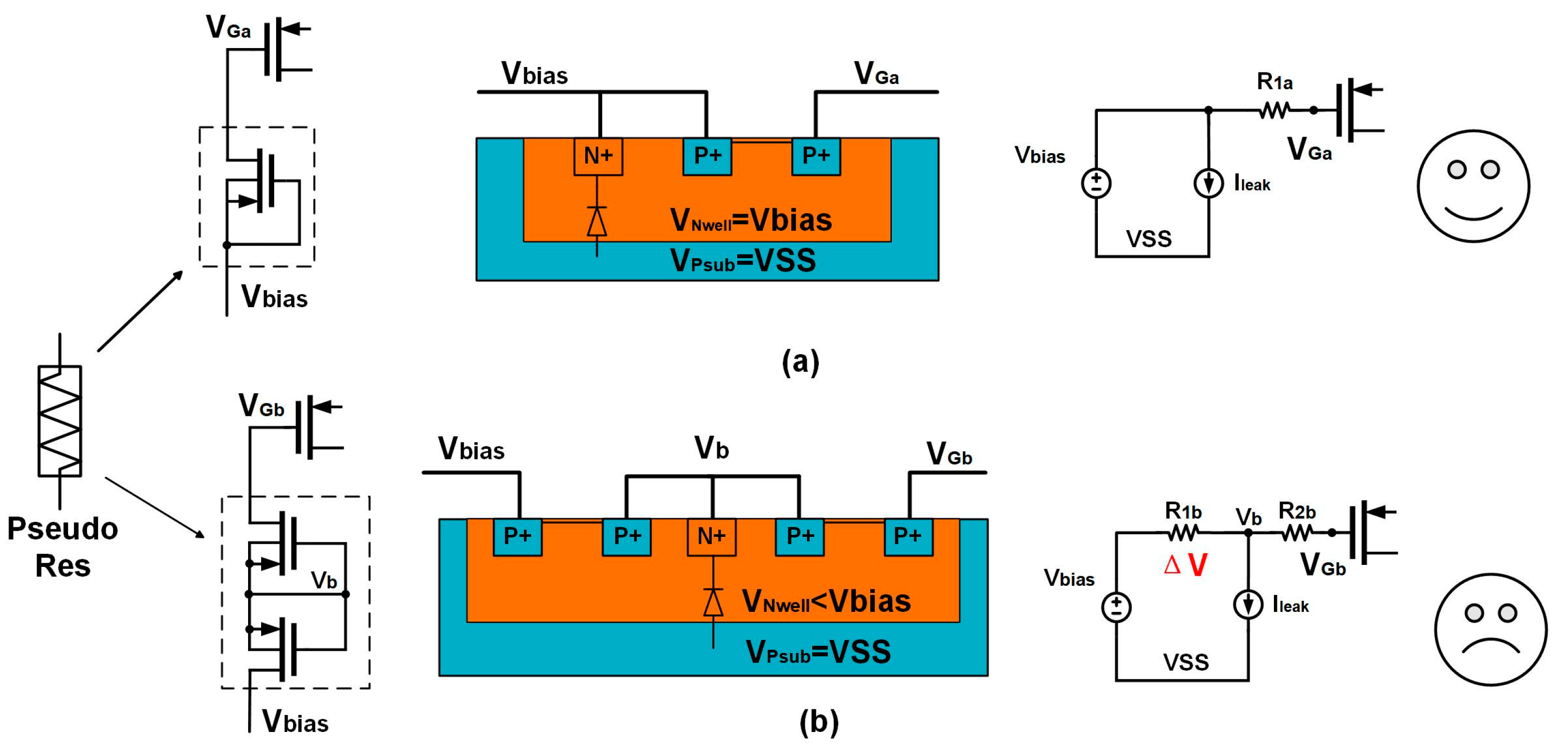
3.2. Design of Analog Front End
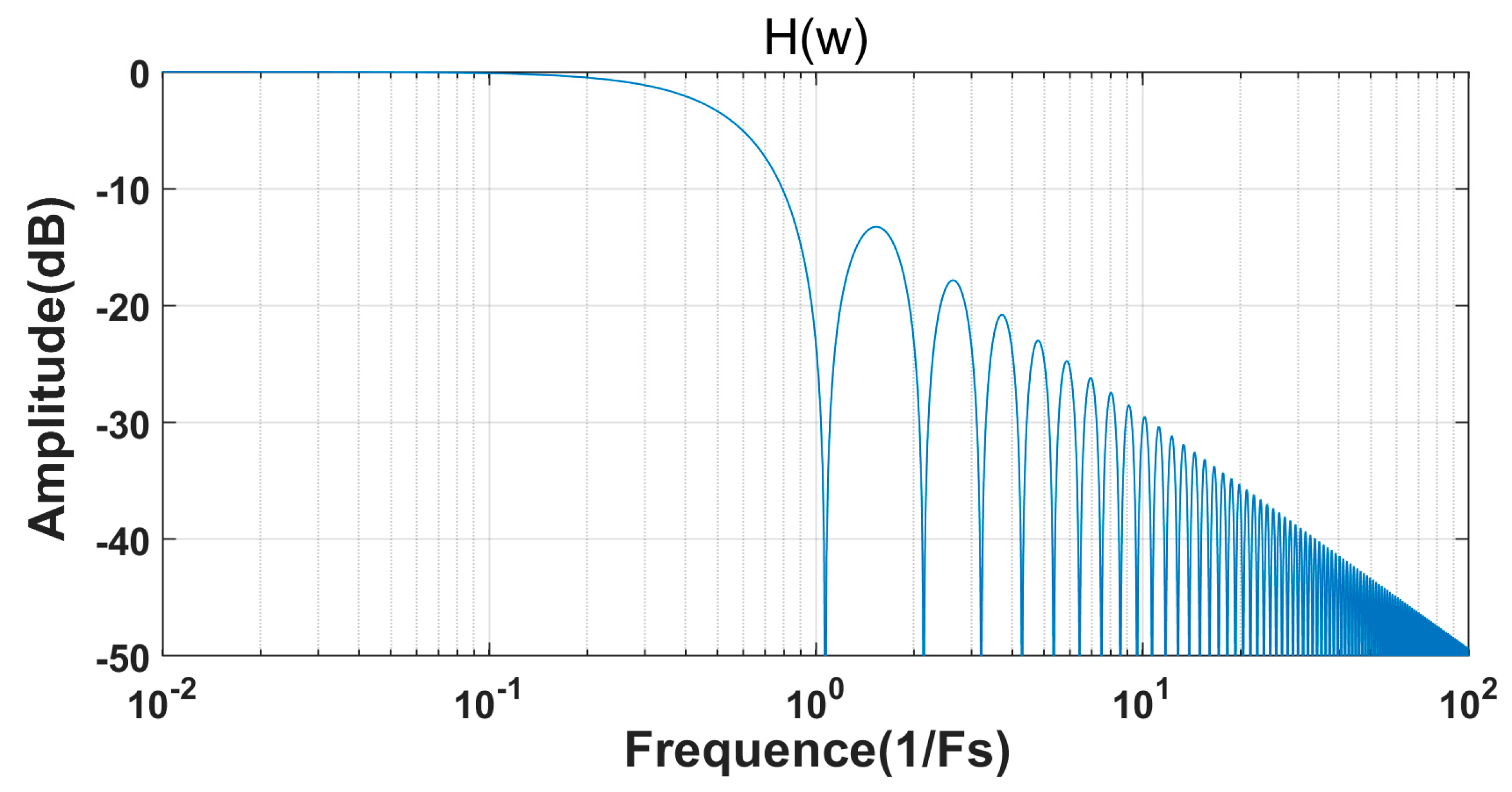
3.3. Design of Digital Logic Control and Data Reconfiguration Circuits
3.4. Design of Current Reference
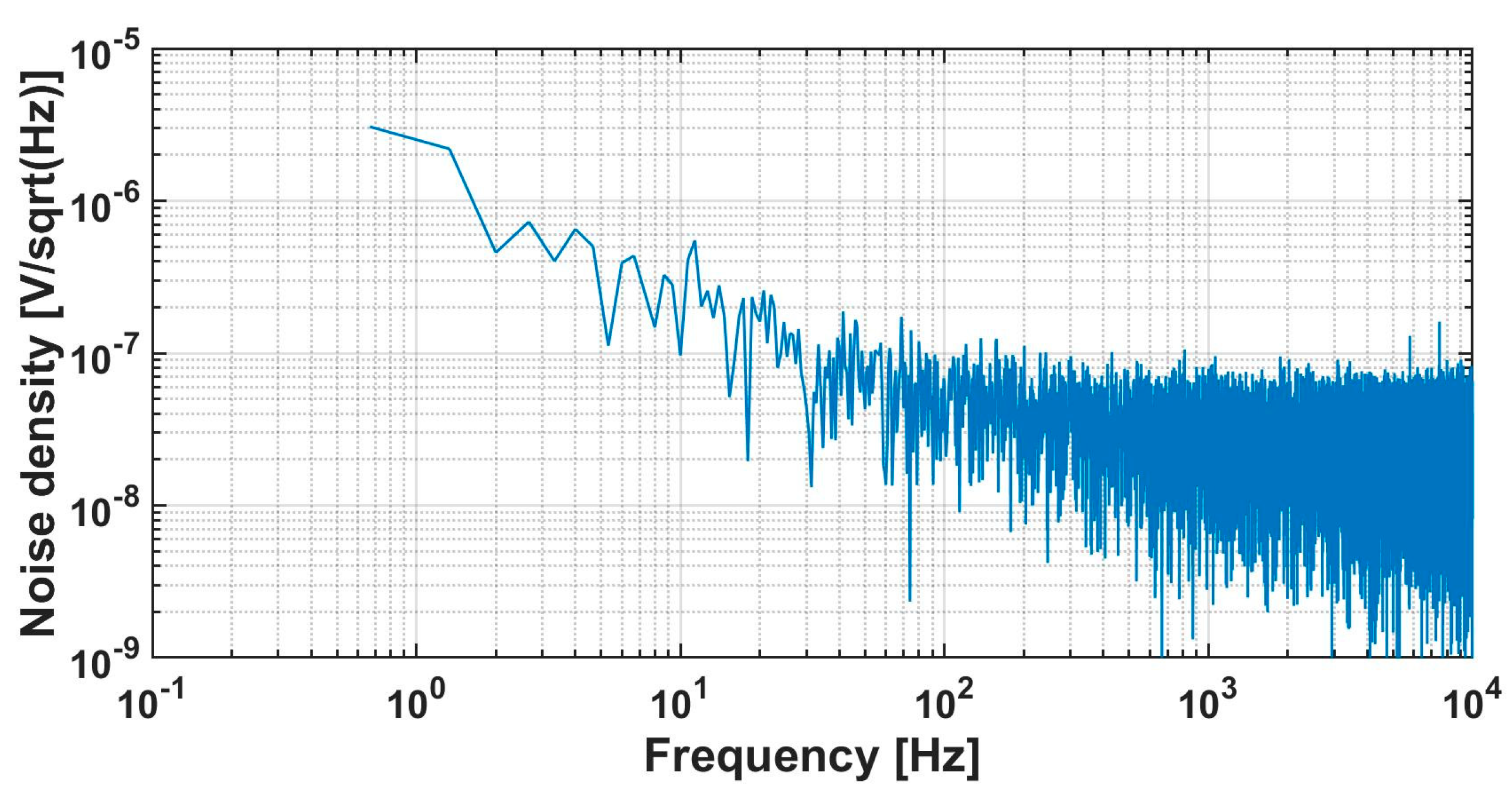
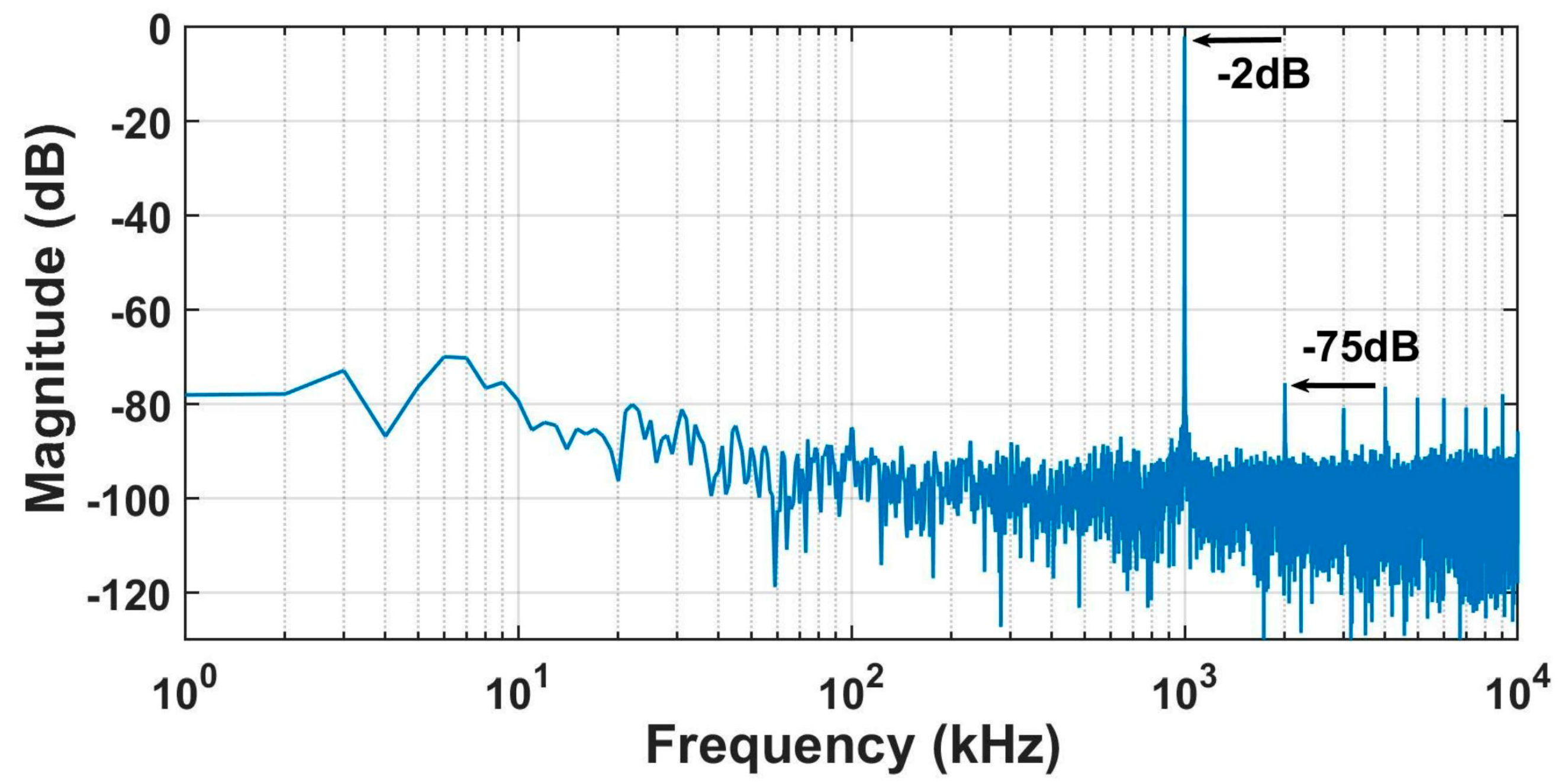
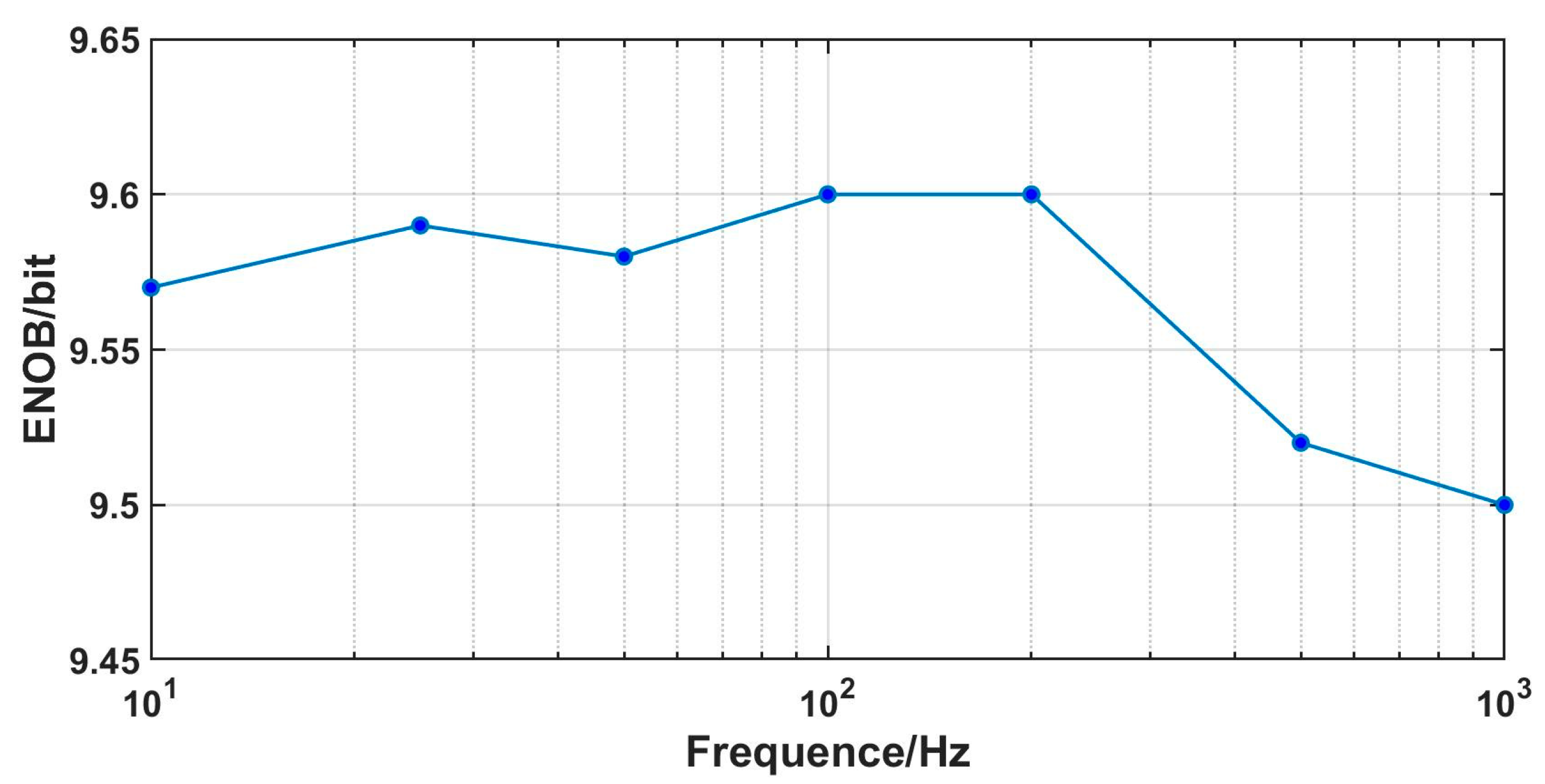
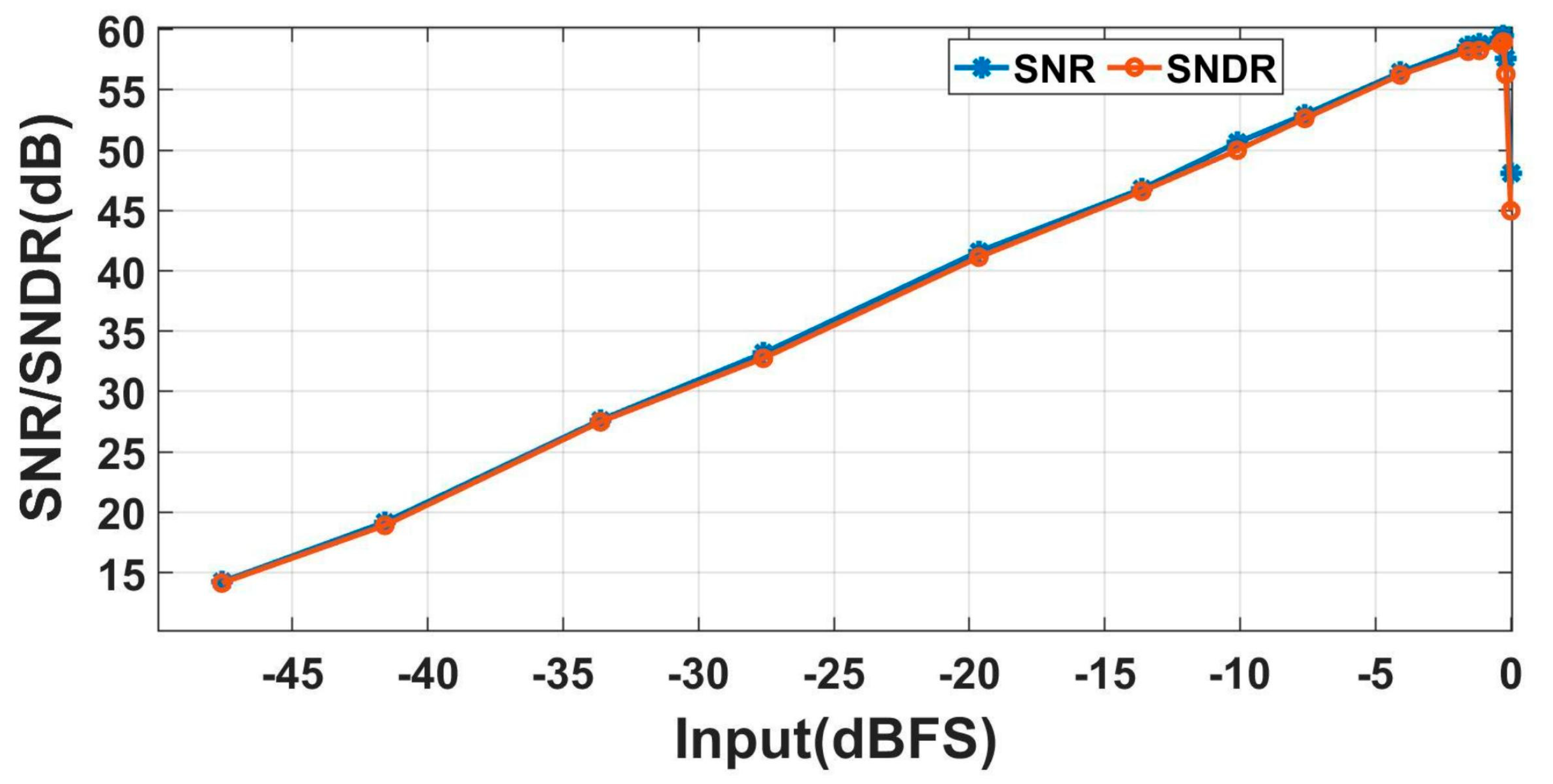
4. Manufacture and Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muller, R.; Le, H.P.; Li, W. A minimally invasive 64-channel wireless μECoG implant. IEEE J. Solid-State Circuits 2014, 50, 344–359. [Google Scholar] [CrossRef]
- Heer, F.; Hafizovic, S.; Franks, W. CMOS microelectrode array for bidirectional interaction with neuronal networks. IEEE J. Solid-State Circuits 2006, 41, 1620–1629. [Google Scholar] [CrossRef]
- Harrison, R.R.; Watkins, P.T.; Kier, R.J. A low-power integrated circuit for a wireless 100-electrode neural recording system. IEEE J. Solid-State Circuits 2006, 42, 123–133. [Google Scholar] [CrossRef]
- Chae, M.S.; Liu, W.; Sivaprakasam, M. Design optimization for integrated neural recording systems. IEEE J. Solid-State Circuits 2008, 43, 1931–1939. [Google Scholar] [CrossRef]
- Aziz, J.N.; Abdelhalim, K.; Shulyzki, R. 256-channel neural recording and delta compression microsystem with 3D electrodes. IEEE J. Solid-State Circuits 2009, 44, 995–1005. [Google Scholar] [CrossRef]
- Shahrokhi, F.; Abdelhalim, K.; Serletis, D. The 128-channel fully differential digital integrated neural recording and stimulation interface. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 149–161. [Google Scholar] [CrossRef]
- Wattanapanitch, W.; Sarpeshkar, R. A low-power 32-channel digitally programmable neural recording integrated circuit. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 592–602. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.M.; Prodanov, D.; Braeken, D. A multichannel integrated circuit for electrical recording of neural activity, with independent channel programmability. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 101–110. [Google Scholar] [CrossRef]
- Gao, H.; Walker, R.M.; Nuyujukian, P.; Hermes, E. A 96-Channel Full Data Rate Direct Neural Interface in 0.13 um CMOS. IEEE J. Solid-State Circuits 2012, 47, 1043–1055. [Google Scholar] [CrossRef]
- Han, D.; Zheng, Y.; Rajkumar, R. A 0.45 V 100-channel neural-recording IC with Sub μW channel consumption in 0.18um CMOS. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 735–746. [Google Scholar]
- Lopez, C.M.; Andrei, A.; Mitra, S. An implanTable 455-active-electrode 52-channel CMOS neural probe. IEEE J. Solid-State Circuits 2013, 49, 248–261. [Google Scholar] [CrossRef]
- Biederman, W.; Yeager, D.J.; Narevsky, N. A 4.78 mm2 fully-integrated neuromodulation SoC combining 64 acquisition channels with digital compression and simultaneous dual stimulation. IEEE J. Solid-State Circuits 2015, 50, 1038–1047. [Google Scholar] [CrossRef]
- Dragas, J.; Viswam, V.; Shadmani, A. In vitro multi-functional microelectrode array featuring 59760 electrodes, 2048 electrophysiology channels, stimulation, impedance measurement, and neurotransmitter detection channels. IEEE J. Solid-State Circuits 2017, 52, 1576–1590. [Google Scholar] [CrossRef]
- Lopez, C.M.; Putzeys, J.; Raducanu, B.C. A neural probe with up to 966 electrodes and up to 384 configurable channels in 0.13 um SOI CMOS. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 510–522. [Google Scholar] [CrossRef]
- Angotzi, G.N.; Malerba, M.; Boi, F. A synchronous neural recording platform for multiple high-resolution CMOS probes and passive electrode arrays. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 532–542. [Google Scholar] [CrossRef]
- Park, S.Y.; Cho, J.; Lee, K. Dynamic power reduction in scalable neural recording interface using spatiotemporal correlation and temporal sparsity of neural signals. IEEE J. Solid-State Circuits 2018, 53, 1102–1114. [Google Scholar] [CrossRef]
- Shiwei, W.; Seyed Kasra, G.; Hosung, C. A compact quad-shank CMOS neural probe with 5120 addressable recording sites and 384 fully differential parallel channels. IEEE Trans. Biomed. Circuits Syst. 2019, 6, 1625–1634. [Google Scholar]
- Zhang, X.; Li, Q.; Chen, C.; Li, Y.; Zuo, F.; Liu, X.; Zhang, H.; Wang, X.; Liu, Y. A Fully Integrated 64-Channel Recording System for Extracellular Raw Neural Signals. Electronics 2021, 10, 2726. [Google Scholar] [CrossRef]
- Yoo, J.; Yan, L.; El-Damak, D.; Altaf, M.A.B.; Shoeb, A.H.; Chandrakasan, A.P. An 8-channel scalable EEG acquisition SoC with patient-specific seizure classification and recording processor. IEEE J. Solid-State Circuits 2013, 49, 214–228. [Google Scholar] [CrossRef]
- Altaf, M.; Yoo, J. A 1.83 μJ/classification 8-channel patient-specific epileptic seizure classification SoC using a non-linear support vector machine. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 49–60. [Google Scholar] [CrossRef]
- Ha, U.; Lee, J.; Kim, M.; Roh, T.; Choi, S.; Yoo, H.-J. An EEG-NIRS multimodal SoC for accurate anesthesia depth monitoring. IEEE J. Solid-State Circuits 2018, 53, 1830–1843. [Google Scholar] [CrossRef]
- Guo, J.; Yuan, J.; Huang, J.; Law, J.K.-Y.; Yeung, C.-K.; Chan, M. 32.9 nV/rt Hz−60.6 dB THD Dual-Band Micro-Electrode Array Signal Acquisition IC. IEEE J. Solid-State Circuits 2012, 47, 1209–1220. [Google Scholar] [CrossRef]
- Li, Q.; Wang, X.; Liu, Y. A 60 nV/<0.01%-THD±200mV-DC-Rejection Bio-Sensing Chopper Amplifier with Noise-Nonlinearity-Cancelling Loop. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 215–219. [Google Scholar]
- Greenwald, E.; So, E.; Wang, Q. A bidirectional neural interface IC with chopper stabilized BioADC array and charge balanced stimulator. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 990–1002. [Google Scholar] [CrossRef] [PubMed]
- Kassiri, H.; Salam, M.T.; Pazhouhandeh, M.R. Rail-to-rail-input dual-radio 64-channel closed-loop neurostimulator. IEEE J. Solid-State Circuits 2017, 52, 2793–2810. [Google Scholar] [CrossRef]
- Kim, C.; Joshi, S.; Courellis, H.; Wang, J.; Miller, C.; Cauwenberghs, G. Sub-μVrms-Noise Sub-μW/Channel ADC-Direct Neural Recording with 200-mV/ms Transient Recovery Through Predictive Digital Autoranging. IEEE J. Solid-State Circuits 2018, 53, 3101–3110. [Google Scholar] [CrossRef]
- Wang, S.; Ballini, M.; Yang, X.; Sawigun, C.; Weijers, J.W.; Biswas, D.; Van Helleputte, N.; Lopez, C.M. A Compact Chopper Stabilized Δ-ΔΣ Neural Readout IC with Input Impedance Boosting. IEEE Open Journal of the Solid-State Circuits Society 2021, 1, 67–78. [Google Scholar] [CrossRef]
- De Dorigo, D.; Moranz, C.; Graf, H.; Marx, M.; Wendler, D.; Shui, B.; Herbawi, A.S.; Kuhl, M.; Ruther, P.; Paul, O.; et al. Fully Immersible Subcortical Neural Probes with Modular Architecture and a Delta-Sigma ADC Integrated Under Each Electrode for Parallel Readout of 144 Recording Sites. IEEE J. Solid-State Circuits 2018, 53, 3111–3125. [Google Scholar] [CrossRef]
- Wendler, D.; De Dorigo, D.; Amayreh, M.; Bleitner, A.; Marx, M.; Willaredt, R.; Manoli, Y. A 0.0046-mm2 Two-Step Incremental Delta–Sigma Analog-to-Digital Converter Neuronal Recording Front End with 120-mVpp Offset Compensation. IEEE J. Solid-State Circuits 2023, 58, 439–450. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, W.; Yang, H.; Hou, Y.; Wang, X.; Liu, Y. A 16-µW 10-kHz BW incremental ΔΣ ADC with automatic EDO canceling for implantable neural recording. IEICE Electronics Express 2024, 21, 20230604. [Google Scholar] [CrossRef]
- Bang, J.-S.; Jeon, H.; Je, M.; Cho, G.-H. A 6.5µW 92.3DB-DR Biopotential-Recording Front-End with 360mVpp Linear Input Range. In Proceedings of the 2018 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 18–22 June 2018; pp. 239–240. [Google Scholar]
- Lee, C.; Jeon, T.; Jang, M.; Park, S.; Kim, J.; Lim, J.; Ahn, J.H.; Huh, Y.; Chae, Y. A 6.5-μW 10-kHz BW 80.4-dB SNDR Gm-C-Based CT ∆∑ Modulator with a Feedback-Assisted Gm Linearization for Artifact-Tolerant Neural Recording. IEEE J. Solid-State Circuits 2020, 55, 2889–2901. [Google Scholar] [CrossRef]
- Wang, S.; Lopez, C.M.; Ballini, M. Leakage compensation scheme for ultra-high-resistance pseudo-resistors in neural amplifiers. Electron. Lett. 2018, 54, 270–272. [Google Scholar] [CrossRef]
- Liu, M.; Pelzers, K.; van Dommele, R.; van Roermund, A.; Harpe, P. A 106nW 10 b 80 kS/s SAR ADC with Duty-Cycled Reference Generation in 65 nm CMOS. IEEE J. Solid-State Circuits 2016, 51, 2435–2445. [Google Scholar] [CrossRef]










| JSSC [13] | TBCAS [14] | TBCAS [17] | JSSC [28] d | JSSC [29] | This Work | |
|---|---|---|---|---|---|---|
| Architecture | AMP + ADC | AMP + ADC | AMP + ADC | ADC only | ADC only | ADC only |
| Process (μm) | 0.18 | 0.13 | 0.13 | 0.18 | 0.18 | 0.18 |
| Supply (V) | 1.8 | 1.2/1.8 | 1.2 | 1.8 | 1.8 | 1.5 |
| Power (μW) /Channel | 16 | 49.06 | 95.1 c | 39.14 | 14.94 | 12 |
| Input Range (mVpp) | - a | - a | - a | 22.5 | 14 | 24 |
| RTI noise (μVrms) | 2.4 (300–3 kHz) 3.6 (1–300 Hz) | 6.36 (0.3 k–3 kHz) | 7.44 (0.3 k–10 kHz) 7.65(0.5–1 kHz) | 12 (1 Hz–10 kHz) | 4.9 (1 Hz–10 kHz) e | 6.9 (1 Hz–10 kHz) |
| THD | - b | 0.4% (10 mVpp) | 0.17% (10 mVpp) | 0.22% (10 mVpp) | 0.078% e (10 mVpp) | 0.036% (15 mVpp) |
| Area (mm2) /Channel | >0.02 | 0.12 | 0.035 | 0.0049 | 0.00462 | 0.0192 |
| EDO tolerance | Rail-to-Rail | Rail-to-Rail | Rail-to-Rail | 22.5 mV | ±60 mV | Rail-to-Rail |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Hou, Y.; Wang, X.; Liu, Y. A 12 μW 10 kHz BW 58.9 dB SNDR AC-Coupled Incremental ADC for Neural Recording. Electronics 2024, 13, 1222. https://doi.org/10.3390/electronics13071222
Zhang X, Hou Y, Wang X, Liu Y. A 12 μW 10 kHz BW 58.9 dB SNDR AC-Coupled Incremental ADC for Neural Recording. Electronics. 2024; 13(7):1222. https://doi.org/10.3390/electronics13071222
Chicago/Turabian StyleZhang, Xiangwei, Ying Hou, Xiaosong Wang, and Yu Liu. 2024. "A 12 μW 10 kHz BW 58.9 dB SNDR AC-Coupled Incremental ADC for Neural Recording" Electronics 13, no. 7: 1222. https://doi.org/10.3390/electronics13071222
APA StyleZhang, X., Hou, Y., Wang, X., & Liu, Y. (2024). A 12 μW 10 kHz BW 58.9 dB SNDR AC-Coupled Incremental ADC for Neural Recording. Electronics, 13(7), 1222. https://doi.org/10.3390/electronics13071222






