An Energy Consumption Model for SRAM-Based In-Memory-Computing Architectures

Abstract

In this paper, a mathematical model for obtaining energy consumption of IMC architectures is constructed. This model provides energy estimation based on the distribution of a specific dataset. In addition, the estimation reduces the required simulation time to create an energy consumption model of SRAM-based IMC architectures. To validate our model with realistic data, the energy consumption of IMC is compared by using NeuroSim V3.0 for the CIFAR-10 and MNIST-like datasets. Furthermore, an application is created with our model to select highest performing quantization mapping based upon the parameters of energy consumption and accuracy.

1. Introduction

The use of machine learning ushered in a new era for a wide variety of fields from speech recognition to image classification. Among these fields, a large amount of work is dedicated to keyword or key image search algorithms and systems. Such tasks are found to be well suited for Deep Neural Network (DNN)-based machine learning implementations. When these are used as sub-units and employed in larger systems, they can act as a trigger for more complex functions. As such, they allow for power reduction by keeping the complex functions powered down unless they are triggered by the lower-power keyword or key image search sub-unit. Such applications can also be referred to as “key-data” detection. Therefore, power consumption of such trigger sub-units, which continuously search for simple trigger data, is critical, and such units need to be carefully designed to reduce system level power consumption. Power optimizations often involve architectural decisions and need to allow designers to estimate power as early as possible during the design cycle. As a result, many studies in the literature have proposed various system architectures to reduce overall energy consumption [1,2,3,4].

To satisfy the requirements during the implementation of machine learning-based “key-data” search algorithms, in-memory-computing (IMC) techniques are often used. This architecture eliminates excessive data transfers between memory and processing units by introducing arithmetic functionality within each memory cell. Additionally, the weight data of DNNs or fully connected layers (FCLs) are also stored in the memory. Thus, using the data and the arithmetic functionality in each memory cell, the output is computed in parallel. Here, each storage element implements single-bit multiplication, which is a part of a larger operation [5]. By employing different types of arithmetic units in memory cells, various types of IMC architectures were developed in [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. These works aim to improve energy consumption, speed, and accuracy. Additionally, inputs with different resolutions, ranging from single-bit precision in [5,6,19] to multi-bit precision, were used [7,8,9,10,11,12] to satisfy the accuracy criteria of various types of neural networks [7]. In addition to these, there are studies carried out at the device level to realize lower-power IMC architectures based on different types of memory cells [24,25].

Regarding speed and accuracy of key-data search algorithms, the wake-up delay of such systems can be in the order of 100 ms, or even as high as 1 s, which is a relatively long duration for microelectronic systems. Last but not least, due to the need for detecting a smaller set of words, images, etc., the system has a relaxed accuracy specification. Hence, a smaller dataset would be enough to train a low-power Deep Neural Network (DNN)-based system that remains always on, searches for keywords, and generates a trigger within 100 ms⁻¹ s of detection. Therefore, it is necessary to enable designers to estimate the energy consumption of such low power AI systems, as early as possible, preferably starting during the architectural exploration phase.

To allow architects to estimate the power consumption of such designs, different types of benchmarking software were proposed to simulate the power consumption and latency of the IMC architecture [14,15]. Best known among these is the NeuroSim benchmark framework. Other benchmarking software with similar features were proposed in [26,27,28,29]. Reported in [14,15], NeuroSim IMC benchmarking software achieves 10.51% power estimation error from results obtained with ASIC power analysis tools using layout parasitic extracted (LPE) netlists. This result was reported to be consistent across three different technology nodes.

However, as the complexity of DNN structures increases, simulation times can reach hours or even days. Moreover, in the case of larger datasets, simulation runtimes will increase further. To speed up such analyses, semi-analytical models were also introduced in papers [30,31,32]. This approach is still based on simulations during which power consumption of a few key blocks is analytically computed and the simulation load is somewhat reduced. However, simulation times can still reach many hours.

In this paper, we propose a mathematical model to predict power consumption for a given dataset within seconds. Our approach stems from the observation that the power of an always-active DNN array would reduce when its switching activity reduces. Combining pre-computed power consumption of always-active circuits and switching activity from different datasets, we can estimate power consumption in mere seconds. We were able to show that the switching activity comes from the logic-1 bits in the pixels of the training dataset. Using the ratio of the number of these bits to the size of the training data gave us the switching factor we needed. Our fully active power numbers are based on a NeuroSim simulation of the DNN. We verified our method, using different types of datasets. The key contributions of our paper are summarized as follows:

(1)

A fully analytical model is proposed to estimate the power and switching activity factor of IMC-based architectures. Using our model, designers can pre-estimate overall power consumption in seconds with an accuracy close to NeuroSim.

(2)

The switching activity factors for MNIST-like datasets as well as the CIFAR-10 dataset are computed. Designers can use these activity factors to improve their power estimations.

(3)

An optimization for lowering the switching activity while maintaining high resolution is proposed. It is shown that this optimization can be completed in orders of magnitude shorter time compared to other simulation methods.

The rest of the paper is organized as follows. Section 2 discusses previous work that is relevant to the subject of IMC modeling. Section 3 describes the theoretical background behind Artificial Neural Networks (ANNs) and the execution of multiply and accumulate (MAC) operations on SRAM-based IMC structures and the power consumption characteristics of these structures. Section 4 proposes an analytical model to predict power consumption and introduces the activity factor. Section 5 compares predictions of the proposed model against equivalent results from NeuroSim, which validates our model. Switching activity factor lists for various CIFAR-10 and MNIST-like datasets are also included. Lastly, an optimization example that lowers switching activity by various quantizations of the dataset is included. Section 6 concludes the work and discusses the possible future work from this study.

2. Related Works

Recently, modeling the power consumption of IMC structures, in addition to the performance of the DNNs they realize, has been a popular topic. In order to extract several parameters of IMC structures, a wide range of methods are presented in various works. Among these methods, some prior works [27,28,29] have introduced simulation software to estimate the mentioned parameters. These simulators primarily focus on the correct estimation of the DNN performance rather than simulation runtime. To reduce this, several optimization methods are proposed. First among these is emulating the overall IMC structure in a Field Programmable Gate Array (FPGA) [30], while others use analytical models [31,32] to accelerate the simulation speed.

2.1. Software Simulation for Estimation of IMC Performance

In [27], a novel circuit-level macro model that estimates the performance of several types of IMC structures such as analog or digital erasable nonvolatile memory (e-NVM) is introduced. This simulator, aka NeuroSim, can estimate circuit performance based on the various process technology information and device properties. So accordingly, this simulator provides designers with the ability to perform a wide range of space exploration. Similarly, Eva-CIM [28] is another system-level evaluation framework that targets to correctly estimate the performance and energy consumption of IMC-based systems.

In [29], a Python-based framework is introduced to correctly estimate the accuracy of a DNN structure. It is mentioned that the model can predict this by considering several design parameters such as an activated row, partial sum quantization configurations, and non-idealities of several blocks in IMC. Similar work in [32] proposed techniques such as using behavioral models. These simulators are primarily designed to enable the designer to estimate the accuracy of a DNN rather than the energy consumption of the IMC structure that implements the DNN.

2.2. Emulation in FPGA for Estimation of IMC

In [30], an emulator is designed to implement IMC in FPGA devices. With the aid of the FPGA device, this work aims for quick and correct estimates of the energy consumption of the hardware and the accuracy of the DNN. However, creating a mimic IMC in an FPGA requires a detailed implementation of the system, and it is difficult to achieve coverage during architectural explorations. This could result in a new challenge to the designer for accelerating the design process.

2.3. Analytical Model for Estimation of IMC

In [31], a uniform modeling framework is introduced to estimate the energy consumption using analytical models rather than architecture-level simulations. In that paper, it is stated that all layers of the DNN structure should be analyzed to estimate activity for each layer. By gathering technology and architecture parameters from the user, the model in [31] estimates the energy by using energy consumption per activity. Although the paper claims to reduce simulation time, it is not clear how fast the proposed rather complex algorithm can be completed. Furthermore, the algorithm introduced in [31] estimates energy for each DNN layer, which can increase the simulation time.

In contrast to these prior works, in this paper, we implemented a fully analytical model for estimating dynamic energy consumption in IMC structures. Our model creates quick estimations of IMC array energy consumption, which can be useful in early architectural explorations.

3. Background

An DNN is a multi-net network chain that mimics the human brain neuron system with a computational model. Similar to the human brain, DNNs involve learning algorithms such as backpropagation, which is commonly used in many machine learning applications. In our study, backpropagation is used to train the Fully Connected Layers (FCLs) using the MNIST dataset. The backpropagation train algorithm consists of three different calculation stages: feedforward, error calculation, and weight update [33]. The three stages are executed in each epoch to train the FCLs. After the training session, in normal operating mode, only the feedforward stage executes to classify certain datasets. Therefore, in our model, we focused only on the power consumption of the feedforward calculation part.

Feedforward calculation is expressed in (1). The calculation involves multiply and accumulate (MAC) operations, since input vector $A_n^k$ is multiplied by the weight matrix $w_n$ and the products are added. (As a side note, index k represents the specific layer in the NN chain). After that, the sum is passed through the activity function $\phi$. For our purpose, the sigmoid function is assumed as the activity function.

$$A_m^{k+1}=\phi [\sum _n(A_n^k.w_{n,m})]$$

(1)

In order to model the energy consumption of the IMC structure faithfully, it is essential to understand the operations during the binary multiplication phase and accumulation phase [33].

3.1. Binary Multiplication Phase

As it is depicted in Figure 1, MAC operations start by loading the input data $\left(A_n^k\right)$ to the word line driver. As it is shown in (2), each row of the SRAM array is activated serially according to the binary value of each bit in $A_n^k\left[j\right]$. In (2), the additional j parameter denotes the index of each bit in $A_n^k$. Next, each 8T-SRAM block in the activated row starts to draw current from bit lines according to their stored $w_{n,m}\left[j\right]$ binary weight data, implementing the multiplication. This product current is sensed via a trans-impedance amplifier (TIA) to digitize the product for the accumulation phase.

$$g\left(x\right)=\left\{\begin{array}{cc}{n}^{th}rowactive\hfill & \mathrm{if}{A}_n^k\left[j\right]=1\hfill \\ n^{th}rowinactive\hfill & \mathrm{if}{A}_n^k\left[j\right]=0\hfill \end{array}\right.$$

(2)

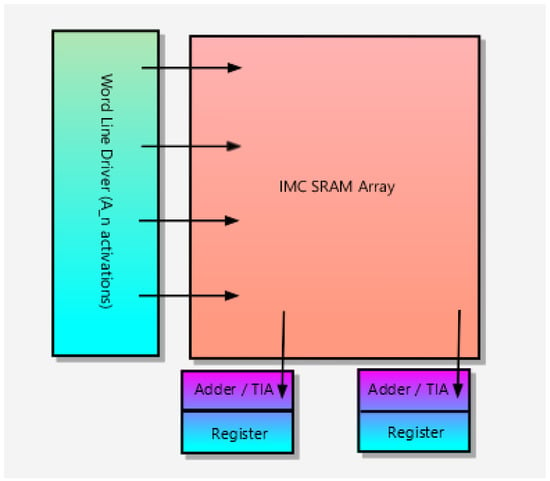
Figure 1. Simplified architecture of SRAM-based IMC architecture.

3.2. Accumulation Phase

Products from the TIA are accumulated by the adder and register. Here, rows of the product matrix are added one by one resulting in a single row, as shown in (3). MAC calculations are repeated according to the bit-length of input activation data for input bit lengths, in the range of $j\in [1\dots N]$ where N denotes the activation data bit length.

$$A_m^{k+1}=\sum _j\sum _n(A_n^k\left[j\right]·w_{n,m}[1:N])·2^j$$

(3)

4. Mathematical Model

This section describes the mathematical concept behind the energy model for IMC architectures. In light of the information given in the previous section, a useful estimate for energy consumption can be based on switching activity factors for different types of applications. Next, the switching activity factor needs to be formally defined.

4.1. Switching Activity Factor

$$AF(\%)=\frac{Amountofoperation}{Maximumlevelofoperation}·100$$

(4)

In (4), the generalized switching expression of activity factor ($AF$) is described. Accordingly, the $AF$ parameter demonstrates the percentage usage of the chip in computation mode. Likewise, energy consumption is also directly proportional to the $AF$ since the active period of the chip is increased with the number of operations.

$$AF(\%)=\frac{{\sum }_m\left(Numberofactiverows\right)}{{\sum }_n\left(Numberoftotalrows\right)}·100$$

(5)

In (5), the expression that defines the switching activity factor ($AF$) for the IMC SRAM arrays is described. As expressed in (2), in the MAC operations, rows of SRAM array are activated according to the $A_n^k\left[j\right]$ activation bit value. For the case of inactivation of a specific SRAM row, all structures such as TIA, registers, and adders remain inactive and these structures are assumed to consume merely negligible static power. For the active SRAM row, the phenomenon is vice-versa.

Hence, it can be deduced that the amount of $A_n^k\left[j\right]=1$ in the total activation data $A_n^k$ directly influences the activity factor of the chip as well as its energy consumption. In compliance with the result, the activity factor ($AF$) is described as

$$AF(\%)=\frac{\sum (Amountof{A}_n^k\left[j\right]=1)}{\sum \left(Totalsizeof{A}_n^k\right)}·100$$

(6)

In other words, the switching factor is defined as the ratio of the “number of logic-1 bits in the training data” to the “size of the training data”.

4.2. Quantization and Histogram of Activation Data

The histogram of certain activation data $\rho \left(x\right)$ has a significant role in modeling energy consumption since it carries information regarding the distribution of $A_n^k$ multi-bit values in the complete dataset. This allows us to create energy models for different datasets and quantization configurations by obtaining their histograms. This procedure is explained below.

Activation data $A_n^k$ is a multi-bit data structure. In order to reduce the dataset to multi-bit activation data, the analog values in the specified dataset need to be quantized. The quantization scheme is illustrated for $q=[7,0]$ in Figure 2.

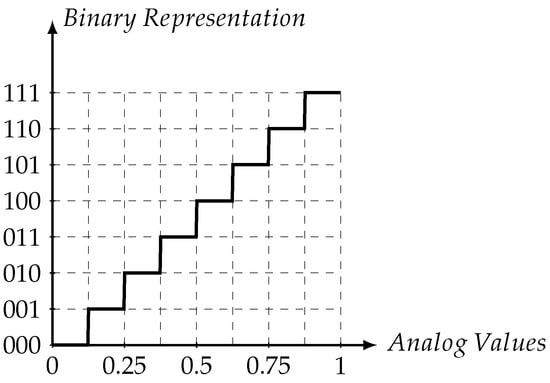
Figure 2. Quantization scheme example for 3-bit $q=[7,0]$.

As depicted in Figure 2, for each analog value, a 3-bit digital value is assigned. After this process, the occurrence of each of n-bit codeword (for 3-bit cases ranging from 000 to 111), is determined. With this information, the frequency of the codewords is defined as function a $\rho \left(x\right)$. Using this information, the number of 1’s, i.e., $A_n^k\left[j\right]=1$, in the total activation data can be easily computed with the aid of Hamming weight function $H\left(x\right)$.

4.3. Energy Modeling

The energy model can be constructed using the histogram data and the Hamming weight function. In the first step, Hamming weights $H\left(x\right)$ of each n-bit codewords are considered. (Hamming weight of an integer equals the number of non-zero bits in its binary representation; for example, $H\left(3\right)$ = 2).

As the Hamming weights of all n-bit codewords are calculated, these data can be used along with the frequency of each n-bit codeword. This frequency is given by function $\rho \left(x\right)$. Combining these two pieces of information, the ratio of ones $A_n^k\left[j\right]=1$ in the dataset can be calculated using the expression described in (7).

$${\mathrm{\Gamma }}_p=\sum (H\left(x\right)\ast \rho \left(x\right))x=1,2,3,\cdots ,2^n$$

(7)

In (7), ${\mathrm{\Gamma }}_p$ denotes the total number of ones in the dataset. This formula allows us to model both $AF$ and energy consumption using the expression of (6). The complete model for $AF$ and energy consumption can be seen in (8) and (9), respectively. For simplicity, ${\mathrm{\Gamma }}_t$ is used to define the total number of bits in the dataset $A_n^k$.

$$AF(\%)={\mathrm{\Gamma }}_p/{\mathrm{\Gamma }}_n·100$$

(8)

$$E=A_1\ast AF(\%)/100+A_2$$

(9)

As it is depicted in (9), energy consumption is modeled as a linear function of $AF(\%)$. In this expression, $A_1$ coefficient, which is the always-active energy consumption, and $A_2$ coefficient, which is the static energy consumption, are combined with $AF(\%)$ to estimate the energy consumption. To illustrate the whole model, the extended version of (9) can be seen in (10).

$$E=A_1\frac{\sum \left(H\right(x)\ast \rho (x\left)\right)}{\sum (n\ast \rho (x\left)\right)}+A_{2}x=1,2,3,\cdots ,2^n$$

(10)

In order to obtain $A_1$ and $A_2$ coefficents, NeuroSim simulations are performed with two sets of training data. One where the input data are completely logic-1 bits, and another where all the input data are logic-0 bits. A more intuitive way of explaining $A_1$ and $A_2$ coefficients related to the device parameters is shown in (11) and (12).

$$A_1=MaximumEnergy-MinimumEnergy$$

(11)

$$A_2=MinimumEnergy$$

(12)

It can be interpreted that the designer will be able to predict energy consumption with (9) for various datasets. We should also highlight that to estimate power consumption using energy consumption data, the latency characteristics reported by NeuroSim can be utilized. By combining the latency with the energy consumption estimates from our model, a power consumption estimate can be obtained.

4.4. Framework of Our Energy Estimation Model

In Figure 3, a framework of our model is described. According to Figure 3, estimation starts by taking the histogram of the dataset. The histogram output of the dataset is an n-sized array where n denotes the bit width of quantization. A histogram array is applied to the input to generate $\%AF$ as shown in the highlighted portion of the block diagram. Eventually, maximum and minimum power consumption of the IMC architecture are also determined. Our proposed analytical model uses exactly these three parameters to estimate energy.

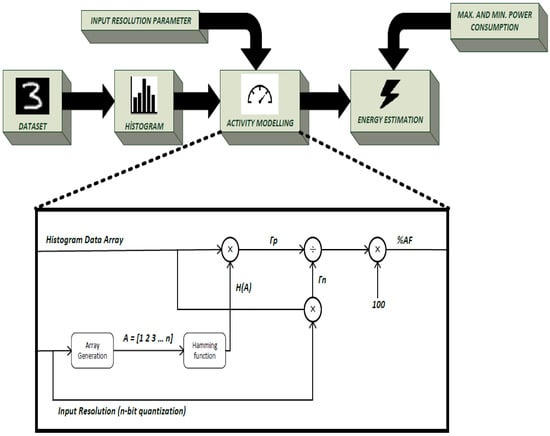
Figure 3. Visualization of our model as a framework.

5. Results

Before examining the results, we would like to point out that, when compared to power consumption results obtained from ASIC power analysis tools, NeuroSim IMC benchmarking software power estimates show an error smaller than 10.51%. This result was reported across three different technology nodes [27]. We also would like repeat that, to obtain power consumption from the energy consumption data, the latency characteristics of the specific IMC architecture reported by NeuroSim can be used. By combining the latency with the energy consumption estimates from our model, power estimates can be calculated.

In this section, we will first compare the energy estimates from NeuroSim to the energy estimates from the proposed analytical model. Next, we will determine the activity factors for a number of datasets; lastly, we will use the proposed analytical model to optimize power for different quantizations of the datasets and show that the proposed method can perform such optimizations much faster than other methods.

5.1. Comparison of Proposed Analytical Model against NeuroSim

NeuroSim simulations were executed by using the DNN structure sized as $400\times 100\times 10$ with 6-bit data words. The energy estimated by the analytıcal model and energy simulated by NeuroSim are compared. In order to expand the comparison, space variants of the input data are generated via a set of quantization maps $q=[a,b]$.

In our case, $8\times 17$ variants of the quantization maps are used. In (13), an overall matrix, which describes all different quantization maps used in our simulation, is shown below.

$$Q={\left[\begin{array}{cccc}[63,32]& [63,31]& \dots & [63,16]\\ [61,30]& [61,28]& \dots & [61,14]\\ ⋮& ⋮& \ddots & ⋮\\ [49,18]& [49,17]& \dots & [49,2]\end{array}\right]}_{8\times 17}$$

(13)

As a reminder, for $q=[a,b]$ mapping, the multi-bit values in the dataset are quantized into the integers between a and b. Afterwards, the energy estimation model matrix $E\left(Q\right)$ is created for each quantization map by substituting each $Q_{i,j}$ into (10). Finally, energy estimated by the model $\left(E\right(Q\left)\right)$ and energy simulated by NeuroSim $\left(Sim\right(Q\left)\right)$ are compared.

Next, an error matrix is created by calculating the error with respect to NeuroSim results (14). Results plotted for comparison and error functions can be seen in Figure 4 and Figure 5, respectively.

$$\%Err\left(Q\right)=\frac{E\left(Q\right)-Sim\left(Q\right)}{Sim\left(Q\right)}·100$$

(14)

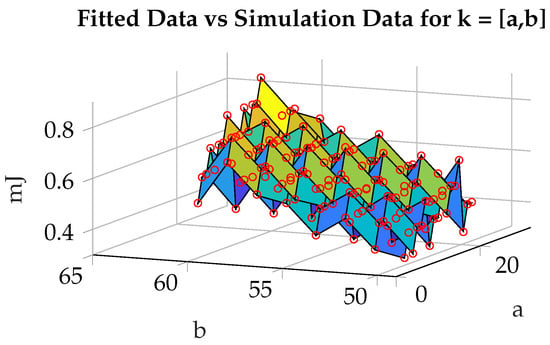
Figure 4. A comparison between analytical energy estimates (3D surface plot) and NeuroSim energy estimates (shown in red dots) for MNIST dataset.

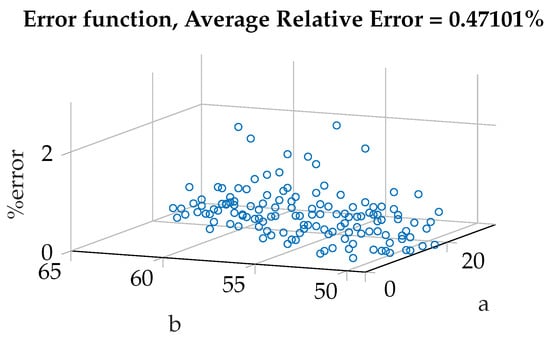
Figure 5. $Err\left(Q\right)$ Error function for MNIST dataset.

In Figure 4, a comparison between analytical energy estimates and NeuroSim energy estimates for MNIST dataset is plotted. As it is seen in Figure 4, our model estimates the energy very close to the NeuroSim results. Similarly, the $Err\left(Q\right)$ error function is plotted in Figure 5. According to this plot, the maximum error does not exceed 2% while the average error is 0.5% for various $q=[a,b]$ quantization maps.

To evaluate the energy estimation accuracy of our analytical model, other MNIST-like datasets (Fashion-MNIST, Sign-MNIST, Handwritten-MNIST, and Noisy-MNIST) and the CIFAR-10 dataset are used when comparing the proposed analytical model against NeuroSim energy estimates. Furthermore, for each dataset, a double comparison is performed to investigate the accuracy of the analytical model for row-by-row and parallel MAC operations. The results of these evaluations and overall performances are summarized in Figure 6. Here, it can be seen that the average errors of the proposed analytical model do not exceed 1.5% for the whole group of datasets.

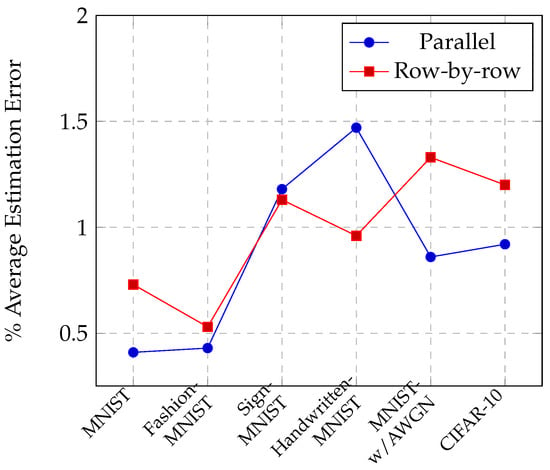
Figure 6. Average estimation error of our model.

5.2. Switching Activity Factor List

In this part, we introduce a list that includes the switching activity of IMC-based structures for frequently used quantization configurations. In most cases, for n-bit quantization, $q=[2^n-1,0]$ mapping is used for the maximum signal-to-quantization-noise ratio ($SQNR$). Therefore, this mapping is used when obtaining the switching activity factors listed in Table 1.

Table 1. Average switching activity list for MNIST-like datasets and CIFAR-10 dataset.

Dataset/Quantization-bits	6-bit	5-bit	4-bit	3-bit	2-bit
MNIST	24.31%	23.9%	24.78%	24.35%	24.35%
Fashion-MNIST	25.81%	25.61%	26.48%	26.14%	28.81%
Sign-MNIST	54.08%	53.97%	55.79%	55.73%	61.3%
Handwritten-MNIST	15.57%	15.61%	15.64%	15.73%	15.09%
MNIST-w/AWGN	45.89%	44.62%	43.77%	40.56%	37.98%
CIFAR-10	50.10%	49.18%	49.71%	48.13%	30.35%

5.3. Example of Fast Optimization Using the Analytical Model: Reducing Activity by Optimizing Input Quantization

As opposed to the frequently used mapping $q=[2^n-1,0]$, during our simulations, we have also observed that better quantization mappings can be found to optimize energy consumption while maintaining DNN accuracy. In order to select such optimal quantization maps $q=[a,b]$, a figure of merit $FOM$ parameter is proposed in (15).

$$FOM=\frac{Quant.Range}{Switch.Activity}=\frac{(a-b)}{AF(\%)}q=[a,b]$$

(15)

Using the evaluation criteria in (15) and our analytical model to estimate power consumption, an optimization for quantization mappings was executed. Resulting mappings as well as switching activity (and hence power) reductions are given in Table 2 and Table 3. Thanks to the quick estimation properties of our model, the improvements are found out in a much quicker way. For each bit-width, the optimal quantization mapping is listed in Table 2. Moreover, Table 3 includes the achieved power savings. As can be seen from Table 2, using the standard $q=[2^n-1,0]$ mapping will not always yield the highest savings. For example, in the MNIST dataset with 6-bit data quantization, it is beneficial to use $q=[48,0]$ instead of $q=[63,0]$ to achieve a reduction in activity factor up to 41.3% while preserving DNN accuracy. As it can be seen from Table 3, it is possible to reduce the energy consumption up to 53% by using different quantization mapping schemes.

Table 2. Optimized quantization mappings for MNIST-like datasets and CIFAR-10 dataset.

Dataset/Quantization-bits	6-bit	5-bit	4-bit	3-bit	2-bit
MNIST	$q=\left[480\right]$	$q=\left[240\right]$	$q=\left[120\right]$	$q=\left[40\right]$	$q=\left[20\right]$
Fashion-MNIST	$q=\left[630\right]$	$q=\left[300\right]$	$q=\left[140\right]$	$q=\left[70\right]$	$q=\left[20\right]$
Sign-MNIST	$q=\left[630\right]$	$q=\left[310\right]$	$q=\left[150\right]$	$q=\left[70\right]$	$q=\left[30\right]$
Handwritten-MNIST	$q=\left[560\right]$	$q=\left[240\right]$	$q=\left[120\right]$	$q=\left[60\right]$	$q=\left[20\right]$
MNIST-w/AWGN	$q=\left[630\right]$	$q=\left[310\right]$	$q=\left[150\right]$	$q=\left[70\right]$	$q=\left[30\right]$
CIFAR-10	$q=\left[630\right]$	$q=\left[310\right]$	$q=\left[150\right]$	$q=\left[70\right]$	$q=\left[20\right]$

Table 3. Reduction in activity factor of in IMC circuitry for MNIST-like datasets and CIFAR-10 dataset.

Dataset/Quantization-bits	6-bit	5-bit	4-bit	3-bit	2-bit
MNIST	−41.3%	−38.08%	−35.27%	−52.9%	−45.02%
Fashion-MNIST	0%	−6.3%	−10.2%	0%	−38.5%
Sign-MNIST	0%	0%	0%	0%	0%
Handwritten-MNIST	−27.60%	−36.50%	−32.47%	−24.3%	−40.8%
MNIST-w/AWGN	0%	0%	0%	0%	0%
CIFAR-10	0%	0%	0%	0%	−38.6%

We also observed the optimization results with respect to the histogram of code-words $\left(\rho \right(x\left)\right)$ in the training data across different datasets. According to these observations, the power savings can be larger for bimodally distributed histograms, whereas more uniformly distributed histograms did not yield significant power reductions.

Finally, our estimation method reduces the power consumption estimation time significantly. A comparison of the simulation times for energy estimation using the proposed analytical model vs. NeuroSim simulator is given in Figure 7 and indicates orders of magnitude of potential savings. It should also be noted that architectural optimizations such as searching for optimal mapping is only possible to perform due to the immense time savings from the proposed analytical model. As such, we believe our method can be useful, especially during initial architectural explorations.

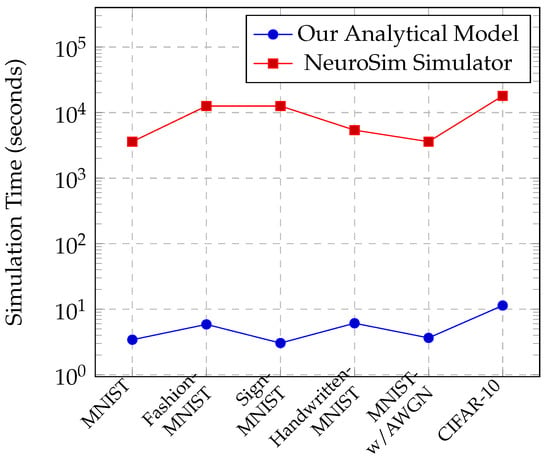
Figure 7. Duration of our model compared to NeuroSim.

It should be noted that while our method provides a very efficient way to estimate power consumption, it does not provide any insight into the DNN accuracy. Even though a fully connected network is assumed as the intended topology, the estimates that were used from NeuroSim can be thought of as an upper limit.

6. Conclusions and Future Works

In this paper, an energy estimation model for IMC architectures is proposed. To create an energy estimation model, we quantified the power reduction due to switching activity. According to that, we were able to show that the switching activity comes from the 1’s in the multi-bit input words of the training data. Using the ratio of the total number of these 1’s to the size of the training data gave us the switching factor we needed. It also allowed us to compute power reductions from the consumption of an always-active circuit.

The proposed model is constructed based on the principle of active and inactive rows in the SRAM array during the IMC computation process. The energy model is compared against NeuroSim for aspects such as average energy estimation error and simulation completion time. According to the comparison, the proposed model is able to model IMC energy consumption for different quantization mappings with an average error lower than 1.5% for six different datasets. Lastly, our model reduces simulation execution time by orders of magnitude $1000\times$ compared to the NeuroSim simulator. Accordingly, the speed of our model offers a great potential during architectural explorations, which can improve the overall design process of IMC chips.

To recap the major contributions of our work is threefold:

• Introducing a very quick power estimation tool that can be very helpful during architectural explorations;
• Tabulating switching activity factors for some appropriate datasets, such as MNIST-like datasets as well as the CIFAR-10 dataset;
• Providing an example use of our algorithm. Here, we proposed an optimization for lowering the switching activity while maintaining high resolution. We showed that this optimization can achieve energy reductions up to 53% while completing in orders of magnitude shorter simulation times compared to other simulation methods.

The possible future improvements of our work are to further expand the context of the activity factors catalog by introducing additional datasets. Moreover, replicating the power consumption simulations using ASIC power analysis tools and FPGA emulators would strengthen the validity of our models. Here, the set of simulations would be reduced to limit the simulation times required for completion. Additionally, since our work is an architectural-level exercise we could not sweep operating conditions such as voltage and temperature. However, if it is really necessary to include the effects of such variations, they can be implemented as extra factors that are functions of temperature and other operating conditions.