Abstract
The evolving landscape of network systems necessitates automated tools for streamlined management and configuration. Intent-driven networking (IDN) has emerged as a promising solution for autonomous network management by prioritizing declaratively defined desired outcomes over traditional manual configurations without specifying the implementation details. This paradigm shift towards flexibility, agility, and simplification in network management is particularly crucial in addressing inefficiencies and high costs linked to manual management, notably in the radio access part. This paper explores the concurrent operation of multiple intents, acknowledging the potential for conflicts, and proposes an innovative reformulation of these conflicts to enhance network administration effectiveness. Following the initial detection of conflicts among intents using a gradient-based approach, our work employs the Multiple Gradient Descent Algorithm (MGDA) to minimize all loss functions assigned to each intent simultaneously. In response to the challenge posed by the absence of a closed-form representation for each key performance indicator in a dynamic environment for computing gradient descent, the Stochastic Perturbation Stochastic Approximation (SPSA) is integrated into the MGDA algorithm. The proposed method undergoes initial testing using a commonly employed toy example in the literature before being simulated for conflict scenarios within a mobile network using the ns3 network simulator.
1. Introduction
Autonomous networks are envisioned to provide the necessary integration of learning and understanding in networks. IDN enables a path towards realizing a network able to comprehend and deploy user requirements irrespective of the underlying infrastructure. Internet Engineering Task Force (IETF) defines intent as “a set of operational goals that a network should meet and outcomes that a network is supposed to deliver, defined in a declarative manner without specifying how to achieve or implement them” [1]. The intent can be characterized as an optimization objective, which serves as a high-level directive provided by a network stakeholder (service subscriber, network operator, administrator, or infrastructure provider) [2]. It entails the determination of a specific key performance indicator (KPI) that the network is expected to achieve, such as “increase handover success to x%” or “reduce load by y%” [3].
1.1. Background
Conflict management and resolution is an exciting challenge for IDN systems [4]. The conflicts can be explicit or implicit based on the deployment stage of an intent [5]. Explicit conflicts will be apparent from the intent expressions, but a IDN system still has to understand the conflict that is apparent to humans. We are more interested in an implicit conflict that becomes apparent only after a set of conflicting actions are determined, usually before deployment as per a determined set of KPIs. For example, a conflict between intent objectives can be due to competing service requirements. In this context, assuring a KPI fulfills the expectation that a particular intent might negatively influence the assurance of a KPI associated with another intent. Moreover, conflicts can stem from a lack of alignment in the target network control parameter values related to KPIs associated with disparate intents [3]. A notable manifestation of such conflict is commonly referred to as a direct target conflict [6]. This category of conflict materializes when multiple intents, each aiming to accomplish distinct objectives, impose contradictory requirements on network control parameters (NCPs). Such a scenario arises when one intent necessitates a reduction in the value of a particular NCPs, while simultaneously, another intent advocates for an increase in the values of the same NCPs.
1.2. Related Works
Banerjee et al. [3] present a closed-loop model, wherein each KPI is managed by a cognitive function (CF) and assumes the presence of a single intent activating two distinct functions, namely mobility robustness optimization (MRO) and mobility load balancing (MLB), both controlling the same parameters in a direct target conflict. The Nash social welfare function is proposed as a solution to ascertain the optimal value of the parameters and propagated to the network operator for decision-making. This work is extended by modeling the network as a Fisher market model, considering diverse intents’ priorities [7]. The Eisenberg–Gale solution is employed to determine optimal values of control parameters, which are tuned to KPI functions. The system’s performance is enhanced by with a reduced computation time. Furthermore, a diverse range of bargaining solutions, such as the Weighted Nash Bargaining Solution (WNBS), the Kalai–Smorodinsky Bargaining Solution (KSBS), and the Shannon Entropy Bargaining Solution (SEBS), is explored in [8] to identify optimal parameter values. The goal is to utilize these methods in an intent conflict resolution framework with the objective of ensuring Jain-based fairness. In another study, Baktir et al. [9] utilize fitness values or penalties associated with each intent to manage conflicting conditions, representing the cost of failure to fulfill or partially fulfill their KPIs. The conflict resolution process assesses the potential impact of KPI to aid the selection of optimal actions to minimize the predicted penalty followed by a controlled execution in the network environment. Furthermore, in the study presented in [10], three distinct intents are examined, each necessitating fulfillment for different services, with packet priority and maximum bit rate identified as the controlling parameters. Conflicts arise when optimizing one target KPI has a detrimental impact on another. To tackle this issue, a model-free multi-agent reinforcement learning approach is employed, where each agent is tasked with adjusting a parameter associated with the intent-defined objective based on intent priorities expressed as penalties. This approach produces a proportional degradation of lower-priority intents to prioritize higher-priority ones.
1.3. Motivation and Contributions
Conflict management and resolution have gained significant attention within the intent-based networking community. Recent studies have explored centralized and distributed coordination-based methods to alleviate the conflicts and manage their impact on the service KPIs. However, to the best of our knowledge, there is a lack of literature discussing the possibility of resolving conflict amongst intents with similar or competing objectives in a multi-intent environment. Utilizing classic optimization theory can provide improvements and optimal conditions to handle conflicts in an efficient way. Hence, the concept of conflict within the IDN environment is redefined by introducing a novel approach that leverages gradients of loss functions associated with each intent. This definition also introduces an inherent conflict detection mechanism without needing an additional step in the resolution process within the system model. The contributions are listed as follows:
- In the proposed framework, the concurrent reception of multiple intents is addressed as a multi-objective optimization problem, with potential conflict situations defined in a novel way and resolution facilitated through the proposed application of the MGDA.
- To utilize MGDA, it is imperative to compute derivatives of the loss function, with the prerequisite being the availability of a closed form of the loss function for each intent. Obtaining closed-form expressions for each intent to facilitate using derivatives is computationally challenging, especially in a dynamic environment. Addressing this challenge, SPSA, a derivative-free method, is employed to approximate gradients to facilitate MGDA in this work to optimize shared NCPs.
- The extensive experimental analysis is performed to test various boundary conditions of the proposed framework and solve the potential of the conflicts.
1.4. Paper Organization
The rest of the paper is organized as follows. Section 2 describes the system model for intents and the definition, management, and resolution of conflicts. Section 3 provides the proposed method for the resolution and optimization of conflicts. Section 4 provides a detailed experimental model and analysis to assess the proposed methodology. Finally, Section 5 concludes the paper along with potential future directions.
2. System Model
This section establishes a model for the intent representation leading to defining a conflict on a generic and intent level. The conflict resolution methodology is established by discussing a model for SPSA and its role when coupled with MGDA.
The set of N intents can be represented as , where denotes the nth intent characterized by the operational goal, , that includes a specific KPI and the corresponding desired magnitude of change or target value denoted by , expressed as pairs
Consider that a received intent, , with a specific directive such as “increase the energy efficiency by 5%” can be formally expressed as , where is energy efficiency and is .
2.1. A New Approach to Defining the ’Conflict’ in IDN
Consider the simultaneous reception of distinct intents, each linked to a unique KPI, , with a specific target value, . Each KPI , such as coverage, interference, and energy efficiency, can be tuned through a defined set of NCPs, , including parameters such as antenna tilt and downlink transmission power, as discussed in [11]. These NCPs can be shared across various operational goals to attain their respective target values . The total set of NCPs for each KPI is denoted as , where denotes the shared NCPs across all intents and denotes the intent-specific NCPs (e.g., , and ). For each intent , there is an associated loss function designed to quantify the disparity between the current state of the performance metric and its target value . This situation can be viewed as a multi-task optimization problem, where diverse intent goals drive the determination of an optimal set of parameters to minimize . Formally, the multi-task objective is expressed as
where is the pre-defined weight (i.e., priority) for nth intent and . In practice, a common objective involves minimizing the average loss with equal weights for all intents as
In the context of optimization, when utilizing the gradient descent directly, the update step can be given by , where represents a positive learning rate. In a given scenario, if the decrease in the loss for , , coincides with an increase in the loss for , , where , this situation can be interpreted as a conflict between intents. Alternatively, if the minimization of the average loss, , leads to an increase in the loss for any , , it can also be characterized as a conflict. In such situations, the occurrence of a conflict concerning gradient vectors can be characterized when two gradients ( and ) associated with opposing loss directions (specifically, when the cosine similarity, represented as , is less than or equal to zero, i.e., , where is the angle between and ), as in Figure 1.
In this defined context, the objective of conflict resolution is to optimize the so that both the average loss and each individual loss are minimized simultaneously. This phenomenon is known as conflicting gradients [12] and has been investigated in the literature [13,14,15,16,17] under the performance evolution of multi-task learning (MTL).
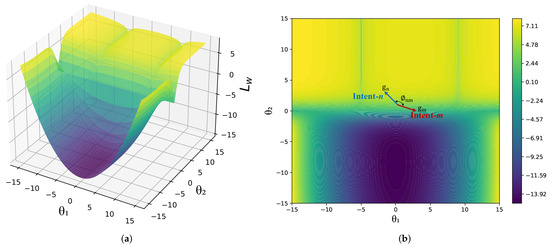
Figure 1.
(a) 3D plot of the average loss function of Toy example [13] based on the shared parameters, and (b) Contour plot of average loss function of Toy example and conflict.
2.2. Multiple Gradient Descent Algorithm (MGDA)
The MGDA [14], embodying an advanced methodology within the domain of a multi-objective optimization, employs the indispensable Karush–Kuhn–Tucker (KKT) conditions as crucial prerequisites for attaining optimality [18]. It is demonstrated that the solution to this optimization problem can be either zero, in which case the resulting point complies with the KKT conditions, or the solution provides a descent direction that enhances performance across all tasks. The simultaneous optimization of multiple interconnected tasks can be effectively managed through the application of MTL. In this particular learning paradigm, a unified model is developed and trained to effectively address a multitude of distinct yet interrelated tasks. The application of the MGDA in this context offers a promising methodology for obtaining a solution that not only furnishes a descent direction but also enhances performance across all tasks concurrently. Multi-objective optimization in terms of gradients can be expressed as
where is the gradient of the loss function of nth intent, is the weights of nth gradient and .
All methods presented in the literature for addressing the challenge of conflicting gradients operate under the assumption that the closed-form expressions of the loss functions for each task are readily accessible, allowing for the direct calculation of gradients by taking the derivatives of the respective loss functions. In the context of the IDN scenario, the computational complexity is attributed to the dynamic nature of the environment, rendering the calculation of gradients through the direct derivation of loss functions for each intent to be a computationally intensive process. This study proposes the application of SPSA within the context of MGDA in IDN to address conflicting intents, eliminating the necessity for closed-form expressions of loss functions. SPSA, as elaborated below, is a derivative-free method explicitly developed to approximate parameters that minimize the objective function by acquiring measurements directly from the environment [19].
2.3. Simultaneous Perturbation Stochastic Approximation (SPSA)
SPSA is a derivative-free optimization method designed to find the optimum input values, , which minimize a multivariate function , defined as
where is the input parameters of . This methodology proves especially advantageous when the function, , lacks a closed-form expression, thereby implying that the exact gradient is not readily available for utilization in gradient descent algorithms. In such scenarios, SPSA relies on noisy and stochastic function measurements, embodying a data-driven and robust approach for optimization in situations where a comprehensive understanding of the characteristics of the function is uncertain or limited [19].
It employs an iterative optimization approach, commencing with , initial input values of , and subsequently updating them using a stochastic approximation of gradient , denoted as , where is the nth element of at the iteration of t and given as
where is the perturbation size and signifies a random perturbation element applied to the nth parameter at the iteration of t, . For iteration, the iterative update of a parameter set, , with gradient approximations to minimize the , is given as
where the step size, , is defined in [20] as
The performance of the SPSA algorithm hinges on the critical choice of the step size, , and perturbation size, , with suggested values for computing and being and , respectively, as recommended in [21].
3. Proposed SPSA-Based MGDA for Conflict Resolution in IDN
The proposed method given in Algorithm 1 utilizes the MGDA for handling conflicting intents and SPSA to approximate the gradients due to the dynamic environment and the absence of a closed form of the loss function for each KPI. The system model, illustrated in Figure 2, outlines the process of receiving intents in the format of KPIs, , and target values, . Subsequently, the system identifies the shared NCPs, , to optimize each KPI. The gradients need to be approximated using the SPSA method to employ MGDA. Initially, the shared parameters are perturbed, and measurements, and , are obtained for each parameter set, and via the ns3 network simulator. Subsequently, losses, and (i.e., ), are computed based on the measurements and the target values that are requested from the intents. Afterward, gradients are estimated to leverage the MGDA algorithm, as outlined in (3), for the minimization of all the losses. Finally, the shared NCPs, , are updated based on the weights obtained from the MGDA algorithm.
| Algorithm 1: Proposed SPSA-based MGDA. |
 |
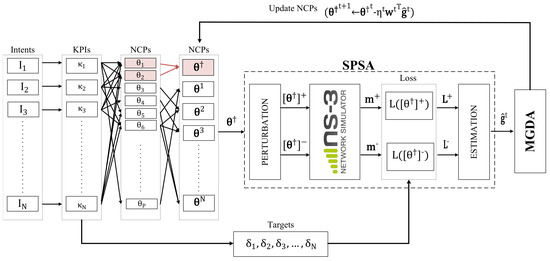
Figure 2.
Proposed SPSA-based MGDA system model , and .
4. Performance Analysis
4.1. SPSA-Based MGDA for Toy Example
The toy example presented in [13] is employed to illustrate the conflicting behavior of gradients in Figure 3 and Figure 4 when solely using the SPSA-based vanilla gradient descent (VGD) algorithm [22]. This scenario assumes the absence of closed-form loss functions (i.e., not utilizing derivatives for gradients), necessitating the measurement in each iteration. Hence, the SPSA algorithm was employed to approximate the gradients of , , and . Figure 3 illustrates contour plots of the loss functions , , and , along with the trajectory for the shared parameters, , when employing VGD to minimize . Furthermore, it is evident that increases after a certain number of iterations, while and consistently decrease when the objective is to minimize using VGD, as depicted in Figure 4. This scenario is defined as a conflict in the previous section.
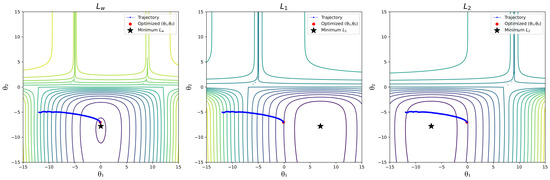
Figure 3.
Trajectories for , and, with SPSA-based VGD (Initial point for ()) is ()).
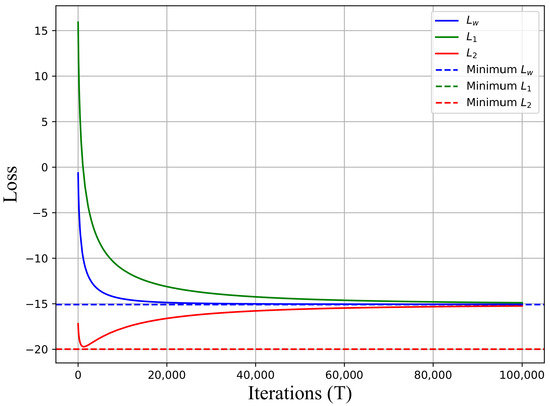
Figure 4.
Minimization of , and, with SPSA-based VGD (Min. points for () is ()).
In contrast, Figure 5 and Figure 6 demonstrate the application of the MGDA algorithm in the same scenario. Figure 5 illustrates the trajectory for the shared parameters, , when utilizing SPSA-based MGDA to minimize . The MGDA method facilitates the reduction of both and when the goal is to minimize , as depicted in Figure 5. This algorithm halts when any tasks, , , or the common objective, , reach the optimum point. In this example, reaches the minimum point, as depicted in Figure 6. However, the VGD algorithm solely concentrates on the common objective, , without considering any contributing tasks, and .
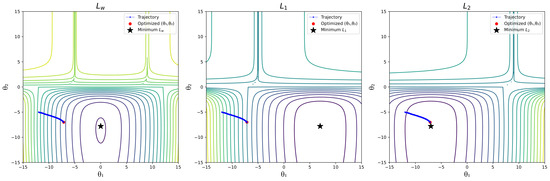
Figure 5.
Trajectories for , and with SPSA-based MGDA (Initial point for ()) is ()).
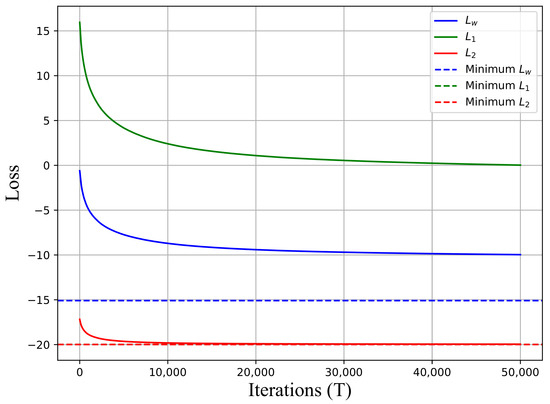
Figure 6.
Minimization of , and, with SPSA-based MGDA (Min. points for () is ()).
4.2. A Conflict Scenario in IDN with KPI Measurement Tools
One of the typical conflicts in the literature revolves around KPIs associated with coverage and interference [7,23,24,25]. This issue often arises due to the inherent trade-off between optimizing coverage, which involves extending the network reach and managing interference, which requires minimizing signal disruptions in neighboring cells. A vital indicator of the coverage within a network is the reference signal receive power (RSRP), which reflects the strength of the signal received by the user equipment. The mean RSRP can be employed as a KPI to provide a representative measurement of signal strength across the entire network by averaging RSRP values from currently active and utilized cells. The mean signal-to-interference ratio (SIR), excluding the influence of background noise registered by receivers, can be employed to evaluate interference in the network. This calculation aids in assessing the extent of inter-cell interference (ICI) and its consequent impact on network capacity and spectral efficiency.
Typically, these conflicting KPIs are commonly controlled by two shared control parameters: Transmission power and Antenna tilt angle [11]. The dynamic adjustment of transmission power and antenna tilt angle is crucial to optimize and balance these conflicting KPIs in wireless communication systems. Increasing transmission power levels diminishes outage probability at the cell edge, ensuring a more robust signal reach. Conversely, reducing power transmission levels effectively minimizes interference, thereby optimizing the network capacity. Similarly, adjusting the antenna tilt plays a pivotal role: reducing the tilt angle extends the coverage area, enhancing coverage in affected regions, whereas increasing tilt concentrates the signal within a smaller area, effectively mitigating inter-cell interference.
4.3. Simulation Setup
A cellular network model with three eNB sites is employed to model conflicts within an IDN approach as a simulation scenario. Among the 100 users, 80 are designated as call-text users, while the remaining 20 are involved in video streaming. This simulation scenario is evaluated using the ns-3 LENA platform, adhering to the parameters outlined in Table 1. The simulation involves two shared control parameters: Transmission power and Antenna tilt angle. The transmission power of the antenna is varied within a range of 30 dBm to 45 dBm, while the mechanical tilt of the antenna is adjusted within a range of to , with incremental adjustments of at each step. In Figure 7, the plot illustrates variations in KPIs (SINR and RSRP) corresponding to the adjustments made to two shared NCPs as illustrated in Figure 8.

Table 1.
Simulation Parameters.
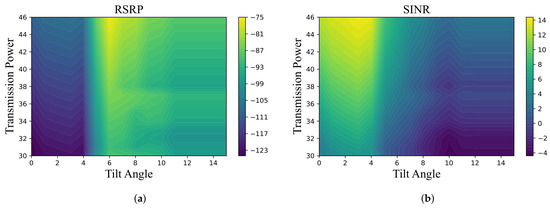
Figure 7.
(a) Variation of mean RSRP and (b) mean SINR with respect to shared parameters: transmission power and tilt angle.
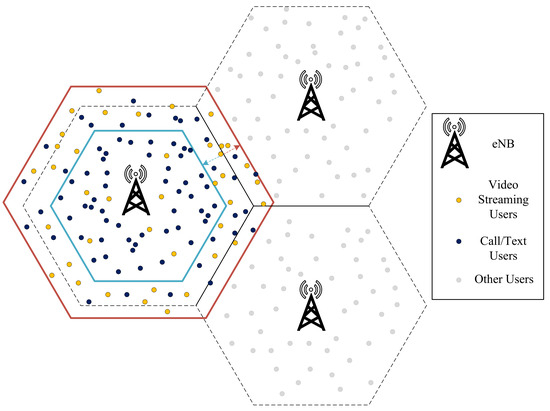
Figure 8.
Simulation scenario.
For each iteration, the simulations are run several times to obtain the measurements required for the objective function in line# 11, 12 of Algorithm 1 and consolidated output parameter measurement for the optimization of conflicting intents. Hence, each simulation runs for 10 s, and the measurements are performed to obtain RSRP and SINR values from the simulator. These values are used to estimate the gradient and optimize the expected output for the intent using MGDA.
4.4. Simulation Results
The initial parameters are set at 40 dBm for transmission power and for antenna tilt angle. The corresponding KPI values for RSRP and SINR with a confidence level are dBm and dB, respectively. The scenario assumes the simultaneous reception of two distinct intents for a sector site, with the target value of SINR set at dB for one intent and dBm for RSRP for the other. The optimization processes exclusively employ the SPSA-based VGD algorithm and the proposed SPSA-based MGDA, and a comparative analysis is conducted. Both algorithms aim to identify optimal parameter values that minimize losses per the specified target values within the intents.
In Figure 9 and Figure 10, two algorithms depict the variations in the loss functions, where denotes the RSRP loss, and represents the SINR loss. It is important to note that the objective function is to minimize the average losses for both algorithms. It is observed that the SPSA-based VGD algorithm successfully minimizes both losses initially, but the loss increases after reaching its minimum value (i.e., achieving the target value), as shown in Figure 9. This illustrates that the SPSA-based VGD algorithm encounters challenges in resolving conflicting situations, as evidenced by the observed increase in the loss after reaching its minimum value. On the other hand, the SPSA-based MGDA ensures the concurrent minimization of all losses without generating conflicts, as depicted in Figure 10. The algorithm concludes its operation when at least one target is achieved.
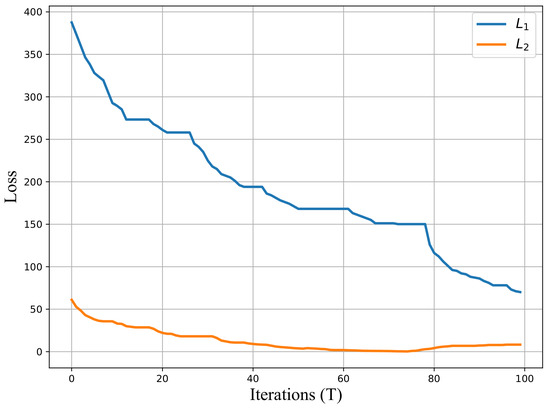
Figure 9.
Minimization of and with SPSA-based VGD.
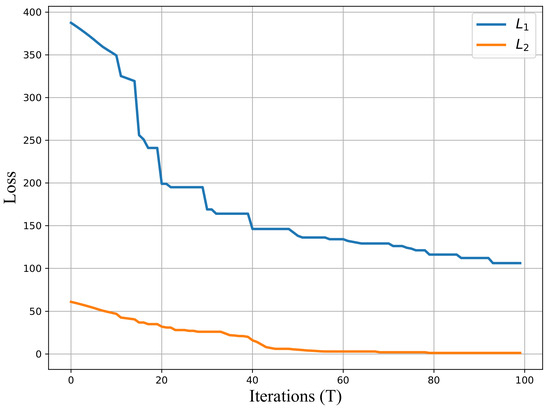
Figure 10.
Minimization of and with SPSA-based MGDA.
5. Conclusions
Conflict management is a critical challenge in emerging IDN owing to its key role in the validation of user intents. This paper proposes a novel approach to handle direct conflicts between competing user intents in order to realize an optimal deployment solution for them. The lack of a closed-form objective function serves as a motivation to employ a gradient-free optimization framework consisting of SPSA and MGDA. The proposed solution involves a perturbed search through the parameter space for selected NCPs (i.e., mechanical tilt and transmit power). Optimal values are determined for these NCPs that satisfy and meet the target values dictated by the user intents. An experimental analysis reinforces the assertions regarding the performance of the proposed solution, as optimal operational values are determined for the NCPs.
The future work expands upon the scope of the proposed solution in a complete intent processing pipeline with an active closed-loop control of an intent’s life cycle. Moreover, the selection criterion for the NCPs and the target values will be determined to tune the proposed algorithm for a generic design applicable in different types of conflicting scenarios.
Author Contributions
Conceptualization, I.C.; Methodology, I.C.; Software, K.M.; Validation, K.M.; Investigation, I.C.; Writing—original draft, I.C.; Writing—review & editing, K.M. and K.K.; Supervision, K.K. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
Author Idris Cinmere is funded for his Ph.D. by the Ministry of National Education in Turkiye (2018).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clemm, A.; Ciavaglia, L.; Granville, L.Z.; Tantsura, J. Intent-Based Networking-Concepts and Definitions. RFC 9315. 2022. Available online: https://www.rfc-editor.org/info/rfc9315 (accessed on 1 February 2024).
- Mehmood, K.; Kralevska, K.; Palma, D. Intent-driven autonomous network and service management in future cellular networks: A structured literature review. Comput. Netw. 2023, 220, 109477. [Google Scholar] [CrossRef]
- Banerjee, A.; Mwanje, S.S.; Carle, G. Contradiction Management in Intent-driven Cognitive Autonomous RAN. In Proceedings of the 2022 IFIP Networking Conference (IFIP Networking), Catania, Italy, 13–16 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- ETSI. Zero-Touch Network and Service Management (ZSM); Intent-Driven Autonomous Networks; Generic Aspects. 2023. Available online: https://www.etsi.org/committee/1431-zsm (accessed on 1 February 2024).
- Telemanagement Forum (TMForum). Intent in Autonomous Networks. Introductory Document IG1253. TMForum. 2022. Available online: https://www.tmforum.org/resources/how-to-guide/ig1253-intent-in-autonomous-networks-v1-0-0/ (accessed on 1 February 2024).
- Mwanje, S.S.; Banerjee, A.; Goerge, J.; Abdelkader, A.; Hannak, G.; Szilágyi, P.; Subramanya, T.; Goser, J.; Foth, T. Intent-driven network and service management: Definitions, modeling and implementation. ITU J. Future Evol. Technol. 2022, 3, 555–569. [Google Scholar] [CrossRef]
- Banerjee, A.; Mwanje, S.S.; Carle, G. Toward Control and Coordination in Cognitive Autonomous Networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 49–60. [Google Scholar] [CrossRef]
- Cinemre, I.; Mehmood, K.; Kralevska, K.; Mahmoodi, T. Direct-Conflict Resolution in Intent-Driven Autonomous Networks. In Proceedings of the European Wireless 2023, 28th European Wireless Conference, Rome, Italy, 2–4 October 2023; pp. 1–6. [Google Scholar]
- Baktir, A.C.; Junior, A.D.N.; Zahemszky, A.; Likhyani, A.; Temesgene, D.A.; Roeland, D.; Biyar, E.D.; Ustok, R.F.; Orlić, M.; D’Angelo, M. Intent-based cognitive closed-loop management with built-in conflict handling. In Proceedings of the 2022 IEEE 8th International Conference on Network Softwarization (NetSoft), Milan, Italy, 27 June–1 July 2022; pp. 73–78. [Google Scholar] [CrossRef]
- Perepu, S.K.; Martins, J.P.; Souza, R.; Dey, K. Intent-based multi-agent reinforcement learning for service assurance in cellular networks. In Proceedings of the GLOBECOM 2022-2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 2879–2884. [Google Scholar] [CrossRef]
- Bandh, T.; Romeikat, R.; Sanneck, H.; Tang, H. Policy-based coordination and management of SON functions. In Proceedings of the 12th IFIP/IEEE International Symposium on Integrated Network Management (IM 2011) and Workshops, Dublin, Ireland, 23–27 May 2011; pp. 827–840. [Google Scholar] [CrossRef]
- Yu, T.; Kumar, S.; Gupta, A.; Levine, S.; Hausman, K.; Finn, C. Gradient surgery for multi-task learning. Adv. Neural Inf. Process. Syst. 2020, 33, 5824–5836. [Google Scholar]
- Liu, B.; Liu, X.; Jin, X.; Stone, P.; Liu, Q. Conflict-averse gradient descent for multi-task learning. Adv. Neural Inf. Process. Syst. 2021, 34, 18878–18890. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Shi, G.; Li, Q.; Zhang, W.; Chen, J.; Wu, X.M. Recon: Reducing Conflicting Gradients from the Root for Multi-Task Learning. arXiv 2023, arXiv:2302.11289. [Google Scholar]
- Navon, A.; Shamsian, A.; Achituve, I.; Maron, H.; Kawaguchi, K.; Chechik, G.; Fetaya, E. Multi-task learning as a bargaining game. arXiv 2022, arXiv:2202.01017. [Google Scholar]
- Senushkin, D.; Patakin, N.; Kuznetsov, A.; Konushin, A. Independent Component Alignment for Multi-Task Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 20083–20093. [Google Scholar]
- Désidéri, J.A. Multiple-gradient descent algorithm (MGDA) for multiobjective optimization. Comptes Rendus Math. 2012, 350, 313–318. [Google Scholar] [CrossRef]
- Spall, J.C. An overview of the simultaneous perturbation method for efficient optimization. Johns Hopkins Apl. Tech. Dig. 1998, 19, 482–492. [Google Scholar]
- Wulff, B.; Schuecker, J.; Bauckhage, C. Spsa for layer-wise training of deep networks. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Proceedings, Part III 27. Springer: Berlin/Heidelberg, Germany, 2018; pp. 564–573. [Google Scholar]
- Spall, J. Implementation of the simultaneous perturbation algorithm for stochastic optimization. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 817–823. [Google Scholar] [CrossRef]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Moysen, J.; Giupponi, L. Self-coordination of parameter conflicts in D-SON architectures: A Markov decision process framework. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 1–18. [Google Scholar] [CrossRef]
- Bag, T.; Garg, S.; Rojas, D.F.P.; Mitschele-Thiel, A. Machine Learning-Based Recommender Systems to Achieve Self-Coordination Between SON Functions. IEEE Trans. Netw. Serv. Manag. 2020, 17, 2131–2144. [Google Scholar] [CrossRef]
- Lateef, H.Y.; Imran, A.; Imran, M.A.; Giupponi, L.; Dohler, M. LTE-advanced self-organizing network conflicts and coordination algorithms. IEEE Wirel. Commun. 2015, 22, 108–117. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).