Abstract
The optimization and allocation of transport cost savings among stakeholders are two important issues that influence the satisfaction of information providers, drivers and passengers in ridesharing recommendation systems. For optimization issues, finding optimal solutions for nonconvex constrained discrete ridesharing optimization problems poses a challenge due to computational complexity. For the allocation of transport cost savings issues, the development of an effective method to allocate cost savings in ridesharing recommendation systems is an urgent need to improve the acceptability of ridesharing. The hybridization of different metaheuristic approaches has demonstrated its advantages in tackling the complexity of optimization problems. The principle of the hybridization of metaheuristic approaches is similar to a marriage of two people with the goal of having a happy ending. However, the effectiveness of hybrid metaheuristic algorithms is unknown a priori and depends on the problem to be solved. This is similar to a situation where no one knows whether a marriage will have a happy ending a priori. Whether the hybridization of the Firefly Algorithm (FA) with Particle Swarm Optimization (PSO) or Differential Evolution (DE) can work effectively in solving ridesharing optimization problems needs further study. Motivated by deficiencies in existing studies, this paper focuses on the effectiveness of hybrid metaheuristic algorithms for solving ridesharing problems based on the hybridization of FA with PSO or the hybridization of FA with DE. Another focus of this paper is to propose and study the effectiveness of a new method to allocate ridesharing cost savings to the stakeholders in ridesharing systems. The developed hybrid metaheuristic algorithms and the allocation method have been compared with examples of several application scenarios to illustrate their effectiveness. The results indicate that hybridizing FA with PSO creates a more efficient algorithm, whereas hybridizing FA with DE does not lead to a more efficient algorithm for the ridesharing recommendation problem. An interesting finding of this study is very similar to what happens in the real world: “Not all marriages have happy endings”.
1. Introduction
Human activities such as daily commutes to work, business travel, leisure trips, manufacturing, logistics, etc., often consume different types of energy and generate enormous amounts of greenhouse gases in the atmosphere, which leads to global warming. Sustainable transport attempts to mitigate global warming through energy-efficient, affordable modes of transport to achieve the benefits of reduced carbon emissions and energy consumption and improved cost savings and accessibility with less reliance on fuels [1,2]. Sustainable transport has become one of the most important topics related to Sustainable Development Goals (SDGs), as transportation is the major driving force behind a growing world demand for energy [3]. As about one-fourth of energy-related emissions come from transport, sustainable transport is mainstreamed across several SDGs in the 2030 Agenda for Sustainable Development [4,5].
The sharing economy concept provides an effective approach to the development of innovative transport models and realizes sustainable transport. In the literature, there were many studies on the effectiveness of applying different sharing-based transport modes, such as ridesharing [6], car-sharing [7,8], bike-sharing [9] and autonomous car-sharing [10], to reduce greenhouse gas emissions. The analysis of [11] compared the greenhouse gas emissions of electrified fleets and gasoline-powered fleets, and it indicated that electrified fleets had 40–45% lower greenhouse gas costs per trip than gasoline-powered fleets. The paper reported in [12] for several car-sharing case studies showed that a 3–18% reduction of greenhouse gas emissions can be achieved. The study also indicated that ridesharing would introduce a much more significant reduction in greenhouse gas emissions. The analysis of [13] indicated that shared mobility services had the potential to eliminate 6.3% of passenger transport emissions on average, and the mitigation potential varied widely across cities. The above discussions indicate the potential for shared mobility services to mitigate greenhouse gas emissions.
Ridesharing is one of the important shared mobility services. It has been applied in different application scenarios to share travel costs, reduce energy consumption and mitigate the negative impact on the environment. These application scenarios include the provision of ridesharing services in universities [14,15] and providing ridesharing services by transport service providers such as Lyft [16], Uber [17], Didi [18], Wingz [19] and Via [20] to the general public. In the literature, different aspects and issues of ridesharing services have been studied. These research issues include studies on detrimental factors influencing the adoption and use of ridesharing by people [21,22] and the optimization of performance [23,24,25], as well as the consideration of social factors and trust factors in ridesharing systems [26,27]. In this study, we will focus on the optimization issue and cost allocation issue in ridesharing recommendation systems.
The optimization issue in ridesharing recommendation systems is used to determine the set of drivers sharing rides and the passengers on each ride according to the requirements of drivers and passengers. Optimization of performance in ridesharing recommendation systems is usually formulated as a nonconvex constrained discrete optimization problem. Finding optimal solutions for nonconvex constrained discrete optimization problems is a challenging issue due to computational complexity. Due to the limitation of classical optimization methods to solve nonconvex constrained discrete optimization problems, many metaheuristic methods such as Firefly Algorithm (FA) [28], Particle Swarm Optimization (PSO) [29], Differentiation Evolution (DE) [30] and their variants [31] have been proposed to find solutions for ridesharing recommendation problems. The hybridization of different metaheuristic approaches has demonstrated its advantages in the literature. For example, there were success stories of hybrid DE/Firefly approaches [32,33] as well as hybridization of Firefly with the PSO approach [34,35,36,37].
The principle of the hybridization of metaheuristic approaches is similar to a marriage of two people with the goal of having a happy ending by helping each other. However, no one knows whether a marriage will have a happy ending a priori. The effectiveness of hybrid metaheuristic algorithms is unknown a priori and depends on the problem to be solved. Whether the hybridization of FA with PSO or DE can work effectively in solving ridesharing recommendation problems needs further study. In the studies reported in [38,39], some preliminary results show the merits of hybridization of FA with PSO or DE. However, only one of the DE mutation strategies was used in the hybrid algorithm to solve ridesharing problems. It is interesting to study whether other well-known DE mutation strategies can work effectively through hybridization with FA to solve ridesharing recommendation problems. In addition, there is a lack of comparative studies on the effectiveness of the hybridization of FA with PSO and the hybridization of FA with different DE mutation strategies to solve ridesharing recommendation problems. Motivated by deficiencies in existing studies, one focus of this paper will be on the development of hybrid metaheuristic algorithms for solving ridesharing optimization problems based on the hybridization of FA with PSO or DE. The hybrid metaheuristic algorithms developed in this paper include a discrete Firefly-PSO (FPSO) algorithm and six discrete Firefly-DEi (FDEi) algorithms, where i , for solving the ridesharing optimization problem.
Besides the optimization issue, the study of how to allocate the benefits of travel cost savings in transportation systems has attracted researchers’ attention in recent years. A review of approaches to allocating cost savings in collaborative transportation systems can be found in [40]. Another focus of this paper is on the development of a method to allocate ridesharing cost savings. The problem of allocating travel cost savings in ridesharing systems can be defined based on the cooperative game theory, as the stakeholders in a ridesharing system can be modeled as the players that form coalitions and cooperate with one another to achieve some goals in ridesharing. These well-known solution approaches to allocating cost savings include the Shapley value [41], nucleolus [42] and proportional methods [43]. Although these well-known solution approaches to allocating travel cost savings are available and well founded, some of these approaches are computationally infeasible for real cases due to complexity issues. Therefore, computationally efficient methods such as proportional methods are usually used in practice. To address this issue, several heuristic proportional methods have been proposed to reduce computational complexity [44,45,46]. These heuristic proportional methods were referred to as the Local Proportional (LP) Method, Fifty–Fifty (FF) Method and Global Proportional (GP) Method in [47,48]. These heuristic proportional methods allocate the benefits among members in a cooperative game based on coalitions that are defined intuitively. In this paper, we defined two coalitions called the driver group and the passenger group (DGPG) in a ridesharing system. Based on DGPG, we developed a new method to divide the benefits (cost savings) among the stakeholders in the ridesharing system. The benefits were first divided into three parts and allocated to information providers, the driver group and the passenger group, respectively. The proportional method was then applied to divide the benefits among the set of drivers in the driver group. Similarly, the proportional method was then applied to divide the benefits among the set of passengers in the passenger group. The developed hybrid metaheuristic algorithms and allocation method had been verified by examples of several application scenarios.
The contributions of this study are twofold. First, we have developed several hybrid metaheuristic algorithms for solving ridesharing problems based on combining FA with PSO or DE approaches and studied the effectiveness of these hybrid metaheuristic algorithms. Besides the optimization of cost savings, a new allocation method has been proposed in this study to improve the number of acceptable shared rides and the number of ridesharing participants. The new allocation method can be applied to deal with different minimal expectations of drivers and passengers by setting a parameter.
The rest of this paper is organized as follows. In Section 2, we will first introduce the ridesharing problem formulation and then define a new proportional method to allocate cost savings. In Section 3, we will first review the standard Firefly Algorithm and then propose several hybrid metaheuristic algorithms for solving the ridesharing cost = saving optimization problems, including the hybrid discrete Firefly-PSO (FPSO) algorithm and six hybrid discrete Firefly-DEi (FDEi) algorithms, where i denotes a specific mutation strategy selected from the six well-known mutation strategies in the Differential Evolution approach. In Section 4, we will present the results for verification of the developed hybrid metaheuristic algorithms and compare the effectiveness of these algorithms. We will also compare the proposed allocation method with the existing methods, including the Local Proportional Method, Fifty–Fifty Method and Global Proportional Method in the literature. We will briefly discuss the results in Section 5 and conclude this paper in Section 6.
2. Optimization Problem in Ridesharing Recommendation Systems and a New Proportional Method to Allocate Cost Savings
This paper focuses on two research issues: (1) a comparative study of applying hybrid metaheuristic algorithms developed based on hybridizing FA with PSO or DE to solve the ridesharing optimization problem and (2) the development of a new cost-saving allocation method and a study of its effectiveness for ridesharing systems. In this section, we will briefly review the ridesharing optimization problem and propose a new cost-saving allocation method for the ridesharing system. The notation used in this section is defined in Table 1.

Table 1.
Notation of symbols, variables and parameters.
A ridesharing recommendation system is defined by a set of drivers, , a set of passengers, , and passengers’ requests, = , where is the origin, is the destination, is the earliest departure time, is the latest arrival time, and is the number of seats requested by passenger ; drivers’ requests = , where is the origin, is the destination, is the earliest departure time, is the latest arrival time, and is the number of seats available for a driver . The ridesharing recommendation system applies proper bid generation procedures such as the ones proposed in [46] to generate the bids: , , for the driver, , and the bids, , , for the passenger, , according to the drivers’ requests, , and passengers’ requests, = , respectively, where and are defined in Table 1. The bids, , , for the driver, , and the bids, , , for the passenger, , will be submitted to the ridesharing recommendation system.
The ridesharing optimization problem is defined by decision variables , , and , . The decision variable is equal to 1 if is a winning bid. Otherwise, the decision variable is equal to 0. The decision variable is equal to 1 if is a winning bid. Otherwise, the decision variable is equal to 0. The objective function is the overall cost savings of the ridesharing system. The ridesharing optimization problem is used to determine the values of the decision variables , , and , such that the objective function in (1) is maximized subject to the following constraints: the demand and supply constraints specified in (2) and (3), the cost-saving constraint specified in (4), the drivers’ single winning bid constraint specified in (5) and the binary values constraint for the decision variables specified in (6) and (7).
s.t.
The above ridesharing optimization problem can be solved by applying different solution approaches. In this study, we will develop several hybrid metaheuristic algorithms to solve the above ridesharing optimization problem based on hybridizing FA with PSO or DE in the next section. Suppose a solution for the above problem is found. A cost-saving allocation method must be applied to divide the cost savings of the solution properly and to allocate the cost savings to the stakeholders of the ridesharing system, including the information provider, drivers and passengers. A cost allocation method can be defined by the portion of allocated to each stakeholder of the ridesharing system. The concept of shared values is used to describe the portion of the cost savings, , allocated to each stakeholder of the ridesharing system. In this paper, we use , and to denote the shared values for the information provider, passenger and driver , respectively. Please refer to Table 2 for the definition of , and . The shared values must satisfy the following constraints , where , and . Based on the concept of shared values, the portion of allocated to the information provider is represented by , where is defined in (8). The portion of allocated to passenger is represented by , where is defined in (9). The portion of allocated to driver is represented by , where is defined in (10). In this paper, we define a new method to allocate cost savings based on the shared values , and defined in Table 2.

Table 2.
The DGPGP method for dividing cost savings among the ridesharing participants.
The shared value, , for the information provider is determined by the ridesharing service provider. Note that the cost savings allocated to the information provider are . Typically, the value of must be set properly such that the cost savings allocated to the information provider are sufficient to maintain the operations of the ridesharing system. However, if the value of is too big, the cost savings allocated to drivers and passengers will not be sufficient to make more drivers and passengers accept ridesharing. Another parameter that influences the cost savings allocated to the passengers and drivers is . The value of must be set properly. The cost savings allocated to the passenger group are , where . The cost savings allocated to passengers are . The cost savings allocated to the driver group are , where . The cost savings allocated to drivers are .
If the value of is too big, the cost savings allocated to drivers will not be sufficient to make more drivers accept ridesharing. If the value of is too small, the cost savings allocated to passengers will not be sufficient to make more passengers accept ridesharing. Therefore, in addition to setting the value of properly, the value of must be set properly such that the cost savings allocated to drivers and passengers are sufficient to make more drivers and passengers accept ridesharing.
Cost savings are one of the key determinant factors for potential users of ridesharing services, including drivers and passengers, to decide whether or not to share a ride. A driver or a passenger may accept to share a ride only if their expected cost savings can be satisfied. To characterize whether a ride can satisfy the expected cost savings of a driver or a passenger, the concept of minimal expected reward rates has been introduced in [47,48]. The minimal expected reward rate is the minimal expected cost savings of a ridesharing participant due to ridesharing divided by the original cost. In this paper, it is assumed that minimal expected reward rate for all drivers is the same and is denoted by . In this paper, it is assumed that minimal expected reward rate for all passengers is the same and is denoted by . A ride is called an acceptable ride if the reward rate for the driver on the ride is greater than or equal to the minimal expected reward rate of drivers, , and the reward rate for each passenger on the ride is greater than or equal to the minimal expected reward rate . The number of acceptable rides and the number of ridesharing participants on acceptable rides are important performance metrics to assess the effectiveness of cost-saving allocation methods for ridesharing systems. We will use these performance metrics to illustrate the effectiveness of the new proposed allocation method.
3. Development of Hybrid Algorithms Based on Hybridization of Firefly Algorithm with PSO or DE
Before presenting the hybrid metaheuristic algorithms developed based on the hybridization of the Firefly Algorithm with the PSO approach or DE approach for solving the ridesharing optimization problem, we first briefly review the Firefly Algorithm. We then introduce the hybrid metaheuristic algorithms. To describe the discrete Firefly Algorithm and the discrete hybrid metaheuristic algorithms, we define the notation in Table 3.
| Procedure 1: CS to map a real value to zero or one |
| Input: Output: Begin If If Generate return End |

Table 3.
Notation of Firefly Algorithm and Hybrid Algorithms.
3.1. Fitness Function
In an evolutionary algorithm, a fitness function is used as an indicator to quantize the quality of solutions in the solution-finding processes. For a constrained optimization problem, a proper fitness function needs to be designed to take into account the quality of a solution in terms of the objective function value and violation of constraints. In the literature, a variety of approaches to dealing with violations of constraints have been proposed. One common concept of these approaches is the use of penalty terms in the fitness function. These approaches are called penalty methods in optimization theory [49]. Although penalty methods can be applied to deal with constraints, they suffer from the drawbacks of performance degradation due to the improper setting of penalty coefficients. For this reason, an alternative approach proposed in [50] is adopted in this study to deal with constraints. This approach discriminates between feasible and infeasible solutions to deal with constraints without penalty coefficients. By applying this approach, the objective function value of the worst feasible solution in the current population is calculated by , where = { is a feasible solution in the current population. The fitness function is defined as , where , , , and .
3.2. Firefly Algorithm
The Firefly Algorithm is a nature-inspired metaheuristic method. It was inspired by fireflies’ flashing patterns and behavior. The Firefly Algorithm mimics the behavior of fireflies: the less bright firefly moves towards the brighter one. In case no brighter one can be found, a firefly moves randomly. In the Firefly Algorithm, a brighter firefly refers to a firefly with a better fitness function value. The underlying assumption of the Firefly Algorithm is that fireflies are attracted to other ones regardless of their sex.
The Firefly Algorithm follows the paradigm of evolutionary algorithms to solve problems. Evolutionary algorithms use the mechanism of reproduction, mutation, crossover and selection in biological evolution to solve problems. Typically, an evolutionary algorithm starts with the initialization of a randomly generated population of candidate solutions. Each candidate solution in the population is referred to as an individual of the population. The quality of candidate solutions is characterized by the fitness function. The individuals in the population evolve from one generation to another. In each generation, the individuals in the population undergo the operations of mutation, crossover and selection to attempt to improve the quality of candidate solutions. The evolution processes terminate when a pre-specified number of generations is reached. There are several common parameters used in an evolutionary algorithm, including population size, , the total number of generations, , and the dimension of the problem, . In addition to these common parameters, there are other parameters specific to each type of metaheuristic approach. For example, the Firefly Algorithm needs the parameters of the light absorption coefficient, , and the attractiveness, . A flowchart of the Firefly Algorithm is shown in Figure 1. The way the -th firefly in position moves toward the -th firefly in the -th dimension and reaches a new position is according to (11), with and being defined in Table 3.
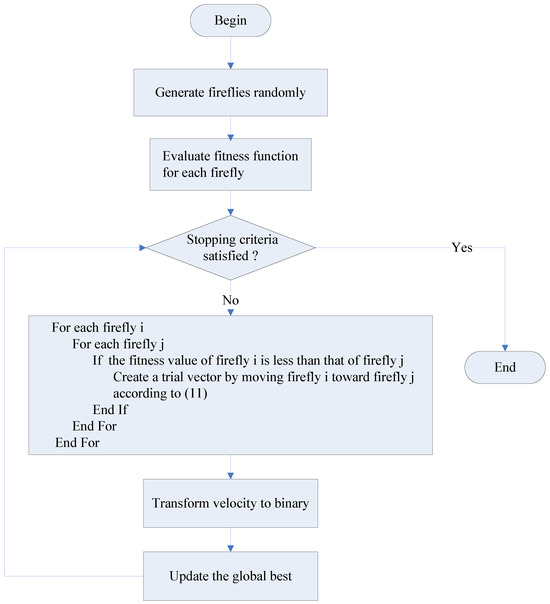
Figure 1.
A flowchart of discrete Firefly Algorithm.
The discrete Firefly Algorithm is defined in Algorithm 1:
| Algorithm 1: Discrete Firefly Algorithm |
| Input: , Output: the global best, Step 1: Generate fireflies in the initial population of swarm Step 2: While () Evaluate the fitness function for For each For each If For Move the i-th firefly toward the j-th firefly in the n-th dimension: Transform to binary and update i-th firefly i as follows: Generate randomly based on uniform distribution End For Evaluate End If End For End For Update the global best End While |
3.3. Discrete Firefly-PSO (FPSO) Algorithm and Discrete Firefly-DEi (FDEi) Algorithm
Hybrid Firefly-based metaheuristic algorithms can be developed by extending fireflies’ behavior. For example, in case one firefly fails to find another better firefly to update its position, the firefly will attempt to fly following the behavior of other approaches, such as PSO and DE, to create a trial solution. Table 4 lists PSO and six DE strategies to create a trial solution in case one firefly fails to find a better one. This way of combining the Firefly Algorithm with PSO or DE approaches to create a new candidate solution leads to hybrid metaheuristic algorithms. Figure 2 shows the flowchart of a discrete hybrid Firefly Algorithm obtained by hybridizing the Firefly Algorithm with a selected strategy to create a trial vector.

Table 4.
The methods to create a trial vector in PSO and DE approaches.
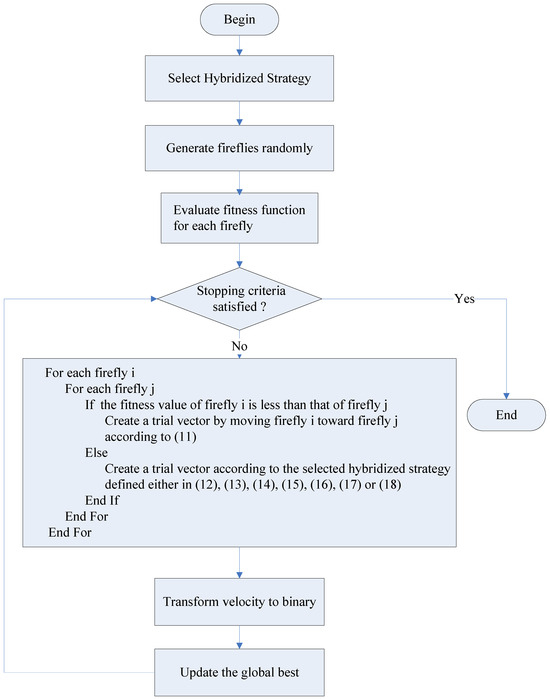
Figure 2.
A flowchart of discrete hybrid Firefly Algorithm with a selected strategy.
The strategy that PSO creates a trial solution is based on Formula (12), which uses two parameters, the cognitive acceleration coefficient, , and the social acceleration coefficient, , to take into account the difference between the current individual and the personal best as well as the difference between the current individual and the global best. The pseudocode of the discrete Firefly-PSO (FPSO) algorithm is shown in Algorithm 2.
| Algorithm 2: Discrete Firefly-PSO (FPSO) Algorithm |
| Input: , Output: the global best, Step 1: Generate fireflies in the initial population of swarm Step 2: While () Evaluate the fitness function for each firefly For each For each If Step 2.1: Fly according to fireflies’ pattern For Move the i-th firefly toward the j-th firefly in the n-th dimension Transform to binary and update -th firefly as follows: Generate randomly based on uniform distribution End For Else Step 2.2: Fly according to particle swarm’s pattern to attempt to increase diversity For Generate , a random variable with uniform distribution Generate , a random variable with uniform distribution Transform each element of the trial vector to one or zero End For End If End For End For Update the global best End While |
The DE approach provides six strategies referred to as DE1, DE2, DE3, DE4, DE5 and DE6 in this paper. These DE strategies can be used to create a trial solution based on either Formula (13) for mutation strategy DE1, Formula (14) for mutation strategy DE2, Formula (15) for mutation strategy DE3, Formula (16) for mutation strategy DE4, Formula (17) for mutation strategy DE5 or Formula (18) for mutation strategy DE6. The differences between these methods are the ways in which to calculate mutant vectors. For example, in DE1, three individuals, , and , are randomly sampled from the current population and then combined according to Formula (13) to calculate the mutant vector. In DE2, the best individual, , and two individuals, and , are randomly sampled from the current population and then combined according to Formula (14) to calculate the mutant vector. In DE3, five individuals, , , , and , are randomly sampled from the current population and then combined according to Formula (15) to calculate the mutant vector. In DE4, the best individual, , and four individuals, , , and , are randomly sampled from the current population and then combined according to Formula (16) to calculate the mutant vector. In DE5, the current individual, , the best individual, , and two individuals, and , are randomly sampled from the current population and then combined according to Formula (17) to calculate the mutant vector. In DE6, the current individual, , the best individual, , and four individuals, , , and , are randomly sampled from the current population and then combined according to Formula (18) to calculate the mutant vector. After the mutant vector has been calculated, the crossover operation will be applied to the mutant vector to find the trial vector. A Firefly Algorithm hybridized with Dei is referred to as the Discrete Firefly-DEi (FDEi) Algorithm. The pseudocode of the FDEi Algorithm is shown in Algorithm 3.
| Algorithm 3: Discrete Firefly-DEi (FDEi) Algorithm |
| Input: , Output: the global best, Step 1: Generate fireflies in the initial population of swarm Step 2: While () Evaluate the fitness function for each firefly For each For each If Step 2.1: Fly according to fireflies’ pattern For Move the i-th firefly toward the j-th firefly in the n-th dimension Transform as follows: Generate randomly based on uniform distribution End For Else Step 2.2: Fly according to particle swarm’s pattern to attempt to increase diversity For Apply Strategy DEi to create the n-th dimension of trial vector Transform each element of the trial vector to one or zero End For End If End For End For Update the global best End While |
4. Results
The hybrid algorithms and the method to allocate cost savings developed in the previous section were tested to compare the effectiveness of different hybridization strategies as well as the proposed cost-saving allocation method. The examples for testing the hybrid algorithms are available for download via the following link:
https://drive.google.com/drive/folders/1DRzq7XubK105XrnSpjVpQGLubj73id5K?usp=sharing (accessed on 29 November 2023).
4.1. Comparison of Hybrid Algorithms
The results presented in this section include the discrete version of the Firefly Algorithm, the PSO algorithm, the Differential Evolution algorithms with the six well-known mutation strategies and the hybrid algorithms developed in this paper. The hybrid algorithm developed by applying the Firefly Algorithm and Differential Evolution with Mutation Strategy i is denoted by FDEi. The hybrid algorithm developed by applying Firefly Algorithm and PSO is denoted by FPSO. The discrete version of Differential Evolution with Mutation Strategy i is denoted by DEi.

Table 5.
Parameters used in all DE, PSO and Firefly algorithms.

Table 6.
Parameters used in all hybrid algorithms.
Based on the parameters, all the algorithms mentioned above were applied to find the solutions for the test cases. We ran each algorithm ten times, and the results were recorded. The average fitness function values and the average generations of the best solutions found by each algorithm were calculated and summarized in Table 7 and Table 8 for population size = 10.

Table 7.
Average fitness function values and average generations for hybrid FDEi algorithms, where I and FPSO algorithm with population size = 10.

Table 8.
Average fitness function values and average generations for native discrete DE algorithms and PSO with population size = 10.
The results in Table 7 and Table 8 show that the average fitness function values achieved by FPSO are the same as the ones found by the PSO for all test cases for = 10. But the average generations for which FPSO found the best solutions are much smaller than those of PSO for all test cases. This indicates that FPSO is superior to PSO in terms of convergence rate. In addition, FPSO outperforms FA in average fitness function values and average generations for most test cases. This indicates that FPSO improves the performance and convergence rate of FA.
The results in Table 7 and Table 8 show that the average fitness function values achieved by FDEi are greater than those found by the DEi and FA for most of the test cases for = 10. However, the average generations for which FDEi found the best solutions are not always smaller than those of DEi for all test cases. This means that FDEi improves the performance but not the convergence rate of FA for = 10.
The results in Table 7 and Table 8 show that the average fitness function values achieved by FPSO are greater than those found by the FDEi for most of the test cases for = 10. In addition, the average generations for which FPSO found the best solutions are smaller lower than those of FDEi for most test cases. This indicates that FPSO outperforms FDEi in terms of performance and convergence rate for = 10.
Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the average fitness function values and (b) average generations for Case 1 through Case 6 with population size = 10.
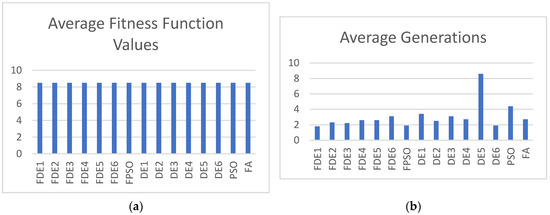
Figure 3.
(a) Average fitness function values; (b) average generations for Case 1 with population size NP = 10.
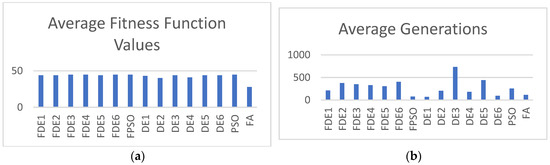
Figure 4.
(a) Average fitness function values; (b) average generations for Case 2 with population size NP = 10.
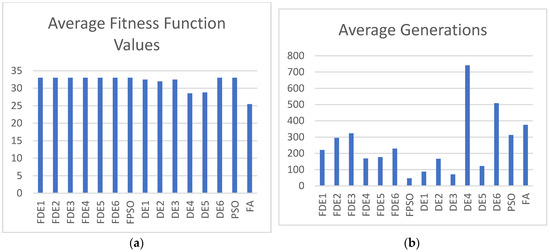
Figure 5.
(a) Average fitness function values; (b) average generations for Case 3 with population size = 10.
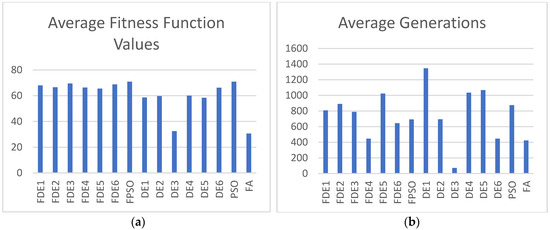
Figure 6.
(a) Average fitness function values; (b) average generations for Case 4 with population size NP = 10.
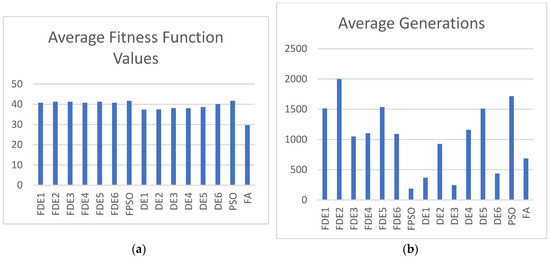
Figure 7.
(a) Average fitness function values; (b) average generations for Case 5 with population size = 10.
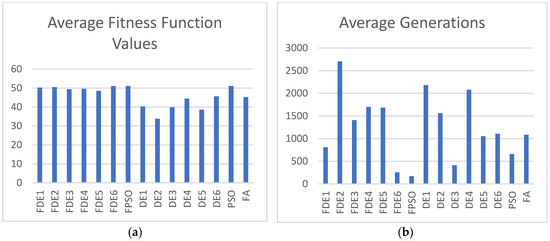
Figure 8.
(a) Average fitness function values; (b) average generations for Case 6 with population size = 10.
Figure 4 shows the average fitness function values and (b) average generations for Case 2 with population size = 10.
The average fitness function values and the average generations for which each algorithm found the best solutions were calculated and summarized in Table 9 and Table 10, respectively, for population size = 30.

Table 9.
Average fitness function values and average generations for hybrid FDEi algorithms, where i and FPSO algorithm with population size = 30.

Table 10.
Average fitness function values and average generations for native discrete DE algorithms and PSO with population size = 30.
The results in Table 9 and Table 10 show that the average fitness function values achieved by FPSO are the same as the ones found by the PSO for all test cases for = 30. But the average generations for which FPSO found the best solutions are much smaller than those of PSO for all test cases. This indicates that FPSO is superior to PSO in terms of convergence rate.
The results in Table 9 and Table 10 show that the average fitness function values achieved by FDEi are greater than or equal to those found by the DEi for all the test cases for = 30. However, the average generations for which FDEi found the best solutions are not and can be much larger than those of DEi for many test cases for = 30. This means that FDEi improves the performance but not the convergence rate of DEi for = 30.
The results in Table 9 and Table 10 show that the average fitness function values achieved by FPSO are the same as those found by the FDEi for all the test cases for = 30. In addition, the average generations for which FPSO found the best solutions are much smaller than those of FDEi for most test cases, with the exception of Case 1. The average generations for which FPSO found the best solutions are either no greater than or much smaller than those of standard PSO and FA for all test cases. This indicates that FPSO improves the performance and convergence rate of PSO and FA.
Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the (a) average fitness function values and (b) average generations for Case 1 through Case 6 with population size = 30.
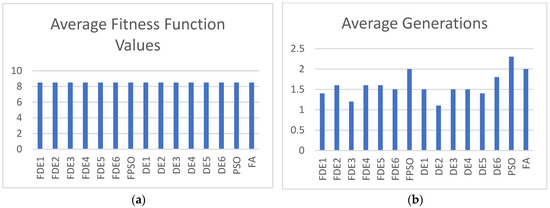
Figure 9.
(a) Average fitness function values; (b) average generations for Case 1 with population size = 30.
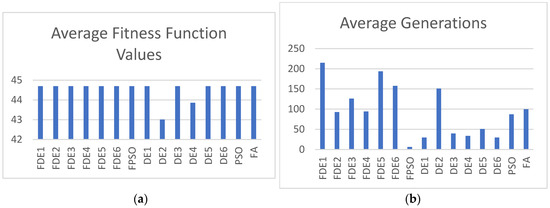
Figure 10.
(a) Average fitness function values; (b) average generations for Case 2 with population size = 30.
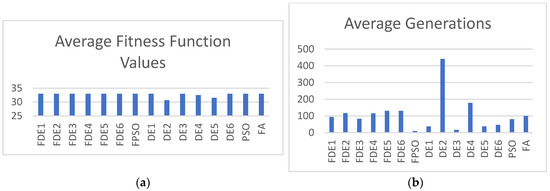
Figure 11.
(a) Average fitness function values; (b) average generations for Case 3 with population size = 30.
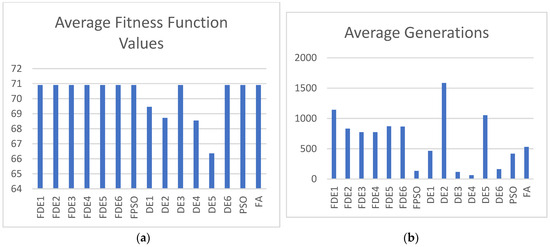
Figure 12.
(a) Average fitness function values; (b) average generations for Case 4 with population size = 30.
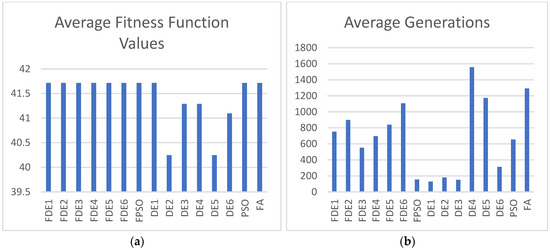
Figure 13.
(a) Average fitness function values; (b) average generations for Case 5 with population size = 30.
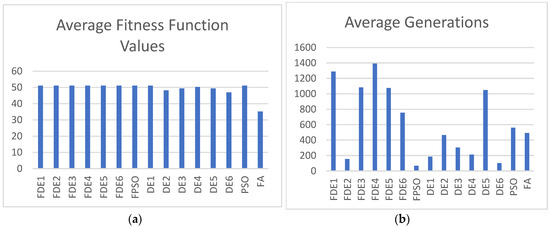
Figure 14.
(a) Average fitness function values; (b) average generations for Case 6 with population size = 30.
In summary, the average fitness function values obtained by the FDEi algorithms tend to increase as the population size changes from 10 to 30. By contrast, the average fitness function values obtained by the FPSO algorithm are the same as the population size changes from 10 to 30. This indicates that the performance of the FPSO algorithm is less sensitive to population size. The results of our experiments indicate that in case one firefly fails to find another better firefly to update its position, allowing the firefly to attempt to fly by following the behavior of PSO to create a trial solution can improve efficiency in searching the solutions. However, in case one firefly fails to find another better firefly to update its position, allowing the firefly to attempt to fly by following the behavior of DE to create a trial solution cannot improve efficiency in searching the solutions.
4.2. Comparison of the Proposed Allocation Method with Existing Methods
Besides the optimization of cost savings in ridesharing systems, a new allocation method was proposed in this study to improve the number of acceptable shared rides and the number of ridesharing participants. In this subsection, we compare the proposed cost-saving allocation method with existing methods, including the FF, LP and GP methods in the literature. The proposed cost-saving allocation method is a parameterized method with the parameters and . For all the experiments, is set to 0.05. The meaning of the parameter is the ratio of the cost savings allocated to all winning passengers to the cost savings allocated to all winning passengers and all winning drivers. The results of this section include two situations called DGPGP1 and DGPGP2 by setting the parameter in the allocation method. In DGPGP1, the parameter is set to 0.5, and in DGPGP2, the parameter is the ratio of the overall original cost of the winning passengers to the overall original cost of the winning passengers and winning drivers. Several scenarios were created to test the performance of DGPGP1 and DGPGP2. The results indicate that either DGPGP1 or DGPGP2 is the best-performing method in comparison with the existing methods, FF, LP and GP, in these experiments.
The results in Table 11 show the number of acceptable rides and the number of ridesharing participants of the proposed allocation method DGPGP1 with = 0.5. Figure 15 and Figure 16 show the bar charts of the number of acceptable rides and the number of ridesharing participants for all cases, respectively. The results indicate that DGPGP1 is the best-performing method compared with FF, LP and GP.

Table 11.
Comparison of the number of acceptable rides and the number of ridesharing participants of the proposed allocation method with those of existing methods for and population size NP = 30, where M/N in each cell of the table denotes the number of acceptable rides (M) and the number of ridesharing participants (N).
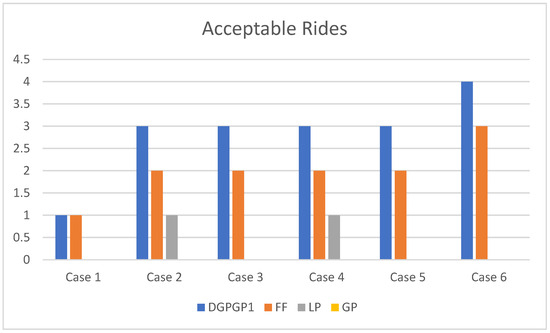
Figure 15.
Comparison of acceptable rides of DGPGP1 with FF, LP and GP for NP = 30.
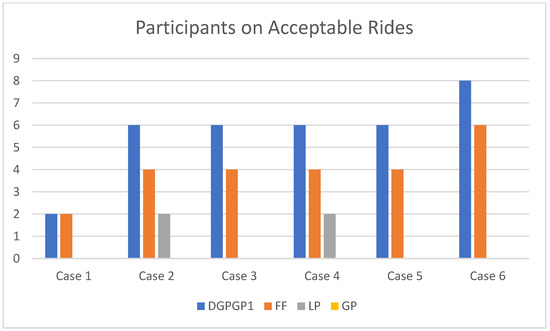
Figure 16.
Comparison of participants on acceptable rides of DGPGP1 with FF, LP and GP for = 30.
The results in Table 12 show the number of acceptable rides and the number of ridesharing participants of the proposed allocation method DGPGP2. Figure 17 and Figure 18 show the bar charts of the number of acceptable rides and the number of ridesharing participants for all cases, respectively. The results indicate that DGPGP2 is the best-performing method compared with FF, LP and GP.

Table 12.
Comparison of the number of acceptable rides and the number of ridesharing participants of the proposed allocation method with those of existing methods for and population size NP = 30, where M/N in each cell of the table denotes the number of acceptable rides (M) and the number of ridesharing participants (N).
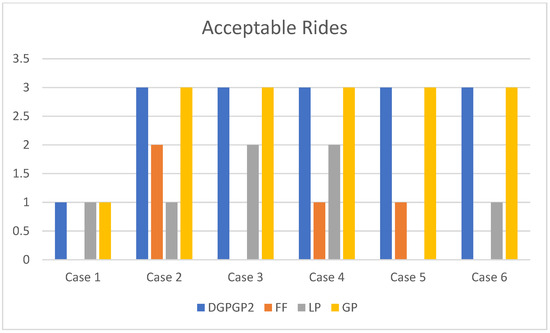
Figure 17.
Comparison of acceptable rides of DGPGP2 with FF, LP and GP for = 30.
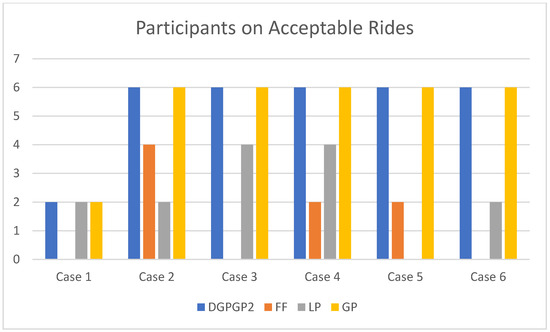
Figure 18.
Comparison of participants on acceptable rides of DGPGP2 with FF, LP and GP for = 30.
5. Discussion
We conducted experiments by applying the seven hybrid Firefly metaheuristic algorithms developed in this study to solve the ridesharing cost-saving optimization problems and compare their effectiveness. The results of the experiments indicate that combining the Firefly Algorithm with PSO or DE approaches can improve the performance of the original Firefly Algorithm. This is due to the ability to improve the search in the solution space by applying other diversified strategies to create potential candidates in case an individual cannot find another one to improve the solution quality using to the Firefly Algorithm. Therefore, the results of the experiments are consistent with our expectations. Another finding of this study is that the efficiency of a hybrid Firefly metaheuristic algorithm depends on the strategy used in the hybridization mechanism. The results of the experiments indicate that the FPSO algorithm, which was developed by hybridizing the Firefly Algorithm with PSO, is more efficient than the FDEi algorithm, which was developed by hybridizing the Firefly Algorithm with Dei. The average generations for which FPSO found the best solutions are smaller than those of the Firefly Algorithm. This indicates that FPSO is more efficient than the Firefly Algorithm. In addition, the average generations for which FDEi found the best solutions are not smaller than those of the Firefly Algorithm. This implies that the FDEi algorithm may not be more efficient than the Firefly Algorithm. In summary, arbitrarily combining two metaheuristic approaches may not always lead to an efficient hybrid metaheuristic algorithm.
As ridesharing or shared mobility systems require efficient decision support methods, several computationally efficient methods to allocate transport cost savings have been proposed in the literature. These methods include the Local Proportional Method, the Fifty–Fifty Method and the Global Proportional Method. These methods were proposed based on the idea of the proportional concept. As the cost-saving allocation method used in ridesharing or shared mobility systems directly influences the financial benefits of the users and the acceptability of ridesharing mode, several studies have started to probe into the performance issue of the cost-saving allocation method in recent years. In this paper, we proposed a new proportional method to allocate transport cost savings. The proposed proportional method to allocate transport cost savings depends on the parameter . In the experiments performed in this study, we considered two special cases of the new proportional allocation method called DGPGP1 and DGPGP2. DGPGP1 is obtained by setting to 0.5, and DGPGP2 is obtained by setting to the ratio of the overall original cost of the winning passengers to the overall original cost of the winning passengers and winning drivers. The results of experiments indicated that both DGPGP1 and DGPGP2 outperform the three existing proportional allocation methods, including the Local Proportional Method, the Fifty–Fifty Method and the Global Proportional Method, in terms of the performance metrics of the number of acceptable rides and the number of ridesharing participants on acceptable rides in ridesharing systems. This indicates that the new proportional allocation method is an effective allocation method.
6. Conclusions
The optimization of transportation cost savings and allocation of cost savings among stakeholders are two issues in ridesharing systems. In this study, we addressed these two issues based on the development of several hybrid metaheuristic algorithms and a new allocation method. As ridesharing problems are typically formulated as discrete optimization problems with constraints, they belong to the category of nonconvex constrained discrete optimization problems. Hybrid metaheuristic approaches are adopted in this study to develop solution algorithms for solving the ridesharing problems. Although the hybridization of different metaheuristic approaches may provide a potentially effective method to improve the performance and/or efficiency of the solution-finding processes in solving optimization problems, the effectiveness of hybridization depends on the metaheuristic approaches used in hybridization and the optimization problems to be solved. Therefore, it is necessary to study the effectiveness of applying the hybridization approach to each specific problem in terms of performance and efficiency. The rationale for hybridization to work is due to the increased diversity through properly combining different metaheuristic approaches in the solution processes to provide more diversified search directions in the solution space. However, the capability to effectively increase the diversified search directions in the solution space is dependent on the metaheuristic approaches selected for hybridization and is unknown a priori. Experiments need to be conducted to know whether an algorithm based on the hybridization of different metaheuristic approaches is able to increase the diversified search directions in the solution space to improve candidate solutions. In this paper, we developed several hybrid metaheuristic algorithms for ridesharing problems by combining the Firefly Algorithm with the PSO approach or DE approach. These hybrid metaheuristic algorithms include Firefly PSO (FPSO), Firefly DE1 (FDE1), Firefly DE2 (FDE2), Firefly DE3 (FDE3), Firefly DE4 (FDE4), Firefly DE5 (FDE5) and Firefly DE6 (FDE6). To study the effectiveness of these hybrid metaheuristic algorithms, we conducted experiments for two different population size parameters. A population size of 10 is used in the first series of experiments to study whether these hybrid metaheuristic algorithms can work effectively in small population sizes. A population size of 30 is used in the second series of experiments to study whether these hybrid metaheuristic algorithms can work effectively in moderate population sizes. The results of the first series of experiments indicate that FPSO either outperforms or performs as well as FDE1, FDE2, FDE3, FDE4, FDE5 and FDE6 in terms of average fitness function values and average generations for most test cases. The results of the second series of experiments indicate that the average fitness function values achieved by FPSO are the same as those found by the FDEi for all the test cases for a population size of 30. In addition, the average generations for which FPSO found the best solutions are much smaller than those of FDEi for most test cases with a population size of 30. The average generations for which FPSO found the best solutions are much smaller than those of standard PSO and FA for all test cases for a population size of 30. This indicates that FPSO improves the efficiency of PSO and FA through hybridization. In summary, hybridizing FA with PSO creates a more efficient algorithm, whereas hybridizing FA with DE does not lead to a more efficient algorithm for the ridesharing recommendation problem. Hybridizing FA with PSO or DE is very similar to marriages in the real world. An interesting finding of this study is very similar to what happens in the real world: “Not all marriages have happy endings.” It is necessary to carefully select the different metaheuristic approaches to be hybridized.
Besides the optimization of cost savings, a new allocation method was proposed in this study to improve the number of acceptable shared rides and the number of ridesharing participants. The new allocation method can be applied to deal with the different minimal expectations of drivers and passengers by setting a parameter . We define two special cases based on the new allocation methods called DGPGP1 and DGPGP2 by setting the parameter to 0.5 and the ratio of the overall original cost of the winning passengers to the overall original cost of the winning passengers and winning drivers, respectively. Several scenarios were created to test the performance of DGPGP1 and DGPGP2. The results indicate that either DGPGP1 or DGPGP2 is the best-performing method for these scenarios compared with the existing methods, FF, LP and GP, in the literature. One of our future research directions is to develop new methods that are computationally efficient and can be effectively applied in ridesharing recommendation systems. Another future research direction is to study the effectiveness of other hybridization methods for ridesharing recommendation systems.
Funding
This research was supported in part by the National Science and Technology Council, Taiwan, under Grant NSTC 111-2410-H-324-003.
Data Availability Statement
Data are available in a publicly accessible repository described in the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sustainable Transportation and Fuels. Available online: https://www.energy.gov/eere/sustainable-transportation-and-fuels (accessed on 20 November 2023).
- AGENDA 21. Available online: https://sustainabledevelopment.un.org/content/documents/Agenda21.pdf (accessed on 20 November 2023).
- Plan of Implementation of the World Summit on Sustainable Development. Available online: https://library.arcticportal.org/1679/1/Johannesburg_Plan_of_Implementation.pdf (accessed on 20 November 2023).
- Sustainable Transport. Available online: https://sdgs.un.org/topics/sustainable-transport (accessed on 20 November 2023).
- Transforming Our World: The 2030 Agenda for Sustainable Development. Available online: https://sdgs.un.org/2030agenda (accessed on 20 November 2023).
- Tafreshian, A.; Masoud, N.; Yin, Y. Frontiers in service science: Ride matching for peer-to-peer ride sharing: A review and future directions. Serv. Sci. 2020, 12, 44–60. [Google Scholar] [CrossRef]
- Ferrero, F.; Perboli, G.; Rosano, M.; Vesco, A. Car-sharing services: An annotated review. Sustain. Cities Soc. 2018, 37, 501–518. [Google Scholar] [CrossRef]
- Narayanan, S.; Chaniotakis, E.; Antoniou, C. ‘Shared autonomous vehicle services: A comprehensive review. Transp. Res. C Emerg. Technol. 2020, 111, 255–293. [Google Scholar] [CrossRef]
- Ricci, M. Bike sharing: A review of evidence on impacts and processes of implementation and operation. Res. Transp. Bus. Manag. 2015, 15, 28–38. [Google Scholar] [CrossRef]
- Hao, M.; Yamamoto, T. Shared autonomous vehicles: A review considering car sharing and autonomous vehicles. Asian Transp. Stud. 2018, 5, 47–63. [Google Scholar]
- Mohan, A.; Bruchon, M.; Michalek, J.; Vaishnav, P. Life Cycle Air Pollution, Greenhouse Gas, and Traffic Externality Benefits and Costs of Electrifying Uber and Lyft. Environ. Sci. Technol. 2023, 57, 8524–8535. [Google Scholar] [CrossRef] [PubMed]
- Amatuni, L.; Ottelin, J.; Steubing, B.; Mogollón, J.M. Does car sharing reduce greenhouse gas emissions? Assessing the modal shift and lifetime shift rebound effects from a life cycle perspective. J. Clean. Prod. 2020, 266, 121869. [Google Scholar] [CrossRef]
- Exploring the Impact of Shared Mobility Services on CO2, Environment Working Paper No. 175. Available online: https://one.oecd.org/document/ENV/WKP(2021)7/en/pdf (accessed on 20 November 2023).
- Bruglieri, M.; Ciccarelli, D.; Colorni, A.; Luè, A. PoliUniPool: A carpooling system for universities. Procedia-Soc. Behav. Sci. 2011, 20, 558–567. [Google Scholar] [CrossRef]
- Liftango. Available online: https://www.newcastle.edu.au/our-uni/campuses-and-locations/transport/rideshare-liftango (accessed on 20 November 2023).
- Lyft. Available online: https://www.lyft.com/ (accessed on 20 November 2023).
- Uber. Available online: https://www.uber.com/ (accessed on 20 November 2023).
- Didi. Available online: https://www.didiglobal.com (accessed on 20 November 2023).
- Wingz. Available online: https://www.wingz.me/ (accessed on 20 November 2023).
- Via. Available online: https://ridewithvia.com/ (accessed on 20 November 2023).
- Hwang, K.; Giuliano, G. The Determinants of Ridesharing: Literature Review; Working Paper UCTC No. 38; The University of California Transportation Center: Los Angeles, CA, USA, 1990; Available online: https://escholarship.org/uc/item/3r91r3r4 (accessed on 20 November 2023).
- Wieding, S.V.; Sprei, F.; Hult, C.; Hult, Å.; Roth, A.; Persson, M. Drivers and barriers to business-to-business carsharing for work trips—A case study of Gothenburg, Sweden. Case Stud. Transp. Policy 2022, 10, 2330–2336. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. Eur. J. Oper. Res. 2012, 223, 295–303. [Google Scholar] [CrossRef]
- Mourad, A.; Puchinger, J.; Chu, C. A survey of models and algorithms for optimizing shared mobility. Transp. Res. Part B Methodol. 2019, 123, 323–346. [Google Scholar] [CrossRef]
- Martins, L.D.C.; de la Torre, R.; Corlu, C.G.; Juan, A.A.; Masmoudi, M.A. Optimizing ride-sharing operations in smart sustainable cities: Challenges and the need for agile algorithms. Comput. Ind. Eng. 2021, 153, 107080. [Google Scholar] [CrossRef]
- Saisubramanian, S.; Basich, C.; Zilberstein, S.; Goldman, C.V. Satisfying Social Preferences in Ridesharing Services. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3720–3725. [Google Scholar]
- Hsieh, F.S. Trust-Based Recommendation for Shared Mobility Systems Based on a Discrete Self-Adaptive Neighborhood Search Differential Evolution Algorithm. Electronics 2022, 11, 776. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Hsieh, F.-S. A Self-Adaptive Meta-Heuristic Algorithm Based on Success Rate and Differential Evolution for Improving the Performance of Ridesharing Systems with a Discount Guarantee. Algorithms 2024, 17, 9. [Google Scholar] [CrossRef]
- Li, J. A Hybrid Differential Evolution Method for Practical Engineering Problems. In Proceedings of the 2009 IITA International Conference on Control, Automation and Systems Engineering (Case 2009), Zhangjiajie, China, 11–12 July 2009; pp. 54–57. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L.; Yang, X.S.; Dai, Y. A Novel Hybrid Firefly Algorithm for Global Optimization. PLoS ONE 2016, 11, e0163230. [Google Scholar] [CrossRef] [PubMed]
- Paital, S.R.; Ray, P.K.; Mohanty, A. Firefly-swarm optimized fuzzy adaptive PSS in power system for transient stability enhancement. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 1969–1976. [Google Scholar]
- Paital, S.R.; Mohanty, A.; Eddy Foo, Y.S.; Krishnan, A.; Beng Gooi, H.; Amaratunga, G.A.J. A Hybrid Firefly-Swarm Optimized Fractional Order Interval Type-2 Fuzzy PID-PSS for Transient Stability Improvement. IEEE Trans. Ind. Appl. 2019, 55, 6486–6498. [Google Scholar]
- Ibrahim, I.M.; Omran, W.A.; Abdelaziz, A.Y. Optimal Sizing of Microgrid System Using Hybrid Firefly and Particle Swarm Optimization Algorithm. In Proceedings of the 22nd International Middle East Power Systems Conference (MEPCON), Assiut, Egypt, 14–16 December 2021; pp. 287–293. [Google Scholar] [CrossRef]
- Aydilek, İ.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Hsieh, F.-S. A Hybrid Firefly-DE algorithm for Ridesharing Systems with Cost Savings Allocation Schemes. In Proceedings of the 2022 IEEE World AI IoT Congress (AIIoT), Seattle, WA, USA, 6–9 June 2022; pp. 649–653. [Google Scholar]
- Hsieh, F.-S. Improve Decision Making Efficiency in Ridesharing Systems through a Hybrid Firefly-PSO algorithm. In Proceedings of the 2023 IEEE World AI IoT Congress (AIIoT), Seattle, WA, USA, 7–10 June 2023; pp. 578–582. [Google Scholar]
- Guajardoa, M.; Ronnqvist, M. A review on cost allocation methods in collaborative transportation. Int. Trans. Oper. Res. 2016, 23, 371–392. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games. Available online: https://www.rand.org/content/dam/rand/pubs/papers/2021/P295.pdf (accessed on 20 November 2023).
- Schmeidler, D. The Nucleolus of a Characteristic Function Game. SIAM J. Appl. Math. 1969, 17, 1163–1170. [Google Scholar] [CrossRef]
- Kalai, E. Proportional solutions to bargaining situations: Intertemporal utility comparisons. Econometrica 1977, 45, 1623–1630. [Google Scholar] [CrossRef]
- Wang, X.; Agatz, N.; Erera, A. Stable Matching for Dynamic Ride-Sharing Systems. Transp. Sci. 2018, 52, 850–867. [Google Scholar] [CrossRef]
- Agatz, N.A.H.; Erera, A.L.; Savelsbergh, M.W.P.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Transp. Res. Part B Methodol. 2011, 45, 1450–1464. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Zhan, F.; Guo, Y. A solution methodology for carpooling systems based on double auctions and cooperative coevolutionary particle swarms. Appl. Intell. 2019, 49, 741–763. [Google Scholar] [CrossRef]
- Hsieh, F.-S. A Comparison of Three Ridesharing Cost Savings Allocation Schemes Based on the Number of Acceptable Shared Rides. Energies 2021, 14, 6931. [Google Scholar] [CrossRef]
- Hsieh, F.-S. Improving Acceptability of Cost Savings Allocation in Ridesharing Systems Based on Analysis of Proportional Methods. Systems 2023, 11, 187. [Google Scholar] [CrossRef]
- Ravindran, A.; Ragsdell, K.M.; Reklaitis, G.V. Enginering Optimization: Methods and Applications, 2nd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).