Distributed Feature Selection for Power System Dynamic Security Region Based on Grid-Partition and Fuzzy-Rough Sets
Abstract
1. Introduction
- (1)
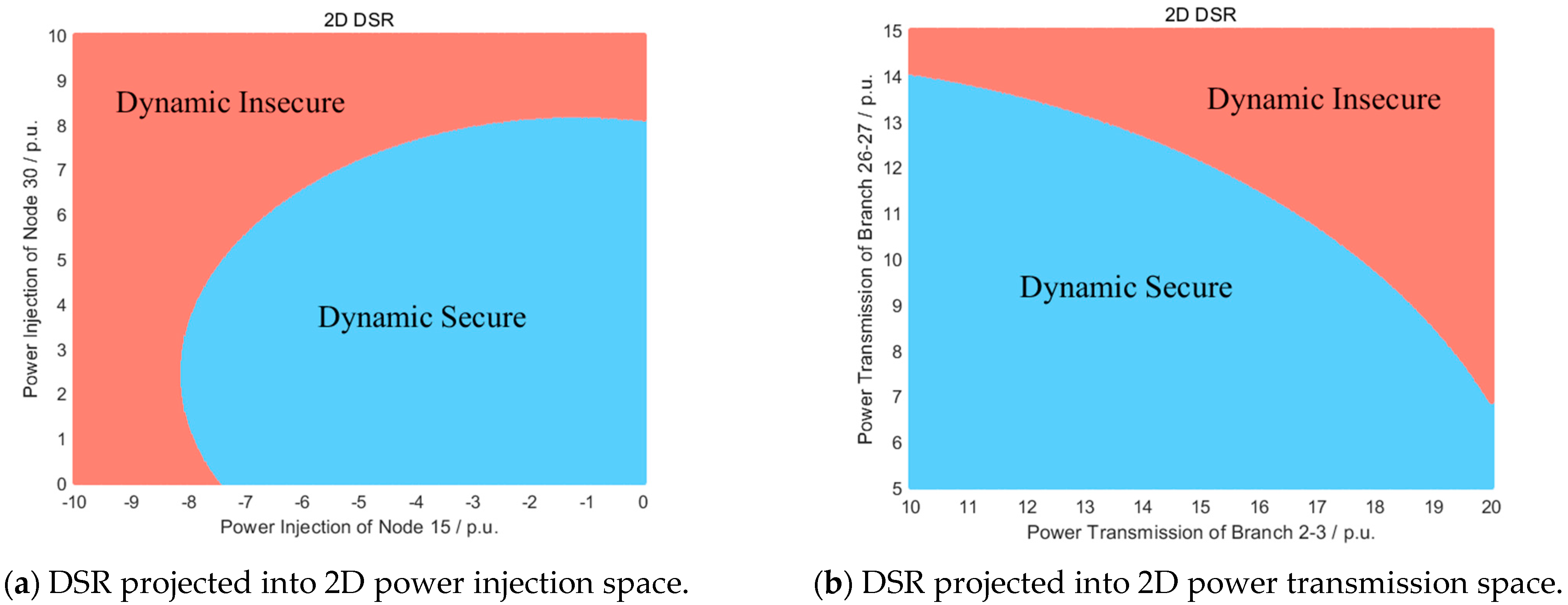
- Considering the need for actual grid dispatching, extend the definition of DSR in power systems from the power injection space to the Cartesian product of the power injection space and power transmission space (referred to as the power space). Meanwhile, considering the changes in topological characteristics brought about by the extension, introduce a support vector machine (SVM) with a Gaussian kernel function to approximate the boundaries of the extended DSR.
- (2)
- Propose a distributed feature selection method based on grid partition and fuzzy-rough sets that can be applied to a power system DSR analysis with high-dimensional features. On the one hand, electrical partition by the Louvain algorithm can allocate the original feature set to multiple computational units for screening, while the connection between different feature subsets is minimized to a relatively low level, thereby avoiding large errors in the distributed results. On the other hand, feature selection based on the FRST is not only efficient but can also effectively take into account the intrinsic connections between features and, thus, improve the screening accuracy.
2. Power System Dynamic Security Region
2.1. Extension of Dynamic Security Region
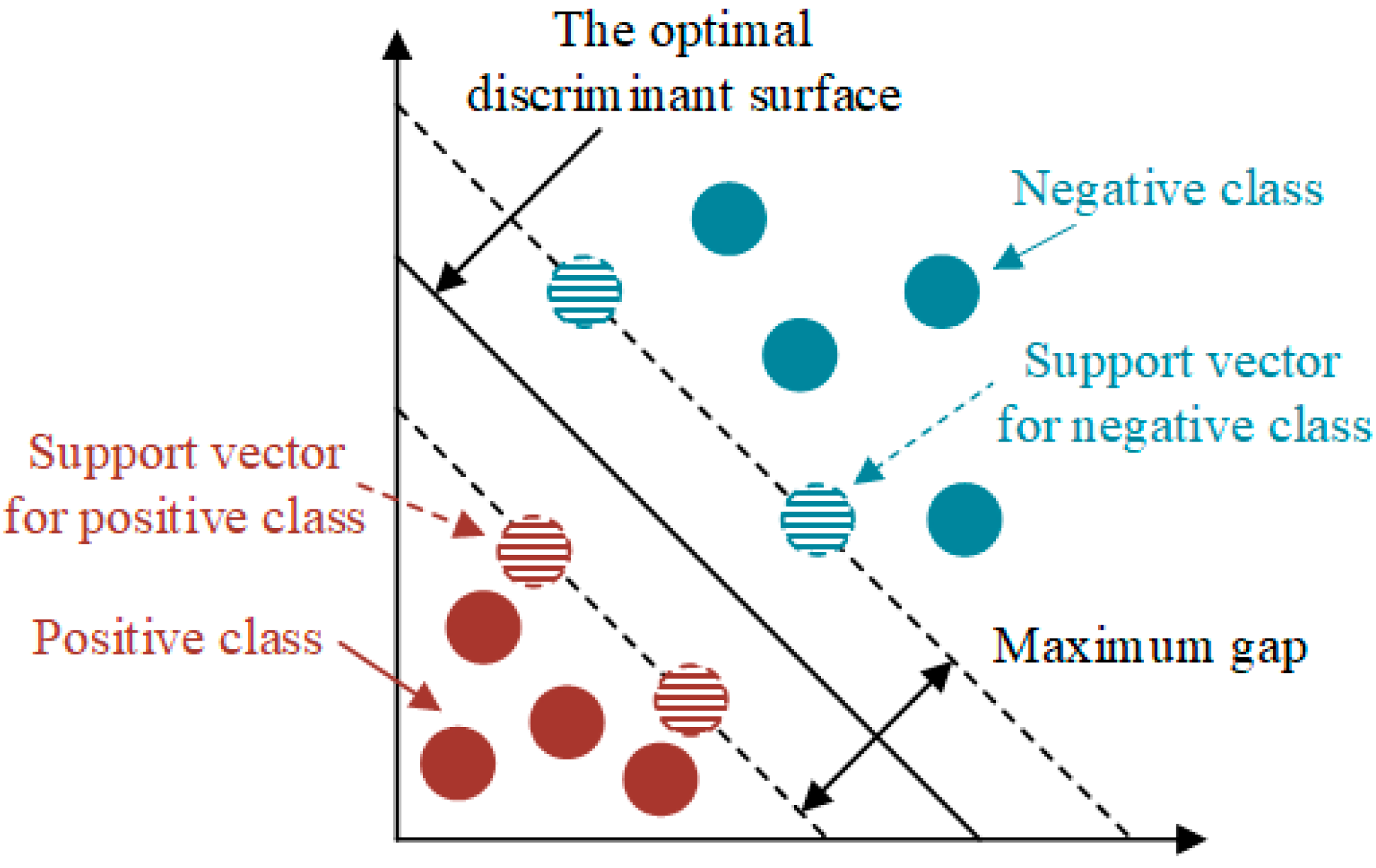
2.2. Approximate Boundaries of Extended Dynamic Security Region
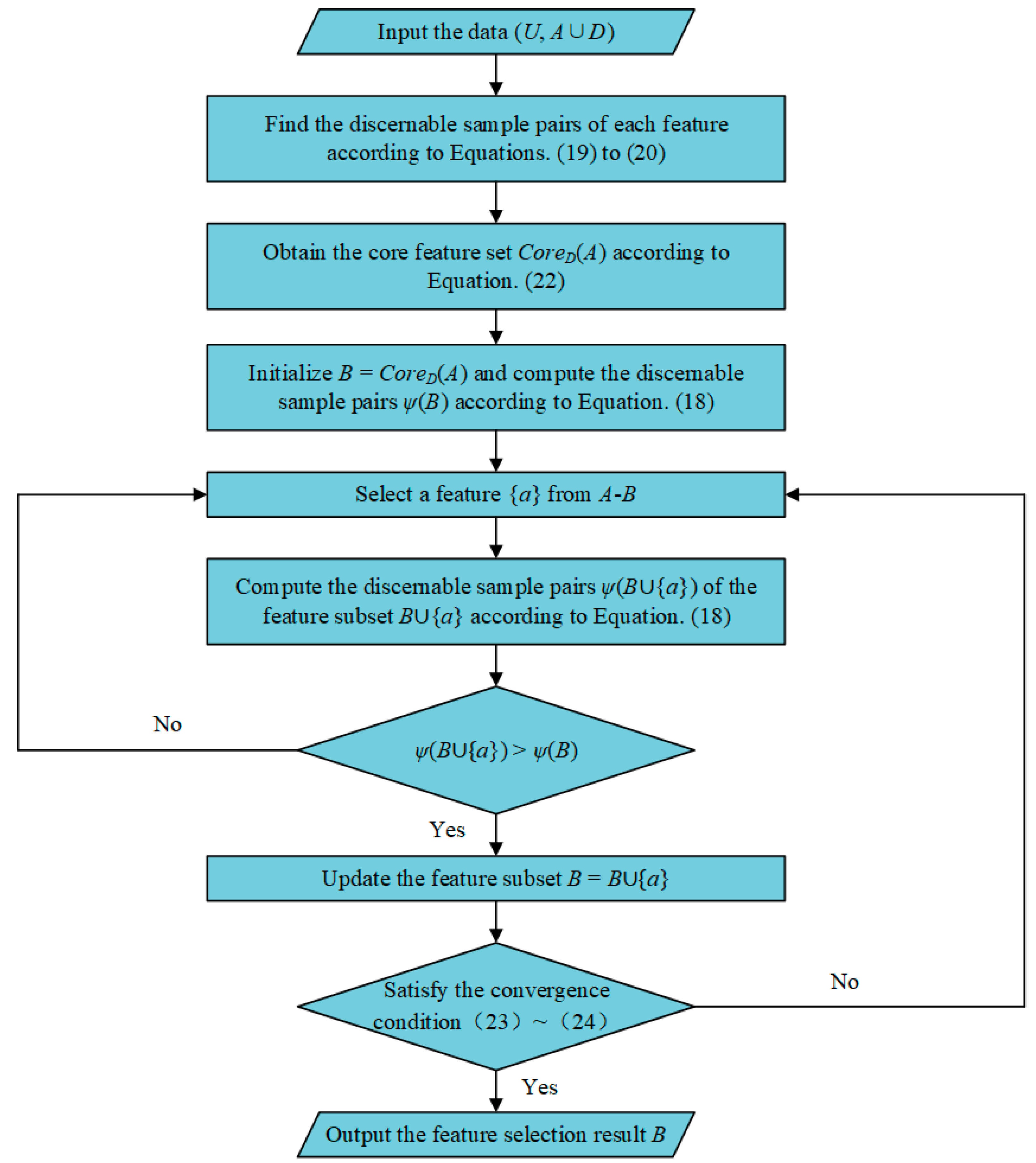
3. Distributed Feature Selection for Dynamic Security Region
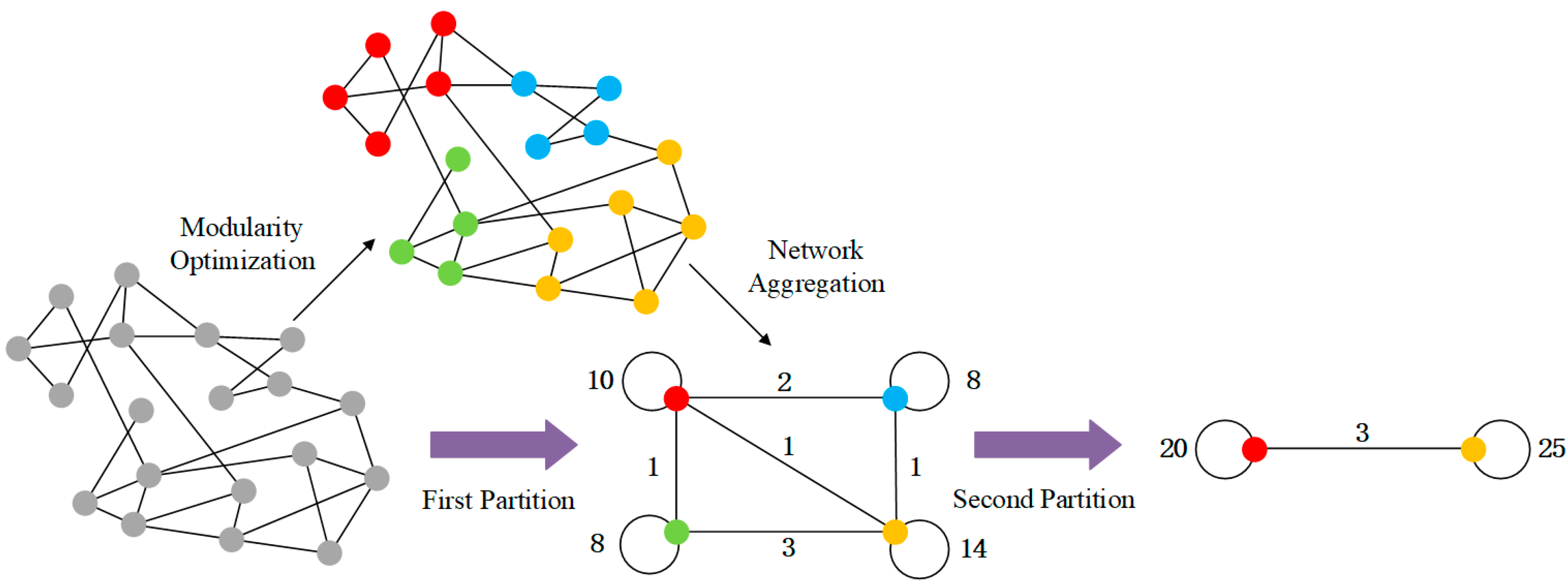
3.1. Louvain Algorithm
3.2. Fuzzy-Rough Set Theory
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations/Nomenclatures | |
| SR | Security Region |
| SSSR | Steady-state Security Region |
| DSR | Dynamic Security Region |
| ROA | Region of Attraction |
| TEF | Transient Energy Function |
| EEAC | Extended Equal Area Criterion |
| RST | Rough Set Theory |
| FRST | Fuzzy-rough Set Theory |
| FSR | Fuzzy Similarity Relation |
| SVM | Support Vector Machine |
| KKT | Karush–Kuhn–Tucker Conditions |
| Variables | |
| The DSR of the power system | |
| The fault to be studied | |
| The power vector to be studied or the class of sample | |
| The lower limit vectors of | |
| The upper limit vectors of | |
| The system state or the sample data | |
| The system state at the instant of fault clearing | |
| The equilibrium point in the state space | |
| The ROA of the power system | |
| The set of that satisfies the constraints | |
| The normal vector of the hyperplane | |
| The mapping function | |
| The displacement term of the hyperplane | |
| The number of sample data | |
| The relaxation variable | |
| The penalty parameter | |
| The kernel function | |
| The width parameter in | |
| The electrical distance between node and node | |
| The elements of the corresponding position in the node impedance matrix | |
| The modularity of the network | |
| The gain of modularity | |
| The sum of the weights of the edges inside partition | |
| The sum of the weights of the edges connected to the nodes in partition | |
| The sum of the weights of all edges in the network | |
| The sum of the weights of the edges from node to other nodes in partition | |
| The sum of the weights of the edges attached to node | |
| The FSR between sample and sample on feature subset | |
| The FSR between sample and sample on feature | |
| The fuzzy upper approximation of sample on feature subset and decision class | |
| The fuzzy lower approximation of sample on feature subset and decision class | |
| Determine whether belongs to decision class | |
| The fuzzy positive region of sample on feature subset | |
| The discernable sample pairs of feature subset | |
| The discernable sample pairs of feature | |
| The decision classes of sample | |
| All possible feature selection results of the data | |
| The core feature set | |
| The decision-making accuracy | |
| The number of test samples | |
| The number of samples with correct decisions in the test samples | |
References
- Xiong, L.; Liu, X.; Liu, Y.; Zhuo, F. Modeling and stability issues of voltage-source converter-dominated power systems: A review. CSEE J. Power Energy Syst. 2020, 8, 1530–1549. [Google Scholar] [CrossRef]
- Bergen, A.R. Power Systems Analysis; Pearson Education India: Bengaluru, India, 2009. [Google Scholar]
- Kundur, P. Power system stability. In Power System Stability and Control; CRC Press: Boca Raton, FL, USA, 2007; Volume 10, ISBN 978-1-4398-8320-4. [Google Scholar]
- Yu, Y.X. Review of study on methodology of security regions of power system. J. Tianjin Univ. 2008, 41, 635–646. [Google Scholar]
- Yu, Y.; Liu, Y.; Qin, C.; Yang, T. Theory and method of power system integrated security region irrelevant to operation states: An introduction. Engineering 2020, 6, 754–777. [Google Scholar] [CrossRef]
- Yu, Y.; Zeng, Y.; Feng, F. Differential topological characteristics of the DSR on injection space of electrical power system. Sci. China Ser. E Technol. Sci. 2002, 45, 576–584. [Google Scholar] [CrossRef]
- Zeng, Y.; Yu, Y. A practical direct method for determining dynamic security regions of electrical power systems. In Proceedings of the International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 2, pp. 1270–1274. [Google Scholar] [CrossRef]
- Xia, S.; Chen, S.; Guo, Z.; Xu, Y. The application of energy sensitivity for practical dynamic security region calculation. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, Y.; Qin, C.; Chang, J.; Zhang, J.; Tu, J. A Method for Building Practical Dynamic Security Region Based on Phase-plane Trajectory. Proc. CSEE 2018, 38, 1905–1912. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Fan, Y. Dynamic Security Regions of Electric Power System Based on Extended Equal-area Criterion. Proc. CSEE 2007, 27, 20–26. [Google Scholar] [CrossRef]
- Liu, H.D.; Li, Q.; Feng, W.; Gao, X.H.; Chang, A.; Li, T. A Rapid Method to Calculate the Hyper-Plane of DSR Based on EEAC. Adv. Mater. Res. 2013, 694, 2993–2996. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z. A review of power system transient stability analysis and assessment. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Maihemuti, S.; Wang, W.; Wang, H.; Wu, J.; Zhang, X. Dynamic security and stability region under different renewable energy permeability in IENGS system. IEEE Access 2021, 9, 19800–19817. [Google Scholar] [CrossRef]
- Liu, Y.L.; Shi, X.J.; Xu, Y. A hybrid data-driven method for fast approximation of practical dynamic security region boundary of power systems. Int. J. Electr. Power Energy Syst. 2020, 117, 105658. [Google Scholar] [CrossRef]
- Ren, Z.; Hu, W.; Ma, K.; Zhang, Y.; Liu, W.; Xiong, J. Dynamic security region algorithm considering sample imbalance and misclassification cost. In Proceedings of the 2021 13th IEEE PES Asia Pacific Power & Energy Engineering Conference (APPEEC), Thiruvananthapuram, India, 21–23 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Karunadsa, P.S.; Annakkage, U.D.; MacDonald, B.A. Dynamic security control using secure regions derived from a decision tree technique. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 3, pp. 1861–1865. [Google Scholar] [CrossRef]
- Zeng, Y.; Fan, J.C.; Yu, Y.X.; Lu, F.; Fang, Y.G. Practical dynamic security regions of bulk power systems. Autom. Electr. Power Syst. 2001, 25, 6–10. [Google Scholar]
- Qiu, L.; Zhao, J.; Jia, H.; Huang, H.; Li, P.; Li, Z. Studies on the section thermal limits based on security region. In Proceedings of the 2013 IEEE International Conference of IEEE Region 10 (TENCON 2013), Xi’an, China, 22–25 October 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Liang, L.; Hu, W.; Zhang, Y.; Ma, K.; Gu, Y.; Tian, B.; Li, H. An algorithm with LightGBM+ SVM fusion model for the assessment of dynamic security region. In Proceedings of the 2021 International Conference on Power System and Energy Internet (PoSEI2021), Chengdu, China, 16–18 April 2021; Volume 256, p. 02022. [Google Scholar] [CrossRef]
- Zhiqiang, G.; Yuan, C.; Yongming, H. Power Systems Intrusion Detection Using Novel Wrapped Feature Selection Framework. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Guangzhou, China, 13–15 November 2020; pp. 446–450. [Google Scholar] [CrossRef]
- Cheng, W.; Zheng, L.; Wu, J. Conditional Mutual Information Based Interpretable Key Feature Selection Method for Power System Security Analysis. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 2907–2911. [Google Scholar] [CrossRef]
- Gu, X.; Li, Y.; Jia, J. Feature selection for transient stability assessment based on kernelized fuzzy rough sets and memetic algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 664–670. [Google Scholar] [CrossRef]
- Chen, Z.; Han, X.; Zhang, H.; Zhao, J.; Mei, S. Feature Selection Method for Power System Transient Stability Status Prediction Considering Class Imbalanced Characteristic. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar] [CrossRef]
- Lee, C.; Shen, Y. Optimal Feature Selection for Power-Quality Disturbances Classification. IEEE Trans. Power Deliv. 2011, 26, 2342–2351. [Google Scholar] [CrossRef]
- Gao, H.; Cai, G.; Yang, D.; Lixin, W.; Hao, Y. Feature selection approach based on FCC-eAI in static voltage stability margin estimation. Electr. Power Autom. Equip. 2023, 43, 168–176. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Ruiz, R. A survey on sparse learning models for feature selection. IEEE Trans. Cybern. 2020, 52, 1642–1660. [Google Scholar] [CrossRef] [PubMed]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Wang, S.; Wang, K.; Zheng, L. Feature selection via analysis of relevance and redundancy. J. Beijing Inst. Technol. 2008, 17, 300–304. [Google Scholar]
- Nguyen, N.A.; Quyen, H.A.; Le, T.N.; Phan, T.T.B. An Improvement Forward Floating Search Algorithm for Feature Selection in Power System Transient Stability Classification; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Tan, B.; Yang, J.; Zhou, T.; Xiao, Y.; Zhou, Q. A Novel Temporal Feature Selection for Time-Adaptive Transient Stability Assessment. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe, Bucharest, Romania, 29 September–2 October 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, T.; Ren, X. Key Feature Selection Method for Intelligent Assessment of Transient Power Angle Stability Based on Physical Mechanism and Improved Relief. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 24–26 August 2022; pp. 632–636. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Yu, Z.; Tian, F. Feature selection of power system transient stability assessment based on random forest and recursive feature elimination. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, T.; Ren, X.; Bao, Y.; Wu, F.; Zhang, J. Comparison and improvement of key feature selection methods for intelligent assessment of transient power angle stability. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 1563–1568. [Google Scholar] [CrossRef]
- Li, P.; Dong, X.; Meng, Q.; Jiming, C. Transient stability assessment method for power system based on Fisher Score feature selection. Electr. Power Autom. Equip./Dianli Zidonghua Shebei 2023, 43, 117. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Geng, H.; Wang, Y.; Zeng, H.; Ding, J. A Holistic Feature Selection Method for Enhanced Short-term Load Forecasting of Power System. IEEE Trans. Instrum. Meas. 2022, 72, 2500911. [Google Scholar] [CrossRef]
- Kong, L.; Qu, W.; Yu, J.; Zuo, H.; Chen, G.; Xiong, F.; Pan, S.; Lin, S.; Qiu, M. Distributed feature selection for big data using fuzzy rough sets. IEEE Trans. Fuzzy Syst. 2019, 28, 846–857. [Google Scholar] [CrossRef]
- Huang, T.; Sun, H.; Guo, Q. Online distributed security feature selection based on big data in power system operation. Autom. Electr. Power Syst. 2016, 40, 137–140. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1951. [Google Scholar]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets and intelligent data analysis. Inf. Sci. 2002, 147, 1–12. [Google Scholar] [CrossRef]
- Gao, S.; Dong, L.; Liao, X.Z.; Gao, Y. Long-Term Wind Power Prediction Based on Rough Set. Appl. Mech. Mater. 2013, 329, 411–415. [Google Scholar] [CrossRef]
- Xiao, Z.; Ye, S.-J.; Zhong, B.; Sun, C.-X. BP neural network with rough set for short term load forecasting. Expert Syst. Appl. 2009, 36, 273–279. [Google Scholar] [CrossRef]
- Gan, S.C.; Zhou, A.H.; Guo, H.; Tang, L. Application of Variable Precision Rough Set in Power Transformer Fault Diagnosis. Appl. Mech. Mater. 2013, 373, 824–828. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Putting rough sets and fuzzy sets together. In Intelligent Decision Support: Handbook of Applications and Advances of the Rough Sets Theory; Springer: Dordrecht, The Netherlands, 1992; pp. 203–232. [Google Scholar] [CrossRef]
- Pai, A. Energy Function Analysis for Power System Stability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]


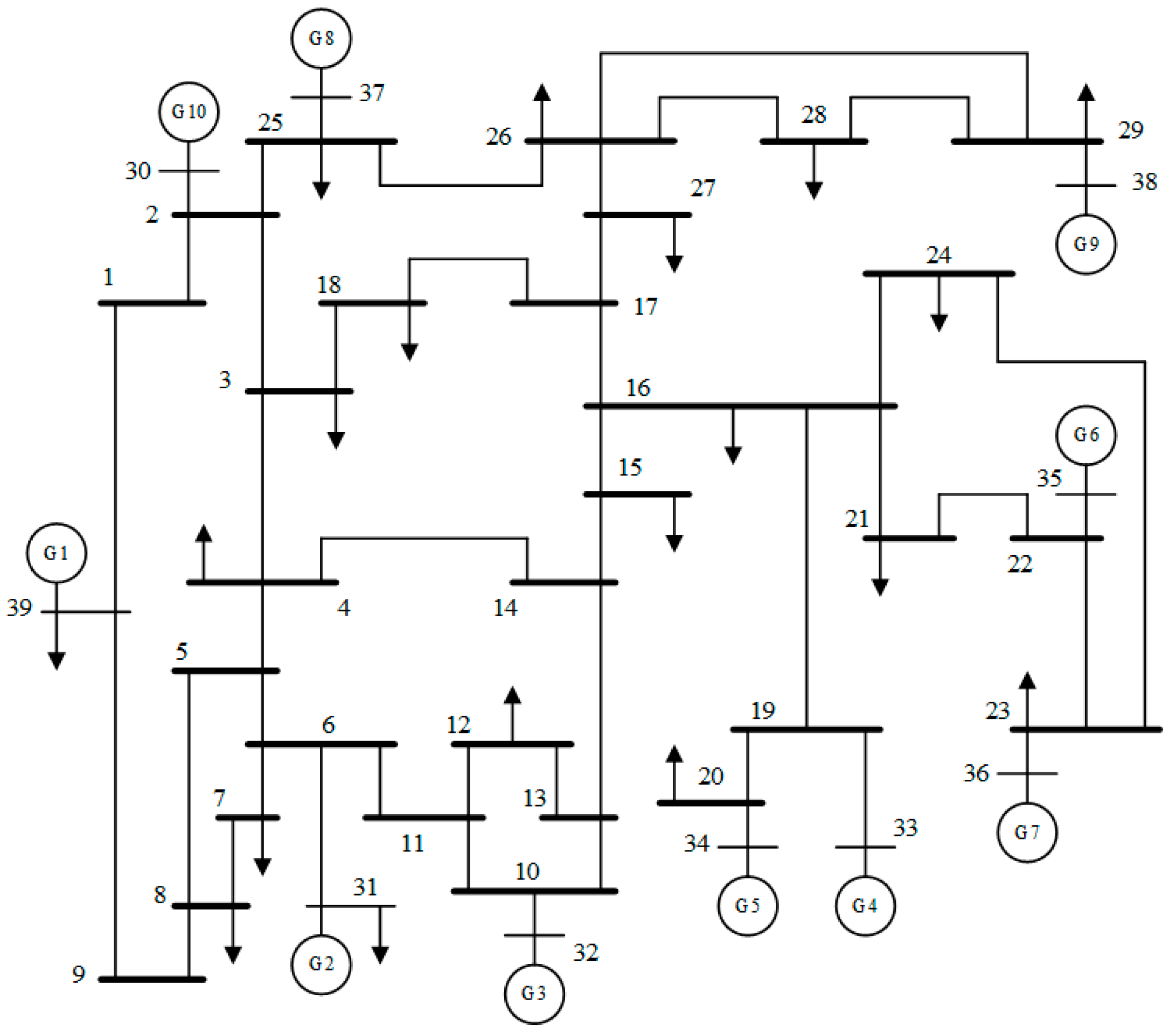
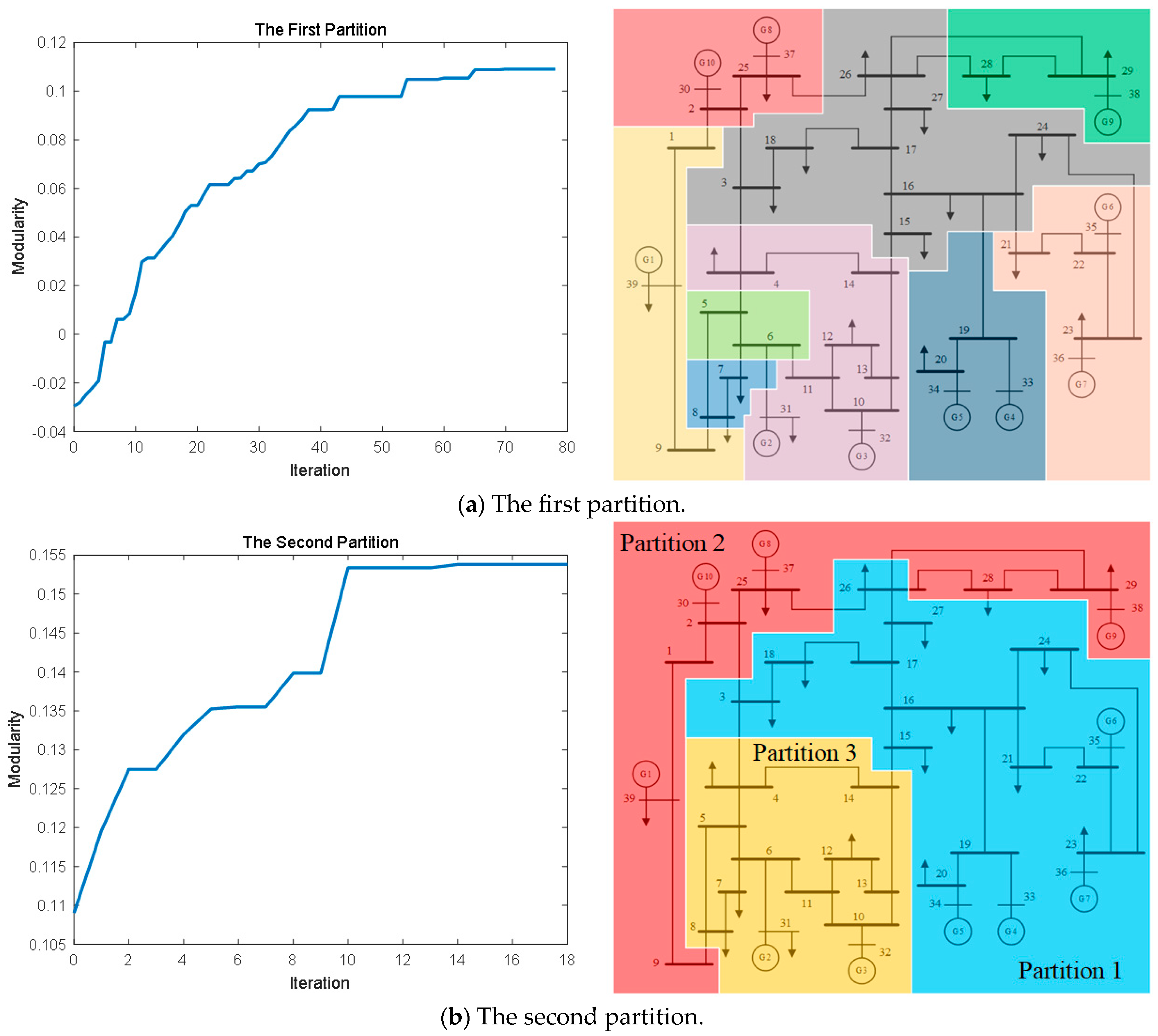
| Partition | Node | Power Injections of Nodes | Power Transmissions of Branches |
|---|---|---|---|
| 1 | 3, 15−24, 26−27, 33−35 | 28 | 80 |
| 2 | 1−2, 9, 25, 28−30, 37−39 | 14 | 42 |
| 3 | 4−8, 10−14, 31−32 | 12 | 62 |
| Total | 54 | 184 | |
| Power Injections of Nodes | Power Transmissions of Branches | Time Costs (s) | DSR Analysis Accuracy (%) | |
|---|---|---|---|---|
| Before Feature Selection | 54 | 184 | - | 91.33 |
| After Centralized Feature Selection | 22 | 36 | 3.6404 | 92.67 |
| After Distributed Feature Selection | 12 + 5 + 5 = 22 | 14 + 16 + 7 = 37 | 0.5768 | 92.67 |
| Power Injections of Nodes | Power Transmissions of Branches | Time Costs (s) | DSR Analysis Accuracy (%) | |
|---|---|---|---|---|
| Relief | 23 | 35 | 0.3047 | 91.67 |
| Fisher Score | 9 | 49 | 0.0042 | 89.67 |
| Mutual Information | 4 | 54 | 39.7484 | 87.00 |
| Proposed Method | 22 | 37 | 0.5768 | 92.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Du, Z.; Zhou, W.; Chen, B. Distributed Feature Selection for Power System Dynamic Security Region Based on Grid-Partition and Fuzzy-Rough Sets. Electronics 2024, 13, 815. https://doi.org/10.3390/electronics13050815
Tan Y, Du Z, Zhou W, Chen B. Distributed Feature Selection for Power System Dynamic Security Region Based on Grid-Partition and Fuzzy-Rough Sets. Electronics. 2024; 13(5):815. https://doi.org/10.3390/electronics13050815
Chicago/Turabian StyleTan, Yefa, Zhaobin Du, Weixian Zhou, and Baixi Chen. 2024. "Distributed Feature Selection for Power System Dynamic Security Region Based on Grid-Partition and Fuzzy-Rough Sets" Electronics 13, no. 5: 815. https://doi.org/10.3390/electronics13050815
APA StyleTan, Y., Du, Z., Zhou, W., & Chen, B. (2024). Distributed Feature Selection for Power System Dynamic Security Region Based on Grid-Partition and Fuzzy-Rough Sets. Electronics, 13(5), 815. https://doi.org/10.3390/electronics13050815





