Digital Functional Blocks Implementation of PWM and Control for a High-Frequency Interleaved Y-Inverter Motor Drive

Abstract

This paper is about the development and demonstration of a motor drive for e-transport applications based on an innovative hybrid Si-SiC dual switching frequency interleaved buck–boost Y-inverter and a single-rotor Halbach machine. In particular, the focus is the implementation of the required discontinuous inverter modulation scheme, input voltage feed-forward and motor currents feedback control loops, as well as over-voltage, over-current, and over-temperature protections, using an off-the-shelf commercial hardware platform enabling straightforward Simulink-environment programming of all parts, while ensuring the high switching frequency capability required by wide-band-gap semiconductors. Experimental results showed good inverter efficiency, transient dynamic response to load changes, input voltage regulation, and fully functional protection capability, validating the proposed approach as a powerful option for reducing system development time and cost.

1. Introduction

Until recently, the prevailing trajectory in the development of traction drives for hybrid and fully electric vehicles (EVs) emphasized increasing primary source voltage levels to reach state-of-the-art bus values of 800 V for power ratings in excess of 100 kW. Such high voltages facilitate the creation of traction drive systems relying solely on an inverter to feed the machine, without the necessity for voltage step-up DC–DC converters on the input side. Recently, however, a trend reversal has been emerging, marked by a considerable reduction in power and, consequently, input voltage ratings [1]. Now, future development is expected to focus more on ways to optimize the volume and weight of the motor by increasing the number of poles in the machine design, and thus increasing the required fundamental frequency and amplitude of the supply voltage, starting from a lower input battery voltage. In relation to that, interest in the adoption of wide-band-gap (WBG) semiconductors is also increasing, as they allow high switching frequencies and high efficiencies even at higher voltage ratings. So, in an effort to compensate the issue of a higher initial cost of the technology, benefits and savings in other parts of the system are being sought for by WBG bespoke designs. A promising solution that emerged within this context, and which is rapidly gaining widespread interest, is the Y-inverter, illustrated in Figure 1. The inverter consists of three DC–DC converters (Figure 1a) that are not modulated with a constant duty-cycle as is usual, but rather with a sinusoidally varying duty-cycle, as illustrated in Figure 1b: this way, each converter synthesizes an output voltage that is still non-zero DC-average, but is obtained from an offset sinusoidal waveform. When the output voltage is higher than the input voltage, the converter operates in boost mode; vice-versa, when the output voltage is lower than the input, the converter operates in buck mode. Via connecting three 120 deg phase-shifted sinusoidally-modulated DC–DC converter cells in Y-configuration as per Figure 1a, the DC offset at the output of each cell is cancelled out in the phase-to-phase or phase-to-neutral voltages of a three-phase load, yielding the required supply voltages and currents for a three-phase machine (Figure 1c). The amplitude of the phase-to-neutral voltage is indicated as V_PN,PEAK in Figure 1b; provided that V_PN,PEAK > V_DC,IN (i.e., V_OUT,PEAK > 2 × V_DC,IN), then the boost capability of the load voltage relative to the input is ensured. In principle, various DC–DC converter topologies can be selected [2,3,4]; in this work, reference is made to the use of a four-switch non-inverting buck–boost architecture, the solution enabling the highest volumetric and gravimetric power density.

The advantages of Y-inversion over the conventional DC–DC boost plus step-down voltage-source inverter (VSI) approach are many-fold [2,3,4,5,6]:

■

No bulky and reliability critical DC-link capacitor is required;

■

Voltage boost capability is inherently possible;

■

Output electro-magnetic signature is greatly improved, both in terms of harmonic content and dV/dt values;

■

Switching losses are greatly reduced, enabling much higher switching frequencies;

■

Selection and operation of input- and output-side devices can be tailored to optimum performance and cost in terms of semiconductor technology, voltage rating, and switching frequency.

A detailed benchmark can be found in [7,8].

In this paper, a motor drive with a nominal rating of 7.5 kW is considered, supplied by a primary battery with a 60 V nominal rating (48 V min; 72 V max). These specifications were derived from an actual commercial light electric vehicle. To demonstrate major improvements in overall power density, a single-rotor Halbach machine was custom designed with a high number of poles and minimum inductances, requiring fundamental electrical frequencies up to about 2 kHz, with phase-to-neutral voltage amplitudes up to 120 V [9].

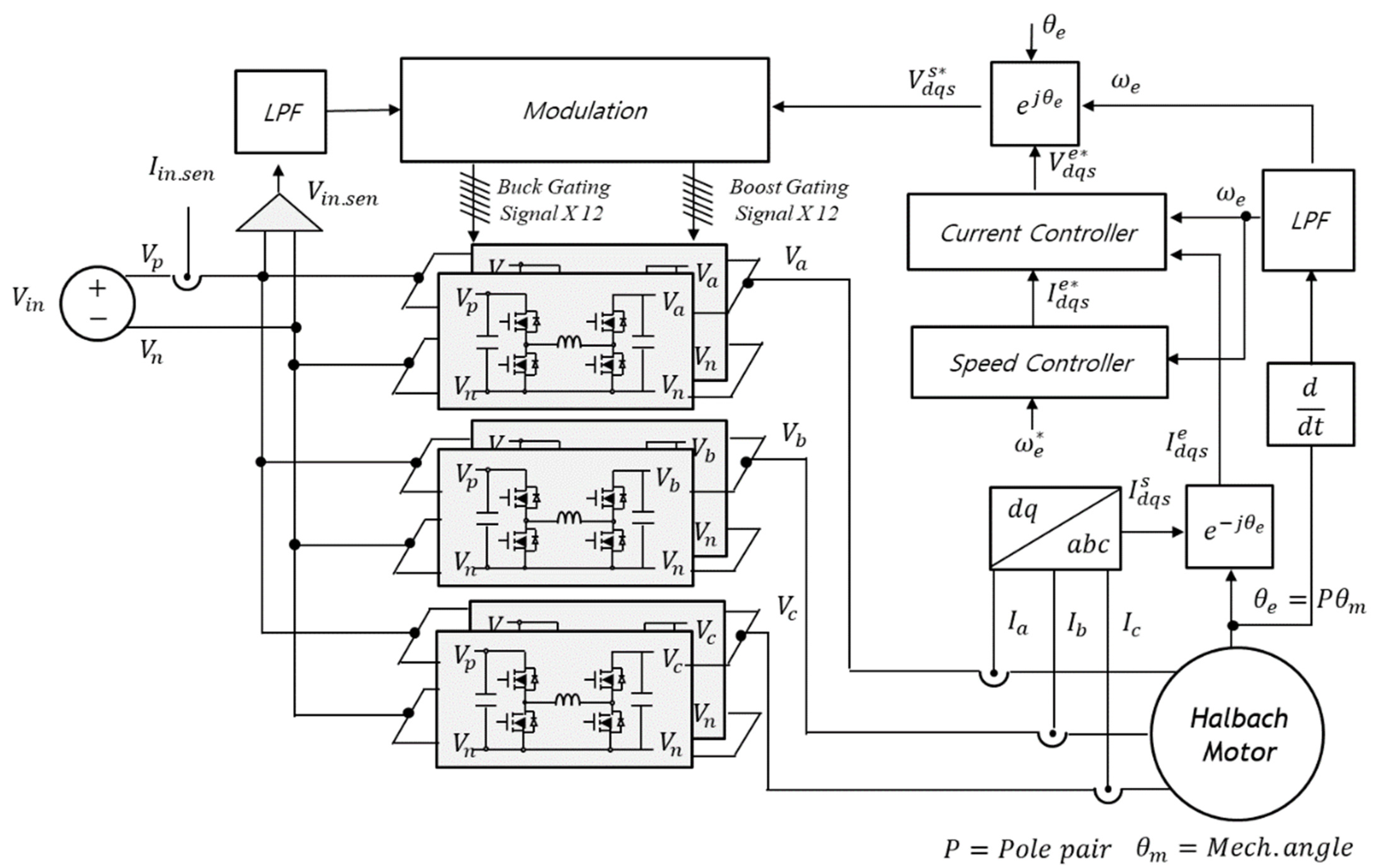
2. Inverter Architecture

2.1. Power Cell Design

The basic cell architecture is shown in Figure 2: a four-switch non-inverting buck–boost converter. As mentioned above, the voltage of the output capacitor is a combination of a DC and an AC voltage component, with the DC voltage offset being removed in a three-phase connection.

In view of the ratings detailed above, input-side transistors can be rated for relatively low voltage (e.g., 100 V). So, either silicon (Si) MOSFETs or gallium nitride (GaN) HEMTs could be chosen. Here, the choice was Si to contain cost. On the output side, 650 V-rated devices are ideal, so that both GaN HEMTs and silicon carbide (SiC) MOSFETs can be considered. Here, SiC MOSFETs were chosen by virtue of their greater maturity and availability from multiple manufacturers. To meet the overall current rating requirements, a single switch on the output was not sufficient. Rather than paralleling multiple devices, we opted for an interleaved implementation of a single cell, so as to reduce the size and electro-thermal stress of passive components. In particular, this design choice is compatible with the use of cross-coupled inductors, in which the equivalent magnetizing current can be significantly reduced [10].

As the Y-inverter’s boost stage has a higher current ripple than the buck’s leg, SiC MOSFET can be applied to the boost stage to strategically reduce ripple. In this paper, we discuss how to implement a three-phase motor system using a commercial hardware and software platform offering the possibility to implement high switching frequencies with extremely simple and straightforward functional block programming.

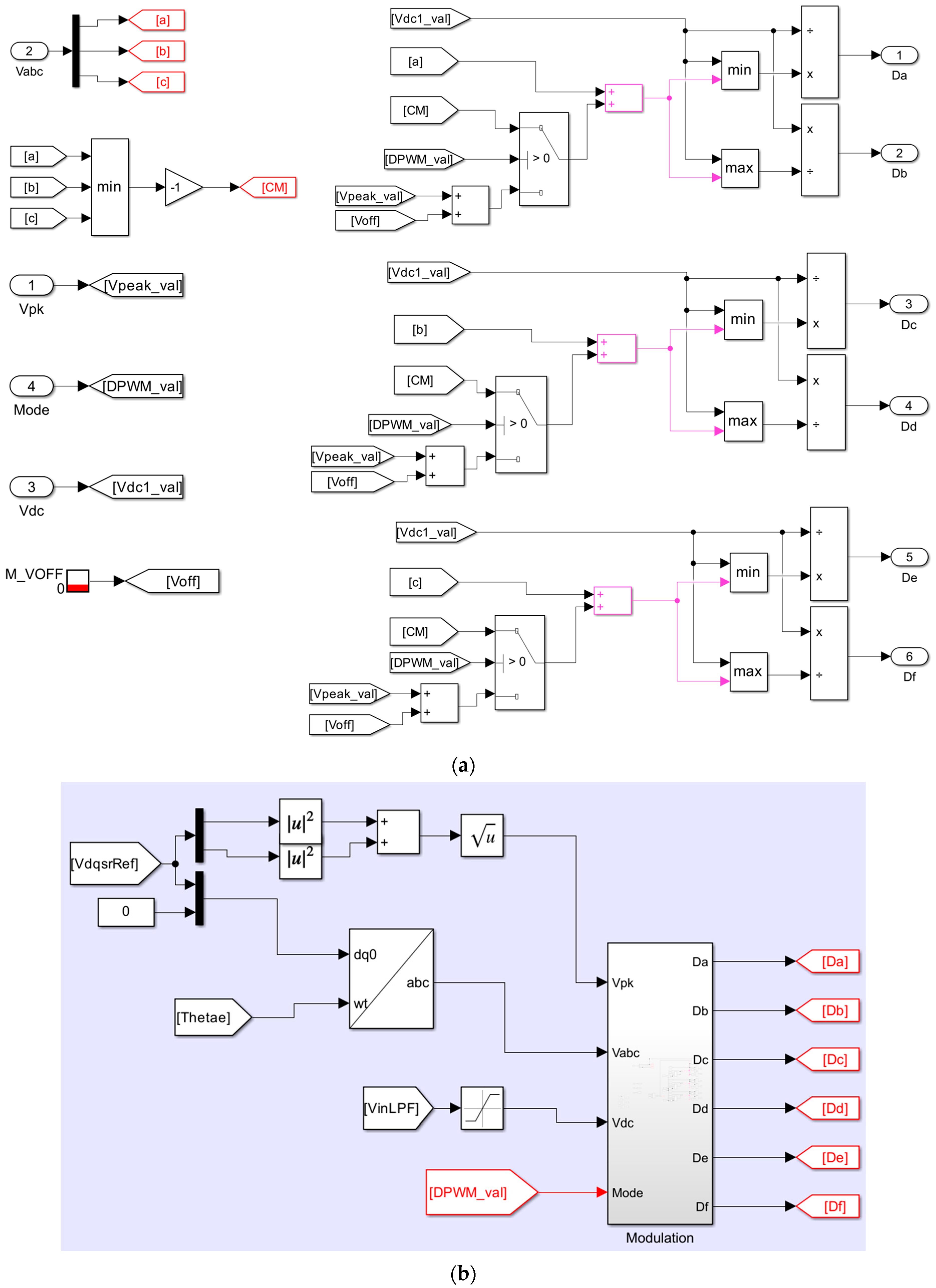
2.2. Modulation Strategy

With relevance to Figure 2, the relationship between the input voltage and the output voltage of one non-inverting buck–boost cell can be expressed as:

$$\frac{V_{abc,n}}{V_{pn}}=\frac{d_{BU}}{1-d_{BO}}=\frac{d_{BU}}{d_{BOC}}=\frac{\widehat{V}}{V_{pn}}·\left[1+\sin \left({\omega }_{F}t\right)\right]$$

(1)

where V_abc.n represents the output capacitor voltage of one of the three phases, and W, V, or U, and V_pn represent the input voltage. d_BU is the duty ratio of the buck converter, d_BO is that of the boost converter, and d_BOC is its complementary (i.e., logic negation) signal.

Based on Equation (1), various modulation strategies are, in principle, possible. For instance:

-

Single-duty: If d_BU = d_BO = d, a single parameter modulation is achieved, with diagonal switch-pairs in the H-bridge cell jointly turned on and off;

-

Dual-duty: This is implemented by maintaining separate variable duty cycles for the buck and boost cells, setting d_BU = 1 during boost-mode operation and, vice versa, setting d_BOC = 1 during buck-mode operation;

-

Hybrid duty: Setting d_BOC = k (with 0 < k < 1) and using only d_BU as the control parameter means that the boost-side leg transistors are operated with constant duty and the buck-side ones with variable duty. Of course, the possibility to set a fixed d_BU value and a variable d_BOC also exists theoretically; however, in the case of sinusoidal modulation, the need to ensure 0 < d_BOC < 1 implies increased complications.

A detailed comparison of various modulation schemes for the Y-inverter is beyond the scope of this paper, but the following observations can be made:

-

The dual-duty solution is the one enabling the lowest maximum voltage across the inductor and thus, the highest power density. Moreover, it minimizes switching losses, as only two devices are switching at any given time, allowing for maximum power density.

-

Single-duty modulation implements a continuous switching pattern of all devices, and thus, of the inductor current controllability; it can be of interest for ensuring good harmonic performance at relatively high output fundamental frequencies.

-

The hybrid-duty approach results in a fully linear control equation and can thus be of interest when a high-performance dynamic response is required while maintaining control simplicity.

In this work, the dual-duty modulation approach is considered, with optimized different values for the switching frequencies of input and output switches.

In Figure 2, $V_{dq}^{\ast }$ is the command voltage required for the load phase voltage expressed in the d-q synchronous reference frame. The electrical angle (θ) can be obtained by multiplying the angular velocity (ω) by the sampling time (T) and the three-phase command voltage from the a-b-c stationary reference frame ($V_{abcs}^{\ast }$). The calculated three-phase command voltage requires the output capacitor voltage of each cell buck–boost converter with the magnitude of the command voltage as a DC offset to be applied to the load. Therefore, the offset voltage may be implemented by adding the magnitude of $V_{dq}^{\ast }$ to each of the three-phase command voltages, as also indicated in Figure 2. However, as errors in the practical implementation of the minimum voltage may occur due to resistance and sensing errors of the capacitor, it may be additionally corrected by an additional arbitrary $\widehat{v_o}$ term. With this approach, sinusoidal PWM (SPWM) was implemented.

Next to SPWM, discontinuous PWM (DPWM) is also considered to reduce the output capacitor voltage peak of the Y-inverter and increase voltage utilization. This is also effective to boost efficiency, as switching is stopped for portions of the period. Here, specifically, a two-thirds discontinuous modulation (TTM) scheme was implemented, with reference voltages shown in Figure 3a, and the corresponding load voltages in Figure 3b. Figure 3c,d report estimated reductions in the boost-side transistors and cell inductor and output capacitor currents amplitudes by adopting SPWM or DPWM.

The selection of this specific DPWM scheme was made after extensive simulation-based benchmarks of the most common DPWM schemes [11,12], because TTM provides the highest efficiency in this particular application, enabling operation at the highest possible switching frequency, and thus with the smallest inductor value.

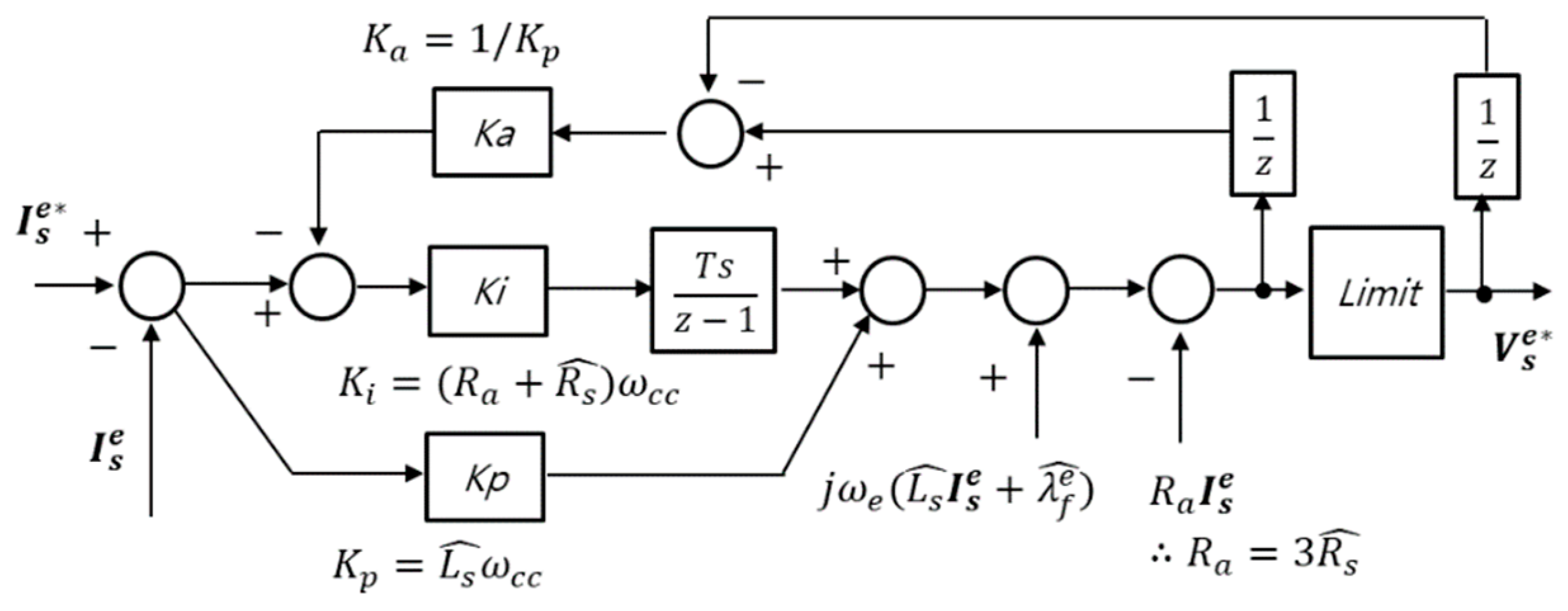
2.3. Control

Figure 4 illustrates the overall control diagram of the Si-SiC hybrid integrated Y-inverter developed in this study. It should be noted that to reduce the current stress on output capacitors, an interleaved configuration was chosen, as opposed to straightforward paralleling of transistors, to achieve the required current rating. So, each phase here consists of two parallel interleaved 180-degree switching frequency phase-shifted cells. Although not exploited here, such a solution also enables the use of cross-coupled inductors, further contributing to the power density optimization of the overall inverter. This solutions appears to increase the number of devices as compared to boost–VSI, but in reality it does not: the number of devices was chosen only to meet the required current rating, which was dictated by the requirement for the machine torque–speed characteristics to be just as high at low-speed high-torque conditions as the DC–DC converter boosting action makes them at high-speed low-torque conditions. So, for the same spec, a boost–VSI system would also likely be designed with interleaved cells in the boost stage to reduce the stress on the DC-link capacitor and parallel devices in the inverter stage.

To operate the motor, a cascaded controller that regulates the speed–phase current is required, utilizing the dq-axis frame as its reference. The controller relies on the electrical machine’s speed ${\omega }_e$, angle θ_e, and motor currents I_a, I_b, and I_c, and then generates the required AC voltages $V_{abcs}^{\ast }$ that the inverter must produce at the machine’s terminals. The required AC motor voltages, including the DC offset voltage, can be generated based on each phase-leg buck–boost converter. Typically, controlling the output voltage of a buck–boost converter requires sensing the output voltage and DC inductor current. Usually, we consider comprising a cascaded output voltage inductor current controller [2]. However, due to its low output capacitance value, the Y-inverter allowed the design of current control using current sensors only if the motor control was compatible with a relatively narrow bandwidth (or slow) response. Nevertheless, in applications such as electric vehicles or systems requiring robust failure tolerance, the design of an interleaved structure proves advantageous. A robust response from the current controller is essential to address hardware imbalances arising from a single-leg failure. Furthermore, when dealing with a low-inductance-based motor featuring a high number of poles, the benefits of wide-band-gap semiconductors-based high switching frequency must be maximized with a fast response controller.

In order to prevent instability in the designed current controller resulting from parameter errors or other disturbances like digital delay and inverter nonlinearity, it was crucial to incorporate a virtual resistor, a technique commonly referred to as the active damping method. With the virtual resistor, the d- and q-axes equivalent circuits in the synchronous reference frame can be deduced, as shown in Figure 5.

$$\left[\begin{array}{c}{v}_{ds}^e\\ v_{qs}^e\end{array}\right]=\left[\begin{array}{cc}{R}_v+R_s+s{L}_{ds}& -{\omega }_e{L}_{qs}\\ {\omega }_e{L}_{ds}& R_v+R_s+s{L}_{qs}\end{array}\right]\left[\begin{array}{c}{i}_{ds}^e\\ i_{qs}^e\end{array}\right]+\left[\begin{array}{c}0\\ {\omega }_e{\lambda }_f^e\end{array}\right]$$

(2)

$$\left[\begin{array}{c}{v}_{ds}^{e\ast }\\ v_{qs}^{e\ast }\end{array}\right]=\left[\begin{array}{cc}\frac{K_{pd}s+K_{id}}{s}& 0\\ 0& \frac{K_{pq}s+K_{iq}}{s}\end{array}\right]\left[\begin{array}{c}{i}_{ds}^{e\ast }-i_{ds}^e\\ i_{qs}^{e\ast }-i_{qs}^e\end{array}\right]+\left[\begin{array}{cc}0& -{\omega }_e\widehat{L_{qs}}\\ {\omega }_e\widehat{L_{ds}}& 0\end{array}\right]\left[\begin{array}{c}{i}_{ds}^e\\ i_{qs}^e\end{array}\right]+\left[\begin{array}{c}0\\ {\omega }_e\widehat{{\lambda }_f^e}\end{array}\right]-R_a\left[\begin{array}{c}{i}_{ds}\\ i_{qs}\end{array}\right]$$

(3)

In (3), if P gains ($K_{pd}, K_{pq}$) are set as ($\widehat{L_{ds}}{\omega }_{cc}, \widehat{L_{qs}}{\omega }_{cc}$), I gains ($K_{id}, K_{iq}$) are set as $\left(\widehat{R_s}+R_v\right){\omega }_{cc}$, and the virtual resistor ($R_v=R_a)$ is set as $\left(3~10\right)\widehat{R_s}$, then the closed loop transfer function can be summarized as a first-order low pass filter between the desired currents ($i_{ds}^{e\ast }, i_{qs}^{e\ast }$) and the response currents ($i_{ds}^e, i_{qs}^e$) with the estimated motor inductances ($\widehat{L_{ds}}, \widehat{L_{qs}}$) and estimated linkage flux ($\widehat{{\lambda }_f^e})$ well matched to the real plant. Based on (3), the current controller was designed as shown in Figure 6, and the anti-windup limiter was considered together with it to limit the output voltage. Here, the anti-windup control gain ($K_a$) is as ($1/K_{pd}, 1/K_{pq}$). The modulation technique used here configured the controller by applying a method devised in a previous study [5].

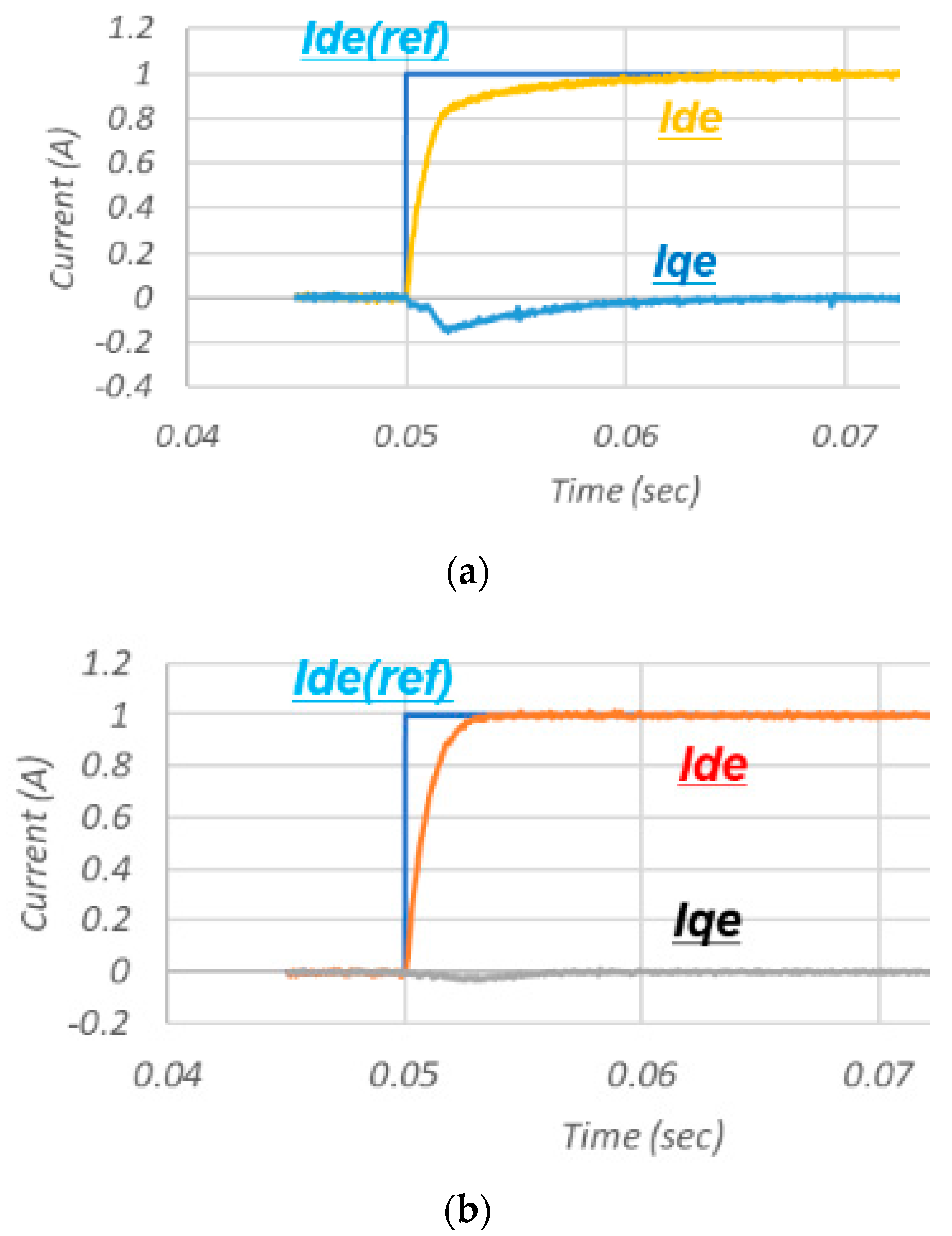
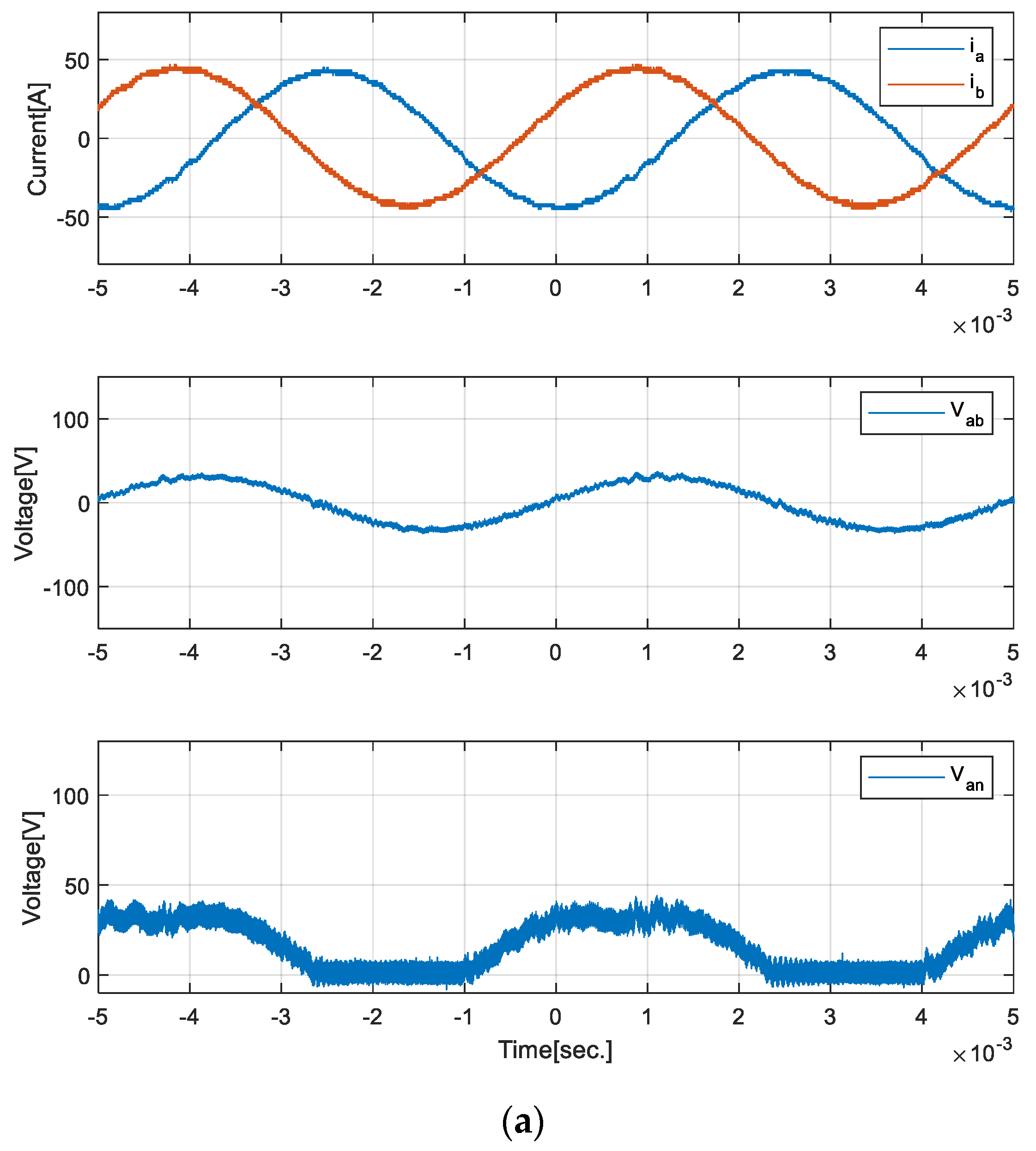
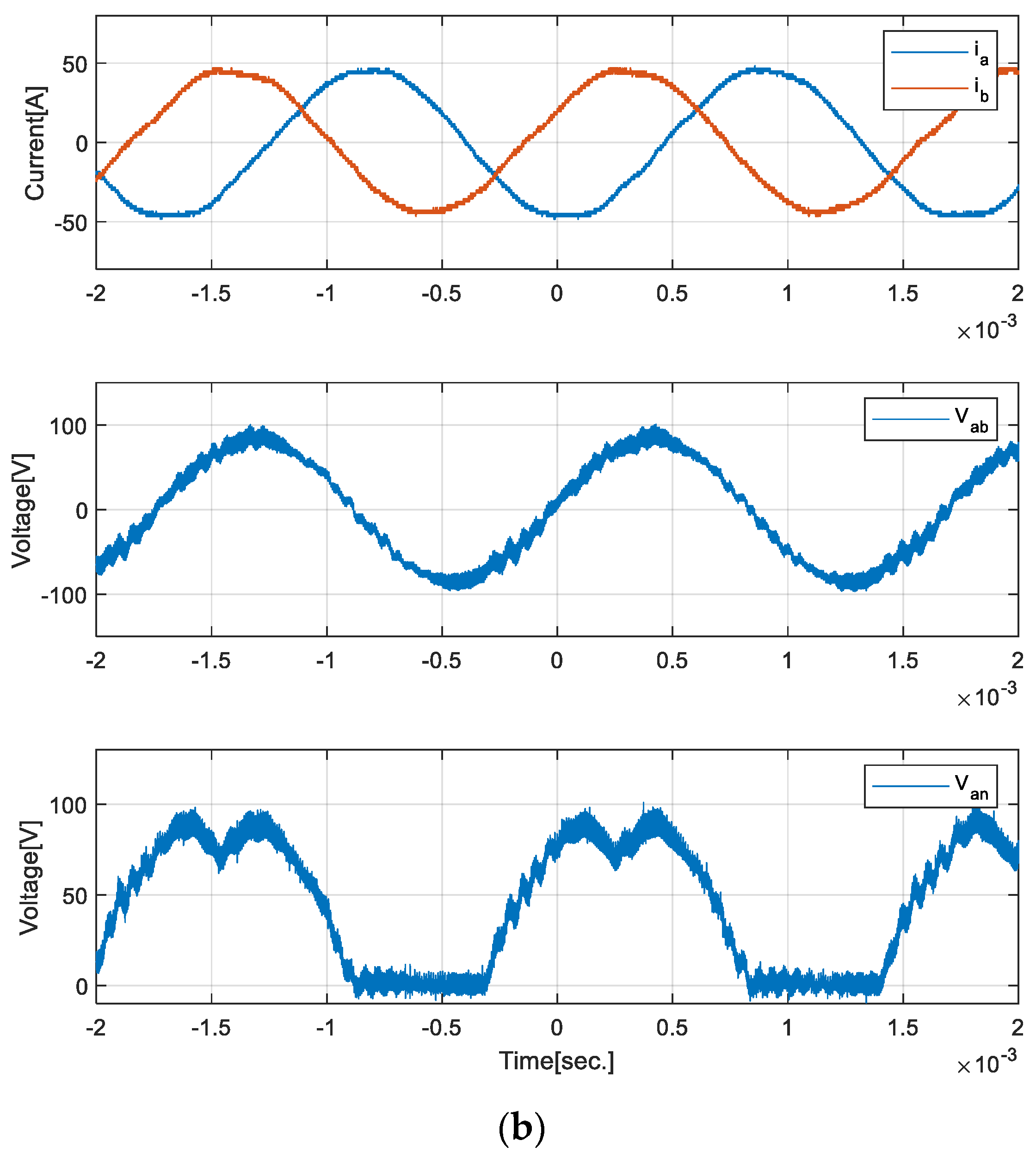
3. Hardware Implementation and Test

The hardware prototype is shown in Figure 7, together with the selected commercial control board [13]. Si MOSFETs on the low-voltage input side are Infineon IPT020N10N3, and SiC MOSFETs on the high-voltage output side are ROHM SCT3017ALHR. Input and output cells are switched with different frequencies, 50 and 150 kHz, respectively, to optimize efficiency. Moreover, to meet power rating requirements, the inverter is implemented by interleaved cells, with a 180 deg phase-shift operation between them [6].

The selected control platform has its own software design kit, which can be installed as a toolbox of Matlab-Simulink for graphic programming of real-time control software. The custom functional blocks allow implementation of the desired functionalities for both simulation and actual automatic code generation. For instance, here, the designed system considered the sampling and feedback controller of a sensor at 50 kHz, while the boost-side SiC MOSFETs require the application of a PWM carrier of 150 kHz. As shown in Figure 8, Clock_0 was designed to be 50 kHz, and Clock_1 was set to 150 kHz. Each specific setting can be found in Figure 5 and Figure 6.

Using the two PWM reference clocks and the carrier-based PWM (CBPWM) function provided by the toolbox, dual switching frequency modulation implementation is straightforward. As the switch of each leg controls the top, and the switch of the bottom needs to consider the dead time, the output mode of the CB-PWM is simply set to Dual (PWM_H + PWM_L); the dead time can also be set by the user, with a value of 200 ns chosen in this case. In addition, as the designed hardware has two parallel power electronic cells for high current input and output, a phase parameter of the CB-PWM can be set to 0 and 0.5 to implement PWM signals with the required 180 degree phase shift.

The required duty-cycle can be implemented by the modulation method described in Section 2.2. Figure 9a shows the toolbox implementation of the three-phase target voltage (V_abc), the vector magnitude of the target voltage (V_pk), the PWM mode (if the value is 0, it calculates the duty for the sinusoidal PWM; in other cases, it generates the duty of the DPWM), and the input voltage magnitude (V_dc) to calculate the duty required for each phase. This configured subsystem is connected to the command voltage (V_aq) and the PWM function, as illustrated in Figure 9b.

Figure 10a shows real-time simulation results of the implemented interleaved carrier signals, while Figure 10b shows real-time simulated output capacitor voltage (top), cross-coupled inductor currents (center), and effective magnetizing current (bottom) for the implemented operation. The results in Figure 10 were obtained with a real-time simulation box [14], for which an interface with the control platform is readily available, also allowing for ease of use in hardware-in-the-loop (HIL) type experiments.

Controller design validation was carried out by means of DC current step response, discussed with the help of Figure 11: in (a), using a conventional controller, the target value was reached in approximately 20 ms; in contrast, employing active damping results in (b), the target value was attained within about 3 ms, a significant improvement (in these tests, the bandwidth cut-off frequency was set at 300 Hz). Based on the above preliminary results, the overall system dynamic performance was assessed using a test light-load motor before its application to the Halbach motor. Figure 12 shows representative results: in (a), the startup performance was validated, and the boosting function with an output voltage surpassing the input voltage was confirmed at maximum speed operation in (b); in (c), bidirectional power transfer capability of the Y-inverter is shown, confirming the current controller’s performance during regenerative braking.

The Halbach motor experimental setup shown in Figure 13 was assembled and used for final characterization.

Figure 14 shows representative waveforms for DPWM, with test conditions of 15.3 N-m torque and motor rotational speeds of 600 rpm and 1800 rpm in (a) and (b), respectively. Under the same load torque, motor terminal currents were approximately 30 amps at different speed conditions, while the phase-to-phase motor voltage was close to an ideal sinusoidal waveform.

Figure 15 reports the results of measured inverter efficiency for other torque and speed conditions. These results include gate-driver losses of around 12 W. The maximum efficiency measured here, for power levels up to about 50% of the maximum rating, was 97%, and it is worth noting how even partial load conditions were characterized by relatively high efficiency.

Finally, Figure 16 shows the measured harmonic distortion using the phase-to-phase motor terminal voltages and motor currents under different speed and load torque conditions: both voltage and current total harmonic distortions were below 5% at all test conditions. Such good results were due not only to the inverter, but also to the Halbach rotor machine design. Some tests carried out with a non-permanent magnet-type machine yielded different harmonic signatures. Details of the Halbach machine’s structure and design can be found in [15,16].

4. Discussion and Conclusions

Results presented demonstrate the suitability of modern control platforms and dedicated functional blocks-based SDK packages to implement real-application control solutions, even for high-frequency switching original inverter topologies and machine structures used in modern traction drives requiring regenerative braking capability. Not shown here explicitly, the same platform and approach were also used to design input and output over-voltage and over-current protections, as well as temperature monitoring and over-temperature shutdown, and their validity was confirmed experimentally in a number of dedicated tests. Definitely a powerful option for research and development laboratory environments, the time-saving opportunities offered by such an approach over alternative solutions requiring explicit programming well compensate the hardware platform cost and could also be used for commercial product delivery.