Multi-Agent Deep Reinforcement Learning-Based Inference Task Scheduling and Offloading for Maximum Inference Accuracy under Time and Energy Constraints

Abstract

The journey towards realizing real-time AI-driven IoT applications is facing a significant hurdle caused by the limited resources of IoT devices. Particularly for battery-powered edge devices, the decision between performing task inference locally or by offloading to edge servers, all while ensuring timely results and conserving energy, is a critical issue. This problem is further complicated when an edge device houses multiple local inference models. The challenge of effectively allocating inference models to tasks between local models and edge server models under strict time and energy constraints while maximizing overall accuracy is recognized as a strongly NP-hard problem and has not been addressed in the literature. Therefore, in this work we propose MASITO, a novel multi-agent deep reinforcement learning framework designed to address this intricate problem. By dividing the problem into two sub-problems namely task scheduling and edge server selection we propose a cooperative multi-agent system for addressing each sub-problem. MASITO’s design allows for faster training and more robust schedules using cooperative behavior where agents compensate for each other’s sub-optimal actions. Moreover, MASITO dynamically adapts to different network configurations which allows for high-mobility edge computing applications. Experiments on the ImageNet-mini dataset demonstrate the framework’s efficacy, outperforming genetic algorithms (GAs), simulated annealing (SA), and particle swarm optimization (PSO) in scheduling times by providing lower times ranging from 60% up to 90% while maintaining comparable average accuracy in worst-case scenarios and superior accuracy in best-case scenarios.

1. Introduction

As advancements in hardware and machine learning algorithms continue to unfold, artificial intelligence (AI) is becoming increasingly pervasive in Internet of Things (IoT) applications. One notable trend driving this evolution is the empowerment of IoT devices to conduct local inference tasks. This shift is propelled by two key factors: the remarkable progress in hardware capabilities and the refinement of machine learning algorithms. Modern IoT devices are equipped with increasingly sophisticated processors and specialized neural processing engines, enabling them to process complex AI computations locally with greater efficiency. Concurrently, machine learning algorithms have undergone significant enhancements, becoming more lightweight, efficient, and capable of running on resource-constrained devices. Together, these advancements enable IoT devices to perform real-time data analysis and decision-making at the edge, reducing latency, conserving bandwidth, and enhancing privacy by minimizing data transmission to central servers [1,2].

In addition to local inference capabilities, the role of inference task offloading to edge servers remains vital, particularly for tasks with higher computational demands and time-sensitive applications, while local inference is advantageous for quick decision-making and reducing reliance on centralized resources, certain AI tasks may exceed the processing capacity of individual IoT devices. In such scenarios, offloading these tasks to edge servers equipped with more powerful hardware and ample computational resources becomes indispensable. This approach not only alleviates the burden on edge devices but also ensures the timely execution of complex computations, critical for meeting stringent response time requirements in time-sensitive applications [3].

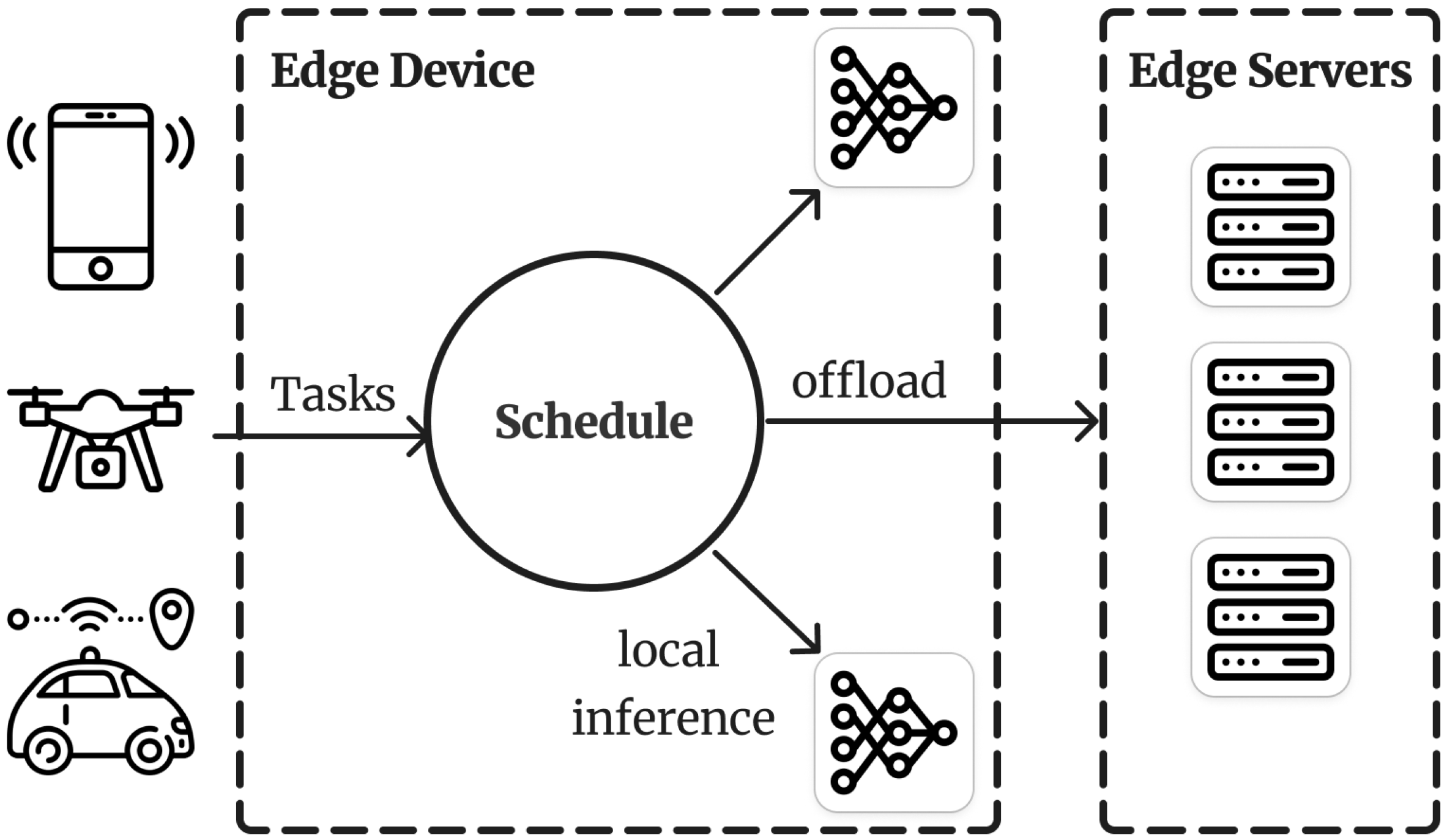
Having multiple local inference models onboard an edge device varying in size and accuracy empowers the system with dynamic adaptability, enabling edge devices to intelligently assign the most suitable model to a task based on various factors such as task properties, device resources, and application parameters (see Figure 1). This dynamic approach leverages the diverse capabilities of different inference models to optimize performance and efficiency in real-time scenarios. By analyzing task requirements, such as computational complexity, accuracy thresholds, and latency constraints, edge devices can intelligently select the most appropriate model from their repertoire to favor accuracy over energy, for example, or speed over accuracy. Simultaneously, considering device resources, including processing power, memory availability, and energy reserves, ensures optimal utilization of onboard resources without overburdening the device. Additionally, by incorporating application-specific parameters, edge devices can tailor inference model selection to align with application objectives and constraints [4].

The challenge of assigning local and edge server inference models to tasks under time and energy constraints while maximizing the accuracy is similar in nature to the unbounded multidimensional knapsack problem [5], which consists of filling a knapsack limited by volume and weight to maximize profit. However, in this case, the aim is to fill a schedule constrained by time and energy with inference models to optimize accuracy. This class of problem falls under the NP-Hard category, lacking any polynomial time solutions. Therefore, in this work, we tackle this complex optimization problem by dividing it into two smaller sub-problems and proposing an edge computing framework for AI-driven edge computing real-time applications, using state-of-the-art deep reinforcement learning methods by leveraging parallel inference between local inference and offloading tasks under time and energy limitations while maximizing inference accuracy.

In real-time IoT applications, such as smart healthcare [6], autonomous vehicles [7,8], and critical resource deployment [9,10], timely decision-making is critical for ensuring safety, efficiency, and responsiveness. By efficiently managing inference tasks at the edge, solving this problem enables the seamless integration of AI capabilities into these systems, enhancing their intelligence and autonomy. Moreover, the optimization of inference task allocation contributes to resource conservation, extending the operational lifespan of battery-powered edge devices and reducing overall energy consumption. Beyond IoT, edge computing, and AI integration, solutions to this problem have implications for broader computing paradigms, including cloud-edge orchestration and distributed computing architectures. Therefore, addressing this challenge not only advances the capabilities of edge computing systems but also paves the way for innovative applications that leverage the synergy between AI and edge technologies.

In the literature, there is a notable lack of research on the subject of inference task scheduling and offloading under constraints, primarily attributed to the novelty of the problem under investigation. Few works such as [11] focus on the decision of whether to process data locally or offload to an edge server based on the probability of the inference resulting in low accuracy while adhering to a given energy constraint. This work represents a smaller subproblem of the more general problem tackled in this work, where their work takes advantage of only a single local inference model with a single-edge server resulting in a binary decision. Moreover, the time aspect is not addressed, which is crucial for real-time applications. On the other hand, the study outlined in [4] strikes more resemblance to our problem, where multiple inference models within the edge device are considered all while adhering to time constraints. However, their investigation overlooks the energy aspect, which holds significance for battery-powered edge devices. Additionally, their system exclusively allows offloading to a single-edge server. This underscores a research gap wherein the overarching problem necessitates attention, considering both time and energy constraints while maximizing inference accuracy through the allocation of inference models from a set of local and edge server models.

Utilizing deep reinforcement learning (DRL) agents to orchestrate inference task scheduling and offloading in edge computing environments, our work seeks to optimize the allocation of inference models, respecting time and energy constraints while maximizing accuracy, thereby advancing the efficacy and efficiency of AI-driven IoT applications. The main contributions of this paper can be summarized as follows:

• We formulate the problem of inference model scheduling between local inference and edge server offloading under time and energy constraints in parallel where we analyze its complexity.
• We propose MASITO, a multi-agent deep reinforcement learning (DRL)-based framework for inference task scheduling and offloading for edge computing consisting of cooperating agents for task scheduling and edge server selection.
• We perform experiments on the framework and compare its performance against other schemes, such as genetic algorithms (GAs), simulated annealing (SA), and particle swarm optimization (PSO), where we prove its effectiveness and advantages over these schemes.

The rest of this paper is organized as follows. Section 2 presents the related works and points out the research gap. In Section 3, we describe the system model. In Section 4, we propose MASITO and explain the framework components. In Section 5, we present the experiment setup and results in addition to analysis of the obtained results. Finally, we conclude this work in Section 6.

2. Related Works

Task offloading in edge computing has attracted significant attention from the research community as a result of its crucial role in optimizing resource utilization and enhancing system performance. Various solutions and architectures have been proposed to address task-offloading problems [3]. In this section, we focus on the multi-access edge computing (MEC) network architecture in which computing resources are placed at the edge of the network, close to end users. This reduces latency and improves efficiency for data processing and service delivery in applications like IoT and mobile networks [12,13,14,15].

For instance, works proposed by Yang et al. (2020) [16], Liu et al. (2019) [17], and Zhang et al. (2021) [18] focus on designing offloading decisions based on data characteristics and network conditions, aiming to minimize latency and maximize throughput. Similarly, solutions proposed by Chen et al. (2021) [19], Li et al. (2020) [20], and Xu et al. (2020) [21] examine task-offloading strategies considering energy consumption and device capabilities, developing energy-aware scheduling algorithms. Additionally, studies by Cozzolino et al. (2023) [22], Abdenacer et al. (2023) [6], and Younis et al. (2019) [23] address both energy and latency, aiming to reduce both metrics or find a balance between them. These approaches are often not suitable for real-time applications, which require meeting strict time constraints and tight energy budgets.

A notable scarcity of studies is found in the literature where explicit time and energy constraints are considered, either individually or in combination. For example, works by Li et al. (2021) [24], Tajallifar et al. (2021) [25], and Liu et al. (2016) [26] propose a time-aware task-offloading framework that processes tasks by priority based on given deadlines to dynamically allocate resources for meeting real-time requirements. Similarly, Zhao et al. (2021) [27] and Jiang et al. (2022) [28] introduce an energy-aware task-offloading approach optimizing energy consumption by balancing workload distribution across edge devices and servers. Furthermore, Mohammad et al. (2020) [29], Azizi et al. (2022) [30], Wang et al. (2019) [31], and Ben et al. (2024) [32,33] tackle the joint optimization of time and energy constraints in task-offloading decisions, using mathematical modeling techniques to formulate the problem as a multi-objective optimization problem. These studies emphasize the necessity of accounting for both time and energy constraints when making task-offloading decisions, underscoring their interdependence and the requirement for comprehensive optimization strategies in edge computing environments.

In the context of inference tasks, accuracy as a task-offloading objective has seen less attention from the research community. With the rise of AI model deployment in IoT, it is becoming an important performance metric. Nikoloska et al. (2020) [11] propose a data selection scheme based on a confidence metric for edge devices to select the data samples which could lead to poor inference accuracy, in which case they are offloaded to the edge server. Fresa et al. (2021) [4] propose a task scheduling and offloading scheme based on LP-Relaxation and dynamic programming where all possible cases of scheduling two inference tasks between the edge device and the edge server are considered.

Various optimization methods have been used to tackle the task-offloading problem in edge computing, reflecting the complexity and diversity of the challenges involved. Traditional optimization techniques, such as Mixed Linear Programming (MLP) [34] and branch and bound [35], have framed task allocation as a mathematical optimization problem, allowing for exact or near-optimal solutions under certain constraints. Additionally, machine learning methods have gained prominence for their capacity to adaptively learn and optimize task-offloading decisions based on historical data and real-time observations [36,37]. Furthermore, metaheuristic algorithms, including genetic algorithms, simulated annealing, and particle swarm optimization, have been employed to address the NP-hard nature of the task-offloading problem by efficiently exploring the solution space and identifying high-quality solutions [32,33,38,39]. Each method presents unique advantages and trade-offs, depending on the specific problem characteristics and the requirements of the edge computing environment.

Deep reinforcement learning (DRL) approaches stand out as highly adaptive schemes, making them suitable for high-mobility edge computing networks. Additionally, with proper configuration and design, DRL schemes can consistently match and outperform metaheuristic schemes while consuming fewer resources. Chen et al. (2021) [19] propose a resource allocation scheme for augmented reality (AR) in single and multi-access edge computing (MEC) systems. Using a DRL multi-agent deep deterministic policy gradient (MADDPG) method, their system managed to minimize energy consumption for each user subject to latency requirements and limited resources. Their proposed system uses MEC servers for offload path planning, which incurs a communication overhead while edge devices wait for plans. Additionally, their proposed DRL agent considers a fixed number of MEC servers. Alfakih et al. (2020) [36] propose a system model consisting of mobile edge computing networks (MECNs) with multiple access points. The edge devices can connect to an MECN through the access points. The edge device uses a state–action–reward–state–action (SARSA) reinforcement learning agent to decide whether to offload the task to the nearest edge server, an adjacent edge server, or the remote cloud. This work relies on networking infrastructure that might not always be available and cost-effective, potentially causing additional delays in real-time applications. Furthermore, the proposed agent has limited actions in terms of deciding which server to offload to, significantly reducing the ability to precisely control the overall task offload latency. Gao et al. (2024) [40] propose Com-DDPG, an offloading strategy for MEC utilizing multi-agent reinforcement learning to improve offloading performance. Within the Internet of Vehicles (IoV) transmission radius, multiple agents collaborate to learn environmental changes, such as the number of mobile devices and task queues, and develop an offloading strategy for edge servers. The method models task dependency, priority, and resource consumption, and formulates communication among agents. Reinforcement learning determines the offloading strategy, with a Long Short-Term Memory (LSTM) network enhancing internal state predictions and a bidirectional recurrent neural network (BRNN) improving communication features among agents. Li et al. (2024) [41] propose a Multi-Action and Environment-Adaptive Proximal Policy Optimization algorithm (MEPPO), an enhancement of the conventional PPO algorithm, aimed at optimizing task scheduling and resource allocation in dynamic Vehicular Edge Computing (VEC) environments. The method encompasses three core aspects: generating task-offloading and priority decisions to reduce service request completion time, dynamically allocating transmit power based on expected transmission distances to minimize energy consumption, and adapting scheduling decisions to varying numbers of vehicle tasks by manipulating the state space of the PPO algorithm. This approach ensures efficient and adaptive management of tasks and resources in real-world scenarios.

In summary, a significant gap in the literature is identified, where inference task-offloading decisions are determined by both time and energy constraints while aiming to maximize overall accuracy. Our work stands out by addressing inference task scheduling and offloading with a strong emphasis on accuracy as a key performance metric. Furthermore, our approach directly integrates time and energy constraints to control scheduling and offloading decisions, focusing on parallel task execution. Additionally, deep reinforcement learning enables rapid scheduling and real-time adaptation to network changes.

3. System Model

We consider a sensing system consisting of edge devices equipped with a set of local inference models $\mathcal{L}=\{1,\dots ,L\}$. These edge devices have access to a set of edge servers $\mathcal{E}$. Each edge server is equipped with a single inference model. The set of edge server inference models is denoted as $\mathcal{S}=\{1,\dots ,S\}$. At each time slot, the edge device receives a set of inference tasks denoted as $\mathcal{J}=\{1,\dots ,J\}$. An edge device constructs a selected set of inference models $\mathcal{M}=\{1,\dots ,M\}$ for each time slot using $\mathcal{S}$ and $\mathcal{L}$. This set is then used to assign inference models to tasks. All notations used in this section are presented in

Table 1. Symbols and notations.

Notation	Description
$\mathcal{L}$	The set of edge device local inference models
$\mathcal{E}$	The set of available edge servers
$\mathcal{S}$	The set of edge server inference models
$\mathcal{M}$	The set of all inference models available to the edge device
$\mathcal{J}$	The set of inference tasks for each time slot
$A_i$	The average top-1 accuracy of model i
$T_i^{\inf }$	The average inference time of model i
$T_i^{\mathrm{lat}}$	The average communication latency for edge server i
$T_{ij}^{\mathrm{off}}$	The estimated time to offload task j to the edge server i
$siz{e}_j$	The size of task j
$b_i$	The bandwidth of the communication channel for edge server i
$T_{ij}^{\mathrm{task}}$	The total time it takes to process task j using model i
$T_i^{\mathrm{resp}}$	The average response time from edge server i
$x_{ij}$	Represents whether an inference model i is assigned to task j
$T_k^{\mathrm{slot}}$	The total time to process a complete time slot k
$T_k^{\mathrm{local}}$	The total local inference time for time slot k
$T_k^{\mathrm{server}}$	The total server time for time slot k
$T^{\mathrm{off}\_\mathrm{accu}}$	Offloading time accumulator
$T^{\inf \_\mathrm{accu}}$	Inference time accumulator
$E_{ij}^{\mathrm{off}}$	The energy cost of offloading task j to edge server i
$c_i$	The average energy cost of transmitting data to edge server i
$E_i^{\mathrm{resp}}$	The energy cost of the inference response
$E_i^{\inf }$	The average energy cost of inference using model i
$E_{ij}^{\mathrm{task}}$	The total energy cost of processing task j using model i
$A_k^{\mathrm{slot}}$	The total accuracy for time slot k
$E_k^{\mathrm{slot}}$	The total energy for time slot k

.

3.1. Inference Accuracy

Edge devices can deploy inference models in several ways. One approach is to use a single tunable model, where adjusting input hyperparameters alters accuracy and inference times. Alternatively, multiple instances of similar models with different internal structures, such as varying layer sizes in Deep Neural Networks (DNNs), can be deployed. Another option is to use diverse types of models with different sizes and top-1 average accuracies. Since the actual top-1 accuracy of each model for a specific inference task is unknown beforehand, we rely on the average accuracy estimated from historical top-1 accuracy measurements. The average top-1 accuracy of model i is denoted as $A_i\mathrm{where}i\in \mathcal{M}$. The average top-1 accuracy of models on edge servers is set to be significantly higher than that of local inference models on edge devices [32].

$$A_j>A_i\forall i\in \mathcal{L},j\in \mathcal{S}$$

3.2. Time Delay Model

The average inference time for each model i denoted as $T_i^{\inf }\mathrm{where}i\in \mathcal{M}$ is estimated using the average historical measured inference times where data pre-processing time is considered part of $T_i^{\inf }$. We define $T_i^{\mathrm{lat}}$ as the average latency of edge server i estimated from previous measurements. $T_i^{\mathrm{lat}}$ is continuously updated after every transmission providing an indirect metric to the mobility of edge devices. Let $T_{ij}^{\mathrm{off}}$ be the estimated time to offload task $j\mathrm{where}i\in \mathcal{J}$ to edge server i. $T_{ij}^{\mathrm{off}}$ can be calculated using the channel bandwidth and the size of task j denoted as $siz{e}_j$ given by

$$T_{ij}^{\mathrm{off}}=\frac{siz{e}_j}{b_i}+T_i^{\mathrm{lat}}$$

where $b_i$ represents the bandwidth of the channel between the edge device and edge server i. The bandwidth can be estimated from historical transmissions.

Let $T_{ij}^{\mathrm{task}}$ be the total time to process a given task j using model i including inference and offloading times.

$$T_{ij}^{\mathrm{task}}=T_i^{\inf }\forall i\in \mathcal{L}j\in \mathcal{J}$$

$$T_{ij}^{\mathrm{task}}=T_i^{\inf }+T_{ij}^{\mathrm{off}}+T_i^{\mathrm{resp}}\forall i\in \mathcal{S}j\in \mathcal{J}$$

where $T_i^{\mathrm{resp}}$ represents the average response time from edge server i given by

$$T_i^{\mathrm{resp}}=\frac{siz{e}_r}{b_i}+T_i^{\mathrm{lat}}$$

where $siz{e}_r$ is a constant representing the response size.

We define $x_{ij}=\{0,1\}$ as a binary variable representing the decision whether an inference model i is assigned to inference task j. Let $T_k^{\mathrm{slot}}$ be the total time to process a complete time slot k. The local inference and offloading are performed in parallel, and therefore we define $T_k^{\mathrm{slot}}$ as the max between the total local inference time $T_k^{\mathrm{local}}$ and the total server time which includes offloading, inference, and response times of all offloaded tasks denoted as $T_k^{\mathrm{server}}$. $T_k^{\mathrm{server}}$ is calculated using Algorithm 1.

$$T_k^{\mathrm{slot}}=max(T_k^{\mathrm{local}},T_k^{\mathrm{server}})\forall k\in \Delta$$

where

$$T_k^{\mathrm{local}}=\sum _{i=1}^L\sum _{j=1}^J{x}_{ij}{T}_i^{\inf }$$

• $T_i^{\mathrm{server}}$ is the total offload, inference, and response times for all tasks offloaded to the edge server with model i.
• $T^{\mathrm{off}\_\mathrm{accu}}$ is a variable to accumulate and track offload times for all edge servers.
• $T_i^{\inf \_\mathrm{accu}}$ is a variable that accumulates and tracks inference times for each edge server with model i.

Algorithm 1: Steps to calculate $T_k^{\mathrm{server}}$

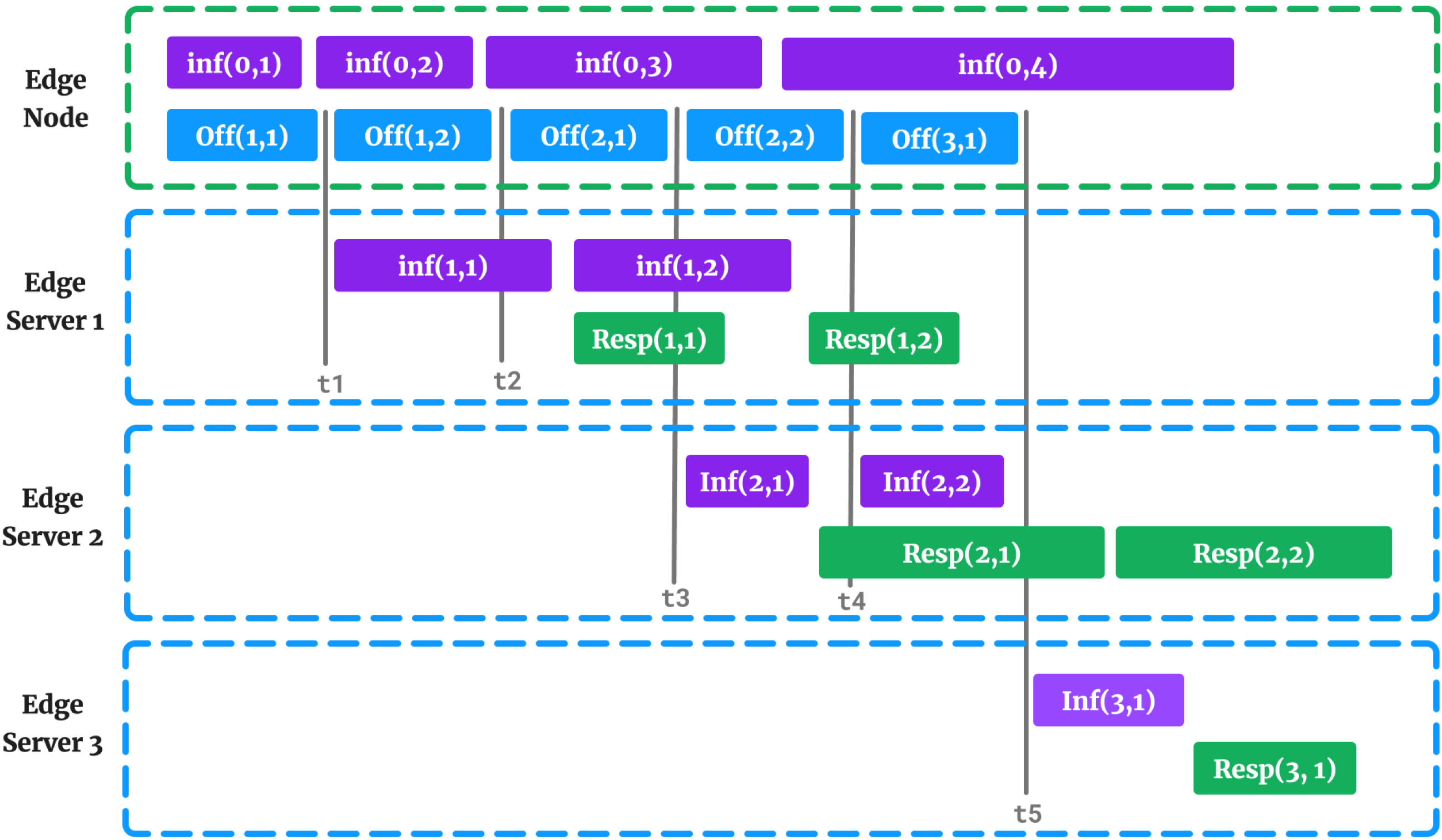
The edge devices, encompassing both standard edge devices and edge servers, are assumed to have two queues as depicted in Figure 2, one for computation and another for communication. This configuration facilitates parallel processing of inference tasks and offloading or receiving data. Figure 3 illustrates an example schedule for nine inference tasks, where four tasks are processed using local inference models, and six tasks are offloaded to three different edge servers. At $t_1$, the scenario is as follows:

$$T^{\mathrm{off}\_\mathrm{accu}}=T_{1,1}^{\mathrm{off}}$$

$$T_1^{\inf \_\mathrm{accu}}=max(T_1^{\inf \_\mathrm{accu}},T^{\mathrm{off}\_\mathrm{accu}})+T_{1,1}^{\inf }$$

$$T_1^{\inf \_\mathrm{accu}}=T^{\mathrm{off}\_\mathrm{accu}}+T_{1,1}^{\inf }=T_{1,1}^{\mathrm{off}}+T_{1,1}^{\inf }$$

$$T_1^{\mathrm{server}}=max(T_1^{\mathrm{server}},T_1^{\inf \_\mathrm{accu}})+T_1^{\mathrm{resp}}$$

$$T_1^{\mathrm{server}}=T_1^{\inf \_\mathrm{accu}}+T_{1,1}^{\mathrm{resp}}=T_{1,1}^{\mathrm{off}}+T_{1,1}^{\inf }+T_{1,1}^{\mathrm{resp}}$$

By following the steps outlined in Algorithm 1 and applying them to the example shown in Figure 3, we obtain the $T_i^{\mathrm{server}}$ values presented in

Table 2. Example values of $T_i^{\mathrm{server}}$ for time steps 2–5.

$t_2$	$T_1^{\mathrm{server}}=T_{1,1}^{\mathrm{off}}+T_{1,1}^{\inf }+T_{1,2}^{\inf }+T_{1,2}^{\mathrm{resp}}$
$t_3$	$T_2^{\mathrm{server}}=T_{1,1}^{\mathrm{off}}+T_{1,2}^{\mathrm{off}}+T_{2,1}^{\mathrm{off}}+T_{2,1}^{\inf }+T_{2,1}^{\mathrm{resp}}$
$t_4$	$T_2^{\mathrm{server}}=T_{1,1}^{\mathrm{off}}+T_{1,2}^{\mathrm{off}}+T_{2,1}^{\mathrm{off}}+T_{2,1}^{\inf }+T_{2,1}^{\mathrm{resp}}+T_{2,2}^{\mathrm{resp}}$
$t_5$	$T_3^{\mathrm{server}}=T_{1,1}^{\mathrm{off}}+T_{1,2}^{\mathrm{off}}+T_{2,1}^{\mathrm{off}}+T_{2,2}^{\mathrm{off}}+T_{3,1}^{\mathrm{off}}+T_{3,1}^{\inf }+T_{3,1}^{\mathrm{resp}}$

. The $T^{\mathrm{server}}$ value is determined as the maximum of all edge server total times. Finally, the total slot time $T^{\mathrm{slot}}$ is calculated by taking the larger value between the total time for local inference $T^{\mathrm{local}}$ and $T^{\mathrm{server}}$.

$$T^{\mathrm{server}}=max(T_1^{\mathrm{server}},T_2^{\mathrm{server}},T_3^{\mathrm{server}})=T_2^{\mathrm{server}}$$

$$T^{\mathrm{slot}}=max(T^{\mathrm{local}},T_2^{\mathrm{server}})=T_2^{\mathrm{server}}$$

3.3. Inference Energy

Let $E_{ij}^{\mathrm{off}}$ be the energy cost of offloading task j to edge server i. $E_{ij}^{\mathrm{off}}$ depends on the offload time $T_{ij}^{\mathrm{off}}$ and $c_i$ the average energy cost of transmitting data to edge server i in one time unit. $c_i$ depends on several factors, including the communication medium such as Wi-Fi, Cellular, Bluetooth, or Zigbee, which affects energy consumption. Each medium has different power requirements, data rates, and transmission ranges, which influence the overall energy cost. The transmission power level of the wireless device impacts energy consumption. Higher transmit power levels generally result in greater energy consumption to maintain communication over longer distances or in environments with obstacles or interference. The power consumed by the wireless device when idle or in standby mode also contributes to the overall energy cost. Signal strength and quality impact energy consumption, especially in wireless communication systems that adapt transmission power based on signal conditions. Maintaining reliable communication may require higher power levels in environments with weak or noisy signals, leading to increased energy consumption. Environmental factors such as interference, obstacles, and electromagnetic noise can affect energy consumption by influencing signal propagation and reception quality. Various optimization techniques, such as data compression, packet aggregation, adaptive modulation, and power control algorithms, can help reduce energy consumption during wireless communication by improving spectral efficiency and minimizing transmission overhead.

The energy cost of offloading task j to edge server i, denoted as $E_{ij}^{\mathrm{off}}$, depends on the offload time $T_{ij}^{\mathrm{off}}$ and $c_i$, the average energy cost per time unit for transmitting data to edge server i. Several factors influence $c_i$, including the communication medium (Wi-Fi, Cellular, Bluetooth, or Zigbee), each with distinct power requirements, data rates, and transmission ranges. Higher transmission power levels generally lead to greater energy consumption, especially for maintaining communication over longer distances or in challenging environments. Additionally, the power consumed by the wireless device in idle or standby mode contributes to the overall energy cost. Signal strength and quality also impact energy consumption, as maintaining reliable communication in weak or noisy signal environments may require higher power levels. Environmental factors such as interference, obstacles, and electromagnetic noise can affect energy consumption by influencing signal propagation and reception quality. Furthermore, optimization techniques like data compression, packet aggregation, adaptive modulation, and power control algorithms can reduce energy consumption by improving spectral efficiency and minimizing transmission overhead [32].

We assume that $c_i$ can be calculated internally by monitoring battery usage and the network adapter’s configurations such as the transmission power. By averaging these measured power usage metrics we can estimate $c_i$. $E_{ij}^{\mathrm{off}}$ is given by the following.

We calculate $c_i$ internally by monitoring battery usage and network adapter configurations, including transmission power levels. By averaging these measured power usage metrics, we can estimate $c_i$. The energy cost $E_{ij}^{\mathrm{off}}$ of offloading task j to edge server i is then given by

$$E_{ij}^{\mathrm{off}}=\frac{T_{ij}^{\mathrm{off}}}{c_i}$$

Similarly, the energy cost of the inference response denoted by $E_i^{\mathrm{resp}}$ is given by

$$E_i^{\mathrm{resp}}=\frac{T_i^{\mathrm{resp}}}{c_i}$$

Let $E_i^{\inf }$ be the average energy cost of performing the inference of an inference task using model i. The inference energy cost is negligible compared to the offloading energy cost. Therefore it is defined as a constant that can be estimated using the inference time and the maximum power consumption of the edge device’s CPU in the worst case under full load. Let $E_{ij}^{\mathrm{task}}$ be the total energy cost of processing task j using model i given by the following.

Let $E_i^{\inf }$ represent the average energy cost of performing inference for a task using model i. Given that the inference energy cost is minimal compared to the offloading energy cost, it is considered constant. This constant can be estimated using the inference time and the maximum power consumption of the edge device’s CPU under worst-case conditions of full load. Let $E_{ij}^{\mathrm{task}}$ denote the total energy cost for processing task j using model i, given by:

$$E_{ij}^{\mathrm{task}}=E_i^{\inf }\forall i\in \mathcal{L}j\in \mathcal{J}$$

$$E_{ij}^{\mathrm{task}}=E_i^{\inf }+E_{ij}^{\mathrm{off}}+E_i^{\mathrm{resp}}\forall i\in \mathcal{S}j\in \mathcal{J}$$

Finally, we define $E_k^{\mathrm{slot}}$ as the total energy consumption for slot k given by

$$E_k^{\mathrm{slot}}=\sum _{i=1}^M\sum _{j=1}^J{x}_{ij}{E}_{ij}^{\mathrm{task}}$$

3.4. Problem Formulation

In this section, we identify two optimization problems. First, the problem of assigning inference models to inference tasks while respecting the given time and energy constraints and maximizing the overall accuracy. Secondly, the problem of selecting an optimal subset of available edge servers which maximizes the average accuracy of produced schedules while reducing the scheduling time.

3.4.1. Inference Task Scheduling Problem

The problem can be formulated as follows:

$$Maximize{A}_k^{\mathrm{slot}}=\sum _{i=1}^M\sum _{j=1}^J{x}_{ij}{A}_i$$

(1)

Where $A_k^{\mathrm{slot}}$ is the total accuracy for a time slot k. Let $E_k^{\mathrm{slot}}$ be the total energy consumption of slot k. Given E and T as the energy and time constraints, respectively, Equation (1) is subject to the following:

$$T_k^{\mathrm{slot}}\le T\forall k\in \Delta$$

(2)

$$E_k^{\mathrm{slot}}\le E\forall k\in \Delta$$

(3)

$$\sum _{i=1}^M{x}_{ij}=1\forall j\in J$$

(4)

Using Equation (2), we guarantee that each parallel processing time of each slot is respecting the time constraint. Similarly, Equation (3) ensures energy consumption for a time slot respects the given constraint. Finally, Equation (4) guarantees each inference task is assigned an inference model that produces a complete solution.

This problem could be thought of as an instance of the well-known classic knapsack problem (KP) in which we are trying to fill our schedule (i.e., a knapsack) with inference models (i.e., pieces) to maximize the accuracy (i.e., profit) while respecting time and energy constraints (i.e., knapsack weight and volume capacities). In this case, the pieces and the knapsack have two dimensions and therefore this problem is an instance of the multi-dimensional KP. Additionally, inference models (i.e., pieces) can be reused to construct a schedule, and therefore the problem becomes an instance of the unbounded multi-dimensional KP (UMdKP). However, since we are considering parallel schedules where inference tasks can be processed locally and in edge servers in parallel, which in UMdKP terms means pieces can be overlapping in the weight dimension (i.e., time) but not in the volume dimension which renders this similarity useless. Alternatively, multiple knapsacks can be considered for each edge server which makes this problem an instance of the multi-knapsack problem (MKP). However, the problem becomes much more difficult to model especially when trying to uphold the time constraint over all knapsacks.

3.4.2. Edge Server Selection Problem

Let ${\mathcal{M}}_k$ be the set of selected edge servers for time slot k. Let $y_j$ be a binary variable representing whether the inference model from edge server j is selected to be part of $\mathcal{M}$.

Objective:

$$Maximize{A}_k=\sum _{i=1}^{\mathcal{L}}{x}_i{A}_i+\sum _{j=1}^{\mathcal{S}}{y}_j{A}_j$$

(5)

Subject to:

$$\sum _{i=1}^{\mathcal{L}}{x}_i+\sum _{j=1}^{\mathcal{S}}{y}_j=|\mathcal{M}|$$

(6)

$$x_i\in \{1,0\},\forall i\in \mathcal{L}$$

$$y_j\in \{1,0\},\forall j\in \mathcal{S}$$

where:

• $A_i$ is the average accuracy of local inference model i.
• $A_j$ is the accuracy of the inference model from edge server j.

This formulation (Equation (6)) ensures that each selected edge server contributes its single inference model to the selected subset $\mathcal{M}$. The binary variable $y_j$ determines the selection of edge servers, and the objective function maximizes the total accuracy obtained from the selected models. Solving this optimization problem provides the optimal or near-optimal solution for selecting the subset $\mathcal{M}$ for each time slot k.

This type of problem is a combinatorial optimization problem known as a subset selection problem, where the goal is to select a subset of elements from a given set while optimizing a certain objective function subject to certain constraints.

In this specific case, we are tasked with selecting a subset $\mathcal{M}$ of inference models from both local models and models hosted on edge servers to perform inference tasks. The objective is to maximize the total accuracy obtained from the selected models while minimizing the cardinality of $\mathcal{M}$ (i.e., selecting the fewest number of models necessary to achieve faster scheduling times and higher accuracy).

Such types of optimization problems can be solved using various methods such as greedy algorithms where we select models based on certain criteria (e.g., highest accuracy or best cost–benefit ratio) until the cardinality constraint is met, while greedy algorithms do not guarantee optimal solutions, they can provide fast and efficient solutions in many cases. Moreover, dynamic programming can also be used if the problem exhibits overlapping subproblems and optimal substructure properties. This approach is particularly useful for problems with small problem sizes and a limited number of feasible solutions. Metaheuristic algorithms such as genetic algorithms, simulated annealing, or particle swarm optimization can be used to explore the solution space and find near-optimal solutions.

4. Multi-Agent DRL-Based Selective Inference Task Scheduling and Offloading Framework (MASITO)

Task scheduling and offloading in edge computing systems involve complex decision-making processes due to dynamic network conditions, varying computational loads, time, and energy constraints. Deep reinforcement learning (DRL) is best suited to handling such complexity by enabling agents to learn optimal decision-making policies through interaction with the environment. Task scheduling and offloading decisions in edge computing systems often need to optimize multiple conflicting objectives, such as adhering to time and energy constraints while maximizing accuracy. DRL algorithms can balance these objectives by learning complex trade-offs and generating efficient scheduling and offloading strategies. DRL agents can adapt to such dynamic environments by continuously learning and updating their policies based on real-time feedback.

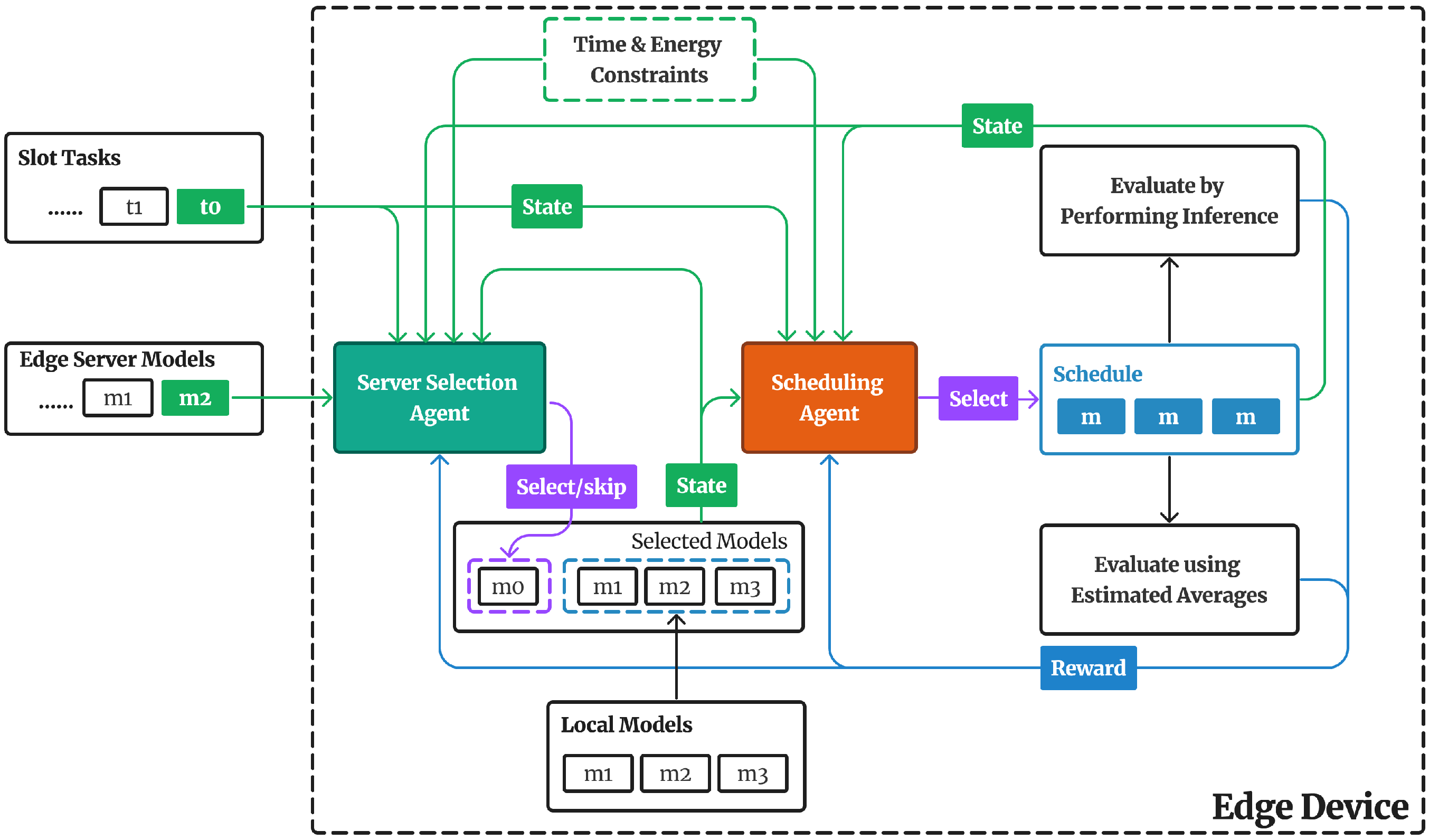
The proposed MASITO framework depicted in Figure 4 takes advantage of DRL and uses two cooperating reinforcement learning agents, namely edge server selection agent and a scheduling agent. At the beginning of each time slot, the agents have access to information about the received tasks for that time slot. In addition to information about local inference models, available edge server models, given constraints, and network status. Using this information the edge server selection agent selects a single-edge server model for each task to be included in the selected set of inference models along with local inference models. This set is then used by the scheduling agent to assign an inference model for each task.

In the context of edge computing, the system state at a given time slot is often primarily influenced by the decisions made in the previous time slot regarding task scheduling and offloading. This characteristic lends itself well to being modeled as a Markov Decision Process (MDP), where the state transition dynamics satisfy the Markov property, meaning the future state depends only on the current state and the action taken. However, accurately determining the transition probabilities between states, especially in finite-state MDPs, can be challenging due to the dynamic and uncertain nature of the network environment, and while existing works often assume that transfer probabilities can be obtained through offline training, this approach may not accurately reflect the real-world network conditions, which are inherently unknown and subject to change. Therefore, to devise an optimal task scheduling and offloading strategy, reinforcement learning agents, specifically scheduling and server selection agents, are trained using model-free deep reinforcement learning (DRL) algorithms like Double Deep Q-Networks (DDQNs). Model-free DRL algorithms learn directly from interactions with the environment without relying on explicit models of the system dynamics, making them suitable for capturing the complex and dynamic nature of edge computing environments. By leveraging DDQNs, these agents can iteratively learn and update their decision-making policies based on real-time feedback, ultimately enabling more adaptive and effective task scheduling and offloading strategies that maximize system performance under time and energy constraints.

4.1. MASITO Design

For each time slot k, the edge device receives a set of inference tasks $\mathcal{J}$. For each task, a fixed-size pool of selected inference models $\mathcal{M}$ consisting of all the local inference models $\mathcal{L}$ in addition to a single slot reserved for a selected edge server model $m_s$ is constructed.

$$\mathcal{M}=\mathcal{L}+m_s$$

The design illustrated in Figure 5 facilitates the operation of DDQNs with fixed inputs and outputs for both agents, enabling them to adapt to the dynamic network of edge servers, which may join and disconnect arbitrarily. The selection of the edge server model $m_s$ is made based on the current inference task to best adhere to the given time and energy constraints. Subsequently, the set of selected inference models is utilized by the scheduling agent to assign a single model to the ongoing inference task. Initially, the schedule $H_k$ for time slot k is initialized with a default local model $m_d$ where $m_d\in \mathcal{L}$. Following each scheduling assignment, the model corresponding to the currently processed task is substituted with the selected model. This design approach ensures the availability of a complete schedule before all time slot tasks are completed, facilitating evaluation at each step, and enabling the computation of a reward representing a single action. This design is advantageous for training agents as it necessitates providing a reward for each action, as opposed to multiple actions where the agent selects inference models for all slot tasks and subsequently receives a single reward.

A schedule $H_k$ undergoes evaluation by computing its total time $T_k^{\mathrm{slot}}$, total energy consumption $E_k^{\mathrm{slot}}$, and total accuracy $A_k^{\mathrm{slot}}$. We identify two methods for evaluating a schedule. The first method relies solely on estimated averages, including inference time, inference energy, and accuracy, for each selected model in a schedule. This approach offers benefits for agents as they receive relatively consistent average values, facilitating faster learning. Additionally, multiple agents can run in parallel to produce a single schedule, resulting in significant speed advantages. This is achievable because only cached average values are needed, eliminating the need for real inference after each selection step. However, relying solely on average estimates may lead to incorrect solutions, especially when outliers such as task sizes and network latency deviate significantly from the estimated average values. Hence, we propose a second approach where inference is performed after every selection step. This yields real inference times, energy consumption, and accuracy, as opposed to estimated averages, allowing the agent to adapt its subsequent actions to address previous sub-optimal actions and better handle outlier data, which can cause unexpected time and energy spikes. Consequently, this approach leads to more accurate schedules. Moreover, during training, the second approach benefits from instant and accurate rewards.

4.2. Inference Task Scheduling

In this section, we propose an MDP model for the inference task scheduling problem.

4.2.1. State Space

The state for the scheduling agent is designed such that given a set of selected inference models $\mathcal{M}$, time and energy constraints T and E, respectively, and currently processed task j, it allows it to estimate $T_k^{\mathrm{slot}}$, $E_k^{\mathrm{slot}}$, and $A_k^{\mathrm{slot}}$ for time slot k. As discussed earlier, we initially start with a default schedule H and start replacing models with selected ones and thus the state is represented as the set of all possible schedules produced from considering all possible actions (i.e., all models in $\mathcal{M}$). A state $s_{k,j}^{\mathrm{sched}}$ for time slot k and task j is given by

$$\begin{array}{cc}\hfill s_{k,j}^{\mathrm{sched}}=\{& \\ & [I{d}_i,T,E,A_k^{\prime \mathrm{slot}},E_k^{\prime \mathrm{slot}},T_k^{\prime \mathrm{server}},T_k^{\prime \mathrm{local}},T_k^{\prime \mathrm{slot}},siz{e}_j,c]\hfill \\ & \forall i\in \mathcal{M}\hfill \\ \hfill \}\end{array}$$

where $I{d}_i$ is the id of the inference model i. T and E represent time and energy constraints, respectively. $siz{e}_j$ is the size of task j. c is the number of remaining tasks in the schedule which gives the agent an indicator of how to spend the constraints budget according to how many tasks are remaining. c can be calculated by subtracting j from the number of tasks per time slot. $A_k^{\prime \mathrm{slot}}$, $E_k^{\prime \mathrm{slot}}$, $T_k^{\prime \mathrm{server}}$, $T_k^{\prime \mathrm{local}}$, $T_k^{\prime \mathrm{slot}}$ are estimated from previous schedule values $A_k^{\mathrm{slot}}$, $E_k^{\mathrm{slot}}$, $T_k^{\mathrm{server}}$, $T_k^{\mathrm{local}}$, $T_k^{\mathrm{slot}}$, respectively, passed by previous state $s_{k,j-1}^{\mathrm{sched}}$ and replacing placeholder default inference model $M_d$ by model $M_i$.

Let $z_i$ be a binary variable representing whether inference model $m_i$ is a local model or belongs to an edge server.

$$z_i=\left\{\begin{array}{cc}0\hfill & m_i\mathrm{is}\mathrm{a}\mathrm{local}\mathrm{model}\hfill \\ 1\hfill & m_i\mathrm{is}\mathrm{an}\mathrm{edge}\mathrm{server}\mathrm{model}\hfill \end{array}\right.$$

$$E_k^{\prime \mathrm{slot}}=E_k^{\mathrm{slot}}-E_d^{\inf }+E_{ij}^{\mathrm{task}}$$

$$A_k^{\prime \mathrm{slot}}=A_k^{\mathrm{slot}}-A_d+A_i$$

$$T_k^{\prime \mathrm{off}\_\mathrm{accu}}=T_k^{\mathrm{off}\_\mathrm{accu}}+z_i{T}_i^{\mathrm{off}}$$

$$T_k^{\prime \mathrm{server}}=max(T_k^{\mathrm{server}},T_k^{\prime \mathrm{off}\_\mathrm{accu}}+z_i(T_i^{\inf }+T_i^{\mathrm{resp}}))$$

$$T_k^{\prime \mathrm{local}}=T_k^{\mathrm{local}}-T_d^{\inf }+(1-z_i)T_i^{\inf }$$

$$T_k^{\prime \mathrm{slot}}=max(T_k^{\prime \mathrm{local}},T_k^{\prime \mathrm{server}})$$

All state values except for ${\mathrm{Id}}_i$ and c are normalized using a min–max approach where instead of using values from different ranges, we scale all values to a range between 0 and 1.

4.2.2. Action Space

The action space for the scheduling agent consists of the index of the selected inference model. The action space $a^{\mathrm{sched}}$ is given by

$$a^{\mathrm{sched}}=\{i\forall i\in \mathcal{M}\}$$

4.2.3. Reward Function

After every action, the resulting schedule is evaluated where we calculate $T_k^{\mathrm{slot}}$, $A_k^{\mathrm{slot}}$, and $E_k^{\mathrm{slot}}$; then, using time and energy constraints we define the reward $r_{k,j}$ for time slot k and task j is given in Equation (7). Let $\widehat{A_k^{\mathrm{slot}}}$, $\widehat{T_k^{\mathrm{slot}}}$, and $\widehat{E_k^{\mathrm{slot}}}$ be the normalized values of $A_k^{\mathrm{slot}}$, $T_k^{\mathrm{slot}}$, and $E_k^{\mathrm{slot}}$, respectively.

$$r_{k,j}=\alpha \widehat{A_k^{\mathrm{slot}}}-\beta |\widehat{T_k^{\mathrm{slot}}}-\widehat{T}|-\gamma |\widehat{E_k^{\mathrm{slot}}}-\widehat{E}|$$

(7)

where $\widehat{T}$ and $\widehat{E}$ are normalized values of T and E, respectively. $\alpha$, $\beta$, and $\gamma$ are weighting coefficients that determine the relative importance of each term in the reward function.

4.3. Edge Server Selection

In this section, we propose an MDP model for the edge server selection problem.

4.3.1. State Space

The state for the edge server selection agent contains information about the network latency and accuracy about the currently evaluated edge server along with the current task j and given constraints. This gives the agent enough context to decide whether to use this edge server for offloading or not. Given $m_s$ as the inference model corresponding to the previously selected edge server, and $m_{s+1}$ as the inference model corresponding to the currently evaluated edge server. We define the state $s_{k,j}^{\mathrm{sel}}$ as follows:

$$s_{k,j}^{\mathrm{sel}}=[T_s^{\mathrm{lat}},T_{s+1}^{\mathrm{lat}},T_k^{\mathrm{server}},T_k^{\mathrm{local}},E_k^{\mathrm{slot}},T,E,{size}_j]$$

where T and E represent time and energy constraints, respectively. ${size}_j$ is the size of the currently processed task j.

4.3.2. Action Space

The action space of the edge server selection agent consists of a binary decision representing whether to use the evaluated edge server $E{S}_1$ or skip it and keep using the previous one $E{S}_0$.

$$a^{\mathrm{sel}}=\{0,1\}$$

The edge server selection agent receives a similar reward to the scheduling agent since they have a common goal of producing the best schedule given the same constraints.

4.4. DDQN for MASITO

Deep Q-Network (DQN) is a reinforcement learning algorithm that combines deep neural networks with Q-learning to learn optimal policies for decision-making in sequential decision-making tasks. At its core, DQN aims to approximate the optimal action-value function, $Q*(s,a)$, which represents the expected cumulative reward when taking action a in state s and then following the optimal policy thereafter. The key innovation of DQN lies in using deep neural networks to approximate the action-value function, enabling it to handle high-dimensional state spaces commonly encountered in real-world applications. DQN learns by iteratively updating the parameters of the neural network to minimize the temporal difference error between the predicted Q-values and the target Q-values. By leveraging experience replay, where past experiences are stored and sampled randomly during training, DQN improves sample efficiency and stability by breaking temporal correlations in the data. Through this process, DQN learns to make optimal decisions by iteratively refining its policy based on feedback received from the environment.

Double Deep Q-Networks (DDQNs) improve upon DQNs by addressing the issue of overestimation bias in action values, which can lead to suboptimal policies. In DDQNs, this bias is mitigated by decoupling action selection from action evaluation through the use of two separate networks, a policy network and a target network (see Figure 6), and while the policy network selects the best action based on the current state, the target network is used to estimate the value of that action. By periodically updating the parameters of the target network with those of the policy network, a DDQN ensures that the target values used to compute the temporal difference error are more stable and less prone to overestimation. This approach results in more accurate and reliable Q-value estimates, leading to improved convergence and ultimately better performance in reinforcement learning tasks compared to the original DQN algorithm. The target Q-value is calculated according to Equation (8). The loss function is given by Equation (9). The target network is updated using Equation (10).

$$Q_{target}(s,a)=r+\gamma Q_t(s^{\prime },{\mathrm{argmax}}_{a^{\prime }}Q(s^{\prime },a^{\prime };\theta );{\theta }^{\prime })$$

(8)

$$L\left(\theta \right)=\mathbb{E}\left[{(r+\gamma Q_t(s^{\prime },{\mathrm{argmax}}_{a^{\prime }}Q(s^{\prime },a^{\prime };\theta );{\theta }^{\prime })-Q(s,a;\theta ))}^2\right]$$

(9)

$${\theta }^{\prime }=\tau \theta +(1-\tau ){\theta }^{\prime }$$

(10)

where $Q(s,a;\theta )$ represents the Q-value predicted by the policy network for state s and action a with parameters $\theta$. $Q_t(s,a)$ represents the target Q-value for state s and action a. r is the immediate reward obtained after taking action a in state s. $s^{\prime }$ is the next state. $\gamma$ is the discount factor determining the importance of future rewards. ${\theta }^{\prime }$ represents the parameters of the target network. $\tau$ is the soft update parameter determining the rate at which the target network parameters are updated.

The deep neural network for the scheduling agent takes an array of size $|\mathcal{M}|\times 10$ and outputs an array of size $|\mathcal{M}|$, while the deep neural network for the edge server selection agent takes an array of size $(|\mathcal{M}|+5)\times 2$ as input and outputs an array of size 2.

Algorithm 2 describes the steps used to train the DDQN agents. It uses an epsilon-greedy strategy where an agent decides between exploring new actions and exploiting known actions based on a parameter $ϵ$. Initially, $ϵ$ is set to ${ϵ}_{max}$ and then each episode is reduced by a factor of ${ϵ}_{decay}$ until it reaches a minimum value of ${ϵ}_{min}$. This ensures sufficient exploration to avoid local optima and a gradual shift towards exploitation leveraging accumulated knowledge for better decision-making. Furthermore, Replay memory is used where past experiences (state, action, reward, next state) are stored in a buffer, allowing the agent to randomly sample mini-batches of these experiences during training. This approach breaks the temporal correlations between consecutive experiences, stabilizing the training process and improving learning efficiency. Algorithm 3 presents the main steps of MASITO illustrated in Figure 5.

Algorithm 2: DDQN Agent Training Algorithm

Algorithm 3: MASITO steps

5. Experimental Results

In this section, we evaluate the performance of MASITO through extensive experiments and comparisons with the following algorithms.

5.1. Baseline Algorithms

Genetic algorithms (GAs) have been extensively utilized in the literature [38,42] for addressing high-dimensional optimization problems due to their versatility and effectiveness. In a GA, a population of candidate solutions, represented as chromosomes, undergoes iterative evolution through processes such as selection, crossover, and mutation, inspired by principles of natural selection and genetics. Selection mechanisms, such as tournament selection, play a crucial role in GA operation by determining which individuals proceed to the next generation based on their fitness. The tournament selection method, employed in our study, involves randomly selecting a subset of individuals from the population and choosing the fittest individual among them to serve as a parent for producing offspring. This approach ensures that individuals with higher fitness have a greater probability of being selected as parents, thereby guiding the evolution of the population toward more optimal solutions. The widespread use of GAs in the literature, coupled with their ability to handle high-dimensional problems and diverse solution spaces, justifies their selection as a baseline for comparison in our study.

Particle swarm optimization (PSO) stands out as a foundational metaheuristic extensively employed in MdKP research [43,44]. Its efficacy in navigating high-dimensional search spaces has established it as a reliable baseline method. Drawing inspiration from the collective behavior observed in natural phenomena like bird flocks or fish schools, PSO operates through a cooperative search mechanism. Individuals, termed particles, iteratively adjust their positions based on personal experiences and swarm knowledge. This collaborative approach enables PSO to explore diverse regions of the search space, adapt to dynamic conditions, and converge toward optimal solutions efficiently. Assessing our proposed framework against PSO provides valuable insights into its effectiveness and competitiveness in addressing the optimization task, and while PSO traditionally caters to continuous search spaces with real-valued vectors, our experiments necessitate its adaptation for discrete search spaces. This adaptation involves representing solutions as integer position vectors, corresponding to inference model indexes, and applying clipping mechanisms to integer velocity vectors after each update to ensure adherence to predefined ranges.

Simulated annealing (SA) has been widely adopted in the literature for both task scheduling [45,46] and the MdKP [47,48], demonstrating its effectiveness. Its stochastic nature, employing a probabilistic acceptance criterion, enables it to navigate complex and multimodal optimization landscapes, making it well-suited for tackling challenging optimization problems. This characteristic allows SA to evade local optima and explore diverse regions of the search space, rendering it a compelling choice as a baseline method.

All compared algorithms utilize an identical fitness function f outlined in Equation (14). The parameters for all implemented algorithms are detailed in

Table 3. Metaheuristic algorithm parameters.

GA	Mutation probability	0.25
	Mutation fading	0.90
	Population	20
	Generations	20
	Tournament size	10
PSO	Swarm size	50
	Iterations	100
SA	Initial temperature	1 × 103
	Cooling rate	1 × 10−1
	Iterations	500

. Python version 3.12 serves as the programming language for the implementation of all algorithms, supplemented by PyTorch for handling inference models. Notably, parameters such as population size and swarm size for GA and PSO have been meticulously tuned to their minimum values offering best accuracy with lowest execution time. Increasing these parameters only results in longer execution times without improvements in accuracy.

$${\delta }_T=\frac{T-T_k^{\mathrm{slot}}}{T}$$

$${\delta }_E=\frac{E-E_k^{\mathrm{slot}}}{E}$$

$${\omega }_T=\left\{\begin{array}{cc}1\hfill & \mathrm{if}({\delta }_T<0)\mathrm{and}(|{\delta }_E|\le {\delta }_{min})\hfill \\ 1-|{\delta }_T|\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

$${\omega }_E=\left\{\begin{array}{cc}1\hfill & \mathrm{if}({\delta }_E<0)\mathrm{and}(|{\delta }_T|\le {\delta }_{min})\hfill \\ 1-|{\delta }_E|\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(12)

$$\omega =\frac{1}{2}{\omega }_T+\frac{1}{2}{\omega }_E$$

(13)

$$f_k=\omega \frac{A_k^{\mathrm{slot}}}{100}$$

(14)

In this context, ${\delta }_T$ and ${\delta }_E$ signify the distance ratio of $T_k^{\mathrm{slot}}$ and $E^{\mathrm{slot}}k$ from the specified constraints T and E, respectively. $\delta min$ denotes the minimum distance ratio at which the constraint is considered fulfilled. Introducing ${\omega }_T$ and ${\omega }_E$ as the time and energy penalties, respectively, the penalties are structured to scale in accordance with the distance from the given constraints. This design compels the agent to minimize the distance and effectively utilize the allocated constraint budget. However, in scenarios where a single constraint imposes a limitation, Equations (11) and (12) ensure that the agent is not forced to maximize both constraints simultaneously. Instead, the penalty for the other constraint is waived as long as it remains within acceptable bounds.

5.2. Experiment Setup

We present a real-world case study employing a laptop as the edge device, as detailed in

Table 4. Edge device parameters.

	Parameter	Value
edge device	Average Response Size	0.1 MB
	$|\mathcal{M}|$	4
	Default Model	ShuffleNet-V2
	CPU	Quad Core @ 3.0 GHz
	RAM	8 GB
	Tasks Per Time Slot	10

. The laptop is equipped with a quad-core processor running at 3.0 GHz and 8 GB of RAM. Connectivity is facilitated through WiFi (802.11ac), linking the edge device to an access point. The access point, in turn, connects to a set of edge servers comprising desktop computers via Ethernet. To ensure the validity of our findings in practical settings, it is crucial to note that the experiments were conducted in an environment devoid of concurrent devices competing for network resources, thus mitigating potential traffic contention issues. In our experiments, we opt to utilize power as a constraint, measured in watts, rather than energy, measured in kWh, for the sake of convenience.

5.3. Experiment Case Study

We use an object detection case study utilizing the ImageNet-mini dataset [49], comprising 3923 images with sizes ranging from 10 KB to 10 MB, to assess the effectiveness of our system. For deployment on the edge device, we select a suite of lightweight object classification inference models, including ResNet-18 and ResNet-34 [50], as well as ShuffleNet-V2 [51]. Conversely, the edge servers are equipped with a more precise and larger inference model, specifically the ResNeXt-101 [52]. During the deployment phase, we conduct tests on these models to estimate their average inference time and accuracy on each machine, as outlined in

Table 5. Inference model parameters.

	Average Accuracy (%)	Average Inference Time (ms)	Size (MB)	Number of Parameters
ShuffleNet-V2	66.15	19.44	5.3	1,366,792
ResNet-18	72.01	28.07	44.7	11,689,512
ResNet-34	76.79	42.45	83.3	21,797,672
ResNeXt-101 (Edge Servers)	87.05	-	319.3	83,455,272

. Notably, the average inference time of edge servers varies across machines due to differences in hardware capabilities and is therefore excluded from the table.

The task scheduling agent undergoes training with parameters detailed in

Table 6. Agent parameters.

	Parameter	Value
Scheduling Agent	${ϵ}_{max}$	1.0
	${ϵ}_{min}$	0.01
	${ϵ}_{decay}$	0.995
	Learning Rate	1 × 10−3
	Replay Memory Capacity	1 × 106
	Batch Size	64
	$\gamma$	0.99
	$\tau$	1 × 10−3
	Update Every N steps	4
	Hidden Layer Size	128
	Hidden Layers	3
Server Selection Agent	Hidden Layer Size	64
	Hidden Layers	3
	${ϵ}_{decay}$	0.985

.

Initially, training commences on a subset comprising 33% of the dataset, spanning 50 episodes, while introducing randomized variations in time and energy constraints within the ranges of $T=[200,250,300,\dots ,500]$ and $E=[10,15,20,\dots ,50]$. In the initial phase of pre-deployment training, edge servers are simulated locally, leveraging high-accuracy inference models while introducing random variations in latency. Once the scheduling agent has attained sufficient training, the subsequent phase entails training the server selection agent. The parameters employed for training the server selection agent align closely with those utilized for the scheduling agent, with exceptions specified in Table 6.

5.4. Evaluation Metrics

We assess the performance of the agents on the remaining 66.66% of the dataset using four key metrics: scheduling time, accuracy, time, and power consumption. Scheduling time, measured in milliseconds, represents the duration required by the algorithm to generate a schedule for a given time slot. This metric is calculated individually for each time slot and then averaged across all slots. Accuracy, time, and power consumption collectively quantify the quality and adherence of the generated schedules to the specified constraints. Each schedule for every time slot undergoes evaluation through inference utilizing the designated inference models. Subsequently, these metrics are aggregated across all time slots to provide a comprehensive assessment across the dataset.

5.5. Performance under Different Number of Iterations

Examining the results depicted in Figure 7, Subplot 1, we note that the scheduling times of GA and PSO exhibit linear scaling in relation to the number of iterations. Notably, a small number of iterations, around 20 for GA, 100 for PSO, is found to be adequate for generating high-accuracy schedules, whereas for SA we find 500 iterations to be sufficient. These values will be used in subsequent experiments. Conversely, while SA initially appears to maintain a constant scheduling time, a closer inspection (refer to Figure 8, Subplot 1) reveals a linear growth pattern, albeit at a slower pace. Interestingly, MASITO remains unaffected by the number of iterations, attributable to its capacity to generate solutions in a single forward pass through the deep neural network.

In Subplot 2, we observe that all schemes yield nearly comparable accuracy solutions, albeit with minor deviations. SA and PSO notably produce higher accuracy schedules with increased iterations.

Subplot 3 highlights MASITO’s distinct advantage in leveraging the available time budget compared to other methods, enabling it to achieve comparable average accuracy. This phenomenon may be attributed to the edge server selection agent’s tendency to choose higher latency and power-cost servers, yielding similar accuracy but garnering higher rewards. This behavior aligns with the reward function design, which penalizes greater deviations from the given constraints, thereby incentivizing the selection of servers that better use the given time and power budgets to maximize the reward.

5.6. Performance Evaluation under Different Time Constraints

To assess MASITO’s performance and accuracy in terms of constraint compliance, we conduct experiments where one constraint is fixed while the other is varied. In Figure 9, we maintain the power constraint at 30W and adjust the time constraint from 200 to 500 ms. Analyzing the results depicted in Figure 9, Subplot 1, we observe that GA, PSO, and SA demonstrate linear growth in scheduling times as the time constraints increase. In contrast, MASITO remains unaffected, maintaining a consistent scheduling time regardless of the time constraint value. Subplot 2 illustrates that all methods yield schedules with increasing accuracy relative to higher time constraints, with MASITO achieving comparable accuracy to GA and SA while surpassing PSO in accuracy, despite exhibiting significantly shorter scheduling times. Notably, in Subplot 3, we observe that all compared algorithms adhere to the specified time constraint, albeit with minor variations for MASITO. This suggests MASITO’s capability to effectively manage time constraints while maintaining high accuracy levels and low scheduling times.

5.7. Performance Evaluation under Different Power Constraints

Similarly, in Figure 10, we fix the time constraint at 500 ms and vary the power constraint from 10 to 30 W. Analyzing Figure 10, Subplot 1, we observe results similar to those previously discussed. However, we note that the power constraint has a more pronounced effect on the scheduling times of GA, PSO, and SA, with a noticeable increase in scheduling times in response to variations in the power constraint, while MASITO remains unaffected. Subplot 2 reveals that the accuracy levels of all compared schemes are mostly similar, with slight variations observed for MASITO. In Subplot 3, we observe that all metaheuristic methods exhibit scheduling times lower than the specified constraint, especially for the 20 W constraint, indicative of a greater reliance on offloading to low-latency edge servers. Conversely, MASITO tries to maintain scheduling times as close as possible to the given constraint in an attempt to maximize rewards. Subplot 4 demonstrates that all compared schemes successfully adhere to the specified power constraint until reaching 40 W, beyond which all schemes reach a time constraint limit and cease to increase power consumption despite having larger power budgets. However, MASITO exhibits less compliance with the power constraint due to the reward function coefficients favoring accuracy and time over power. This issue could be addressed by adjusting these coefficients, albeit potentially at the expense of accuracy.

5.8. Performance Evaluation under Varying Number of Edge Servers

In this section, we assess the scalability of the framework by fixing both time and energy constraints at 500 ms and 30 W, respectively, while varying the number of available edge servers, as demonstrated in Figure 11. This enables us to monitor changes in scheduling time with larger networks and determine whether the compared methods capitalize on the available resources. Upon examining Figure 11, Subplot 2, we observe that as the number of available edge servers increases, MASITO consistently generates solutions on par with or occasionally surpassing those of GA, PSO, and SA. This can be attributed to the server selection agent’s adeptness at making optimal decisions in selecting the best servers, while operating at lower scheduling times. Subplot 3 highlights MASITO’s ability to fully leverage the allocated time constraint budget to maximize rewards, contrasting with other schemes that often opt for solutions with lower times. Lastly, in Subplot 4, MASITO is observed to allow for higher power solutions than the specified power constraint, prioritizing time compliance and higher accuracy at the expense of power constraint adherence as a strategic compromise to maximize rewards. This behavior can be fine-tuned by adjusting the coefficients of the reward function to achieve a more balanced trade-off between time, accuracy, and power constraints.

6. Conclusions

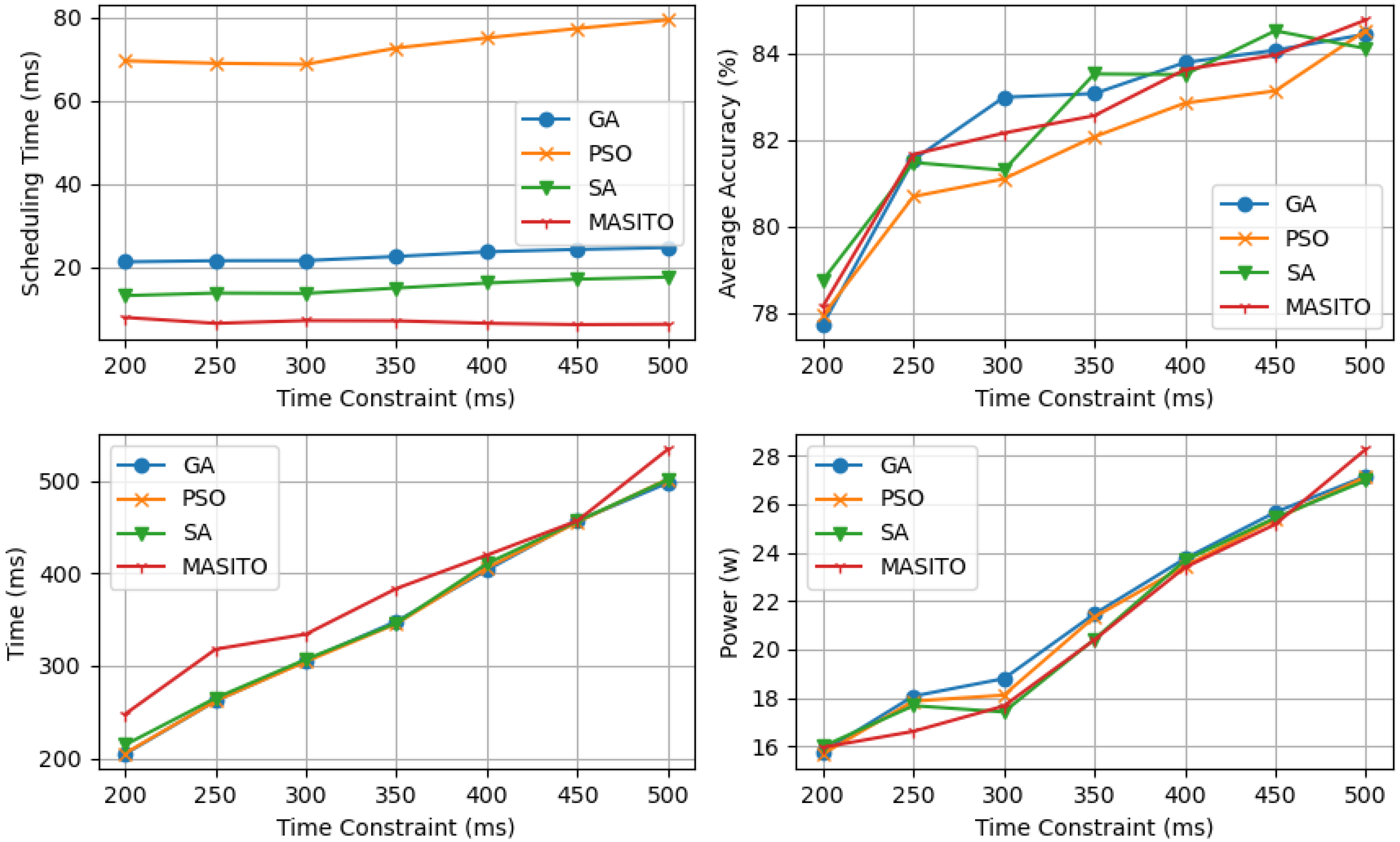
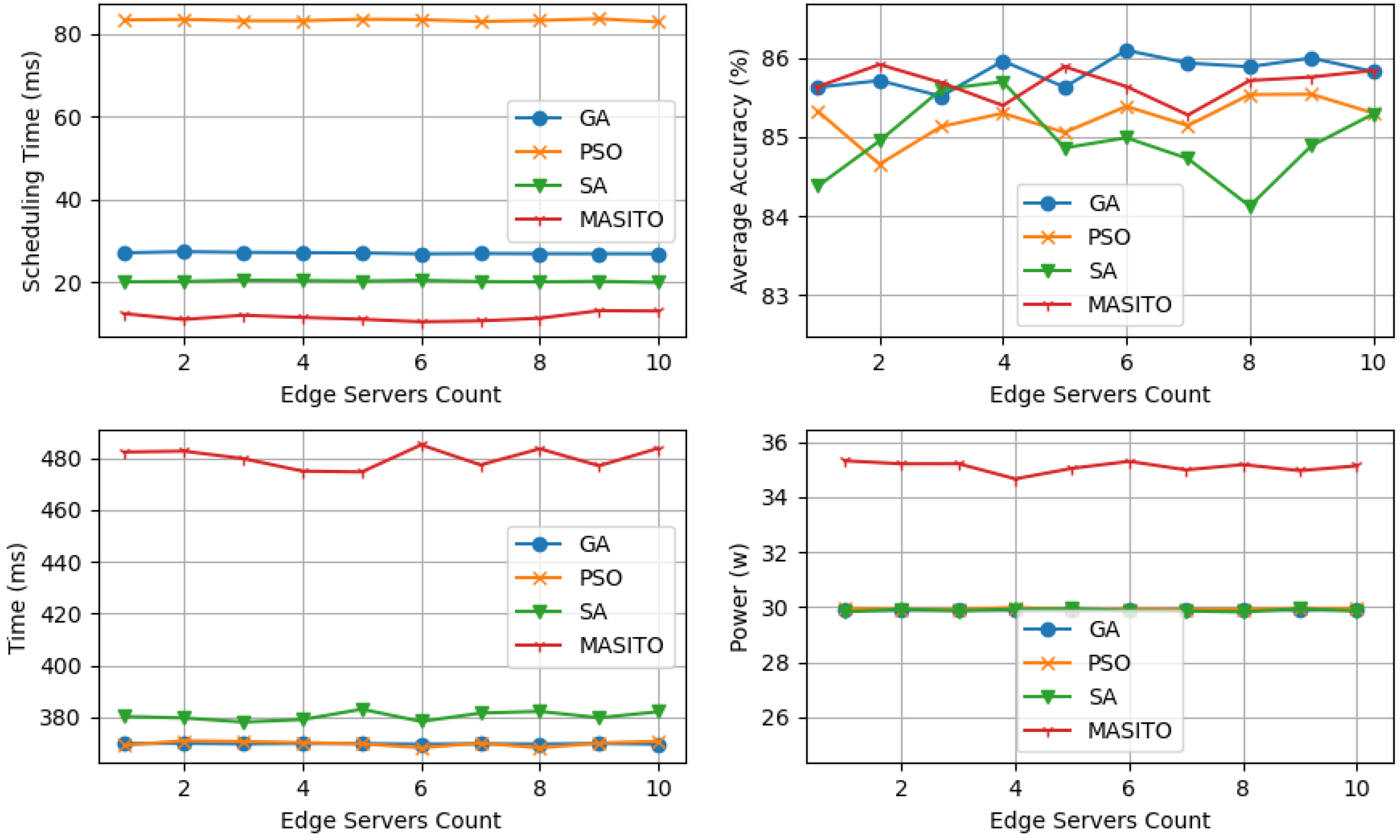
In this study, we address the challenging optimization problem of selective inference task scheduling and offloading under time and energy constraints while prioritizing accuracy maximization. Demonstrated to be strongly NP-Hard, we propose MASITO, a novel framework-leveraging cooperative multi-deep reinforcement learning agents. Our approach involves the deployment of a scheduling DRL agent tasked with allocating inference models to inference tasks, balancing between local inference and offloading to edge servers. Additionally, a complementary DRL agent is devised to select optimal edge servers for each inference task based on specified time and energy constraints. These agents operate synergistically, compensating for each other’s sub-optimal actions, and are seamlessly integrated into MASITO to dynamically adapt to diverse network configurations, facilitating applications in high-mobility edge computing environments. Experimental validation on the ImageNet-mini dataset underscores the efficacy of our framework against genetic algorithms (GAs), particle swarm optimization (PSO), and simulated annealing (SA) which reveal MASITO’s superiority in maintaining consistently lower scheduling times regardless of constraints and the number of edge servers, a critical factor for real-time applications. Moreover, MASITO demonstrates comparable average accuracy in worst-case scenarios and superior accuracy in best-case scenarios. Furthermore, MASITO exhibits the potential for continuous improvement with increased data processing.

Looking ahead, we propose two avenues for future research. Firstly, we advocate for the implementation of a federated learning scheme among edge devices to facilitate the sharing of learned experiences, expediting the convergence to optimal agents. Secondly, we suggest the development of an automated system capable of adapting the reward function coefficients dynamically according to specific application scenarios, enhancing the adaptability and robustness of MASITO in diverse real-world settings.