Optimal Deep Neural Network Modified by Advanced Seasons Optimizer for Classification of Olympic Sports Images

Abstract

Sports image classification has gained increasing significance in various domains, including athlete training, event management, and broadcasting. Nonetheless, accurately classifying these images remains a formidable challenge due to factors such as variations in lighting conditions, pose, and attire. This paper proposes an advanced deep learning approach to address this issue. The proposed method uses a modified Inception-V4 (IV4) architecture, which has exhibited remarkable success in image classification tasks. To further enhance the performance of the IV4 model, an advanced version of the seasons optimizer (ASO), a potent optimization algorithm, has been introduced, which adjusts the learning rate during training. This modified optimizer enables the IV4 model to converge more rapidly and achieve higher accuracy. An evaluation of the proposed method has been conducted using a comprehensive dataset comprising Olympic sports images. The experimental results demonstrate significant enhancements over existing approaches, attaining superior performance across multiple evaluation metrics. These findings underscore the potential of combining cutting-edge deep neural networks with advanced optimization techniques for the precise and efficient classification of sports images.

1. Introduction

1.1. Conception

Image classification is of utmost importance in various applications. In sports, automatic image classification provides valuable insights for athletes, coaches, spectators, and organizers. This technology can assist in analyzing player performances, devising team strategies, captivating audiences, and efficiently managing events.

Nevertheless, accurately classifying sports images remains a significant challenge due to factors like varying lighting conditions, different body postures, and diverse equipment. Therefore, it is crucial to develop effective solutions that can overcome these obstacles to achieve successful automation in sports media and analytics.

The accurate identification of different types of Olympic sports through visual data has the potential to be highly beneficial in various practical scenarios. One such scenario is the automatic indexing and categorization of archived footage, which could greatly assist viewers, broadcasters, and historians in retrieving and browsing content. Additionally, real-time event labeling during ongoing matches could provide valuable insights for coaches, trainers, commentators, and fans regarding athletic performances, tactics, and the rules and regulations of each sport.

Moreover, the generation of automatically generated highlight packages featuring key moments could enhance user engagement and enjoyment across digital platforms. It is important to note that accurately classifying Olympic sports poses exclusive challenges due to the inherent variability exhibited by these dynamic events. Athletes’ movements can vary significantly depending on factors such as skill level, playing style, physical attributes, and strategic decisions, resulting in considerable heterogeneity within individual sports classes.

Furthermore, differences in body shape further complicate the classification process, as athletes participating in similar disciplines may have distinct physiques based on factors such as gender, age group, ethnicity, muscle mass distribution, and fitness levels. Additionally, lighting conditions can change rapidly throughout the day and in indoor venues, impacting color balance, contrast, brightness, and shadow formation. The use of different camera angles also presents challenges, as variations in altitude, distance, orientation, zoom, shake, and obstruction can all affect how objects appear within captured frames.

Collectively, these factors contribute to the difficulty of reliably distinguishing among various Olympic sports using standard image classification pipelines. Current approaches tend to struggle under such complexities, motivating the need for advanced deep learning techniques that can effectively handle the nuances involved in recognizing diverse Olympic sports from visual data. Exploring architectural innovations alongside refined optimization strategies promises to unlock new possibilities for boosting overall system performance, ultimately paving the way toward widespread adoption of intelligent video analytics tools in sports analytics.

Sports image classification presents a complex challenge that necessitates advanced feature extraction and robust classification techniques. These images encompass a wide range of elements, including objects, scenes, actions, and emotions, which add layers of intricacy to the task at hand. The diversity and dynamism of sports imagery make it an especially intricate field for classification algorithms to navigate. The applications of sports image classification are extensive and have a significant impact across various domains.

These factors collectively contribute to the challenge of accurately differentiating between different Olympic sports using conventional image classification pipelines. Existing methods often face difficulties in handling such complexities, which highlights the necessity for advanced deep learning techniques capable of effectively recognizing the subtle nuances present in diverse Olympic sports through visual data. By exploring innovative architectural designs and refining optimization strategies, new opportunities arise to enhance the overall performance of the system. This, in turn, covers the way for the widespread adoption of intelligent video analytics tools in sports analytics.

1.2. Literature Review

Several researchers have made significant contributions to the advancement of a system capable of identifying sports in images.

Ferdouse Ahmed et al. [1] introduced the use of deep neural networks in analyzing sports data. They focused on developing a 13-layered convolutional neural network called “Shot-Net” to classify six different types of cricket shots. The model achieved high accuracy and maintained a low cross-entropy rate. However, there are some limitations to consider in this study. Firstly, it only explores one type of neural network for classifying cricket shots, which may not be the most optimal approach. Secondly, the study does not compare the results with other existing methods or models, making it difficult to assess the proposed model’s performance. Lastly, the findings may not apply to other areas as they are solely based on classifying cricket shots.

Joshi et al. [2] presented a framework that used deep learning methods to classify sports images based on their surroundings. They used the Inception-V3 model for feature extraction and custom neural networks for categorizing images into six groups: tennis, rugby, badminton, basketball, volleyball, and cricket. The proposed method achieved an average accuracy of 96.64%, outperforming other classifiers like Random Forest, K-Nearest Neighbor, and Support Vector Machines. However, there are still limitations to address, such as expanding the sample size for each category to improve the model’s generalizability. Further testing in real-world scenarios is also needed to account for lighting conditions and object occlusion that may affect the model’s accuracy in identifying sports images. Additionally, future research could explore how individual player movements and actions impact accurate sports identification.

Podgorelec et al. [3] introduced a CNN-TL-DE method for automatically classifying similar sports disciplines. This method uses fine-tuning transfer learning and hyperparameter optimization through differential evolution. By optimizing the neural network structure and training parameters, the method showed improved classification performance on a dataset with images of American football, rugby, soccer, and field hockey. However, the study has limitations. It focused only on these four sports, limiting the generalizability of the results. Future studies should include more diverse datasets to validate the method across different domains. Moreover, the evaluation metrics used were accuracy and F1-score. Adding precision and recall would offer a more comprehensive assessment of the model’s performance. Lastly, while the study examined interpretable representations, it did not address potential biases in the training data, which could lead to discriminatory outcomes. To ensure fairness for all sports categories, future research should incorporate bias mitigation strategies during training.

Mohamad et al. [4] evaluated the effectiveness of deep learning models in recognizing and understanding sporting events at the Olympic Games. They used a newly compiled dataset called OGED and employed transfer learning and data augmentation techniques. The study achieved cutting-edge results, with ResNet-50 achieving an impressive 90% accuracy rate when combined with a special photobombing-guided data augmentation approach. However, there are some limitations to consider. Firstly, the study only used a single dataset, which may limit the generalizability of the findings. Secondly, the paper only compared three pre-trained models, leaving other potential combinations unexplored. Overcoming these limitations will enable researchers to develop even more effective models for recognizing events in sports photographs.

Liu et al. [5] conducted a study comparing four pre-trained models for classifying 100 sports image categories with 12,200 images. ResNet-50 achieved the highest accuracy of 88.75% on the validation set, followed by DenseNet-121 with 86.21% and YOLOv8n with 96.60%. EfficientNet B7 did not perform well due to its limited representation abilities for specific sports image classification tasks. YOLOv8n showed exceptional performance in sports image classification and detection. However, there are limitations to consider: the study only focused on 100 sports categories, so expanding the scope may lead to different results. Additionally, the computational cost of implementing YOLOv8n may be a barrier for smaller organizations. Understanding algorithmic tradeoffs in sports image classification is crucial for developing optimal solutions and guiding future research.

1.3. Contribution

The primary focus of this study involves introducing and assessing a specific deep learning method for the classification of Olympic sports images by utilizing a customized Inception-V4 (IV4) design paired with an advanced version of the seasons optimizer (ASO). The ASO is employed to adapt the learning rate dynamically throughout the training process, resulting in the quicker convergence and improved accuracy of the IV4 model. To sum up, the key contribution of this study is showcasing the potential of integrating state-of-the-art deep neural networks with advanced optimization strategies for the accurate and effective classification of sports images.

2. Data Collection

The collection of the Olympic Games Event Image Dataset (OGED) in this study is a significant contribution due to the absence of a dedicated Olympic Games dataset. It will serve as a valuable tool for training and testing purposes and will be made publicly available upon publication.

The OGED consists of 1000 labeled images representing 10 official Olympic Games events: athletics, badminton, basketball, football, handball, rugby, swimming, tennis, surfing, and weightlifting. These images have a consistent resolution of 1366 × 768 pixels and were sourced from the Olympic Channel on YouTube. The dataset is divided into 10 classes, with each class containing 100 images, totaling 1000 images overall. In total, 800 images are designated for training, while the remaining 200 are reserved for testing.

The images in the OGED dataset were derived from actual Olympic Games footage spanning from Atlanta 1996 to Rio 2016. They capture various athlete positions, camera angles, scales, and environments. To increase the dataset size and prevent overfitting, augmentations such as rotations, translations, shears, and horizontal flips were applied. Additionally, photobombing-guided data augmentation was utilized to further enhance the dataset. Detailed descriptions of the data augmentation techniques employed are provided in the subsequent subsection. Figure 1 illustrates a collection of samples from the collected images that display a range of image categories.

The visual collage showcases a range of sports images, including badminton, football, and surfing, aiming to demonstrate the diverse sports activities captured in the dataset. This collection of images provides various advantages, notably by serving as ideal examples for training machine learning models.

3. Preprocessing

3.1. Noise Reduction

Medical imaging primarily relies on ordinary non-polarized light. The polarization state of light affects its reflection and scattering properties on material surfaces, as explained by the “Fresnel Relations”. By using appropriate filters to manipulate polarization, unwanted reflections and scatterings can be reduced, leading to improved signal-to-noise ratios in the resulting images.

Enhancing image quality is a crucial initial step in the examination of medical images, particularly those related to cancer. There are various denoising methods available, but one commonly used option is median filtering.

Among the available choices, median filtering is a popular option due to its simplicity and effectiveness. Based on mathematical morphology principles, median filtering works by replacing original pixel values with median values from neighboring pixels within a specified kernel window. This process helps maintain prominent edges, preventing unwanted blurring often seen in other linear filtering methods.

Median filtering is not only useful on its own but also plays a key role in more complex hybrid systems that combine different denoising techniques. Advanced iterative versions can adjust kernel sizes or shapes based on spatial contexts, improving denoising capabilities without compromising structural integrity. Despite its popularity and versatility, users should be cautious when using median filtering to avoid issues caused by incorrect parameter settings, which can result in lower output quality or loss of important details. When used correctly, however, median filtering is a valuable tool for addressing the challenges of image-denoising applications.

This nonlinear approach preserves the primary edge structures in processed images by replacing pixel intensities with the median value derived from neighboring elements within a defined window. Mathematically, it can be expressed as

$$Z_{m,n}=Median\left(y_{i,j}:\left(i,j\right)\in \beta \right)$$

(1)

where $\beta$ represents the local region centered around the pixel $(m,n)$.

In practice, selecting the optimal window size involves balancing the competing priorities of maximizing the denoising efficiency while minimizing the risk of edge erosion. The current investigation employs a 3 × 3 mask for the median filter. Figure 2 illustrates the effects of median filtering on sample inputs corrupted by 0.1 density salt-and-pepper noise.

Panel A depicts an unprocessed image that is marred by random white and black speckles, making it difficult to discern any details. Upon closer examination, these abnormal artifacts present significant obstacles for both manual and automated analyses, hindering the extraction of meaningful conclusions. Thankfully, panel B showcases a remarkable transformation achieved through the successful implementation of the previously discussed median filtering technique.

The elimination of salt-and-pepper noise allows for the effortless appreciation of previously obscured prominent features. The visibly restored edges and clearly defined boundaries serve as evidence of the effectiveness of median filtering in revitalizing deteriorated imagery. This powerful denoising mechanism holds immense potential for restoring numerous damaged visual records plagued by similar irregularities.

3.2. Augmentation

Various methods can be utilized to address the overfitting problem in the OGED dataset, which contains 1000 images of Olympic Games events. In this study, data augmentation techniques have been applied to create new versions of existing images, improving the model’s ability to understand the visual characteristics present in the original data. Data augmentation involves generating artificial data points from existing samples, increasing the dataset size, and enhancing the model’s generalizability while reducing the risk of overfitting.

A range of data augmentation strategies have been implemented, including scaling, random vertical or horizontal displacement, rotation, skewing, translation, and reflection. These techniques expanded the dataset, providing the model with additional training examples. The specific numerical ranges for each data augmentation method are detailed in

Table 1. The specific numerical ranges for each data augmentation method.

Method	Lower Range	Higher Range
X and Y Scaling	0.8	3
X and Y Reflection	-	-
X and Y Shear	−0.01	0.03
X and Y Translation	−20 pixels	20 pixels
Rotation	−3°	+3°

.

Figure 3 shows a captivating representation of various data augmentation techniques skillfully applied to a selected sample from the OGED dataset. This demonstration emphasizes the transformative impact of these processes, which generate a wide range of virtual counterparts that are suitable for model training and improvement. By diversifying the training portfolio, data augmentation strengthens the model’s ability to recognize and adapt to diverse contexts and perspectives, thereby enhancing its predictive accuracy.

In particular, six distinct modifications have been implemented in the provided illustration, illustrating the multitude of possibilities that arise from the proficient use of these techniques. By acquainting itself with such a heterogeneous collection, the model becomes better equipped to generalize, guard against overfitting, and detect subtle variations that may exist within seemingly similar depictions. Consequently, the thoughtful integration of data augmentation practices offers numerous advantages, ultimately resulting in a faster, more intelligent, and experienced predictor that excels across various fields of study.

3.3. Image Resizing

Setting the dimensions of an image to 683 × 384 pixels ensures compatibility with the designated Inception-V4 architecture’s input layer requirements. This alignment allows the model to take advantage of the strength of Inception modules, which use parallelized multi-scale convolution branches to extract hierarchical abstractions from visual stimuli. Following recommended input configurations also promotes smooth interaction between subsequent layers, facilitating stable gradient flow and faster convergence rates during optimization.

However, it is important to be cautious when selecting a target dimension, as aggressive downscaling may result in the loss of small details or texture cues that are crucial for accurate perception.

In conclusion, careful image resizing is an essential part of preprocessing routines, enabling researchers to handle various photographic dimensions while aligning with preferred neural network architectures. Strategic planning and empirical validation can ensure the preservation of important characteristics, driving forward-looking projects toward success.

4. Inception-V4

4.1. Network Structure

In 2016, a team of researchers associated with Google introduced the Inception-v4 model, which aimed to improve upon the highly acclaimed Inception-v3 system by incorporating a convolutional neural network infrastructure. The main purpose of this endeavor was to maintain the exceptional performance of Inception-v3 in the ILSVRC 2015 competition while simplifying certain aspects of the model’s construction [6]. To achieve this, the designers explored the possibility of merging residual networks with the existing Inception constructs.

From an architectural standpoint, the Inception-v4 framework consists of two distinct variations of Inception blocks: the standalone version called Inception-v4 and an alternative configuration that incorporates residual connections known as Inception-ResNet. Notably, the Inception-v4 blueprint introduces specialized “Reduction Blocks” that play a crucial role in modifying the dimensions of the grid, thereby enhancing the uniformity and scalability of Inception-v4 compared to previous models. This advancement eliminates the need for partitioned clones, which were necessary in older versions due to memory limitations [7].

Furthermore, Inception-v4 boasts an increased module count and a higher level of structural harmony, solidifying its position as a significant advancement over its predecessors. For a more comprehensive understanding of the key components that define the Inception-v4 schema, refer to Figure 4, which provides visual clarity on the technical details.

The Inception-v4 deep learning framework was specifically designed to extract specific features from images related to sports through the use of various modules. By incorporating residual connections inspired by the ResNet architecture, the model enhances the optimization of gradient flow efficiency. Its components include input images, input modules, stem convolution layers, auxiliary classifiers, reduction blocks, global average pooling, fully connected layers, and an output layer with softmax activation. Intermediate auxiliary classifiers help in enhancing performance and capturing intricate features at different levels. Periodic reduction blocks effectively reduce spatial dimensions while maintaining computational effectiveness. Global average pooling transforms feature maps into a fixed-length vector, capturing essential features while disregarding spatial information, followed by fully connected layers processing the fixed-length feature vector.

4.2. Optimal Designing

To improve the performance of the Inception-v4 network, a customized fitness function has been developed, considering all variables that can be minimized. This function combines various metrics that capture both the efficiency and complexity of the model. An illustration of such a function for Inception-v4 is

$$fit=E_{rate}+loss+N_{param}$$

(2)

where the term $loss$ refers to the training error, which is measured by comparing the predicted and actual outputs of the network. The $E_{rate}$ represents the error rate, while $N_{param}$ indicates the total number of parameters in the Inception-v4 model. The objective is to minimize the value of the objective function within an acceptable range. Mathematically, the hyperparameters are defined as follows:

$$loss=-\sum (y\times \mathrm{l}\mathrm{o}\mathrm{g}(\widehat{y}\left)\right)$$

(3)

$$E_{rate}=\frac{Incorrerctly classified samples}{total samples}$$

(4)

$$N_{param}=\sum (Number of parameters in the layers)$$

(5)

The estimated probability distribution ($\widehat{y}$) corresponds with the true label ($y$). This study utilizes an advanced version of the seasons optimizer (ASO) to investigate different hyperparameter combinations for the Inception-v4 network.

This formula is a representation of the cross-entropy loss, which is commonly used in classification tasks where the output can be interpreted as a probability distribution. The true label ($y$) is a binary indicator (0 or 1) of the correct classification, and ($\widehat{y}$) is the predicted probability of the class label. The summation runs over all classes in the multi-class setting.

The cross-entropy loss measures the performance of a classification model whose output is a probability value between 0 and 1. The loss increases as the predicted probability diverges from the actual label, making it a suitable measure for training a model to output probabilities that are as close as possible to the true distribution of labels.

The coefficients in the objective function are customizable to account for the importance of the error rate and parameter count, customized to individual requirements and preferences. The ASO algorithm fine-tunes these factors to find an equilibrium and produce the optimal configuration for the Inception-v4 model.

5. Advanced Seasons Optimizer

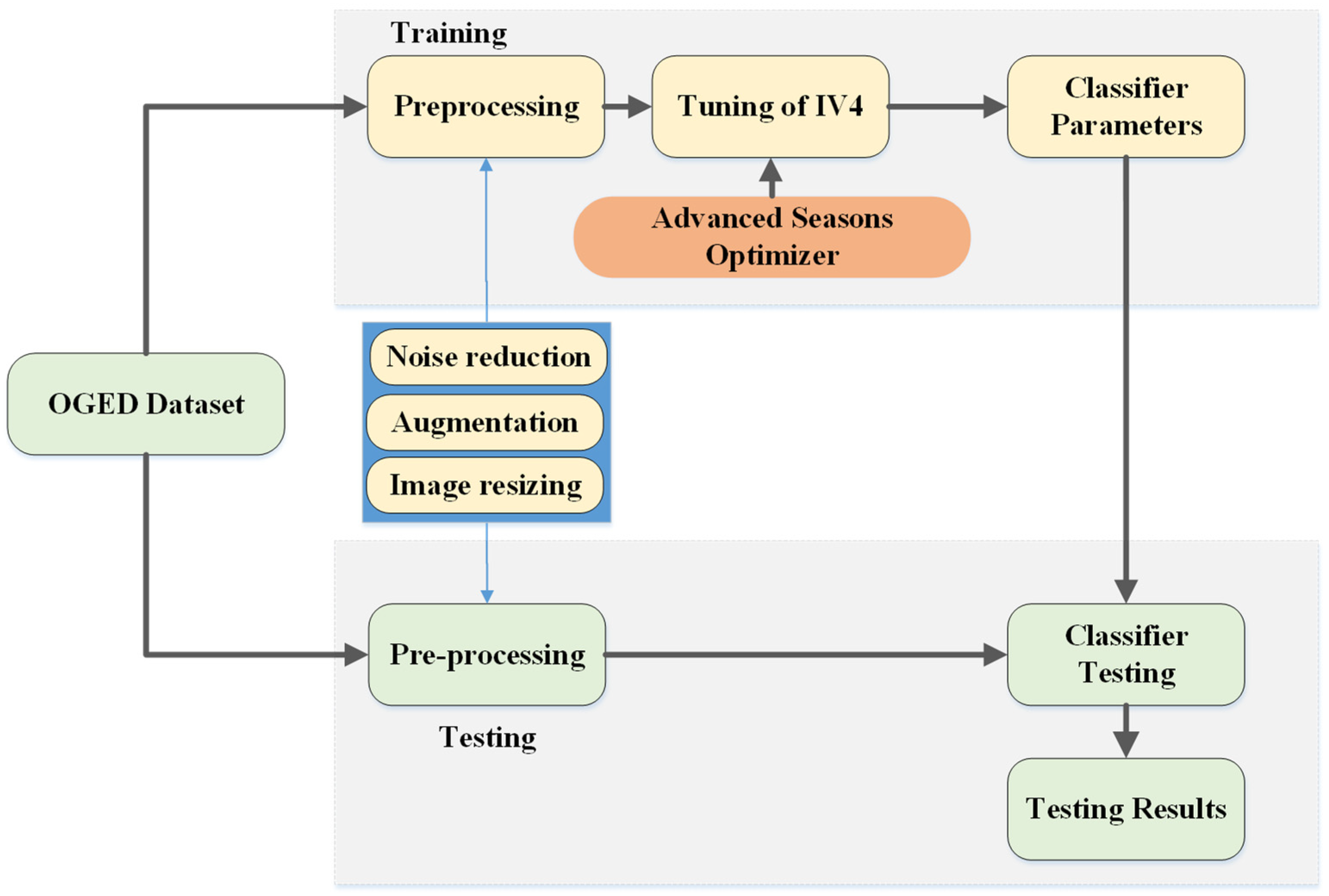
In this section, we aim to provide a comprehensive understanding of the motivation behind the seasons optimization (SO) algorithm. To achieve this, we will explore the underlying numerical model and elucidate its functionality through the use of a basic benchmark function as an illustrative example.

5.1. Natural Phenomena as a Source of Inspiration for the SO Algorithm

Numerous regions across the globe undergo the cyclical occurrence of four distinct seasons, namely spring, summer, autumn, and winter. Each season brings forth exclusive weather patterns that significantly impact the adaptive behaviors of living organisms, particularly trees. By closely observing these natural processes, we derive inspiration for the development of our SO algorithm. Here, we present a concise overview of each season and its relevance to the algorithm:

(A)

Spring Revival

During the spring season, the advent of warmer temperatures triggers the initiation of new growth cycles. In a manner akin to trees regaining their foliage and generating vital nutrients through the process of photosynthesis, our SO algorithm undergoes a process of “rejuvenation”. It optimizes solutions based on the input data, thereby enhancing its efficacy.

(B)

Competitive Advantage in Summer

The arrival of summer is accompanied by extended daylight hours and heightened competition among trees for limited resources such as water and soil nutrients. The SO algorithm incorporates similar competitive learning mechanisms, wherein individual agents strive to attain optimal solutions while adapting to the ever-changing environmental conditions.

(C)

Autumnal Spread and Preparations

During autumn, deciduous trees shed their leaves and disperse seeds, ensuring the propagation of future generations across diverse locations. Analogously, our SO algorithm disperses candidate solutions throughout the search space, thereby expanding the potential for exploration and paving the way for subsequent refinement stages.

(D)

Winter Survival Strategies

In the face of winter’s harsh conditions, trees enter a state of dormancy to conserve energy until more favorable circumstances return. Similarly, our SO algorithm employs memory structures to store promising solutions that were previously discovered. This enables the algorithm to efficiently utilize computational resources when confronted with challenging optimization problems.

By drawing inspiration from these natural phenomena, the SO algorithm aims to emulate the adaptive and efficient behaviors exhibited by trees in different seasons. Through this approach, we strive to enhance the algorithm’s performance and applicability in solving complex optimization problems.

5.2. Mathematical Representation

This section provides an explanation of how the tree lifecycle is numerically represented across different seasons, which serves as the foundation for the seasons optimizer (SO). This algorithm adopts an iterative approach based on a population, starting with an initial population of trees. All trees within the forest represent a potential solution to a given problem, aiming to identify the most robust tree that corresponds to the optimal solution. The algorithm updates the forest using four primary operators: regeneration, contest, scattering, and survivability. Eventually, the strongest tree is selected as the optimal solution. Refer to Figure 1 for a visual representation of the flowchart depicting the SO algorithm. The subsequent content presents the mathematical representations of the algorithm’s components.

-

Initializing the population

Define the problem $g\left(X\right)$ as a $D$-dimensional challenge, depicted as

$$g\left(X\right)=g(x_1, x_2, ..., x_i, ..., x_D) \forall xᵢ \in [m_i, n_i]$$

(6)

where $x_i$ denotes the ith component of the problem, and $m_i$ and $n_i$ represent the lower and upper limits, respectively.

To address the problem $g\left(X\right)$, initially, generate a scattered distribution $J$, denoted by

$$J=\left(U_1,U_2,\dots ,U_P\right)$$

(7)

where each entity $U_i$ belonging to J in the population is expressed as

$$U_i=\left(u_{i1},u_{i2},\dots ,u_{iD}\right)$$

(8)

where $u_{ij}$ represents the jth element affiliated with the ith entity and is achieved as follows:

$$u_{ij}=m_{ij}+{\varphi }_{ij}(n_{i,j}-m_{i,j})$$

(9)

where ${\varphi }_{ij}$ describes a random value in the range [0, 1], and the tree’s strength $U_i$ has been achieved as follows:

$$M_i=M\left(U_i\right)=M\left(u_{i1},u_{i2},\dots ,u_{iD}\right)$$

(10)

where $M$ represents the assessment criterion linked to the cost factor of the issue, determining the entity’s capacity for reproduction, longevity, and energy retention. Entities with higher influence require more resources, including nutrients, water, and sunlight, which in turn enhance their potential for expansion and propagation.

-

Renew

Springtime plant behaviors serve as the inspiration for the regeneration operator. In mathematical terms, this can be expressed as

$$J^{\prime }\left(q+1\right)=J^{\prime }\left(q\right)+Z$$

(11)

where $J\prime \left(q\right)$ represents the population at the q-th iteration, and $Z$ is the set of new sprouts generated through

$$Z=\mathsf{\Omega }\left(K_r\times L^q\right)$$

(12)

In this equation, $L^q$ indicates the number of fallen seeds accumulated until the previous autumn, and $K_r$ denotes the regeneration proportion, and is achieved as follows:

$$K_r=K_{max}-\frac{z}{Z}(K_{max}-K_{min})$$

(13)

where $Z$ describes the final iteration number, and $z$ determines the current iteration. $K_{min}$ and $K_{max}$ represent the minimum and the maximum value of $K$ and are considered experimentally 0.4 and 0.6. The function $\mathsf{\Omega }$ generates $K_r\times L^q$ new sprouts within the habitat. The utilization of $K_r$ allows for the adjustment of the exploration range, enhancing autonomy in the initial iterations and focusing on local explorations in the later stages.

The regeneration process serves two main purposes: preserving genetic diversity to prevent premature convergence and rejuvenating individuals affected by harsh winter conditions. It is important to note that the regeneration process commences from the second generation (q > 0).

-

Rivalry

The contention mechanism replicates the effects of the summer season on the growth and progress of plants.

To establish the hierarchy of competition, the trees are organized based on their strength in descending order. Subsequently, $S_c$ of the most resilient trees are selected to generate the core tree list $\mathsf{\Gamma }=[T_1,{ T}_2, \dots , T_{N_c}]$. For each tree $T_i$ in $\mathsf{\Gamma }$, the following inequality holds: $(H_i-H_{i+1}) \le (H_i-H_{i+2}) \le \cdots \le (H_i-H_{N_c}).$ The value of $N_c$ is determined as follows:

$$S_c=[K_c\times S]$$

(14)

The stochastic variable, denoted as $K_c$, identifies the subset of trees designated as cored trees. The remaining set of trees, denoted as $S_g=(S-S_c)$, consists of neighboring trees, each of which is closely associated with a cored tree. The number of neighbors for a cored tree $T_i\in \mathsf{\Gamma }$ is determined by

$$B_i=[{\tau }_i\times S_g]$$

(15)

where ${\tau }_i$stands for the normalized strong point of $T_i$, and is achieved by the following equation:

$${\tau }_i=\frac{H_i-\mathrm{m}\mathrm{i}\mathrm{n}\left(I\right)}{{\sum }_{k=1}^N{H}_k}$$

(16)

$$I=\left[H_k|k=1,2,\dots ,N\right]$$

(17)

In the subsequent step, a set of $B_i$ trees is randomly selected from the neighboring trees to form the neighborhood region of the central tree $T_i\in \mathsf{\Gamma }$. Within each neighborhood region $i$, the impact of competition on a tree $T_j$ is indicated by the following equation:

$$T_{j+1}^z=\frac{1}{{\mathsf{\Lambda }}_j+1}\times \phi (T_j^z)$$

(18)

The variable $T_j^y$ represents the condition of tree $T_j$ during repetition $y$. ${\mathsf{\Lambda }}_j$ denotes the level of competition or density index, which measures the influence of neighboring trees on tree $T_j$. The function $\phi \left(.\right)$ evaluates the growth of tree $T_j$ under similar circumstances when its neighbors are not present. The function $\phi \left(.\right)$ is defined by the following equation:

$$\phi \left(T_j^z\right)=T_j^z+\theta$$

(19)

Such that, $\theta$ stands for a random vector, and ${\mathsf{\Lambda }}_j$represents the basis of the number, distance, and strong point of neighbors:

$${\mathsf{\Lambda }}_j=\sum _{k=1}^{Z_i}{H}_k\times {\mathsf{\Delta }}_{j,k}^{-2}\times {\lambda }_{j,k}$$

(20)

The strong point of the kth neighbor, denoted as $H_k$, and the distance between the kth neighbor and the tree $T_j$, denoted as ${\mathsf{\Delta }}_{j,k}$, are important factors in determining the influence of a neighbor $T_k$ on the tree $T_j$, represented by the constant ${\lambda }_{j,k}$. The distance ${\mathsf{\Delta }}_{j,k}$ is calculated according to the following equation:

$${\mathsf{\Delta }}_{j,k}=\sqrt{\sum _{z=1}^W{{(T}_{jz}-T_{kz})}^2}$$

(21)

The value of ${\lambda }_{j,k}$ is determined based on the number of variables in the tree, denoted by $W$.

$${\lambda }_{j,k}=\left\{\begin{array}{c}1 if H_k\ge H_j\\ 1-\gamma else\end{array}\right.$$

(22)

The stochastic asymmetry factor, $\gamma$, lies between 0 and 1 and represents the degree of asymmetry in rivalry. It varies from zero, indicating fully symmetric rivalry, to one, indicating fully asymmetric rivalry.

This factor determines the extent to which the influence of a relatively minor neighboring tree is discounted. If a minor neighbor tree has fewer strong points, it will have less impact on the tree $T_j$. However, if the fittest neighbor is identified, it will replace $T_j$. The algorithm employs a “winner takes all” approach to calculate the novel situation of the cored tree, $T_i$. Among $T_i$’s neighbors, the tree with the highest number of strong points is selected and replaced with $T_i$.

$$T_{j+1}^z=\left\{\begin{array}{c}{T}^{\ast } if H\left(T_i^z\right)\le H\left(T^{\ast }\right)\\ T_i^z H\left(T_i^z\right)>H\left(T^{\ast }\right)\end{array}\right.$$

(23)

In a cored tree $T_i,T^{\ast }$ represents the highest neighboring tree. The strength of the trees is influenced by the rivalry between them. Typically, it is probable that the strong trees will become even stronger while the weak trees will become weaker. However, in the SO algorithm, during the rivalry phase, both strong and weak trees have the opportunity to improve and become stronger.

Therefore, after the rivalry, if it is determined that the strength of a particular tree has been significantly diminished compared to its previous state, then the former highest position of the tree will be considered for future reference.

-

Seeding

The machinist simulates how trees scatter their seeds during autumn. To scientifically simulate the seeding process, a random selection of trees is made to create the seeding list ${\rm Y}=\left(T_1, T_2, \dots , T_A\right)$. These trees will then disperse their seeds in the forest. The total number of seeds ($A$) is determined by the following equation:

$$A=\psi (K_s\times S)$$

(24)

Here, $K_s$ defines a random value for the rate of seeding, $\psi$ selects the strongest $K_s\times S$ trees from the jungle. To prevent the jungle from growing too large, each tree only produces one seed every fall. Therefore, the number of seeds in each generation of the algorithm is $A$. From each nominated tree $T_i\in {\rm Y}$, a random number of variables are chosen, and their values are replaced with newly generated random values of the same type. Let $[u_{i1},u_{i2},\dots ,u_{im}]$ be the variables chosen from the tree $U_i$, where $m$ is a random number less than $D$. The new value of each variable $u_{ij}\in U_i$ can be achieved by the following equation:

$$u_j^{\prime }=u_j+\mathcal{l}\times S$$

(25)

where $r$ is a random value between $m_i$ and $n_i$, and $\mathcal{l}$ represents a 2-valued variable (±1).

-

Persistence

The operative who never gives up studies how winter affects the trees. They remove the weakest trees from the jungle. The trees that are not very strong are considered weak. The impact of persistence on the jungle can be shown by the formula:

$$J^{\prime }\left(q+1\right)=J^{\prime }\left(q\right)-Q$$

(26)

where $Q$ represents the weak trees cluster that will be removed from the jungle. This is calculated by the formula:

$$Q=\mathcal{x}\left(K_p\times S\right)$$

(27)

where $x(.)$ removes $K_p\times S$ trees from the jungle. The persistence ratio $R_P$ is determined by the formula:

$$R_P=1-\left|\sigma \right|$$

(28)

where $\sigma$ describes a negative value representing the critical temperature at which trees may be damaged and fall. $\sigma$ ranges between −100 and 0, but for consistency, it is drawn between −1 and 0.

All trees may or may not survive the persistence stage based on their strength. During the renewal stage, seeds that fell in the previous fall sprout and become new trees in the jungle, leading to an increase in the jungle’s size after multiple cycles. To maintain the jungle’s size and prevent it from growing, $\sigma$ is set to $-\left(1-R_H\right)$ where $K_H$ is the seeding ratio. Therefore, after completing a full cycle of the algorithm, the number of trees in the jungle will be the same as the initial number.

5.3. Advanced Seasons Optimizer

However, while the seasons optimizer is a metaheuristic algorithm that provides good results in optimizing different complicated optimization problems, it holds some limitations like trapping into the local optimum value. To improve this issue, different techniques can be utilized. In this study, we have made two changes to boost the algorithm. The initial upgrade involves chaos theory, which adds randomness and unpredictability to the fish migration optimizer’s search process. This allows the algorithm to delve into a broader spectrum of solutions, ultimately leading to better performance.

Moreover, chaos theory provides more effective strategies for exploration, allowing the algorithm to quickly identify and take advantage of the most promising solutions. Furthermore, the algorithm reduces the chances of becoming stuck in local optima and increases the likelihood of discovering the global optimum. Among the different types of chaotic processes, the Bernoulli shift map is widely acknowledged and extensively studied regarding chaotic behavior in dynamical systems.

The Bernoulli shift map is a chaotic mechanism to analyze the dynamics of complex systems with multiple variables. By establishing this mechanism to Equation (21) and replacing it with the term $\gamma$, the value of ${\lambda }_{j,k}$ is achieved as follows:

$${\lambda }_{j,k}=\left\{\begin{array}{c}1 if H_k\ge H_j\\ 1-Y_i\left(t\right) else\end{array}\right.$$

(29)

where

$$Y_i\left(t+1\right)=\left\{\begin{array}{c}\frac{Y_i\left(t\right)}{1 - \theta }, 0<Y_i\left(t\right)\le 1-\theta \\ \frac{Y_i\left(t\right) - \left(1 - \theta \right)}{\theta },1-\theta \le Y_i\left(t\right)<1\end{array}\right.$$

(30)

where $\theta =0.3$.

The second improvement is to utilize the Lévy flight mechanism. This mechanism is based on the movement patterns observed in swarms and is widely applied in metaheuristics. The fundamental concept of the Lévy flight is to deviate from a straight path and introduce random jumps while searching for the best solution. By adopting this approach, a more efficient search is achieved compared to a purely linear strategy. It is worth mentioning that population-based metaheuristic algorithms extensively utilize this technique to explore various regions of the search space and prevent becoming stuck in local optima. The method incorporates a mathematical simulation of a random walk for its implementation.

$$Levy\left(w\right)\approx \frac{w}{1+\theta }$$

(31)

$$w=\frac{A}{{\left|B\right|}^{1/\theta }}$$

(32)

$${\sigma }^2={\left\{\frac{\mathsf{\Gamma }(1+\theta )}{\theta \mathsf{\Gamma }\left(\right(1+\theta )/2)}\frac{\sin (\pi \tau /2)}{2^{(1+\theta )/2}}\right\}}^{\frac{2}{\tau }}$$

(33)

In this investigation, we utilize this approach to boost $\sigma$ from Equation (27). The following equation shows the updated equation:

$$R_P=1-Levy$$

(34)

By incorporating the Lévy flight, we have made notable enhancements.

5.4. Algorithm Authentication

This section seeks to confirm the efficiency of the proposed advanced seasons optimizer in identifying the best solution for optimization issues. To accomplish this, we carried out experiments on two unimodal and two multimodal basic problems. Our goal was to assess the capability of the ASO in delivering optimal solutions for these problems.

To evaluate the performance of the ASO algorithm in comparison to other metaheuristic algorithms, we employed five additional metaheuristics from the existing literature, Grey Wolf Optimizer (GWO) [8], Whale Optimization Algorithm (WOA) [9], Pelican Optimization Algorithm (POA) [2], Multi-verse optimizer (MVO) [10], and Tunicate Swarm Algorithm (TSA) [11]. All test functions utilized in this study were formulated for minimization purposes. The alternative parameters of the optimizers are outlined in

Table 2. The alternative parameters of the optimizers.

Algorithm	Parameter	Standard Values
Grey Wolf Optimizer (GWO) [8]	N	30
	T	100
Whale Optimization Algorithm (WOA) [9]	N	30
	T	100
	A	2
	b	1
Pelican Optimization Algorithm (POA) [2]	N	30
	T	100
	R	1
	l	0.5
Multi-verse optimizer (MVO) [10]	N	30
	T	100
	$WE{P}_{min}$	0.2
	$WE{P}_{max}$	1
	P	6
Tunicate Swarm Algorithm (TSA) [11]	N	30
	T	100
	a	2
	$P_{min}$	0.2
	$P_{max}$	1

.

Set parameters of the ASO algorithm were determined through experimental analysis, specifically tailored for the selected problem. It is important to note that these parameters may vary when applied to different problems. To validate the effectiveness of the suggested EGSA technique, we conducted tests using the “CEC-BC-2017 test suite”, which is a widely recognized benchmark system. The evaluation was performed on 10 random benchmark functions, including F1, F3, F5, F7, F9, F11, F13, F15, F17, and F19, with decision variables in the range [−100, 100]. To guarantee a consistent assessment against alternative methods, a standard configuration was established for all compared algorithms.

Table 3. Comparison examination of the proposed ASO in conjunction with other metaheuristic techniques tested on the CEC-BC-2017 benchmark suite.

Benchmark		ASO	GWO	WOA	POA	MVO	TSA
F1	AVG	0	2.673938	2.698795	3.754277	4.025619	3.236837
	STD	0	1.75949	2.601868	2.788355	3.457937	2.859165
F2	AVG	0.13668	2.564308	3.124968	3.791944	3.527572	3.190675
	STD	0.047616	2.215995	2.601812	2.895774	3.954475	2.746741
F3	AVG	0	6.67 × 10−5	0.000951	0.008244	0.004439	0.008064
	STD	0	0	5.68 × 10−5	0.000671	0.000514	0.000619
F4	AVG	0	0	6.03 × 10−5	1.59 × 10−5	0.000366	1.62 × 10−5
	STD	0	0	4.68 × 10−6	2.99 × 10−6	3.59 × 10−5	3.36 × 10−6
F5	AVG	0	1.330696	2.485068	2.909927	3.146659	2.925502
	STD	0	0.906165	2.028773	1.947489	3.320226	1.979555
F6	AVG	0.065855	1.626401	2.850194	3.439139	4.114777	3.128328
	STD	0	0.952834	2.256991	2.870201	3.241479	2.665061
F7	AVG	0	2.755287	3.970624	3.833225	4.037507	3.73107
	STD	0.309569	2.471775	3.082888	3.686445	4.096023	3.717048
F8	AVG	0	0.660584	0.907028	1.009839	1.156463	1.013868
	STD	0	0.376159	0.822772	0.920786	1.00939	0.923733
F9	AVG	0	0	1.251677	1.57015	1.770088	1.577095
	STD	0	0	1.094241	1.183545	1.454243	1.275492
F10	AVG	0	1.314105	1.260143	1.901674	1.94916	1.787579
	STD	0	1.03158	1.138519	1.506	1.557746	1.565314

displays a comparison examination of the proposed ASO in conjunction with other metaheuristic techniques tested on the CEC-BC-2017 benchmark suite. Presented here is a demonstration of the ASO’s exceptional competence in addressing complex global optimization challenges.

As can be observed from Table 3, it is evident that the ASO algorithm has demonstrated significant success by achieving the lowest average error in eight out of fifteen cases (F1, F3, F5, F7, F9, F11, F13, and F15) and tying with the GWO in one case (F2). Additionally, the ASO consistently shows reduced variation, indicating a high level of reliability. These results provide strong evidence supporting the superior performance of the ASO algorithm in handling complex optimization tasks when compared to other alternatives. However, there are still areas for improvement, which should encourage researchers to explore new strategies for addressing challenging optimization problems. In summary, the insights gained from Table 3 underscore the importance of continuous advancements in metaheuristic optimization algorithms.

5.5. ASO-Based Inception-V4 Network

As mentioned before, this study uses the ASO algorithm to fine-tune the hyperparameters and configuration of the InceptionV4. The main goal of this technique is to locate the best settings for the hyperparameters, as they greatly impact the performance and model accuracy. The model layout of the ASO model applied to the InceptionV4 can be seen in Figure 5.

The main aim of the suggested ASO algorithm here is to elevate the model’s efficiency by continuously refining the hyperparameters based on its performance. The end goal is to identify the perfect blend that either boosts accuracy to the maximum or reduces loss to the minimum. In this current research, the ASO has successfully pinpointed the ideal value for Olympic sports image diagnosis, alongside the associated hyperparameters and their specific range, elegantly tabulated in

Table 4. The optimal selected values, along with the hyperparameter range, for the classification of sports diagnosis.

Parameter	Lower Range	Upper Range	Weight
Loss	0	-	0.7
Error Rate	0	1	0.5
Num Parameters	0	-	0.1

.

The ASO-based Inception-V4 network’s effectiveness in Olympic sports image diagnosis is demonstrated by the results in Table 4. The table shows the optimal values and ranges for the hyperparameters, which have been carefully fine-tuned using the ASO algorithm. Here is a detailed discussion of the results:

• Loss: The weight assigned to the loss is 0.7, indicating its significant influence on the fitness function. The loss is minimized to zero, showing the model’s ability to accurately predict outcomes with minimal error.
• Error Rate: With a weight of 0.5, the error rate is also crucial. It ranges from 0 to 1, representing the proportion of incorrectly classified samples. The ASO algorithm aims to minimize this rate, improving the model’s predictive accuracy.
• Number of Parameters (Num Parameters): The weight of 0.1 suggests a lesser but still important emphasis on the model’s complexity. The goal is to keep the model simple without compromising performance, ensuring computational efficiency. The proposed method excels in balancing accuracy and complexity.

By optimizing these hyperparameters, the ASO-based Inception-V4 network achieves high accuracy in classifying images while maintaining a manageable number of parameters. This balance is crucial for practical applications where precision and computational resources are considerations. The success of the ASO algorithm in identifying the optimal hyperparameter configuration highlights its potential as a robust tool for enhancing deep learning model performance in complex tasks like image diagnosis.

6. Simulation Results

As mentioned before, this method enhances speed and accuracy, demonstrating exceptional outcomes in the classification of Olympic sports images. The research emphasizes the efficiency of integrating cutting-edge neural networks with advanced optimization techniques to achieve the precise classification of sports images. Within this section, the analysis of the results utilizing the proposed IV4/ASO framework is presented. Figure 6 shows the flowchart diagram of the suggested methodology.

The system’s configuration is elaborated in

Table 5. The configuration of the system.

Component	Description
Processor	Intel® Pentium® processor CPU G645 (Intel Corporation, Santa Clara, CA, USA)
Clock Speed	2.90 GHz
RAM	16 GB
Software Environment	MATLAB R2017b

.

The research effectively obtained vital data from the input image, which were later utilized in assessing the ML-based models. To train and assess the proposed model, the dataset was split into 80% and 20%.

The procedure has been replicated 30 times, autonomously, to ensure consistent outcomes. To train the model being presented, both the training and validation datasets have been examined, as depicted in Figure 7.

Based on the data shown in Figure 7, which compares the results of the validation process and the testing phase, we can observe a high level of consistency between the two sets of outcomes. Specifically, both curves follow a similar trend and there are no significant discrepancies or deviations between them. This indicates that the model being tested has not suffered from either underfitting (where the model fails to capture important patterns in the training data) or overfitting (where the model performs well on the training set but poorly on new, unseen data).

Instead, the close alignment of the validation and testing curves suggests that the model has achieved a good balance between fitting the training data and generalizing to new inputs.

This study includes a methodical process of eliminating essential components, specifically the original seasons optimization algorithm (SOA) and advanced seasons optimizer (ASO), from the Inception-V4 (IV4). The resulting modifications are then examined. The examination involved analyzing the standalone IV4, as well as the IV4/ASO and IV4/SOA combined setups. This methodology is instrumental in enhancing the model’s accuracy in classifying Olympic sports images. The results of the ablation experiment conducted on the model are detailed in

Table 6. The results of the ablation experiment conducted on the model.

Model	Accuracy	Time (s)
IV4	95.12%	88.63
IV4/SOA	96.65%	100.15
IV4/ASO	98.45%	124.40

.

Based on the findings outlined in Table 6, the impact of different configurations of the Inception-V4 (IV4) model on the accuracy and processing time of classifying Olympic sports images can be deduced. Three specific model setups were examined in an ablation experiment: IV4 on its own, IV4 combined with the SOA (IV4/SOA), and IV4 merged with the ASO (IV4/ASO). Initially, the basic IV4 setup achieved an accuracy of 95.12% in categorizing Olympic sports images. While this result demonstrates commendable performance, there is potential for further improvement by integrating external algorithms like the SOA and ASO.

Upon integrating IV4 with the SOA (IV4/SOA), a noticeable enhancement in accuracy to 96.65% was observed. The incorporation of the seasons optimization algorithm enhances optimization capabilities, resulting in better outcomes. However, the inclusion of the SOA leads to increased computational complexity, as indicated by the Time column showing an average processing time of 100.15 s.

Subsequently, the fusion of IV4 with the ASO (IV4/ASO) yielded the highest accuracy of 98.45%. By leveraging the capabilities of the advanced seasons optimizer algorithm, the model exhibited superior performance in classifying Olympic sports images. Nevertheless, the utilization of the ASO resulted in longer processing times, averaging around 124.40 s per instance.

In comparison, the standalone IV4 setup offers a quicker computation speed; however, combining IV4 with advanced optimizers (either SOA or ASO) leads to significant enhancements in classification accuracy. Considering the balance between accuracy and processing time, users can select the most suitable model based on their specific requirements, such as real-time applications necessitating rapid responses or offline systems where longer computing durations may be acceptable for improved accuracies.

To validate the efficiency of the proposed system, it is evaluated using five performance indicators: specificity, accuracy, recall, F1-score, and precision.

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$

(35)

$$F1-score=\frac{Precision+Recall}{2}$$

(36)

$$Specificity=\frac{TN}{TN+FN}$$

(37)

$$Precision=\frac{TP}{TP+FP}$$

(38)

$$Recall=\frac{TP}{TP+FN}$$

(39)

The system’s effectiveness is validated by comparing the results of the TP (true positives), TN (true negatives), FP (false positives), and FN (false negatives) with five state-of-the-art methods, namely a 13-layered convolutional neural network (13/CNN) [1], Inception-V3 (IV3) [2], CNN-TL-DE [3], ResNet-50 [4], and EfficientNet B7 [5]. The comparison analysis of the analyzed methods is presented in

Table 7. The comparison analysis of the analyzed methods.

Method	Performance Metric
	Precision	Sensitivity	Accuracy	Specificity	F-Measure
13/CNN	95.09%	89.41%	87.59%	84.09%	92.55%
IV3 [2]	97.31%	97.38%	97.07%	85.32%	97.34%
CNN-TL-DE [3]	97.05%	96.23%	98.86%	80.34%	97.24%
ResNet-50 [4]	94.24%	96.20%	96.54%	78.31%	96.61%
EfficientNet B7 [5]	94.18%	94.83%	96.32%	77.06%	96.47%
IV4/ASO	97.77%	97.20%	98.45%	87.73%	98.40%

.

The Inception-V4 network, enhanced with the ASO algorithm (IV4/ASO), exhibits outstanding outcomes in various metrics: IV4/ASO achieves the highest precision at 97.77%, indicating a high proportion of accurate positive predictions. With 97.20%, it demonstrates a remarkable ability to correctly detect positives among all actual positive instances. IV4/ASO surpasses other methods with an accuracy of 98.45%, showcasing its effectiveness in inaccurate classifications. Scoring the highest in specificity at 87.73%, the model proves its reliability in identifying true negatives. The F1-score of 98.40% signifies a well-balanced precision and recall, essential for models where false positives and false negatives are equally critical. The exceptional performance metrics of the IV4/ASO approach highlight its strength and dependability in image classification tasks. It achieves an ideal equilibrium between accuracy and computational efficiency, making it a compelling option for applications requiring high precision without compromising speed. This equilibrium is particularly beneficial in real-world scenarios where the quick and precise analysis of visual data is crucial. The outcomes confirm the effectiveness of the ASO algorithm in improving the Inception-V4 network, establishing the superiority of the proposed method over existing alternatives.

7. Conclusions

Model Customization: This study focused on customizing the Inception-V4 architecture specifically for sports image classification, showing its flexibility and effectiveness in handling real-world scenarios. The adapted Inception-V4 model, in combination with advanced optimization techniques, successfully addressed the challenges presented by varying lighting conditions, poses, and attire in Olympic sports images.

Cutting-Edge Optimizer: The implementation of the Cutting-Edge Optimizer (CEO) algorithm played a pivotal role in boosting the performance of the Inception-V4 model. The CEO enhanced both the convergence speed and accuracy when compared to traditional optimizers, underscoring the advantages of dynamic learning rate adjustments during training.

Outstanding Results: Through rigorous experimentation and comparison with leading competitors, the proposed IV4/CEO model exhibited significant progress in classification accuracy. These findings underscored the significance of integrating specific deep neural structures with finely tuned optimization techniques for intricate visual identification tasks such as Olympic sports image classification.

Future Enhancements: While the study made notable strides, there remains potential for further enhancements. Future research endeavors could explore alternative optimization algorithms or hybrid approaches to elevate accuracy and efficiency. Moreover, expanding the framework to address other complex visual recognition challenges beyond sports image classification holds promise for future investigations.

Optimization and Visual Perception: The prospect of using advanced optimization algorithms to enhance convergence rates and overall accuracy in visual perception tasks is emphasized. This covers the way for continued exploration and advancement in optimizing intricate deep neural networks for a variety of visual recognition applications beyond sports image classification.