The Method of Elementary Solvers in SPICE

Abstract

Circuit simulators are fundamentally used for solving electric circuit problems with different degrees of complexity in which node voltages and branch currents are the unknowns. This is fully understandable since they were originally created for this specific task. However, behind the curtains, powerful simulation engines based on a variety of numerical techniques operate so as to always comply with Kirchhoff’s current and voltage laws. In this paper, it is shown how a simple circuital configuration, referred to as the elementary solver, consistent in two behavioral current sources in series, can be used to solve mathematical problems that go beyond electronics. Of course, the intention is not to substitute mathematical packages with well-proven calculus capacity but to increase the scope of circuit simulators for their application in other areas of research or simply for educational purposes. It is worth mentioning that no special programming skills are required (except a basic knowledge of the available tools and language) and, furthermore, that the user can operate exclusively in a graphical environment. It is shown, throughout a series of selected examples, how the method of elementary solvers (MES) works, providing a new and practical dimension to the applicability of circuit simulators.

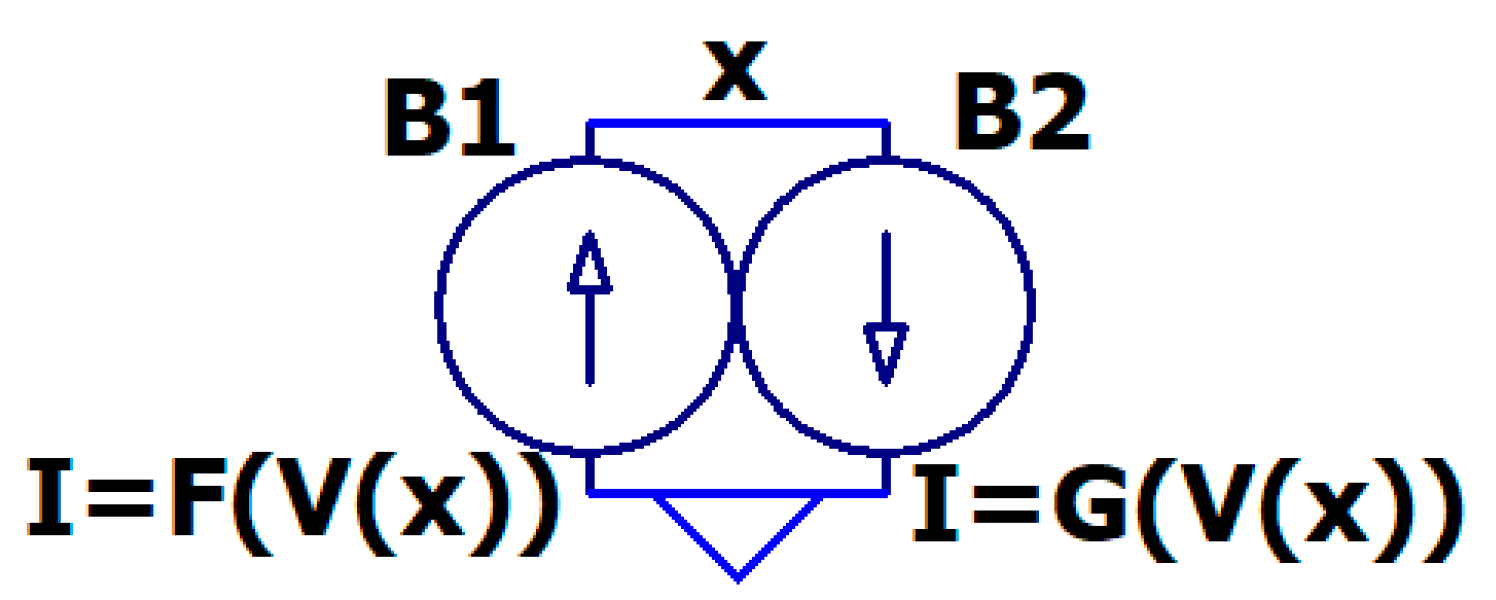
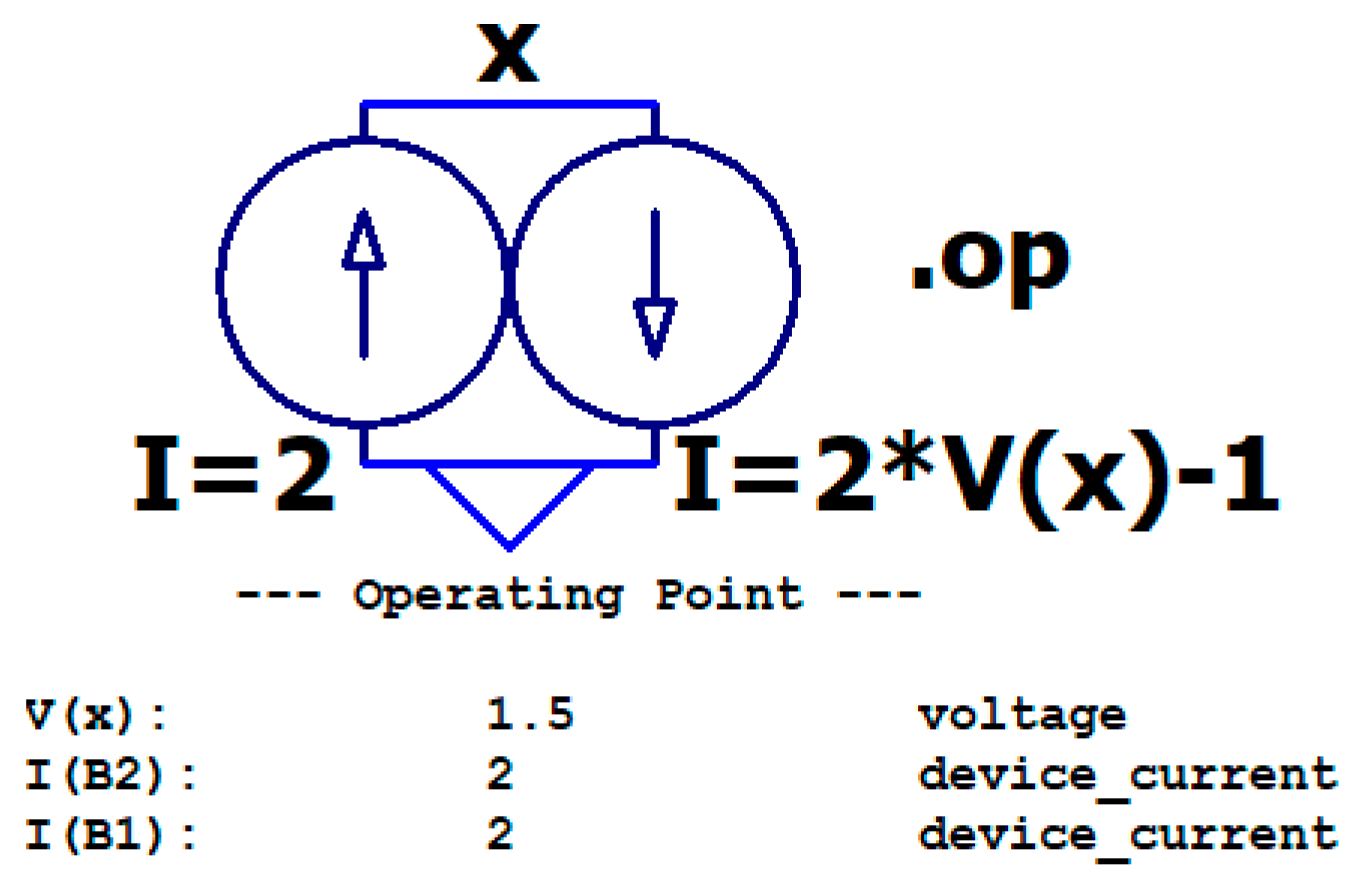
1. Introduction

This paper is not about electric circuits. It is about the use of a specific electric circuit for solving mathematical problems that can be expressed as a single equation or as a system of equations. However, before getting into the topic, it is worth mentioning that, to our knowledge, the approach we are going to follow is different from previous proposals. The idea that we can represent equations associated with mathematical, physical, engineering, biological, epidemiological, etc., problems in terms of electric components is not new of course and the literature has plenty of cases of such applications [1,2,3,4]. For instance, very often, if we need a derivator or an integrator we think of a combination of components such as resistors, capacitors, inductances, opamps, etc. But why do we not make direct use of the behavioral components circuit simulators offer instead? In this way, we can straightforwardly benefit from the heart of the simulation engines upon which circuit simulators are built without establishing correspondence with any specific electric circuit. At the end, a circuit simulator is nothing but an equations solver. However, the question is whether it is possible or not to define a very elemental electrical cell suitable for solving a wide variety of problems without requiring specialized programming skills. Of course, we are not thinking of substituting mathematical packages of proven calculus capacity to this purpose. We are thinking about something simple and adaptable, and in any case, expressible by means of a few commands and directives. In order to accomplish this objective, we are going to use the LTSpice XVII simulator from Analog Devices [5], but any other circuit simulator would be appropriate in principle. LTSpice is a free SPICE simulator software that offers a powerful simulation engine and, perhaps what is relevant to our aim, an easy to use graphical interface which can be combined with a waveform viewer. LTSpice is available both for Windows and MacOS. Apart from the numerous papers, webpages, tutorials, and videos on LTSpice, some books have been recently published [6,7,8,9].

We will refer to the proposed electric cell as the elementary solver (ES). This cell simply consists in two behavioral current sources (B-sources B1 and B2) connected in series with a central node x as illustrated in Figure 1. F and G are two functions of the voltage V(x), i.e., the unknown. The triangle at the bottom of the mesh indicates the connection to ground (this is always required!). Because of the particular arrangement considered, the cell automatically complies with Kirchhoff’s current law (ΣI = 0) at node x.

However, since B1 and B2 can be somehow regarded as a parallel combination too, the voltage drops across them must also coincide because of Kirchhoff’s voltage law (ΣV = 0). At the end, V(x) is the value required to equalize the currents (F[V(x)] = G[V(x)]), i.e., the solution of the problem we want to solve.

For the sake of clarity, Figure 2 shows an elementary introductory example. The equation to be solved is 2 = 2·x − 1, with x as the unknown. Since x is a label in the circuit, we have to refer to the voltage value at node x, i.e., V(x). Of course, we can always rewrite the proposed equation as 0 = 2·x − 3 if necessary. .op is the LTSpice directive for the DC operating point (stationary solution). For time-dependent problems, a transient analysis .tran must be invoked instead. The solution V(x) = 1.5, i.e., x = 1.5 can be found in the bottom panel of Figure 2. Notice also that I(B1) = I(B2) as expected (this must always be checked!). If the user prefers to work in text mode, the script corresponding to the circuit shown in Figure 2 can be found in the “SPICE Netlist” window.

If, because of the complexity of the problem we want to solve, the operating point cannot be found with successive linear approximations as is conducted using the Newton–Raphson (NR) iteration method, it is always advisable to try a different method. The corresponding directives are indicated in

Table 1. List of directives corresponding to the numerical methods used by LTSpice.

Method	Directive to Disable
Direct Newton Iteration	.options noopiter
Adaptive Gmin Stepping	.options gminsteps = 0
Adaptive Source Stepping	.options srcsteps = 0
Pseudo Transient	.options ptrantau = 0

and they can be added to the circuit diagram.

It is also worth mentioning that in many cases, the variable time, which is always assumed positive and reserved for transient problems, can be used with an alternative meaning, for example, as the abscissa in a 2D coordinate problem. If a negative x-axis is required, the .step directive and discretized versions of the derivatives must be considered for .op conditions. Even though LTSpice can deal with complex numbers, mainly for frequency analysis, in this paper we will exclusively focus on the real axis.

2. Selected Examples

In this section, a number of selected problems will be presented and discussed, mainly in connection with their practical implementation. The examples reported below do not pretend to cover all cases and situations. They are just presented for illustrative purposes and many of them are widely discussed in the literature. In some cases, exact solutions or approximations are included for comparison. We will also make extensive use of behavioral voltage sources as function plotters. Since this is not a course on mathematical calculus (neither on any other discipline!), for the sake of simplicity, we will skip derivations and details. Please pay attention to the definition of the current sources B1 and B2. If inadvertently exchanged, computational errors can arise.

2.1. Solution of a Nonlinear Equation: Lambert W Function

We start this selection with an extension of the problem presented in Figure 2. Here, we will focus the attention on the solution of a transcendental equation. Contrary to the previous example, the solution to the equation is as follows:

W·exp(W) = z

(1)

where z > −1/e is a real number which cannot be expressed in terms of elementary functions. W(z) is called the Lambert W function and can be found in combinatory analysis, combustion problems, electric circuits, population dynamics, etc. [10]. When z changes, the principal branch of W is generated. The corresponding ES with the stepped z parameter is shown in Figure 3a. A closed-form Hermite–Padé approximation for W(z) is also included in the schematics [11]. Figure 3b illustrates both the numerical and approximate results for W(z).

2.2. Analysis of a Function: Polynomial Case

This second selected example focuses on the analysis of a cubic polynomial function such as the one below:

f(x) = x³ − x² − 16x − 20

(2)

In this case, not only the function f but also its first and second derivatives are plotted as a function of the argument (see the set of voltage plotters in Figure 4a). First, notice that the discrete forms of the derivatives are used (central case difference). h is the discretization step. Second, in order to find the roots of the function (zeroes of f) and of its first derivative (local extremes of f), a shift z in the function argument is introduced. Recall that the circuit simulator only provides a single solution (we are dealing with a conventional electric circuit!). The shift is compensated by a second voltage source of value z at the ES output port. The roots must be read in the y-axis of the plot as indicated by the horizontal lines (see Figure 4b). A reasonable range for z must be initially provided. Notice that horizontal asymptotes can also be identified as minimums/maximums since the first derivative could reach values close to zero in those regions. Switching between the root values can also occur randomly because of the NR iteration method. Trying different z steps is also advisable.

2.3. Indirect Integration: Gamma Function

This exercise deals with the fundamental theorem of calculus which states that the integral of a function f over a fixed interval is equal to the difference of the antiderivative F evaluated at the ends of the interval. We will use the theorem to calculate the gamma function, which can be considered an extension of the factorial function to non-integer values [12,13]. We will limit the analysis here to the positive real axis. Notice that the intention here is not to find an approximate expression for the gamma function but to play with the ES. The gamma function is the integral from 0 to ∞ of the function (see Figure 5a):

f(z) = t^z−1·exp(−t)

(3)

Using time as the integration variable, we construct the gamma function through the stepped parameter z. In fact, Figure 5b shows the so-called lower incomplete gamma function which is a function of the upper integration limit t. The gamma function corresponds to the last point in each curve, once the curves level off. These points are plotted in Figure 5c as a function of z. The results are compared with Stirling’s approximation for the factorial function given by the following equation:

F(z)~(2π)^1/2·z^z−1/2·exp(−z)

(4)

Although we have used the ES as an indirect integrator, we can also integrate the function f using the integration command idt directly, which can be obtained by clicking on the w port shown in Figure 5a.

2.4. Recursion: Explicit Newton–Raphson Method

In this exercise, the NR method is explicitly used [14]. The delay function is used to generate the recursive computation required to find the roots of a polynomial of degree 3 (Figure 6a). The roots of f are plotted in Figure 6b (zoomed plot). The stepped parameter z is used for shifting the initial condition of the iterative process. For completeness, a voltage plotter is included in order to generate the function graph. Figure 6c describes the analyzed function and indicates its roots.

2.5. System of Linear Equations: Matrix Inversion

This simple algebra exercise consists in finding the inverse of a 2 × 2 matrix with the coefficients b₁₁ = 5, b₁₂ = 2, b₂₁ = −7, and b₂₂ = −3 (see Figure 7). This is nothing but the solution of a linear equation system. The exercise can easily be extended to higher dimensions. The solution is given by the matrix a₁₁ = 3, a₁₂ = 2, a₂₁ = −7, and a₂₂ = −5. The blue numbers on top of the ESs are obtained by clicking on the corresponding connection node. The method can also be adapted for the computation of the eigenvalues and eigenvectors of a matrix if an additional equation for the determinant (det[A-λI] = 0) is added.

2.6. System of Nonlinear Equations: Optimum Solution

In this example, a system of nonlinear equations needs to be solved. The optimum solution (minimum error) is looked for. As shown in Figure 8a, the problem consists of solving three coupled nonlinear equations with three unknowns. If solved under the .op directive, the solution provided by the simulator seems to be a priori correct (see Figure 8b) though a message in the Error Log window indicates that the “Direct Newton iteration failed to find .op point (Use .option noopiter to skip)”. If the noopiter option is enable then, the solution shown in Figure 8c is obtained. This is the solution we were looking for since it provides the smallest error. The main message is that even if the solution seems to be correct (because of the currents matching), always substitute the solution into the equations and check the resulting error. The other alternative numerical methods provide the same optimum solution. Notice that, in this case, LTSpice does not require an initial guess for solving the problem. Instead, commercial software arrives at the same solution using the initial guess (1,1,0).

2.7. First-Order Autonomous Differential Equation: Newton’s Law of Heat Transfer

With this simple exercise, we start the series of differential equation problems. In this case, we have to solve the first-order autonomous differential equation:

dT/dt = k·(M − T)

(5)

which can be linked to Newton’s law of cooling and heating [15]. In this context, t is the time, T is the temperature, M the equilibrium temperature, and k a positive constant.

Additionally, T(t = 0) = T₀ is the initial temperature (T₀ > M: cooling, T₀ < M: heating). Figure 9a illustrates the corresponding circuit schematic. ddt is the derivative with respect to time. Two post-processing directives are included here: one measures the time (time_ch) required for the system to reach a ±10% value of the equilibrium temperature and the other directive computes the temperature (temp) reached after 1 s (see Figure 9a’s insets). Temperatures are plotted as a function of the initial condition T₀ in Figure 9b.

2.8. First-Order Non-Autonomous Differential Equation: Redefinition of the Time Coordinate

In this case, the differential equation to be solved is as follows:

dy/dx = 1 − 2·y·x

(6)

Notice that not only the function y but also the variable x appear now in the right-hand side of (6). In order to solve this equation, we will use the variable time as the x coordinate for positive values of x and −time for negative values of x. The corresponding circuital diagram is shown in Figure 10a. Notice that the derivative with respect to time must also be reversed. The solutions for positive and negative values of x as a function of the integration constant c are reconstructed in Figure 10b.

2.9. Delayed Differential Equation: Logistic Model

This exercise consists in finding the solution of the delayed logistic equation (Hutchinson’s equation) [16]:

dx/dt = k·x(t)·[1 − x(t − τ)]

(7)

where x is the magnitude of interest, t the time, k a constant, and τ the time delay.

Equation (7) is frequently found in biological problems that require the representation of resource regeneration times, maturation periods, feeding times, reaction times, etc. Time delays introduce perturbations in the solution which deviate the system state from its equilibrium condition. The corresponding schematic is shown in Figure 11a along with its solution as a function of τ in Figure 11b. For τ ≈ 0, the logistic function (Verhulst’s equation) is recovered. Figure 11c illustrates the evolution of the system state in the phase space using, as the derivative function, the current flowing through one of the generators. Notice that different behaviors are obtained: from closed orbits, there are decaying orbits to an attraction point. The schematic includes two measurement directives for the maximum and minimum of the oscillation amplitudes around the stationary state. Figure 11d shows the expected Hopf bifurcation (transition to a periodic solution) as a function of the delay time [17]. Measurements are taken after the transient regime.

2.10. First-Order Integro-Differential Equation: When Integrals and Derivatives Meet

In this exercise, integrals and derivatives are combined in the same expression to form an integro-differential equation. This is a nonlinear problem which can be analytically solved as a sum of exponential functions. The equation to be solved is as follows:

2·exp(−3·t) = deriv(x) +3·x + 2·integ(x)

(8)

deriv() and integ() stand for the time derivative and integral, respectively. Figure 12a shows the corresponding circuit diagram using the ES, and Figure 12b shows the solution to the proposed equation as a function of the initial condition (red curves). The solution corresponding to the initial condition x(t = 0) = 0 is shown in blue.

2.11. Second-Order Differential Equation: Harmonic Oscillator

Second-order differential equations can also be solved using MES. This kind of problem requires two initial conditions, one for the function and one for the derivative. If the second derivative operator ddt(ddt()) is used, then we just need to define the initial condition of f. The initial condition for the derivative is assumed to be null. This is the case illustrated in Figure 13a. The equation to be solved corresponds to the classical pendulum formula:

d²x/dt² = −sin(x)

(9)

where x is the angle with respect to the vertical. Notice that the equation is solved without invoking the linear approximation for the angular amplitude of the oscillation. The oscillation period T is measured for different initial angles. In addition, the numerical results are compared with approximations of increasing order (see the series combination of voltages sources). The results are illustrated in Figure 13b.

Instead, Figure 14a shows the case in which initial conditions are provided both for the function and the derivative. The example corresponds to a linear oscillator with a drag force proportional to the velocity:

m·d²x/dt² = −k·x − g·dx/dt

(10)

Notice that the second-order differential equation is decomposed now into two first-order differential equations. Figure 14b illustrates the cases corresponding to the free, underdamped, and overdamped responses. This problem is also associated with linear circuit theory (RLC circuits).

2.12. Differential Equation with Control Parameter: Frequency-Dependent Memristor Model

The memory state of a memristor (the so-called fourth element of circuit theory [18]) can be described by a balance-type differential equation of the following form [19]:

dx/dt = (1 − x)/T_S − x/T_R

(11)

where T_S = exp[−η_S·(S − V_S)] and T_R = exp[η_R·(S + V_R)] are called the set and reset characteristic times, respectively. η_S and η_R are called the transition rates, and V_S and V_R are called the set and reset voltages, respectively (see Figure 15a). Here, the memory state is driven by a triangular signal S (voltage) with a variable period P (see Figure 15c). A conditional expression in the memory equation expressed by the ES is introduced so as to avoid interference between positive and negative voltages.

Figure 15b illustrates the hysteretic behavior of the memristor memory state as a function of the applied stimulus (control parameter). Figure 15c,d show that when the signal period increases (signal frequency decreases), the half-way memory state (S-value@x = 1/2) shifts towards lower values both for the set and reset processes. This means that if we kept the maximum voltage constant and we increase the frequency, then, the memristor behavior coincides with that of a resistor (collapse of the memory window).

2.13. System of Nonlinear Differential Equations: Lotka–Volterra Model

The Lotka–Volterra equations are a system of first-order nonlinear differential equations that describe the dynamics of a biological system in which two species interact [20]. This is also called the predator–prey model. The population dynamics are described by a system of differential equations:

dx/dt = a·x − b·x·y

(12)

dy/dt = −c·y + d·x·y

(13)

where x represents the prey and y the predator. The derivatives describe the instantaneous growth rates of both populations. a, b, c, and d are positive constants (see Figure 16a). The solution corresponding to the initial condition x(0) = 10 is shown in Figure 16b. Figure 16c illustrates the orbits in the phase space.

2.14. Recurrence Relation: Logistic Map

The logistic map is a recurrence relation often used as a reference to illustrate how complex chaotic behavior can arise from a simple nonlinear equation [21]. The logistic map is expressed as follows:

x_n+1 = r·x_n·(1 − x_n)

(14)

where x_n is a number between zero and one and r a positive number in the range [0,4]. As r changes, the amplitude and frequency content of the logistic map exhibits different behaviors. The iteration is carried out with the help of the delay function (see Figure 17a). Figure 17b shows the variety of behaviors than can be observed for different values of r. Figure 17c shows the onset of the first bifurcation. Unfortunately, the evolution of the chaotic behavior cannot be fully visualized using the proposed scheme. Nevertheless, some specific curves can indeed be obtained such as the 2D Poincaré plot for r = 4 (see Figure 17d). In this case, use tran 0 25 5 10E3 for a better resolution.

2.15. System of Nonlinear Differential Equations: SIR Model with Vital Dynamics

Mathematical models of epidemics are often expressed as a system of nonlinear differential equations. The SIR model represents the evolution of different population groups: S, susceptible; I, infected or infectious; and R, recovered [22]. Recovered people are considered immune so that they can no longer be infected again. The SIR model with vital dynamics includes birth (c in (15)) and natural death (c in (17)) processes. The equations (normalized) governing the whole process are as follows:

dS/dt = −a·S·I + c·(1 − S)

(15)

dI/dt = a·S·I + (b + c)·I

(16)

dR/dt = b·I − c·R

(17)

The model circuital diagram is shown in Figure 18a. Typical curves obtained with Equations (12)–(14) are illustrated in Figure 18b. The curves shown in Figure 18c were obtained by sweeping the vital dynamics parameter c. Figure 18d shows the infectious–susceptible plot and how its maximum shifts towards lower values as the maximum of S increases. This information is obtained through the measurement directives in the bottom line of the model diagram.

2.16. System of Nonlinear Differential Equations: Lorenz Model

Another example of a coupled set of nonlinear time-dependent differential equations is that of the Lorenz system [23]. The Lorenz equations arise in a number of areas such atmospheric convection problems, lasers, dynamos, chemical reactions, electric circuits, etc. In particular, the Lorenz attractor is a set of chaotic solutions that when plotted in the phase space exhibits a typical “butterfly” plot. Figure 19a shows the model diagram for the three differential equations that constitute the Lorenz model. The trajectories obtained for a particular combination of parameters (those often used in the literature) are shown in Figure 19b.

2.17. Discrete Fractal Curve: 2D Random Walk

A random walk is a stochastic process that describes a path in the space consistent in a succession of random steps [24,25]. In this case, a 2D random walk with steps ±1 was generated. Recurrence is carried out using the delay function again and uncorrelated randomness is introduced in the x and y directions through an if statement (see Figure 20a). Discretization of the variables is performed using the floor function. The model schematic calculates the escape time for a given distance (radius) as well as the location of the escape point. The escape velocity is defined as the escape radius divided by the escape time. All this information is obtained from the post-processing directives at the bottom of the model schematic and can be found in the “SPICE error log” window under the view tab (see Figure 20b). Figure 20c illustrates five different trajectories with origin at (0,0). Figure 20d shows a detail of one of the trajectories.

2.18. Parabolic Partial Differential Equation: 1D Heat Equation

In this example, the 1D heat equation is analyzed [26]. To solve this problem, we are going to use for the first time a 1D chain of ESs. This equation is strongly connected to other several problems including probability theory (Brownian motion) and financial mathematics (Black–Scholes equation). For instance, this problem can be associated with a rod heated at one extreme with the other extreme subjected to a fixed temperature. The equation can be modified so as to incorporate internal heat generation. The corresponding equation is given below:

dT/dt = α·d²T/dx²

(18)

where α is a constant. In this exercise, we have assumed a temperature pulse with logistic rise and fall times for the boundary condition and null temperatures for the initial conditions (see Figure 21a). Each ES corresponds to a different location along the rod being heated at one extreme (N0). The second derivative was discretized using the central difference scheme. As shown in Figure 20b, the temperature increases and decreases at each node with a certain delay related to its position along the rod.

2.19. Hyperbolic Partial Differential Equation: 1D Wave Equation

The wave equation describes the evolution of waves (sound, water, seismic, electromagnetics) as a function of space and time. The equation requires initial and/or boundary conditions depending on the problem we want to solve. The equation reads as follows:

d²A/d²t = α·d²A/dx²

(19)

where A can represent the displacement of a string and α is a parameter related to the velocity of the wave. In our case, a sinusoidal pulse is applied to one extreme of the string (N0) while the opposite extreme is kept fixed (N6) (see Figure 22a). The solution at each node as a function of time is shown in Figure 22b. Notice that we have deliberately used a discretization step h = 1 (included in the constant α). Appropriate boundary conditions at N6 can represent the vibration of a free string. The displacement amplitude as a function of the position at various times (like a photograph of the string) can be found using post-processing directives.

2.20. Stochastic Differential Equation: Ornstein–Uhlenbeck Process

A stochastic differential equation (SDE) is a differential equation which includes a noise term [27]. The result is a stochastic process. SDEs find application in a plethora of fields including physics, probability, mathematical finance, evolutionary biology, etc. In physics, the Ornstein–Uhlenbeck (OU) process describes the velocity of a Brownian particle under the influence of friction. The process is also called mean-reverting since the trajectories tend to fluctuate around the mean value μ with reversion velocity ρ. The OU SDE is sometimes written as the Langevin equation:

dx/dt = ρ·(μ − x) + σ·η(t)

(20)

where σ is the magnitude of the fluctuations (volatility) and η(t) is white noise (time derivative of a Wiener process). In the framework of SPICE, we identify (17) with a pseudo-OU (pOU) process since the differential time dt is not accessible. Caution should be exercised in considering dt as a fixed increment. We assume that η(t) is a normally distributed random number with zero mean and unit variance. Figure 23a presents the corresponding ES: q is the random number generator seed, z is the sampling number per unit time (maximum timestep << 1/z), and x0 is the process initial value. Three sets of measurements are considered. They are used for calculating and checking the average value and variance of the individual processes. In all the cases, an auxiliary generator is used to calculate the square of the average value. In the case of a uniform distribution in the range [0,1], these values are 0.5 and 1/12. In the case of a normal distribution, these values are 0 and 1 (see Figure 22b). The normally distributed random numbers are calculated using the Box–Muller algorithm [28]. Again, care has to be taken with the generated data since they do not strictly follow a normal distribution (we use marked data points to see the correlations). The last directives calculate the statistical features of the pOU process including a ± 3 standard deviation confidence band (measured from 0.5 s to 1 s after the transient). The simulation results are shown in Figure 23c. Notice how the different trajectories fluctuate around the average value. This is the mean-reverting effect. A more detailed discussion about the solution of SDEs using MES will be reported elsewhere.

2.21. Control System: When Physics Meets Mathematics Meets Electronics

In this last example, we solve a physical problem using the method of elementary solvers and we combine it with electronics. This example is just for illustrative purposes and shows the potentiality of the proposed method when different aspects of a complex problem are combined.

Let us consider a 2D furnace with a liquid inside with its top edge open to the air (room temperature, rt) and the rest of the edges at a given temperature (maximum temperature, maxt or rt). The region of interest (blue region) is discretized as illustrated in Figure 24. We are not going to pay attention to details such as the discretization step or the properties of the liquid. The problem requires solving the heat equation with changing boundary conditions. The graphic approach is still valid although it is a bit cumbersome because the finite difference method in 2D needs to be used. Instead, the text-mode method is preferred here and of course is the best option when working with higher dimensions or larger problems. The idea here is that the temperature at the center of the furnace is measured using a constant current biased diode. The initial condition is room temperature rt everywhere inside the furnace. Then, the walls of the furnace are heated up to a temperature maxt. When the threshold temperature thrt is reached at the center of the structure (yellow spot), then the wall’s temperature is set back to rt. When T drops below thrt, the heating source is switched on again. Of course, this is in the end a very simple control problem. The process dynamics is illustrated in Figure 25, where the liquid temperature, the wall’s temperature, and the reference temperature are shown. The oscillations are a consequence of the thermal inertia of the system.

For completeness, Figure 26 shows the transductor circuit. The scheme illustrates the circuit and the fitting result for the voltage-temperature dependence of the particular diode considered (1N4148). LTSpice does not allow a dynamic change in the device temperature. Notice that the relationship is linear except at the highest temperatures. The temperature of the diode is finally found using an ES. The complete script is reported in Figure 27. The script can be further simplified using subcircuits, but it is presented this way for clarity. The script can be opened as .txt file in LTSpice and executed. No circuit schematic is required.

3. Conclusions

This paper reports a method for numerically solving an equation or a system of equations using a circuit simulator. In particular, LTSpice was considered in this work for its great versatility. The use of a basic circuit cell formed by two current sources connected in series, called an elementary solver, is demonstrated through the presentation of several examples. The simple and graphical way of programming are among the main advantages of the proposed method. The method of elementary solvers extends the range of applicability of circuit simulators to other areas of research and education.