Abstract
The study of lateral steering control for Automated Driving Systems identifies new control solutions more often than new control problems. This is likely due to the maturity of the field. To prevent repeating efforts toward solving already-solved problems, what is needed is a cohesive way of evaluating all developed controllers under a wide variety of environmental conditions. This work serves as a step in this direction. Four controllers are tested on five maneuvers representing highways and collision avoidance trajectories. Each controller and maneuver combination is repeated on five sets of environmental conditions or Operational Design Domains (ODDs). The design of these ODDs ensures the translation of these experimental results to real-world applications. The commercial software, CarSim 2020, is extended with Simulink models of the environment, sensor dynamics, and state estimation performances to perform highly repeatable and realistic evaluations of each controller. The results of this work demonstrate that most of the combinations of maneuvers and ODDs have existing cheap controllers that achieve satisfactorily safe performance. Therefore, this field’s research efforts should be directed toward finding new control problems in lateral path tracking rather than proposing new controllers for ODDs that are already solved.
1. Introduction
The vision of cars that can drive themselves (now called Automated Driving Systems) has been a dream of science fiction since the 1950s [1]. They are thought to be capable of greatly improving road safety and efficiency [2]. A key enabling technology is the control of the steering wheel to safely perform driving tasks. We term this technology lateral motion control. When lateral motion control is constrained to only modify the direction of the front wheels of the vehicle, we call this front steering control. A benefit to constraining lateral motion control to this type of actuation is that this actuation is quite prevalent across passenger vehicles. Therefore, the research on this technology is readily applicable to many passenger vehicles.
The design of a front steering controller that tracks some path or trajectory has been a heavily researched topic since the 1950s [1]. Before the late 1990s, most controllers focused on speeds lower than typical highway driving [3]. One notable exception is [4], which developed a steering controller for a 1965 Plymouth Sedan. Various controllers were tested in wet and dry road conditions between 50 and 80 mph. However, their success was mostly limited to low-curvature roads. Also around that time, the US Department of Transportation’s Intelligent Transportation Systems program began researching Automated Highway Systems. However, such efforts were not limited to just the United States. An overview of the advances during this time is found in [2].
Due to the maturity of this research area, it is not surprising that consumers have access to automated steering systems. In 2021, 50% of new vehicle models offer sustained Lane Keeping Assistance, which commonly uses some form of lateral steering control [5]. Insight into the control techniques used by these systems is not publicly available, except for Comma.ai’s open-source Openpilot [6]. This system uses a Deep Neural Network to extract a future waypoint directly from a forward-facing camera. This waypoint is used in separate Longitudinal and Lateral Model Predictive Control-based local planners to generate a reference path. A steering controller then tracks the reference path using a PID feedback control law with a feed-forward controller.
With knowledge of only one commercially deployed controller, very little can be said about these Lane Keeping Assistance systems. In particular, it is difficult to investigate their safety. However, their existence proves that many companies feel they can achieve safe automated steering at highway speeds. The natural question to ask is: what are their limitations? This question is close to the heart of this work: determining under which conditions lateral front steering controllers fail to meet pre-specified performance requirements.
To understand the limitations of the commercially available steering controllers (such as Lane Keep Assist), we can use the terms and definitions from [7,8] to discuss their limitations. We begin by pointing out that the systems analyzed in [5] are examples of Active Safety Systems and not Automated Driving Systems (ADS). The Lane Keep Assist investigated in [5] requires an attentive driver capable of interrupting the controller quickly after any issue occurs. This requirement significantly increases the level of acceptable risk in the design of a lateral steering controller. This suggests that the lateral steering controller can fail in some Operational Design Domains (ODDs). If true, this suggests that the problem of designing a sufficiently safe lateral controller for operation in some ODDs is still unsolved. However, it is not possible to say under which ODDs, if any, these controllers will fail. This conclusion is further qualified by the observation that there is not enough information to show that the front steering controller is the cause of the limited ODD. For instance, the perception system (i.e., a forward-looking camera), and not the steering controller, may be the cause of the limited ODD. Therefore, there must be efforts dedicated towards evaluating these Active Safety Systems in a wide variety of ODDs to understand their limitations and the cause of those limitations. After that, research and development efforts can be more efficiently allocated.
Active Safety Systems are not the only types of systems that would benefit from such an effort. When the steering controller is designed for an ADS, the system cannot be designed with the assumption that a human can take over. To simplify this problem, constraints are often imposed on the ODD. This typically takes the form of isolating geographic regions where the ADS is allowed to operate (geofencing). Robo-taxi companies Cruise and Waymo use this strategy. Both companies have deployed or are testing ADSs in cities such as Las Vegas, Nevada; Phoenix, Arizona; Houston, Texas; and San Francisco, California. The lack of cities that experience adverse weather throughout the year suggests that modern ADSs cannot yet be safely deployed in adverse weather or road conditions. While this is due, in part, to the degraded sensor performances in adverse weather conditions [9], another reason for this may be that controlling the vehicle in these conditions is more challenging.
Despite decades of research on lateral steering controllers, the question of how well they perform in various ODDs remains insufficiently answered. A major cost of not sufficiently answering this question is that only a subset of the US population will be able to experience the safety and economic benefits of ADS. The current deployment of robo-taxis focuses on the most profitable and easiest ODDs. These ODDs consist of densely populated areas with good weather throughout the year. Examples are found in the deployment locations of Cruise and Waymo in 2023. Populations that live outside these domains will not benefit from the technology until safe operation can be sustained for enough of the year to provide a profitable business. Therefore, it is of paramount importance to focus attention on studying the performance of steering controllers in a wide variety of ODDs, not just the ones that are most easily driven.
At a high level, this work seeks to answer the question of what the limitations of modern lateral steering controllers are. This question is motivated by the desire to have a single lateral steering control architecture that is capable of achieving useful and pre-specified performance requirements across a variety of ODDs. The framing of this question requires the answer to be dependent on the ODD, which will help the steering control research community to focus more directly on challenging ODDs.
Through a proper choice of steering controllers and ODDs, experimental analysis will indicate combinations of maneuvers and ODDs where steering controllers need to be improved and where they currently meet requirements. In particular, we partition requirements into three types: safety, comfort, and security. This study focuses only on safety requirements, which is considered as the steering controller’s ability to keep the vehicle within some pre-defined path error. This study does not treat requirements relating to the comfort of passengers (this will be the subject of further research). This study also does not treat the case in which adversaries are attempting to influence the performance of the controllers, which we call security requirements. This final set of requirements is rather new and emerging [10].
The steering control literature is vast, so a small sample of steering control algorithms is selected, as will be explained in Section 2.1. The controllers are chosen in an attempt to provide information on what will be the most successful future direction of research. To compare these controllers, several maneuvers and environmental conditions are developed in Section 2.5. Together, they constitute samples of existing ODDs that need to be solved to achieve SAE Level 5 driving [8]. To compare each controller on the same ODDs in a highly repeatable manner, CarSim 2020 is extended with various models as explained in Section 2.3. This simulation realistically captures the most significant phenomena in highway driving. It combines models of the environment and its associated disturbances with a high-fidelity vehicle model that captures tire–road interactions and powertrain dynamics. To compare each controller objectively, several metrics are proposed in Section 2.6. Finally, the results are presented and discussed in Section 3.
Research similar to this study can be found in [11,12], which uses a single lane change and a double lane change maneuver to evaluate a set of lateral motion controllers. They study the performance under nominal, model discrepancies, low friction, and sensor noise disturbances. However, both references use a low-fidelity simulator (not yet validated) to evaluate each controller. This choice greatly diminishes the reliability of their results. However, it comes with the benefit that they are able to run many simulations very quickly, enabling Monte Carlo studies, which is suitable for their comparison of controllers.
The results presented in this work build upon and greatly extend those of [11,12]. The extension is so great that several arguments can be proposed as a result of the observations detailed in Section 3. These arguments can be further supported by the work of [11,12]. When compared to these references, our work approaches controller comparison more systematically, rigorously, and practically. This is achieved mainly by introducing a set of ODDs. Model discrepancies are inherently captured because CarSim 2020 is used to simulate the vehicle dynamics while a dynamic bicycle car model is used to design the controllers. Sensor noises are included by appropriate simulation of sensors and fusion algorithms. Furthermore, a larger variety of maneuvers are used to evaluate each controller. Finally, the controllers studied in this work are wholly different from the ones studied in [11,12] (except for the Linear Quadratic Regulator).
The main contribution of this work is the systematic investigation of controllers in realistic ODDs. Through this investigation, various other contributions are made. A significant result of this work is to show that simple linear and nonlinear controllers can achieve sufficient performance in many ODDs without requiring special retuning for each ODD. A secondary contribution of this work is that it shows the extent to which collision avoidance maneuvers can be used to predict performance on highway trajectories. For instance, the performance of a steering controller in a modified version of ISO 3888’s [13] double lane change (commonly known as the Moose Test) will be compared to the performance of that same controller on an existing highway. Altogether, these contributions are preliminary work toward a standardized method of comparing steering controllers. It also serves to provide evidence for promising research directions focused on developing a robust steering controller that meets performance requirements in all ODDs.
2. Materials and Methods
2.1. Controller Selection
The previous section briefly discussed the history and size of the literature on steering controllers. It is common in survey papers to group controllers based on the model that they use and the type of control methodology, such as kinematic, dynamic, nonlinear, linear, and online-optimal [11,12,14,15,16]. Controllers that are developed based on the geometry of the control task rather than the dynamics of the vehicle are insufficient for high-speed operation, where inertial effects are significant [11,14,15].
A similar conclusion is drawn for kinematic controllers, but not without controversy [17,18]. Controllers that use kinematic models have found success when used in Model Predictive Control (MPC) techniques, often with additional algebraic terms to compensate for tire dynamics or inertial effects [17,18,19,20]. The drawback of using MPC, or any online optimization-based method, is the high computation cost. Most applications mitigate this with simplified models, hence the kinematic model’s popularity. However, even when using simplified models, their computational effort is often greater than controllers implemented using filters. This computational cost may not be necessary to achieve robust performance on highways. To show this, we constrain the controllers considered in this investigation to “cheap” controllers. “Cheap” refers to controllers that do not use large amounts of computational resources (both processor time and memory).
To further explain this definition, we may consider online (implicit) Model Predictive Control such as in [18]. This controller requires the computer onboard the vehicle to solve a quadratic program every time step. The number of iterations is not fixed, so there is no guarantee that the optimal solution will be reached within the duration of the time step. In this way, there is often a need for a fast CPU that can reliably reach the optimal solution before the next time step (with more time for secondary computation tasks like communication). However, it is possible to stop the solver after a set number of iterations and use the resulting sub-optimal solution. Doing so can sacrifice constraint violations and performance. In practice, this is not always the case [18]. There also exists explicit MPC implementations that shift the high computation time to high memory consumption (which is sometimes preferable) [21]. In [22], an explicit MPC controller is developed using the same model formulation described later in Section 2.1.3. Both forms of MPC are considered expensive controllers since they require either high computation time or memory usage. Further discussion on this is presented in Section 2.2.
By contrast, the Linear Quadratic Regulator (LQR), presented in Section 2.1.3, computes the steering angle by multiplying a 1-by-4 vector with a 4-by-1 vector. The small number of calculations therefore classifies this controller as cheap. Further discussion of each controller’s requirements on computational resources is discussed in Section 2.2. This aspect of cheap control poses a central hypothesis of this investigation: satisfactory control performance is achievable without online optimal techniques for some practical ODDs.
To achieve highway driving, the steering controller must ensure stability and safe performance at high speeds. Therefore, when selecting controllers from the literature to compare against, control implementations that have been demonstrated at high velocities are preferred over controllers that have been tested at low velocities. Some controllers that have been tested in both high and low velocities will also be considered.
It is well known that the vehicle’s dynamics vary significantly with longitudinal velocity [3,4,23]. How to properly handle this has been the source of research since the 1970s. In the 1980s, several control solutions were based on controllers scheduled on the vehicle’s longitudinal velocity [24,25]. The main argument is that gain scheduling the controller on velocity is required to meet tight performance requirements across the velocity range of the vehicle. Conversely, in the 1990s, arguments were made that a single LTI controller, properly designed using robust control techniques, is capable of achieving sufficient performance [26,27,28]. The argument made in these works is that a single LTI controller is simpler than a gain-scheduled one, and yet performance requirements can still be met. However, what happens when more is asked of the lateral motion controller? The arguments in favor of a single, robust controller is centralized around lane keeping control. If the driving task is made more complex, then the controller’s requirements become more challenging to meet. This has been the motivation to combine robust control techniques with LPV techniques. The combination of these approaches is well developed in [29,30,31,32,33,34,35]. The application of one of these control techniques to path following control is well executed in [36]. Further comparison of LPV controllers is carried out in [37]. A recent overview of LPV and adaptive techniques more generally can be found in [38]. The argument presented by these works is that with increased performance requirements, LPV control is necessary. Moving to robust LPV methods increases the mathematical complexity of the control synthesis over LTI robust methods. It also increases the online computation time and memory consumption over that of LTI controllers because the LPV dynamic output feedback controller must be stored, and the gains must be computed at each time-step. However, it might be possible to reduce this increase in computation time by turning to Event-triggered control (also called aperiodic control) [39]. Such a technique increases the mathematical complexity of the control synthesis, but with added benefit of reducing online compute resources. Ref. [40] shows this benefit with a comparison of various control techniques.
This discussion therefore proposes additional preferences on the controllers selected for investigation. In addition to considering controllers validated on real-world systems, preference will be given to techniques that have low mathematical complexity, low calibration effort, small online compute requirements, and good safety performance. To investigate if an LTI controller is capable of achieving similar performance as LPV controllers, an LTI controller will also be considered in this comparison.
Most nonlinear controllers are designed to operate at various speeds even if their tuning parameters need to be scheduled with velocity [15,23,41]. Some linear controllers, such as PID and LQR, are easily extended to parameter-varying control at the cost of additional compute resources and complexity.
The following three controllers are selected from the controllers surveyed in [11,14,15,16]. Each is chosen because (1) they do not require online optimization, (2) they have been demonstrated on full-scale vehicles at high speeds, and (3) they are either already scheduled with velocity or are easily extended to schedule with velocity.
- Nonlinear Feedback and Feed-forward control (FDBK + FFW) [23];
- Target and Control Driver Model (TandC) [41];
- Discrete-Time Infinite-Horizon Linear Quadratic Regulator (LQR). (Formally, this acronym should be DTLQR or dLQR, but since there is no other LQR formulation to differentiate from, LQR is used instead) [42].
A fourth controller will also be included in this comparison, which is a parameter-varying extension of the Youla Parameterization technique with Interpolation Conditions [43]. Although not yet available in the literature, the design of this controller will be the subject of a future publication. This interpolation technique (without the LPV extension) has shown success in various automotive applications: [44,45,46].
2.1.1. Nonlinear Feedback and Feed-Forward Control
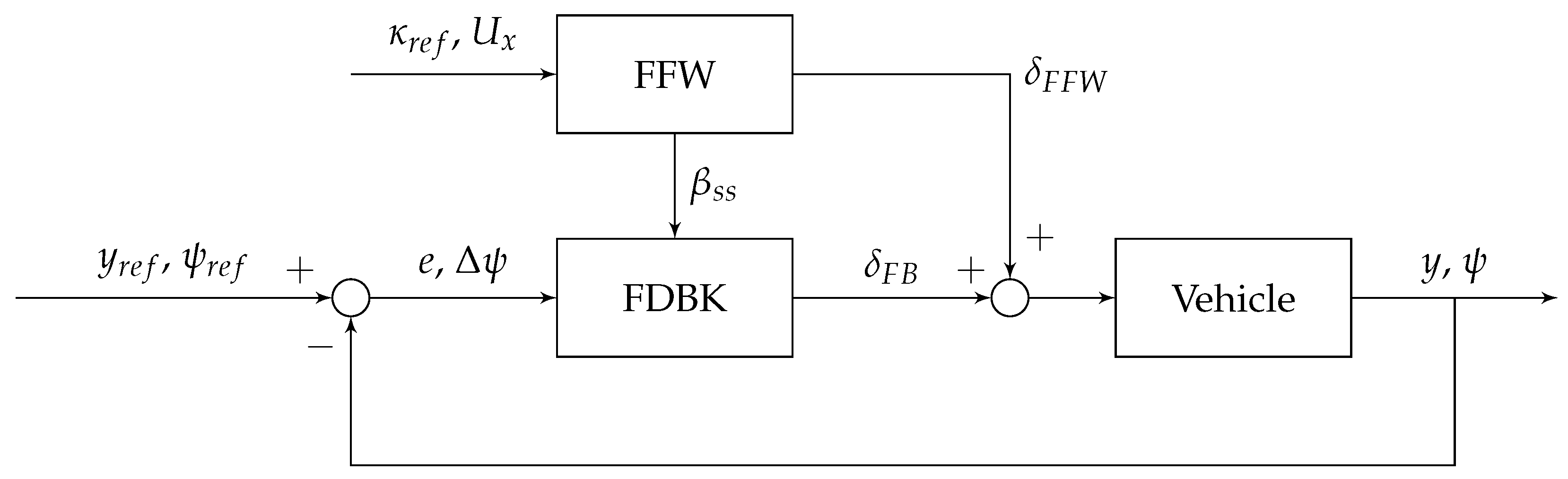
The first controller, shown in Figure 1, is an example of a nonlinear controller. It uses a nonlinear feed-forward controller with proportional feedback. This controller is experimentally validated on an Audi TTS in racing conditions [23]. Several other papers extend this methodology to drifting maneuvers and a wide variety of road surfaces [47,48,49]. The feed-forward utilizes a Fiala tire model to predict the required steering angle, , and steady-state body-slip angle, , from the reference curvature, . Note that this computation occurs in the feedforward controller and is not the result of a separate estimator. The feedback law for the system shown in Figure 1 is given by Equation (1), where is the feedback gain, e is the lateral error at c.g., is the look-ahead distance, and is the yaw error at the center of gravity.
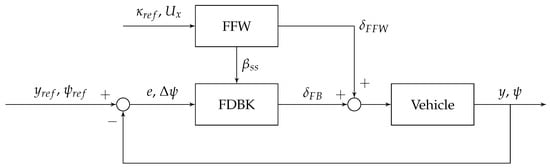
Figure 1.
FDBK + FFW control diagram.
There are two tuning parameters: the look-ahead distance and the controller gain. The closed-loop pole locations are given by the eigenvalues of Equation (2).
The original form of this controller (using constant gains) was found to be insufficient across the wide range of velocities at which the vehicle can operate. Therefore, the gains are scheduled with longitudinal velocity to achieve improved performance across all velocities. It was observed that the dominant poles of the closed-loop system move with respect to both control parameters. With this knowledge, an optimization routine, Algorithm 1, is created that achieves desirable natural frequencies, , and damping ratios, , of the most dominant poles.
| Algorithm 1 FDBK + FFW Gain Optimization Routine |
| for each do |
| while do |
| while do |
| Compute |
| Compute |
| end while |
| end while |
| end for |
Algorithm 1 describes a search over a grid of values of and that move the closed-loop dominant poles close to the desired pole locations. The density of the grid is determined by the magnitudes of and . The fact that the dominant pole’s is sensitive to and the pole’s is sensitive to is exploited in the nested while loops. The resulting dominant poles of the closed loop system will therefore not have exactly the same values as the desirable pole locations. The distance between the poles and their desired locations can be decreased by making the grid more dense, but at the cost of increasing computation.
It was found that if the desired closed-loop poles were held constant throughout the velocity range, the resulting gains were large, resulting in large actuator effort. To keep the gains low, the routine’s hyperparameters, and , are scheduled with longitudinal velocity, . The result is that the closed loop system’s dominant pole locations are also scheduled with longitudinal velocity.
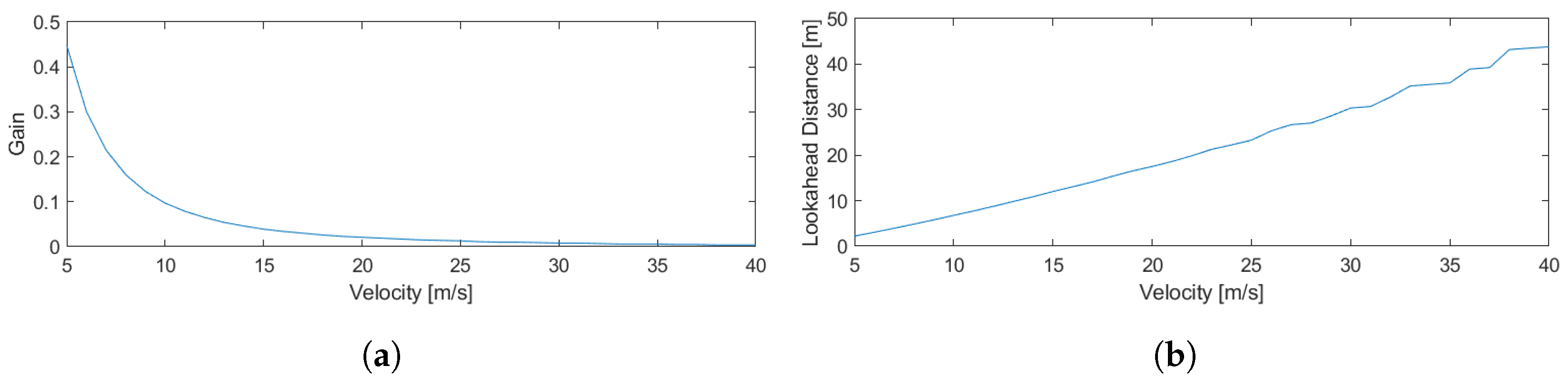
To tune the hyperparameters, simulations are run on the single and double lane change trajectories under nominal and realistic conditions. These conditions are explained in Section 2.5. The resulting gains are shown in Figure 2.
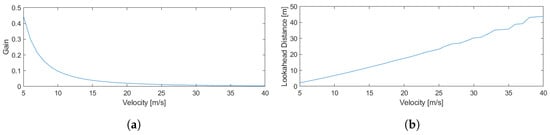
Figure 2.
FDBK + FFW gains with respect to velocity. (a) FDBK + FFW . (b) FDBK + FFW .
2.1.2. Target and Control Driver Model
The second controller is an example of driver model-based controllers [50]. This particular controller is one of the most mature and experimentally validated controllers in the literature. It has been tested extensively on an articulated bus, and extended with various fault tolerant systems [41,51]. It also has been experimentally validated on a sedan at moderate speeds [52]. However, in [52], the original formulation is modified by replacing the feedback integral controller with a Youla–Kucera parameterized controller. This enabled the controller to be adapted online to the type of maneuver the vehicle was performing (either lane change or lane keeping). Such extensions show promise in improving the base performance of this controller. If this controller shows good results, there would be good motivation to focus research on controllers of this form.
The original controller can be implemented in several ways. The version implemented in this study is given in Equation (3) [50].
where the variables are defined in Table 1.

Table 1.
T&C control law variables.
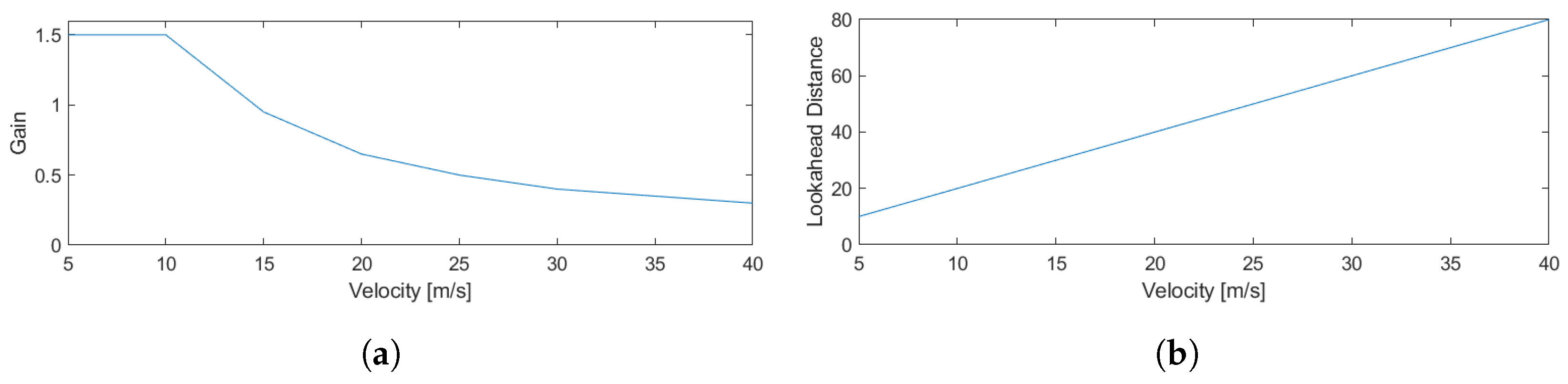
The T&C controller has only two gains to tune: the look-ahead gain, , and the controller gain, , which must be scheduled with longitudinal velocity to ensure stability across the vehicle’s velocity range. Similar to the FDBK + FFW controller, these gains are tuned offline using a simple grid search optimization technique. However, the resulting closed-loop pole locations exhibit more coupled dependence on and than the FDBK + FFW controller. To overcome this, Algorithm 2 computes the closed-loop poles and the corresponding disk margin [53] (a robust version of classical gain and phase margins that considers combinations of both gain and phase margins) over a grid of gains [53]. Then, using a cost function, the optimal gains are selected. This approach is covered in Algorithm 2. The resulting gains are shown in Figure 3.
| Algorithm 2 T&C Gain Optimization Routine |
| for each do |
| Compute for all and |
| Remove all and where |
| compute disk margin (skew parameter set to 0) |
| end for |
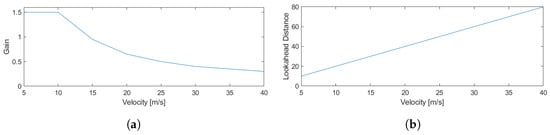
Figure 3.
T&C gains with respect to velocity. (a) T&C . (b) T&C .
The hyperparameters, , , are weights on the controller gain, look-ahead gain, and disk margin, respectively. These hyperparameters are tuned in the same way as the Algorithm 1’s hyperparameters.
The trajectory of the optimal controller gain with respect to velocity closely resembles the one computed in [54], indicating that this routine is similar to the one developed by the authors of the T&C driver model.
2.1.3. Linear Quadratic Regulator
The third controller is the well-known Linear Quadratic Regulator (LQR), which is used to represent LTI controllers. The controller is developed using the error state model from [42], which is reproduced for completeness in Equation (5).
where the variables are defined the same as in previous sections. In particular, is the lateral position error [m] and is the yaw orientation error [rad]. This model defines the control input to the bicycle car as the front steer angle and the exogenous input as the desired yaw rate. In [42], the desired yaw rate is considered a measurable disturbance that is rejected with a feed-forward controller. This is considered a disturbance because the states are formulated as error states and therefore should not be allowed to drive the states away from zero.
The LQR method produces a state feedback controller, which requires access to all of the states of the model. In all controllers, this work assumes access to and , but not necessarily and . However, this is relatively easily solved by using a digital filter that differentiates each measured state and low passes the output at a suitably high frequency to reduce noise. The ability to access and is explained further in Section 2.3.
The design of this LQR controller is well explained in [42] except that this study uses the discrete-time version since the controller is sampled during simulation. The LQR cost function provides five tuning parameters: a weighting on each state and the steering angle. One may begin with Bryson’s Rule [55]; however, simulation results on the single and double lane change maneuvers showed significant actuator effort. So the R value was increased iteratively until the actuator effort was brought to a more acceptable level, . Due to this large value, the system’s performance is not very sensitive to the weighting matrix on the states, Q. So to simplify the tuning effort, it is set as the identity matrix.
A final tuning option is the choice of constant velocity when computing the state feedback gains. Through further simulations, it was found that better performance is achieved when the set velocity is equal to or greater than the testing velocity. Therefore, the longitudinal velocity is set as 30 m/s. While this set velocity is higher than any velocity used in this study, it is chosen because it is the reasonable upper bound of the vehicle’s operating range and provides good performance at all velocities.
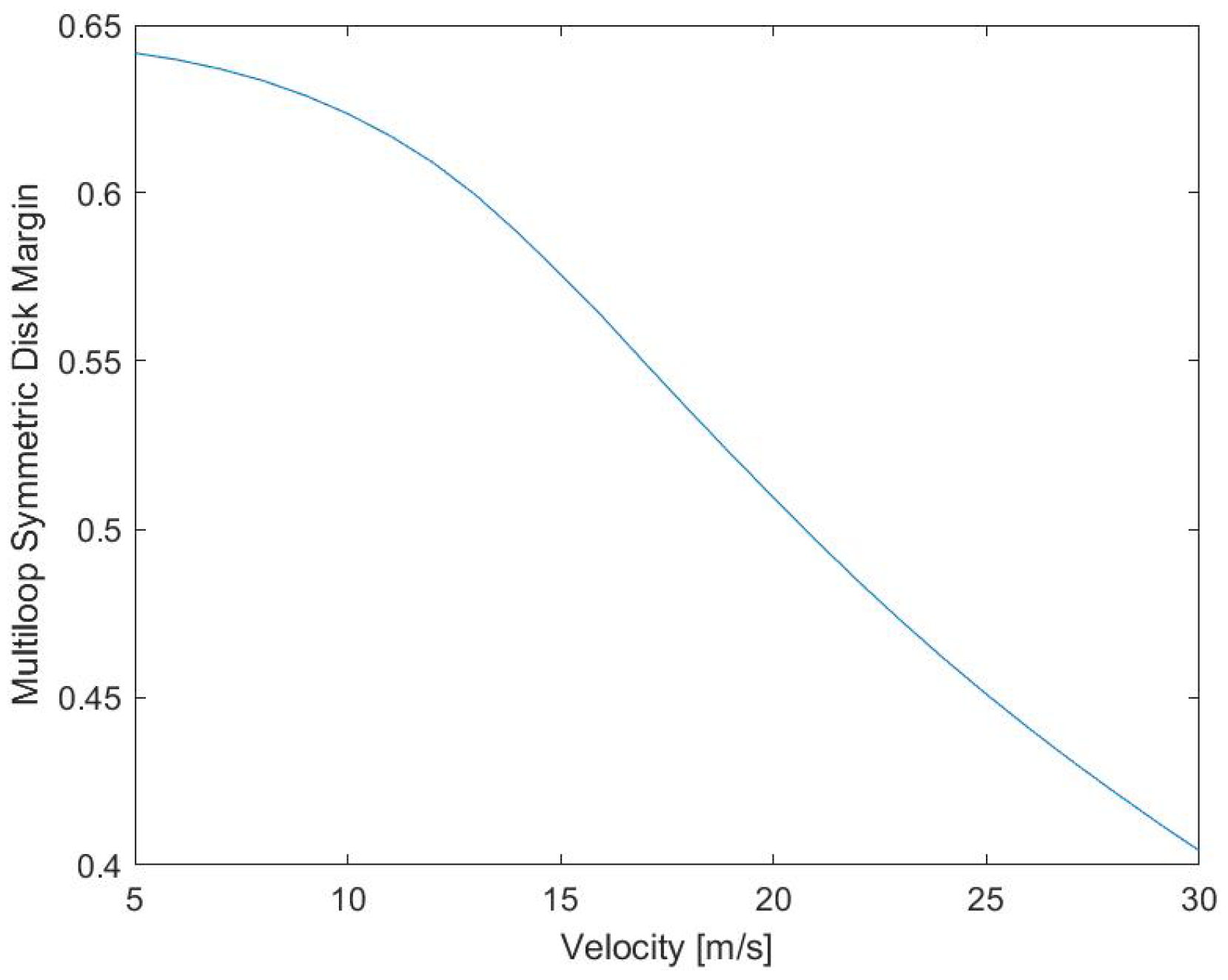
This choice of tuning is further motivated by an analysis of the disk margins when the system operates at velocities other than 30 m/s. To perform this analysis, the disk margin is computed (with the skew parameter set to 0) considering input and output disturbances [53]. The plant used in this analysis is frozen at a velocity ranging between 5 and 30 m/s. The resulting disk margin values, shown in Figure 4, represents the maximum radius of the symmetric disk in the complex plane that contains stable disturbances. The results show that robustness increases as the system’s velocity decreases. Therefore, the closed-loop system becomes more robustly stable at lower velocities, motivating the decision to tune the controller at the highest feasible velocity rather than some other lower velocity. However, the cost of improved robustness is decreased performance at lower velocities.
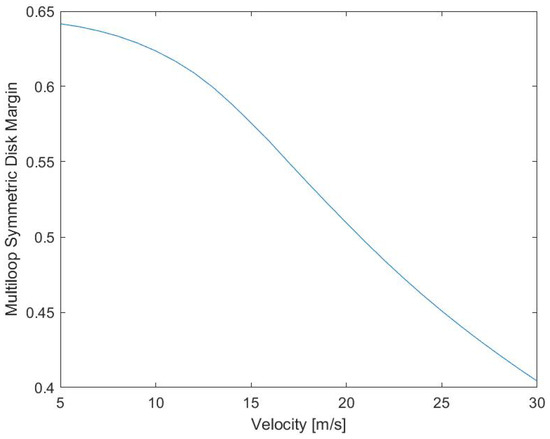
Figure 4.
Multiloop symmetric disk margin for LQR controller across velocity range.
2.1.4. Linear Parameter Varying Youla Controller
One significant control technique not represented by these three is the frequency-based approach. To address this, we use a control methodology that is a Linear Parameter-Varying (LPV) extension of the Youla Parameterization Interpolation methods from [43]. The development of this control methodology will be addressed in a later publication. This controller uses the error state model from [42], where the longitudinal velocity is the scheduling parameter, and a look-ahead distance is used to compute the model’s output. This look-ahead distance has been the subject of research for decades and is well known to be very beneficial in steering control at high speeds because it compensates for the system’s phase lag [1,3,4,56]. This technique is similar to the LPV Coprime factorization used in [52], except where [52] uses Coprime factorization, this technique uses Interpolation Conditions to ensure internal stability.
Interpolation Conditions require the Complementary Sensitivity Transfer Function, to equal a specific value when evaluated at a pole or zero. Similarly, these conditions can be presented as conditions on the Sensitivity Transfer Function, , with the relation . This method allows the control designer to derive conditions that permit a wide variety of transfer functions that guarantee internal stability. Refer to [43] for more discussion.
The Interpolation Conditions are as follows [43]:
and
where
where, p are the locations of unstable poles of the plant and is the multiplicity of the ith unstable pole. By treating as a frozen parameter, the plant (the transfer function from to y) is given by
where the coefficients, , are functions of . Two poles are always at the origin. For understeer vehicles, the other two poles are stable. The two zeros are also stable for the vehicle used in this study.
We can study the relationship between the number of poles and zeros required by the Interpolation Conditions for this plant by assuming
The condition is automatically satisfied. The condition (which comes from the pole at the origin having a multiplicity of 2) requires . To ensure the system is realizable, . Also, M and N must be integers. Therefore, there must be at least 1 pole and therefore at least 1 zero. Furthermore, the number of poles and zeros influence the location of the poles and zeros. Further constraints can be derived by requiring the Youla parameter to be proper.
However, this choice of is mostly useful for analysis purposes and does not allow much flexibility in tuning. To overcome this challenge, a new form of is proposed in Equation (10).
where Equation (11) guarantees internal stability.
This new form provides a zero to meet the condition . The two pairs of second-order poles provide both tuning parameters as well as ensure that the Youla Parameter, is proper. The additional pole provides flexibility in shaping the high-frequency responses of and .
Having selected a suitable the controller transfer function can then be computed. This is similar to the model-matching problem [57,58,59]. The difference is that in the model-matching problem the reference model transfer function is unconstrained, whereas in this technique the reference model transfer function is constrained by the Interpolation Conditions.
The closed-loop system is fully determined by , , , , and . The challenge is to set these parameters to achieve robust performance and limited actuator effort. To overcome this problem, the parameters are tuned to approximate an analogous H-infinity loop-shaping control problem. This analogous problem is solved for the LTI plant at velocity intervals of 5 m/s for 5–40 m/s. The process is explained in Algorithm 3. The nomenclature used is as follows: is the Youla Parameter transfer function from reference signal r to actuator input u, is the plant transfer function, and is the complementary sensitivity transfer function from r to output y. Each transfer function is also a function of . , in particular, is a function of because the weighting filters used in the loop-shaping problem were also parameterized by to allow the closed-loop bandwidth to increase with increasing velocity. This flexibility allows for an improved balance of the performance–robustness trade-off throughout the system’s velocity range.
| Algorithm 3 LPV Youla Tuning Routine |
| Require: dB |
| for each do |
| Compute |
| Compute as solution to H-infinity loop shaping problem |
| end for |
The last step in the algorithm is to approximate with by setting the poles of close to the dominant poles of . This achieves a low system order while balancing sensitivity requirements and actuator constraints. In effect, it is a low-order approximation of the H-infinity solution.
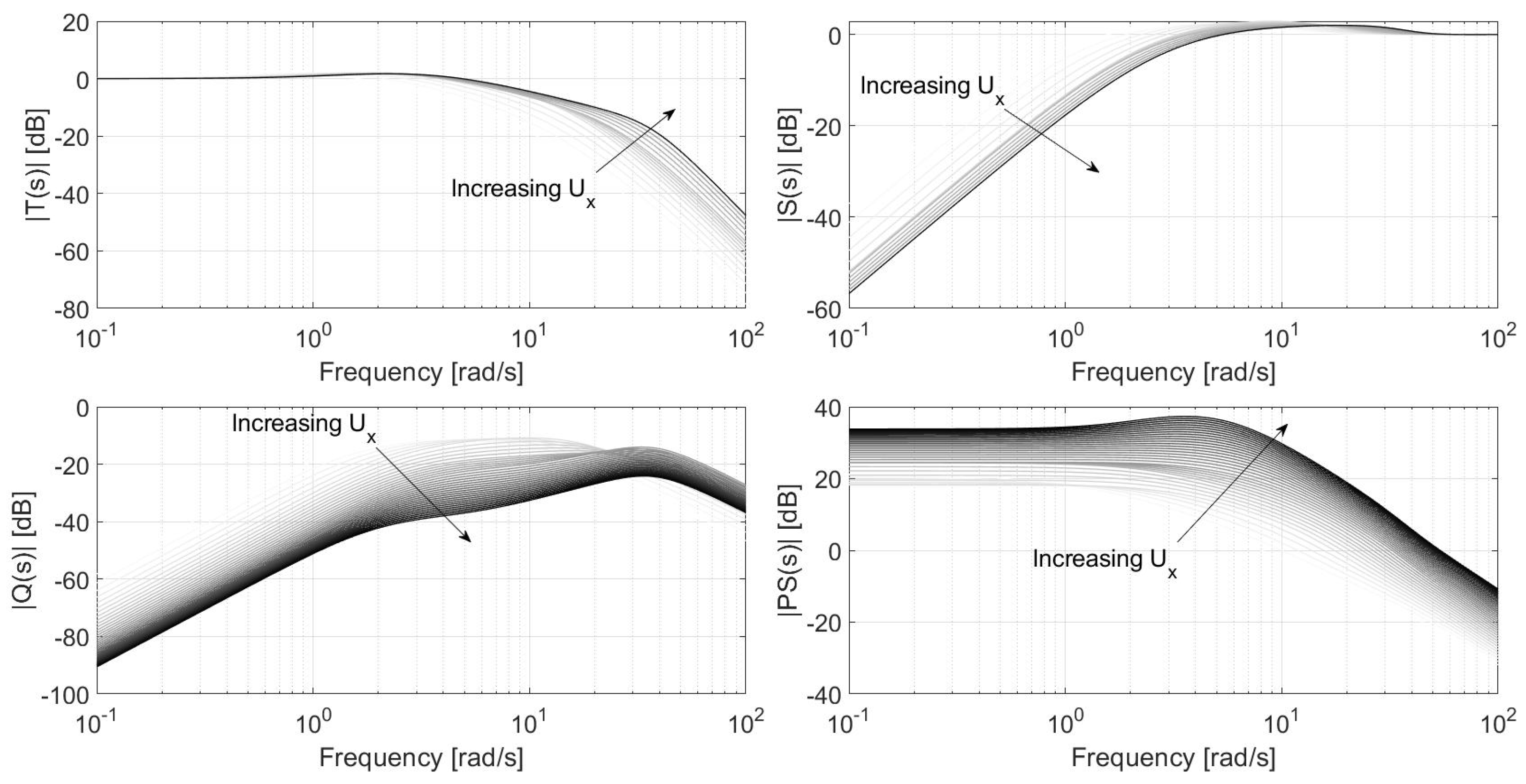
The result of this tuning routine is that at velocities above 20 m/s, the parameters varied very little. To simplify tuning, is held constant for velocities above 20 m/s. However, even though the reference model transfer function does not change when the velocity is above 20 m/s, the computed controller still varies because the plant varies. The resulting bode plots of the gang of four, , , , and , are shown in Figure 5. Here, is the sensitivity transfer function, and is the product of with . Figure 5 shows the frequency response of each transfer function as velocity increases in the range 5–40 m/s, represented as the transition from white to black colored lines.
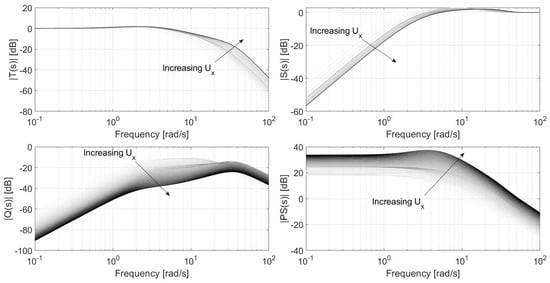
Figure 5.
LPV Youla gang of four.
Several observations are worth noting.
- The bandwidth of increases as velocity increases.
- remains less than 5 dB.
- remains close to −10 dB until higher velocities are reached (≈20 m/s). After that, as velocity increases, decreases. This is a direct result of setting constant for velocities above 20 m/s.
- has a rather large DC gain that increases with velocity.
- increases as velocity increases.
These observations suggest that this controller will be robust to parameter variations, require less actuator effort as velocity increases, but suffer from actuator disturbances such as bump steer and unmodeled steering actuator effects. The tuning of the design can be adjusted to mitigate these effects at the cost of reduced tracking performance. This is the fundamental trade-off between robustness and performance. Furthermore, it is worth noting that the look-ahead error response to curvature is captured by . Therefore, this closed-loop system should reject the reference path’s curvature when its frequency content is below 2–3 rad/s. However, when this frequency content is high, the system cannot reject this.
2.2. Computational Comparison
The cheapness of each controller relates to the amount of computer resources each controller requires when implemented on a physical system. Chiefly, this work is concerned with the CPU usage and the memory consumption. All controllers are simulated at a sampling rate of 50 Hz. This update frequency is easily achievable by most real-time systems, especially since each controller has small computational requirements.
The FDBK + FFW controller requires enough memory to store three 1D lookup tables. Two are for the front and rear inverse tire models. The size of these lookup tables can be very small (<25 elements) before closed-loop performance is effected. The third is for the scheduled parameter-varying gain in Equation (1). The size of this table depends on the number of gains the design requires. A total of 36 gains was found to provide sufficient performance. This controller requires very little computational power, since it multiplies and adds a series of double precision values and performs lookup table operations.
The T&C controller requires enough memory to store two 1D lookup tables and the state of the 1D integrator. One table for the look-ahead distance , and one table for the integral feedback gain in Equation (3). Each of these tables use only 8 elements. The computational load is also quite low. All that is needed is to compute Equation (3) as well as to perform the numerical integration.
The LQR controller is the cheapest controller considered since it needs to only store the feedforward gain and the feedback gain. The computational load is also very small, since it needs only to compute the feedforward command by multiplication of two scalars and the feedback command by multiplication of two vectors.
The LPV Youla controller requires slightly more memory than the other controllers, since it is an LPV dynamic output feedback controller. This means that there must be enough memory to store the numerator and denominator of each digital filter (there are 8 filters in this design) and the digital filter states. However, this memory requirement is still small because the resulting controller is of order 5. In total, there are 2 2D lookup tables. One is for the digital filter numerator coefficients, and one is for the denominator coefficients. The computational cost is very small since all that is required is to perform digital filtering and the lookup operation. There are also a wide variety of other methods that can be employed to implement this controller such as using the discrete state space model instead of the digital filter. This would require more and larger lookup tables, but they should not be prohibitively large. Finally, the unique formulation of this controller permits the derivation of a function of each digital filter coefficient as a function of the vehicle velocity , allowing for lookup tables to be avoided altogether.
Altogether, these four controllers are cheap when compared to more expensive controllers such as MPC. By comparison, the explicit MPC (a computationally efficient version of MPC) developed in [22] required nearly 0.52 s in Simulink to compute a suitable actuator command. By contrast, it takes Matlab 2021b less than 0.01 s to perform 1000 evaluations of a lookup table with 100 elements in it (Windows PC with Ryzen 5 CPU). It takes Matlab less than 0.01 s to perform 1000 matrix multiplications between two vectors with 100 elements. These simple computation experiments greatly overestimate the amount of time required to compute new control actions for the selected controllers. Furthermore, [60] developed an explicit MPC using a four-state system, resulting in almost 5000 polyhedral regions. Each region needs to be stored in memory. The selected controllers need only store small (<100 elements) lookup tables in memory. While it is true that there are techniques to greatly reduce the memory and computation of explicit MPC [61], they still do not approach the computation efficiency of the controllers studied here.
2.3. Simulation
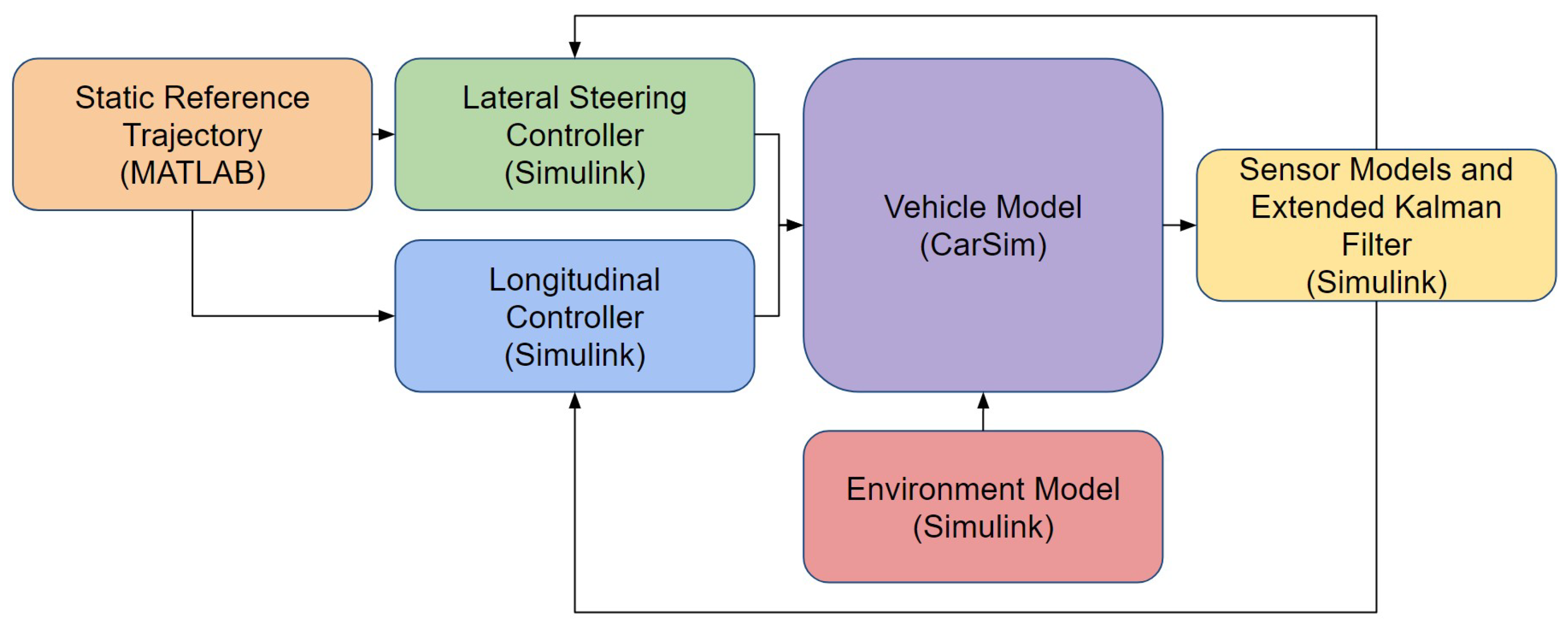
The simulator used to evaluate each controller is summarized in Figure 6.
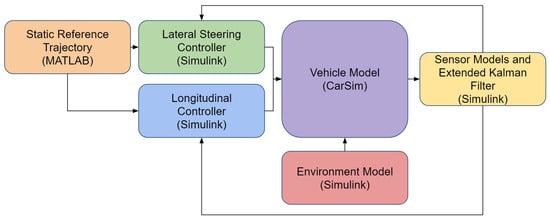
Figure 6.
High-level overview of simulator architecture.
The selection of the vehicle to model has a significant impact on the results of this study. Many of the chosen controllers have already been demonstrated on high-performance sedan-like vehicles [23,47,52,62]. Furthermore, according to data collected on vehicle model sales in the US in 2023 [63], 15 of the top 20 best-selling vehicle models are either pickup trucks and SUVs (including smaller hatchbacks). Only 5 of the top 20 best-selling vehicle models are sedans. When totalling the number of sales for the top 20 sold models [63], sedans account for approximately less than 20%. Furthermore, the current vehicle models operated by robotaxi companies (Waymo, Cruise, and Motional) are SUV vehicles (Jaguar I-Pace, Chevy Bolt, and Ioniq 5, respectively). Therefore, by simulating an SUV, this study (1) differentiates itself from what has been done before, (2) uses the most popular vehicle type sold in the US, and (3) is very practical and useful for the ADS industry.
Finally, before moving on, it is worth noting that by selecting an SUV model, the control task is made more challenging. The performance requirements are tighter since the vehicle is larger. Furthermore, it is generally true that SUVs are less maneuverable than smaller sedans. Therefore, it is predicted that the controllers under study would perform even greater than what is shown subsequently. However, this prediction is made with little empirical study and should be considered appropriately.
The vehicle model in Figure 6 models an SUV that comes with the commercial software CarSim 2020. This vehicle is a full sized SUV equipped with Electronic Stability Control and Antilock Braking System. The front suspension is independent and the rear suspension is a solid axle. The powertrain model is specified to 250 kW with a 7 speed automatic transmission and four-wheel drive. Each tire is modeled using CarSim’s internal table model with simple camber and relaxation length for a 265/70 R17 tire. The inputs to the CarSim model are steering wheel torque, throttle percentage, and brake pressure. Two low-level PID controllers are developed in Simulink to abstract the interface. The first PID controller tracks a reference steering wheel angle by commanding a steering wheel torque. The second PID controller tracks a desired velocity using a combination of throttle percentage and brake pressure. To separate the two commands, the output of the second PID controller is split into positive and negative components. When positive, throttle percentage is commanded. When negative, brake pressure is commanded.
The CarSim model also supports road friction inputs for each tire–road interface, vertical displacement for each tire, and external wind magnitude and direction. These inputs constitute the Environment Model’s interface with the vehicle model. These Environment Models will be explained further in Section 2.5.
In addition to the vehicle and environmental models, sensor models and an Inertial Navigation System (INS) algorithm are implemented. This is shown in Figure 6 as consuming the output of the vehicle model. The three sensors that are modeled are the Inertial Measurement Unit (IMU), Wheel Speed Sensor (WSS), and the Global Positioning System (GPS). The IMU provides accelerations and angular rotations at 200 Hz. The WSS provides longitudinal velocity at 200 Hz. The GPS provides position, orientation, and velocity in the global coordinate frame at 2 Hz. The Extended Kalman Filter (EKF) proposed in [64] fuses these three signals to improve localization at 200 Hz. The algorithm developed in [64] fuses more sensors than those modeled here, so those update steps are not used. This algorithm validates the previous assumption that the controller has access to and .
The simulation supports two different modes of operation for the sensor models and EKF: Real-Time Kinematic (RTK) GPS-based INS and Differential GPS (DGPS)-based INS. The parameters of the sensor models and EKF are tuned to match the RTK INS performance and the DGPS INS performance of the AsteRx-i3 D Pro + from Septentrio. When in RTK mode, the EKF provides global positions approximately 6–8 cm within the ground truth (root mean square). When in DGPS mode, the EKF provides global position accuracies of approximately 10–20 cm (root mean square).
Before moving on from the sensor models, it is worth noting a phenomenon that is also modeled: jumps in position estimates. The GPS model provides the EKF with measurements at a drastically different update rate and accuracy than the predictions using the IMU measurements. The IMU and WSS measurements are used by the particle mass model to estimate position of the ego vehicle at 200 Hz. This is the so-called model update step. The noise in each sensor is integrated in this step such that there is drift in the position update. Then, at 2 Hz, the GPS provides high-precision position information in the so-called measurement update step. Tuning the gains of the EKF is therefore a balance between trusting the measurements and the model estimations. If the model updates are trusted too much, the drift in the model updates can be large. Then, when the measurement update step occurs, the estimate jumps to a more accurate estimate. If the model updates are trusted too little, the estimation quality deteriorates until a measurement update occurs. Therefore, a balance is struck in the EKF tuning between smoothness and variance. In the RTK configuration, this balance is easy to achieve, but in the DGPS configuration, jumps ranging between 10 and 40 cm must be tolerated to ensure acceptable performance levels.
In addition to modeling the sensors, the output of the EKF is delayed by a value that is sampled from a Gaussian distribution. This is to model the delay associated with the processing time of various sensor information, which varies stochastically. With a proper estimate of the mean of this delay, its effects can be mitigated by forward extrapolating the signals, as is done in [64]. However, in this work, we assume the delay is unknown and normally distributed, so it is not accounted for in the design process of the EKF or the design of the lateral or longitudinal controllers.
As Figure 6 shows, the control architecture uses decoupled lateral and longitudinal controllers. Typical Automated Driving System software architectures require perception modules and planner modules [2,6,14,51,54]. However, since neither of these modules are the subject of our current study, their contribution is eliminated by assuming static trajectories. These trajectories are provided to both the longitudinal and lateral controllers. The full path (the trajectory without the time parameter) is provided to the lateral controller. The distance along the path and the time associated with each waypoint are given to the longitudinal controller. In this way, the longitudinal controller’s task is to position the vehicle along the path exactly where the trajectory desires. The lateral controller’s task is to keep the vehicle as close to the path as possible.
This separation of lateral and longitudinal dynamics has significant impacts on the overall control of the system, especially when operating on low-friction surfaces or at the limits of tire saturation. The primary reason for using this separation is that it must be imposed when implementing a lateral steering controller. All of the controllers investigated in this work control only lateral and yaw vehicle dynamics. This choice is motivated by the successes realized in [47,48,49]. These works present empirical proof that it is possible to design a lateral motion controller that achieves good performance in a wide range of tasks and ODDs without explicitly considering longitudinal dynamics. In particular, their steering controllers sustain large body-slip angles when drifting, good performance when driving at the limits of handling, and achieve good performance in reduced road friction [48,49].
2.4. Reference Generation
The goal of this work is to experimentally evaluate each controller in rural roads and highways across a variety of environmental conditions. This necessitates the generation of references that represent driving on typical highways and rural roads. However, driving on typical roads includes a variety of maneuvers that must be safely completed such as lane keeping, lane changing, overtaking, and collision avoidance.
Lane keeping maneuvers are captured in this work by using two existing sections of highways in California: CA-17 and I-15; both of these are collected from OpenStreetMap [65]. These sections are selected because they are the locations of a large number of vehicle collisions every year in California. To capture lane changing and overtaking maneuvers another trajectory, called "S Road", is manually created to present higher-than-normal curvatures. This maneuver is generated by first creating a high-curvature road. Then, an overtaking maneuver is manually created on this high-curvature road. The result is an aggressive highway maneuver.
Collision avoidance maneuvers are quite different from these three trajectories. Collision avoidance maneuvers are typically composed of a series of very high, but short-duration, peaks in road curvature. The single lane change (SLC) and double lane change (DLC) maneuvers are commonly used in the literature to test the performance of steering controllers [14,15,66]. Both names come from the number of lanes crossed during an abrupt overtaking maneuver. They are specified by ISO 3888 [67]. While the design of the single and double lane changes is motivated by actual driving, it is not clear how well they predict steering controller performance on actual highways. The inclusion of actual highway trajectories allows for the direct study of this question.
ISO 3888 specifies the SLC and DLC tests to be conducted with an expert driver, whose task is to enter the test at a high speed and keep the vehicle within a bounded area. When this test is performed by an ADS, the local planner must determine a path that keeps the vehicle within the bounded area. Because this investigation is not focused on trajectory generation or optimization, the trajectory is generated offline and held static for all controllers and ODDs.
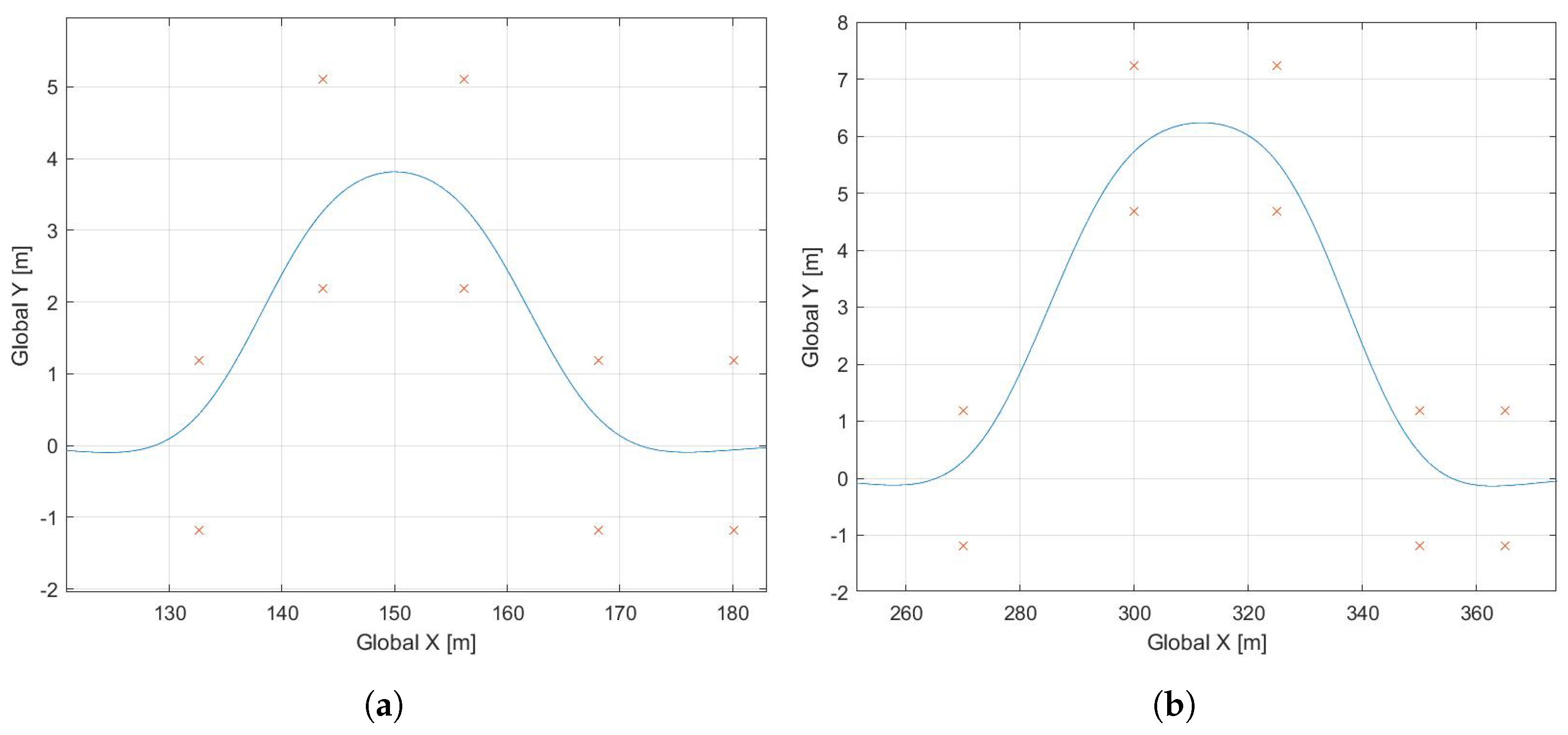
The trajectories are generated in two steps: (1) the generation of a two-dimensional, continuous path, and (2) the assignment of a velocity profile to the path. A continuous path is one whose zeroth, first, and second derivatives are continuous. This provides a smooth reference that can be followed with low error. To generate the path, a cubic spline, parameterized by the cumulative chord length [68], interpolates the waypoints extracted from the OpenStreetMap data. This allows for any amount of spatial sampling of the path (i.e., the path is composed of waypoints that are spaced 0.1 m from each other along the path). For the collision avoidance paths, the waypoints are initially centered between each cone in the ISO specification. Then, a cubic smoothing spline interpolation algorithm [69] is used to adjust the waypoints so that they generate a smoother path. This step is iterated by increasing the desired smoothness of the spline until the path is approximately the vehicle’s track width away from the nearest cone. Finally, the same method used for the highway maneuvers is applied to generate the final trajectory. The SLC and DLC paths are shown in Figure 7a,b. The crosses indicate the cone locations specified by the associated standard.
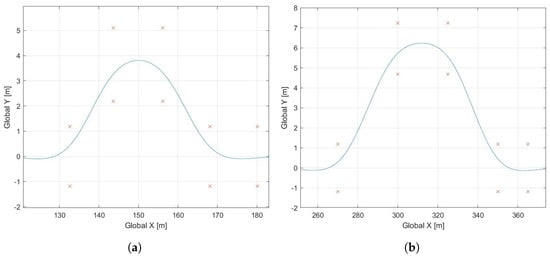
Figure 7.
Collision avoidance paths. (a) Top-down view of the single lane change path. (b) Top-down view of the double lane change path.
The specifications of the five trajectories used in this study are listed in Table 2.

Table 2.
Trajectory specifications.
2.4.1. Dynamic Feasibility
Dynamic feasibility is often a requirement imposed on trajectories generated by a planner. When a reference is dynamically feasible, the system, under perfect control, is capable of tracking the references with zero error. To explain this further, consider a vehicle driven manually for some duration. Now assume the pose of the vehicle is recorded perfectly for the duration of the test. The recorded poses constitute a dynamically feasible trajectory because the trajectory of poses has been performed already.
However, in practice, this trajectory generation method is impractical, so a model is used to generate the trajectories. In this sense, the generated trajectories are dynamically feasible according to the model used for generation. A path that is dynamically feasible according to a bicycle car model is not guaranteed to be dynamically feasible with the physical car because of the modeling errors in the bicycle car. Therefore, dynamic feasibility is closely related to modeling discrepancies.
Having defined these concepts, the trajectories in Table 2 are dynamically feasible according to the chord-length-parameterized cubic spline model. However, this is not a very accurate model of the vehicle. This is made worse when the road conditions vary because the velocity profile is generated on assumptions of maximum lateral and longitudinal accelerations.
One option to address this is to replace the cubic spline model with a higher-fidelity model such as a bicycle car and explicitly include road conditions such as road friction. A simpler method is to limit the maximum velocity on the path according to steady-state analysis of velocity, lateral accleration, curvature, and road friction. By lowering the maximum velocity quadratically with the lowered road friction, the resulting tire forces may not exceed the reduced saturation limit. However, the velocities should not be lowered too much to the point where the maneuvers no longer capture their designed intention.
To determine how much to lower the maximum velocity of the maneuvers, we can derive the relationship between the vehicle’s longitudinal velocity, , and the road–tire static friction coefficient, , as is shown in Equation (12). This relationship attempts to guarantee that the references remain dynamically feasible even when the road friction is diminished. The success of this approach is looked at more closely in Section 3.
where is the road’s curvature and g is Earth’s gravity constant. This relationship can now be used to determine a safe velocity for each maneuver at different values of .
2.4.2. Reference Extraction
There are several ways to pass the generated trajectory to the lateral and longitudinal controllers. One way to pass the trajectory to the lateral controller is to discard the temporal information and treat the trajectory as a path. However, now the challenge is to determine which waypoint on the path to use as a reference. This is solved with a closest-point algorithm. This comes at the cost of additional computing and, more significantly, introduces the pose estimator’s dynamics and noise into the reference. By using a closest-point algorithm, the reference becomes a function of the current pose estimate, therefore forwarding noise from the sensors and estimation algorithms to the references. If this noise occurs in the same frequency range as the controller, no feedback controllers can mitigate this noise because it is in the reference, not the feedback.
Further expanding on the lateral controller, once the steering angle is computed, it is typically passed to a low-level steering controller, sometimes referred to as a smart actuator. This is the motivation for the PID controller developed in Simulink to track a desired steer angle by providing a torque request to CarSim 2020. While some lateral controllers consider steering actuator dynamics [36], we assume the dynamics are unknown. The reason for this is that it is often the case that Automated Driving Systems are developed on an existing vehicle with its own low-level steering actuator controllers. Depending on the Original Equipment Manufacturer, these controllers can be difficult to obtain information on or to model accurately. To account for this, each controller is tuned to account for actuator constraints indirectly. This is part of the reason for the hyperparameter tuning of each controller. This more closely resembles a realistic control development task when the control developers are given a system and not given full information on the system.
To control the longitudinal dynamics, a cascade controller is developed. The outer loop controller tracks the time-scheduled distance along the path. The outer loop controller provides a target velocity that is then tracked by the inner loop controller, which uses the throttle and brake pedals. Both the inner and outer controllers are PID controllers for simplicity. Sometimes, the single and double lane change tests specify that the throttle should not be used once entering the lane change (known as an off-throttle test). However, in this investigation, the longitudinal controller will be used to maintain proper longitudinal position, allowing these tests to be completed using the throttle or brakes (if needed).
2.5. ODD Definitions
Having defined the trajectories and control architecture, the next step is to define the test conditions. By selecting specific parameters of the disturbance models, we can create numerous ODDs. Table 3 defines disturbance parameters for 5 ODDs. The first ODD is called nominal and is where the feedback is without noise or delay, the friction is maximal, there is no wind, and the vertical road noise is minimal. The goal of this domain is to provide an upper bound on performance. All controllers should perform well in this domain.

Table 3.
Operational Design Domain (ODD) Specifications.
The second ODD is realistic. It uses minimal vertical road noise, minimal wind (but with gusts), maximal friction, and feedback provided by the Extended Kalman Filter tuned to match Real-Time Kinematic Inertial Navigation System (RTK INS) performance levels. It also includes stochastic feedback delay as previously described. All ODDs, except for Nominal, use feedback delay with a mean of 60 ms with a standard deviation of 10 ms. Altogether, the Realistic ODD simulates a well-maintained road in ideal weather conditions.
The third ODD, Rural, is identical to the second except that the vertical road noise is increased and so is the wind speed. This simulates a moderately maintained road with moderate to high wind speeds. It also uses degraded feedback performance. This is reasonable since RTK requires a ground station, and some rural roads might be outside the range of that ground station.
The fourth ODD, Rainstorm, simulates driving in a rainstorm on a moderately-maintained road. The last ODD uses the highest vertical road noise, high wind speed, and the lowest road friction to simulate driving in a blizzard.
2.6. Metrics
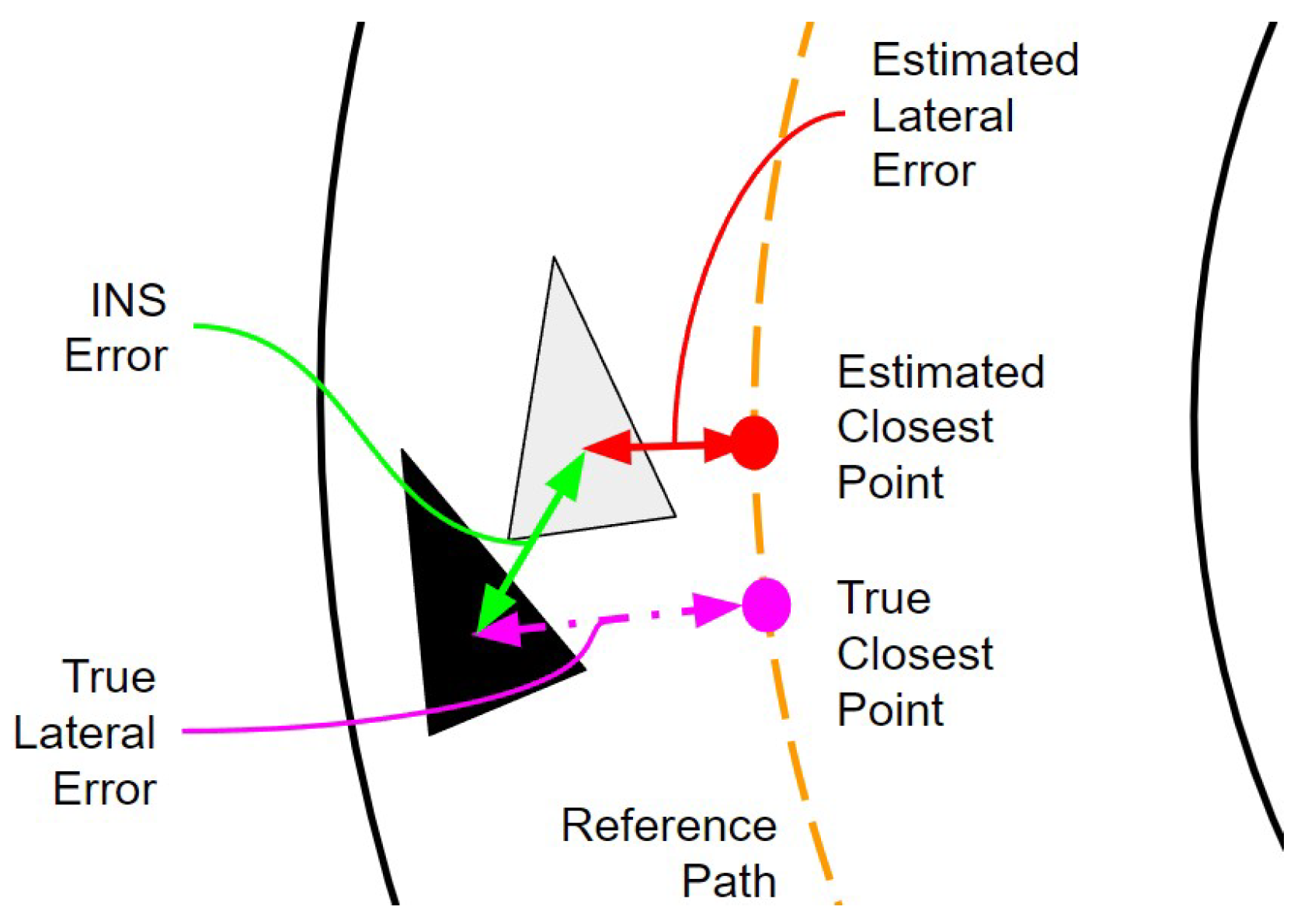
The motivating question behind this study is the following: under which conditions do these controllers perform insufficiently? This is most simply answered by setting a maximum value of acceptable lateral error. However, since the position is estimated with an Inertial Navigation System, there are two possible definitions of lateral error. Both definitions are visualized in Figure 8 with the double-sided arrows. The estimated lateral error, shown in the red double-sided arrow, is the projection of the distance between the estimated vehicle pose (grey triangle) and the estimated closest point (red dot) onto a unit vector that is both normal to the reference path and intersects the estimated vehicle’s position. The estimated closest point and the true closest point (purple dot) are not the same because the estimated closest point must be computed online with the estimated vehicle pose. The true lateral error, shown with the double-sided purple arrow, is defined the same as the estimated lateral error, except it uses the true vehicle pose (black triangle) and the true closest point.
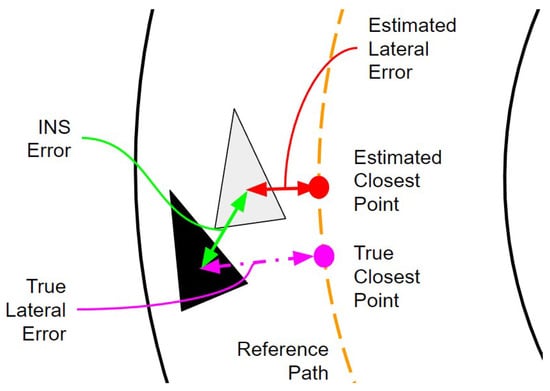
Figure 8.
Visualization of true and estimated lateral error definitions.
As the INS error decreases, the distance between the estimated and true closest points decreases. It is also worth noting, that these differences are independent of the vehicle’s yaw angle.
Having specified the two forms of lateral error, we can now provide a maximum value of acceptable true lateral error based on the lane and vehicle’s widths. However, such a deterministic requirement oversimplifies the uncertainty in everyday driving. To mitigate this, we reframe the question as a probabilistic one: how often do the controllers’ true lateral errors exceed some deterministic limit? Therefore, we propose a new metric:
where , is the width of a lane (3.6 m), is the track width of the vehicle (1.725 m), is the probability of failure, is the maximum acceptable lateral error, are the samples of the true lateral error, N is the number of samples, denotes a translation between the logical output to an integer (true maps to 1, false maps to 0), and is a threshold of lateral error, beyond which, the simulation is canceled and determined as incomplete. Using reduces the amount of compute time needed to simulate all combinations. Tuning this value requires finding a balance between reducing simulation time and capturing all successful simulations. It was found that a value of 2 m establishes an acceptable balance.
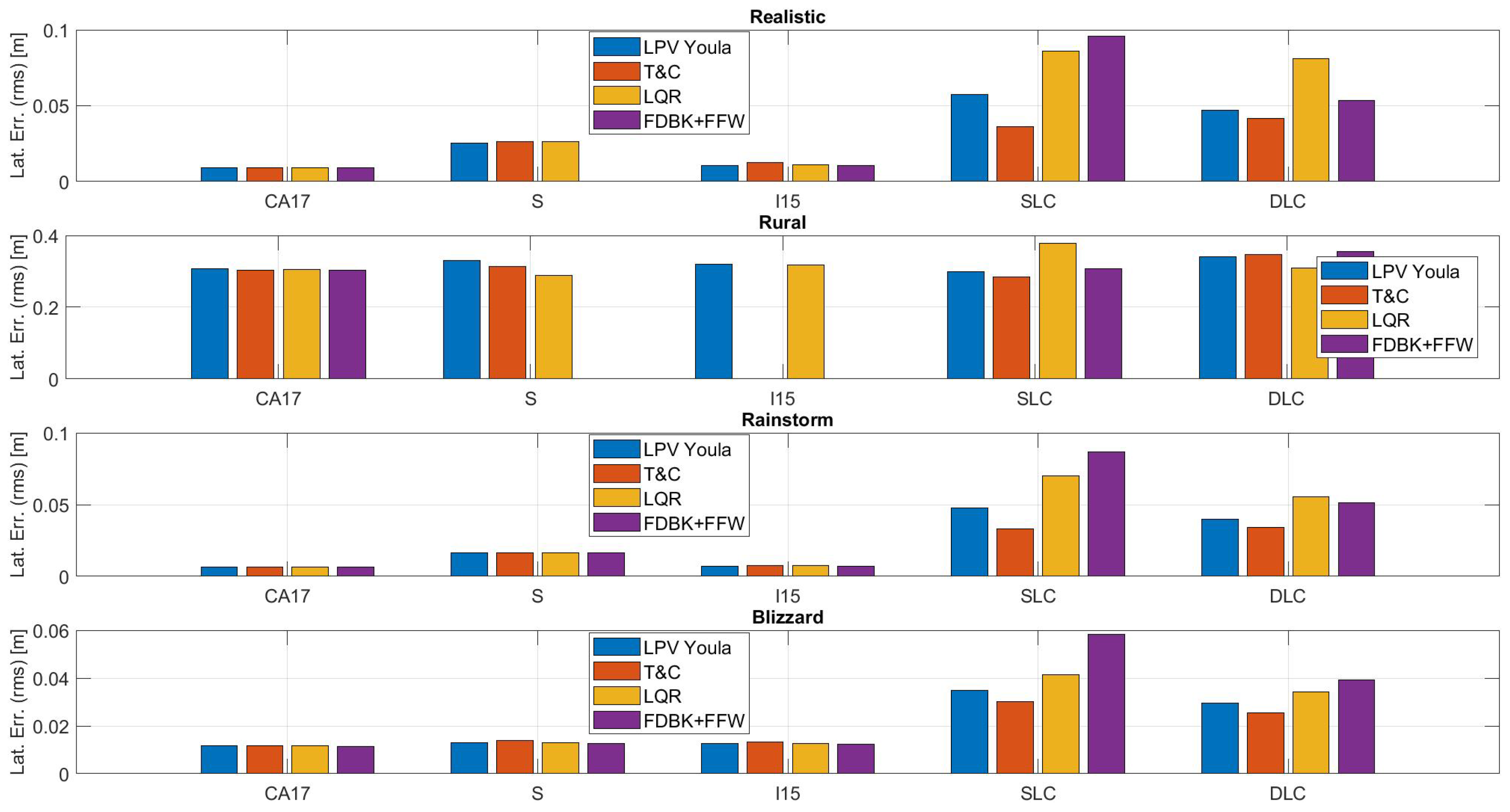
True lateral error is used in this definition instead of estimated lateral error because it includes the INS performance. A reasonable question to ask is if the INS performance changes between each controller. The simulation results in Figure 9 show that the INS performance is relatively consistent across controllers. The reader will notice that the INS performance for collision avoidance maneuvers varies more. This is because they are much shorter durations (the data during the speeding up portion is removed) and so the variance is higher. The absent bars in Figure 9 are the result of the controller achieving a probability of failure of 1 during some point in the maneuver. This is discussed further in Section 3.
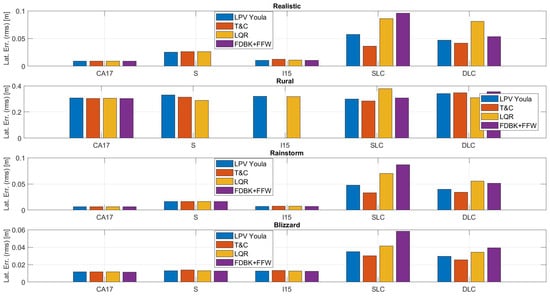
Figure 9.
INS performance across all ODDs.
In addition to quantifying the level of sufficient performance, there is still the need to quantify each controller’s relative performance and relative robustness. For relative performance, we use the root mean square (L2 norm) to capture the average performance of each controller, respectively. Finally, to quantify robustness we may compare the change in these scalar metrics between each ODD.
3. Results and Discussion
One hundred experiments are simulated to analyze the performance of all four controllers on all five maneuvers across five ODDs. The large number of experiments is not amenable to presenting plots of each experiment. So instead, summary statistics are presented in this section’s figures. However, a plot of various signals versus simulation time is useful to demonstrate each controller’s performance.
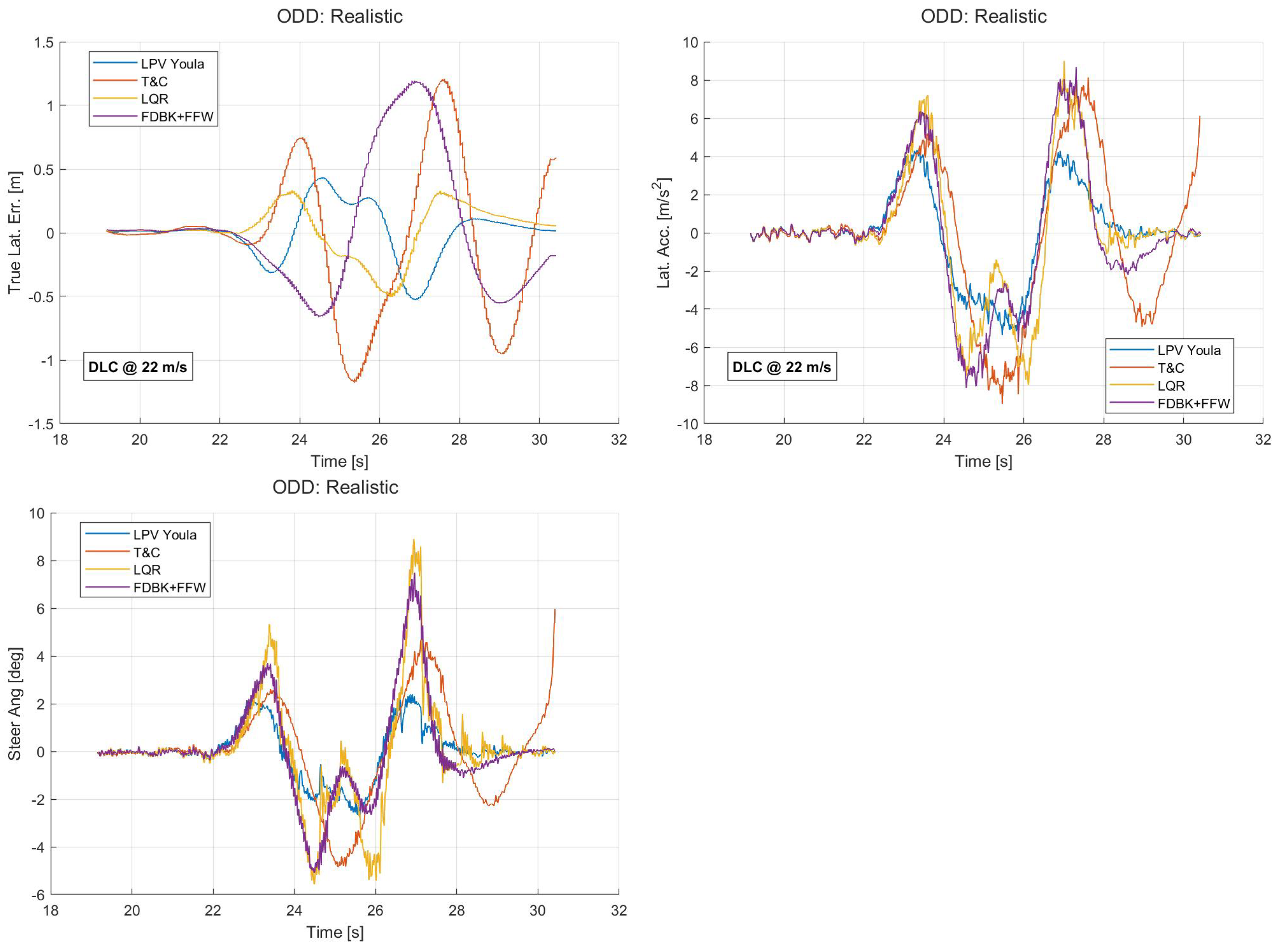
The simulation results for the DLC maneuver in the Realistic ODD are presented in Figure 10. The first plot shows the true lateral error (True Lat. Err.). By comparison, the LQR and LPV Youla controllers achieve the lowest tracking error. The second plot shows the lateral acceleration (Lat. Acc.), which is useful in evaluating how close the vehicle is to its physical limit. The plot shows that all of the controllers command the vehicle to a peak lateral acceleration greater than 4 m/. All controllers, except LPV Youla, reach as high as 8 m/. The third plot shows the steering angle measured at the tire. By comparison, the LPV Youla controller uses the lowest amount of actuator effort (as measured by maximum absolute steering angle). The LQR controller uses the greatest amount of actuator effort.
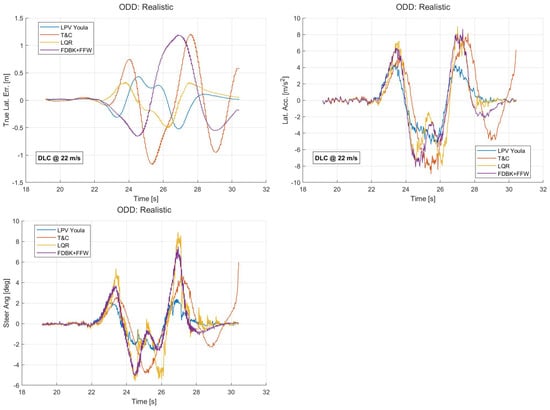
Figure 10.
Simulation results for DLC maneuver in realistic ODD.
The maximum lateral acceleration experienced in each maneuver is useful when quantifying how hard the vehicle is being pushed to its physical limits. Table 4 presents the minimum of all controller’s maximum absolute lateral accelerations for each maneuver and ODD. The presented values show that many of the maneuvers (especially the “S” maneuver) are very aggressive. The resulting average performance of each controller will be shown in the following subsection.

Table 4.
Minimum of all controllers’ maximum absolute lateral acceleration (m/).
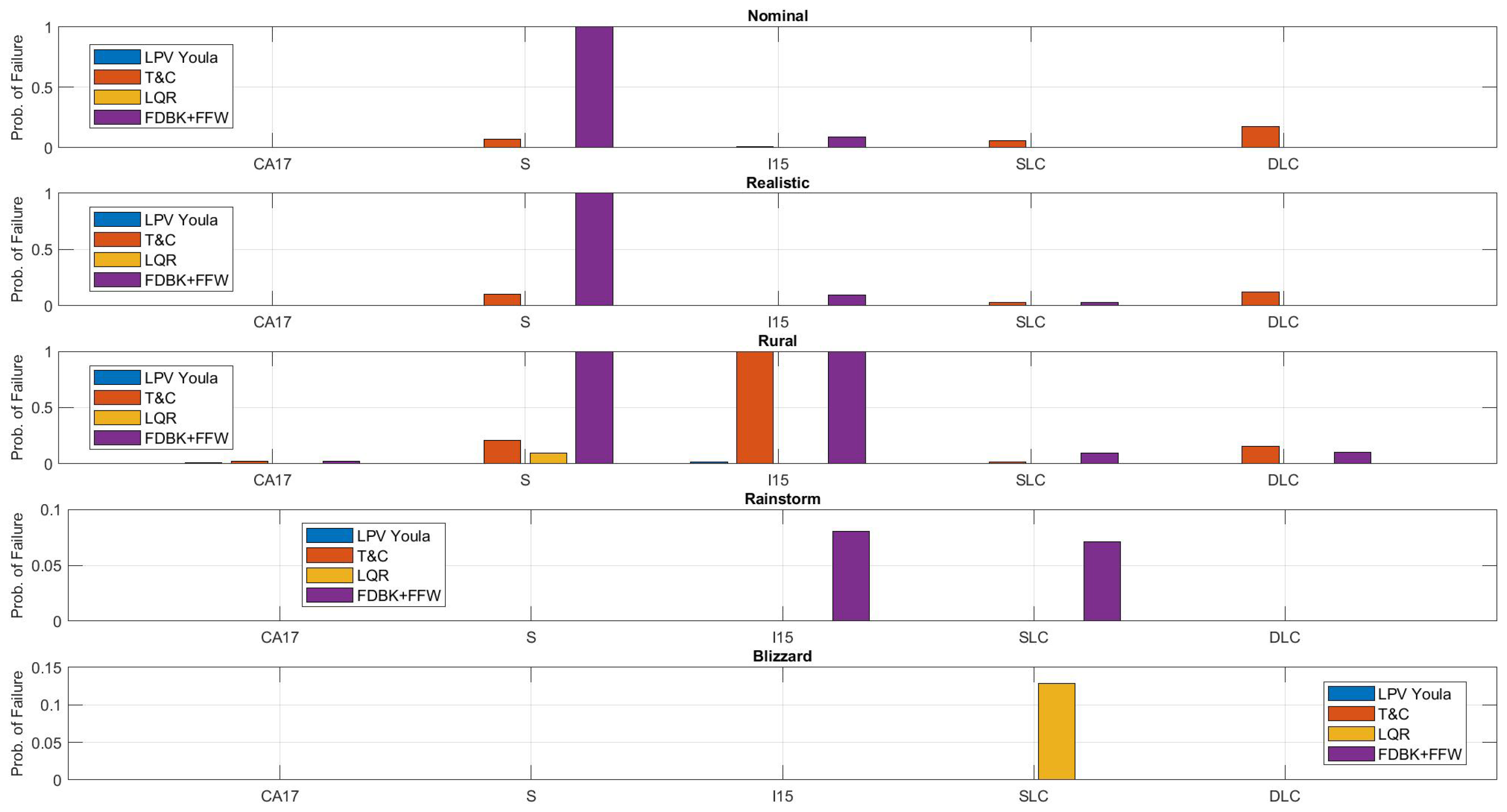
The next set of results to consider are the probabilities of failure, , for each controller, which is shown in Figure 11. We begin with these results because they directly answer the core question of this work: which Operational Design Domain (ODD) has an existing control solution? For an ODD to be considered solved, there must exist at least one controller that achieves a for all maneuvers.
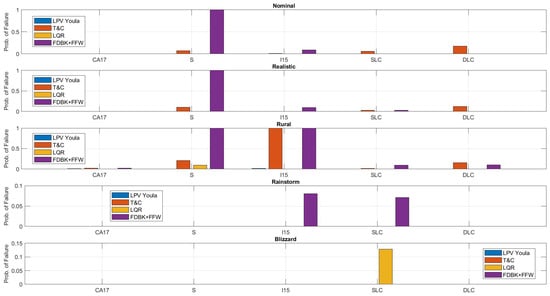
Figure 11.
Probability of failure across all ODDs.
Figure 11 shows that all of the ODDs have at least one controller that achieves a for all maneuvers. This suggests that there are controllers that provide a solution to all ODDs. The ODD with the most frequent nonzero probability of failure is the Rural ODD. The reason this ODD is so difficult is because precise control is required to achieve , and this is challenging when the INS uses DGPS. The DGPS configuration of the simulation almost doubles the lateral INS error. This results in a smaller budget of acceptable error for the lateral controller. Also, as the INS error increases, the dynamics of the INS play a more significant role.
Before proceeding to discuss Figure 12 and Figure 13 it is necessary to explain the cause of the controllers that achieve . This is summarized in Table 5.
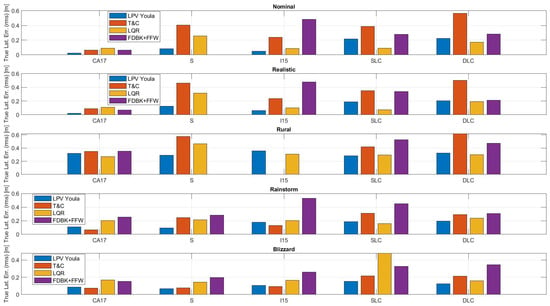
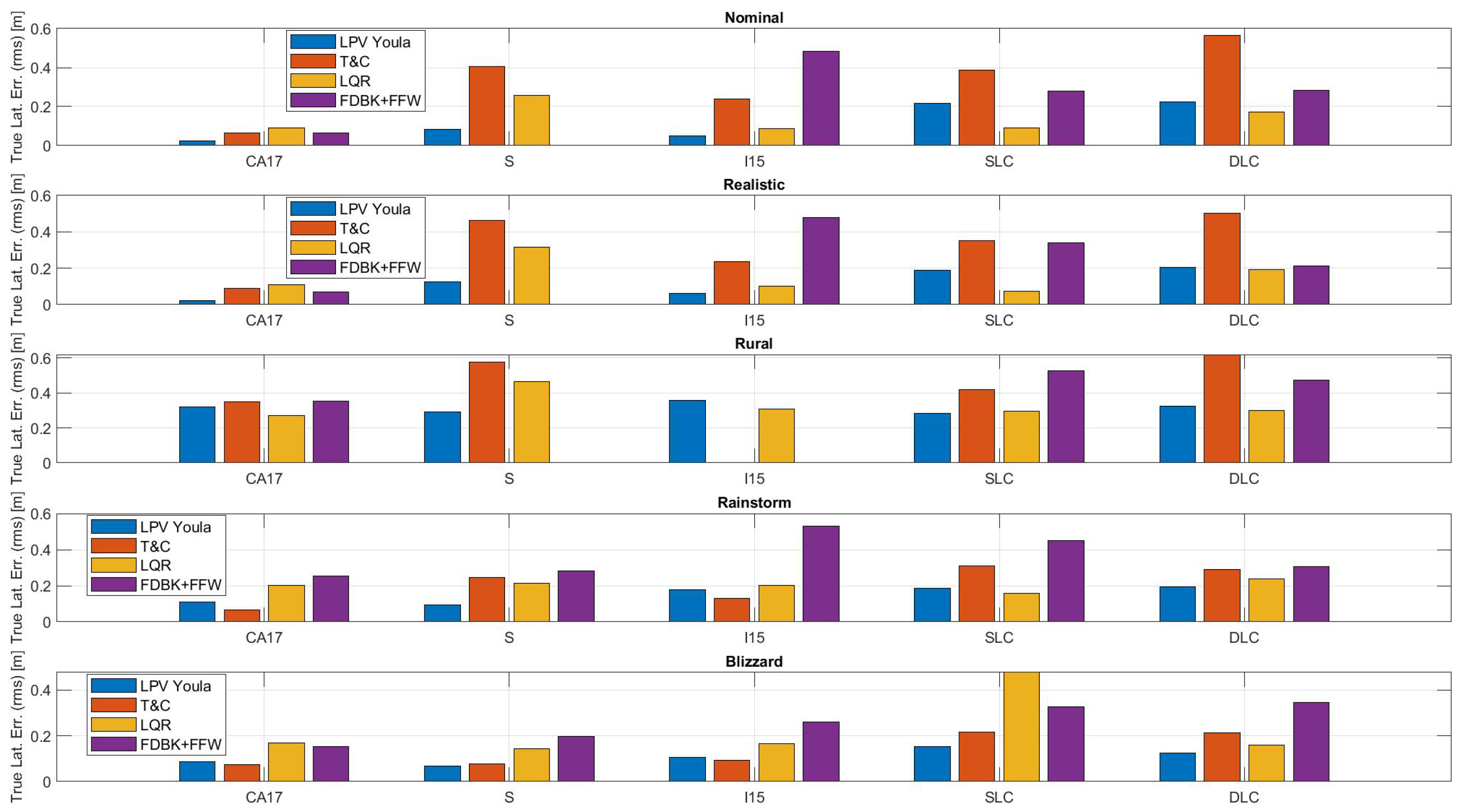
Figure 12.
True lateral error (RMS) across all ODDs.
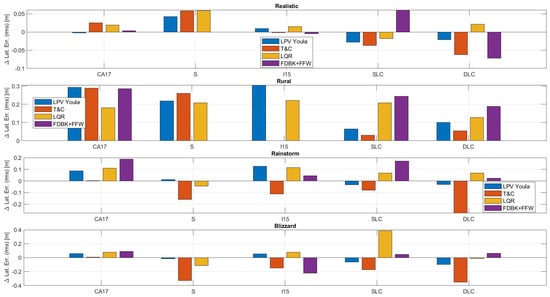
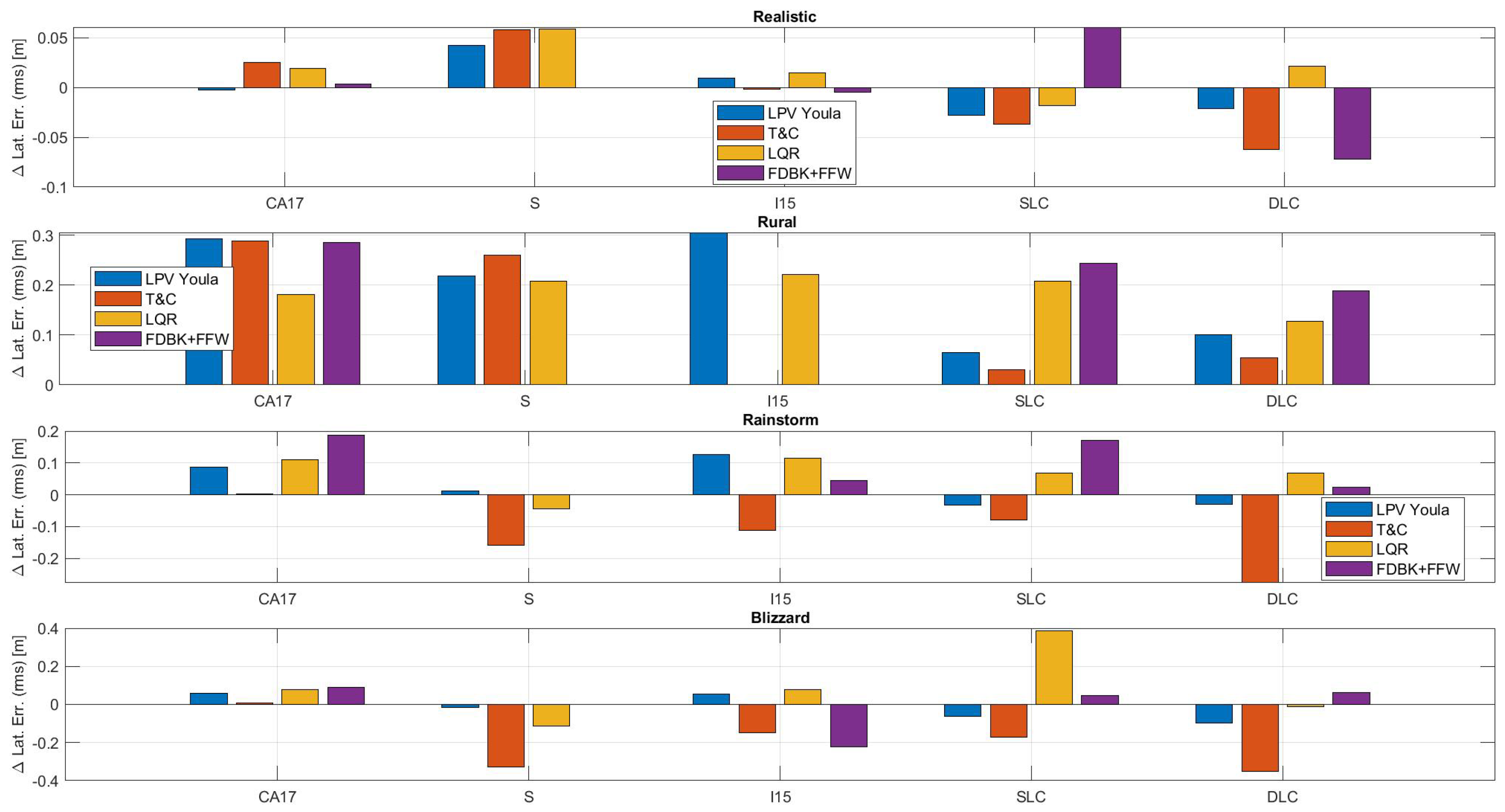
Figure 13.
Change in true lateral error (RMS) with respect to Nominal.

Table 5.
Cause of Failures in Experiments.
Most controllers have zero or low in the Rainstorm and Blizzard ODDs. Since this result is contrary to the typical belief that controlling a car is more difficult in rainy and snow conditions than in dry conditions, it suggests that the method of modifying the trajectories to ensure dynamic feasibility is overly conservative. In other words, the assumed relationship between and results in improving the dynamic feasibility so much so that achievable performance is also improved. These results show there are likely additional variables that affect the controller performance. Such a conclusion has been demonstrated for real-world vehicles [70].
Furthermore, the ODD specifications in Table 3 would benefit from more environmental variables. One oversimplification is that the INS performance is the same for Realistic, Rainstorm, and Blizzard ODDs. In reality, INS performance can deteriorate in severe weather conditions. Assuming that the accuracy of the RTK-INS degrades to that of DGPS is difficult to validate. Further work is needed to determine how to degrade the INS performance to better simulate adverse weather conditions.
The results of this work demonstrate that it is feasible to find one controller capable of achieving safe performance in a wide variety of ODDs for a wide variety of driving tasks. The methods used in this work represent another step towards such a set of benchmarks with which all steering controllers can be evaluated.
3.1. Relative Performance
Figure 12 shows the RMS value of the true lateral error for all controllers, maneuvers, and ODDs. Again, the absent bars correspond to the controllers that achieved . It is worth emphasizing here that the LQR and FDBK + FFW controllers use a feedforward controller, while the LPV Youla and T&C controllers do not.
The controller that tends to have the lowest average lateral error across all maneuvers and ODDs is the LPV Youla controller. The LQR controller tends to achieve the second lowest lateral error. Finally, the FDBK + FFW and T&C controllers tend to be the worst-performing controllers.
The difference in performances of the same controller between the collision avoidance maneuvers (SLC and DLC) and the highway maneuvers suggests that using collision avoidance to validate a controller does not guarantee the controller’s generalizability to other tasks. If a controller is developed for both highway lane-keeping tasks and collision avoidance tasks, it should be tested on both types of paths.
The maximum absolute true lateral error of each controller is not shown because the trends between controllers, maneuvers, and ODDs are the same. Furthermore, Figure 11 also presents information related to the maximum absolute performance of each controller. So, its inclusion does not add any additional information to the reader.
3.2. Relative Robustness
Figure 13 shows the change in true lateral error RMS for each ODD with respect to the Nominal ODD. While it is expected that the changes should be positive (the performance deteriorates), Figure 13 shows that some controllers improve in average performance with respect to the Nominal ODD. This is because of the previously mentioned velocity modifications to each maneuver for each ODD. This figure more clearly shows that the strategy used to modify the maneuver’s velocity is overly conservative.
Figure 13 most clearly shows each controller’s robustness with respect to the environmental conditions. The small changes observed in the Realistic ODD results show that all controllers are relatively robust against RTK feedback errors, system delays, and small wind gusts. The general increase in lateral error for the Rural ODD show that all controllers suffer in performance when the feedback error is increased, and when the road surface quality is decreased. For highway maneuvers, it appears that the LQR controller changes the least. However, the results differ for the collision avoidance maneuvers, where the T&C controller degrades the least in performance. FDBK + FFW suffers the most in the Rural ODD. This is likely because this controller uses only a proportional feedback gain and relies heavily on its feedforward controller. The closed loop performance is therefore more fragile than the other more intricate feedback controllers.
The results for the Rainstorm and Blizzard ODD show that most controllers can reject high winds and diminished road friction. The T&C controller improves the most in the Rainstorm and Rural ODDs.
4. Conclusions
This work uses a custom, high-fidelity simulator to evaluate four controllers on five maneuvers in five ODDs. By framing this comparison with ODDs, environmental disturbances can be grouped to form simulations of realistic scenarios. Through the combination of all five maneuvers and the five ODDs, 25 unique scenarios are used to evaluate if a controller can achieve pre-defined performance requirements. The reference trajectories are designed to represent a wide range of possible maneuvers, including lane-keeping, overtaking on a highly curved road, and abrupt collision avoidance maneuvers.
The results in Figure 11, Figure 12 and Figure 13 show that all of the five ODDs considered have controllers capable of achieving a pre-defined performance requirement. More significantly, all of these controllers require incredibly low computational power. This suggests that more computationally heavy controllers, such as Model Predictive Control, are not needed to solve these ODDs.
The claims in this work are rather significant, so before concluding, it is necessary to qualify the results. A large number of assumptions were made in this work that simplified these ODDs into simpler (and solvable) problems. The assumptions that may have the most significant influence on these results are as follows:
- Vehicle model and performance requirements: This work used a very simple method to derive lateral performance requirements for controller development. However, there exist several factors that this simple method neglects [71]. Specifically, the choice of vehicle significantly impacts these results. This work uses a full-size SUV, whose track width is 1.7 m, which is a rather wide passenger vehicle. If a smaller vehicle, such as a sedan (typically around 1.5 to 1.6 m track width), were used in this study, the required maximum lateral error would have increased. Conversely, if a larger vehicle, such as a commercial truck, were used, the maximum lateral error would have decreased.
- Stochastic disturbances: One simulation was performed per controller, route, and ODD combination. The underlying assumption is that this simulation represents the worst case in that condition, which is a rather significant oversimplification. In the future, the simulator’s real-time factor can be improved and a Monte Carlo experiment can be used to evaluate the worst-case, average, and best-case performance of each controller. In this sense, it makes sense to redefine the probability of failure accordingly.
- Longitudinal control: The longitudinal control performance is not considered in this work. However, the longitudinal controller must also meet pre-defined performance requirements.
- Reliable sensors: Section 2.3 described a system architecture that uses an EKF to fuse information from a GPS, IMU, and Wheel Speed Sensor. Therefore, the results presented in this work rely on the assumption that each of these sensors are available. For IMUs and Wheel Speed Sensors, this is not too great an assumption. However, assuming GPS is available is more significant. This is partly the motivation for introducing the Rural ODD, in which the RTK-GPS is assumed unavailable, but DGPS is available. More investigation is needed by the research community to develop robust, multi-modal localization techniques that can provide quality feedback to the controller in GPS-denied areas.
- Simplified road disturbances: The vertical road disturbances are modeled as colored noise according to ISO 8608 [13]. This neglects potholes and other sudden road jumps. These types of disturbances might present destabilizing conditions that are not captured in this work.
- Adverse weather conditions assumed to be uniform: The adverse weather conditions (Rainstorm and Blizzard ODDs) assume the road friction is uniform (with the addition of colored noise). In reality, puddles and ice patches can exist that cause large and sudden changes in friction. Furthermore, the simulation is incapable of simulating hydroplaning. All of these disturbances greatly complicate simulating adverse weather conditions.
The outcome of this work is to suggest that there exist many solutions to control the front steering actuator of an Automated Driving System (ADS) to follow a wide variety of maneuvers under a wide variety of conditions within a safe margin (as determined by the requirements derivation). The key qualifier in this statement is the use of “safe margin”. This is to say that if safety is the only concern, then there are several solutions that are satisfactory. However, safety is rarely the only interest. Specifically, comfort is often a secondary performance requirement.
Comfort has not been addressed in this work. This investigation was primarily concerned with evaluating the safety of various controllers in different ODDs. The result has been that the ODDs under study can be considered solved by some of the controllers present in the literature. However, the resulting performances may not be comfortable enough for passengers (or for component lifetime). For normal highway driving, comfort is very important. Further work on lateral steering controllers should be focused on evaluating the comfort of various controllers on various ODDs. Only after a comfortable and safe performance is achieved can an ODD be truly considered as solved by the literature.
In addition to considering comfort, further work in this area should be directed away from developing new, more complex controllers for lane-keeping in ideal weather conditions. Instead, more focus should be given to understanding and modeling the significant disturbances that make driving in adverse road conditions challenging and dangerous. This will require significant on-vehicle testing in adverse weather conditions. Additionally, more effort should be spent on developing longitudinal and lateral control architectures capable of achieving specified joint performances derived from safety requirements. Again, this will require a combination of simulation and real-world testing to validate results.
Author Contributions
Conceptualization, T.V.; methodology, T.V.; writing, T.V.; supervision, F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Department of Transportation’s Automated Driving System Demonstration Grant awarded to Texas A & M Engineering Experiment Station for the project entitled “AVA: Automated Vehicles for All”.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gardels, K. Automatic Car Controls for Electronic Highways; Technical Report; General Motors Research Labs: Warren, MI, USA, 1960. [Google Scholar]
- Ioannou, P.A. (Ed.) Automated Highway Systems; Springer: New York, NY, USA, 1997. [Google Scholar]
- Guldner, J.; Tan, H.S.; Patwardhan, S. Analysis of Automatic Steering Control for Highway Vehicles with Look-down Lateral Reference Systems. Veh. Syst. Dyn. 1996, 26, 243–269. [Google Scholar] [CrossRef]
- Fenton, R.; Melocik, G.; Olson, K. On the steering of automated vehicles: Theory and experiment. IEEE Trans. Autom. Control 1976, 21, 306–315. [Google Scholar] [CrossRef]
- Consumer Reports Inc. Understanding the Current State of Vehicle Automation; Technical Report; Consumer Reports Inc.: Yonkers, NY, USA, 2021. [Google Scholar]
- Comma Ai Openpilot 0.9.4 Release. 2023. Available online: https://github.com/commaai/openpilot/releases/tag/v0.9.4 (accessed on 10 May 2024).
- SAE Standard J3063_202103; Active Safety Systems Terms and Definitions. SAE International: Warrendale, PA, USA, 2021. [CrossRef]
- SAE Standard J3016_202104; Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. SAE International: Warrendale, PA, USA, 2021. [CrossRef]
- Zhang, Y.; Carballo, A.; Yang, H.; Takeda, K. Perception and sensing for autonomous vehicles under adverse weather conditions: A survey. ISPRS J. Photogramm. Remote Sens. 2023, 196, 146–177. [Google Scholar] [CrossRef]
- Ding, F.; Shan, H.; Han, X.; Jiang, C.; Peng, C.; Liu, J. Security-Based Resilient Triggered Output Feedback Lane Keeping Control for Human–Machine Cooperative Steering Intelligent Heavy Truck Under Denial-of-Service Attacks. IEEE Trans. Fuzzy Syst. 2023, 31, 2264–2276. [Google Scholar] [CrossRef]
- Calzolari, D.; Schürmann, B.; Althoff, M. Comparison of trajectory tracking controllers for autonomous vehicles. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Heß, D.; Althoff, M.; Sattel, T. Comparison of trajectory tracking controllers for emergency situations. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast City, Australia, 23 June 2013; pp. 163–170. [Google Scholar] [CrossRef]
- ISO 8608:2016; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. International Organization for Standardization: Geneva, Switzerland, 2016.
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; Technical Report; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Betz, J.; Zheng, H.; Liniger, A.; Rosolia, U.; Karle, P.; Behl, M.; Krovi, V.; Mangharam, R. Autonomous Vehicles on the Edge: A Survey on Autonomous Vehicle Racing. IEEE Open J. Intell. Transp. Syst. 2022, 3, 458–488. [Google Scholar] [CrossRef]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive Active Steering Control for Autonomous Vehicle Systems. IEEE Trans. Control Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Matute, J.A.; Marcano, M.; Diaz, S.; Perez, J. Experimental Validation of a Kinematic Bicycle Model Predictive Control with Lateral Acceleration Consideration. IFAC-PapersOnLine 2019, 52, 289–294. [Google Scholar] [CrossRef]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An Improved Kinematic Model Predictive Control for High-Speed Path Tracking of Autonomous Vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Lee, J.; Chang, H.J. Analysis of explicit model predictive control for path-following control. PLoS ONE 2018, 13, e0194110. [Google Scholar] [CrossRef] [PubMed]
- Kapania, N.R.; Gerdes, J.C. Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef]
- Fenton, R.; Selim, I. On the optimal design of an automotive lateral controller. IEEE Trans. Veh. Technol. 1988, 37, 108–113. [Google Scholar] [CrossRef]
- Cormier, W.; Fenton, R. On the steering of automated vehicles—A velocity-adaptive controller. IEEE Trans. Veh. Technol. 1980, 29, 375–385. [Google Scholar] [CrossRef]
- Ackermann, J.; Sienel, W. Robust Control for Automatic Steering. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 795–800. [Google Scholar] [CrossRef]
- Guldner, J.; Utkin, V.; Ackermann, J. A sliding mode control approach to automatic car steering. In Proceedings of the 1994 American Control Conference—ACC ’94, Baltimore, MD, USA, 29 June–1 July 1994; Volume 2, pp. 1969–1973. [Google Scholar] [CrossRef]
- Ackermann, J.; Guldner, J.; Sienel, W.; Steinhauser, R.; Utkin, V. Linear and nonlinear controller design for robust automatic steering. IEEE Trans. Control Syst. Technol. 1995, 3, 132–143. [Google Scholar] [CrossRef]
- Gahinet, P.; Apkarian, P. A linear matrix inequality approach to H-infinity control. Int. J. Robust Nonlinear Control 1994, 4, 421–448. [Google Scholar] [CrossRef]
- Apkarian, P.; Biannic, J.M.; Gahinet, P. Self-scheduled H-infinity control of missile via linear matrix inequalities. J. Guid. Control. Dyn. 1995, 18, 532–538. [Google Scholar] [CrossRef]
- Apkarian, P.; Gahinet, P.; Becker, G. Self-scheduled H-infinity control of linear parameter-varying systems: A design example. Automatica 1995, 31, 1251–1261. [Google Scholar] [CrossRef]
- Apkarian, P.; Adams, R.J. Advanced gain-scheduling techniques for uncertain systems. In Advances in Linear Matrix Inequality Methods in Control; SIAM: Philadelphia, PA, USA, 2000; pp. 209–228. [Google Scholar]
- Apkarian, P.; Tuan, H.D. Parameterized LMIs in control theory. SIAM J. Control Optim. 2000, 38, 1241–1264. [Google Scholar] [CrossRef]
- Gahinet, P. Explicit controller formulas for LMI-based H-infinity synthesis. Automatica 1996, 32, 1007–1014. [Google Scholar] [CrossRef]
- Chilali, M.; Gahinet, P. H-infinity design with pole placement constraints: An lmi approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]
- Corno, M.; Panzani, G.; Roselli, F.; Giorelli, M.; Azzolini, D.; Savaresi, S.M. An LPV Approach to Autonomous Vehicle Path Tracking in the Presence of Steering Actuation Nonlinearities. IEEE Trans. Control Syst. Technol. 2021, 29, 1766–1774. [Google Scholar] [CrossRef]
- Kapsalis, D.; Sename, O.; Milanés, V.; Martinez, J.J. Gain-scheduled steering control for autonomous vehicles. IET Control Theory Appl. 2020, 14, 3451–3460. [Google Scholar] [CrossRef]
- Atoui, H.; Sename, O.; Milanes, V.; Martinez-Molina, J.J. Toward switching/interpolating LPV control: A review. Annu. Rev. Control 2022, 54, 49–67. [Google Scholar] [CrossRef]
- Heemels, W.P.; Johansson, K.H.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3270–3285. [Google Scholar]
- Viadero-Monasterio, F.; Nguyen, A.T.; Lauber, J.; Boada, M.J.L.; Boada, B.L. Event-Triggered Robust Path Tracking Control Considering Roll Stability Under Network-Induced Delays for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14743–14756. [Google Scholar] [CrossRef]
- Tan, H.S.; Huang, J. Design of a High-Performance Automatic Steering Controller for Bus Revenue Service Based on How Drivers Steer. IEEE Trans. Robot. 2014, 30, 1137–1147. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Farhad Assadian, K.R.M. Robust Control: Youla Parameterization Approach; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2022. [Google Scholar]
- Arasteh, E.; Assadian, F. A Comparative Analysis of Brake-by-Wire Smart Actuators Using Optimization Strategies. Energies 2022, 15, 634. [Google Scholar] [CrossRef]
- Filipozzi, L.; Assadian, F. Control of Over-Actuated Systems—From Practical to Theoretical Concepts with Application in Hybrid Powertrain Speed Control Development. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Guillen, S.; Assadian, F. Unique approaches to integrating semi-active suspension and active anti-roll bar control systems. Int. J. Veh. Des. 2022, 90, 98–115. [Google Scholar] [CrossRef]
- Kapania, N.R.; Gerdes, J.C. Learning at the Racetrack: Data-Driven Methods to Improve Racing Performance over Multiple Laps. IEEE Trans. Veh. Technol. 2020, 69, 8232–8242. [Google Scholar] [CrossRef]
- Goh, J.Y.; Goel, T.; Christian Gerdes, J. Toward Automated Vehicle Control Beyond the Stability Limits: Drifting Along a General Path. J. Dyn. Syst. Meas. Control 2019, 142, 021004. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, eaaw1975. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.S.; Huang, J. Experimental Development of a New Target and Control Driver Steering Model Based on DLC Test Data. IEEE Trans. Intell. Transp. Syst. 2012, 13, 375–384. [Google Scholar] [CrossRef]
- Huang, J.; Tan, H.S. Control System Design of an Automated Bus in Revenue Service. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2868–2878. [Google Scholar] [CrossRef]
- Mahtout, I.; Navas, F.; Gonzalez, D.; Milanes, V.; Nashashibi, F. Youla-Kucera Based Lateral Controller for Autonomous Vehicle. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 3281–3286. [Google Scholar] [CrossRef]
- Seiler, P.; Packard, A.; Gahinet, P. An Introduction to Disk Margins [Lecture Notes]. IEEE Control Syst. Mag. 2020, 40, 78–95. [Google Scholar] [CrossRef]
- Luan, B.C.; Lee, I.H.; Tan, H.S.; Li, K.; Yuan, D.; Chou, F.C. Design and Field Testing of a Lane Following Control System with a Camera Based on T&C Driver Model. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; Routledge: London, UK, 1975. [Google Scholar]
- Guldner, J.; Tan, H.S.; Patwardhan, S. Study of design directions for lateral vehicle control. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 10–12 December 1997; Volume 5, pp. 4732–4737. [Google Scholar] [CrossRef]
- Chen, C.T. Linear System Theory and Design; Saunders College Publishing: Philadelphia, PA, USA, 1984. [Google Scholar]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 104. [Google Scholar]
- McFarlane, D.C.; Glover, K. Robust Controller Design Using Normalized Coprime Factor Plant Descriptions; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Metzler, M.; Tavernini, D.; Sorniotti, A.; Gruber, P. An explicit nonlinear MPC approach to vehicle stability control. In Proceedings of the 14th International Symposium on Advanced Vehicle Control, Tsinghua University, Beijing, China, 16–20 July 2018. [Google Scholar]
- Grancharova, A.; Johansen, T.A.; Tøndel, P. Computational aspects of approximate explicit nonlinear model predictive control. In Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007; pp. 181–192. [Google Scholar]
- de Gelder, E.; Elrofai, H.; Saberi, A.K.; Paardekooper, J.P.; Op den Camp, O.; de Schutter, B. Risk Quantification for Automated Driving Systems in Real-World Driving Scenarios. IEEE Access 2021, 9, 168953–168970. [Google Scholar] [CrossRef]
- Smith, C. 20 Best-Selling Cars in the US in 2023. Available online: https://www.motor1.com/features/703891/best-selling-cars-2023/ (accessed on 26 April 2024).
- Wischnewski, A.; Stahl, T.; Betz, J.; Lohmann, B. Vehicle Dynamics State Estimation and Localization for High Performance Race Cars. IFAC-PapersOnLine 2019, 52, 154–161. [Google Scholar] [CrossRef]
- Contributors, O. Planet Dump. 2023. Available online: https://planet.openstreetmap.org (accessed on 10 May 2024).
- Chatzikomis, C.; Sorniotti, A.; Gruber, P.; Zanchetta, M.; Willans, D.; Balcombe, B. Comparison of Path Tracking and Torque-Vectoring Controllers for Autonomous Electric Vehicles. IEEE Trans. Intell. Veh. 2018, 3, 559–570. [Google Scholar] [CrossRef]
- ISO 3888-1:2018; Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre—Part 1: Double Lane-Change. International Organization for Standardization: Geneva, Switzerland, 2018.
- Floater, M.S. On the deviation of a parametric cubic spline interpolant from its data polygon. Comput. Aided Geom. Des. 2008, 25, 148–156. [Google Scholar] [CrossRef]
- Cubic Smoothing Spline—MATLAB. Available online: https://www.mathworks.com/help/curvefit/csaps.html. (accessed on 29 December 2023).
- Betz, J.; Heilmeier, A.; Wischnewski, A.; Stahl, T.; Lienkamp, M. Autonomous Driving—A Crash Explained in Detail. Appl. Sci. 2019, 9, 5126. [Google Scholar] [CrossRef]
- Vidano, T.; Assadian, F. Control Performance Requirements for Automated Driving Systems. Electronics 2024, 13, 902. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).