Novel Hybrid SOR- and AOR-Based Multi-User Detection for Uplink M-MIMO B5G Systems

Abstract

The Internet of Things (IoT) is one of the most important wireless sensor network (WSN) applications in 5G systems and requires a large amount of wireless data transmission. Therefore, massive multiple-input multiple-output (M-MIMO) has become a crucial type of technology and trend in the future of beyond fifth-generation (B5G) wireless network communication systems. However, as the number of antennas increases, this also causes a significant increase in complexity at the receiving end. This is a challenge that must be overcome. To reduce the BER, confine the computational complexity, and produce a form of detection suitable for 4G and B5G environments simultaneously, we propose a novel multi-user detection (MUD) scheme for the uplink of M-MIMO orthogonal frequency division multiplexing (OFDM) and universal filtered multi-carrier (UFMC) systems that combines the merits of successive over-relaxation (SOR) and accelerated over-relaxation (AOR) named mixed over-relaxation (MOR). Herein, we divide MOR into the initial and collaboration stages. The former will produce the appropriate initial parameters to improve feasibility and divergence risk. Then, the latter achieves rapid convergence and refinement performance through alternating iterations. The conducted simulations show that our proposed form of detection, compared with the BER performance of traditional SOR and AOR, can achieve $99.999\%$ and $99.998\%$ improvement, respectively, and keep the complexity at $\mathcal{O}\left(N^2\right)$. It balances BER performance and complexity with fewer iterations.

1. Introduction

International mobile telecommunications (IMT) [1,2,3] have formulated the architecture and goals in the future for fifth-generation (5G) systems [4,5,6], such as enhanced mobile broadband (eMBB), ultra-reliable and low-latency communications (URLLC), and massive machine-type communications (mMTC). They bring users a better experience and inject new vitality into the fields of the Internet of Things (IoT) [7,8,9], industrial automation, telemedicine, and driverless driving. Among them, the IoT is one of the critical application technologies for 5G wireless communication [10,11], and wireless transmission services have become an influential means of transmitting IoT messages. To meet various applications of the IoT, wireless communication transmission of large amounts of information to data collection centers and extension to big data analysis is an essential requirement for eMBB and URLLC (i.e., beyond 5G (B5G) technology [12,13,14] will be forced to bear massive amounts of data while being more time-saving than the previous systems).

Apart from the demand increase in data rate and spectral efficiency in the evolution of wireless communication systems, single-carrier modulation technology has disadvantages such as poor resistance to channel delays, a high bit error rate (BER), and significant bandwidth demand. Therefore, it is insufficient for most current applications. Thus, many researchers have developed multi-carrier modulation technology to cut a bandwidth into many subchannels and use multiple subcarriers to transmit signals and combat the above shortcomings. Orthogonal frequency-division multiplexing (OFDM) is one of the most popular technologies among multiple-carrier modulation schemes [15,16]. Although the spectrum overlaps, its subcarriers are orthogonal. Therefore, each subcarrier will not affect one another. Furthermore, its robustness to channel delay and resistance to inter-symbol interference (ISI) is proven [17]. Unfortunately, OFDM still has some disadvantages that are not conducive to B5G [18,19,20], such as strict synchronization requirements, high sidelobe losses, and inter-carrier interference (ICI), which need to be improved. To approach the needs of B5G systems simultaneously, it is necessary to find new multi-carrier waveforms to combat the shortcomings of OFDM and support higher data rates, low latency, and looser synchronization techniques. Universal filtered multi-carrier (UFMC) [21,22] is a feasible candidate multi-carrier waveform that combines the advantages of OFDM and filter bank multi-carrier (FBMC) [23,24], is resistant to ICI, and has less out-of-band emissions (OOBMs) to reduce sidelobe losses. In addition, UFMC is compatible with the same architecture as OFDM regarding the channel model [25,26,27].

Regarding the challenges of B5G wireless communication systems, to further stimulate the advantages of UFMC and provide better spectral efficiency, previous researchers have proposed the massive multiple-input multiple-output (M-MIMO) architecture as an essential type of technology for advanced wireless communication [28,29] which provides better link reliability and higher spectral efficiency. Due to coherent combination [30], the transmit power is inversely proportional to the number of transmit antennas. Thus, as the number of transmit antennas increases, the energy efficiency, signal throughput diversity gain, array gain, capacity gain, and beamforming gain will also be improved and can be obtained efficiently [31,32].

As for the current standard optimum detectors, maximum likelihood (ML) [33] has the best BER performance, but many researchers are distressed and discouraged due to its complexity. The main reason for this is that the complexity grows exponentially with the number of antennas, severely impacting hardware costs, while traditional linear detector methods, such as zero forcing (ZF) [34] and the minimum mean square error (MMSE) [35], have BER performance levels that are only inferior to ML. Regrettably, they still involve the calculation of the inverse matrix, which keeps the complexity high. To deal with the hazards of inverse matrices, many researchers have dedicated themselves to proposed methods based on iterative algorithms to avoid the annoying inverse matrices in mathematical operations, such as the Neumann series (NS) method, Gauss–Seidel (GS) method, Jacobi (JA) method, successive over-relaxation (SOR) method, and accelerated over-relaxation (AOR) method proposed by Liu et al. [36], Wu et al. [37], Kong et al. [38], Gao et al. [39], and Hadjidimos et al. [40], respectively. These detectors avoid the inverse matrix operation by linear iteration and then reduce the complexity from $\mathcal{O}\left(N^3\right)$ to $\mathcal{O}\left(N^2\right)$. However, their performance has yet to reach the required level of the current day and still needs improvement. Given this, Ning et al. [41] and Hu et al. [42] proposed a symmetric successive over-relaxation (SSOR) method and a symmetric accelerated over-relaxation (SAOR) method based on SOR and AOR, respectively, which utilize two similar symmetric matrices for iteration so that the performance can be better than the previous SOR method and AOR method. Even so, their performance results are unsatisfactory. Therefore, Yu et al. [43] and the authors in our previous work [44], through the two-stage structure proposed SOR method and AOR method combined with the Chebyshev algorithm, namely Chebyshev successive over-relaxation (CSOR) and Chebyshev accelerated over-relaxation (CAOR) techniques, respectively, produced efficient performance.

To reduce the high complexity of the linear detector caused by the increased transmitter antenna of M-MIMO and still maintain its BER performance, this study proposes a more advanced novel detection method combining the merits of the SOR and AOR methods to promote a balance between calculated complexity and BER performance. Simultaneously, we provide one option for disparate needs. Herein, we divide the proposed algorithm into two parts to improve the feasibility and reduce the risk of divergence. The first part, named the initial stage, involves preprocessing the parameters required for the proposed detection, such as the iteration matrix, matched filter (MF) compensation vector, and initial estimation signal. In the second part, called the collaboration stage, the parameters processed in the first part are mixed with the respective characteristics of SOR and AOR through the collaborative architecture to speed up convergence and refine performance. It is worth noting that this study cooperates with the SOR and AOR methods to achieve efficient performance through the joint architecture, which offsets their shortcomings and provides the effect of each compensating the other’s performance. Therefore, we named it mixed over-relaxation (MOR). The simulation results show that MOR detection only needs moderate computational complexity and good BER performance and is achievable with uplink multi-user M-MIMO OFDM and UFMC systems simultaneously. These are merits and features that other previous works do not present.

The rest of this paper is organized as follows. Section 2 introduces the system model adopted in this paper. Section 3 reviews some traditional iterative methods and the novel MOR detection method proposed in this study. The simulation results, complexity analysis, and verification of the proposed method are given in Section 4. Section 5 provides a concluding remark to summarize the paper.

2. System Model

This section will illustrate the architecture of the OFDM [17,26,45] and UFMC [21,23,26] systems and then briefly describe the M-MIMO channel model [17,28,46], channel estimation method, and standard MMSE detector [47], which acts as a benchmark for comparing BER performance.

2.1. OFDM Systems

As shown in Figure 1, the input data are first modulated by quadrature amplitude modulation (QAM) and inserted into pilot tones to generate a QAM symbol signal. The signal of the QAM symbol is serial-to-parallel (S/P) conversion and performs an N-point inverse fast Fourier transform (IFFT). Finally, parallel-to-serial (P/S) conversion is used to generate OFDM signals. It can be expressed as follows  [26]:

$$x_{OFDM}\left[n\right]=\sum _{k=0}^{N-1}X\left[k\right]e^{{\displaystyle \frac{j2\pi kn}{N}}},0\le n\le \left(N-1\right),$$

(1)

where $X\left[k\right]$ is the QAM symbol signal and N is the number of subcarriers.

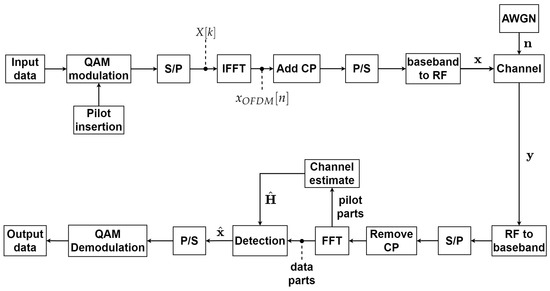
Figure 1. A system block diagram of the OFDM transceiver.

To better combat inter-symbol interference (ISI), adding a cyclic prefix (CP) to the OFDM signal can effectively avoid the occurrence of ISI, and according to [48], the length of the CP has been adopted and proven to be a quarter of the number of subcarriers. Before the signal is transmitted to the channel, the OFDM signal is converted from baseband to a radio frequency (RF) through a process called upconversion and sent to the receiving end through the channel.

At the receiving terminal, the channel’s RF signal output must first be converted into a baseband signal by the downconversion function. Then, the serial signal is altered to its parallel form using the S/P converter. Because a CP is added to the OFDM signal at the transmitter, the receiver must remove its CP component first and then perform an N-point fast Fourier transform (FFT). Herein, the signal includes two parts: the pilot and data parts, which must be separated. The pilot part is provided to the channel estimator to estimate the channel matrix, and the channel matrix mixes the data part into the detector to obtain the complex signal transmitted by the transmitter. Finally, the output data are produced through P/S conversion and QAM demodulation.

2.2. UFMC Systems

The UFMC system is a B5G candidate waveform extended by the OFDM system architecture to obtain a prompted spectrum efficiency. As shown in Figure 2, the input data are first modulated by QAM and inserted into pilot tones to generate QAM symbol signals. At this time, the QAM symbol signals are converted into S/P form and divided into B sub-bands, each with M QAM sub-symbol signals. To allow vector operations to be performed on the grouped sub-bands, each sub-band needs zero padding to the subcarrier length N. Then, each sub-band is subjected to N-point IFFT and multiplied by a finite impulse response (FIR) filter of a length L individually. Finally, vector addition and P/S conversion of all sub-band signals are performed to obtain the UFMC signal, whose vector length is $\left(N+L-1\right)$. The UFMC signal $x_{UFMC}\left[n\right]$ can be expressed as follows [26]:

$$x_{UFMC}\left[n\right]=\sum _{b=1}^B\sum _{l=0}^{L-1}\sum _{m=0}^{N-1}X\left[b,m\right]e^{{\displaystyle \frac{j2\pi mn}{N}}}{f}_b\left(l\right),0\le n\le \left(N+L-1\right),$$

(2)

where $X\left[b,m\right]$ is the QAM symbol signal after zero padding, its length is $N\times 1$, and $f_b\left(l\right)$ is the FIR filter for each sub-band. In this study, for the UFMC system, $f_b\left(l\right)$ is adopted based on the Dolph–Chebyshev filter, which can be written as [49,50]

$$f_b\left(l\right)=h_b\left(l\right)e^{{\displaystyle \frac{j2\pi }{N}}\left({\displaystyle \frac{N-N_{ZG}}{2}}+\left(b - {\displaystyle \frac{1}{2}}\right)n + {\displaystyle \frac{N}{2}}\right)l}, 0\le l\le \left(L-1\right),$$

(3)

where $N_{ZG}$ is the zero padding for each sub-band and $h_b\left(l\right)$ is the Dolph–Chebyshev prototype FIR filter, whose equation is [49,50]

$$h_b\left(l\right)={\left(-1\right)}^l{\displaystyle \frac{cos\left[N{cos}^{-1}\left[\mu cos\left({\displaystyle \frac{\pi l}{N}}\right)\right]\right]}{cosh\left[N{cosh}^{-1}\left(\mu \right)\right]}},$$

(4)

in which $\mu =cos\left[{\displaystyle \frac{1}{N}}{cosh}^{-1}\left({10}^{\alpha }\right)\right]$, $\alpha$ is the attenuation parameter, which is a positive real number and determines the relative sidelobe attenuation of the filter. In front, the signal is transmitted to the channel as the OFDM mentioned earlier, and the UFMC signal is upconverted and sent to the receiving end through the channel.

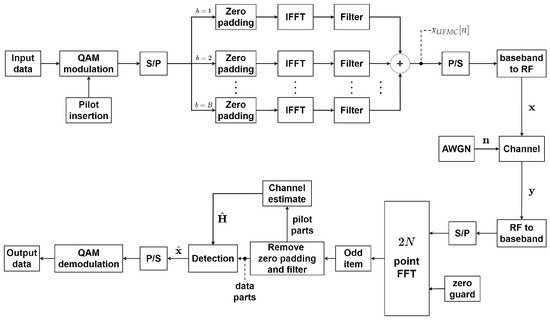
Figure 2. A system block diagram of the UFMC transceiver.

Similar to the aforementioned OFDM receiver, the UFMC channel output signal is downconverted and then S/P converted. At this time, when performing a $2N$-point FFT, it is necessary to first zero fill the received signal to twice the subcarrier length and then downsample it to recover the signal, which is performed to extract the odd-numbered elements after the FFT [25,26,27]. As in the previous subsection, separating the pilot and data parts is necessary. The pilot part is provided to the signal estimator to estimate the channel matrix, and the channel matrix mixes the data part into the detector to obtain the complex signal transmitted by the transmitter. Finally, the output data are obtained through P/S conversion and QAM demodulation.

2.3. Multi-User M-MIMO Channel Model

For the uplink M-MIMO scenario [28,29] in this article, we assumed that there was a total of $K{N}_t$ user antennas, denoted as $N_T$, and mounted $N_R$ antennas at the base station, where K is the number of users and each user has $N_t$ transmission antennas. In terms of setting the number of antennas, to ensure optimal detector performance and minimize thermal noise interference and channel estimation bias, we set the number for $N_R$ to be much larger than the total number of user antennas $N_T$. Moreover, the signal transmitted into the channel and the received signal can be denoted as $\mathbf{x}={\left[x_1,x_2,\dots ,x_{N_T}\right]}^T$ and $\mathbf{y}={\left[y_1,y_2,\dots ,y_{N_R}\right]}^T$, respectively. Furthermore, we use bold lowercase letters and bold capital letters to represent vectors and matrices, respectively, to make them easier to read. Therefore, the channel model can be expressed as follows [51,52]:

$$\mathbf{y}=\mathbf{H}\mathbf{x}+\mathbf{n},$$

(5)

where $\mathbf{H}\in {\mathbb{C}}^{N_R\times N_T}$ and $\mathbf{n}$ is the $N_R\times 1$ noise vector. To be clear, we have rewritten this as

$$\left[\begin{array}{c}{y}_1\\ ⋮\\ y_{N_R}\end{array}\right]=\left[\begin{array}{ccc}{h}_{11}& \cdots & h_{1N_T}\\ ⋮& \ddots & ⋮\\ h_{N_{R}1}& \cdots & h_{N_R{N}_T}\end{array}\right]\left[\begin{array}{c}{x}_1\\ ⋮\\ x_{N_T}\end{array}\right]+\left[\begin{array}{c}{n}_1\\ ⋮\\ n_{N_R}\end{array}\right].$$

(6)

Now, we will use the Rayleigh fading channel matrix [53] to simulate the outdoor environment for the above matrix $\mathbf{H}$. Without loss of generality, considering that the realistic environment has many external factors, we set up a channel with two independent and identically distributed (i.i.d.) paths and a Gaussian distribution that obeyed unit variance and a zero mean to align with the compatible actual environment [44]. The noise vector adopted additive white Gaussian noise (AWGN) that conformed to an i.i.d. and complex Gaussian distribution.

Here, we used a comb-type pilot structure [54] to measure the Rayleigh fading channel at the base station, which periodically inserted pilot tones into the subcarriers. Furthermore, we estimated the channel matrix with the least squares (LS) channel estimation method [55] with the pilot tones, and the result can be expressed as

$${\widehat{\mathbf{H}}}_{LS}={\left({\mathbf{X}}_p^H{\mathbf{X}}_p\right)}^{-1}{\mathbf{X}}_p^H{\mathbf{Y}}_p={\mathbf{X}}_p^{-1}{\mathbf{Y}}_p,$$

(7)

where ${\mathbf{X}}_p$ and ${\mathbf{Y}}_p$ denote the transmitted and received signals’ pilot tones, respectively.

As for the detector, it estimates the transmitted signal through the estimated channel matrix and the matched filter (MF). In light of this, according to [35,47,52], the traditional linear MMSE detection algorithm has been proven to be nearly optimal for uplink MIMO systems, and the estimation of its transmitted signal can be expressed as

$${\widehat{\mathbf{x}}}_{MMSE}={\left({\widehat{\mathbf{H}}}^H\widehat{\mathbf{H}}+{\sigma }^2{\mathbf{I}}_{N_T}\right)}^{-1}{\widehat{\mathbf{H}}}^H\mathbf{y}={\mathbf{W}}^{-1}{\mathbf{y}}^{MF},$$

(8)

where ${\sigma }^2$ denotes the noise variance, $\widehat{\mathbf{H}}$ is the channel estimation matrix, $\mathbf{W}$ is the filter matrix of MMSE, which is equal to $\left({\widehat{\mathbf{H}}}^H\widehat{\mathbf{H}}+{\sigma }^2{\mathbf{I}}_{N_T}\right)$, and ${\mathbf{y}}^{MF}$ is MF’s output, which is equivalent to ${\widehat{\mathbf{H}}}^H\mathbf{y}$.

3. Proposed Scheme

To clarify our proposed method, we will briefly describe the conventional SOR [39,56] and AOR [40,44] methods, including their convergence behavior. Immediately afterward, we will introduce our proposed MOR method, which allows improved BER performance and complexity balance with fewer iterations. Moreover, we will briefly discuss and derive convergence in Appendix A.

3.1. Overview of the Conventional SOR Method

According to [56], we consider a linear system whose mathematical equation can be expressed as

$$\mathbf{A}\mathbf{x}=\mathbf{b},$$

(9)

where $\mathbf{A}$ is a symmetric positive definite matrix, $\mathbf{x}$ is an arbitrary complex vector, and $\mathbf{b}$ the MF output of the received signal $\mathbf{y}$ after channel estimation. We can denote $\mathbf{b}$ as $\mathbf{b}={\widehat{\mathbf{H}}}^H\mathbf{y}={\mathbf{y}}^{MF}$, and it is a nonzero complex vector (i.e., $\mathbf{b}\in {\mathbb{C}}^n\setminus \left\{0\right\}$). Moreover, $\mathbf{A}$ can be decomposed into

$$\mathbf{A}=\mathbf{D}-\mathbf{L}-\mathbf{U},$$

(10)

in which $\mathbf{D}$, $-\mathbf{L}$, and $-\mathbf{U}$ are $\mathbf{A}$’s diagonal, lower, and upper triangular matrices, respectively. Then, the SOR iteration equation can be expressed as

$${\mathbf{x}}^{(i+1)}={\left(\mathbf{D}-\omega \mathbf{L}\right)}^{-1}\{\left[\left(1-\omega \right)\mathbf{D}+\omega \mathbf{U}\right]{\mathbf{x}}^{\left(i\right)}+\omega \mathbf{b}\},$$

(11)

where $\omega$ is the relaxation parameter. Herein, we replace ${\left(\mathbf{D}-\omega \mathbf{L}\right)}^{-1}$ and $\left[\left(1-\omega \right)\mathbf{D}+\omega \mathbf{U}\right]$ with ${\mathbf{M}}_{SOR}$ and ${\mathbf{N}}_{SOR}$, respectively, and further define the matrix ${\mathbf{G}}_{SOR}$, called the iteration matrix of SOR, which is expressed as

$${\mathbf{G}}_{SOR}={\mathbf{M}}_{SOR}{\mathbf{N}}_{SOR}.$$

(12)

Then, Equation (11) can be simplified and written as

$${\mathbf{x}}^{(i+1)}={\mathbf{G}}_{SOR}{\mathbf{x}}^{\left(i\right)}+{\mathbf{d}}_{SOR},$$

(13)

where ${\mathbf{d}}_{SOR}$, the MF compensation vector of SOR, comes from ${\mathbf{M}}_{SOR}$ multiplied by $\mathbf{d}$, where $\mathbf{d}$ is $\omega \mathbf{b}$.

The linear iterative algorithm judges its convergence using the spectral radius $\rho \left(\mathbf{G}\right)$ of matrix $\mathbf{G}$ as the criterion, which is defined as follows [44,57]:

$$\rho \left(\mathbf{G}\right)\triangleq \underset{\lambda \in \rho \left(\mathbf{G}\right)}{max}\left|\lambda \right|,$$

(14)

where $\lambda$ is the eigenvalue of $\mathbf{G}$. Moreover, Equation (11) will converge if $\rho \left({\mathbf{G}}_{SOR}\right)$ satisfies

$$\rho \left({\mathbf{G}}_{SOR}\right)=\underset{1<c<N_T}{max}\left|{\lambda }_c\right|<1.$$

(15)

According to [56], the SOR iterative algorithm has been proven to converge when it satisfies $0<\omega <2$.

3.2. Overview of the Conventional AOR Method

The conventional AOR iterative algorithm [40] is an extended version of the SOR iterative algorithm that, through a combination of relaxation parameters $\omega$ and acceleration parameters $\gamma$, obtains better performance, and the equation is as follows:

$${\mathbf{x}}^{(i+1)}={\left(\mathbf{D}-\gamma \mathbf{L}\right)}^{-1}\{\left[\left(1-\omega \right)\mathbf{D}+\left(\omega -\gamma \right)\mathbf{L}+\omega \mathbf{U}\right]{\mathbf{x}}^{\left(i\right)}+\omega \mathbf{b}\},$$

(16)

Similar to the SOR method, to simplify Equation (16), we define the matrix ${\mathbf{G}}_{AOR}$, called the iteration matrix of AOR, as

$${\mathbf{G}}_{AOR}={\mathbf{M}}_{AOR}{\mathbf{N}}_{AOR},$$

(17)

where ${\mathbf{M}}_{AOR}={\left(\mathbf{D}-\gamma \mathbf{L}\right)}^{-1}$ and ${\mathbf{N}}_{AOR}=\left[\left(1-\omega \right)\mathbf{D}+\left(\omega -\gamma \right)\mathbf{L}+\omega \mathbf{U}\right]$. Then, Equation (16) can be written as

$${\mathbf{x}}^{(i+1)}={\mathbf{G}}_{AOR}{\mathbf{x}}^{\left(i\right)}+{\mathbf{d}}_{AOR},$$

(18)

where ${\mathbf{d}}_{AOR}$ is the MF compensation vector of AOR, equal to ${\mathbf{M}}_{AOR}$ multiplied by $\mathbf{d}$. From Equation (14), we see that Equation (16) will converge if it satisfies

$$\rho \left({\mathbf{G}}_{AOR}\right)=\underset{1<c<N_T}{max}\left|{\lambda }_c\right|<1.$$

(19)

According to [44], when satisfying $0<\omega <2$, $0<\gamma <2$, and $\omega =\gamma$, the AOR iterative algorithm has been proven to converge.

3.3. Proposed MOR Method

After reviewing the previous subsections, we developed a novel detection combining the advantages of conventional SOR and AOR to improve BER performance and balance the complexity, which we call mixed over-relaxation (MOR). As shown in Figure 3, the first part is the initial stage, and some parameters required by the iterative algorithm must be processed. In the first step, we define the iteration matrix of MOR according to the iteration matrices ${\mathbf{G}}_{SOR}$ and ${\mathbf{G}}_{AOR}$ mentioned earlier in Section 3.1 and Section 3.2, respectively, which are written as follows:

$${\mathbf{G}}_{MOR}={\mathbf{G}}_{AOR}{\mathbf{G}}_{SOR}.$$

(20)

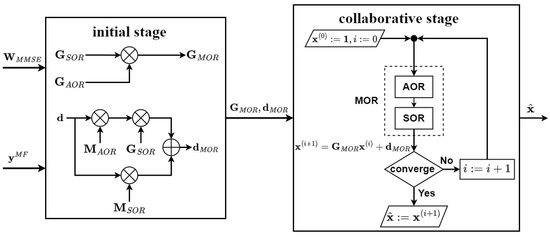
Figure 3. A block diagram of the proposed detection scheme.

Aside from that, we performed a mixed operation on the MF compensation vectors in the SOR and AOR iterative equations for better BER performance. Here, the MOR MF compensation signal ${\mathbf{d}}_{MOR}$ can be described as follows:

$${\mathbf{d}}_{MOR}=\left({\mathbf{G}}_{AOR}{\mathbf{M}}_{SOR}+{\mathbf{M}}_{AOR}\right)\mathbf{d}.$$

(21)

Next, to obtain appropriate initial $\omega$ and $\gamma$ values, we must first calculate the spectral radius of ${\mathbf{G}}_{MOR}$. The definition of the spectral radius $\rho \left({\mathbf{G}}_{MOR}\right)$ is the same as in Equation (14) in the previous subsection, and it can be written as

$$\rho \left({\mathbf{G}}_{MOR}\right)\triangleq \underset{\lambda \in \rho \left({\mathbf{G}}_{MOR}\right)}{max}\left|\lambda \right|,$$

(22)

Therefore, we can find the mathematical equations [44] for $\omega$ and $\gamma$:

$$\omega ={\displaystyle \frac{1}{\sqrt{1-{\mu }^2}}},$$

(23)

$$\gamma ={\displaystyle \frac{2}{1+\sqrt{1-{\mu }^2}}},$$

(24)

where $\mu$ is $\rho \left({\mathbf{G}}_{MOR}\right){|}_{\omega =1,\gamma =0}$.

The second part we call the collaboration phase. As shown in the MOR algorithm block (collaboration stage) proposed in Figure 3, we joined the relaxation characteristics of the SOR iteration algorithm and the acceleration ability of the AOR iteration algorithm. Through the collaborative architecture, SOR and AOR assist each other in estimating the better signal and apply the appropriate initialization $\omega$ and $\gamma$ to obtain the MOR iteration matrix ${\mathbf{G}}_{MOR}$ and MF compensation vector ${\mathbf{d}}_{MOR}$. The experimental results prove that the proposed MOR method has a faster convergence speed and better BER performance. Moreover, its iteration equation can be simplified as follows:

$${\mathbf{x}}^{(i+1)}={\mathbf{G}}_{MOR}{\mathbf{x}}^{\left(i\right)}+{\mathbf{d}}_{MOR}.$$

(25)

It is worth noting that the parameters generated in the initial stage in Figure 3 only need to be calculated once, which include the iterative matrix ${\mathbf{G}}_{MOR}$, MF compensation vector ${\mathbf{d}}_{MOR}$, and initial estimate signal ${\mathbf{x}}^{\left(0\right)}$, which are provided to the collaboration stage for iterative calculation. The procedure of the proposed MOR detection method is shown in Algorithm 1. As for its convergence of MOR, we will derive this in detail in Appendix A. Therefore, we know that MOR will converge when $0<\omega <2$ and $0<\gamma <2$. Aside from that, we can compare the convergence conditions of SOR and AOR to MOR and find that MOR does not increase the convergence difficulty and also does not limit $\omega =\gamma$ as AOR does, which means that MOR has higher flexibility in choosing $\omega$ and $\gamma$.

Algorithm 1 Proposed MOR detection algorithm.

Receiver signal input: ${\mathbf{W}}_{MMSE}={\widehat{\mathbf{H}}}^H\widehat{\mathbf{H}}+{\sigma }^2{\mathbf{I}}_{N_T}\triangleq \mathbf{A}$, and $\mathbf{A}=\mathbf{D}+\mathbf{L}+\mathbf{U}$ ${\mathbf{y}}^{MF}={\widehat{\mathbf{H}}}^H\mathbf{y}\triangleq \mathbf{b}$ The first part: (initial stage) ${\mathbf{M}}_{SOR}={\left(\mathbf{D}-\omega \mathbf{L}\right)}^{-1}$, ${\mathbf{N}}_{SOR}=\left[\left(1-\omega \right)\mathbf{D}+\omega \mathbf{U}\right]$ ${\mathbf{M}}_{AOR}={\left(\mathbf{D}-\gamma \mathbf{L}\right)}^{-1}$, ${\mathbf{N}}_{AOR}=\left[\left(1-\omega \right)\mathbf{D}+\left(\omega -\gamma \right)\mathbf{L}+\omega \mathbf{U}\right]$ ${\mathbf{G}}_{SOR}={\mathbf{M}}_{SOR}{\mathbf{N}}_{SOR}$, ${\mathbf{G}}_{AOR}={\mathbf{M}}_{AOR}{\mathbf{N}}_{AOR}$ ${\mathbf{G}}_{MOR}={\mathbf{G}}_{AOR}{\mathbf{G}}_{SOR}$ $\mathbf{d}=\omega \mathbf{b}$, ${\mathbf{d}}_{MOR}=\left({\mathbf{G}}_{AOR}{\mathbf{M}}_{SOR}+{\mathbf{M}}_{AOR}\right)\mathbf{d}$ $\omega ={\displaystyle \frac{1}{\sqrt{1-{\mu }^2}}}$, $\gamma ={\displaystyle \frac{2}{1+\sqrt{1-{\mu }^2}}}$, $\mu =\rho \left({\mathbf{G}}_{MOR}\right){|}_{\omega =1,\gamma =0}$ Set $i:=0$ and ${\mathbf{x}}^{\left(0\right)}:=\mathbf{1}$ The second part: (collaborative stage) While not converging, do ${\mathbf{x}}^{\left(i+1\right)}={\mathbf{G}}_{MOR}{\mathbf{x}}^{\left(i\right)}+{\mathbf{d}}_{MOR}$ $i:=i+1$ End Set $\widehat{\mathbf{x}}:={\mathbf{x}}^{\left(i+1\right)}$ Receiver signal output: The estimate of the transmitted signal vector $\widehat{\mathbf{x}}$

4. Simulation Results and Complexity Analysis

4.1. Simulation Results and Discussion

In this section, some numerical simulations will be performed to evaluate and verify the performance of our proposed novel receiver. Moreover, we use the famous Matlab(Version R2022a) mathematical software tool to simulate the numerical results and graphics, execute Monte Carlo 500,000 for each graph, and use Microsoft Excel for calculations and statistical tables. Considering the OFDM multi-carrier technology, UFMC multi-carrier technology, and $N_R\times N_T$ uplink multi-user M-MIMO environment described in Section 2, as shown in Table 1, we fed the same total data volume of 512 to experiment with the two systems equitably, and the pilot tone insertion interval was 0.05. Therefore, each symbol inserted 25 pilot tones and 1024 QAM modulation. For the particular parameters of OFDM in the 4G environment and UFMC in the B5G environment, the former needed to set a cyclic prefix (CP) whose length was one quarter of the subcarrier (i.e., 128), and the volume of the data was equal to the number of subcarriers. In the latter, the size of subcarrier N was 1024, the number of sub-bands B was 16, and each sub-band was allocated a data volume of 32 (i.e., M). It is worth noting that the product of the two could not be greater than the number of subcarriers N (i.e., the total data amount needed to be less than or equal to the number of subcarriers), in which the number of zero padding was the subcarrier minus the data amount and would be divided into the starting and tailing of the data vector (i.e., 256). According to [58,59,60], the UFMC waveform adopted the Chebyshev FIR filter, where the filter length L was 43 and the side attenuation was 40. In addition, we assumed that the channel was a two-multipath flat Rayleigh fading channel with AWGN, and the receiver could obtain channel state information (CSI) through the least squares (LS) estimation scheme. We chose SOR [39], AOR [40], SSOR [41], SAOR [42], CSOR [43], and CAOR [44] as the BER performance and complexity comparison objects of the proposed MOR scheme and used the MMSE as the BER performance benchmark. Moreover, we briefly describe the features of previously published works and our proposed MOR scheme in Table 2.

Table 1. Enumerate parameters used in simulation scenarios.

Parameter	Value
Common parameters
Modulation scheme	1024 QAM
Volume of data	512
Amount of pilot data in one symbol	25
The maximum SNR (dB)	50
Channel type	Rayleigh fading channel
Number of users K	8
Number of transmission antennas in one user $N_t$	2
Number of channel taps	2
Noise	AWGN
Channel estimation	LS
The number of experiments for Monte Carlo (times)	500,000
OFDM specific parameters
CP length	128
UFMC specific parameters
Number of subcarriers N	1024
Number of sub-bands B	16
Number of subcarriers in each sub-band M	32
Amount of zero padding in each sub-band $N_{ZG}$	256
Filter type	Chebyshev FIR filter
Filter length L	43
Filter sidelobe attenuation (dB)	40

Table 2. Brief descriptions of our proposed scheme and previously published works.

Scheme	Brief Description
SOR [39]	SOR is a linear iterative method, and it was derived from adding relaxation parameters $\omega$ to the Gauss–Seidel iterative algorithm.
AOR [40]	The AOR iterative algorithm is an extension of the SOR iterative algorithm. It is a linear iterative method derived through the relaxation parameter $\omega$ and the newly added acceleration parameter $\gamma$.
SSOR [41]	SSOR combines two SOR sweeps in a semi-iterative architecture to produce an iterative matrix similar to a symmetric matrix.
SAOR [42]	SAOR combines two AOR sweeps in a semi-iterative architecture to produce an iterative matrix similar to a symmetric matrix.
CSOR [43]	The CSOR method combines the SOR iterative algorithm and the recursive characteristics of the Chebyshev polynomials.
CAOR [44]	The CAOR method combines the AOR iterative algorithm and the recursive characteristics of the Chebyshev polynomials.
MOR	Our proposed MOR method joins the characteristics and abilities of both the SOR and AOR iterative algorithms to accelerate iterative convergence and obtain efficient BER performance through a collaborative architecture.

To verify and roughly observe the characteristics between the OFDM and UFMC waveforms regarding BER performance and the power spectral density (PSD), we conducted some experiments to demonstrate their disparity, as shown in Figure 4 and Figure 5. In Figure 4, we can see that the UFMC effectively improved the BER performance when $N_R\times N_T=64\times 16$ and utilized the MMSE detector. Especially when the SNR level was 35 dB, the UFMC and OFDM BER performance values were $2.061\times {10}^{-5}$ and $9.886\times {10}^{-4}$, respectively, which could be improved by approximately $97.916\%$. As for the PSD, which is an agreeable index of the impact of OOBMs, as shown in Figure 5, we can observe that under the same environment and data volume, the UFMC had better OOBM resistance than OFDM, which means it resisted intercarrier interference (ICI) better [22,61]. By combining the BER performance and PSD simulation results, we know that the UFMC had better BER performance and could achieve better OOBM resistance, which is expected in future B5G wireless communication systems.

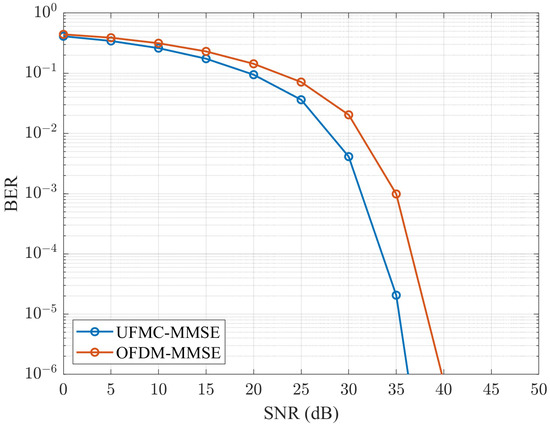
Figure 4. An MMSE BER performance comparison for OFDM vs. UFMC with $N_R\times N_T=64\times 16$ and $K=8$.

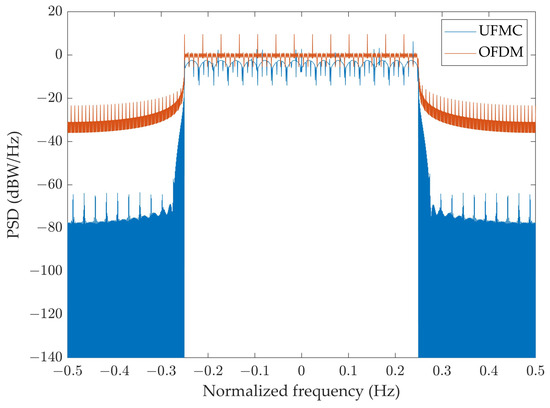
Figure 5. A PSD comparison for OFDM vs. UFMC.

Next, we will explore MOR detectors that can be applied to 4G and B5G multi-carrier technologies. To obtain the appropriate relaxation parameter $\omega$ and acceleration parameter $\gamma$, we first used Equations (23) and (24) to obtian the preliminary relaxation parameter $\omega$ and acceleration parameter $\gamma$. Apart from this, as shown in Figure 6 and Figure 7, the acceleration parameter $\gamma$ and relaxation parameter $\omega$ are depicted for different relaxation parameter $\omega$ values and acceleration parameter $\gamma$ values for our proposed method in the OFDM and UFMC, respectively, comparing the BER performance graphs when the iteration number i was 4, $N_R\times N_T$ was $64\times 16$, and the SNR was at 35 dB. We can observe in Figure 6a,b that if $\gamma$ was the curve of $1.1$, the BER performance would improve, whereas the BER performance would decrease, and the best BER performance was when $\omega$ was equal to $1.2$. Similarly, we also observed the same values of $\omega$ and $\gamma$ in Figure 6 and Figure 7. In light of this, choosing a $\gamma$ value close to $1.1$ and $\omega$ value close to $1.2$ would have the best estimate. Meanwhile, the experimental simulation data in Figure 6 and Figure 7 were consistent with the theoretical calculation values of Equations (23) and (24). It is worth noting that regardless of whether the MOR operated in the OFDM or UFMC, the optimal values of $\omega$ and $\gamma$ were the same, which is ideal. This means that the MOR-optimized BER performance could still be obtained without recalculation if applied to 4G or B5G systems, substituting $\omega$ with $1.1$ and $\gamma$ with $1.2$.

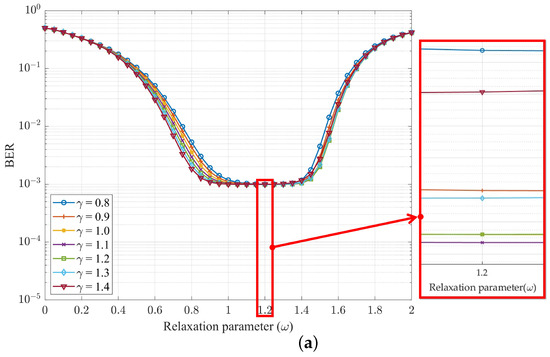
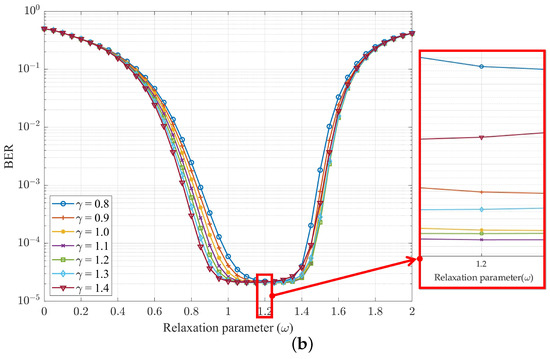
Figure 6. BER performance of MOR method relative to $\omega$ with SNR $=35$ dB, $N_R\times N_T=64\times 16$, $K=8$, and number of iterations i of 4 for (a) OFDM and (b) UFMC.

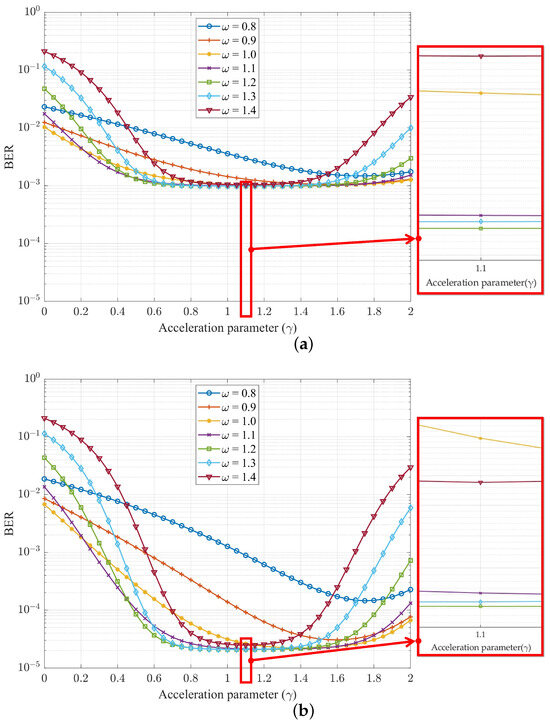
Figure 7. BER performance of MOR method relative to $\gamma$ with SNR $=35$ dB, $N_R\times N_T=64\times 16$, $K=8$, and number of iterations i of 4 for (a) OFDM and (b) UFMC.

Figure 8 and Figure 9 depict the BER performance comparison of different detection methods when the iteration number i was 3 and 4, respectively. Among them, Figure 8a and Figure 9a apply to the OFDM system, and Figure 8b and Figure 9b apply to the UFMC system. In Figure 8a,b, we can observe that when the iteration number i was equal to 3, our proposed method was already close to the performance of the MMSE. Moreover, when the SNR was at 40 dB, we compared the BER performance of MOR and related it to that of the CAOR, and for the OFDM system, it was approximately $1.395\times {10}^{-6}$ and $8.563\times {10}^{-3}$, respectively, an improvement of $99.984\%$. The UFMC system’s results were roughly $3.878\times {10}^{-8}$ and $7.773\times {10}^{-3}$, respectively, an improvement of $99.999\%$. As shown in the numerical values, the BER performance of our new method was significantly improved compared with CAOR, let alone other iterative detection methods. In addition, as shown in Figure 9a,b, when the iteration number i was equal to 4, the BER performance of our method overlapped with the MMSE method.

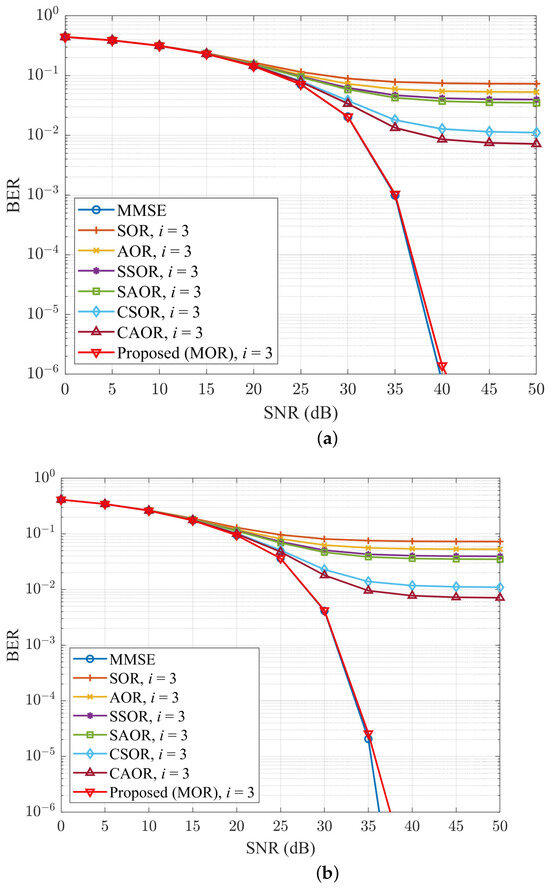
Figure 8. BER performance comparison for different detection methods with $N_R\times N_T=64\times 16$, $K=8$, and number of iterations i of 3, for (a) OFDM and (b) UFMC.

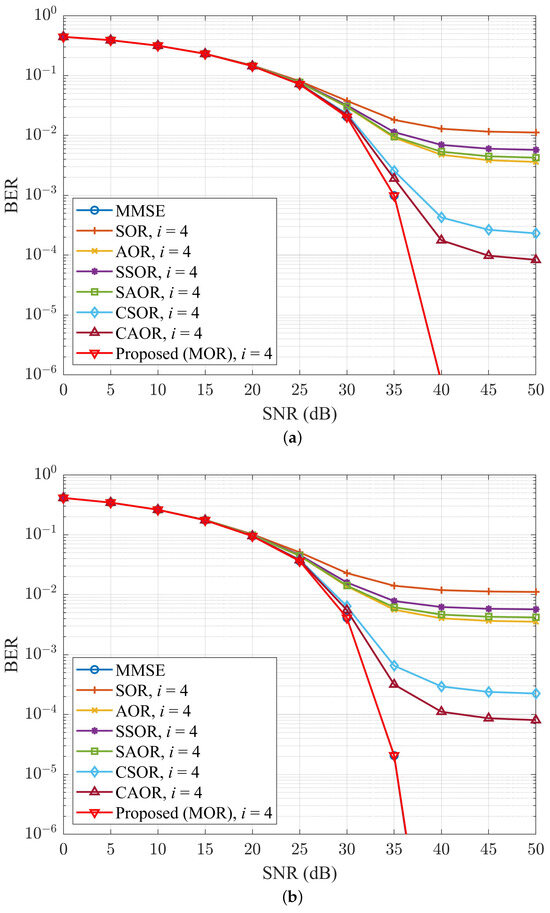
Figure 9. BER performance comparison for different detection methods with $N_R\times N_T=64\times 16$, $K=8$, and number of iterations i of 4 for (a) OFDM and (b) UFMC.

Following this, we will observe when the number of base station antennas $N_R$ increases, as shown in Figure 10 and Figure 11, which depict the BER performance comparison of different detection methods run in OFDM and UFMC systems when the number of base station antennas $N_R$ was 128 and 256, respectively, while the fixed iteration number i was 2. In Figure 10a, we can observe that when the SNR was at 35 dB and $N_R$ was 128, the MOR and CAOR BER performance of the OFDM system were approximately $1.838\times {10}^{-5}$ and $6.030\times {10}^{-3}$, respectively, an improvement of $99.695\%$; In Figure 10b, the MOR and CAOR BER performance of the UFMC system were approximately $6.208\times {10}^{-7}$ and $4.955\times {10}^{-3}$, respectively, an improvement of $99.987\%$. In Figure 11, when $N_R$ kept increasing to 256, whether the OFDM or UFMC system was used, MOR only needed two time iterations, and the BER performance already overlapped with the MMSE.

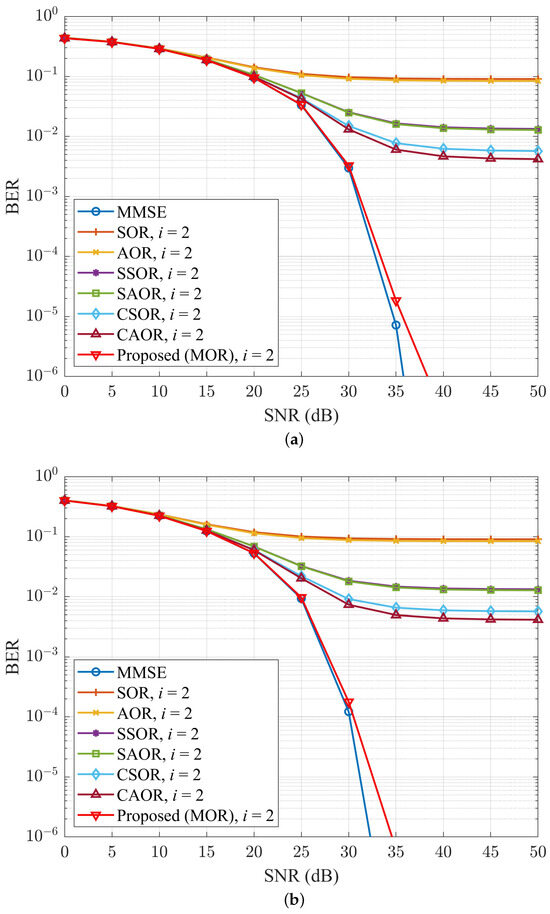
Figure 10. BER performance comparison for different detection methods with $N_R\times N_T=128\times 16$, $K=8$, and number of iterations i of 2 for (a) OFDM and (b) UFMC.

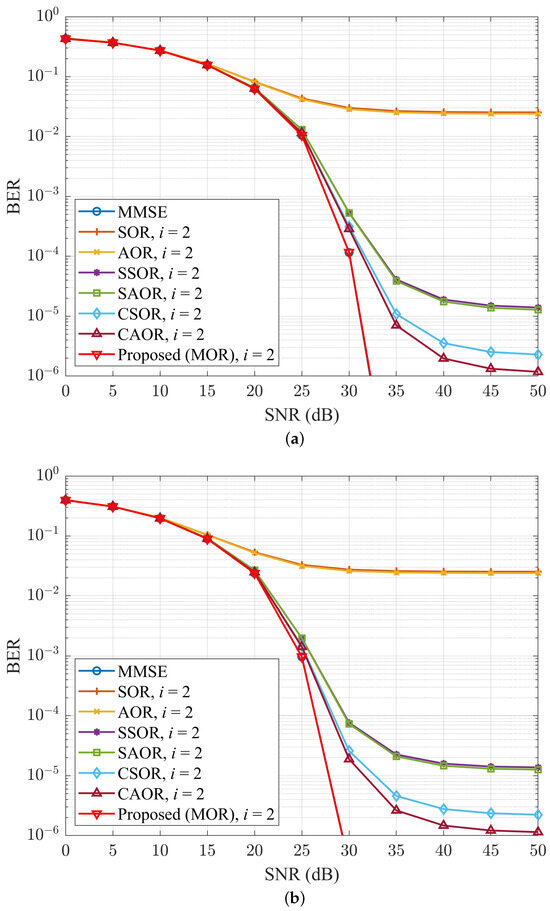
Figure 11. BER performance comparison for different detection methods with $N_R\times N_T=256\times 16$, $K=8$, and number of iterations i of 2 for (a) OFDM and (b) UFMC.

To analyze the BER performance of different detector methods varies with the ratio of $N_R$ to the total number of user antennas $N_T$, we denoted this as $\beta$, which is called the antenna ratio [52]. Figure 12 and Figure 13 show the variations in BER performance of different detector methods for OFDM and UFMC systems when the iteration number i was 2 and 3, respectively. From Figure 12 and Figure 13, we took some samples to look at the BER improvement, as shown in Table 3 and Table 4, respectively. For example, when $\beta$ was equal to 16, the MOR and CAOR of the OFDM system were approximately $1.174\times {10}^{-4}$ and $2.862\times {10}^{-4}$, respectively, an improvement of $58.979\%$.

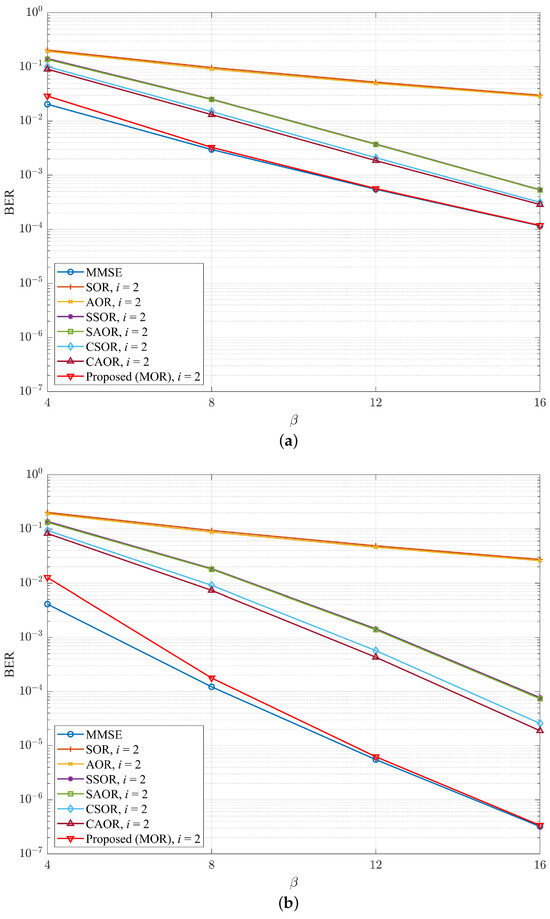
Figure 12. (a) OFDM and (b) UFMC, BER vs. $\beta$ for different detection schemes when the number of iterations i was 2 and the SNR was 30 dB.

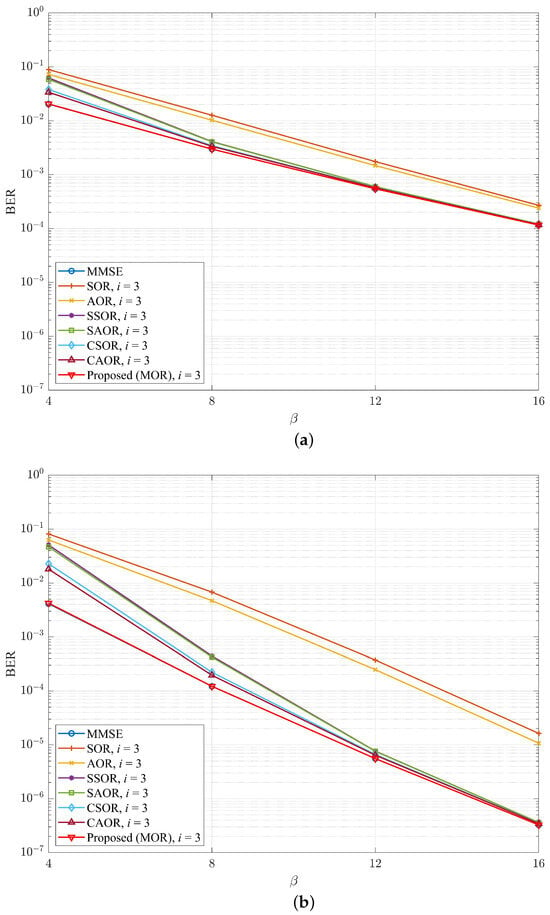
Figure 13. (a) OFDM and (b) UFMC, BER vs. $\beta$ for different detection schemes when the number of iterations i was 3 and the SNR was 30 dB.

Table 3. Comparison of BER improvement of MOR vs. previous works at $\beta =16$ for the OFDM system.

Number of Iterations	CAOR [44]	CSOR [43]	SAOR [42]	SSOR [41]	AOR [40]	SOR [39]
$i=2$	$58.979\%$	$62.589\%$	$77.826\%$	$78.116\%$	$99.589\%$	$99.608\%$
$i=3$	$2.026\%$	$2.310\%$	$4.290\%$	$4.315\%$	$51.695\%$	$57.018\%$

Table 4. Comparison of BER improvement of MOR vs. previous works at $\beta =16$ for the UFMC system.

Number of Iterations	CAOR [44]	CSOR [43]	SAOR [42]	SSOR [41]	AOR [40]	SOR [39]
$i=2$	$98.214\%$	$98.690\%$	$99.542\%$	$99.563\%$	$99.998\%$	$99.999\%$
$i=3$	$5.717\%$	$6.395\%$	$9.784\%$	$9.958\%$	$96.957\%$	$97.998\%$

As shown by the numerical values, we could find that the gap in BER performance of all iterative methods had a decreasing trend. Undoubtedly, as the $\beta$ values grew, BER performance was improved with more antennas due to the spatial diversity gain [62,63]. Above all, our proposed method achieved the best BER performance compared with the abovementioned detection methods regardless of the value of $\beta$. Simultaneously, as the number of antennas kept increasing, the required iterations were also relatively reduced.

To further illustrate the impact of the numerical antenna ratio $\beta$ on BER performance, in Table 5 and Table 6, we compare the degree to which the BER performance of each iterative method was close to the MMSE when the number of iterations i was 2 and 3 in the form of a logarithm value (i.e., to obtain a more demarcated numerical comparison, we took the logarithm operation $log\left(·\right)$ and denoted it as a separation rate between the MMSE) of the BER distance between each detection method and the traditional MMSE, and the data came from the simulation data in Figure 12 and Figure 13. We can observe that in Table 5 and Table 6, under different $\beta$ conditions, the distance between MOR and the traditional MMSE was the smallest. For instance, in the OFDM and UFMC, when $\beta$ was 16 and i was 2, the BER separation rates between MOR and the MMSE were $0.0061$ and $0.0215$, respectively. Aside from that, when $\beta$ was 8 and i was 3, the BER separation rate of MOR and the MMSE was $0.0001$ and $0.0005$, respectively, which means the proposed method was already extremely close to the MMSE. Furthermore, when $\beta$ was 16 and i was 3, the BER separation rate between MOR and the MMSE in the OFDM and UFMC was 0 and $-0.0007$, respectively. As shown in the numerical value, the distance in the UFMC system was already negative, which means that the BER performance distance ratio between MOR and the MMSE was less than one. Hence, the value became a negative value after the logarithm operation $log\left(·\right)$. In light of this, the separation rate value was smaller, and the BER performance of the detector was closer to the MMSE.

Table 5. Comparison of BER performance separation rates between all detectors and MMSE in different $\beta$ under an iteration number i of 2 and SNR at 30 dB for (a) OFDM and (b) UFMC.

Scheme	$\mathit{\beta }=4$	$\mathit{\beta }=8$	$\mathit{\beta }=12$	$\mathit{\beta }=16$
		(a)
SOR [39]	$1.0008$	$1.5153$	$1.9799$	$2.4129$
AOR [40]	$0.9777$	$1.4873$	$1.9552$	$2.3921$
SSOR [41]	$0.8439$	$0.9307$	$0.8355$	$0.6660$
SAOR [42]	$0.8276$	$0.9239$	$0.8284$	$0.6603$
CSOR [43]	$0.6947$	$0.7013$	$0.5836$	$0.4330$
CAOR [44]	$0.6482$	$0.6449$	$0.5303$	$0.3930$
Proposed MOR	$0.1522$	$0.0399$	$0.0138$	$0.0061$
		(b)
SOR [39]	$1.6925$	$2.8858$	$3.9460$	$4.9298$
AOR [40]	$1.6674$	$2.8555$	$3.9195$	$4.9080$
SSOR [41]	$1.5252$	$2.1803$	$2.4161$	$2.3807$
SAOR [42]	$1.5076$	$2.1693$	$2.3989$	$2.3610$
CSOR [43]	$1.3578$	$1.8727$	$2.0138$	$1.9043$
CAOR [44]	$1.3017$	$1.7794$	$1.8911$	$1.7695$
Proposed MOR	$0.4893$	$0.1636$	$0.0528$	$0.0215$

Table 6. Comparison of BER performance separation rates between all detectors and MMSE in different $\beta$ under an iteration number i of 3 and SNR at 30 dB for (a) OFDM and (b) UFMC.

Scheme	$\mathit{\beta }=4$	$\mathit{\beta }=8$	$\mathit{\beta }=12$	$\mathit{\beta }=16$
		(a)
SOR [39]	$0.6406$	$0.6283$	$0.5046$	$0.3667$
AOR [40]	$0.5523$	$0.5364$	$0.4307$	$0.3160$
SSOR [41]	$0.4857$	$0.1397$	$0.0415$	$0.0192$
SAOR [42]	$0.4594$	$0.1354$	$0.0410$	$0.0191$
CSOR [43]	$0.2707$	$0.0643$	$0.0220$	$0.0102$
CAOR [44]	$0.2197$	$0.0514$	$0.0186$	$0.0089$
Proposed MOR	$0.0026$	$0.0001$	0	0
		(b)
SOR [39]	$1.2935$	$1.7443$	$1.8282$	$1.6979$
AOR [40]	$1.1828$	$1.5852$	$1.6505$	$1.5160$
SSOR [41]	$1.0907$	$0.5603$	$0.1396$	$0.0448$
SAOR [42]	$1.0539$	$0.5384$	$0.1365$	$0.0440$
CSOR [43]	$0.7417$	$0.2591$	$0.0766$	$0.0280$
CAOR [44]	$0.6407$	$0.2048$	$0.0633$	$0.0248$
Proposed MOR	$0.0102$	$0.0005$	$0.0001$	$-0.0007$

To understand the convergence of different detectors under different numbers of base station antennas $N_R$, Figure 14, Figure 15 and Figure 16 show the relationship between the iteration number i and BER performance in OFDM and UFMC systems when $N_R$ was 64, 128, and 192, respectively. While $N_R$ was 64 and the SNR was 37 dB, as shown in Figure 14, MOR almost converged at four iterations, which can also be verified by Figure 9. Moreover, at the same iteration count of four, when comparing MOR to CAOR, the BER performance in the OFDM and UFMC systems improved by $80.540\%$ and $99.705\%$, respectively. Similarly, as shown in Figure 15, when $N_R$ increased to 128, the SNR level was 33 dB, and MOR nearly converged while only needing three iterations. In other words, at the same iteration count of three, when comparing MOR to CAOR, the BER performance in the OFDM and UFMC systems improved by $35.220\%$ and $88.542\%$, respectively. As for $N_R$ increasing to 192 and the SNR being at 31 dB, as shown in Figure 16, we found that the MOR method could approach convergence in only two iterations for either the OFDM or UFMC systems. Compared with CAOR, their BER performance increased by $84.196\%$ and $99.776\%$, respectively. Echoing the previous antenna ratio $\beta$ analysis, M-MIMO would enhance the BER performance when increasing the number of base station antennas $N_R$. Moreover, our proposed MOR algorithm had the best BER performance and the fastest convergence speed among the abovementioned detectors.

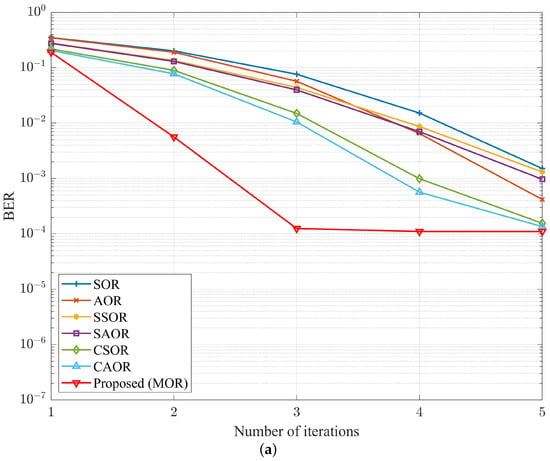
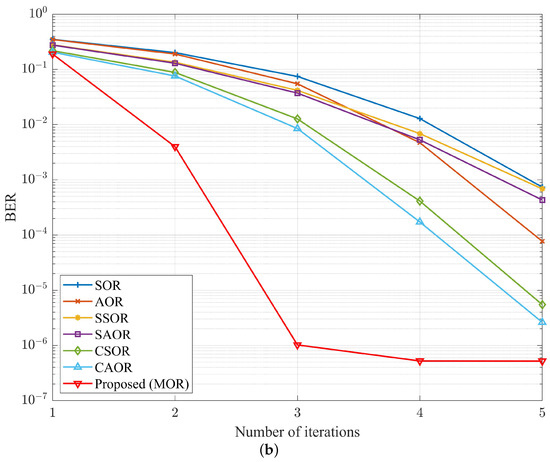
Figure 14. BER performance vs. number of iterations with $N_R\times N_T=64\times 16$, $K=8$, and SNR $=37$ dB for (a) OFDM and (b) UFMC.

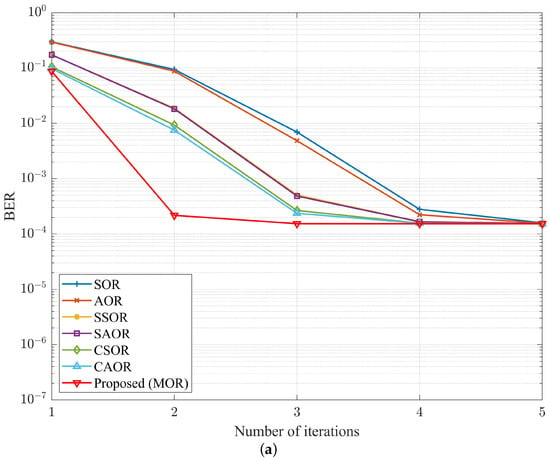
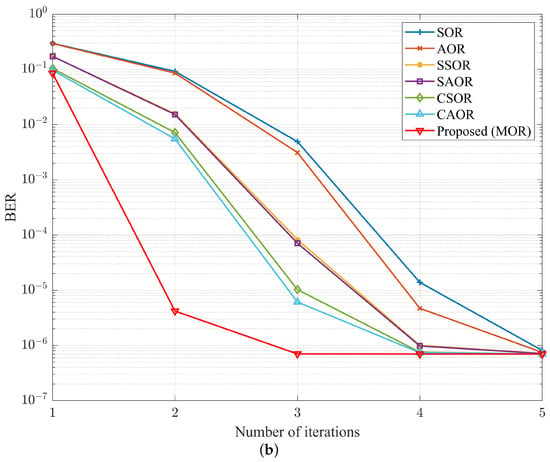
Figure 15. BER performance vs. number of iterations with $N_R\times N_T=128\times 16$, $K=8$, and SNR $=33$ dB for (a) OFDM and (b) UFMC.

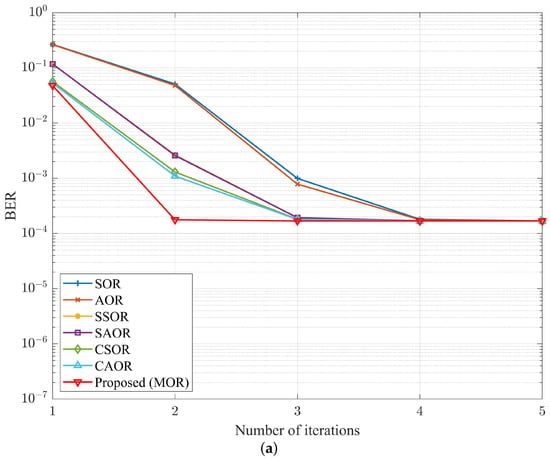
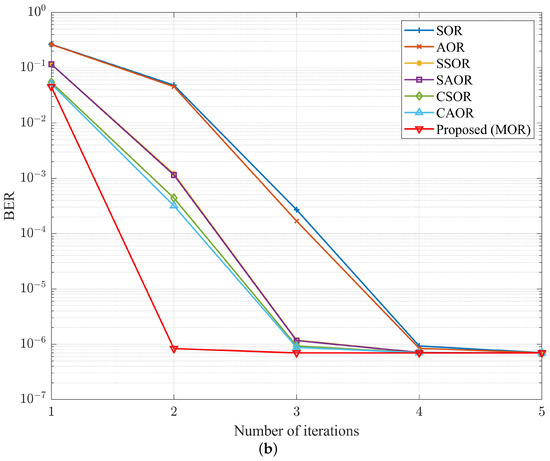
Figure 16. BER performance vs. number of iterations with $N_R\times N_T=192\times 16$, $K=8$, and SNR $=31$ dB for (a) OFDM and (b) UFMC.

To more clearly observe the numerical evolution of the number of iterations and BER performance under different numbers of antennas, where $N_R$ was 128 and 192, as well as the progress of each method approaching the MMSE, we organized the data into Table 7 and Table 8 from Figure 15 and Figure 16, respectively. Similar to Table 5 and Table 6, to obtain a clear numerical comparison, we took the logarithm operation $log\left(·\right)$ of the BER distance between each detector and the MMSE at iteration numbers i from 2 to 5. In Table 7a,b, we observe that MOR was quite near the MMSE in only three iterations when $N_R$ was 128 and the SNR was at 36 dB. Compared with CAOR, the separation rate with the MMSE in the OFDM system was $0.0006$ and $0.1891$, respectively, being shortened by $0.1885$, while in the UFMC system, the values were $0.0020$ and $0.9429$, respectively, being compressed by $0.9409$. In Table 8, $N_R$ increased to 192. The MOR scheme was extremely close to the MMSE and only needed two iterations. Moreover, there was a significant gap with other iteration methods. It is worth noting that in Table 7b and Table 8b, when the iteration number i reached 5 and 4, respectively, the BER separation rate between MOR and the MMSE was already a negative value. To summarize Table 7 and Table 8, the MOR detector had the fastest convergence and was closest to the optimal BER performance compared with thte other methods, whether in the OFDM or UFMC systems. Moreover, the experimental results in Figure 14, Figure 15 and Figure 16 show that in addition to Appendix A theoretically proving the convergence of the MOR scheme, it is also verified convergence from the experimental data.

Table 7. Comparison of BER performance separation rates between all detectors and MMSE in different iteration numbers when $N_R\times N_T=128\times 16$ and SNR level was 33 dB for (a) OFDM and (b) UFMC.

Scheme	$\mathit{i}=2$	$\mathit{i}=3$	$\mathit{i}=4$	$\mathit{i}=5$
		(a)
SOR [39]	$2.7875$	$1.6570$	$0.2604$	$0.0162$
AOR [40]	$2.7573$	$1.5006$	$0.1624$	$0.0089$
SSOR [41]	$2.0874$	$0.5203$	$0.0370$	$0.0037$
SAOR [42]	$2.0766$	$0.5002$	$0.0355$	$0.0036$
CSOR [43]	$1.7833$	$0.2392$	$0.0104$	$0.0003$
CAOR [44]	$1.6917$	$0.1891$	$0.0070$	$0.0002$
Proposed MOR	$0.1517$	$0.0006$	0	0
		(b)
SOR [39]	$5.1212$	$3.8485$	$1.2989$	$0.0649$
AOR [40]	$5.0897$	$3.6505$	$0.8284$	$0.0304$
SSOR [41]	$4.3528$	$2.0726$	$0.1591$	$0.0101$
SAOR [42]	$4.3387$	$2.0076$	$0.1460$	$0.0091$
CSOR [43]	$4.0115$	$1.1673$	$0.0344$	$0.0010$
CAOR [44]	$3.8973$	$0.9429$	$0.0238$	$0.0010$
Proposed MOR	$0.7785$	$0.0020$	$0.0002$	$-0.0001$

Table 8. Comparison of BER performance separation rates between all detectors and MMSE in different iteration numbers when $N_R\times N_T=192\times 16$ and SNR level was 31 dB for (a) OFDM and (b) UFMC.

Scheme	$\mathit{i}=2$	$\mathit{i}=3$	$\mathit{i}=4$	$\mathit{i}=5$
		(a)
SOR [39]	$2.4801$	$0.7712$	$0.0305$	$0.0011$
AOR [40]	$2.4547$	$0.6671$	$0.0219$	$0.0006$
SSOR [41]	$1.1957$	$0.0596$	$0.0039$	$0.0004$
SAOR [42]	$1.1855$	$0.0587$	$0.0039$	$0.0004$
CSOR [43]	$0.8873$	$0.0321$	$0.0009$	0
CAOR [44]	$0.8124$	$0.0269$	$0.0006$	0
Proposed MOR	$0.0208$	0	0	0
		(b)
SOR [39]	$4.8419$	$2.5898$	$0.1252$	$0.0044$
AOR [40]	$4.8152$	$2.3851$	$0.0834$	$0.0015$
SSOR [41]	$3.2391$	$0.2311$	$0.0077$	$0.0003$
SAOR [42]	$3.2191$	$0.2232$	$0.0077$	$0.0003$
CSOR [43]	$2.8017$	$0.1264$	$0.0035$	$0.0003$
CAOR [44]	$2.6612$	$0.1017$	$0.0022$	$0.0003$
Proposed MOR	$0.0286$	$0.0008$	$-0.0001$	$-0.0001$

Finally, to verify M-MIMO affecting the capability of the OFDM and UFMC systems, Table 9 shows the improvement range of various iterative methods in the OFDM and UFMC as $N_R$ increased, which can be referred to in Figure 12. We know that no matter whether the OFDM or UFMC system was used, when the number of antennas increased in the M-MIMO environment, all schemes could obtain significantly improved BER performance, of which the amount of gain in the UFMC was slightly higher than that of the OFDM system, which means that the UFMC system had better adaptability to M-MIMO. Also, the proposed MOR detector is entirely compatible with M-MIMO environments in both OFDM and UFMC systems and has better spatial diversity gain. It is worth noting that MOR can be used seamlessly for the 4G environment of the OFDM system and B5G environment of the UFMC system. Therefore, the proposed MOR detector is highly competitive in the 4G and B5G environments.

Table 9. BER improvement rates of different detection schemes when iteration number i was 2 and SNR was 33 dB for $N_R=128$, 192, and 256 for (a) OFDM and (b) UFMC.

Scheme	${\mathit{N}}_{\mathit{R}}=128$	${\mathit{N}}_{\mathit{R}}=192$	${\mathit{N}}_{\mathit{R}}=256$
(a)
SOR [39]	$52.373\%$	$74.435\%$	$85.341\%$
AOR [40]	$52.902\%$	$74.528\%$	$85.265\%$
SSOR [41]	$82.208\%$	$97.369\%$	$99.613\%$
SAOR [42]	$81.815\%$	$97.369\%$	$99.612\%$
CSOR [43]	$85.210\%$	$97.312\%$	$99.689\%$
CAOR [44]	$85.543\%$	$97.923\%$	$99.685\%$
Proposed MOR	$88.750\%$	$98.050\%$	$99.795\%$
(b)
SOR [39]	$53.632\%$	$75.869\%$	$96.501\%$
AOR [40]	$54.283\%$	$75.998\%$	$86.430\%$
SSOR [41]	$86.601\%$	$98.955\%$	$99.944\%$
SAOR [42]	$86.397\%$	$98.954\%$	$99.944\%$
CSOR [43]	$90.299\%$	$99.392\%$	$99.973\%$
CAOR [44]	$91.097\%$	$99.478\%$	$99.977\%$
Proposed MOR	$98.600\%$	$99.951\%$	$99.997\%$

4.2. Computational Complexity Analysis

In this subsection, we evaluate the computational complexity of the proposed detection method in terms of the number of complex multiplications and additions (CMAs) compared with other mentioned detection methods in this article [39,40,41,42,43,44]. Table 10 shows the algebraic expressions of the computational complexity of different iterative methods, where i and $N_T$ represent the number of iterations and the number of user antennas, respectively. Furthermore, iterative methods for inverse matrices require $\left(2N_T^2-N_T\right)$ CMAs [64]. Relatively, the iterative procedure of our proposed MOR method utilizes Equation (25), where ${\mathbf{G}}_{MOR}={\mathbf{M}}_{SOR}{\mathbf{N}}_{SOR}{\mathbf{M}}_{AOR}{\mathbf{N}}_{AOR}$ and ${\mathbf{d}}_{MOR}=\left({\mathbf{M}}_{AOR}+{\mathbf{G}}_{AOR}{\mathbf{M}}_{SOR}\right)\mathbf{d}$ require $\left(6N_T^2-2N_T\right)$ and $3N_T^2$ CMAs, respectively. Because there are two stages within our proposed MOR algorithm, with the first being the initial stage that involves spending $\left(9N_T^2-2N_T\right)$ CMAs for initialization calculation and the second being the collaboration stage to perform the iterative work by Equation (25), requiring $i\left(2N_T^2\right)$ CMAs. Therefore, the total complexity of our proposed method is $\left(9N_T^2-2N_T\right)+i\left(2N_T^2\right)$. In addition, Table 11 shows the numerical complexity of each detector when $N_T$ is 16 and the number of iterations is from 2 to 5. Furthermore, to be more straightforward, the numerical complexity is presented using a bar chart in Figure 17.

Table 10. Algebraic expressions of computational complexity for different detectors.

Iteration Methods	Complex Multiplications and Additions (CMAs)
SOR [39]	${\displaystyle \frac{1}{2}}\left(5N_T^2+N_T\right)+i\left(2N_T^2+N_T\right)$
AOR [40]	$3N_T^2+3i{N}_T^2$
SSOR [41]	$\left(5N_T^2+N_T\right)+2i\left(2N_T^2+N_T\right)$
SAOR [42]	$6N_T^2+6i{N}_T^2$
CSOR [43]	${\displaystyle \frac{1}{2}}\left(5N_T^2+N_T\right)+i\left(2N_T^2+3N_T\right)$
CAOR [44]	$3N_T^2+3i\left(N_T^2+N_T\right)$
Proposed MOR	$\left(9N_T^2-2N_T\right)+i\left(2N_T^2\right)$

Table 11. Numerical complexity comparison for different detectors with $N_T=16$.

Iteration	CMAs	CMAs	CMAs	CMAs
Methods	$i=2$	$i=3$	$i=4$	$i=5$
SOR [39]	1704	2232	2760	3288
AOR [40]	2304	3072	3840	4608
SSOR [41]	3408	4464	5520	6576
SAOR [42]	4608	6144	7680	9216
CSOR [43]	2280	3096	3912	4728
CAOR [44]	2400	3216	4032	4848
Proposed MOR	3296	3808	4320	4832

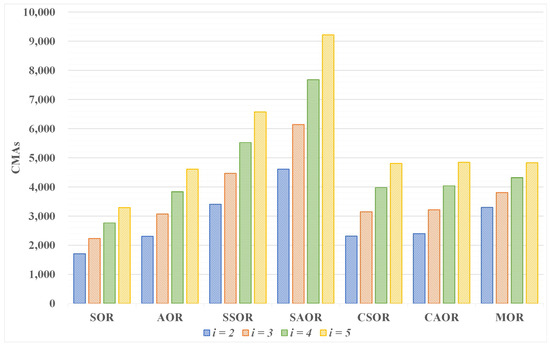
Figure 17. Bar chart of computational complexity for different detectors with $N_T=16$.

Here, considering both the BER performance and complexity factors under discussion, we observe from Table 11 and Figure 8 that in the case of three iterations, although the complexity of our proposed method was about $15.546\%$ slightly higher than CAOR, we found that MOR could significantly surpass CAOR in the OFDM and UFMC systems, not to mention other detectors. On the other hand, it can be observed that when the iteration number i was 3, the MOR complexity only required 3808 CMAs, which could outperform the CAOR BER performance with an iteration number i of 5 (needing 4848 CMAs). When further observing the impact of increasing the number of base station antennas $N_R$ on the BER performance and complexity, it can be found from Figure 15 and Figure 16 that as $N_R$ increased, the number of iterations required by the iterative method gradually decreased, and the proposed MOR algorithm especially only required three iterations and two iterations, respectively. In light of the above discussion, we know that as the number of antennas $N_R$ increased, it could arrive at convergence using a small amount of iterations, simultaneously reducing the complexity. Therefore, overall, the computational complexity of MOR was lower than that of other detectors, and it had good BER performance.

5. Conclusions

This paper proposes a novel collaborative architecture receiver that mixes the relaxation characteristics of the SOR iteration algorithm and the acceleration ability of the AOR iteration algorithm to improve the convergence rate and obtain significant BER performance compared with the other iterative methods. Of course, combining the best convergence merits and complementarity of AOR and SOR is crucial to achieving such excellent BER performance. The numerical results verified that compared with the BER performance of different detection methods under the same environment, it outperformed other detection methods and was simultaneously close to the performance of the MMSE. For the complexity issue, although the proposed method adds a little computational load compared with CSOR and CAOR detectors under consistent iteration numbers, fortunately, due to our proposed MOR detector only needing a small amount of iteration to convergence, simultaneously, the BER performance approached the MMSE the most. In other words, our proposed method can achieve outstanding BER performance and only needs moderate complexity compared with other detectors that require more iterations. In addition, by applying MOR to 4G and B5G environments through experiments, we can verify that it can be ideally used and realize its merit.

Finally, the B5G system is an essential driver of advanced wireless sensor networks. Applications, such as the AIoT face numerous computing and transmission challenges. Therefore, it will be an inevitable trend to develop technologies that meet the requirements of eMMB, URLLC, and mMTC. We propose that the MOR algorithm be applied to M-MIMO systems, which possess lower complexity and BERs, contributing to the demand for large-scale transmission, low latency, and high accuracy in this field. Simultaneously, it is an algorithm worth looking forward to in further development.