RoCS: Knowledge Graph Embedding Based on Joint Cosine Similarity
Abstract
:1. Introduction
- We propose a joint cosine similarity method to calculate the complex vector similarity as a scoring function.
- Our approach combines the rotational properties of the complex vector model RotatE to reason about a variety of important relational patterns.
- We have experimentally verified that the proposed RoCS provides a significant improvement over RotatE and achieves results close to or even higher than the current state-of-the-art.
2. Related Work
3. RoCS
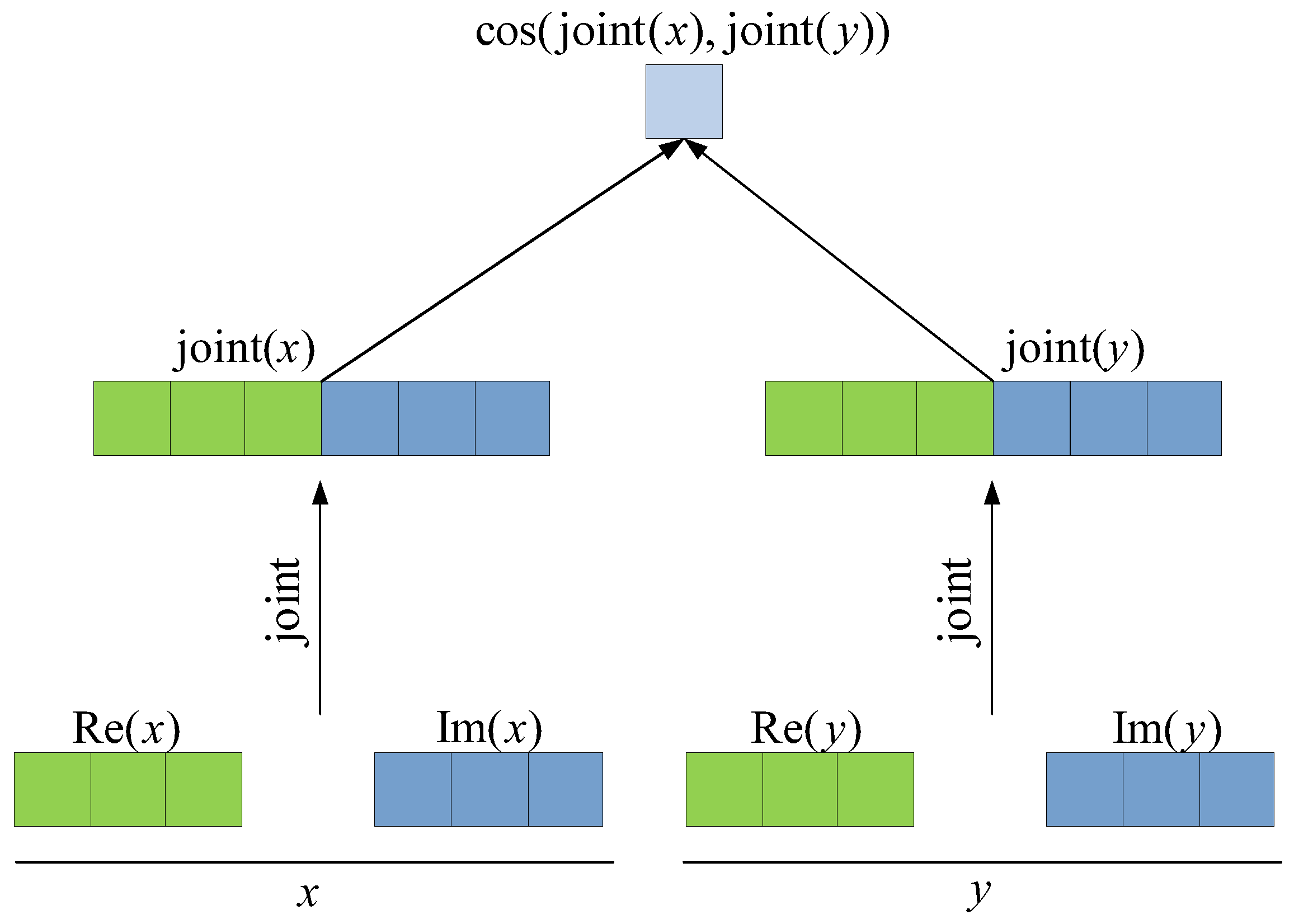
3.1. Joint Cosine Similarity of Complex Vectors
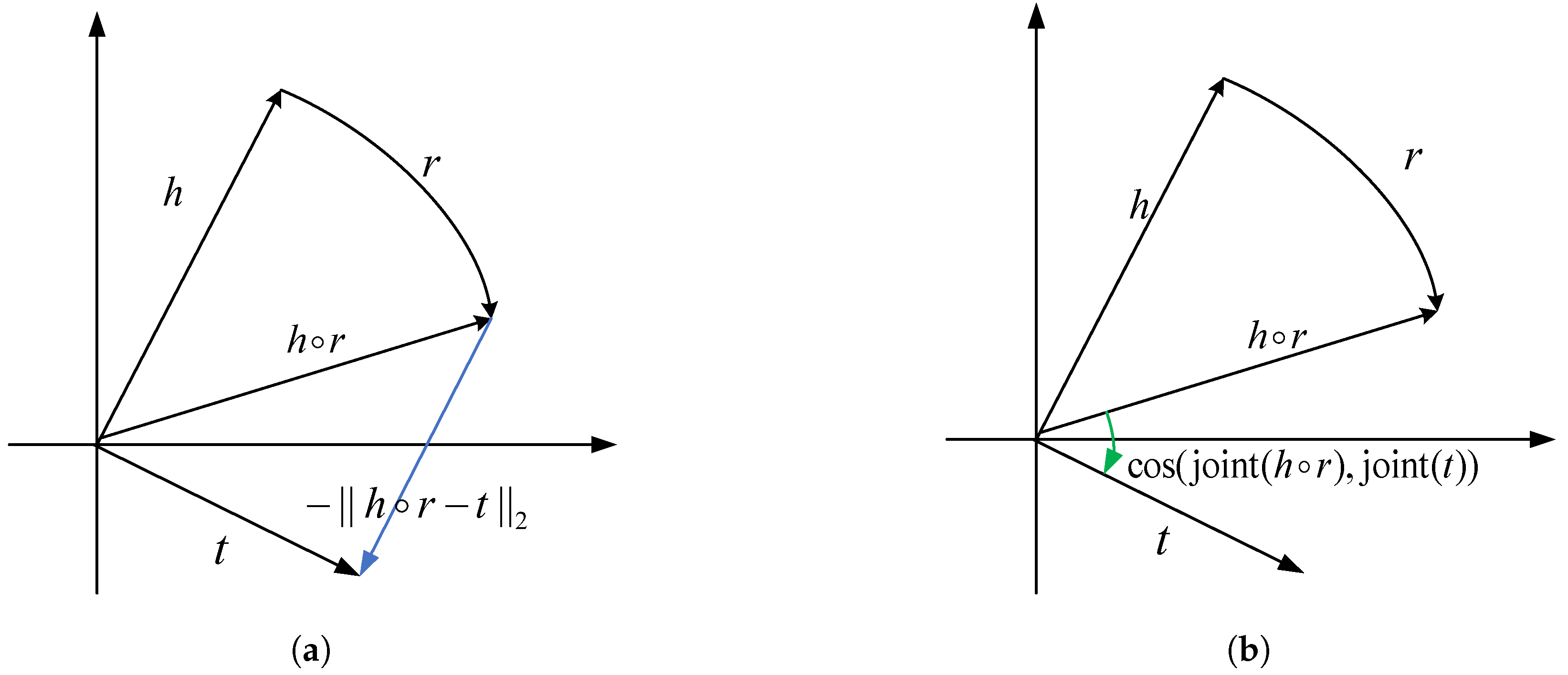
3.2. Scoring Function Based on Joint Cosine Similarity
3.3. Training
3.4. Discussion
3.4.1. Infer Patterns of the Relations
3.4.2. Connection with Existing Methods
4. Experiment
4.1. Experimental Setup
4.1.1. Datasets
4.1.2. Evaluation Criterion
4.1.3. Baselines
4.1.4. Experimental Details
4.2. Compare RotatE
4.3. Comparison with Current SOTA Models
4.4. Comparing Complex Vector Embeddings
4.5. Ablation Study
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge graph embedding: A survey of approaches and applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Philip, S.Y. A survey on knowledge graphs: Representation, acquisition, and applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 494–514. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, J.; Li, D.; Li, P. Knowledge graph embedding based question answering. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, Australia, 11–15 February 2019; pp. 105–113. [Google Scholar] [CrossRef]
- Zhang, F.; Yuan, N.J.; Lian, D.; Xie, X.; Ma, W.Y. Collaborative knowledge base embedding for recommender systems. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 353–362. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Xie, X.; Guo, M. DKN: Deep knowledge-aware network for news recommendation. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 1835–1844. [Google Scholar] [CrossRef]
- Yang, B.; Mitchell, T. Leveraging Knowledge Bases in LSTMs for Improving Machine Reading. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Vancouver, BC, Canada, 30 July–4 August 2017. [Google Scholar] [CrossRef]
- Qin, Z.; Cen, C.; Jie, W.; Gee, T.S.; Chandrasekhar, V.R.; Peng, Z.; Zeng, Z. Knowledge-graph based multi-target deep-learning models for train anomaly detection. In Proceedings of the 2018 International Conference on Intelligent Rail Transportation (ICIRT), Singapore, 12–14 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, C.; Li, K.; Zou, X.; Cheng, Z.; Wei, W.; Tian, Q.; Zeng, Z. Hierarchical Semantic Graph Reasoning for Train Component Detection. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4502–4514. [Google Scholar] [CrossRef] [PubMed]
- Miller, G.A. WordNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; pp. 1247–1250. [Google Scholar] [CrossRef]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 697–706. [Google Scholar] [CrossRef]
- Yang, B.; tau Yih, W.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. Conference Track Proceedings. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T. Holographic embeddings of knowledge graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. Available online: https://dl.acm.org/doi/10.5555/3016100.3016172 (accessed on 18 December 2023).
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; Available online: https://dl.acm.org/doi/10.5555/3045390.3045609 (accessed on 18 December 2023).
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion knowledge graph embeddings. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 2735–2745. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 26, 2787–2795. Available online: https://dl.acm.org/doi/10.5555/2999792.2999923 (accessed on 18 December 2023).
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; Volume 28. Available online: https://dl.acm.org/doi/10.5555/2893873.2894046 (accessed on 18 December 2023).
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Ebisu, T.; Ichise, R. Toruse: Knowledge graph embedding on a lie group. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Geometry interaction knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2022; Volume 36, pp. 5521–5529. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. Available online: https://dl.acm.org/doi/10.5555/3045118.3045167 (accessed on 18 December 2023).
- Singhal, A. Modern information retrieval: A brief overview. IEEE Data Eng. Bull. 2001, 24, 35–43. [Google Scholar]
- Dai, A.M.; Olah, C.; Le, Q.V. Document Embedding with Paragraph Vectors. arXiv 2015, arXiv:1507.07998. [Google Scholar]
- Thongtan, T.; Phienthrakul, T. Sentiment classification using document embeddings trained with cosine similarity. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics: Student Research Workshop, Florence, Italy, 28 July–2 August 2019; pp. 407–414. [Google Scholar] [CrossRef]
- Toutanova, K.; Chen, D. Observed versus latent features for knowledge base and text inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, Beijing, China, 26–31 July 2015; pp. 57–66. [Google Scholar] [CrossRef]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Balažević, I.; Allen, C.; Hospedales, T.M. Tucker: Tensor factorization for knowledge graph completion. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019. [Google Scholar] [CrossRef]
- Amin, S.; Varanasi, S.; Dunfield, K.A.; Neumann, G. LowFER: Low-rank Bilinear Pooling for Link Prediction. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 257–268. [Google Scholar]
- Jin, L.; Yao, Z.; Chen, M.; Chen, H.; Zhang, W. A Comprehensive Study on Knowledge Graph Embedding over Relational Patterns Based on Rule Learning. In Proceedings of the International Semantic Web Conference, Athens, Greece, 6–10 November 2023; Springer: Cham, Switzerlnd, 2023; pp. 290–308. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A three-way model for collective learning on multi-relational data. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; Volume 11, pp. 809–816. Available online: https://dl.acm.org/doi/10.5555/3104482.3104584 (accessed on 18 December 2023).
- Vashishth, S.; Sanyal, S.; Nitin, V.; Agrawal, N.; Talukdar, P. Interacte: Improving convolution-based knowledge graph embeddings by increasing feature interactions. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3009–3016. [Google Scholar]
- Chen, C.; Li, K.; Wei, W.; Zhou, J.T.; Zeng, Z. Hierarchical graph neural networks for few-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 240–252. [Google Scholar] [CrossRef]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the European Semantic Web Conference, Heraklion, Crete, Greece, 3–7 June 2018; Springer: Cham, Switzerland, 2018; pp. 593–607. [Google Scholar] [CrossRef]
- Luo, C.; Zhan, J.; Xue, X.; Wang, L.; Ren, R.; Yang, Q. Cosine normalization: Using cosine similarity instead of dot product in neural networks. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Springer: Cham, Switzerland, 2018; pp. 382–391. [Google Scholar] [CrossRef]
- Kryszkiewicz, M. The cosine similarity in terms of the euclidean distance. In Encyclopedia of Business Analytics and Optimization; IGI Global: Hershey, PA, USA, 2014; pp. 2498–2508. [Google Scholar] [CrossRef]
- Kazemi, S.M.; Poole, D. Simple embedding for link prediction in knowledge graphs. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montreal, QC, Canada, 3–8 December 2018; pp. 4284–4295. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
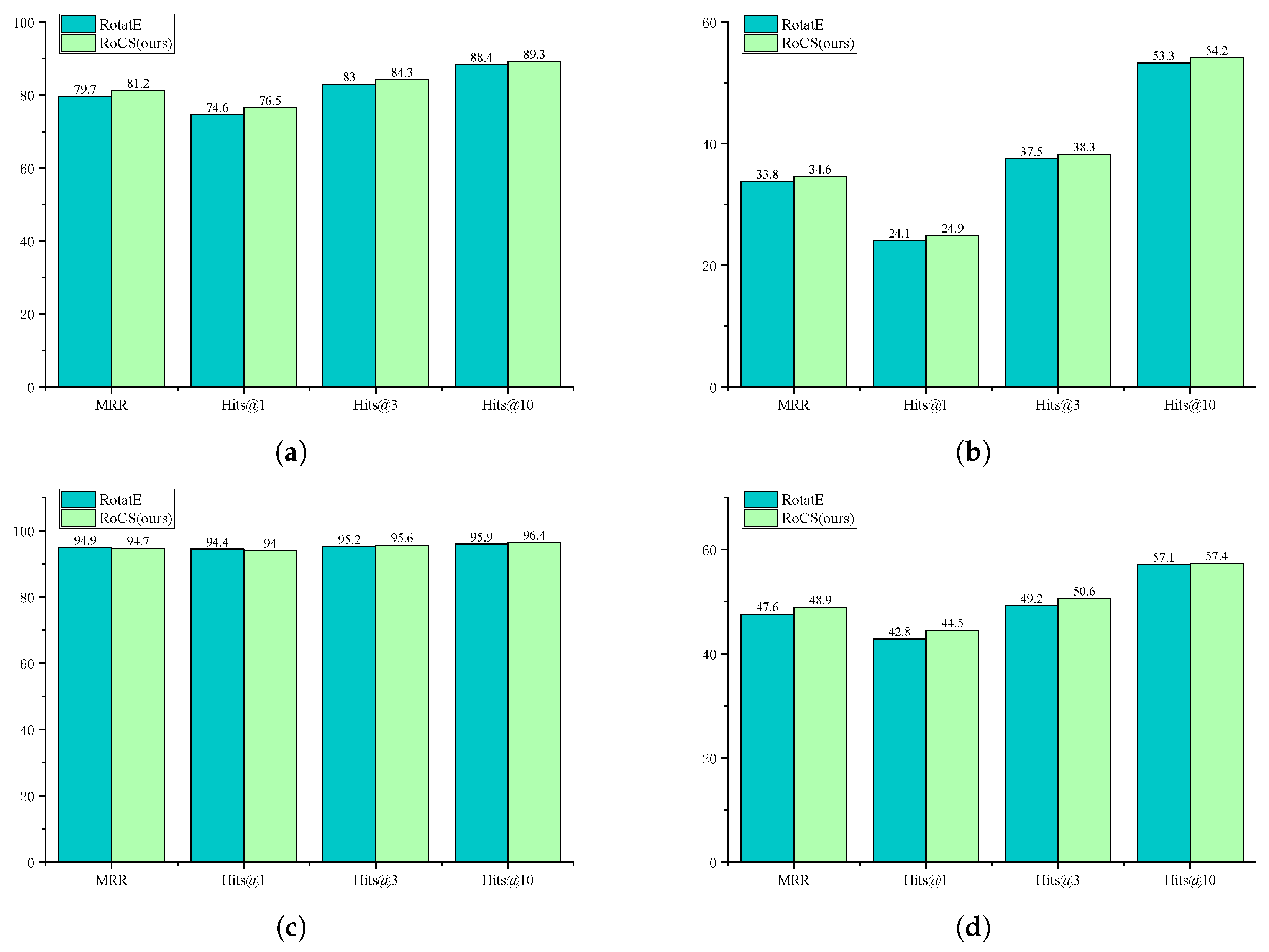
| Models | Scoring Function | Representation Space | Score Range |
|---|---|---|---|
| TransE [16] | Unbounded | ||
| DistMult [12] | Unbounded | ||
| ComplEx [14] | Unbounded | ||
| ConvE [27] | Unbounded | ||
| RotatE [17] | Unbounded | ||
| QuatE [15] | Unbounded | ||
| LowFER [29] | Unbounded | ||
| RoCS (ours) | Bounded |
| Dataset | #Entity | #Relation | #Train | #Valid | #Test |
|---|---|---|---|---|---|
| FB15K | 14,951 | 1345 | 483,142 | 50,000 | 59,071 |
| FB15K-237 | 14,541 | 237 | 272,115 | 17,535 | 20,466 |
| WN18 | 40,943 | 18 | 141,442 | 5000 | 5000 |
| WN18RR | 40,943 | 11 | 86,835 | 3034 | 3134 |
| Models | WN18 | WN8RR | ||||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hits@1 | Hits@3 | Hits@10 | MRR | Hits@1 | Hits@3 | Hits@10 | |
| TransE [16] | 49.5 | 11.3 | 88.8 | 94.3 | 22.6 | - | - | 50.1 |
| DistMult [12] | 79.7 | - | - | 94.6 | 43.0 | 39.0 | 44.0 | 49.0 |
| ComplEx [14] | 94.3 | 93.5 | 94.6 | 95.6 | 46.0 | 39.0 | 43.0 | 48.0 |
| ConvE [27] | 94.2 | 93.9 | 94.4 | 94.7 | - | - | - | - |
| SimplE [37] | 94.7 | 94.3 | 95.0 | 95.4 | - | - | - | - |
| TorusE [20] | 94.1 | 93.6 | 94.5 | 94.7 | 44.0 | 41.0 | 46.0 | 51.0 |
| RotatE [17] | 94.9 | 94.4 | 95.2 | 95.9 | 47.6 | 42.8 | 49.2 | 57.1 |
| QuatE [15] | 95.0 | 94.5 | 95.4 | 95.9 | 48.8 | 43.8 | 50.8 | 58.2 |
| TuckER [28] | 95.3 | 94.9 | 95.5 | 95.8 | 47.0 | 44.3 | 48.2 | 52.6 |
| LowFER [29] | 95.0 | 94.6 | 95.2 | 95.8 | 46.5 | 43.4 | 47.9 | 52.6 |
| RoCS (ours) | 94.7 | 94.0 | 95.6 | 96.4 | 48.9 | 44.5 | 50.6 | 57.4 |
| Models | FB15K | FB15K-237 | ||||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hits@1 | Hits@3 | Hits@10 | MRR | Hits@1 | Hits@3 | Hits@10 | |
| TransE [16] | 46.3 | 29.7 | 57.8 | 74.9 | 29.4 | - | - | 46.5 |
| DistMult [12] | 65.4 | 54.6 | 73.3 | 72.8 | 24.1 | 15.5 | 26.3 | 41.9 |
| ComplEx [14] | 69.2 | 59.9 | 75.9 | 84.0 | 32.5 | 23.7 | 25.6 | 50.1 |
| ConvE [27] | 74.5 | 67.0 | 80.1 | 87.3 | - | - | - | - |
| SimplE [37] | 72.7 | 66.0 | 77.3 | 83.8 | - | - | - | - |
| TorusE [20] | 73.3 | 67.4 | 77.1 | 83.2 | 24.7 | 15.8 | 27.5 | 42.8 |
| RotatE [17] | 79.7 | 74.6 | 83.0 | 88.4 | 33.8 | 24.1 | 37.5 | 53.3 |
| QuatE [15] | 78.2 | 71.1 | 83.5 | 90.0 | 34.8 | 24.8 | 38.2 | 55.0 |
| TuckER [28] | 79.5 | 74.1 | 83.3 | 89.2 | 35.8 | 26.6 | 39.3 | 54.4 |
| LowFER [29] | 82.4 | 78.2 | 85.2 | 89.7 | 35.9 | 26.6 | 39.6 | 54.4 |
| RoCS (ours) | 81.2 | 76.5 | 84.3 | 89.3 | 34.6 | 24.9 | 38.3 | 54.2 |
| Models | WN18 | WN8RR | FB15K | FB15K-237 | ||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hits@10 | MRR | Hits@10 | MRR | Hits@10 | MRR | Hits@10 | |
| 89.2 | 95.4 | 47.0 | 55.7 | 78.0 | 89.0 | 32.1 | 50.9 | |
| RotatE | 94.9 | 95.9 | 47.6 | 57.1 | 79.7 | 88.4 | 33.8 | 53.3 |
| RoCS(ours) | 94.7 | 96.4 | 48.9 | 57.4 | 81.2 | 89.3 | 34.6 | 54.2 |
| Models | WN18 | WN8RR | FB15K | FB15K-237 | ||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hits@10 | MRR | Hits@10 | MRR | Hits@10 | MRR | Hits@10 | |
| RoReCS | 63.7 | 90.7 | 36.7 | 44.5 | 49.1 | 65.9 | 23.1 | 33.4 |
| RoAddCS | 92.1 | 95.2 | 46.0 | 52.1 | 68.5 | 79.0 | 28.0 | 44.9 |
| RoCS | 94.7 | 96.4 | 48.9 | 57.4 | 81.2 | 89.3 | 34.6 | 54.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Luo, J.; Deng, S.; Guo, X. RoCS: Knowledge Graph Embedding Based on Joint Cosine Similarity. Electronics 2024, 13, 147. https://doi.org/10.3390/electronics13010147
Wang L, Luo J, Deng S, Guo X. RoCS: Knowledge Graph Embedding Based on Joint Cosine Similarity. Electronics. 2024; 13(1):147. https://doi.org/10.3390/electronics13010147
Chicago/Turabian StyleWang, Lifeng, Juan Luo, Shiqiao Deng, and Xiuyuan Guo. 2024. "RoCS: Knowledge Graph Embedding Based on Joint Cosine Similarity" Electronics 13, no. 1: 147. https://doi.org/10.3390/electronics13010147
APA StyleWang, L., Luo, J., Deng, S., & Guo, X. (2024). RoCS: Knowledge Graph Embedding Based on Joint Cosine Similarity. Electronics, 13(1), 147. https://doi.org/10.3390/electronics13010147






