HeMGNN: Heterogeneous Network Embedding Based on a Mixed Graph Neural Network

Abstract

Network embedding is an effective way to realize the quantitative analysis of large-scale networks. However, mainstream network embedding models are limited by the manually pre-set metapaths, which leads to the unstable performance of the model. At the same time, the information from homogeneous neighbors is mostly focused in encoding the target node, while ignoring the role of heterogeneous neighbors in the node embedding. This paper proposes a new embedding model, HeMGNN, for heterogeneous networks. The framework of the HeMGNN model is divided into two modules: the metapath subgraph extraction module and the node embedding mixing module. In the metapath subgraph extraction module, HeMGNN automatically generates and filters out the metapaths related to domain mining tasks, so as to effectively avoid the excessive dependence of network embedding on artificial prior knowledge. In the node embedding mixing module, HeMGNN integrates the information of homogeneous and heterogeneous neighbors when learning the embedding of the target nodes. This makes the node vectors generated according to the HeMGNN model contain more abundant topological and semantic information provided by the heterogeneous networks. The Rich semantic information makes the node vectors achieve good performance in downstream domain mining tasks. The experimental results show that, compared to the baseline models, the average classification and clustering performance of HeMGNN has improved by up to 0.3141 and 0.2235, respectively.

1. Introduction

In the era of big data, a large amount of data and their rich and detailed relationships are collected and stored, which constitutes various complex networks containing rich topological and semantic information. These complex networks provide a good carrier for describing and analyzing complex systems in the real world [1,2]. However, the huge structure of the network also brings unprecedented challenges to the analysis based on the network. How to efficiently realize the expression and mining of networks has become an important problem.

In recent years, network embedding methods have been widely used in network analysis due to their high performance and interpretability in encoding graph structures [3,4]. The network embedding method can extract the semantic information implied in the network topology, and then map the network data into the vectorized space to help obtain the vectorized representation of nodes so as to realize the quantitative analysis of large-scale networks and provide basic structured data for the subsequent domain learning tasks [5,6].

Metapath-based models are the mainstream models of the embedded representation of heterogeneous networks [7,8]. Because the node type and relationship type are the most basic heterogeneous semantic information in heterogeneous networks, a metapath is designed as a path composed of a series of different types of nodes and their relationships. Researchers manually design metapaths according to domain knowledge, and use metapaths to guide the process of random walking and finally obtain the embedding of nodes [9,10]. However, the strategy of manually determining the metapath brings instability to the embedding of nodes. In addition, most of the current research focuses on generating the embedding of target nodes based on the aggregation of information of homogeneous neighbor nodes, while ignoring the role of heterogeneous neighbor nodes in the embedding process. How to automatically generate metapaths and integrate information from homogeneous and heterogeneous neighbor nodes are the main challenges of heterogeneous network embedding research.

This paper proposes a new network embedding model, named HeMGNN, for heterogeneous networks. HeMGNN adopts an end-to-end learning process and does not need to rely on domain knowledge to set metapaths in advance, so as to effectively avoid the dependence of the learning process on the human experience. HeMGNN automatically generates and filters the metapaths that meet the metapath screening rules in the multiplication process of adjacency matrices. According to the extracted metapaths, HeMGNN maps the heterogeneous network into homogeneous subgraphs and bipartite subgraphs and obtain the embedding of target nodes by aggregating the information of homogeneous neighbors and heterogeneous neighbors.

The main contributions of this paper are as follows:

• HeMGNN is a general heterogeneous network embedding model that can handle the embedding tasks for any type of heterogeneous network.
• HeMGNN can automatically generate and filter out the metapaths closely related to the domain tasks, so as to avoid the limitation of the manual selection of metapaths.
• HeMGNN can learn the embedding of target nodes by aggregating the information of homogeneous and heterogeneous neighbors, so as to ensure the richness of information in node embedding.

2. Related Work

Heterogeneous network embedding is a bridge between the original data of the network and the network application tasks. It can map the nodes in a network into low-dimensional dense vectors on the basis of retaining the topology information and semantic information of the network. Among them, the embedding methods based on metapaths are the most mainstream technology of network representation learning.

Inspired by the random-walk strategy of DeepWalk [11] in homogeneous networks, researchers use node types and relation types to design metapaths to guide the paths of a random walk. The algorithms of Metapath2vec [12] and HERec [13] use this strategy to achieve the retention of specific relationships between nodes. The Hin2vec algorithm makes multiple predictions based on the target set of relationships to be learned, jointly training the potential node vectors and metapaths of the task under a set of relations specified in the form of metapaths in a given heterogeneous network [14]. The DDRW algorithm combines the truncated random walk with hierarchical Softmax, and cooperates with the classification objective function to capture the similarity between nodes [15]. The ProxEmbed algorithm simulates the random-walk sequence as the “time” evolution process between nodes and realizes the embedding of nodes on the basis of investigating the heterogeneity of nodes [16]. The CAHNE algorithm generates the context sequence of nodes by a breadth-first search (BFS) and realizes the embedding of nodes by combining the structural information of the sequence and the importance of nodes [17]. The D2AGE algorithm recombines multiple random-walk paths generated between node pairs into a directed acyclic graph through BFS and uses LSTM to embed the node sequence [18]. The W-MetaGraph2Vec algorithm uses a random-walk mechanism based on a topic-driven metagraph to guide the generation of heterogeneous neighborhoods of nodes [19]. The ARWR-GE algorithm preserves the high-order neighbor information of nodes through a random walk and uses adversarial learning to obtain node embedding [20]. The HIN-DRL algorithm adopts a random-walk-based dynamic representation learning to learn the embedding of nodes under different timestamps [21]. The MBRep algorithm extracts the salient motif structures from the original heterogeneous network, applies a weighted biased random walk to the motif-level higher-order network using the Skip-gram model, and obtains the embedding of nodes in the heterogeneous network [22].

Some researchers use a metapath to find the neighbor nodes of the target node and encode the target node by aggregating the information of the neighbor nodes and metapaths. Taking the idea of the GATs algorithm [23] on homogeneous graphs, the HAN algorithm obtains the embedding of a target node by fusing the information of neighbor nodes and metapaths through a node-level and semantically level attention mechanism [24]. Based on the autoencoder model SDNE [25] on the homogenous graph, the BL-MNE algorithm was proposed to learn the embedding of nodes on the basis of investigating the first-order and second-order adjacency relations in the metapaths [26]. Referring to the representation-learning algorithm DGI [27] on the homogeneous graph, the HDGI algorithm uses the graph convolution module and semantic-level attention mechanism to capture the metapath information to achieve node embedding [28].

Network embedding methods based on metapaths can integrate the information of the metapaths and neighbor nodes into the embedded vector of the target nodes. However, the strategy of manually determining the metapaths brings an instability to the performance of these methods. Moreover, most of the current research focuses on aggregating the information of the homogeneous neighbors in the metapaths to generate the embedding of target nodes, while ignoring the role of information from heterogeneous neighbors.

This paper proposes a HeMGNN model to provide solutions to the above problems. HeMGNN can automatically generate and select metapaths. At the same time, it examines the information of homogeneous and heterogeneous neighbor nodes in the metapaths to generate the embedding of target nodes.

3. Overall Architecture of the HeMGNN Model

Before discussing the architecture of the HeMGNN model in detail, we first introduce some relevant definitions used in the HeMGNN model.

3.1. Definitions

Definition 1:

Heterogeneous network

A heterogeneous network is a graph structure composed of different types of nodes and different types of edges between nodes. Formally, a heterogeneous network is defined as $\mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A},\mathcal{R}\}$. Specifically, $\mathcal{V}$ is a set of nodes, $\mathcal{E}$ is a set of edges; $\mathcal{A}$ and $\mathcal{R}$ are sets of node types and edge types, respectively. The detailed notation is shown in Table 1.

Table 1. Notations and explanations.

Notation	Explanation
$\mathcal{G}$	Heterogeneous network
$\mathcal{V}$	Set of nodes
$\mathcal{E}$	Set of edges
$\mathcal{A}$	Set of node types
$\mathcal{R}$	Set of edge types
$\mathsf{\Phi }$	Metapath
$A^{\mathsf{\Phi }}$	Metapath-based adjacency matrix
$X$	Initial feature matrix of the node

Definition 2:

Metapath

In a heterogeneous network, a metapath is a path composed of different types of nodes and their relationships. Formally, a metapath Φ is defined as $v_1\stackrel{R_1}{\to }{v}_2\stackrel{R_2}{\to }\cdots \stackrel{R_{n-1}}{\to }{v}_n$. Specifically, $R=R_1◦R_2◦\cdots ◦R_{n-1}$ defines an edge relationship between nodes $v_1$ and $v_n$. For example, the metapath A–P–A can be denoted as ${\Phi }_{APA}$.

Definition 3:

Adjacency Matrix of a Metapath

If there is a metapath ${\Phi }_i$ connecting the node $v_s$ to the node $v_t$, it can be considered that $v_s$ and $v_t$ are neighbors. At this point, the adjacency matrix $A^{{\Phi }_i}\in {\mathbb{R}}^{\left|v_s\right|\ast \left|v_t\right|}$ under the metapath ${\Phi }_i$ can be constructed, where $A_{xy}^{{\Phi }_i}=1$, indicating that the node $v_x$ and the node $v_y$ are connected through metapath ${\Phi }_i$, otherwise $A_{xy}^{{\Phi }_i}=0$.

3.2. Framework of the HeMGNN Model

Figure 1 presents a schematic diagram of the overall framework of the HeMGNN model. The structure of the HeMGNN model is divided into two modules: the metapath subgraph extraction module and node embedding mixing module. In the metapath subgraph extraction module, HeMGNN automatically generates and filters the metapaths, and maps the reserved metapaths to the set of subgraphs $\{G^{{\mathsf{\Phi }}_1},G^{{\mathsf{\Phi }}_2},\cdots ,G^{{\mathsf{\Phi }}_n}\}$. Specifically, according to the initial adjacency matrix $\left\{A\right\}$ of the heterogeneous network, a series of metapaths representing high-order relationships between nodes are generated through the progressive multiplication of the adjacency matrices. According to the screening principle of metapaths proposed in this paper, the set of metapaths $\{{\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,\dots ,{\mathsf{\Phi }}_P\}$ that meet the requirements is automatically screened. According to whether the types of head and tail nodes in one metapath are the same, the metapaths are mapped into two sets. One is the set of “homogeneous subgraphs”, which is mapped by the metapaths with the same type of head and tail nodes. The other is the set of “bipartite subgraphs”, which is mapped by the metapaths with different types of head and tail nodes. In the node embedding mixing module, the embedding models suitable for the homogeneous subgraph and bipartite subgraph are constructed. By aggregating the information of homogeneous neighbors and heterogeneous neighbors, the embedding of target nodes in the two kinds of graph structures is obtained. The attention mechanism in the metapath semantic level is used to fuse the embedding of the same target node so as to obtain the final embedding vector of the node. On this basis, the performance of node embedding is verified by the domain tasks.

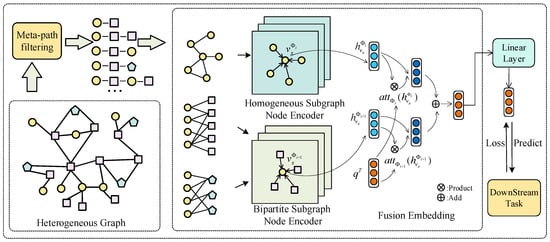
Figure 1. Framework of the HeMGNN model.

3.2.1. Metapath Subgraph Extraction Module

In the metapath subgraph extraction module, HeMGNN automatically generates and filters the metapaths. At the same time, these extracted metapaths are mapped to the homogeneous subgraphs or bipartite subgraphs according to the types of head nodes and tail nodes in the metapaths. The detailed process is as follows:

Step 1: According to the types of edges in the network, the corresponding nodes and the relationship between nodes are extracted, and on this basis, the initial adjacency matrices of heterogeneous network are constructed. Taking heterogeneous citation networks as an example, the initial adjacency matrices will include the adjacency matrix composed of homogeneous nodes, such as of A (author)–A (author), and the adjacency matrix composed of the heterogeneous nodes, such as the adjacency matrix of A (author)–P (paper). The initial adjacency matrix reflects the first-order direct connection between nodes in heterogeneous networks.

Step 2: Based on the initial adjacency matrices, the higher-order relationship between nodes is obtained through the progressive multiplication of the adjacency matrices. Considering the one-to-one correspondence between the adjacency matrix and network topology, a series of metapaths will be generated automatically with the multiplication of adjacency matrices. In order to automatically eliminate the redundant and low semantic metapaths, this paper proposes the screening principle of metapaths.

Principle 1: Nodes of the same type can appear, at most, twice in the same metapath. This principle is formulated based on the principles of three levels of influence in social networks. Limiting the number of occurrences of nodes of the same type in the metapath can prevent the generation of overly long metapaths. Because in a long metapath, the information transmission between the head and tail nodes will be greatly attenuated, and the semantics conveyed by the metapath will be too complex to understand.

Principle 2: There can be up to three different types of heterogeneous nodes in the metapath. Usually, when the metapath contains several different types of nodes, the information transmission ability between the head and tail nodes will be greatly reduced. Consider two metapaths generated on heterogeneous citation networks: ${\mathsf{\Phi }}_1$ = “Author1-Paper1-Conference1-Paper2” and ${\mathsf{\Phi }}_2$ = “Author1-Paper1-Conference1-conference address1-Conference2-Paper2”. Compared to metapath ${\mathsf{\Phi }}_1$, there are more heterogeneous nodes from different types in metapath ${\mathsf{\Phi }}_2$, resulting in a weaker information transmission between its head and tail nodes. Meanwhile, the semantics represented by metapath ${\mathsf{\Phi }}_2$ are too complex to understand.

According to Principle 1 and Principle 2, the maximum length of a metapath is limited to five. This will greatly remove some metapaths of low semantic information.

Principle 3: Sub-paths whose head-to-tail node relationship is <1:1> cannot appear in one metapath. For example, metapath ${\mathsf{\Phi }}_1$ = “Author1-Paper1-Conference1-Paper2-Conference1” will be filtered out, because the head-to-tail relationship in sub-path of “Conference1-Paper2-Conference1” is <1:1>. This sub-path does not bring valuable information transmission because an article can only be published in one conference.

Principle 4: Metapaths unrelated to domain tasks will be deleted. Suppose that the current task is to classify author nodes, then only the metapaths with a head or tail node as the author type could be retained.

Step 3: According to the type of head and tail nodes in the metapaths, the adjacency matrices of metapaths are mapped into two graph structures: one are homogeneous subgraphs, which represent the adjacency relationship between the homogeneous nodes; the other are bipartite subgraphs, which represent the adjacency relationship between the heterogeneous nodes.

3.2.2. Node Embedding Mixing Module

In the node embedding mixing module, the nodes in the homogeneous subgraph and bipartite subgraph are embedded, and then the embedding of the same node is fused to obtain the final representation vector of the node. Two different embedding strategies are used to encode the nodes in the homogeneous subgraphs and bipartite subgraphs. One is the node encoder based on a graph convolution neural network, and the other is the node encoder based on a Transformer-based attention mechanism. In the fusion process of the node embedding, a semantic attention mechanism is used to fuse the embeddings of the same target node, so as to find the final representation vector of the node.

(A)

Node Encoder based on a Graph Convolutional Neural Network

GCN and GCMC are used to realize the embedding of nodes in a homogeneous subgraph and a bipartite subgraph respectively. GCN adopts the convolution method of first-order spectral graphs to obtain the embedding of the target node by aggregating the information of the first-order neighbors. The embedding process using GCN is shown in Formula (1):

$$H^{heo}=\left(D^{{\mathsf{\Phi }}_i-\frac{1}{2}}{A}^{{\mathsf{\Phi }}_i}{D}^{{\mathsf{\Phi }}_i-\frac{1}{2}}\right)X{W}^{{\mathsf{\Phi }}_i},$$

(1)

where $H^{heo}$ represents the node embedding encoded by the homogenous graph, and $X$ represents the initial feature matrix of the node. $D^{{\mathsf{\Phi }}_i}$ represents the degree matrix under metapath ${\mathsf{\Phi }}_i$, $A^{{\mathsf{\Phi }}_i}$ represents the adjacency matrix under metapath ${\mathsf{\Phi }}_i$. $W^{{\mathsf{\Phi }}_i}$ is the parameter matrix for embedding metapath ${\mathsf{\Phi }}_i$.

GCMC is a graph convolutional auto-encoder model [29] applied on bipartite graphs, which aggregates the information of heterogeneous neighbor nodes in a similar way to GCN. However, in order not to lose the initial semantic information of the target node, the GCMC integrates the features of the target node itself and the features of heterogeneous neighbor nodes to generate the embedding of the target node. The process of node embedding using GCMC is shown as:

$$H^{bio}=X{W}_1^{{\mathsf{\Phi }}_i}+{\tilde{A}}^{{\mathsf{\Phi }}_i}Z{W}_2^{{\mathsf{\Phi }}_i},$$

(2)

$H^{bio}=X{W}_1^{{\mathsf{\Phi }}_i}+{\tilde{A}}^{{\mathsf{\Phi }}_i}Z{W}_2^{{\mathsf{\Phi }}_i}$ where $H^{bio}$ represents the node embedding after the bipartite subgraph encoding, $X$ represents the initial feature matrix of the node, $Z$ represents the initial feature matrix of the heterogeneous neighbor node, ${\tilde{A}}^{{\mathsf{\Phi }}_i}=C^{{\mathsf{\Phi }}_i}\circ A^{{\mathsf{\Phi }}_i}$, $C^{{\mathsf{\Phi }}_i}$ is the normalized matrix, ${\mathrm{c}}_{ij}={\left(\sqrt{\left|{\mathcal{N}}_i\right|\left|{\mathcal{N}}_j\right|}\right)}^{-1}$, and ${\mathcal{N}}_i$ is the degree of the i node.

(B)

Node Encoder based on a Transformer Attention Mechanism

The idea of using Transformer-based attention mechanism to generate the node embedding is inspired by HGT [30]. In this strategy, the target node is used as a query, and the neighbor nodes are used as keys, and the attention weights of neighbor nodes are calculated by using the attention mechanism. The embedding of the target node will be generated by the weighted aggregation of the information of neighbor nodes. The process of node embedding using a Transformer-based attention mechanism is shown in Formulas (3) and (4):

$$H^{{\mathsf{\Phi }}_i}=M_{Att}^{{\mathsf{\Phi }}_i}\cdot V_{\left(z\right)},$$

(3)

$$M_{Att}^{{\mathsf{\Phi }}_i}=\genfrac{}{}{0pt}{}{Softmax}{{\forall }_{xϵ\mathcal{N}\left(z\right)}}\left(Q_{\left(x\right)}·W_{Att}^{{\mathsf{\Phi }}_i}{·K}_{\left(z\right)}^T\circ A^{{\mathsf{\Phi }}_i}\right),$$

(4)

$$K_{\left(z\right)}=K–Linear\left(Z\right),$$

(5)

$$Q_{\left(x\right)}=Q–Linear\left(X\right),$$

(6)

$$V_{\left(z\right)}=V–Linear\left(Z\right),$$

(7)

where $H^{{\mathsf{\Phi }}_i}$ is the node embedding generated under metapath ${\mathsf{\Phi }}_i$, $M_{Att}$ represents the weighted adjacency matrix, $X$ is the initial feature matrix of the target node, and $Z$ is the initial feature matrix of the neighbor nodes. $Q_{\left(x\right)}$ is the query vector matrix of the target nodes, $K_{\left(z\right)}$ is the key vector matrix of the neighbor nodes, and $V_{\left(z\right)}$ is the value vector matrix of the neighbor nodes. $W_{Att}^{{\mathsf{\Phi }}_i}$ represents the parameter matrix under metapath ${\mathsf{\Phi }}_i$. The $Q_{\left(x\right)}$ matrix is obtained by the linear mapping of $X$, and the $K_{\left(z\right)}$ and $V_{\left(z\right)}$ matrices are obtained by the linear mapping of $Z$. ‘∘’ is the Hadamard product, which can act on two matrices of the same type to realize the product operation of the corresponding elements.

(C)

Node Embedding Fusion based on a Semantic Level Attention Mechanism

The embeddings of the same node learned from different metapaths will contain different semantics information. This paper adopts an attention mechanism of the semantic level to measure the weight of semantic information under different metapaths. Then, the final embedding of the node will be obtained by a weighted aggregation of the node embeddings generated by different metapaths. Formulas (8) and (9) give the process of node embedding fusion.

$$H=\sum _{i=1}^P{Att}_{{\mathsf{\Phi }}_i}\cdot H^{{\mathsf{\Phi }}_i},$$

(8)

$${Att}_{{\mathsf{\Phi }}_i}=Softmax\left(W_{{\mathsf{\Phi }}_i}\right)=\frac{{exp}^{\left(W_{{\mathsf{\Phi }}_i}\right)}}{{\sum }_{j=1}^P{exp}^{\left(W_{{\mathsf{\Phi }}_i}\right)}},$$

(9)

$$W_{{\mathsf{\Phi }}_i}=U_{{\mathsf{\Phi }}_i}\cdot Q^T,$$

(10)

$$U_{{\mathsf{\Phi }}_i}=\mathrm{T}\mathrm{a}\mathrm{n}\mathrm{h}\left(H^{{\mathsf{\Phi }}_i}W+B\right),$$

(11)

Specifically, $H$ represents the final embedding matrix. $H$ is obtained by a weighted fusion of the node embedding matrix $H^{{\mathsf{\Phi }}_i}$. $W_{{\mathsf{\Phi }}_i}$ represents the weight matrix of metapath ${\mathsf{\Phi }}_i$ under the self-attention mechanism. The weight of the metapath ${Att}_{{\mathsf{\Phi }}_i}$ is obtained by the Softmax function to normalize $W_{{\mathsf{\Phi }}_i}$. $W_{{\mathsf{\Phi }}_i}$ is obtained by multiplying the key vector matrix $U_{{\mathsf{\Phi }}_i}$ and the query vector matrix $Q^T$. The key vector matrix $U_{{\mathsf{\Phi }}_i}$ is obtained by $H^{{\mathsf{\Phi }}_i}$ through a layer of MLP mapping, which uses $Tanh$ as the activation function. $W$, $B$, and $Q^T$ are the training parameters of the model.

3.2.3. Loss Function

This paper takes the cross-entropy between the predicted category and the actual category of the node as the loss function of HeMGNN, and performs the iterative process of the model by minimizing the cross-entropy. The calculation of cross-entropy is shown in Formula (12):

$$L=-\sum _{iϵD}{Y}_i\ln \left(Softmax\left(H_i·W\right)\right),$$

(12)

where $D$ is the dataset. $Y_i$ represents the true label of node $i$, $H_i$ represents the embedding of node $i$, and $W$ is the classifier parameter.

3.2.4. Complexity Analysis

Algorithm 1 shows the algorithm of the heterogeneous network embedding by using HeMGNN. It can be seen that HeMGNN adopts parallel processing when encoding nodes, that is, HeMGNN operates all the metapaths at the same time, which will improve the running speed of the model.

Specifically, the time complexity of HeMGNN is mainly reflected in the node embedding mixing module. The time complexity of this module is $\mathcal{O}(c_1\left(A\right)+c_2(B\left)\right)$. Where $c_1$ and $c_2$ represent the number of homogenous graphs and bipartite graphs, respectively. $A$ is the computational complexity of the homogenous graph encoder, and $B$ is the computational complexity of the bigraph encoder.

If the encoding process of nodes is based on a convolution neural network, the time complexity of this process is $\mathcal{O}(c_1\left(n^2{d}_1^{\prime }+n{d}_1^{\prime }{d}_1^{″}\right)+c_2(n{d}_1^{\prime }{d}_1^{″}+nm{d}_2^{\prime }+n{d}_2^{\prime }{d}_2^{″}\left)\right)$. If the encoding process of nodes is based on a Transformer-based attention mechanism, the time complexity of this process is $\mathcal{O}({(c}_1+c_2)(n{d}_1^{\prime }{d}_1^{″}+2m{d}_2^{\prime }{d}_2^{″}+n{d}_1^{″}{d}_2^{″}+nm(d_1^{″}+d_2^{″}\left)\right)$. $n$ is the number of target nodes, and $m$ is the number of heterogeneous nodes. In particular, in the encoding method based on the Transformer-based attention mechanism, m = n when encoding the homogeneous subgraph. $d_1^{\prime }$ and $d_1^{″}$ are the initial feature dimension and the final feature dimension of the target node. $d_2^{\prime }$ and $d_2^{″}$ are the initial and final embedding dimensions of the heterogeneous nodes. Usually, $d_1^{″}$ = $d_2^{″}$. In the embedding fusion part, the time complexity is $\mathcal{O}({(c}_1+c_2)n{d}_1^{″})$. It can be found that the time complexity of most operations in the model has a linear relationship with the nodes’ number of n and m, and the number of metapath matrices ${(c}_1+c_2)$ also has a linear relationship, which makes the node embedding mixing module have a lower time complexity. Meanwhile, in the metapath subgraph extraction module and node embedding module, HeMGNN uses multiplication based on a sparse matrix to process the inner product of the matrix. This method can transform the matrix multiplication operation from the operation based on a two-dimensional table to the operation based on a linear table through the sequential traversal of the elements in the matrix, so as to greatly reduce the time complexity of the matrix multiplication operation.

Algorithm 1: Algorithm of HeMGNN.

Input:    The heterogeneous network $\mathcal{G}=\{\mathcal{V},\mathcal{E},\mathcal{A},\mathcal{R}\}$                The node feature $\left\{h_{v_j},\forall v_j\in \mathcal{V}\right\}$,                The metapath set $\{{\mathsf{\Phi }}^{heo},{\mathsf{\Phi }}^{bio}\}$, Output: The final embedding $\{h_{v_j}^{mixed},\forall v_j\in \mathcal{V}\}$,                The metapath attention weight {${\alpha }_{\mathsf{\Phi }},\mathsf{\Phi }\in {\{\mathsf{\Phi }}_i^{heo},{\mathsf{\Phi }}_i^{bio}\}$}. 1: for ${{\mathsf{\Phi }}_i\in \{\mathsf{\Phi }}_i^{heo},{\mathsf{\Phi }}_i^{bio}\}$ do 2:       for $v_j\in \mathcal{V}$ do 3:             find the neighbors ${\mathcal{N}}_{v_j}$ of $v_j$ in metapath ${\mathsf{\Phi }}_i$; 4:             if ${\mathsf{\Phi }}_i\in {\mathsf{\Phi }}_i^{heo}$ 5:                 $h_{v_j}^{heo}=aggregate for homogeneous subgraph(h_{{\mathcal{N}}_{v_j}})$; 6:             end if 7:             if ${\mathsf{\Phi }}_i\in {\mathsf{\Phi }}_i^{bio}$ 8:                 $h_{v_j}^{bio}=aggregate for bipartite subgraph(h_{{\mathcal{N}}_{v_j}})$; 9:             end if 10:      Calculate the weight of metapath ${\alpha }_{{\mathsf{\Phi }}_i}$; 11:      End 12: Mix embeddings under metapaths $h_{v_j}^{mixed}=\sum _{{{\mathsf{\Phi }}_i\in \{\mathsf{\Phi }}_i^{heo},{\mathsf{\Phi }}_i^{bio}\}}{\alpha }_{{\mathsf{\Phi }}_i}·h_{v_j}^{{\mathsf{\Phi }}_i}$ 13: End 14: Calculate Cross-Entropy 15: $L=-\sum _{iϵD}{Y}_{i}ln(Softmax(H_{v_j}·W))$; 16: Back propagation and update parameters in HeMGNN; 17: Return ${\{h}_{v_j}^{mixed}\}\{{\alpha }_{{\mathsf{\Phi }}_i}\},v_j\in \mathcal{V}$

4. Experiments and Analysis

This paper constructs heterogeneous networks from three different fields to verify the performance of the HeMGNN model.

4.1. Datasets

Table 2 gives the datasets used in our experiments. The specific information of the datasets is as follows:

Table 2. Information about the three datasets.

Dataset	Node Type	Nodes	Edge Type	Edges	Labels
DBLP	Author (A) Conference (C) Paper (P) Term (T)	4057 20 14,376 8920	P–A P–C P–T	19,645 14,376 114,625	Author (4)
Yelp	Business (B) Reservation (R) Service (S) Stars_level (L) User (U)	2614 2 2 9 1286	B–L B–R B–S B–U	2614 2614 2614 30,839	Business (3)
IMDB	Movie (M) Director (D) Actor (A)	4278 2081 5257	M–D M–A	4278 12,828	Movie (3)

DBLP: DBLP is a heterogeneous citation network dataset extracted from the DBLP website. It contains four heterogeneous nodes: 4057 authors, 14,376 papers, 20 conferences, and 8920 terms. Among them, the label of the author node can be obtained according to his/her research field, and can be divided into four types: Database, Data mining, Information retrieval, and Machine learning.

Yelp: Yelp is a heterogeneous business network dataset. It contains five types of heterogeneous nodes: 2614 merchants, 1286 users, 2 service types, 2 booking types, and 7 star ratings. Among them, the merchant nodes are labeled and divided into three types: Mexico, Burgers, and Gastropubs.

IMDB: IMDB is a heterogeneous movie rating network dataset, which is a data subset extracted from the IMDB website. It contains three types of heterogeneous nodes, including 4278 films, 2081 directors, and 5257 actors. Among them, the movie nodes are labeled and divided into three categories: Action, Comedy, and Drama.

4.2. Baseline Models

In order to verify the performance of the node embedding using the HeMGNN model, we compared it with the existing network embedding models. These models include models based on random walking, adversarial learning, Maximize mutual information, and Transformer-based attention, etc. The details of these baseline models are as follows:

• Metapath2vec [12]: Metapath2vec is a random-walk-based model whose underlying architecture is the Word2vec model.
• Hin2vec [14]: Hin2vec is a metapath-based model. It designs a logical binary classifier to predict whether there is a specific relationship between two given nodes, so as to effectively learn model parameters to learn the embeddings of nodes and metapaths.
• HeGAN [31]: HeGAN is an adversarial learning-based model, which uses a generator to generate false neighbors of the target node, and uses a discriminator to distinguish the authenticity of neighbor nodes.
• HAN [23]: HAN is a semi-supervised embedding model based on an attention mechanism, which uses node-level and semantic-level attention mechanisms to obtain information from the specified metapaths.
• HDGI [28]: HDGI is an unsupervised representation learning model, which uses metapaths to capture the semantic structure in heterogeneous graphs, and uses a graph convolution module and a semantic-level attention mechanism to obtain the local representation of nodes.
• HGT [30]: HGT is a Transformer-based representation learning model. The model uses the self-attention mechanism in a Transformer to calculate the attention on each edge of the target node and reserves a set of weight parameters for each node pair.

In the HeMGNN model, if the node embedding process is based on a graph convolution neural network, HeMGNN will use a one-layer GCN and one-layer GCMC encoders to embed the nodes in a homogeneous subgraph and bipartite subgraph respectively, and the activation function of the encoder is Relu. If the Transformer-based attention mechanism is used to embed the nodes, HeMGNN will use one layer of HGT with the single-head attention and the activation function is Gelu.

For all of the models, the initial features of nodes are encoded with one-hot encoding or random encoding, because we hope that these models can only obtain information from the structure of the heterogeneous network without being affected by the features of the initial nodes. In addition, in order to make a fair comparison with the baseline models, the embedded dimension of the nodes obtained from each model is set to 64 dimensions.

4.3. Experiments’ Results

This paper uses the classification and clustering tasks on three datasets to test the performance of the node embedding generated by each model. The hyperparameters in training the HeMGNN model are set as follows: a one-layer graph encoder is used for each subgraph; the hidden layer is 64 dimensions for each encoder; Relu is used as the activation function; and the Dropout rate is 0.2–0.4. The L2 regularization factor is set to λ = 0.01 in each graph encoder.

The KNN algorithm is used to perform the classification task of nodes, where the number K of the nearest neighbors is set to 5, and the algorithm will iterate 100 times. Macro-F1 and micro-F1 are used to evaluate the classification effect. We use 20% of the data as the training set and the remaining 80% as the verification set.

A K-means clustering algorithm is used to perform the clustering task of nodes, where the number K of clusters is set as the number of label categories of supervised nodes in each dataset, and the model will iterate 100 times. The NMI and ARI indexes are used to evaluate the effect of clustering under each model.

4.3.1. Classification and Clustering Results

Table 3 shows the classification performance of each model on three datasets. “HeMGNN-C” represents the HeMGNN model based on a graph convolutional neural network. “HeMGNN-T” is the Transformer-based HeMGNN model. “Mac-F1” and “Mic-F1” represent the performance evaluation indicators of Macro-F1 and Micro-F1, respectively. Max(Δ) represents the maximum improvement of the HeMGNN model compared to the baseline models under each indicator.

Table 3. The classification performance of models.

MODEL	DBLP		YELP		IMDB		ALL_DATA
	Mac-F1	Mic-F1	Mac-F1	Mic-F1	Mac-F1	Mic-F1	Mac-F1_avg	Mic-F1_avg
Metapath2vec	0.6985	0.6874	0.4534	0.5171	0.3933	0.4051	0.515	0.5365
Hin2vec	0.605	0.594	0.4011	0.3541	0.325	0.3261	0.4437	0.4247
HeGAN	0.7544	0.7702	0.4578	0.5264	0.4057	0.4177	0.5393	0.5714
HAN	0.8525	0.8629	0.6132	0.6847	0.5123	0.5124	0.6593	0.6866
HDGI	0.7153	0.7259	0.4096	0.4429	0.4445	0.4466	0.5231	0.5384
HGT	0.9246	0.9304	0.4832	0.5374	0.377	0.3779	0.5949	0.6152
HeMGNN-C	0.9272	0.9347	0.6913	0.7408	0.5384	0.5409	0.7189	0.7388
HeMGNN-T	0.9168	0.9223	0.6159	0.6982	0.4792	0.4818	0.6706	0.7007
Max(∆)	0.3222	0.3407	0.2902	0.3867	0.2134	0.2148	0.2752	0.3141

It can be seen that among all the models, HeMGNN-C achieves the best classification effect on these three datasets. Compared to the baseline models, the average performance of HeMGNN-C on Mac-F1 and Mic-F1 indicators has improved by up to 0.2752 and 0.3141, respectively. The performance of HeMGNN-T is slightly lower than that of HeMGNN-C, but its classification performance is also better than all the baseline models. In addition, in the baseline models, all semi-supervised models outperform unsupervised models in classification performance. This is because compared with the semi-supervised models, the unsupervised models cannot distinguish the importance of different metapaths, which affects the effect of node embedding to a certain extent.

Table 4 shows the clustering performance of each model on three datasets. It can be seen that the Transformer-based attention HeMGNN-T model achieves the best performance on all three datasets. Compared to the baseline models, the average performance of HeMGNN-T on the NMI and ARI indicators has improved by up to 0.2235 and 0.2046, respectively. The performance of HeMGNN-C is inferior to that of the HeMGNN-T, and inferior to the baseline models of HAN and HGT. However, the HeMGNN-C model outperforms the other four baseline models.

Table 4. The Clustering performance of models.

MODEL	DBLP		YELP		IMDB		ALL_DATA
	NMI	ARI	NMI	ARI	NMI	ARI	NMI_avg	ARI_avg
Metapath2vec	0.4577	0.4806	0.1102	0.1443	0.0115	0.0151	0.1931	0.2133
Hin2vec	0.442	0.4699	0.2324	0.24	0.0102	0.0105	0.2282	0.2401
HeGAN	0.5546	0.572	0.2544	0.2608	0.0366	0.0376	0.2818	0.2901
HAN	0.6557	0.6721	0.3909	0.4167	0.0572	0.017	0.3679	0.3686
HDGI	0.6076	0.6267	0.2334	0.2011	0.0187	0.037	0.2865	0.2882
HGT	0.7103	0.7675	0.2485	0.2238	0.0315	0.0353	0.3301	0.3422
HeMGNN-C	0.4656	0.4248	0.3783	0.4127	0.0635	0.0156	0.3024	0.2843
HeMGNN-T	0.7259	0.7876	0.4656	0.4248	0.0583	0.0413	0.4166	0.4179
Max(∆)	0.2839	0.3628	0.3554	0.2805	0.0533	0.0308	0.2235	0.2046

By comparing the performance of the node embedding in the classification and clustering tasks under each model, it can be seen that the HeMGNN model performs best. The results show that the HeMGNN model proposed in this paper can generate better node embeddings for the domain tasks. At the same time, the result also indicates that using different encoding methods to learn node embedding in the HeMGNN model has a different bias for the different domain tasks. The encoding method based on a graph convolution neural network is more suitable for the classification task of nodes, and the encoding method based on Transformer-based attention is more suitable for the clustering task of nodes.

4.3.2. Ablation Experimental Results

The HeMGNN model integrates the information of homogeneous and heterogeneous neighbor nodes when generating the embedding of target nodes. In order to verify the necessity of information transmission of homogeneous and heterogeneous neighbors in node embedding, an ablation experiment is designed in this paper. Taking the node classification task as an example, this study examines the classification performance of the model when only aggregating information of homogeneous neighbors or only aggregating the information of heterogeneous neighbors, and compares the results with the complete HeMGNN model.

Table 5 shows the results of the ablation experiment. Among them, “HeMGNN-C” and “HeMGNN-T” represent the graph convolutional neural network-based and Transformer-based HeMGNN models, respectively. “-hom” represents the model that only aggregates the homogeneous neighbor information. For example, “HeMGNN-C-hom” represents the HeMGNN-C model, which only aggregates the homogeneous neighbor information. “-bi” represents the model that only aggregates heterogeneous neighbor information. For example, “HeMGNN-C-bi” represents the HeMGNN-C model only aggregating the heterogeneous neighbor information. The Macro-F1 score is used to evaluate the classification performance of each model.

Table 5. The ablation experiment results.

Model	DBLP	Yelp	IMDB
HeMGNN-C-hom	0.816	0.6287	0.4667
HeMGNN-C-bi	0.8583	0.4245	0.4011
HeMGNN-C	0.9272	0.6913	0.5384
HeMGNN-T-hom	0.8831	0.5682	0.3605
HeMGNN-T-bi	0.9007	0.5098	0.3665
HeMGNN-T	0.9168	0.6159	0.4792

It can be seen that whether under the model of HeMGNN-C or HeMGNN-T, the performance of fusing the information in a homogeneous subgraph and bipartite subgraph is better than that of using a homogeneous subgraph or bipartite subgraph alone. In the current heterogeneous network embedding methods, most of them focus on embedding the target node by using the information transmitted by the homogeneous neighbors, while ignoring the information of the heterogeneous nodes. The HeMGNN model integrates the information of the homogeneous and heterogeneous neighbors of the target nodes, which makes the node embedding generated contain richer semantic and topological information, so as to achieve better results in downstream mining tasks.

4.3.3. Experimental Results of Running Time

By taking the DBLP dataset as an example, Figure 2 shows the results of the running time of each model. All the models are tested under the same hardware conditions.

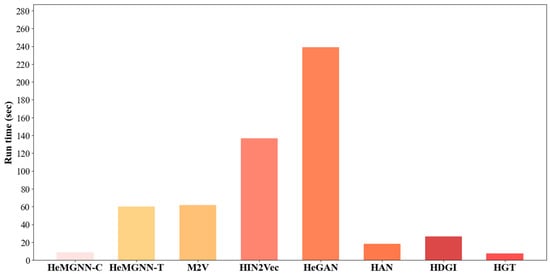
Figure 2. The running time of different models (taking the DBLP dataset as an example).

It can be seen that among all the models, the HeMGNN-C model and the HGT model need the shortest running time. The HGT model directly aggregates the information of neighbor nodes to encode target the nodes, resulting in a small architecture and fast training speed. Although the HeMGNN-C model also trains fast because it uses a sparse matrix for operation, it is based on metapaths to obtain the adjacency relationship between nodes. The training speed of the HeMGNN-T model is slower than that of the HeMGNN-C model, and the baseline models of HGT, HAN, and HDGI. It is because HeMGNN-T uses a random initialization to generate the initialization vector of nodes, and the subsequent matrix operations are based on the dense matrices, which brings HeMGNN-T a higher time consumption in matrix operations. Among the baseline models, the HIN2Vec model and the HeGAN model have the longest time consumption. HIN2Vec requires the input of the relationships between nodes generated by random walking for model training, which results in a longer running time. The HeGAN model takes a Generative Adversarial Network (GAN)-based architecture, it needs more time to train the generators and discriminators. In summary, compared with the baseline models, the HeMGNN model not only performs well in downstream classification and clustering tasks, but also has higher advantages in running time.

4.3.4. Discussion

In the current research on embedding heterogeneous networks, how to choose reasonable metapaths and how to aggregate the information of neighboring nodes are two keys to improve the performance of network embedding. This article proposes the HeMGNN model to make a in-depth discussion on these two issues. The contribution of the HeMGNN model is mainly in the following two aspects.

Firstly, HeMGNN takes progressive multiplication on the adjacency matrixes of the initial heterogeneous network to generate the metapaths. Based on the four general screening principles proposed, HeMGNN can screen out the metapaths closely related to the downstream tasks. Meanwhile, HeMGNN uses semantic-level attention to distinguish the contributions of different metapaths in the network embedding process.

Secondly, HeMGNN aggregates information from both the homogeneous and heterogeneous neighboring nodes to encode the target node. Compared with the current embedding models that only aggregate the information of homogeneous neighbors, HeMGNN can learn more abundant semantic information in the network, thus providing node vectors rich in semantics for downstream mining tasks.

The experimental results show that compared with the state-of-art network embedding models, the node vectors generated by the HeMGNN model achieve the best classification and clustering performance. The results of ablation experiments show that aggregating the information of homogeneous and heterogeneous neighbor nodes at the same time can more fully retain the semantic information in the network than only aggregating the information of homogeneous neighbors.

In addition, the HeMGNN model adopts an end-to-end mode, which can automatically learn the embedding of nodes without any manual intervention. These characteristics make the HeMGNN model highly versatile, which can be used in different heterogeneous networks in different fields.

5. Conclusions

Most heterogeneous network embedding models only focus on the information transmitted by homogeneous neighbors when encoding the target node, while ignoring the information transmitted by heterogeneous neighbors. The HeMGNN model proposed in this article integrates both the homogeneous and heterogeneous neighbor information of the target node, enabling the generated node vectors to embed richer semantic and topological information, thereby improving the performance of the node vectors in downstream mining tasks.

The HeMGNN model can automatically generate and filter out metapaths related to domain mining tasks, effectively avoiding the excessive dependence of the embedding process on artificial prior knowledge. Furthermore, the information of homogeneous and heterogeneous neighbors is integrated into the HeMGNN model to encode the target nodes. The experimental results on three heterogeneous networks in different fields show that the node vectors learned from the HeMGNN model achieve the best classification and clustering performance compared to all baseline models. This indicates that the node vectors generated by the HeMGNN model contain richer and more valuable information.

The HeMGNN model adopts an end-to-end mode, which can automatically learn the embedding of nodes without any manual intervention. These characteristics make the HeMGNN model highly versatile, which has been fully verified by experimental results on three different datasets in different fields. However, the HeMGNN model is a semi- supervised model that requires a small number of annotated samples during model training. However, in practical applications, labeling large-scale heterogeneous networks is a very time-consuming task. Continuing to design a universal unsupervised architecture based on HeMGNN is a challenging task in the future.

Meanwhile, the experimental results indicate that node embeddings generated based on different encoders have different biases on downstream tasks. At the same time, different encoders also have different sensitivities for different initial node feature encoding methods. The experimental results show that the GCN encoder is sensitive to the one hot encoding, while the Transformer-based encoder leans more towards the Gaussian random initialization vectors. Identifying the mechanisms of these phenomena and applying them to the design of network embedding models is also an interesting work for the future.