Abstract
Chemical-reaction optimization not only increases the yield of chemical processes but also reduces impurities and improves the performance of the resulting products, contributing to important innovations in various industries. This paper presents a novel barycentric kernel for chemical-reaction optimization using Bayesian optimization (BO), a powerful machine-learning method designed to optimize costly black-box functions. The barycentric kernel is specifically tailored as a positive definite kernel for Gaussian-process surrogate models in BO, ensuring stability in logarithmic and differential operations while effectively mapping concentration space for solving optimization problems. We conducted comprehensive experiments comparing the proposed barycentric kernel with other widely used kernels, such as the radial basis function (RBF) kernel, across six benchmark functions in concentration space and three Hartmann functions in Euclidean space. The results demonstrated the barycentric kernel’s stable convergence and superior performance in these optimization scenarios. Furthermore, the paper highlights the importance of accurately parameterizing chemical concentrations to prevent BO from searching for infeasible solutions. Initially designed for chemical reactions, the versatile barycentric kernel shows promising potential for a wide range of optimization problems, including those requiring a meaningful distance metric between mixtures.
1. Introduction
Chemical-reaction optimization aims to maximize functional properties of chemical reactions, such as yield [1,2]. Conducting chemical experiments in the lab can be time-consuming and expensive, which limits the number of reaction conditions that can be observed. As a result, the field of cheminformatics has sought computer-assisted methods to accelerate the chemical-reaction optimization process [3]. The fundamental idea behind computer-assisted chemical-reaction optimization is predicting the properties of unobserved points. While various regression models have been proposed for chemical-reaction optimization, selecting an appropriate model remains a challenge due to the unique characteristics of this domain. One challenge is that the observed data available for the regression model is limited due to its cost. Another challenge is that the reaction conditions space is often high-dimensional and non-linear. These challenges make chemical-reaction optimization problems hard to solve with the artificial neural network models outperforming in other domains. Therefore, Bayesian optimization (BO) has emerged as a popular method for chemical-reaction optimization [4,5,6]. BO is expected to find a global optimum in a multi-dimensional space [7].
In our research, we introduce a barycentric kernel for BO. This kernel calculates covariances between points in concentration space and is based on the barycentric distance, a more mathematically sophisticated metric in concentration space. Unlike other reaction conditions, such as temperature or reactants, concentrations are continuous scalars and conjugated fractions of 1. The conjugated fraction implies that if a fraction in a mixture increases, the other fractions must decrease accordingly. Thus, the concentration data should carefully consider conjugated constraints between the chemicals in the same mixture [8,9]. The barycentric distance accounts for this conjugation, enabling the barycentric kernel to perform better in concentration space. We conducted experiments on benchmark functions and chemical-reaction datasets to compare the convergence of the barycentric kernel with other popular kernels, such as the radial basis function (RBF) kernel. Our results indicate that the barycentric kernel converges stably in experiment space with concentration data, which makes this method promising for chemical-reaction optimization.
This paper presents the barycentric metric and generalizes it to n-dimensions. The barycentric space is equivalent to the chemical concentration space. We investigated the effects of dimensionalities on the barycentric kernel and compared our kernel in a cubic space, which is not a concentration space.
State-of-the-art techniques in chemical-reaction optimization have employed various approaches, such as genetic algorithms, particle swarm optimization, and deep-learning models. However, these methods often struggle with limited data. Despite the limited observed data, BO is iterative, allowing chemists to perform regression repeatedly, obtain recommendations, and conduct experiments to observe the ground-truth value of given points until satisfactory results are achieved.
2. Preliminary
2.1. Bayesian Optimization and Kernels
Bayesian optimization (BO) is a powerful optimization technique widely used in various domains. It is particularly suited to problems that require an expensive evaluation process. The core idea of BO is to construct a probabilistic model of the objective function and utilize this model to guide the optimal search.
BO consists of an acquisition function and a surrogate model. Gaussian-process regression (GP) and expected improvement functions (EI) are among the most common configurations of BO. GP is a stochastic model that assumes a prior distribution for the function and updates this distribution based on observed function evaluations [10]. The prior distribution is used as a predictive variance to provide additional explanatory power to the chemist during optimization. EI balances exploitation and exploration throughout the optimization process [11].
GP has two essential components: a mean function and a kernel. It is reasonable to set the mean function to constant when there is insufficient information. The kernel defines and calculates the covariance between data points, and the covariance matrix of the data forms a surrogate model for the objective function. The kernel should reflect the characteristics of the space the GP wants to explore [12].
2.2. Concentration Space
Concentration space is a space in which coordinates represent the fractions of specific materials in a mixture [13]. Consider a mixture M composed of i number of ingredients with concentrations . Since each concentration is a fraction of the mixture, concentrations are constrained such that after normalization by the amount of the mixture. Additionally, since each of is a fraction of the mixture, there is a second constraint: . Each vector can represent each ingredient, and the mixture can be considered as a linear combination of these ingredients.
2.3. Barycentric Coordinate System and Distance
The barycentric coordinate system is a mathematical representation of a point in a simplex, which generalizes a triangle to higher dimensions. In this coordinate system, a point in a simplex is represented as a set of weights that determine its position relative to the vertices of the simplex. Each weight corresponds to a vertex of the simplex, and the sum of the weights equals 1. The weights are unique for each point in the simplex [14]. These properties make the barycentric coordinate system a valuable tool for representing points in high-dimensional spaces, such as the concentration space of chemical mixtures.
A space of fraction generated by the basis set of ingredients forms a simplex on . For example, Figure 1 is a simplex in with vertices , , and . The i-dimensional barycentric coordinate can be mapped to by the given constraint [15].
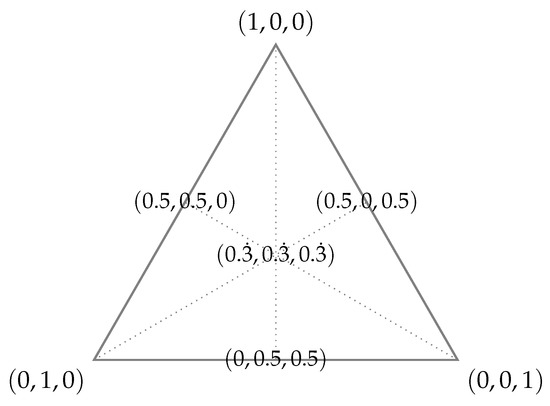
Figure 1.
Example of a two-dimensional simplex in three-dimensional cartesian coordinate. The points on the simplex are on the barycentric coordinate system.
3. Methodology
3.1. Barycentric Metrics
A mixture M is a simplex in the space , which can be mapped to . The simplex represents the space of barycentric coordinates , where . A barycentric metric can define the distance between two mixtures. Defining the metric in a ternary coordinate system allows you to measure the distance between mixtures in concentration space, subject to the constraints and . For the barycentric metric, consider the metric, defined as follows.
This definition of the barycentric metric allows us to calculate the distance between mixtures in concentration space. This metric provides a natural way to measure distance in coordinate-constrained spaces, such as the concentration space of a chemical mixture. In addition, the barycentric metric is not restricted to mixtures in concentration space. Still, it can be applied to any , making it versatile for measuring distance in higher dimensional spaces.
3.2. Barycentric Kernel
We developed a barycentric kernel for Bayesian optimization in the concentration space of chemical mixtures. The barycentric kernel is designed to handle the unique characteristics of the concentration space, considering the constraints on the coordinates. The kernel function is the exponential of the negative norm of the distance between two mixtures. The negative sign and the exponential function make the barycentric kernel a covariance kernel, ensuring stability in logarithm and differential and guaranteeing the positive definiteness of the kernel matrix.
The barycentric kernel provides a meaningful distance metric between mixtures, allowing Bayesian optimization to search for the optimum over the concentration space. The kernel function is an exponential function of the barycentric distance as (10).
where is the barycentric distance between and . This kernel can be effectively used for concentration data to encode chemical-reaction optimization.
We designed the barycentric kernel as a definite positive kernel for Bayesian optimization in the concentration space, equivalent to the chemical concentration space. We demonstrate that the barycentric kernel can effectively map the concentration space and solve chemical-reaction optimization problems. Using the barycentric kernel in Bayesian optimization, we can more accurately model the relationships between points in the concentration space and improve the optimization process for chemical-reaction datasets. We built a model to compare the barycentric kernel to other popular kernels, such as a radial basis function (RBF) kernel. The barycentric kernel is expected to outperform other kernels in capturing the unique properties of the concentration space.
3.3. Implementation
We implement the barycentric kernel functions in Python to ensure compatibility with Scikit-learn, a popular machine-learning library. This implementation allows for seamless integration with existing tools and methods provided by the library. The barycentric kernels are designed to replace Gaussian process regression kernels for Bayesian optimization in barycentric or concentration space. This allows us to leverage the unique properties of barycentric kernels to better model and optimize chemical reactions in concentration space.
The implemented barycentric-kernel class takes the barycentric coordinates of two points as input and returns the log-transformed covariance between the two points. This design choice provides a meaningful distance metric between mixtures, resulting in a stable, positive, static covariance kernel. In addition, the barycentric-kernel class is inherited from Scikit-learn’s kernel class, ensuring compatibility with other components in the library. This implementation makes it simple to use barycentric kernels as a drop-in replacement for traditional kernels in Bayesian optimization, allowing users to take full advantage of the benefits they offer for optimizing chemical reactions in concentration space.
The barycentric-kernel implementation has been made publicly available on GitHub, allowing researchers and practitioners to access and utilize the code in their projects efficiently. The repository, found at https://github.com/saankim/barycentric (accessed on 28 April 2023), includes detailed documentation and usage instructions.
4. Experiments
4.1. Experimental Setup
In our experimental study, we compared the performance of the Barycentric kernel (our proposed kernel) with several other kernels, including radial basis, Matern and Laplace (widely used kernels), Constant and White (baseline kernels), and DotProduct (a simple kernel). This comparison aimed to comprehensively understand how the barycentric kernel performs against various kernels in optimization problems.
We evaluated the kernels on six different benchmark functions in the concentration space, where the barycentric kernel is specifically designed to excel. By comparing the barycentric kernel’s performance to that of other widely used kernels on these benchmark functions, we aimed to gain valuable insights into its practical utility.
The first three benchmark functions we tested were well-known Hartmann functions with dimensions of 3, 4, and 6. These functions commonly assess optimization algorithms and are generally convex with a few local minimums. The Hartmann functions are defined within each dimension’s Euclidean coordinate space. To model the concentration space, we mapped the n-1-dimensional simplex within the cubic space and used it as the problem space for optimization. These functions also allowed us to examine the impact of dimensionality on the kernels’ performance.
The remaining three benchmark functions were emulator functions based on pre-trained artificial neural networks using chemical datasets. The EmulBOB dataset comprises colors created by mixing different proportions of five colored dyes, resulting in a five-dimensional space [16]. The EmulCN9 dataset involves colors created by mixing three colored dyes (red, green, and blue) in varying amounts, leading to a three-dimensional space [16]. Lastly, the PCE10 dataset consists of the degradation of polymer blends for organic solar cells under light exposure with a four-dimensional space [17].
In addition to the concentration space, we evaluated the Euclidean-space kernels using the Hartmann functions. This allowed us to test the performance of the Barycentric kernel under both simplex (concentration space) and cubic (Euclidean space) conditions, demonstrating its effectiveness and versatility compared to other kernels specifically designed for cubic spaces.
Our experiments tested seven kernels, including the Barycentric kernel, on six benchmark functions in the concentration space. We also experimented with the same seven kernels in Euclidean space using three Hartmann functions. Each experimental condition was repeated 40 times with different random seeds to ensure the consistency of the results. The Bayesian optimizer observed 30 iterations before terminating each trial.
4.2. Results
The values are normalized by minimum and maximum from their space. The normalized value reflects is how close to the known minimum the optimum that the optimizer, based on each kernel, found. One hundred means the optimizer observed the optimum before 30 iterations.
In the first table, Table 1, we present the results of the Bayesian optimizer on concentration space. The best result is marked in bold, and the second-best result is underlined. It is evident from the table that the barycentric kernel consistently finds a competitive optimum during the iterations. The White and Constant kernel does not infer information through iterations, so they perform worst, as shown in Table 1. However, it is essential to note that the emulation benchmark functions are relatively simple, necessitating further investigation using another method, such as the survival test presented in Table 2. We also found that the Matern kernel finds a good optimum. We also investigate this in Table 2. The Laplace kernel shows great performance on the Hartmann functions. The barycentric kernel is defeated on the Hartmann6D. This result is because the barycentric kernel is sensitive to dimensionality.

Table 1.
Normalized results of the Bayesian optimizer on the concentration space.

Table 2.
p-Values of the survival test of Bayesian optimizer on the concentration space, emulation benchmark functions.
Table 2 shows the resulting p-values of the survival test of the Bayesian optimizer on concentration space, specifically for the emulation benchmark functions. We conducted a survival test by fitting the Kaplan–Meier survival curve. The survival test compares the barycentric kernel with others from the perspective of the probability of finding the optimum in more than 90% convergence (normalized y value). This additional analysis provides information about the convergence speed (iteration count until finding 90% of the optimum). The result shows that the barycentric kernel converges relatively faster than other kernels, especially compared with the Matern kernel in EmulCN9 and EmulPCE10 and the Laplace kernel in EmulBOB, EmulCN9, and EmulPCE10. Thus, the Matern and Laplace kernels are relatively better in Table 1 but cannot converge as quickly as the barycentric kernel.
In contrast to the previous two paragraphs, which focus on concentration space, the third paragraph discusses the results of the Bayesian optimizer on Euclidean space. Table 3 presents the normalized result, similarly to Table 1. Table 3 shows that the barycentric kernel can also find optimum in the Euclidean space. Since the barycentric kernel is based on the mixture of the fraction of ingredients, the conjugated effect disappears when the dimensionality of the search space increases. Thus, the barycentric kernel performs worse in six or more dimensions in Euclidean space.

Table 3.
Normalized results of the Bayesian optimizer on the Euclidean space.
These three tables thoroughly examine the barycentric kernel’s performance in various contexts. By comparing its performance in both concentration and Euclidean spaces, we can better understand the potential advantages and limitations of the barycentric kernel when used in chemical-reaction optimization and other applications.
In addition, we created a heatmap visualization; Figure 2 is an example of the entire history of optimization results. The figure shows the history of the optimizer performed on the Hartman3D in cubic space. The values from each random seed are aggregated by their average. The figure shows that the barycentric kernel converges faster than other kernels in a small space, even if the space is not simplex (concentration space). Since this optimization experiment set the goal of minimization, the color of each cell should be close to purple during iterations.
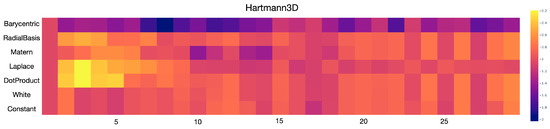
Figure 2.
This is a heatmap of 30 iterations performed on the Hartmann 3D function in concentration space.
5. Conclusions
In conclusion, our research focused on developing a new approach to optimizing problems in concentration space, the barycentric kernel, with specific application to chemical-reaction optimization. Our kernel can be used efficiently in small spaces, including concentration datasets. The barycentric kernel provides a meaningful distance metric between mixtures, ensuring stability under algebraic and differential operations while ensuring the positive definiteness of the kernel matrix. While the kernel was designed with chemical reactions in mind, it is versatile enough to be applied to other scenarios involving fractional composition, such as the softmax output of a classification neural network.
Our experiments compared the barycentric kernel with several other popular kernels and a baseline kernel for six benchmark functions in concentration space and three Hartmann functions in Euclidean space. The results demonstrated the barycentric kernel’s effectiveness and versatility in various optimization problems. We performed 30 iterations for each experimental condition to ensure consistency of results, further solidifying the practical utility of the barycentric kernel in both concentration and Euclidean space.
It is important to note that while the barycentric kernel was designed with chemical reactions in mind, its potential applications are not limited to this domain. The kernel’s ability to perform effectively in various fractional configurations, such as the softmax output of a classification neural network, highlights its adaptability and usefulness in a wide range of optimization problems. As a result, the barycentric kernel represents a promising avenue for future research and development in optimization, particularly in problems that require a meaningful distance metric between mixtures.
Author Contributions
Conceptualization, S.K. and J.K.; methodology, S.K. and J.K.; software, S.K.; validation, S.K. and J.K.; formal analysis, S.K. and J.K.; investigation, S.K. and J.K.; resources, S.K.; writing—original draft preparation, S.K.; writing—review and editing, S.K. and J.K.; visualization, S.K.; supervision, J.K.; project administration, S.K. and J.K.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ICT Creative Consilience Program (IITP-2023-2020-0-01821) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).
Data Availability Statement
The data and code used in this study are publicly available, ensuring the transparency and reproducibility of our research. The code for the barycentric kernel and the experimental setup can be accessed through our GitHub repository at the following URL: https://github.com/saankim/barycentric (accessed on 28 April 2023). This repository includes the Python implementation of the barycentric kernel, the benchmark functions, and the chemical reaction datasets.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, C.J.; Pomberger, A.; Felton, K.C.; Grainger, R.; Barecka, M.; Chamberlain, T.W.; Bourne, R.A.; Johnson, C.N.; Lapkin, A.A. A Brief Introduction to Chemical Reaction Optimization. Chem. Rev. 2023, 123, 3089–3126. [Google Scholar] [CrossRef] [PubMed]
- Lam, A.Y.; Li, V.O. Chemical reaction optimization: A tutorial. Memetic Comput. 2012, 4, 3–17. [Google Scholar] [CrossRef]
- James, J.; Lam, A.Y.; Li, V.O. Evolutionary artificial neural network based on chemical reaction optimization. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 2083–2090. [Google Scholar]
- Shields, B.J.; Stevens, J.; Li, J.; Parasram, M.; Damani, F.; Alvarado, J.I.M.; Janey, J.M.; Adams, R.P.; Doyle, A.G. Bayesian reaction optimization as a tool for chemical synthesis. Nature 2021, 590, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Lobato, J.M.; Hoffman, M.W.; Ghahramani, Z. Predictive entropy search for efficient global optimization of black-box functions. Adv. Neural Inf. Process. Syst. 2014, 27, 918–926. [Google Scholar]
- Nega, P.W.; Li, Z.; Ghosh, V.; Thapa, J.; Sun, S.; Hartono, N.T.P.; Nellikkal, M.A.N.; Norquist, A.J.; Buonassisi, T.; Chan, E.M.; et al. Using automated serendipity to discover how trace water promotes and inhibits lead halide perovskite crystal formation. Appl. Phys. Lett. 2021, 119, 041903. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J. Composition Search of Perovskite Solar Cell with Neural Network and Bayesian Optimization. In Proceedings of the Korean Society of Broadcast Engineers Summer Conference, June 2022; pp. 493–495. [Google Scholar]
- Wang, H.; Xu, Y.; Shi, B.; Zhu, C.; Wang, Z. Optimization and intelligent control for operation parameters of multiphase mixture transportation pipeline in oilfield: A case study. J. Pipeline Sci. Eng. 2021, 1, 367–378. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Khan, N.; Zhu, C.; Gao, Y. Effects of the Surfactant, Polymer, and Crude Oil Properties on the Formation and Stabilization of Oil-Based Foam Liquid Films: Insights from the Microscale. J. Mol. Liq. 2023, 373, 121194. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian processes in machine learning. Lect. Notes Comput. Sci. 2004, 3176, 63–71. [Google Scholar]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Shahriari, B.; Bouchard-Côté, A.; Freitas, N. Unbounded Bayesian optimization via regularization. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Cadiz, Spain, 9–11 May 2016; pp. 1168–1176. [Google Scholar]
- Schrier, J. Solution Mixing Calculations as a Geometry, Linear Algebra, and Convex Analysis Problem. J. Chem. Educ. 2021, 98, 1659–1666. [Google Scholar] [CrossRef]
- Floater, M.S. Generalized barycentric coordinates and applications. Acta Numer. 2015, 24, 161–214. [Google Scholar] [CrossRef]
- Zolotov, V. Scalar product and distance in barycentric coordinates. arXiv 2022, arXiv:2212.11712. [Google Scholar]
- Roch, L.M.; Häse, F.; Kreisbeck, C.; Tamayo-Mendoza, T.; Yunker, L.P.; Hein, J.E.; Aspuru-Guzik, A. ChemOS: An orchestration software to democratize autonomous discovery. PLoS ONE 2020, 15, e0229862. [Google Scholar] [CrossRef] [PubMed]
- Langner, S.; Häse, F.; Perea, J.D.; Stubhan, T.; Hauch, J.; Roch, L.M.; Heumueller, T.; Aspuru-Guzik, A.; Brabec, C.J. Beyond ternary OPV: High-throughput experimentation and self-driving laboratories optimize multicomponent systems. Adv. Mater. 2020, 32, 1907801. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).