Abstract
Time series forecasting has been performed for decades in both science and industry. The forecasting models have evolved steadily over time. Statistical methods have been used for many years and were later complemented by neural network approaches. Currently, hybrid approaches are increasingly presented, aiming to combine both methods’ advantages. These hybrid forecasting methods could lead to more accurate predictions and enhance and improve visual analytics systems for making decisions or for supporting the decision-making process. In this work, we conducted a systematic literature review using the PRISMA methodology and investigated various hybrid forecasting approaches in detail. The exact procedure for searching and filtering and the databases in which we performed the search were documented and supplemented by a PRISMA flow chart. From a total of 1435 results, we included 21 works in this review through various filtering steps and exclusion criteria. We examined these works in detail and collected the quality of the prediction results. We summarized the error values in a table to investigate whether hybrid forecasting approaches deliver better results. We concluded that all investigated hybrid forecasting methods perform better than individual ones. Based on the results of the PRISMA study, the possible applications of hybrid prediction approaches in visual analytics systems for decision making are discussed and illustrated using an exemplary visualization.
1. Introduction
Time series forecasting is a key component used in various fields to predict future events and identify trends. Common use cases include the prediction of stock prices [1], electrical loads [2,3], or tourist numbers [4]. Other domains in which predictions play an important role are, e.g., environmental research [5], mobility research [6], and healthcare [7,8]. The forecasting models have evolved steadily over time. Early methods for time series prediction relied on purely statistical procedures such as regression analyses [9,10,11]. These statistical methods work well for data with linear relationships. For nonlinear data, artificial intelligence models, especially neural networks, have been established [1,2,3]. Recently, hybrid methods that combine statistical methods with deep learning approaches have been developed to make more accurate predictions [4,12,13]. Before applying hybrid forecasting methods, the data can be divided into different components. “Wavelet transform” functions such as “discrete wavelet transform” (DWT) can be used [14,15,16] to divide the data into linear and nonlinear components [17]. Various evaluation methods can be used to measure the quality of forecast results. Metrics such as root mean square error (RMSE) and mean absolute percentage error (MAPE) are measured frequently. Per definition, visual analytics is the combination of automated analysis methods and interactive visualizations that enables analytical reasoning [18,19,20] and supports the decision-making processes in various domains [21] for a variety of tasks [22,23]. Decision making often depends on the temporal component of data and the progressions and trends within them [24]. Therefore, the most accurate possible prediction of temporal sequences plays a crucial role in visual analytics systems. The recently emerged hybrid forecasting approaches can potentially integrate valid predictions into visual analytics systems. These approaches could make an important contribution to the quality of the decision-making process.
Although hybrid forecasting methods make up a large part of the publications on forecasting techniques, there is currently no systematic review and analysis of the quality of different hybrid approaches compared to their corresponding individual models. This fact leads us to analyze in this systematic review reports on hybrid forecasting methods that have measured the quality of the individual statistical models and the neural networks, as well as that of their hybrid approach. To identify the relevant literature in this area, we use the established methodology according to PRISMA for this review, which has emerged in the BMC research but is also increasingly applied in computer science [25] and other domains to analyze literature in a structured and systematic way.
According to PRISMA, this systematic literature review aims to determine whether hybrid approaches provide better prediction results than their corresponding individual models. Based on the results of the PRISMA study, future applications of these hybrid approaches in visual analytics systems for decision making are considered.
Our procedure for conducting the PRISMA study in this work is structured as follows. At the beginning of our work, we first present our methodology, including our search strategy and the associated databases. Using the PRISMA flow graph created for this systematic literature search, we present the individual filtering steps and the inclusion and exclusion criteria. Subsequently, we present the papers included in the review. For this purpose, we have divided the papers into five subcategories. We present each paper individually and briefly explain its goals, underlying data, proposed hybrid prediction approach, and evaluation results they scored for their corresponding individual models and the hybrid approach. In the following discussion, the results of the PRISMA study are summarized, and the evaluation scores are presented in a table. Furthermore, in the second part of the discussion, the application of hybrid forecasting approaches in visual analytics is discussed based on an exemplary visualization. Finally, a summary is drawn. Our main contribution is the systematic review of hybrid prediction approaches with their corresponding error values that can be used in decision support systems, particularly in visual analytics.
2. Methods
The following literature review follows the established PRISMA methodology. To identify the most accurate studies, it is necessary to establish the research objectives, define adequate search terms, and select suitable databases.
The research objective of the following systematic literature review is the investigation of hybrid methods, combining statistical methods and neural networks, for time series forecasting concerning prediction accuracy. We focused on the two metrics root mean squared error (RMSE) and mean absolute percentage error (MAPE) to evaluate the quality of the investigated works. These two metrics provide information on prediction accuracy and are frequently specified by authors to measure prediction quality.
where is the actual value, is the predicted value, and n is the number of forecast values. These metrics are error rates; thus, a lower RMSE or MAPE result represents a more accurate prediction.
In order to identify all relevant works, it was first necessary to identify all meaningful keywords. These keywords also include the various statistical methods and neural networks used in the context of hybrid forecasting, since it cannot be assumed that all authors declare their prediction approach as hybrid. ARIMA appeared as a frequently used statistical method. Therefore, we have approved ARIMA and all derivatives such as SARIMA. In the field of forecasting through artificial intelligence methods, LSTM-, RNN-, CNN-, GNN-, and ANN-networks could be identified.
We performed our review in the following three single source databases:
- IEEE (through the IEEE Xplore platform);
- Elsevier (through the ScienceDirect platform);
- ACM (through ACM Digital Library).
These single-source databases were complemented by a multi-database search on the platform “Web of Science”, allowing for simultaneous searching of databases such as Springer Nature, Wiley Online Library, Emerald, MDPI, Hindawi, Tech Science Press, Cambridge University Press, JAPS, TandFO, and World Scientific. We chose these databases to cover as many studies as possible while minimizing the number of duplicates. The search was limited to English and publications dating from 2019 to 2022 to have the latest and most performing models since things are evolving rapidly in these fields. Table 1 presents the specific search queries.

Table 1.
Table of search queries and filters applied to the different databases.
As summarized in Figure 1, a total of 1435 records were identified from the different databases. A total of 176 duplicates were detected and removed using Citavi. Three independent researchers conducted the screening process. Through title and abstract screening, 960 records were excluded, and 475 reports remained. These 475 reports were filtered based on various inclusion and exclusion criteria. Works that were critical or borderline quality were discussed by three independent researchers in detail, and a joint decision was made. We included reports comparing their proposed hybrid models with each other and with the individual models. We also included reports that presented a hybrid model between a statistical model and a neural network, such as ARIMA-LSTM, but not corresponding to an autoregressive neural network (NAR). We excluded reports that proposed no hybrid models, hybrid statistical models, single neural networks, or autoregressive neural networks. Moreover, at least RMSE or MAPE had to be calculated and specified in the reports. Some reports could not be reported because the results were only presented graphically or due to a lack of precision in the methods used. Finally, only the models implemented separately in several studies were selected to avoid confirmation bias on single samples. As the research did not include tests on comparable populations or even data, no risk of bias was assessed. Because the data from each study inevitably produce widely varying results, only the most important conclusions were considered in this review. In addition, according to PRISMA guidelines, risk of bias is required mainly for BMC domains, but only in certain circumstances in informatics. At last, 21 reports were selected to be included in the review for further investigation. Data regarding the quality of the forecasting models were extracted from the reports by three independent scientists and then cross-checked to ensure quality.
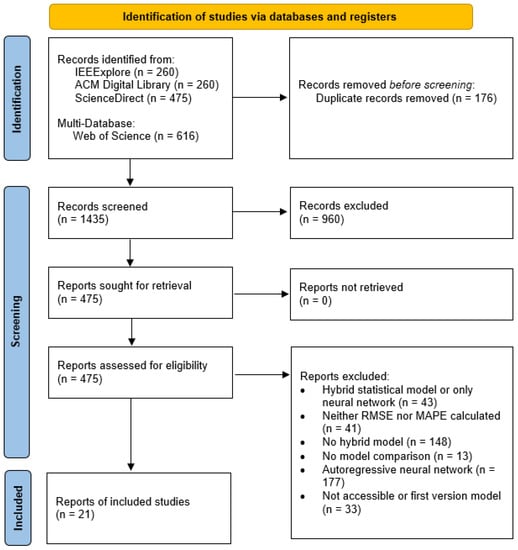
Figure 1.
PRISMA flow chart showing the filtered results for each filter step according to [26].
3. Results
In the following, the works included in the review are briefly summarized, and the results are presented regarding RMSE and MAPE scores. The results were rounded to a maximum of five decimal places. The included reports can be roughly divided into five groups. The first group is hybrid approaches that use ARIMA and LSTM [27,28,29,30,31]. In the second group are approaches that use SARIMA and LSTM [4,5,32]. SARIMA is an extension of the ARIMA model, which also considers seasonality. In the fourth group of studies, models using neural networks more rarely implemented than LSTM were studied [7,8,33,34,35]. In this group are works that combined ARIMA with back propagation neural networks (BPNN) [33,34,35] or works that combined ARIMA with generalized regression neural networks (GRNN) [7,8]. In the last group are models that include wavelet transform decomposition that allows for the separation of linear and nonlinear parts of a temporal series a priori to the actual forecasting [8,36,37,38].
3.1. Hybrid Approaches Combining ARIMA and LSTM
Temur et al. predicted housing sales in Turkey using ARIMA, LSTM, and a hybrid approach combining both [27]. According to Temur et al., their work bridges a gap, as studies conducted in Turkey and other countries increasingly focus on house prices. They used a 124-month data set ranging from 2008 to 2018. Their individual ARIMA model (RMSE: 16.745/MAPE: 0.121) performed better than their LSTM model (RMSE: 21.757/MAPE: 0.150). Their ARIMA-LSTM model (RMSE: 13.252/MAPE: 0.072) outperformed both individual models [27]. In another work, Temur et al. [29] proposed a hybrid approach using ARIMA and LSTM to estimate a monthly sales quantity budget [29]. They stated that they used ARIMA as a linear model, an LSTM RNN as a nonlinear model, and a hybrid ARIMA-LSTM model, which was, according to them, to improve the system’s performance. They stated that their hybrid model (RMSE: 685.570/MAPE: 0.133) gave lower errors in comparison to their single ARIMA model (RMSE: 871.961/MAPE: 0.254) and their single LSTM model (RMSE: 813.579/MAPE: 0.245) [29]. Li et al. proposed an approach to predict soil temperatures [30]. Their work states that predicting soil temperatures is a crucial topic in Earth sciences. The data contain temporal and spatial variations, which multiple factors affect. They propose a special hybrid approach that integrates ARIMA directly into the output layer of a multichannel long short-term memory model (LSTM) to characterize the deterministic part and the stochastic component [30]. According to the authors, the integration aims to learn the features that occurred in a short-term pattern. They tested their approach with half-hour data from two synoptic stations in Laegern and Fluehli in Switzerland. Li et al. stated that their hybrid model, the ARIMA-LSTM model (RMSE: 0.74359), gave lower error rates in comparison to their single ARIMA model (RMSE: 0.96946) and their single LSTM model (RMSE: 0.94749) [30]. Yu et al. proposed a hybrid ARIMA-LSTM approach to predict persistent organic pollutant (POP) concentration [28]. According to Yu et al., a persistent organic pollutant concentration sequence contains linear and nonlinear components. They propose an intelligent data analysis system combining ARIMA and an LSTM to analyze and predict the POPs concentrations in the Great Lakes region. Using multiple evaluation indicators, they evaluated their intelligent data analysis system with other single baseline models. They stated that their system delivered the smallest MAE, RMSE, and SMAPE values on all data sets. Moreover, they stated that their system could predict the trends of concentration changes well, and the predicted values are closer to true values, which prove that it can effectively improve the precision of prediction. They used their system to predict the concentration values of sites in the Great Lakes region for the next five years. According to them, their prediction presented a large fluctuation in concentrations as a trend for each year, but the overall trend was decreasing. For their second test data set, they had the lowest errors with their ARIMA model (RMSE: 48.686), LSTM model (RMSE: 23.193), and their hybrid model (RMSE: 14.726) [28]. Mailman and Arabaci predicted the Canadian, American, and Australian dollar exchange rates and the British pound [31]. According to them, exchange rate data are very dynamic and nonlinear, making forecasting those exchange rates very difficult. They applied a total of ten different single models. Their hybrid ARIMA-LSTM approach delivered the best results (RMSE: 0.0143/MAPE: 0.204). Aside from their ARIMA model (RMSE: 0.02223/MAPE: 0.487) and their LSTM model (RMSE: 0.0155/MAPE: 0.241), they also tested MLP (RMSE: 0.01856/MAPE: 0.259), which outperformed the ARIMA model but not the LSTM model [31].
3.2. Hybrid Approaches Combining SARIMA and LSTM
Sun et al. focused their work on predicting the global average sea level [5]. They stated that sea level variations often contain linear and nonlinear characteristics, making it hard to predict them with a single model. They stated that SARIMA is suitable for the linear characteristics of their data but not for the nonlinear part of the data. To tackle this problem, they proposed an approach to decompose the data into trend, seasonal, and random terms. They achieved good results for their SARIMA model (RMSE: 1.667/MAPE: 1.236) and their LSTM model (RMSE: 1.718/MAPE: 1.251), and the most promising results for their hybrid SARIMA-LSTM (RMSE: 1.155/MAPE: 0.837) approach [5]. Peirano et al. proposed an approach for inflation forecasting, which according to them, has been and continues to be an important issue for global economies [32]. For that cause, monitoring inflation indicators to make national decisions and policies is a crucial task. For the planning of strategic national investments, inflation forecasts over longer periods are necessary [32]. A bad forecast of inflation can lead to significant economic difficulties. They propose a hybrid SARIMA-LSTM model to forecast the inflation rate in emerging economies. They stated that their hybrid SARIMA-LSTM model gave lower error rates (RMSE: 0.00272) in comparison to their ARIMA model (RMSE: 0.00283) and their LSTM model (RMSE: 0.00553) [32]. Wu et al. proposed an approach to predict tourist demand [4]. According to them, most other studies focused on data that are on a quarterly or monthly basis forecast daily for tourist arrivals in Macau SAR in China. They achieved results of their SARIMA model (RMSE: 2598.5/MAPE: 1.006) and their LSTM (RMSE: 3799.76/MAPE: 1.953), but the best scores were for their hybrid SARIMA-LSTM (RMSE: 2524.59/MAPE: 0.79565) approach. They also tested an ARIMA model (RMSE: 3070.28/MAPE: 1.320), scoring worse than the SARIMA model [4].
3.3. Hybrid Approaches Combining ARIMA or SARIMA and an ANN
The next group of works combined ARIMA or SARIMA with ANNs [39,40,41,42]. Wang et al. proposed an approach to forecast shale gas production in Texas and Pennsylvania [39]. They state that forecasting the production in those two states can lead to better prediction results for shale gas production in the United States. They used linear and nonlinear forecasting methods to improve their forecasting accuracy. They developed two hybrid forecasting techniques, namely the nonlinear metabolic grey model–Autoregressive Integrated Moving Average Model (NMGM-ARIMA) and the Autoregressive Integrated Moving Average Model–Artificial neural network (ARIMA-ANN). They used a data set of sixty samples to test their forecasting techniques. As their ARIMA-ANN delivered more promising results than their NMGM-ARIMA approach, only the ARIMA-ANN is considered in this review. They achieved results for their ARIMA model (RMSE: 0.00685/MAPE: 2.78) and for their ANN (RMSE: 0.00595/MAPE: 2.4), but the best scores were for their hybrid ARIMA-ANN (RMSE: 0.0045/MAPE: 1.72) approach [39]. Belmahdi et al. proposed an ARIMA-ANN to forecast daily global solar radiation (DGSR) based on data from three Moroccan cities [40]. They state that daily global solar radiation data are based on different meteorological parameters, which make them difficult to forecast. They measured the forecasting performance of their ARIMA model and the ANN separately, as well as the performance of the hybrid ARIMA-ANN. They achieved for their ARIMA model results of (RMSE: 950.42/MAPE: 64.848) and their ANN (RMSE: 772.28/MAPE: 52.583). They achieved the best results for their hybrid ARIMA-ANN model (RMSE: 486.77/MAPE: 32.964) [40]. Azad et al. and Yu et al. proposed SARIMA-ANN approaches [41,42]. Azad et al. proposed an approach to predict water levels [41]. They state that predicting water levels is a different task because of spatio-temporal changes. For their predictions, they used data derived from the Red Hills Reservoir in India, where that reservoir is an important drinking and irrigation water supplier. They achieved good results for their SARIMA model (RMSE: 891.994/MAPE: 79810.15) and their ANN model (RMSE: 806.062/MAPE: 66032.258). They achieved the best results for their hybrid SARIMA-ANN (RMSE: 430.728/MAPE: 34323.06) approach [41]. Yu et al. proposed their hybrid approach for electricity load dynamics [42]. They state that an accurate electric load forecast is possible due to its inherent seasonality and strict periodicity. They tested their approach on different scenarios, such as seasons, holidays, weekends, and extreme weather conditions. They achieved for their ARIMA model results of (RMSE: 29.40/MAPE: 4.32) and for their ANN (RMSE: 36.00/MAPE: 5.20). They achieved the lowest error score for their hybrid ARIMA-ANN (RMSE: 17.60/MAPE: 2.60) approach [41].
3.4. Hybrid Approaches Combining ARIMA and BPNN or GRNN
Yu et al. [33] proposed an approach to forecasting clothing sales to ease the planning process of clothing producers and sellers. They state that clothing sales data contain linear and non-linear factors. They also state that, for this reason, single forecasting methods are not ideal for these types of data. They achieved the best results on the linear factor of their data with ARIMA (RMSE: 27.684) and the best results for the non-linear component with a BPNN (RMSE: 15.503). Their proposed hybrid ARIMA-BPNN model had the lowest error, with an RMSE of 12.543 [33]. Hadwan et al. proposed a rather general approach for time series forecasting [35]. Their proposed method consists of three forecasting models. They propose an ARIMA model and a back propagation neural network, which they state has an adaptive slope and momentum parameters. The third model they tested is a hybrid ARIMA-BPNN model, which is suitable for linear and non-linear modeling, according to them. They tested their approach on two different data sets. The first data set contained information about the consumer price index (CPI), which they used to predict indices of the CPI. The second data set contained information on cancer patients in the Ibb Province in Yemen, which they used to predict the expected number of cancer patients. They measured the performance of both models using the metrics mean square error, mean absolute error, root mean square error, and mean absolute percentage error. They achieved the best RMSE values for their hybrid approach to the cancer data set. The ARIMA model had an RMSE of 1.252, and the BPNN model had an RMSE of 0.896. The best results delivered their hybrid ARIMA-BPNN model with an RMSE of 0.453 [35]. Hua proposed a forecasting method to predict the gross domestic product (GDP), which is, according to them, an important indicator to evaluate the macroeconomic situation of a country or region and reflects the economic health of a country [34]. According to them, information about GDP development can be used to develop economic strategies and macroeconomic policies. They state that the majority of current methods of forecasting the GDP are only considering linear methods. Their proposed hybrid forecasting approach combines ARIMA and BPNN. The two singular models’ predicted values were combined by taking an average of the weights to obtain the predicted values for the linear part of their hybrid model. The predicted values for the improved hybrid model were obtained by taking an average of the weighted residuals of both singular models, predicting the non-linear residuals using BPNN, and then adding the predicted values of the two parts together. Hua achieved for his ARIMA model (MAPE: 2.80) better results than for his single BPNN model (MAPE: 3.70) and the highest forecast quality for his proposed hybrid ARIMA-BPNN (MAPE: 1.88) method [34]. Wang et al. propose an approach for forecasting in the medical domain to increase disease prevention concerning hemorrhagic fever with renal syndrome (HFRS), which is according to them, a threat to public health in China [8]. They proposed a hybrid ARIMA-GRNN model. They obtained slightly better results for their single ARIMA model (RMSE: 220.6269/MAPE: 21.02) than for their single GRNN (RMSE: 202.1684/MAPE: 19.20) and the best results for their hybrid ARIMA-GRNN approach (RMSE: 196.4682/MAPE: 17.83). Wang et al. [8] conclude that their approach could be used as a decision-making tool in the context of HFRS prevention and control [8]. Li et al. also propose an approach in the medical domain [7]. They propose an approach to forecasting tuberculosis incidence based on data on the incidences in Lianyungang City from January 2007 to June 2016. They propose a hybrid approach using ARIMA and a GRNN model. Li et al. [7] achieved better results for their hybrid ARIMA-GRNN model (RMSE: 0.2805/MAPE: 8.8797) than for their single ARIMA model (RMSE: 0.2553/MAPE: 5.7222) in short-term tuberculosis incidence forecasting in the Chinese population. Moreover, they highlighted that especially the fitting and forecasting of the peak and trough of the incidence worked best with the hybrid approach [7].
3.5. Hybrid Approaches Using Wavelet Transform Decomposition
Cheng et al. proposed an approach to forecasting ground-level ozone concentration, which is very important, according to them, as ground-level ozone harms human health and vegetation growth [36]. As a data set, they use information about the ground-level ozone in ozone concentrations in Shenzhen. They tested various decomposition algorithms, data sets, and factors. They state that wavelet transform is superior compared to other formulas such as empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), and complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) in terms of performance in their case [36]. They propose their hybrid approach as WD-LSTM-SVR. Their approach first decomposed the data into multiple dimensions using wavelet decomposition (WD). They then trained and forecasted each layer of the data with both LSTM and SVR. Their hybrid WD-LSTM-SVR approach provided better results (RMSE: 4.7383/MAPE: 7.9348) than their single models. Their LSTM had an RMSE of 12.2361 and a MAPE score of 23.2028 [36]. Wu et al. proposed a hybrid forecasting approach for precipitation amounts and droughts of northern Chinese provinces using monthly data over a long period from 1967 to 2017 for three stations [43]. Their proposed method consists of combining ARIMA and LSTM through discrete wavelet transformation. Their hybrid model achieved an RMSE of 0.06633 and MAPE of 0.51, outperforming the RMSE and MAPE of their single ARMIA model (RMSE: 0.13342/MAPE: 0.72) and their single LSTM model (RMSE: 0.07/MAPE: 0.56) [43]. Zhang et al. proposed WA-ARMA-BP, a coupled model that combines autoregressive wavelet transform, ARMA, and a BPNN to forecast groundwater depth using leave-one-out cross-validation (LOO-CV) [37]. They use groundwater depth recordings from 1981 to 2021 of a district in the northwest of China. The evaluation of the model took place through RMSE. Their hybrid approach shows better results (RMSE: 0.0136) than their single ARMA model (RMSE: 0.05) or single BPNN model (RMSE: 0.0797) [37]. Eua-Arporn et al. proposed EWT-ARIMA-ANN using empirical wavelet transform combined with ARIMA, and an ANN [38]. A total of four data sets (Sunspot, AQI, Gasoline, and CO2) were used to evaluate the models’ performance. The empirical wavelet transform disassembles the original data series into subseries containing unique features at different frequency horizons. The EWT-ARIMA-ANN approach reaches an RMSE of 13.966 while the single ARIMA reaches an RMSE of 17.385 and 18.561 for the single ANN [38].
4. Discussion
In the following discussion, we first discuss the results of the PRISMA study. We will then discuss the potential of incorporating these hybrid forecasting techniques into visual analytics systems for decision making.
4.1. Hybrid Forecasting Methods
In this PRISMA study, we considered and discussed in detail various implementations of hybrid approaches to time series forecasting. Here, in some cases, very different approaches for very different data sets from completely different domains were chosen by the authors for their predictions. The domains ranged from economy to environmental science and medical topics. In the domain of economy, for example, inflation rates were predicted using indices [32], exchange rates were predicted [31], or the GDP of a country was predicted [34]. Much of the work has made predictions in the area of the environment and Rarth science. Among other things, there were predictions for soil temperature [30], persistent organic pollutant (POP) concentrations [28], sea and water levels [5,41], groundwater depths [37] or ground-level ozone concentrations [36]. In the medical domain, authors proposed approaches to predict the incidences of diseases to prevent and control them [7,8].
Two more general approaches for forecasting were presented by Hadwan et al., and they were applied to different data sets [35,38]. Hadwan et al. used their hybrid ARIMA-BPNN forecasting approach to forecast consumer price index data and cancer data. Their approach yielded promising results for both data sets, with slightly better results for the cancer data set [35]. Eua-Arporn et al. used their hybrid EWT-ARIMA-ANN model, which used empirical wavelet transform combined with ARIMA and an ANN, to predict four different data sets (Sunspot, AQI, Gasoline, and CO2). Their hybrid prediction model delivered better results than their individual models for all data sets [38].
We subdivided the findings of our PRISMA study into the five following groups:
- Group 1: Hybrid approaches that use ARIMA and LSTM [27,28,29,30,31];
- Group 2: Approaches that use SARIMA and LSTM [4,5,32];
- Group 3: The next group of works combined ARIMA or SARIMA with ANNs [39,40,41,42];
- Group 4: Approaches using more rarely implemented neural networks [7,8,33,34,35];
- Group 5: Approaches that include wavelet transform decomposition [8,36,37,38].
Overall, however, it is noticeable that most work examined in this review presented hybrid approaches using ARIMA or its derivate SARIMA in combination with LSTM. This also includes works that first separated the linear and non-linear components using wavelet transformers.
Table 2 summarizes the different forecasting approaches and their quality. To evaluate the collected results from the different works, the difference between RMSE and MAPE can be used to compare the models. These two evaluation methods for measuring the differences between the predicted and actual values should yield lower values for the best-fitting models. It is impossible to say which of these approaches provides the best overall results for all data, as the prediction results are highly dependent on the underlying data. However, based on the collected information, it can be concluded that the hybrid models provide better predictions regarding RMSE and MAPE values for all approaches presented. Moreover, this improvement is present for both predominantly nonlinear and linear data, illustrated in the table by comparing the values of the individual models.

Table 2.
RMSE and MAPE scores for the individual models and the proposed hybrid approaches. The scores were rounded to a maximum of five decimal places.
4.2. Application of Hybrid Forecasting Approaches in Visual Analytics
The results of the PRISMA study validate the great potential of hybrid approaches to predicting time series from different domains. Hybrid forecasting methods have already been used in many application domains and have delivered promising results. Even if the same models are applied to different data sets, the corresponding hybrid models outperform the statistical models commonly used in visual analytics and show significantly better results. The hybrid approaches could be integrated into visual analytics transformation pipelines to improve the quality of decision-making processes further.
We applied the concept of hybrid prediction approaches to an existing visual analytics system [22,23,24].
Figure 2 shows an exemplary application of a forecast visualization that shows the temporal development of a technology with forecast results using an integrated hybrid approach in a visual analytics system [22,24,25]. The future prediction is displayed through lower saturation measured by the standard deviation values of the prediction algorithm.
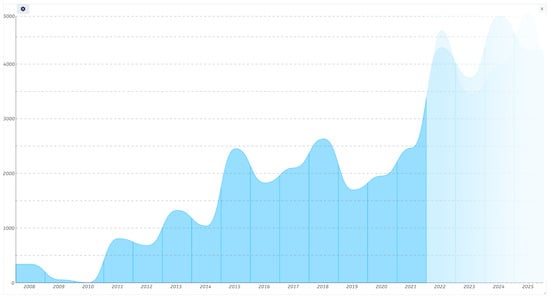
Figure 2.
Exemplary application of an integrated hybrid approach in a visual analytics system [22,24,25]. The future prediction is illustrated through lower saturation measured by the standard deviation values of the prediction algorithm. The x-axis shows the years from 2008 to 2025 in one-year steps. On the y-axis, the number of scientific publications from 0 to 5000 is shown in steps of 1000.
Integrating hybrid forecasting methods into existing visual analytics approaches and systems for decision making holds great potential. For example, these concepts could enhance existing systems for strategic decision making [24] through better predictions of the future course of emerging technologies and thus improve corporate foresight through visual analytics. Another example of applying these hybrid forecasting methods could be the monitoring and observation of competitors and leading domain experts. The more precise predictions could be used to predict the future influence of individuals, which could also support the decision-making process [44].
5. Conclusions
As part of this work, a systematic literature review was conducted using the PRISMA methodology [26]. First, important keywords and relevant databases were identified, and the search process was documented in detail using a PRISMA flow chart. The results were filtered based on in- and exclusion criteria, and the included reports are presented in detail. Furthermore, a table with the evaluation results (RMSE and MAPE) was presented, summarizing the results. We observed that all presented hybrid prediction approaches outperformed the individual methods based on the RMSE and MAPE scores of the proposed models. Since the differences in RMSE or MAPE are often small, future work could supplement and validate the results with Diebold–Mariano tests [45]. Two models were examined that presented a more general approach to time series forecasting from different data sets. This more abstract use of the same models on different data with good results is the first important step toward more general models that could be incorporated into visual analytics systems. Based on these results, we discussed the applications and future trajectories implicated for visual analytics systems through the new hybrid models. For this purpose, we considered an exemplary concept that illustrated integrating hybrid forecasting methods into a visual analytics system. The exemplary visualization is only intended as a first step in this direction. Possible further integrations of these hybrid approaches could use subsets of data or, as in the proposed case, documents at a macro level and make predictions at runtime. We concluded that the hybrid approaches hold the potential to enhance prediction accuracy and thus improve visual analytics systems for decision making.
Author Contributions
Identification of databases, L.B.S. and K.N; identification of search queries, L.B.S. and C.A.S.; identification of publications, L.B.S., C.A.S. and M.B.; deduplication, L.B.S. and C.A.S.; publication screening L.B.S., C.A.S. and M.B.; data extraction, L.B.S., C.A.S. and M.B.; discussion of results, L.B.S., C.A.S. and M.B.; review and editing, L.B.S., C.A.S., M.B. and K.N; visualization, L.B.S., C.A.S. and K.N; supervision, K.N.; project administration, L.B.S., C.A.S., M.B. and K.N; revisions, L.B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the Hessian Center for AI (hessian.AI), Germany.
Acknowledgments
We thank Marie Laurent from Polytech Clermont who supported this literature review during her internship in the Human-Computer Interaction and visual analytics research group. This work was conducted within the research group on human–computer interaction and visual analytics at Darmstadt University of Applied Sciences (https://vis.h-da.de (accessed on: 24 April 2023)). This work was partially funded by the Hessian Center for AI (hessian.AI), Germany.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PRISMA | Preferred Reporting Items for Systematic reviews and Meta-Analyses |
| ARIMA | Auto-Regressive Integrated Moving Average |
| SARIMA | Seasonal Auto-Regressive Integrated Moving Average |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Networks |
| GNN | Graph Neural Network |
| GRNN | General Regression Neural Network |
| ANN | Artificial Neural Network |
| BPNN | Back Propagation Neural Network |
| NMGM | Nonlinear Metabolic Grey Model |
| DGSR | Daily Global Solar Radiation |
| LOO-CV | Leave-One-Out Cross-Validation |
| MLP | Multilayer Perceptron |
| SVR | Support Vector Regression |
| WD | Wavelet Decomposition |
| DWT | Discrete Wavelet Transformxy |
| EWT | Empirical Wavelet Transform |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| MAE | Mean Average Error |
| SMAPE | Squared Mean Average Percentage Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
| ACM | Association for Computing Machinery |
| IEEE | Institute of Electrical and Electronics Engineers |
| MDPI | Multidisciplinary Digital Publishing Institute |
| JAPS | Journal of Animal and Plant Sciences |
| TandFO | Taylor and Francis Online |
| NAR | Autoregressive Neural Network |
| POP | Persistent Organic Pollutant |
| CPI | Consumer Price Index |
| GDP | Gross Domestic Product |
| HFRS | Hemorrhagic Fever with Renal Syndrome |
References
- Shao, X.; Ma, D.; Liu, Y.; Yin, Q. Short-term forecast of stock price of multi-branch LSTM based on K-means. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 1546–1551. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric load forecasting in smart grids using Long-Short-Term-Memory based Recurrent Neural Network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using Deep Neural Networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7046–7051. [Google Scholar] [CrossRef]
- Wu, D.C.W.; Ji, L.; He, K.; Tso, K.F.G. Forecasting Tourist Daily Arrivals with a Hybrid Sarima-Lstm Approach. J. Hosp. Tour. Res. 2021, 45, 52–67. [Google Scholar] [CrossRef]
- Sun, Q.; Wan, J.; Liu, S. Estimation of Sea Level Variability in the China Sea and Its Vicinity Using the SARIMA and LSTM Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3317–3326. [Google Scholar] [CrossRef]
- Wei, S.Y.; Zhang, J. Short-Term Passenger Flow Prediction of Railway Epidemic Based on SARIMA—LSTM Combined Model. IEEE Access 2022. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Song, H.; Liu, Q.; He, B.; Shi, P.; Ji, Y.; Xu, D.; Wang, J. Application of a hybrid model in predicting the incidence of tuberculosis in a Chinese population. Infect. Drug Resist. 2019, 12, 1011–1020. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.W.; Shen, Z.Z.; Jiang, Y. Comparison of autoregressive integrated moving average model and generalised regression neural network model for prediction of haemorrhagic fever with renal syndrome in China: A time-series study. BMJ Open 2019, 9, e025773. [Google Scholar] [CrossRef]
- Wang, E.; Galjanic, T.; Johnson, R. Short-term electric load forecasting at Southern California Edison. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–3. [Google Scholar] [CrossRef]
- Goswami, K.; Kandali, A.B. Electricity Demand Prediction using Data Driven Forecasting Scheme: ARIMA and SARIMA for Real-Time Load Data of Assam. In Proceedings of the 2020 International Conference on Computational Performance Evaluation (ComPE), Shillong, India, 2–4 July 2020; pp. 570–574. [Google Scholar] [CrossRef]
- Putra, J.A.; Basbeth, F.; Bukhori, S. Sugar Production Forecasting System in PTPN XI Semboro Jember Using Autoregressive Integrated Moving Average (ARIMA) Method. In Proceedings of the 2019 6th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Bandung, Indonesia, 18–20 September 2019; pp. 448–453. [Google Scholar] [CrossRef]
- Shelatkar, T.; Tondale, S.; Yadav, S.; Ahir, S. Web Traffic Time Series Forecasting using ARIMA and LSTM RNN. ITM Web Conf. 2020, 32, 03017. [Google Scholar] [CrossRef]
- Wang, D.; Meng, Y.; Chen, S.; Xie, C.; Liu, Z. A Hybrid Model for Vessel Traffic Flow Prediction Based on Wavelet and Prophet. J. Mar. Sci. Eng. 2021, 9, 1231. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-term offshore wind power forecasting—A hybrid model based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and deep-learning-based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Zeng, Z.; Khushi, M. Wavelet Denoising and Attention-based RNN-ARIMA Model to Predict Forex Price. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Qiu, J.; Du, Q.; Wang, W.; Yin, K.; Chen, L. Short-Term Performance Metrics Forecasting for Virtual Machine to Support Anomaly Detection Using Hybrid ARIMA-WNN Model. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; Volume 2, pp. 330–335. [Google Scholar] [CrossRef]
- Khandelwal, I.; Adhikari, R.; Verma, G. Time Series Forecasting Using Hybrid ARIMA and ANN Models Based on DWT Decomposition. Procedia Comput. Sci. 2015, 48, 173–179. [Google Scholar] [CrossRef]
- Keim, D.; Kohlhammer, J.; Ellis, G.; Mansmann, F. (Eds.) Mastering the Information Age: Solving Problems with Visual Analytics; Eurographics Association: Goslar, Germany, 2010. [Google Scholar]
- Keim, D.A. Designing Pixel-Oriented Visualization Techniques: Theory and Applications. IEEE Trans. Vis. Comput. Graph. 2000, 6, 59–78. [Google Scholar] [CrossRef]
- Kovalerchuk, B.; Andonie, R.; Datia, N.; Nazemi, K.; Banissi, E. (Eds.) Visual Knowledge Discovery with Artificial Intelligence: Challenges and Future Directions. In Integrating Artificial Intelligence and Visualization for Visual Knowledge Discovery; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–27. [Google Scholar] [CrossRef]
- Kohlhammer, J.; May, T.; Hoffmann, M. Visual Analytics for the Strategic Decision Making Process. In GeoSpatial Visual Analytics; Amicis, R.D., Stojanovic, R., Conti, G., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 299–310. [Google Scholar]
- Nazemi, K.; Burkhardt, D. Visual Analytics for Analyzing Technological Trends from Text. In Proceedings of the 2019 23rd International Conference Information Visualisation (IV), Paris, France, 2–5 July 2019; pp. 191–200. [Google Scholar] [CrossRef]
- Nazemi, K.; Burkhardt, D.; Kock, A. Visual analytics for technology and innovation management. Multimed. Tools Appl. 2021, 81, 14803–14830. [Google Scholar] [CrossRef]
- Nazemi, K.; Feiter, T.; Sina, L.B.; Burkhardt, D.; Kock, A. Visual Analytics for Strategic Decision Making in Technology Management. In Integrating Artificial Intelligence and Visualization for Visual Knowledge Discovery; Kovalerchuk, B., Nazemi, K., Andonie, R., Datia, N., Banissi, E., Eds.; Springer International Publishing: Cham, Swizterland, 2022; pp. 31–61. [Google Scholar] [CrossRef]
- Sina, L.B.; Nazemi, K. Visual Analytics for Systematic Reviews According to PRISMA. In Proceedings of the 2022 26th International Conference Information Visualisation (IV), Vienna, Austria, 19–22 July 2022. [Google Scholar]
- Page, M.J.; Moher, D.; Bossuyt, P.M. PRISMA 2020 explanation and elaboration: Updated guidance and exemplars for reporting systematic reviews. BMJ 2021, 372, n160. [Google Scholar] [CrossRef] [PubMed]
- Soy Temur, A.; Akgun, M.; Temur, G. Predicting housing sales in turkey using arima, LSTM and hybrid models. J. Bus. Econ. Manag. 2019, 20, 920–938. [Google Scholar] [CrossRef]
- Yu, L.; Wu, C.; Xiong, N.N. An Intelligent Data Analysis System Combining ARIMA and LSTM for Persistent Organic Pollutants Concentration Prediction. Electronics 2022, 11, 652. [Google Scholar] [CrossRef]
- Temur, A.S.; Yildiz, S. Comparison of Forecasting Performance of ARIMA LSTM and HYBRID Models for The Sales Volume Budget of a Manufacturing Enterprise. Istanb. Bus. Res. 2021, 50, 15–45. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, Y.; Yu, F. A Novel Multichannel Long Short-Term Memory Method With Time Series for Soil Temperature Modeling. IEEE Access 2020, 8, 182026–182043. [Google Scholar] [CrossRef]
- Yilmaz, F.M.; Arabaci, O. Should Deep Learning Models be in High Demand, or Should They Simply be a Very Hot Topic? A Comprehensive Study for Exchange Rate Forecasting. Comput. Econ. 2021, 57, 217–245. [Google Scholar] [CrossRef]
- Peirano, R.; Kristjanpoller, W.; Minutolo, M.C. Forecasting inflation in Latin American countries using a SARIMA-LSTM combination. Soft Comput. 2021, 25, 10851–10862. [Google Scholar] [CrossRef]
- Yu, S.; Dong, H.; Chen, Y.; He, Z.; Shi, X. Clothing Sales Forecast Based on ARIMA-BP Neural Network Combination Model. In Proceedings of the 2019 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 29–31 July 2019; pp. 367–372. [Google Scholar] [CrossRef]
- Hua, S. Back-Propagation Neural Network and ARIMA Algorithm for GDP Trend Analysis. Wirel. Commun. Mob. Comput. 2022, 2022, 1967607. [Google Scholar] [CrossRef]
- Hadwan, M.; Al-Maqaleh, B.M.; Al-Badani, F.N.; Khan, R.U.; Al-Hagery, M.A. A Hybrid Neural Network and Box-Jenkins Models for Time Series Forecasting. CMC-Comput. Mater. Contin. 2022, 70, 4829–4845. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, Q.; Peng, Y.; Huang, X.-F.; He, L.-Y. Multiple strategies for a novel hybrid forecasting algorithm of ozone based on data-driven models. J. Clean. Prod. 2021, 326, 129451. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Wang, X.; Zhou, W. Groundwater Depth Forecasting Using a Coupled Model. Discret. Dyn. Nat. Soc. 2021, 2021, 6614195. [Google Scholar] [CrossRef]
- Eua-Arporn, B.; Huang, S.L.; Kuruoglu, E.E. Enhancing Neural Network Based Hybrid Learning with Empirical Wavelet Transform for Time Series Forecasting. In Proceedings of the 2021 IEEE 33rd International Conference on Tools with Artificial Intelligence (ICTAI), Washington, DC, USA, 1–3 November 2021; pp. 386–390. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, F. Integrating linear and nonlinear forecasting techniques based on grey theory and artificial intelligence to forecast shale gas monthly production in Pennsylvania and Texas of the United States. Energy 2019, 178, 781–803. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; El Bouardi, A. A hybrid ARIMA-ANN method to forecast daily global solar radiation in three different cities in Morocco. Eur. Phys. J. Plus 2020, 135, 925. [Google Scholar] [CrossRef]
- Azad, A.S.; Sokkalingam, R.; Daud, H.; Adhikary, S.K.; Khurshid, H.; Mazlan, S.N.A.; Rabbani, M.B.A. Water Level Prediction through Hybrid SARIMA and ANN Models Based on Time Series Analysis: Red Hills Reservoir Case Study. Sustainability 2022, 14, 1843. [Google Scholar] [CrossRef]
- Yu, K.W.; Hsu, C.H.; Yang, S.M. A Model Integrating ARIMA and ANN with Seasonal and Periodic Characteristics for Forecasting Electricity Load Dynamics in a State. In Proceedings of the 2019 IEEE 6th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 17–19 April 2019; pp. 19–24. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, J.; Yu, H.; Liu, D.; Xie, K.; Chen, Y.; Hu, J.; Sun, H.; Xing, F. The Development of a Hybrid Wavelet-ARIMA-LSTM Model for Precipitation Amounts and Drought Analysis. Atmosphere 2021, 12, 74. [Google Scholar] [CrossRef]
- Sina, L.; Burkhardt, D.; Nazemi, K. Visual Dashboards in Trend Analytics to Observe Competitors and Leading Domain Experts. In Proceedings of the CERC 2020, CEUR Workshop Proceedings, Belfast, UK, 10–11 September 2020; Volume 2815, pp. 222–235. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).